Lossless Compression on MRI Images Using SWT

Abstract

Medical image compression is one of the growing research fields in biomedical applications. Most medical images need to be compressed using lossless compression as each pixel information is valuable. With the wide pervasiveness of medical imaging applications in health-care settings and the increased interest in telemedicine technologies, it has become essential to reduce both storage and transmission bandwidth requirements needed for archival and communication of related data, preferably by employing lossless compression methods. Furthermore, providing random access as well as resolution and quality scalability to the compressed data has become of great utility. Random access refers to the ability to decode any section of the compressed image without having to decode the entire data set. The system proposes to implement a lossless codec using an entropy coder. 3D medical images are decomposed into 2D slices and subjected to 2D-stationary wavelet transform (SWT). The decimated coefficients are compressed in parallel using embedded block coding with optimized truncation of the embedded bit stream. These bit streams are decoded and reconstructed using inverse SWT. Finally, the compression ratio (CR) is evaluated to prove the efficiency of the proposal. As an enhancement, the proposed system concentrates on minimizing the computation time by introducing parallel computing on the arithmetic coding stage as it deals with multiple subslices.

Introduction

Recent developments in health-care practices and development of distributed collaborative platforms for medical diagnosis have resulted in the development of an efficient technique to compress medical data. Telemedicine applications involve image transmission within and among health-care organizations using public networks. In addition to compressing the data, this requires handling of security issues when dealing with sensitive medical information systems for storage, retrieval, and distribution of medical data. Some of the requirements for compression of medical data include high compression ratio and the ability to decode the compressed data at various resolutions.

In order to provide a reliable and efficient means for storing and managing medical data, computer-based archiving systems such as picture archiving and communication systems (PACS) and Digital Imaging and Communications in Medicine (DICOM) standards were developed. Health Level Seven (HL7) standards are widely used for exchange of textual information in health-care information systems. With the explosion in the number of images acquired for diagnostic purposes, the importance of compression has become invaluable in developing standards for maintaining and protecting medical images and health records.

Compression offers a means to reduce the cost of storage and increase the speed of transmission; thus, medical images have attained a lot of attention towards compression. These images are very large in size and require lot of storage space.

The image compression techniques are broadly classified into two categories depending whether or not an exact replica of the original image could be reconstructed using the compressed image. These are as follows:

1. Lossless technique

2. Lossy technique

In lossless compression techniques, the original image can be perfectly recovered from the compressed (encoded) image. They are also called noiseless since they do not add noise to the image and are also known as entropy coding since they use statistics/decomposition techniques to eliminate/minimize redundancy. Lossless compression is used only for a few applications with stringent requirements such as medical imaging. Lossless compression is preferred for artificial images such as technical drawings, text, and medical-type images, icons, or comics. Some of the techniques included in lossless compression are run length encoding, Huffman encoding, LZW coding, area coding, etc.

The acronym EBCOT is derived from the description “embedded block coding with optimized truncation” which identifies some of the major contributions of the algorithm. The EBCOT algorithm is related in various degrees to much earlier work on scalable image compression. Scalable compression refers to the generation of a bit stream which contains embedded subsets, each of which represents an efficient compression of the original image at a reduced resolution or increased distortion [1]. The terms “resolution scalability” and “SNR scalability” are commonly used in connection with this idea.

In EBCOT, each subband is partitioned into relatively small blocks of samples, the samples called code-blocks. EBCOT generates a separate highly scalable (or embedded) bit stream for each code-block, B_i. The bit stream associated with B_i may be independently truncated to any of a collection of different lengths, Rⁿ_i, where the increase in reconstructed image distortion resulting from these truncations is modeled by Dⁿ_i. An enabling observation leading to the development of the EBCOT algorithm is that it is possible to independently compress relatively small code-blocks (say 32 × 32 or 64 × 64 samples each), with an embedded bit stream consisting of a large number of truncation points, Rⁿ_i, such that most of these truncation points lie on the convex hull of the corresponding rate-distortion curve. To achieve this efficient, fine embedding, the EBCOT block coding algorithm builds upon the fractional bit plane coding ideas [1].

Several techniques based on the (3D) discrete cosine transform (DCT) have been proposed for volumetric data coding. These techniques fail to provide lossless coding coupled with quality and resolution scalability, which is a significant drawback for medical applications. This paper gives an overview of several state-of-the-art 3D wavelet coders that do meet these requirements and proposes new compression methods exploiting the quadtree and block-based coding concepts, layered zero-coding principles, and context-based arithmetic coding. Additionally, a new 3D DCT-based coding scheme is designed and used for benchmarking. The proposed wavelet-based coding algorithms produce embedded data streams that can be decoded up to the lossless level and support the desired set of functionality constraints. Moreover, objective and subjective quality evaluation on various medical volumetric data sets shows that the proposed algorithms provide competitive lossy and lossless compression results when compared with the state of the art [2].

The mesh-based schemes have been shown to be effective for the compression of 3D brain computed tomography data also. Adaptive mesh-based schemes perform marginally better than the uniform mesh-based methods, at the expense of increased complexity. Lossless uniform and adaptive mesh-based coding schemes are proposed for MR image sequences. Context-based source modeling is used to exploit the intraframe and interframe correlations effectively. However, any other context-based modeling can be used in conjunction with both mesh-based schemes [3].

2D integer wavelet transform is used to decorrelate the data and an intraband prediction method to reduce the energy of the subbands by exploiting the anatomical symmetries typically present in structural medical images [4, 5]. A modified version of the EBCOT, tailored according to the characteristics of the data, encodes the residual data generated after prediction to provide resolution and quality scalability.

In [6, 7], the bit stream reordering procedure is based on a weighting model that incorporates the position of the VOI and the mean energy of the wavelet coefficients. The background information with peripherally increasing quality around the Volume Of Interest (VOI) allows for placement of the VOI into the context of the 3D image.

Several compression methods for medical images have been proposed, some of which provide resolution and quality scalability up to lossless reconstruction [8–13].

Methodologies

Wavelet-Based Compression

For image compression, loss of some information is acceptable. Among all of the above lossy compression methods, vector quantization requires many computational resources for large vectors; fractal compression is time consuming for coding; predictive coding has inferior compression ratio and worse reconstructed image quality than those of transform-based coding [14]. So, transform-based compression methods are generally best for image compression. For transform-based compression, JPEG compression schemes based on DCT have some advantages such as simplicity, satisfactory performance, and availability of special purpose hardware for implementation.

However, because the input image is blocked, correlation across the block boundaries cannot be eliminated. This results in noticeable and annoying “blocking artifacts” particularly at low bit rates. Wavelet-based schemes achieve better performance than other coding schemes like the one based on DCT. Since there is no need to block the input image and its basis functions have variable length, wavelet-based coding schemes can avoid blocking artifacts. Wavelet-based coding also facilitates progressive transmission of images.

Block Coding Algorithm

EBCOT stands for embedded block coding with optimal truncation. Every subband is partitioned into little blocks (for example, 64 × 64 or 32 × 32), called code-blocks. Every code-block is codified independently from the other ones thus producing an elementary embedded bit stream. The algorithm can find some points of optimal truncation in order to minimize the distortion and support its scalability. It uses the wavelet transform to subdivide the energy of the original image into subbands. Coefficients are coded after having done an appropriate quantization specified by the standard. Each subband is divided into code-blocks before being compressed. A bit plane encoder is used; it encodes the information belonging to a code-block by grouping it in bit planes, starting from the most significant one. After that, less significant bit planes will be encoded.

Proposed Method

The main objective of the system is to effectively implement lossless compression by reducing the amount of data required to represent a digital image. The architecture of the proposed system is shown in Fig. 1. The system proposes to implement a lossless codec using an entropy coder. The original 3D medical image is given as input, and it is converted to 2D slices. Using segmentation, extract the brain mass (region of interest) alone from the 2D slice. The extracted information from 2D slices is decimated using 2D stationary wavelet transform (SWT). The decimated coefficients are compressed in parallel using embedded block coding with optimized truncation of the embedded bit stream. These bit streams are decoded and reconstructed using inverse SWT. As an enhancement, the system concentrates on minimizing the time computation by introducing parallel computing on the arithmetic coding stage as it deals with multiple subslices.

Fig. 1.

Architecture of the proposed system

ROI Extraction

The volumetric data of the brain MRI is converted to 2D MRI slices by iterating on the stack. The proposed system needs to compress the image in a lossless manner, the important information extracted from the whole brain image. A segmentation algorithm is used to extract the brain mass alone and eliminate other parts using threshold pixel values [15, 16].

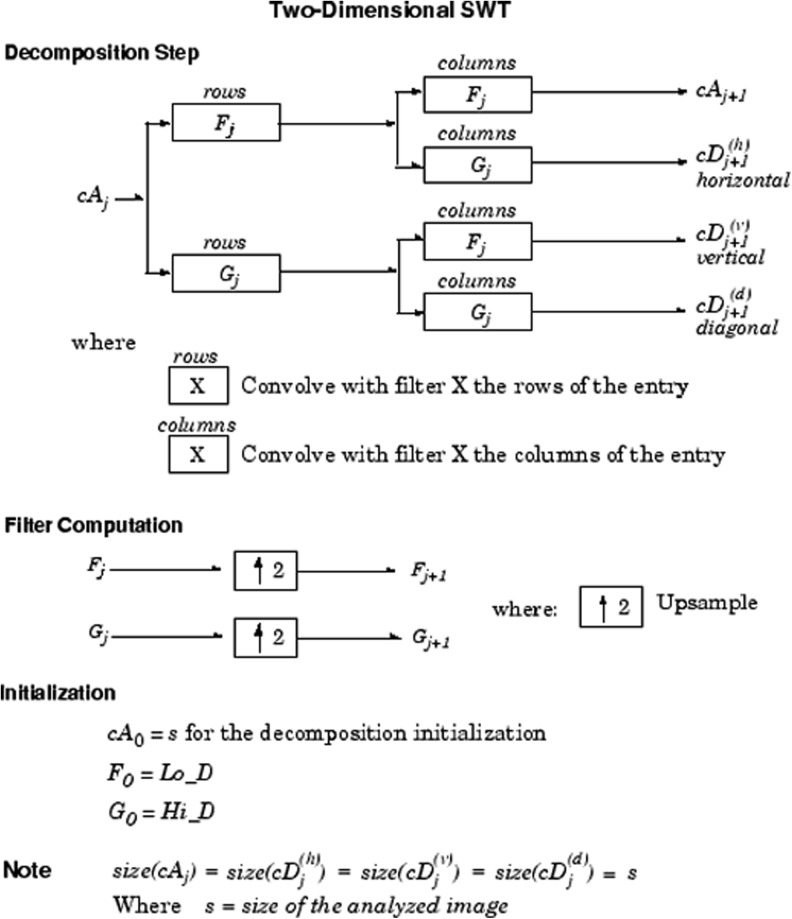
2D Stationary Wavelet Transform

Because of their inherent multi-resolution nature, wavelet-coding schemes are especially suitable for applications where scalability and tolerable degradation are important. Wavelet transform decomposes a signal into a set of basis functions. Here, 2D SWT filters are compared to 2D DWT filters because of the time-space shifts that DWT creates after applying any operation on wavelet coefficients. Compared with the traditional wavelet transform, the SWT has several advantages. First, each subband has the same size, so it is easier to get the relationship among the subbands. Second, the resolution can be retained since the original data is not decimated [17]. Also, at the same time, the wavelet coefficients contain much redundant information which helps to reduce the size of the image.

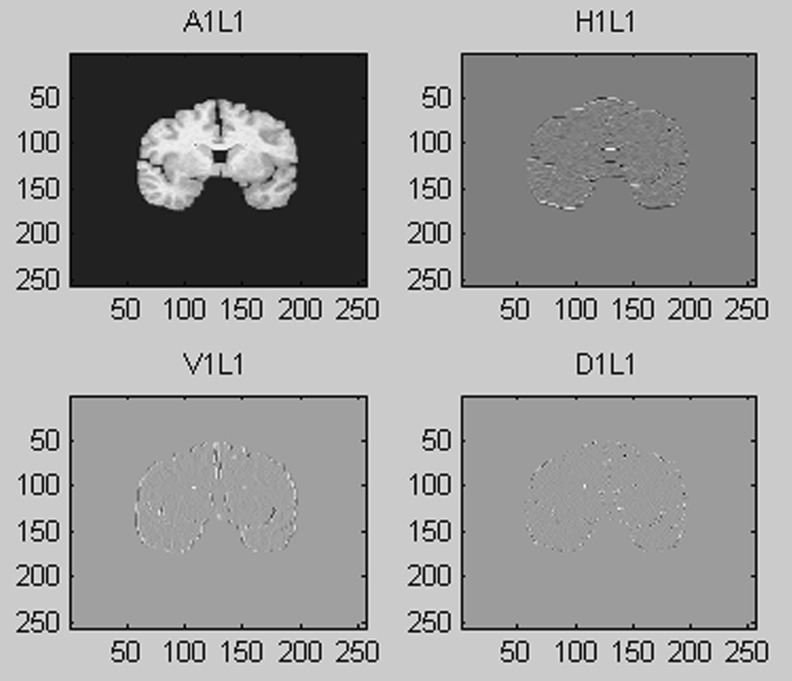
In Fig. 2, F_j and G_j represent high-pass and low-pass filters at scale j, resulting from interleaved zero padding of filters F_j − 1 and G_j − 1 (j > 1). cA₀ is the original image, and the output of scale j, cA_j, would be the input of scale j + 1. cA_j + 1 denotes the low-frequency (LF) estimation after the stationary wavelet decomposition, while cD_j + 1^(h), cD_j + 1^(v), and cD_j + 1^(d) denote the high-frequency (HF) detailed information along the horizontal, vertical, and diagonal directions, respectively.

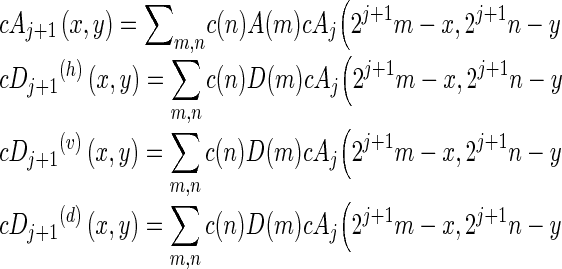where F[·] and G[·] represent the low-pass and high-pass filters, respectively, and cA₀(x, y) = f(x, y).

Fig. 2.

2D stationary wavelet transform

EBCOT Encoding

Encoding is performed by using block coding algorithm mentioned in methodologies.

Bit Plane Coding

A bit plane of a digital discrete signal (such as image or sound) is a set of bits corresponding to a given bit position in each of the binary numbers representing the signal. For example, for 16-bit data representation, there are 16 bit planes: the 1st bit plane contains the set of the most significant bit and the 16th contains the least significant bit. It is possible to see that the first bit plane gives the roughest but the most critical approximation of values of a medium, and the higher the number of the bit plane, the less is its contribution to the final stage. Thus, adding a bit plane gives a better approximation. If a bit on the nth bit plane on an m-bit data set is set to 1, it contributes a value of 2^{(m − n)}; otherwise, it contributes nothing. Therefore, bit planes can contribute half of the value of the previous bit plane.

A bit plane encoder is used; it encodes the information belonging to a code-block by grouping it in bit planes, starting from the most significant one. After that, less significant bit planes will be encoded [18].

Arithmetic Coding

Arithmetic coding is a form of variable-length entropy encoding that converts a string into another form that represents frequently used characters with fewer bits and infrequently used characters with more bits with the goal of using fewer bits in total. As opposed to other entropy-encoding techniques that separate the input message into its component symbols and replace each symbol with a code word, arithmetic coding encodes the entire message into a single number which is a fraction n where (0.0 ≤ n < 1.0). It is also called a statistical technique since it is based on probabilities like all the other techniques. The code extracted for the entire sequence of symbols is called a tag or an identifier.

Arithmetic coding is also a coding technique in which a message is encoded as a real number in an interval from one to zero. Arithmetic coding typically has a better compression ratio than Huffman coding as it produces a single symbol rather than several separate code words. Arithmetic coding is performed by providing symbols and probabilities for each symbol and a message that has to be coded. The arithmetic coding technique, though it gives a better performance than Huffman coding, has some disadvantages. In this coding technique, the whole codeword must be received for the symbols to be decoded, and if a bit is corrupted in the code word, the entire message could become corrupt.

The proposed system uses an arithmetic encoder to code the outputs of bit planes. It encodes the symbols and produces the histogram count of encoded pixels.

Parallel Computing

Parallel computing lets us solve data-intensive problems using multi-core processors. The proposed system uses parallel computing to implement arithmetic coder operations such that it shares the memory of the processors connected in a pool. Thus, a MATLAB pool is constructed by interconnecting two systems, where the unused memory will be used to compute the arithmetic coder operations. This limits the time computation and increases the processing quality and speed.

EBCOT Decoding

The coded sequence is decoded using the arithmetic decoder. It decodes the symbol sequence and returns a row vector which is to be reshaped as a matrix. This reshaped matrix along with its appropriate bit planes has to undergo bit plane decoding. All the decimated blocks have to be decoded using bit plane decoding. The decoded image is reconstructed using inverse SWT.

Performance Analysis

The proposed system determines the efficiency of compression using compression ratio, peak signal to noise ratio (PSNR), and bits per pixel (Table 1). The compression ratio is used to measure the ability of data compression by comparing the size of the image being compressed to the size of the original image.

Table 1.

Experimental results of MRI images for different compression techniques

Modality (Slices:Pixel per slice:Bits Per Pixel)	Compression method
	JPEG 2000	EBCOT	Proposed method
	CR (bit rate/bits per pixel)
MRI (30:256 × 256:8)	8.29:1 (2.58 bpp)	3.33:1 (4.80 bpp)	17.5324 (0.9126 bpp)
MRI (40:256 × 256:16)	8.29:1 (2.58 bpp)	3.33:1 (4.80 bpp)	16.9826 (0.9421 bpp)
	PSNR (bit rate/bits per pixel)
MRI (30:256 × 256:8)	24.45 (0.063 bpp)	22.11:1 (0.063 bpp)	41.6729 (0.9126 bpp)
MRI (40:256 × 256:16)	24.45 (0.063 bpp)	22.11:1 (0.063 bpp)	41.5884 (0.9421 bpp)

Two of the error metrics used to compare the various image compression techniques are the mean square error (MSE) and the PSNR. The MSE is the cumulative squared error between the compressed and the original image, whereas PSNR is a measure of the peak error. The mathematical formulae for the two are

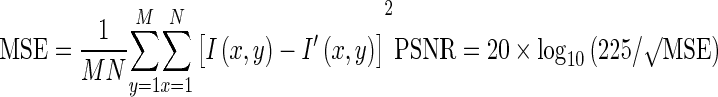where I(x, y) is the original image, I′(x, y) is the approximated version (which is actually the decompressed image), and M and N are the dimensions of the images.

A lower value for MSE means lesser error, and as seen from the inverse relation between the MSE and PSNR, this translates to a high value of PSNR. Logically, a higher value of PSNR is good because it means that the ratio of signal to noise is higher. Table 2 shows experimental results compared with encoding and decoding time.

Table 2.

Experimental results based on time

Modality (Slices:Pixels per slice:Bits per slice)	JPEG 2000		EBCOT		Proposed method
	EcT	DcT	EcT	DcT	EcT	DcT
MRI (30:256 × 256:8)	4.01	3.18	4.10	3.18	1.20	1.06
MRI (40:256 × 256:16)	4.43	3.35	4.48	3.57	2.64	1.12

EcT encoding time, DcT decoding time

Conclusion

Telemedicine applications involve image transmission within and among health-care organizations using public networks. These things resulted in the development of an efficient technique to compress medical data. This work proposes to implement a lossless codec using an entropy coder. This approach exploits the properties of SWT and EBCOT encoding in order to provide lossless compression for 3D brain images.

Future work involves compressing other types of medical images with this proposed system using parallel computing.

Experimental Results

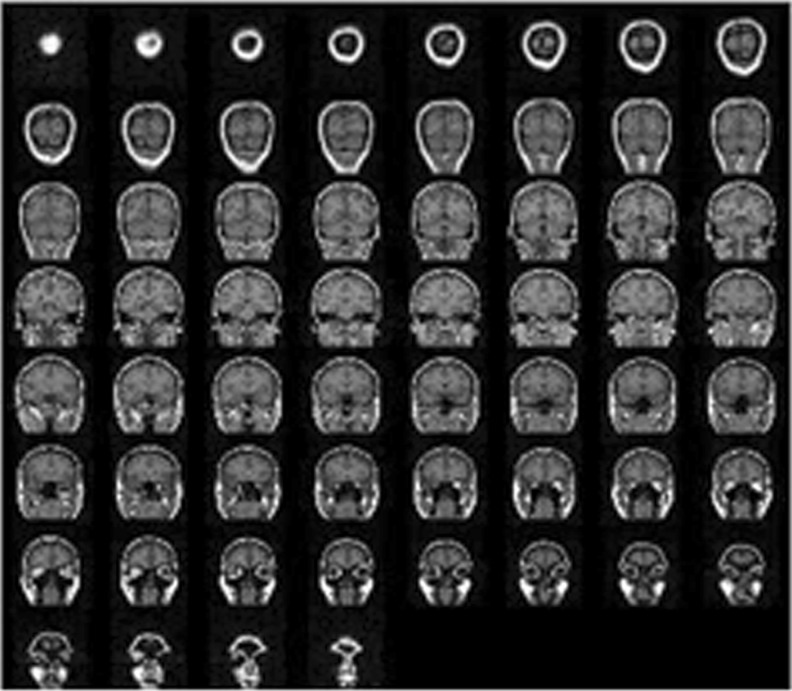
Figures 3, 4, 5, 6, 7, and 8 show the experimental results.

Fig. 3.

2D slices

Fig. 4.

Stationary wavelet transform

Fig. 5.

Region of interest

Fig. 6.

Encoded image

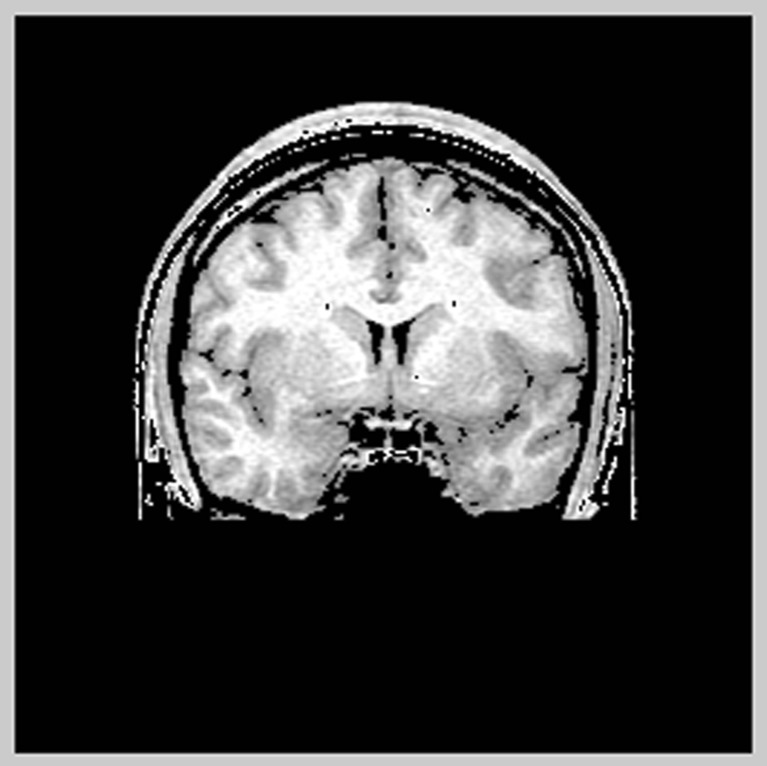
Fig. 7.

Decoded image

Fig. 8.

Reconstructed image