Estimating Population Treatment Effects From a Survey Subsample

Abstract

We considered the problem of estimating an average treatment effect for a target population using a survey subsample. Our motivation was to generalize a treatment effect that was estimated in a subsample of the National Comorbidity Survey Replication Adolescent Supplement (2001–2004) to the population of US adolescents. To address this problem, we evaluated easy-to-implement methods that account for both nonrandom treatment assignment and a nonrandom 2-stage selection mechanism. We compared the performance of a Horvitz-Thompson estimator using inverse probability weighting and 2 doubly robust estimators in a variety of scenarios. We demonstrated that the 2 doubly robust estimators generally outperformed inverse probability weighting in terms of mean-squared error even under misspecification of one of the treatment, selection, or outcome models. Moreover, the doubly robust estimators are easy to implement and provide an attractive alternative to inverse probability weighting for applied epidemiologic researchers. We demonstrated how to apply these estimators to our motivating example.

Use of population-based cohorts and nationally representative surveys lends external validity to a study: Their inclusion allows inferences to be made about the target population of interest. In contrast, inferences drawn from studies that use nonrepresentative samples may be valid for the study sample but may not be generalizable. External validity (also known as transportability (1)) of results derived from population-based cohorts and surveys is threatened when estimation is performed on a nonrandom subsample. Subsample effect estimates may not be generalizable to the population if the selection probabilities depended on effect modifiers and if subsample sampling weights were not utilized (2, 3). In the present article, we compare practical estimators of the population average treatment effect (PATE). These estimators simultaneously account for nonrandomized treatment assignment and subsample selection from a population-based cohort, thereby addressing internal and external validity.

The present study was motivated by the problem of generalizing a treatment effect estimated in a subsample that was created using a 2-stage selection process. In the first stage, adolescents were selected into a nationally representative survey of US adolescent mental health, the National Comorbidity Survey Replication Adolescent Supplement (NCS-A) (4). In the second stage, a subsample of these participants had biomarker data measured. Our interest was in estimating the effect of a nonrandomized treatment, (residence in a disadvantaged neighborhood) on cortisol slope (i.e., the rate of decline in cortisol levels over the course of an interview). Our scenario is different from the missing data pattern generally considered in the causal inference and missing data literature because we did not observe any data for individuals not in the survey. Our goal was to harness the available data and the nationally representative sample to generalize our results to the US population of adolescents. This required accounting for possible confounding due to the nonrandomized treatment assignment and possible lack of external validity due to the 2-stage selection mechanism.

Previous research has suggested and evaluated methods for generalizing results from randomized trials to target populations (2, 3), but there little has been written that extends this to observational studies. Doubly robust methods, which are consistent (i.e., converge to the true population average effect as the sample size goes to infinity) under certain types of model misspecification, have been used to adjust for nonrandom treatment assignment and/or nonrandom selection, right-censoring, or missing data (5–13). However, implementation of these estimators can be challenging. This may contribute to the continued popularity of the simpler Horvitz-Thompson inverse probability weighted (IPW) estimators, despite concerns about their efficiency and robustness (14). A recent advance is that targeted maximum likelihood estimation (TMLE) was implemented in standard statistical software (11), thereby facilitating its accessibility. However, we know of no studies that have used TMLE in the context of survey data with weights. Furthermore, although a discussion of these methods is taking place in the biostatistics literature, it has yet to receive much attention in the epidemiology literature.

We first present results from a simulation study in which we compare the performances of different estimators under correct model specification and various model misspecifications. We compare 3 estimators: IPW; a doubly robust, weighted least-squares (DRWLS) estimator; and a TMLE (15, 16). We then demonstrate how to apply these methods to the motivating example: using data from a subsample of the NCS-A to estimate the effect of residence in a disadvantaged neighborhood on cortisol slope in the target population of US adolescents. We aim to provide practical guidance on how to generalize average effect estimates from a survey subsample to a target population in the presence of measured confounders, effect heterogeneity, and nonrandom subsample selection.

METHODS

We consider a scenario in which individuals are selected into a survey with known probabilities. Treatment information and covariates are fully observed for all participants selected into the survey, but outcome data are only available for a subset of the survey sample. Let W be the vector of baseline covariates, A be a binary (0/1) variable indicating treatment, Δ_svy be a binary variable indicating selection into the survey sample, Δ_sub be a binary variable indicating selection into the subsample, and Y be a continuous outcome of interest. In the language of potential outcomes, Y_1i is the outcome for individual i under treatment A = 1; similarly, Y_0i is the outcome for individual i under treatment A = 0. The difference in these potential outcomes is the individual treatment effect.

Our estimand of interest is the PATE, E(Y₁ − Y₀), with the expectation taken across the target population (17). Other average treatment effects (ATEs) could be considered where the expectation is taken with respect to different target populations, for example, the survey sample ATE, E(Y₁ – Y₀|Δ_svy = 1), and the subsample ATE, E(Y₁ – Y₀|Δ_sub = 1). In Web Appendix 1 (available at http://aje.oxfordjournals.org/), we show identification for each ATE under the assumptions of known survey sampling weights (a typical assumption in the survey literature (18)), no unmeasured confounders, consistency, and positivity.

We compare 3 methods for estimating the PATE. The R code (R Foundation for Statistical Computing, Vienna, Austria) necessary to implement each is provided in Web Appendix 2.

Inverse probability weighting estimation

The IPW estimator uses inverse probability of treatment and selection weights that are obtained by multiplying inverse probability of survey selection weights, inverse probability of treatment weights, and inverse probability of subsample selection weights, as shown in equation 1. Inverse probability of survey selection weights are known and defined as follows:

$$w^{{\mathrm{\Delta }}_{\mathrm{svy}}=1}=\frac{1}{P({\mathrm{\Delta }}_{\mathrm{svy}}=1|\mathbf{W})}.$$

Inverse probability of treatment weights for each a in {0,1} are defined as follows:

$$w^{A=a|{\mathrm{\Delta }}_{\mathrm{svy}}=1}=\frac{I(A=a)}{P(A=a|{\mathrm{\Delta }}_{\mathrm{svy}}=1,\mathbf{W})}.$$

Inverse probability of subsample selection weights for each a in {0,1} are defined as follows:

$$w^{{\mathrm{\Delta }}_{\mathrm{sub}}=1|A=a,{\mathrm{\Delta }}_{\mathrm{svy}}=1}=\frac{I({\mathrm{\Delta }}_{\mathrm{sub}}=1)}{P({\mathrm{\Delta }}_{\mathrm{sub}}=1|A=a,{\mathrm{\Delta }}_{\mathrm{svy}}=1,\mathbf{W})}.$$

For each a in {0,1}, define

$$\begin{array}{rl}{w}^{A=a,{\mathrm{\Delta }}_{\mathrm{svy}}=1,{\mathrm{\Delta }}_{\mathrm{sub}}=1}& =\frac{1}{P({\mathrm{\Delta }}_{\mathrm{svy}}=1|\mathbf{W})}\times \frac{I(A=a)}{P(A=a|{\mathrm{\Delta }}_{\mathrm{svy}}=1,\mathbf{W})}\\ & \times \frac{I({\mathrm{\Delta }}_{\mathrm{sub}}=1)}{P({\mathrm{\Delta }}_{\mathrm{sub}}=1|A=a,{\mathrm{\Delta }}_{\mathrm{svy}}=1,\mathbf{W})}\\ & =\frac{I(A=a,{\mathrm{\Delta }}_{\mathrm{sub}}=1,{\mathrm{\Delta }}_{\mathrm{svy}}=1)}{P(A=a,{\mathrm{\Delta }}_{\mathrm{sub}}=1,{\mathrm{\Delta }}_{\mathrm{svy}}=1|\mathbf{W})}.\end{array}$$ (1)

The above weights are inverse conditional probabilities, which can be estimated using logistic regression. For example, P(A = a|Δ_svy = 1,W) can be estimated using predicted probabilities from a logistic regression in which A is the outcome and W is a vector of covariates among those in the survey. The IPW estimator of the PATE is calculated using the above weights for the r individuals in the subsample:

$$\begin{array}{rl}\widehat{\text{PATE}}& =\frac{{\sum }_{i=1}^r{Y}_i{w}_i^{A=1,{\mathrm{\Delta }}_{\mathrm{svy}}=1,{\mathrm{\Delta }}_{\mathrm{sub}}=1}}{{\sum }_{i=1}^r{w}_i^{A=1,{\mathrm{\Delta }}_{\mathrm{svy}}=1,{\mathrm{\Delta }}_{\mathrm{sub}}=1}}\\ & -\frac{{\sum }_{i=1}^r{Y}_i{w}_i^{A=0,{\mathrm{\Delta }}_{\mathrm{svy}}=1,{\mathrm{\Delta }}_{\mathrm{sub}}=1}}{{\sum }_{i=1}^r{w}_i^{A=0,{\mathrm{\Delta }}_{\mathrm{svy}}=1,{\mathrm{\Delta }}_{\mathrm{sub}}=1}}.\end{array}$$ (2)

Targeted maximum likelihood estimation

For the TMLE, we modified the implementation available in the tmle package in R (11), as described in Web Appendix 2. Additional details of TMLE implementation for estimating an ATE with survey sample data are provided in Web Appendix 1. Below we summarize the main steps involved.

1. Obtain predicted values, ${\hat{Y}}^0$, of the outcome conditional on the treatment and covariates using a linear regression of Y as a function of A and W among participants for whom Y is observed. Although we use a linear regression for comparability with DRWLS estimation, described below, it is also possible to use data-adaptive methods (e.g., machine learning) and a variety of outcome types.

2. For every individual i, compute the covariate $H_i=A_i{w}_i^{A=1,{\mathrm{\Delta }}_{\mathrm{svy}}=1,{\mathrm{\Delta }}_{\mathrm{sub}}=1}-(1-A_i)w_i^{A=0,{\mathrm{\Delta }}_{\mathrm{svy}}=1,{\mathrm{\Delta }}_{\mathrm{sub}}=1}$.

3. Compute the estimated coefficient $\hat{\beta }$ in a regression of Y on H using ${\hat{Y}}^0$ as an offset. Using G-computation, compute the difference between the counterfactual outcomes predicted by this regression under assignment to A = 1 and to A = 0 for each participant in the survey sample. The TMLE is calculated as a weighted sum of this difference across the survey sample participants using the survey weights.

Readers unfamiliar with G-computation should read the introduction by Snowden et al. (19). Briefly, G-computation uses the marginal distribution of covariates in a standardization procedure. This can be thought of as an extension of standardizing mortality rates by the age distribution in a standard population—a common epidemiologic practice. One fits a model of the outcome as a function of treatment and covariates in the observed sample and then applies the model to the distribution of covariates in the standard population to predict the counterfactual outcomes for each individual.

Doubly robust, weighted least-squares estimation

The DRWLS estimator combines weighted regression with G-computation. This estimator was first suggested by Marshall Joffe, reported in an article by Robins et al. (14), and it has been previously evaluated (5, 14). It uses the following steps:

1. Use $w^{A=a,{\mathrm{\Delta }}_{\mathrm{svy}}=1,{\mathrm{\Delta }}_{\mathrm{sub}}=1}$ as weights in a weighted least-squares linear regression of Y given A and W among participants in the subsample. Using G-computation, predict counterfactual outcomes standardized to the survey sample.

2. Use the counterfactual outcomes to estimate the survey sample ATE.

3. Weight this estimate by the survey weights to estimate the PATE.

TMLE and DRWLS estimators are doubly robust. In our application, double robustness means that the estimators are consistent if either the outcome model is correct or the combined treatment-selection weights $w_i^{A=a,{\mathrm{\Delta }}_{\mathrm{svy}}=1,{\mathrm{\Delta }}_{\mathrm{sub}}=1}$ from equation 1 are correct.

SIMULATION STUDY

Overview and set-up

We consider a simplified case with 2 continuous covariates: W = [W₁, W₂]′. Let the observed data O = (Δ_svy = 1, W, A, Δ_sub, Δ_subY). We assume Δ_svy probabilities are known, there are no unobserved confounders, and no additional intermediate variables are observed between A and Y. Figure 1 depicts the data-generating mechanism.

Figure 1.

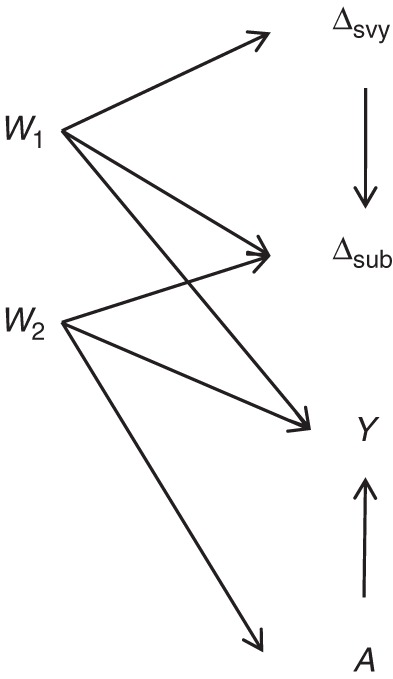
The data-generating mechanism used in our study. A, treatment variable; Δ_sub, selection into the subsample variable; Δ_svy, selection into the survey variable; W₁, summary baseline covariate; W₂, summary baseline covariate; Y, outcome variable.

The simulation is designed to be similar to the case study, which is detailed further below. Figure 2 provides a diagram of the complete data and the observed data. Under the causal inference framework that we are using, it is assumed that the observed data-generating process consists of several steps, the specific order of which is necessary for the identification result and corresponding methods implementation (20). First, selection into the survey is determined, where the probability of selection depends on W₁. For researchers designing the survey, W₁ is known for all individuals in the population. For all other analysts, W₁ is not observed for those not selected into the survey. Second, for all individuals selected into the survey, we observe W₂ and A, where the probability of A = 1 depends on W₂. Third, selection into the subsample (Δ_sub) is determined, where the probability of selection depends on W₁ and W₂. Fourth, for those in the subsample, we observe 1 of 2 counterfactuals, Y₀ or Y₁, which correspond to the treatment A actually received. We include a detailed description of the data-generating process and code to implement it in Web Appendix 3.

Figure 2.

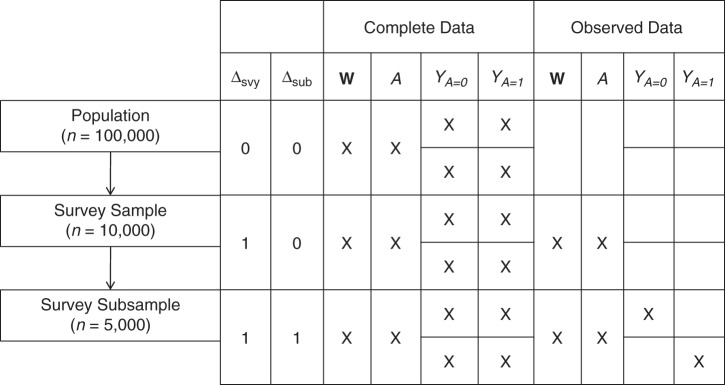
Simulation set-up. X in a box indicates that data was present. A, treatment variable; Δ_sub, selection into the subsample variable; Δ_svy, selection into the survey variable; W, the vector of summary baseline covariates; Y, outcome variable.

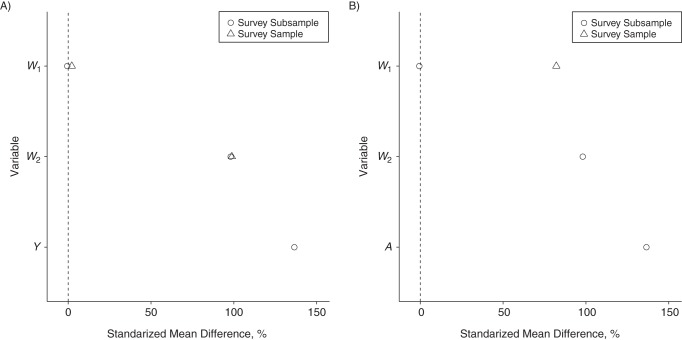
As seen in Figure 1, W₂ acts as a confounder. W₁ directly modifies the treatment effect and is related to selection into the survey and subsample. Figure 3 provides a summary of imbalance in W₁, W₂, and Y across treatment groups and W₁, W₂, and A across selection groups. A consistent estimate of the subsample ATE requires adjustment for confounding by W₂. A consistent estimate of the PATE also requires adjustment for differential selection by W₁.

Figure 3.

Balance across A) treatment and B) selection groups in the simulation. The standardized mean difference is the difference in means between the 2 groups standardized by the standard deviation in the first group. W₁, summary baseline covariate; W₂, summary baseline covariate; Y, outcome variable.

The simulation reflects practical positivity violations (i.e., when subsets of the sample have large weights) similar to the case study. Table 1 gives the treatment and selection weights for both the simulation and the case study.

Table 1.

Characteristics of Selection and Treatment Weights^a,b in the Simulation and Case Study, National Comorbidity Survey Replication Adolescent Supplement, 2001–2004

Weight	Simulation			Case Study
	Mean (SD)	Minimum	Maximum	Mean (SD)	Minimum	Maximum
$w^{{\mathrm{\Delta }}_{\mathrm{svy}}=1}$	1.009 (1.009)	0.020	20.300	0.948 (1.166)	0.041	13.460
$w^{A=1|{\mathrm{\Delta }}_{\mathrm{svy}}=1}|A=1$	0.994 (0.607)	0.529	13.600	0.931 (0.878)	0.377	8.799
$w^{A=0|{\mathrm{\Delta }}_{\mathrm{svy}}=1}|A=0$	0.998 (0.655)	0.491	16.580	1.020 (0.826)	0.641	19.180
$w^{{\mathrm{\Delta }}_{\mathrm{sub}}=1|A=1,{\mathrm{\Delta }}_{\mathrm{svy}}=1}|{\mathrm{\Delta }}_{\mathrm{sub}}=1$	1.009 (0.562)	0.339	7.148	0.995 (0.631)	0.332	5.914
$w^{{\mathrm{\Delta }}_{\mathrm{sub}}=1|A=0,{\mathrm{\Delta }}_{\mathrm{svy}}=1}|{\mathrm{\Delta }}_{\mathrm{sub}}=1$	1.003 (0.593)	0.280	6.044	1.002 (0.574)	0.401	5.598
$w^{{\mathrm{\Delta }}_{\mathrm{sub}}=1,A=1|{\mathrm{\Delta }}_{\mathrm{svy}}=1}|{\mathrm{\Delta }}_{\mathrm{sub}}=1,A=1$	0.992 (1.177)	0.182	22.620	0.883 (1.110)	0.152	14.560
$w^{{\mathrm{\Delta }}_{\mathrm{sub}}=1,A=0|{\mathrm{\Delta }}_{\mathrm{svy}}=1}|{\mathrm{\Delta }}_{\mathrm{sub}}=1,A=0$	0.995 (0.565)	0.269	7.907	1.069 (1.558)	0.315	24.860
$w^{{\mathrm{\Delta }}_{\mathrm{sub}}=1,A=1,{\mathrm{\Delta }}_{\mathrm{svy}}=1}|{\mathrm{\Delta }}_{\mathrm{sub}}=1,A=1$	1.023 (3.421)	0.006	84.080	1.079 (2.699)	0.009	34.380
$w^{{\mathrm{\Delta }}_{\mathrm{sub}}=1,A=0,{\mathrm{\Delta }}_{\mathrm{svy}}=1}|{\mathrm{\Delta }}_{\mathrm{sub}}=1,A=0$	0.993 (1.687)	0.0116	17.910	1.303 (2.990)	0.019	53.160

Abbreviations: A, treatment variable; Δ_sub, selection into the subsample variable; Δ_svy, selection into the survey variable.

^a The simulation weights shown are the true weights. In the case study, the survey weights were assumed known and the remaining weights were estimated.

^b Weights were stabilized by including the marginal probability in the numerator to facilitate comparison. For example, $w^{A=1|{\mathrm{\Delta }}_{\mathrm{svy}}=1}|A=1={\displaystyle \frac{\text{mean}(P(A=1|{\mathrm{\Delta }}_{\mathrm{svy}}=1,\mathbf{W}))}{P(A=1|{\mathrm{\Delta }}_{\mathrm{svy}}=1,\mathbf{W})}}.$

We evaluate how well IPW, TMLE, and DRWLS estimators perform in estimating the PATE when all models are correctly specified and when 1 or more models are misspecified (see Table 2 for model specifications). We include misspecification of multiple models simultaneously but caution that performance in these scenarios depends on the particulars of the data-generating process and misspecifications (14). Performance is evaluated by mean percent bias, mean variance, mean-squared error (MSE), and 95% confidence interval coverage across the 1,000 simulations. For each simulation iteration, variance and the 95% confidence interval are estimated from 500 bootstrapped samples. The percentile method is used for the confidence interval.

Table 2.

Model Specifications

Specification	Treatment Model	Subsample Selection Model	Outcome Model
Correct specification	A ∼ W2	Δsub ∼ W1 + W2	Y ∼ A + W2 + AW1
	W2 = Sum(Z1:Z16)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
		W2 = Sum(Z1:Z16)	W2 = Sum(Z1:Z16)
Moderately misspecified treatment	A ∼ W2mod	Δsub ∼ W1 + W2	Y ∼ A + W2 + AW1
	W2mod = Sum(Z2:Z16)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
		W2 = Sum(Z1:Z16)	W2 = Sum(Z1:Z16)
Majorly misspecified treatment	A ∼ W1	Δsub ∼ W1 + W2	Y ∼ A + W2 + AW1
	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
		W2 = Sum(Z1:Z16)	W2 = Sum(Z1:Z16)
Moderately misspecified outcome	A ∼ W2	Δsub ∼ W1 + W2	Y ∼ A + W2mod + AW1
	W2 = Sum(Z1:Z16)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
		W2 = Sum(Z1:Z16)	W2mod = Sum(Z2:Z16)
Majorly misspecified outcomea	A ∼ W2	Δsub ∼ W1 + W2	Y ∼ A + AW1
	W2 = Sum(Z1:Z16)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
		W2 = Sum(Z1:Z16)
Majorly misspecified outcomea	A ∼ W2	Δsub ∼ W1 + W2	Y ∼ A + W2 + W1
	W2 = Sum(Z1:Z16)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
		W2 = Sum(Z1:Z16)	W2 = Sum(Z1:Z16)
Moderately misspecified selection	A ∼ W2	Δsub ∼ W1mod + W2	Y ∼ A + W2 + AW1
	W2 = Sum(Z1:Z16)	W1mod = Sum(Z2:Z6)	W1 = Sum(Z1:Z6)
		W2 = Sum(Z1:Z16)	W2 = Sum(Z1:Z16)
Majorly misspecified selection	A ∼ W2	Δsub ∼ W1	Y ∼ A + W2 + AW1
	W2 = Sum(Z1:Z16)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
			W2 = Sum(Z1:Z16)
Misspecified treatment and selection	A ∼ W1	Δsub ∼ W1	Y ∼ A + W2 + AW1
	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
			W2 = Sum(Z1:Z16)
Misspecified treatment and outcome	A ∼ W1	Δsub ∼ W1 + W2	Y ∼ A + W2 + W1
	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
		W2 = Sum(Z1:Z16)	W2 = Sum(Z1:Z16)
Misspecified selection and outcome	A ∼ W2	Δsub ∼ W1	Y ∼ A + W2 + W1
	W2 = Sum(Z1:Z16)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
			W2 = Sum(Z1:Z16)
Misspecified treatment, selection, and outcome	A ∼ W1	Δsub ∼ W1	Y ∼ A + W2 + W1
	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)	W1 = Sum(Z1:Z6)
			W2 = Sum(Z1:Z16)

Abbreviations: A, treatment variable; Δ_sub, selection into the subsample variable; W₁, summary baseline covariate; W₂, summary baseline covariate; W_1mod, misspecified summary baseline covariate; W_2mod, misspecified summary baseline covariate; Y, outcome variable; Z, individual baseline covariate that contributes to summary baseline covariate.

^a There were 2 versions of the majorly misspecified outcome model.

Results

Table 3 provides a summary of method performance. Generally, under correct and incorrect model specification, DRWLS estimation outperforms TMLE and IPW estimation, which corroborates the results of other simulations involving practical positivity violations (5, 14). Under correct specification of all models, DRWLS estimation and TMLE perform similarly and outperform IPW estimation in terms of variance and MSE. This result reflects known efficiency problems with IPW estimators that have been thoroughly discussed in the biostatistics literature but are perhaps less well known among epidemiology audiences (14). TMLE and IPW estimators perform similarly and worse than DRWLS estimators in terms of percent bias and 95% confidence interval coverage under correct model specification. This result may seem surprising, and we discuss it further below.

Table 3.

Method Performance Under Correct Specification and Misspecification Across the 1,000 Simulations

Specification	IPW				DRWLS				TMLE
	Mean % Bias	Mean Variance	95% CI Coveragea	MSE	Mean % Bias	Mean Variance	95% CI Coveragea	MSE	Mean % Bias	Mean Variance	95% CI Coveragea	MSE
Correct specification	−6.7	8.225	85.0	10.978	0.2	0.203	93.0	0.219	−8.4	0.252	77.9	0.402
Moderately misspecified treatment	−30.3	7.708	79.3	10.692	−0.1	0.203	94.4	0.207	−7.2	0.234	81.7	0.334
Majorly misspecified treatment	−176.0	5.154	15.8	55.133	0.0	0.202	94.4	0.206	−7.2	0.225	81.7	0.326
Moderately misspecified outcome	−6.7	8.225	85.0	10.978	−0.8	0.266	94.5	0.282	−6.1	0.306	87.2	0.376
Majorly misspecified outcomeb	−6.7	8.225	85.0	10.978	−3.4	1.031	91.0	1.168	−0.2	0.920	93.5	1.104
Majorly misspecified outcomeb	−6.7	8.225	85.0	10.978	−13.1	2.247	79.8	3.285	3.4	10.441	85.5	14.800
Moderately misspecified selection	−197.6	3.677	9.0	66.382	−0.2	0.193	94.9	0.193	−7.2	0.218	81.0	0.320
Majorly misspecified selection	−6.8	5.701	87.8	6.23	−0.1	0.201	94.2	0.208	−7.2	0.23	80.3	0.329
Majorly misspecified treatment and selection	−169.2	4.174	15.1	50.242	−0.8	0.198	94.5	0.203	−7.7	0.22	80.8	0.326
Majorly misspecified treatment and outcome	−176	5.154	15.8	55.133	−10.1	2.359	83.4	3.039	−14.9	9.796	84.6	14.64
Majorly misspecified selection and outcome	−6.8	5.701	87.8	6.23	−15.3	2.148	80.8	3.009	−68.7	9.697	89.4	23.395
Majorly misspecified treatment, selection, and outcome	−169.2	4.174	15.1	50.242	−15.1	2.339	82.3	3.235	−6.6	8.986	85.9	13.278

Abbreviations: DRWLS, doubly robust weighted least-squares estimator; IPW, inverse probability weighted estimator; MSE, mean-squared error; TMLE, targeted maximum likelihood estimator.

^a The 95% confidence interval coverage is percentage of simulations for which the 95% confidence interval contains the true population average treatment effect.

^b There were 2 versions of the majorly misspecified outcome model.

The advantages of DRWLS estimation and TMLE over IPW estimation are pronounced under misspecification of the treatment or selection models. This result is expected, because IPW estimation relies exclusively on the inverse probability weights to account for nonrandom subsample selection and nonrandom treatment assignment. In contrast, because DRWLS estimators and TMLE are doubly robust, they will be consistent under misspecification of the treatment or subsample selection models if the outcome model is correctly specified.

Under correct specification of all models, we expect estimates from IPW, DRWLS, and TMLE to be consistent. However, in several studies (e.g., 5–7, 14, 21, 22), authors have warned that both IPW estimators and doubly robust estimators are sensitive in scenarios of practical positivity violations, as is the case in this simulation. We may expect IPW estimation to be the most sensitive to positivity violations, because there is no outcome model to use for extrapolation. When the outcome model is correctly specified, we expect the DRWLS estimator and TMLE to outperform the IPW estimator because of successful extrapolation using the outcome model. This is true for DRWLS estimation but not for this implementation of TMLE, which performs similarly to IPW estimation in terms of percent bias and 95% confidence interval coverage. This is because in fitting the model used in G-computation, DRWLS estimation uses the combined treatment-selection weights for the treatment and selection conditions that were actually observed, whereas TMLE uses the combined treatment-selection weights for the observed and unobserved counterfactual treatment and selection conditions. If individuals usually receive their most likely treatment and selection assignment, then using the counterfactuals can result in greater positivity violations and thus poorer performance of TMLE as compared with DRWLS estimators.

We examined the extent to which there is a penalty for unnecessary adjustment for nonrandom treatment assignment or sample selection. We considered 2 scenarios for each of the treatment and subsample selection models (Table 4). In this limited simulation, there were no noticeable penalties for overadjustment. Table 5 shows the results from the more extreme second scenario. Results from the first scenario were similar.

Table 4.

Model Misspecification: Overadjustment

Description	Treatment Model	Subsample Selection Model	Outcome Model
Moderate treatment overadjustment
True model	Random	Δsub ∼ W1 + W2	Y ∼ A + W2 + AW1
Misspecified model	A ∼ W2	Δsub ∼ W1 + W2	Y ∼ A + W2 + AW1
Major treatment overadjustment
True model	Random	Δsub ∼ W1 + W2	Y ∼ A + W2 + AW1
Misspecified model	A ∼ W2 + W22	Δsub ∼ W1 + W2	Y ∼ A + W2 + AW1
Moderate selection overadjustment
True model	A ∼ W2	Δsub ∼ W1	Y ∼ A + W2 + AW1
Misspecified model	A ∼ W2	Δsub ∼ W1 + W2	Y ∼ A + W2 + AW1
Major selection overadjustment
True model	A ∼ W2	Random	Y ∼ A + W2 + AW1
Misspecified model	A ∼ W2	Δsub ∼ W1 + W2	Y ∼ A + W2 + AW1

Abbreviations: A, treatment variable; Δ_sub, selection into the subsample variable; W₁, summary baseline covariate; W₂, summary baseline covariate; Y, outcome variable.

Table 5.

Results Under Misspecification of the Treatment and Selection Models Across the 1,000 Simulations

Estimatora	Treatment Model				Selection Model
	Mean % Bias	Mean Variance	95% CI Coverageb	MSE	Mean % Bias	Mean Variance	95% CI Coverageb	MSE
Correct specification
IPW	−1.887	6.625	88.8	7.330	−1.330	2.358	93.5	2.353
DRWLS	−0.036	0.195	95.1	0.197	−0.731	0.179	94.5	0.178
TMLE	−6.554	0.227	82.6	0.296	−2.696	0.178	92.3	0.192
Overadjustment
IPW	−1.967	6.619	89.4	7.291	−1.855	2.208	93.0	2.269
DRWLS	−0.037	0.195	95.1	0.197	−0.733	0.179	94.5	0.178
TMLE	−6.554	0.227	82.5	0.296	−2.699	0.178	92.2	0.192

Abbreviations: DRWLS, doubly robust weighted least squares estimator; IPW, inverse probability weighted estimator; MSE, mean-squared error; TMLE, targeted maximum likelihood estimator.

^a Adjustment when the treatment and selection mechanisms are completely random.

^b The 95% confidence interval coverage is percentage of simulations for which the 95% confidence interval contains the true population average treatment effect.

CASE STUDY

Overview and set-up

We now apply the estimators evaluated in the simulation to generalize the effect of disadvantaged neighborhood residence on cortisol slope to the population of US adolescents. The NCS-A has been described previously (4, 23–25). Neighborhood disadvantage was measured using an established scale (26) that had been used previously with NCS-A residence data geocoded to census tracts (27). Cortisol is a hormone involved in the hypothalamic-pituitary-adrenal axis (28). Salivary cortisol samples were taken immediately before and after the survey interview. Cortisol slope was defined as (preinterview level − postinterview level)/length of interview. Cortisol samples were assayed for a subsample of 2,490 participants because of budget limitations. Treatment and covariate data were available for all participants. Analysis of the relationship between neighborhood disadvantage and cortisol slope among the subsample of participants with cortisol data has been previously reported (27). We excluded those adolescents whose cortisol levels may not have been at risk to be influenced by a stressful neighborhood environment (e.g., current smokers, drug users, persons taking birth control, those using steroid inhalers) as well as 8 influential outliers, for a total of 6,566 participants in the survey sample and 1,600 participants with cortisol measurements. Informed assent and consent were obtained from each adolescent and his/her parent or guardian. The Human Subjects Committees of Harvard Medical School and the University of Michigan approved recruitment and consent procedures.

Web Figure 1 depicts the extent to which 1) NCS-A participants for whom we had cortisol measures compare to participants without across possible confounding variables and 2) NCS-A participants who lived in disadvantaged neighborhoods compared with those from nondisadvantaged neighborhoods. Participants for whom we did and did not have cortisol measurements were similar except for age, average bedtime on the weekends, the amount of time during the participant's life his or her mother worked, and the interview taking place in the summer. In contrast, participants who lived in disadvantaged neighborhoods differed from those in nondisadvantaged neighborhoods in terms of expected demographic variables like race, income, and maternal educational level.

The survey weights and estimated inverse probability of treatment and selection weights for these case study data are shown in Table 1. Positivity violations can be a substantial issue in observational studies (29, 30), and we see evidence of practical positivity violations here. The survey weights are given and assumed known (25). Unlike in the simulation, we do not know the true treatment and selection models. Consequently, it is likely that multiple models are misspecified with the degree of misspecification unknown. For details on model specification and weight estimation, see Web Appendix 4.

Results

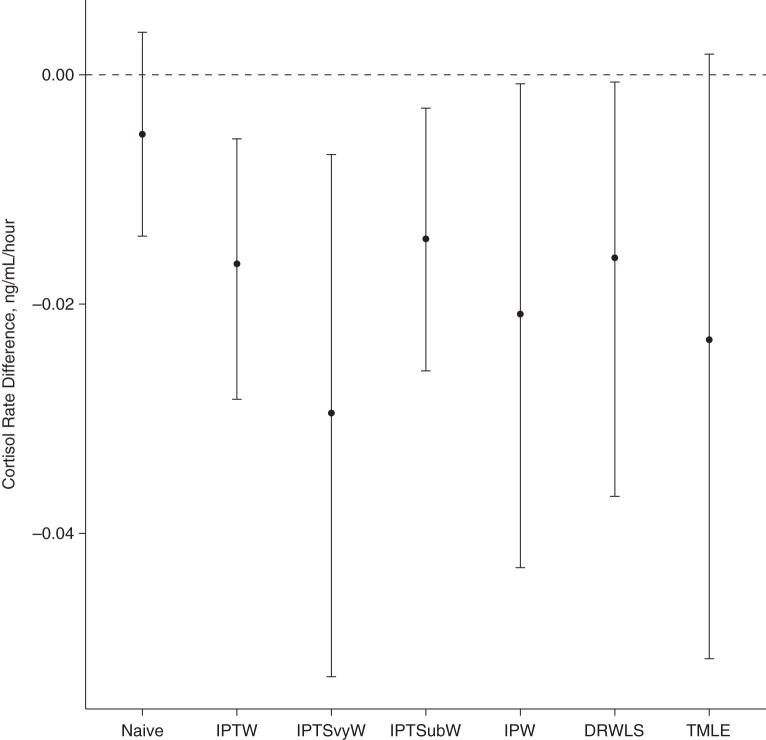
Figure 4 plots the estimates and 95% confidence intervals for the expected effect of living in a disadvantaged neighborhood on cortisol slope using different methods. The 95% confidence intervals were calculated with the percentile method using 1,000 bootstrapped samples. Results when the 8 outliers were included are shown in Web Figure 2. The relative performance of the estimators was similar.

Figure 4.

Illustrative example: average effect estimates and 95% confidence intervals using data from the National Comorbidity Survey Replication Adolescent Supplement (2001–2004) subsample. The inverse probability of treatment weighted estimator (IPTW) estimates the average treatment effect in the survey subsample. The inverse probability of treatment and survey sample selection weighted estimator (IPTSvyW) also estimates the average treatment effect in the survey subsample. The inverse probability of treatment and subsample selection weighted estimator (IPTSubW) estimates the average treatment effect in the survey sample. The inverse probability weighted (IPW) estimator, doubly robust, weighted least-squares (DRWLS) estimator, and targeted maximum likelihood estimator (TMLE) estimate the population average treatment effect.

We first present simpler methods in which we adjust for none or only some of the sources of nonrandomness. These methods may be biased for the primary estimand of interest—the PATE—but may consistently estimate other estimands, specifically, the survey sample ATE or the subsample ATE.

Under the naïve approach, there is no bias correction. The inverse probability of treatment weighted estimator adjusts for nonrandom assignment of the treatment only. If the treatment model is correctly specified, the inverse probability of treatment weighted estimate will be consistent for the NCS-A subsample ATE but may be biased for the PATE. The inverse probability of treatment and survey sample selection weighted estimator adjusts for nonrandom treatment assignment and selection into the survey. If there is nonrandom subsample selection, it may be biased for the population and survey sample ATEs. The inverse probability of treatment and subsample selection weighted estimator adjusts for nonrandom treatment assignment and nonrandom subsample selection. If the 2 models are correctly specified, the inverse probability of treatment and subsample selection weighted estimator will consistently estimate the survey sample ATE but may be biased for the PATE. In the presence of treatment effect heterogeneity when subsample selection probabilities depend on effect modifiers, the subsample ATE, survey sample ATE, and PATE may differ. We see evidence of this in Figure 4. Although the estimates of the subsample ATE and survey sample ATE appear similar, they are slightly more negative than the estimate of the PATE.

The IPW, TMLE, and DRWLS estimators adjust for nonrandom assignment of the treatment, nonrandom selection into the survey sample, and nonrandom selection into the subsample. Under correct model specification, these methods are consistent estimators of the PATE. TMLE and DRWLS estimators have the additional advantage of double robustness. Using DRWLS estimation, we conclude that the cortisol rate difference comparing US adolescents in disadvantaged versus nondisadvantaged neighborhoods likely falls between −3.68 and −0.06 × 10⁻² ng/mL/hour.

The wider TMLE 95% confidence interval relative to the IPW 95% confidence interval may seem surprising, given that TMLE was more efficient than IPW estimation in the simulation under correct model specification and under most model misspecifications. However, in scenarios in which the outcome regression model was misspecified to exclude treatment effect heterogeneity (either alone or in addition to other misspecified models, including the realistic scenario in which all models are misspecified), TMLE was not more efficient than IPW estimation. In these scenarios, the TMLE confidence interval was wider than the IPW and DRWLS confidence intervals by amounts that were the same as or more extreme than those from the case study in several hundred of the 1,000 simulation draws. This reflects the fact that under practical positivity violations and model misspecification, TMLE is not necessarily expected to have a smaller confidence interval width than does IPW estimation.

Just as we assess whether there are penalties for unnecessary adjustment for nonrandom treatment and nonrandom subsample selection in the simulation study (see Table 5), we compare case study results using more parsimonious and less parsimonious models. When more parsimonious subsample selection models are used, the confidence interval of each of the estimators slightly narrows but relative performance stays the same. Interval width is insensitive to parsimony in the treatment model (see Web Appendix 5 and Web Figure 3).

DISCUSSION

We evaluated estimators of the PATE in the presence of treatment effect heterogeneity, nonrandom treatment assignment, a 2-stage selection process, and practical positivity violations. Using a simulation study, we found that a DRWLS estimator and a TMLE have lower MSE than an IPW estimator under correct model specification and in all but 2 model misspecification scenarios. DRWLS estimation had the lowest percent bias and variance and best confidence interval coverage under correct model specification and in most model misspecification scenarios. We derived the efficient influence function and presented a TMLE that incorporated survey sampling weights in Web Appendix 1, which can be easily implemented using the available tmle package in R (code presented in Web Appendix 2).

We agree with others (2, 3, 6, 14) that estimating an average effect standardized to a population of interest is a practical goal. It can increase the interpretability and applicability of a study's conclusions, provided one recognizes the assumptions and limitations involved. First, a PATE will not provide information about treatment effect heterogeneity. Second, estimation can be difficult in the presence of positivity violations. In cases in which the weights are highly variable, a sensitivity analysis that varies model specifications is recommended (14), and there exist methods to identify possible resulting biases (22, 31). Nonparametric methods of model specification may improve robustness to model misspecification (32).

Our demonstration of the poor performance of an IPW estimator is not new. IPW estimators have well-known efficiency problems and can be biased because of structural or practical positivity violations (14). Much has been published on this in the biostatistics literature (e.g., 7, 14), but IPW estimation continues to be widely used by epidemiologists, perhaps because it is straightforward to implement in standard statistical software. We hope demonstrating the similarly straightforward implementation of DRWLS estimation and TMLE coupled with their superior performance over IPW estimation in terms of MSE will cause use of these estimators to gain popularity.

We evaluated the robustness of our simulation results in a series of sensitivity analyses. First, we truncated the most extreme 2% of treatment and selection weights. This may lessen both bias and variance that are due to extreme weights, though it may also increase bias due to misspecification (22, 33). Generally, this resulted in a higher percent bias across estimators (bias was particularly high for IPW), smaller variance, larger MSE for IPW estimation, and lower MSE for DRWLS estimation and TMLE. Optimal truncation strategies have been examined (34); identifying the best one for the data-generating mechanism considered here is an area for future work. Second, we reran the simulations after removing positivity violations in the data-generating distributions. This resulted in consistent estimates, 95% confidence interval coverage of approximately 95%, and substantially lower variance and MSE across estimators when the models were correctly specified. In this case, TMLE and DRWLS estimators clearly outperformed the IPW estimator. Third, we modified the data-generating mechanism so that both W₁ and W₂ were associated with probability of treatment and probability of selection. Performance of the DRWLS estimator was similar and performance of the IPW estimator and TMLE worsened because of greater positivity violations. Fourth, we repeated simulations under no effect heterogeneity. Weights were unchanged in this scenario, but finite sample bias improved because of less data sparsity. Percent bias and confidence interval coverage improved for IPW estimation and TMLE. Variance and MSE improved for all estimators.

In our simulation and example, we considered a scenario in which the full set of covariates was measured in the larger survey sample and selection into the subsample only affected missingness of the outcome variable. One could also conceive of scenarios in which the general missing data pattern (due to nonresponse, sample selection, or right-censoring) extends to some subset of covariates. We explain how such a scenario would alter our assumptions and estimator performance in Web Appendix 6.

Our simulation study has some limitations. First, simulations can only give a rough approximation of the sampling distribution of the estimators (14). Second, there are a dozen or more estimators that could have been assessed and compared, including other implementations of TMLE (6, 13, 35). We chose to focus on a smaller set of estimators that are particularly straightforward to implement and used the implementation of TMLE that is available in the R software package (11). Other estimators and TMLE implementations may have outperformed those we considered, in particular the TMLE implementation, in which the weights are incorporated into a weighted logistic regression model for the updated outcome expectation instead of as part of covariate H (defined in step 2 of the TMLE description) (36). Future work should develop easy-to-use software packages that implement these estimators. Third, the approach shown in this article is not a fully design-based survey analysis. For example, we ignored survey sampling strata in our bootstrapping procedure. This is another area for future work.

In conclusion, we compared estimators of an average effect standardized to a target population in the presence of nonrandom treatment assignment, a 2-stage selection process, treatment effect heterogeneity, and practical positivity violations. This scenario can apply to generalizing results from a survey subsample to a specified target population (2, 3). We demonstrated that the DRWLS estimator and TMLE outperform an IPW estimator in terms of MSE and that DRWLS estimation generally performs best in terms of percent bias, variance, and confidence interval coverage in our practical positivity violation scenario, even under misspecification of one or more of the treatment, selection, or outcome models. Moreover, DRWLS estimation and TMLE are easy to implement. Lastly, we demonstrated how a DRWLS estimator and TMLE can be applied to everyday research questions, providing an attractive alternative to IPW estimation for applied epidemiologic researchers.