Accounting for linkage disequilibrium in genome-wide association studies: A penalized regression method

Abstract

Penalized regression methods are becoming increasingly popular in genome-wide association studies (GWAS) for identifying genetic markers associated with disease. However, standard penalized methods such as LASSO do not take into account the possible linkage disequilibrium between adjacent markers. We propose a novel penalized approach for GWAS using a dense set of single nucleotide polymorphisms (SNPs). The proposed method uses the minimax concave penalty (MCP) for marker selection and incorporates linkage disequilibrium (LD) information by penalizing the difference of the genetic effects at adjacent SNPs with high correlation. A coordinate descent algorithm is derived to implement the proposed method. This algorithm is efficient in dealing with a large number of SNPs. A multi-split method is used to calculate the p-values of the selected SNPs for assessing their significance. We refer to the proposed penalty function as the smoothed MCP and the proposed approach as the SMCP method. Performance of the proposed SMCP method and its comparison with LASSO and MCP approaches are evaluated through simulation studies, which demonstrate that the proposed method is more accurate in selecting associated SNPs. Its applicability to real data is illustrated using heterogeneous stock mice data and a rheumatoid arthritis.

1. INTRODUCTION

With the rapid development of modern genotyping technology, genome-wide association studies (GWAS) have become an important tool for identifying genetic factors underlying complex traits. From a statistical standpoint, identifying SNPs associated with a trait can be formulated as a variable selection problem in a sparse, high-dimensional model. The traditional multivariate regression methods are not directly applicable to GWAS because the number of SNPs in an association study is usually much larger than the sample size.

The LASSO (least absolute shrinkage and selection operator) provides a computationally feasible way for variable selection in high-dimensional settings [14]. Recently, this approach has been applied to GWAS for selecting important SNPs [19]. It has been shown that the LASSO is selection consistent if the predictors meet the irrepresentable condition [23]. This condition is stringent, and there is no known mechanism to verify it in GWAS. Zhang and Huang [22] studied the sparsity and bias of LASSO in high-dimensional linear regression models. It is shown that under reasonable conditions, the LASSO selects a model with the correct order of dimensionality. However, the LASSO tends to over-select unimportant variables. Therefore, direct application of the LASSO to GWAS tends to generate findings with high false positive rates. Another limitation of the LASSO is that, if there is a group of variables among which the pairwise correlations are high, then the LASSO tends to select only one variable from the group and does not care which one is selected [25].

Several methods that attempt to improve the performance of LASSO have been proposed. The adaptive LASSO [24] uses adaptive weights on penalties so that the oracle properties hold under mild regularity conditions. In the case that the number of predictors is much larger than the sample size, adaptive weights cannot be initiated easily. The elastic net method [25] can effectively deal with certain correlation structures in the predictors by using a combination of ridge and LASSO penalties. Fan and Li [4] introduced a smoothly clipped absolute deviation (SCAD) method. Zhang [21] proposed a flexible minmax concave penalty (MCP) which attenuates the effect of shrinkage that leads to bias. Both SCAD and MCP belong to the family of quadratic spline penalties, and both lead to oracle selection results [21]. The MCP has a simpler form and requires weaker conditions for the oracle properties. We refer to [21] and [10] for detailed discussion.

However, the existing penalization methods for variable selection do not take into account the specifics of SNP data. SNPs are naturally ordered along the genome with respect to their physical positions. In the presence of linkage disequilibrium (LD), adjacent SNPs are expected to show similar strength of association. Making use of the LD information from adjacent SNPs is highly desirable as it may help better delineate association signals while reducing randomness observed in single SNP analysis. Fused LASSO [15], which penalizes differences of adjacent coefficients, is not appropriate for this purpose, since the effect of association for a SNP (as measured by its regression coefficient) is only identifiable up to its absolute value—a homozygous genotype can be equivalently coded as either 0 or 2 depending on the choice of reference allele.

We propose a new penalized regression method for identifying important SNPs in GWAS. The proposed method uses a novel penalty, which we shall refer to as the smoothed minimax concave penalty or SMCP, for sparsity and smoothness in absolute values (of regression coefficients). The SMCP is a combination of the MCP and a penalty consisting of the squared differences of the absolute effects of adjacent markers. The MCP promotes sparsity in the model and selects important SNPs. The penalty for the squared differences of absolute effects takes into account the natural ordering of SNPs and adaptively incorporates the LD information between adjacent SNPs. It explicitly uses correlation between adjacent markers and penalizes the differences of genetic effects at adjacent SNPs with high correlations. We derive a coordinate descent algorithm for implementing the SMCP method. We use a resampling method for computing the p-values of selected SNPs to assess their significance.

The rest of the paper is organized as follows. Section 2 introduces the proposed SMCP method. Section 3 presents a genome-wide screening incorporating the proposed SMCP method. Section 4 describes a coordinate descent algorithm for estimating model parameters and discusses the selection of tuning parameters and calculation of p-value. Section 5 conducts simulation and compares with LASSO and MCP. Section 6 applies the proposed method to two real data sets. Finally, Section 7 provides a summary and discusses some related issues.

2. THE SMCP METHOD

For the purpose of SNP selection, we use the MCP, which is defined as

$$\rho (t;{\lambda }_1,\gamma )={\lambda }_1{\int }_0^{\mid t\mid }{(1-x/(\gamma {\lambda }_1))}_{+}dx.$$

Here λ₁ is a penalty parameter, and γ is a regularization parameter that controls the concavity of ρ. x₊ = x1_{x≥0}. The MCP can be easily understood by considering its derivative, which is

$$\stackrel{.}{\rho }(t;{\lambda }_1,\gamma )={\lambda }_1{\left(1-\mid t\mid /(\gamma {\lambda }_1)\right)}_{+}sgn(t),$$

where sgn(t) = −1, 0, or 1 if t < 0, = 0, or > 0, respectively. As |t| increases from 0, MCP begins by applying the same rate of penalization as LASSO, but continuously relaxes that penalization until |t| > γλ₁, a condition under which the rate of penalization drops to 0. It provides a continuum of penalties where the LASSO penalty corresponds to γ = ∞ and the hard-thresholding penalty corresponds to γ → 1+. We note that other penalties, such as LASSO or SCAD, can also be used to replace MCP. We choose MCP because it possesses all the desirable properties of a penalty function and is computationally simple [10, 21].

Let p be the number of SNPs, and β_j be the effect of the jth SNP in a working model that describes the relationship between phenotype and markers. Assume that the SNPs are ordered according to their physical locations on the chromosomes. Adjacent SNPs in high LD are expected to have similar strength of association with the phenotype. To adaptively incorporate LD information, we propose the following penalty that encourages smoothness in |β|s at neighboring SNPs:

$$\frac{{\lambda }_2}{2}\sum _{j=1}^{p-1}{\zeta }_j{(\mid {\beta }_j\mid -\mid {\beta }_{j+1}\mid )}^2,$$ (1)

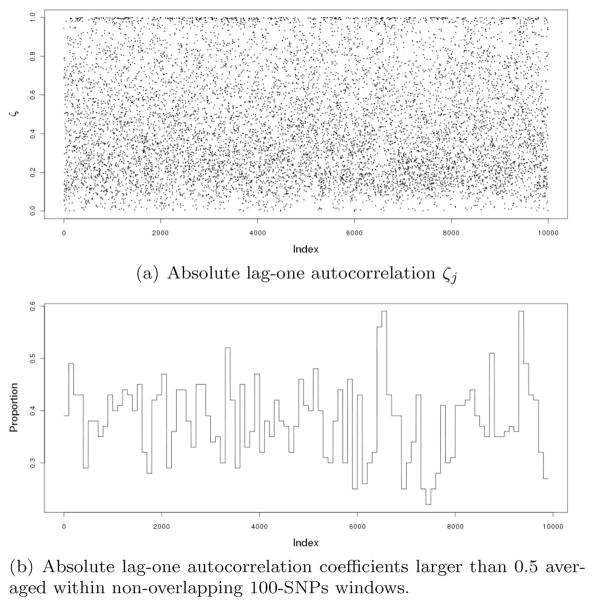
where the weight ζ_j is a measure of LD between SNPs j and j+1. This penalty encourages |β_j| and |β_j+1| to be similar to an extent inversely proportional to the LD strength between the corresponding SNPs. Adjacent SNPs in weak LD are allowed to have larger differences in their |β|s than if they are in stronger LD. The effect of this penalty is to encourage smoothness in |β|s for SNPs in strong LD. By using this penalty, we expect a better delineation of the association pattern in LD blocks that harbor disease variants while reducing randomness in |β|s in LD blocks that do not. Note that there is no monotone relationship between ζ and the physical distance between two SNPs. While it is possible to use other LD measures, we choose ζ_j to be the absolute value of lag one autocorrelation coefficient between the genotype scores of SNPs j and j+1. The values of ζ_j for the rheumatoid arthritis data used by Genetic Analysis Workshop 16, the data set to be used in our numerical study, are plotted for chromosome 6 (Fig. 1(a)). The proportion that ζ_j > 0.5 over non-overlapping 100-SNP windows is also plotted (Fig. 1(b)).

Figure 1.

Plots of absolute lag-one autocorrelation ζ_j on Chromosome 6 from Genetic Analysis Workshop 16 Rheumatoid Arthritis data.

Denote β = (β₁, …, β_p)′. Denote g(β) as the loss function based on a working model for the relationship between the phenotype and markers. For given penalty parameters λ₁ and λ₂, the SMCP estimate β̂ is defined as the minimizer of the objective function

$$g(\mathit{\beta })+\sum _{j=1}^p\rho (\mid {\beta }_j\mid ;{\lambda }_1,\gamma )+\frac{{\lambda }_2}{2}\sum _{j=1}^{p-1}{\zeta }_j{(\mid {\beta }_j\mid -\mid {\beta }_{j+1}\mid )}^2.$$ (2)

The SNPs corresponding to β̂_j ≠ 0 are selected as being potentially associated with response.

3. GENOME-WIDE SCREENING INCORPORATING LD

A basic method for GWAS is to conduct genome-wide screening of a large number of dense SNPs individually and look for those with significant associations with phenotype. Although several important considerations, such as adjustment for multiple comparisons and possible population stratification, need to be taken into account in the analysis, the essence of existing genome-wide screening approaches is single-marker based analysis without considering the structure of SNP data. In particular, the possible LD between two adjacent SNPs is not incorporated in analysis.

Our proposed SMCP method can be used for screening a dense set of SNPs incorporating the LD information in a natural way. To be specific, here we consider the standard case-control design for identifying SNPs that are potentially associated with response. Let the phenotype be scored as 1 for cases and −1 for controls. Let n_j be the number of subjects whose genotypes are non-missing at SNP j. The standardized phenotype of the ith subject with non-missing genotype at SNP j is denoted by y_ij. The genotype at SNP j is scored as 0, 1, or 2 depending on the number of copies of a reference allele in a subject. Let x_ij denote the standardized genotype score satisfying Σ_i x_ij = 0 and ${\sum }_{i=1}^{n_j}{x}_{ij}^2=n_j$.

Consider the penalized criterion

$$L_n(\mathit{\beta })=\frac{1}{2}\sum _{j=1}^p\frac{1}{n_j}\sum _{i=1}^{n_j}{(y_{ij}-x_{ij}{\beta }_j)}^2+\sum _{j=1}^p\rho (\mid {\beta }_j\mid ;{\lambda }_1,\gamma )+\frac{{\lambda }_2}{2}\sum _{j=1}^{p-1}{\zeta }_j{(\mid {\beta }_j\mid -\mid {\beta }_{j+1}\mid )}^2.$$ (3)

Here the loss function is

$$g(\mathit{\beta })=\frac{1}{2}\sum _{j=1}^p\frac{1}{n_j}\sum _{i=1}^{n_j}{(y_{ij}-x_{ij}{\beta }_j)}^2.$$ (4)

We note that switching the reference allele used for scoring the genotypes changes the sign of β_j, but |β_j| remains the same. It may be counter-intuitive to use a quadratic loss in (4) for case-control designs. However, it may actually be sensible. Regardless how the phenotype is scored, the least squares regression slope at SNP j (i.e., a regular single SNP analysis) equals

$$\sum _{i=1}^{n_j}{y}_{ij}{x}_{ij}/\sum _{i=1}^{n_j}{x}_{ij}^2=2({\widehat{p}}_{1j}-{\widehat{p}}_{2j})/{\phi }_j(1-{\phi }_j),$$

where φ_j is the proportion of cases computed from the subjects with non-missing genotype, and p̂_1j and p̂_2j are the allele frequencies of SNP j in cases and controls, respectively. This shows that β_j in the squared loss function (4) can be interpreted as the effect size of SNP j. In the classification literature, quadratic loss has also been used for indicator response variables [7].

An alternative loss function for binary phenotype would be the sum of negative marginal log-likelihood functions based on working logistic regression models. We have found that the selection results using this loss function are in general similar to those based on (4). In addition, the computational implementation of the coordinate descent algorithm described in the next section using the loss function (4) is much more stable and efficient and can easily handle tens of thousands of SNPs.

4. COMPUTATION

In this section, we first present a coordinate descent algorithm for the proposed SMCP method. Then we discuss methods of selecting tuning parameters and evaluating p-values for the selected SNPs.

4.1 Coordinate descent algorithm

In this section, we derive a coordinate descent algorithm for computing the solution to (3). This algorithm was originally proposed for criteria with convex penalties such as LASSO [8, 20]. It has been proposed to calculate nonconvex penalized regression estimates [3, 10]. This algorithm optimizes a target function with respect to one parameter at a time and iteratively cycles through all parameters until convergence. It is particularly suitable for problems such as SMCP that have a simple closed form solution in a single dimension but lack a closed form solution in higher dimensions.

We wish to minimize the objective function L_n(β) in (3) with respect to β_j while keeping all other β_k, k ≠ j, fixed at their current estimates. Thus only the terms involving β_j in L_n matter. That is, this problem is equivalent to minimizing R(β_j) defined as

$$\begin{array}{l}R({\beta }_j)=\frac{1}{2n_j}\sum _{i=1}^{n_j}{(y_{ij}-x_{ij}{\beta }_j)}^2+\rho (\mid {\beta }_j\mid ;{\lambda }_1,\gamma )+\frac{1}{2}{\lambda }_2[{\zeta }_j{(\mid {\beta }_j\mid -\mid {\stackrel{\sim }{\beta }}_{j+1}\mid )}^2+{\zeta }_{j-1}{(\mid {\stackrel{\sim }{\beta }}_{j-1}\mid -\mid {\beta }_j\mid )}^2]\\ =C+a_j{\beta }_j^2+b_j{\beta }_j+c_j\mid {\beta }_j\mid ,j=2,\dots ,p-1,\end{array}$$

where C is a term free of β_j, β̃_j+1 and β̃_j−1 are the current estimates of β_j+1 and β_j−1, respectively, and a_j, b_j, and c_j are determined as follows:

• For |β_j| < γλ₁,

  $$\begin{array}{l}{a}_j=\frac{1}{2}\left(\frac{1}{n_j}\sum _{i=1}^{n_j}{x}_{ij}^2+{\lambda }_2({\zeta }_{j-1}+{\zeta }_j)-\frac{1}{\gamma }\right),\\ b_j=-\frac{1}{n_j}\sum _{i=1}^{n_j}{x}_{ij}{y}_{ij},\end{array}$$
  and

  $$c_j={\lambda }_1-{\lambda }_2(\mid {\stackrel{\sim }{\beta }}_{j+1}\mid {\zeta }_j+\mid {\stackrel{\sim }{\beta }}_{j-1}\mid {\zeta }_{j-1}).$$ (5)
• For |β_j| ≥ γλ₁,

  $$\begin{array}{l}{a}_j=\frac{1}{2}\left(\frac{1}{n_j}\sum _{i=1}^{n_j}{x}_{ij}^2+{\lambda }_2({\zeta }_{j-1}+{\zeta }_j)\right),\\ c_j=-{\lambda }_2(\mid {\stackrel{\sim }{\beta }}_{j+1}\mid {\zeta }_j+\mid {\stackrel{\sim }{\beta }}_{j-1}\mid {\zeta }_{j-1}),\end{array}$$ (6)

  while b_j remains the same as in the previous situation.

Note that function R(β_j) is defined for j ≠ 1 or p. It can be defined for j = 1 by setting β̃_j−1 = 0 and for j = p by setting β̃_j+1 = 0 in the above two situations.

Minimizing R(β_j) with respect to β_j is equivalent to minimizing $a_j{\beta }_j^2+b_j{\beta }_j+c_j\mid {\beta }_j\mid$, or equivalently,

$$a_j{\left({\beta }_j+\frac{b_j}{2a_j}\right)}^2+c_j\mid {\beta }_j\mid .$$ (7)

The first term is convex in β_j if a_j > 0. In the case |β_j| ≥ γλ₁, a_j > 0 is trivially true. In the case |β_j| < γλ₁, a_j > 0 holds when γ > 1.

Let β̂_j denote the minimizer of R(β_j). It has the following explicit expression:

$${\widehat{\beta }}_j=-\text{sign}(b_j)·\frac{{(\mid b_j\mid -c_j)}_{+}}{2a_j}.$$ (8)

This is because if c_j > 0, minimizing (7) becomes a regular one dimensional LASSO problem. β̂_j is the soft-threshold operator. If c_j < 0, it can be shown that β̂_j and b_j are of opposite signs. If b_j ≥ 0, expression (7) becomes

$$a_j{\left({\beta }_j+\frac{b_j}{2a_j}\right)}^2-c_j{\beta }_j.$$

Hence β̂_j = −(b_j − c_j)/2a_j < 0. If b_j < 0, then |β̂_j| = β̂_j and β̂_j = − (b_j + c_j)/2a_j > 0. In summary, expression (8) holds in all situations.

The novel penalty (1) affects both a_j and c_j. Both 2a_j and c_j are linear in λ₂. As λ₂ increases, 2a_j increases at the rate ∂(2a_j)/∂λ₂ = ζ_j−1 + ζ_j, while c_j decreases at the rate ∂c_j /∂λ₂ = |β̃_j+1|ζ_j + |β̃_j−1|ζ_j−1. In the case of |b_j| − c_j ≥ 0, these are the rates of change for the denominator and numerator of |β̂ _j| = (|b_j| − c_j)₊/(2a_j). The change in |β̂_j| is more complicated as it involves the intercepts of its numerator and denominator. In terms of |β̃_j+1| and |β̃_j−1|, β̂_j is larger when these two values are larger. Since b_j does not depend on λ₂, as λ₂ increases, more SNPs will satisfy |b_j| − c_j ≥ 0 and thus be selected.

We note that a_j and b_j do not depend on β_j. They only need to be computed once for each SNP. Only c_j needs to be updated after all β_j s are updated. In the special case of λ₂ = 0, the SMCP method becomes the MCP method. Then even c_j no longer depends on β̃_j−1 and β̃_j+1: c_j = λ₁ if |β_j| < γλ₁, and c_j = 0 otherwise. Expression (8) gives the explicit solution for β_j.

Generally, an iterative algorithm is required to estimate these parameters. Let ${\stackrel{\sim }{\mathit{\beta }}}^{(0)}={({\stackrel{\sim }{\beta }}_1^{(0)},\dots ,{\stackrel{\sim }{\beta }}_p^{(0)})}^{\prime }$ be the initial value of the estimate of β. The proposed coordinate descent algorithm proceeds as follows:

1. Compute a_j and b_j for j = 1, …, p.

2. Set s = 0.

3. For j = 1, …, p,

   1. Compute c_j according to expressions (5) or (6).

   2. Update ${\stackrel{\sim }{\beta }}_j^{(s+1)}$ according to expression (8).

4. Update s ← s + 1.

5. Repeat Steps 3 and 4 until the estimate of β converges.

In practice, the initial values ${\beta }_j^{(0)}$, j = 1, …, p are set to be 0. Each β_j is then updated in turn using the coordinate descent algorithm described above. One iteration completes when all β_j s are updated. In our experience, convergence is typically reached after about thirty iterations.

Convergence of this algorithm follows from Theorem 4.1(c) of [16]. This can be shown as follows. The objective function can be written as $f(\mathit{\beta })=f_0(\mathit{\beta })+{\sum }_{j=1}^J{f}_j({\beta }_j)$ where

$$f_0(\mathit{\beta })=\frac{1}{2}\sum _{j=1}^p\frac{1}{n_j}\sum _{i=1}^{n_j}{(y_{ij}-x_{ij}{\beta }_j)}^2+\frac{{\lambda }_2}{2}\sum _{j=1}^{p-1}{\zeta }_j{(\mid {\beta }_j\mid -\mid {\beta }_{j+1}\mid )}^2,$$

and f_j (β_j) = ρ(|β_j|; λ₁, γ). Since f is regular in the sense of (5) in [16] and ${\sum }_{j=1}^J{f}_j({\beta }_j)$ is separable, the coordinate descent solution converges to a coordinatewise minimum of f, which is also a stationary point of f.

Now we consider in detail property of the second penalty. Assume that λ₁ and λ₂ are fixed, and we want to solve the objective function (2). Suppose that in step s − 1, β_j−1 has been updated. Consider the values of estimate under adjacent steps, and define $\delta =\mid {\stackrel{\sim }{\beta }}_{j-1}^{(s)}\mid -\mid {\stackrel{\sim }{\beta }}_{j-1}^{(s-1)}\mid$. Further assume that at step s − 1, only ${\stackrel{\sim }{\beta }}_{j-1}^{(s-1)}$ is non-zero and δ is usually positive. We now go into step s to update β_j.

• If corr(x_j, x_j−1) > 0, then ζ_j−1 = corr(x_j, x_j−1). We have $c_j^{(s)}=c_j^{(s-1)}-{\lambda }_2\delta {\zeta }_{j-1}$. Note that $c_j^{(s)}<c_j^{(s-1)}$, since ζ_j−1 > 0. From expression (8), we know that ${\beta }_j^{(s)}$ will be nonzero if c_j is less than |b_j|. One can see that when the correlation is stronger (i.e. ζ_j−1 is larger) and/or λ₂ is larger, $c_j^{(s)}$ is smaller. Consequently, ${\stackrel{\sim }{\beta }}_j^{(s)}$ is more likely to be nonzero. The sign of β̃_j is also positive if it is not zero. It makes sense that the correlation between the (j − 1)th and jth predictors is assumed to be positive.

• It is similar when corr(x_j, x_j−1) < 0.

Thus, incorporating the second penalty increases the chance that adjacent SNPs with high correlations will be selected together.

4.2 Tuning parameter selection

There are various methods that can be applied, including AIC, BIC, cross-validation and generalized cross-validation. However, they are all based upon the performance of prediction error. In GWAS, it is rare that disease markers are part of SNP data, which consequently results in non-true models for SNP data. Hence, the methods mentioned above may be inadequate in GWAS. Wu et al. [19] used a predetermined number of predictors to select the tuning parameter and implemented a combination of bracketing and bisection to search for the optimal tuning parameter. We adopt Wu et al.’s method [19]. For this purpose, tuning parameters λ₁ and λ₂ are re-parameterized as τ = λ₁ + λ₂ and η = λ₁/τ. The value of η is fixed beforehand. When η = 1, the SMCP method becomes the MCP method.

The value of τ that selects the predetermined number of predictors is determined through bisection as follows. Let r(τ) denote the number of predictors selected under τ. Let τ_max be the smallest value for which all coefficients are 0. τ_max is the upper bound for τ. From (5), ${\tau }_{max}={max}_j\mid {\sum }_{i=1}^{n_j}{x}_{ij}{y}_{ij}\mid /(n_j\eta )$. To avoid undefined saturated models, τ cannot be zero or too close to zero. Its lower bound, denoted by τ_min, is set at τ_min = ετ_max for a preselected ε. Setting ε = 0.1 works well in our numerical study. Initially, we set τ_l = τ_min and τ_u = τ_max. If r(τ_u) < s < r(τ_l), then we employ bisection. This involves testing the midpoint ${\tau }_m=\frac{1}{2}({\tau }_l+{\tau }_u)$. If r(τ_m) < s, replace τ_u by τ_m. If r(τ_m) > s, replace τ_l by τ_m. This process is repeated until r(τ_m) = s. Our simulation study suggests that the regularization parameter γ also has an important impact on the results. Based on our experience, γ = 6 is a reasonable choice.

4.3 p-values for the selected SNPs

The use of p-value is a traditional way to evaluate the significance of estimates. Unfortunately, there are no straightforward ways to compute standard errors of penalized linear regression estimates. We use the multi-split method proposed by [11] to obtain p-values. This is a simulation-based method that automatically adjusts for multiple comparisons.

In each iteration, the multi-split method proceeds as follows:

1. Randomly split data into two disjoint sets of equal size: D_in and D_out. The case: control ratio in each set is the same as in the original data.

2. Fit the SMCP method with subjects in D_in. Denote the set of selected SNPs by S.

3. Assign a p-value P̃_j to SNP j in the following way:

   1. If SNP j is in set S, set P̃_j as the p-value computed using D_out in the regular linear regression where SNP j is the only predictor.

   2. If SNP j is not in set S, set P̃_j = 1.

4. Define the adjusted p-value as P_j = min{P̃_j |S|, 1}, j = 1, …, p, where |S| is the size of set S.

This procedure is repeated B times for each SNP. Let $P_j^{(b)}$ denote the adjusted p-value for SNP j in the bth iteration. For π ∈ (0, 1), let q_π be the π-quantile of { $P_j^{(b)}/\pi$; b = 1, …, B}. Define Q̃_j (π) = min{1, q_π}. Meinshausen et al. [11] proved that Q̃_j (π) is an asymptotically correct p-value, adjusted for multiplicity. They also proposed an adaptive version that selects a suitable value of quantile based on data:

$$Q_j=min\left\{1,(1-log{\pi }_0)\underset{\pi \in ({\pi }_0,1)}{inf}{\stackrel{\sim }{Q}}_j(\pi )\right\},$$

where π₀ is chosen to be 0.05. It was shown that {Q_j, j = 1, …, p}, can be used for both FWER (family-wise error rate) and FDR control.

5. SIMULATION STUDIES

To make the LD structure as realistic as possible, genotypes are obtained from a rheumatoid arthritis (RA) study provided by the Genetic Analysis Workshop (GAW) 16 (more details described in Section 6). This study involves 2,062 individuals. Four hundred of them are randomly chosen. Five thousand SNPs are selected from chromosome 6. For individual i, its quantitative phenotype y_i is generated as:

$$y_i={\mathit{x}}_i^{\prime }\mathit{\beta }+{\epsilon }_i,i=1,\dots ,400,$$

where x_i (which is a vector of length 5,000) represents the genotype data of individual i, and β is the vector of genetic effect whose elements are all 0 except that (β₂₂₈₇, …, β₂₂₉₈) = (−0.3, 0.2, −0.25, 0.2, −0.6, 0.7, −0.5, 0.4, −0.5, 0.3, −0.6, 0.2) and (β₂₃₀₀, …, β₂₃₁₈) = (0.25, −0.4, 0.2, −0.5, −0.25, 0.3, −0.4, −0.4, 0.15, 0.3, −0.4, 0.4, −0.5, 0.2, − 0.3, 0.16, 0.36, −0.2, 0.1). ε_i is the residual sampled from a normal distribution with mean 0 and standard deviation 1.5.

For binary phenotype y_i, the linear predictor is generated in the same way as for the quantitative trait. Then, the binary response variables are generated from Bernoulli distributions with probability $Pr(y_i=1\mid x_i)=\frac{1}{1+e^{-({\beta }_0+x_i^{\prime }\mathit{\beta })}}$ where β₀ = 0.

For the quantitative trait, the loss function g(β) is given in expression (4), whereas for the binary trait, two loss functions, including the marginal quadratic loss (4) and marginal negative likelihood loss (Appendix: expression (10), are used in simulation.

To evaluate the performance of SMCP, we use false discovery rate (FDR) and false negative rate (FNR) which are defined as follows. Let β̂_j denote the estimated value of β_j, then

$$\text{FDR}=\frac{\#\text{of}\text{SNPs}\text{with}{\widehat{\beta }}_j\ne 0\text{but}{\beta }_j=0}{\#\text{of}\text{SNPs}\text{with}\widehat{\beta }\ne 0}$$

and

$$\text{FNR}=\frac{\#\text{of}\text{SNPs}\text{with}{\widehat{\beta }}_j=0\text{but}{\beta }_j\ne 0}{\#\text{of}\text{SNPs}\text{with}\beta \ne 0}.$$

The mean and standard deviation of the number of true positives, FDR and FNR for various values of η for SMCP, LASSO and MCP over 100 replications are reported in Table 1. In each replication, 50 SNPs are selected. It can be seen that for different values of η, FDR and FNR change in the same direction, since the number of selected SNPs is fixed. As the number of true positives increases, the number of false negatives and the number of false positives decrease. Overall, SMCP outperforms MCP and LASSO in terms of true positives and FDR. For the binary trait, we see that although the marginal negative log-likelihood loss is better than the marginal quadratic loss, it is still sensible to use the marginal quadratic loss (4) to identify phenotype-associated SNPs.

Table 1.

Mean (standard deviation) of the number of true positive, false discovery rate (FDR) and false negative rate (FNR) over 100 simulation replications. There are 31 associated SNPs

γ	η	Quantitative Trait			Binary Trait*			Binary Trait**
		TP	FDR	FNR	TP	FDR	FNR	TP	FDR	FNR
1.8	0.05	29.99(0.22)	0.40(0.01)	0.03(0.01)	21.48(3.89)	0.57(0.08)	0.31(0.13)	24.43(4.45)	0.51(0.09)	0.21(0.14)
	0.06	29.84(0.39)	0.40(0.01)	0.04(0.01)	21.60(4.17)	0.57(0.08)	0.30(0.13)	23.70(5.17)	0.53(0.10)	0.24(0.17)
	0.08	29.56(0.57)	0.41(0.01)	0.05(0.02)	21.57(3.72)	0.57(0.07)	0.30(0.12)	23.31(4.73)	0.53(0.09)	0.25(0.15)
	0.1	28.76(0.82)	0.42(0.02)	0.07(0.03)	20.99(3.91)	0.58(0.08)	0.32(0.13)	23.43(3.99)	0.53(0.08)	0.24(0.13)
	0.2	27.31(0.60)	0.45(0.01)	0.12(0.02)	19.51(3.72)	0.61(0.07)	0.37(0.12)	22.59(3.99)	0.55(0.08)	0.27(0.13)
	0.3	26.66(0.65)	0.47(0.01)	0.14(0.02)	18.79(3.79)	0.62(0.08)	0.39(0.12)	21.80(4.13)	0.56(0.08)	0.30(0.13)
	0.4	26.37(0.56)	0.47(0.01)	0.15(0.02)	18.02(4.01)	0.64(0.08)	0.42(0.13)	21.61(3.85)	0.57(0.08)	0.30(0.12)
	0.5	26.11(0.53)	0.48(0.01)	0.16(0.02)	17.52(3.49)	0.65(0.07)	0.43(0.11)	20.49(4.03)	0.59(0.08)	0.34(0.13)
	0.6	25.77(0.66)	0.48(0.01)	0.17(0.02)	17.78(3.42)	0.64(0.07)	0.43(0.11)	19.55(4.08)	0.61(0.08)	0.37(0.13)
	0.7	25.30(0.69)	0.49(0.01)	0.18(0.02)	17.50(3.05)	0.65(0.06)	0.44(0.10)	19.40(3.88)	0.61(0.08)	0.37(0.13)
	0.8	24.84(0.72)	0.50(0.01)	0.20(0.02)	17.57(3.24)	0.65(0.06)	0.43(0.10)	19.42(3.42)	0.61(0.07)	0.37(0.11)
	0.9	24.23(0.85)	0.52(0.02)	0.22(0.03)	17.35(3.42)	0.65(0.07)	0.44(0.11)	17.35(3.70)	0.65(0.07)	0.44(0.12)
	MCP	23.77(0.80)	0.52(0.02)	0.23(0.03)	17.83(3.23)	0.64(0.06)	0.42(0.10)	17.72(3.19)	0.65(0.06)	0.43(0.10)
3	0.05	29.69(0.60)	0.41(0.01)	0.04(0.02)	20.85(4.05)	0.58(0.08)	0.33(0.13)	23.73(5.14)	0.53(0.10)	0.23(0.17)
	0.06	29.44(0.73)	0.41(0.01)	0.05(0.02)	20.84(4.15)	0.58(0.08)	0.33(0.13)	22.33(4.54)	0.55(0.09)	0.28(0.15)
	0.08	28.20(0.74)	0.44(0.01)	0.09(0.02)	20.98(4.18)	0.58(0.08)	0.32(0.13)	22.79(4.46)	0.54(0.09)	0.26(0.14)
	0.1	27.78(0.63)	0.44(0.01)	0.10(0.02)	20.24(3.95)	0.60(0.08)	0.35(0.13)	22.64(4.35)	0.55(0.09)	0.27(0.14)
	0.2	26.88(0.69)	0.46(0.01)	0.13(0.02)	18.84(4.10)	0.62(0.08)	0.39(0.13)	22.03(4.00)	0.56(0.08)	0.29(0.13)
	0.3	26.39(0.58)	0.47(0.01)	0.15(0.02)	18.23(3.44)	0.64(0.07)	0.41(0.11)	21.16(4.30)	0.58(0.09)	0.32(0.14)
	0.4	26.16(0.47)	0.48(0.01)	0.16(0.02)	17.97(3.57)	0.64(0.07)	0.42(0.12)	20.72(3.83)	0.59(0.08)	0.33(0.12)
	0.5	25.92(0.61)	0.48(0.01)	0.16(0.02)	18.35(3.33)	0.63(0.07)	0.41(0.11)	20.92(4.04)	0.58(0.08)	0.33(0.13)
	0.6	25.51(0.66)	0.49(0.01)	0.18(0.02)	17.40(3.48)	0.65(0.07)	0.44(0.11)	18.76(3.77)	0.62(0.08)	0.39(0.12)
	0.7	25.08(0.69)	0.50(0.01)	0.19(0.02)	17.33(3.09)	0.65(0.06)	0.44(0.10)	19.40(3.65)	0.61(0.07)	0.37(0.12)
	0.8	24.43(0.81)	0.51(0.02)	0.21(0.03)	17.71(3.03)	0.65(0.06)	0.43(0.10)	18.56(3.42)	0.63(0.07)	0.40(0.11)
	0.9	24.15(0.90)	0.52(0.02)	0.22(0.03)	17.55(3.22)	0.65(0.06)	0.43(0.10)	17.86(3.85)	0.64(0.08)	0.42(0.12)
	MCP	23.90(0.88)	0.52(0.02)	0.23(0.03)	17.31(3.00)	0.65(0.06)	0.44(0.10)	17.15(3.24)	0.66(0.06)	0.45(0.10)
6	0.05	29.19(0.80)	0.42(0.02)	0.06(0.03)	21.24(3.91)	0.58(0.08)	0.31(0.13)	23.80(4.17)	0.52(0.08)	0.23(0.13)
	0.06	28.48(0.77)	0.43(0.02)	0.08(0.02)	20.33(3.93)	0.59(0.08)	0.34(0.13)	22.50(4.73)	0.55(0.09)	0.27(0.15)
	0.08	27.72(0.49)	0.45(0.01)	0.11(0.02)	20.83(3.63)	0.58(0.07)	0.33(0.12)	22.97(4.61)	0.54(0.09)	0.26(0.15)
	0.1	27.56(0.54)	0.45(0.01)	0.11(0.02)	19.39(4.09)	0.61(0.08)	0.37(0.13)	22.09(4.33)	0.56(0.09)	0.29(0.14)
	0.2	26.68(0.66)	0.47(0.01)	0.14(0.02)	18.51(3.12)	0.63(0.06)	0.40(0.10)	21.44(3.82)	0.57(0.08)	0.31(0.12)
	0.3	26.27(0.55)	0.47(0.01)	0.15(0.02)	18.57(3.52)	0.63(0.07)	0.40(0.11)	21.65(4.10)	0.57(0.08)	0.30(0.13)
	0.4	25.92(0.58)	0.48(0.01)	0.16(0.02)	18.07(3.44)	0.64(0.07)	0.42(0.11)	20.07(4.38)	0.60(0.09)	0.35(0.14)
	0.5	25.61(0.68)	0.49(0.01)	0.17(0.02)	17.29(3.50)	0.65(0.07)	0.44(0.11)	19.87(3.57)	0.60(0.07)	0.36(0.12)
	0.6	25.00(0.72)	0.50(0.01)	0.19(0.02)	18.14(3.39)	0.64(0.07)	0.41(0.11)	19.33(3.58)	0.61(0.07)	0.38(0.12)
	0.7	24.76(0.77)	0.50(0.02)	0.20(0.02)	17.78(3.75)	0.64(0.08)	0.43(0.12)	18.23(3.75)	0.64(0.07)	0.41(0.12)
	0.8	24.42(0.90)	0.51(0.02)	0.21(0.03)	17.57(3.10)	0.65(0.06)	0.43(0.10)	17.49(3.91)	0.65(0.08)	0.44(0.13)
	0.9	24.02(0.90)	0.52(0.02)	0.23(0.03)	17.42(3.18)	0.65(0.06)	0.44(0.10)	17.32(3.45)	0.65(0.07)	0.44(0.11)
	MCP	23.83(0.88)	0.52(0.02)	0.23(0.03)	17.33(3.24)	0.65(0.06)	0.44(0.10)	17.41(3.27)	0.65(0.07)	0.44(0.11)
∞	0.05	28.52(0.80)	0.43(0.02)	0.08(0.03)	20.82(3.55)	0.58(0.07)	0.33(0.11)	22.57(4.13)	0.55(0.08)	0.27(0.13)
	0.06	28.01(0.67)	0.44(0.01)	0.10(0.02)	20.91(3.39)	0.58(0.07)	0.33(0.11)	22.86(4.21)	0.54(0.08)	0.26(0.14)
	0.08	27.53(0.58)	0.45(0.01)	0.11(0.02)	19.79(3.66)	0.60(0.07)	0.36(0.12)	22.88(4.48)	0.54(0.09)	0.26(0.14)
	0.1	27.30(0.63)	0.45(0.01)	0.12(0.02)	19.77(3.83)	0.60(0.08)	0.36(0.12)	22.46(4.12)	0.55(0.08)	0.28(0.13)
	0.2	26.55(0.69)	0.47(0.01)	0.14(0.02)	18.25(3.40)	0.64(0.07)	0.41(0.11)	20.84(4.16)	0.58(0.08)	0.33(0.13)
	0.3	26.19(0.54)	0.48(0.01)	0.16(0.02)	18.44(3.23)	0.63(0.06)	0.41(0.10)	20.18(4.06)	0.60(0.08)	0.35(0.13)
	0.4	25.81(0.60)	0.48(0.01)	0.17(0.02)	18.12(3.47)	0.64(0.07)	0.42(0.11)	19.99(4.04)	0.60(0.08)	0.36(0.13)
	0.5	25.40(0.68)	0.49(0.01)	0.18(0.02)	17.83(3.05)	0.64(0.06)	0.42(0.10)	19.73(3.76)	0.61(0.08)	0.36(0.12)
	0.6	25.15(0.77)	0.50(0.02)	0.19(0.02)	18.18(3.14)	0.64(0.06)	0.41(0.10)	18.35(3.89)	0.63(0.08)	0.41(0.13)
	0.7	24.50(0.79)	0.51(0.02)	0.21(0.03)	17.79(3.10)	0.64(0.06)	0.43(0.10)	18.11(3.63)	0.64(0.07)	0.42(0.12)
	0.8	24.34(0.89)	0.51(0.02)	0.21(0.03)	17.28(3.55)	0.65(0.07)	0.44(0.11)	18.17(3.54)	0.64(0.07)	0.41(0.11)
	0.9	24.11(0.88)	0.52(0.02)	0.22(0.03)	16.45(3.22)	0.67(0.06)	0.47(0.10)	17.34(3.32)	0.65(0.07)	0.44(0.11)
	LASSO	23.86(0.80)	0.52(0.02)	0.23(0.03)	17.43(3.31)	0.65(0.07)	0.44(0.11)	17.08(3.29)	0.66(0.07)	0.45(0.11)

^*The data is fitted with marginal quadratic loss (4).

^**The data is fitted with marginal negative log-likelihood loss (9, Appendix).

To further investigate the performance of SMCP, MCP and LASSO, we look into a specific simulated data set. For the quantitative trait, the 50 SNPs selected by the three methods and their p-values obtained using the multi-split method are reported in Table 4 (Appendix). For the binary trait, the selected SNPs and their p-values are reported in Table 5 and Table 6 (Appendix) using the marginal negative log-likelihood and marginal quadratic loss, respectively. It is apparent that the number of true positives is much higher for the SMCP method than for the MCP and LASSO methods. For the quantitative trait, SMCP selects 28 out of 31 true response-associated SNPs, while LASSO selects 23 (Appendix: Table 4). The multi-split method can effectively assign p-values for the selected SNPs: with SMCP, 9 out of 22 false positives are significant, whereas 21 out of 28 true positives are significant. In comparison, with MCP, 14 out of 27 false positives are significant, and 16 out of 23 true positives are significant. With LASSO, 11 out of 27 false positives are significant, and 17 out of 23 true positives are significant. Similar results are obtained for the binary trait. The difference between results in Table 5 and Table 6 (Appendix) is not significant, suggesting that it is sensible to use the quadratic loss for binary trait in GWAS.

6. APPLICATION TO REAL DATA

6.1 Application to heterogeneous stock mice data

We use a dataset publicly available from the Welcome Trust Center. This data resource, which also includes pedigree information, was based on an advanced intercross mating among 8 inbred strains over 50 generations of random mating [17]. It is expected that the use of pseudorandom breeding for over 50 generations should result in an average distance between recombinants of < 2 cM. The average LD, as measured by R² between adjacent markers, is 0.62 [9]. We refer to the original publication for more detailed descriptions [17, 18]. This dataset includes full phenotypic records on 2,202 mice, and each was genotyped for 13,459 SNP markers. The phenotype of interest is the starting weight. After deleting observations with missing phenotypes and alleles with minor allele frequency less than 0.05, there are 1,928 mice and 10,074 SNP markers in 19 autosomes.

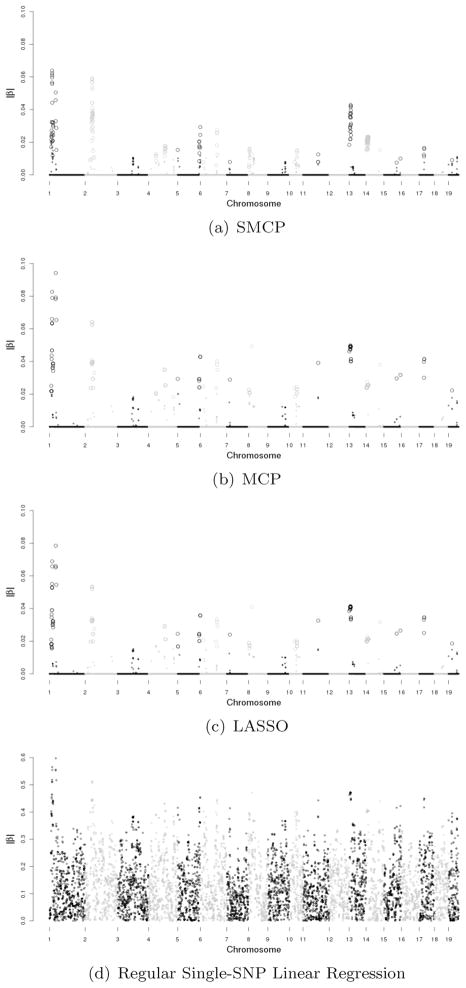
The SNPs on the whole genome are analyzed simultaneously. By using different predetermined numbers of SNPs, we find that 400 SNPs are appropriate for this dataset. For the SMCP method, the value of tuning parameter τ is 2.006 with η = 0.05. For the MCP method (η = 1 and γ = 6), the tuning parameter τ is 0.099. For the LASSO method (η = 1 and γ = ∞), the tuning parameter τ is 0.099. p-values of the selected SNPs are computed using the multi-split method. Fig. 2 shows the Manhattan plots for all three methods plus regular single-SNP linear regression. For SMCP, MCP and LASSO, the large dots represent SNPs with significant estimates, while the small dots are for SNPs with insignificant estimates.

Figure 2.

Genome-wide plot of |β| estimates for heterogeneous stock mice data. (Large dots for significant estimates and small dots for insignificant estimates in SMCP, MCP and LASSO.)

For MCP and LASSO, they identify exactly the same 400 SNPs with slightly different p-values. For SMCP, MCP and LASSO, respectively, 199, 200 and 199 SNPs are significant. The rough pattern of the significant SNPs can be found in Fig. 2. The SNPs that are significant under at least one but not all methods are listed in Table 2.

Table 2.

Significant SNPs (p-value <= 0.05) selected by at least one method for heterogeneous stock mice dataset

Gene	Chr	Position	SNP name	SMCP		MCP		LASSO
				Estimates	p-value*	Estimates	p-value*	Estimates	p-value*
Prdm14	1	13115662	rs13475730	−0.019	0.052	−0.022	0.039	−0.018	0.023
Ncoa2	1	13219271	rs3654377	−0.020	0.052	−0.022	0.039	−0.018	0.023
Ncoa2	1	13373071	rs3655978	0.020	0.052	0.022	0.039	0.018	0.023
Eya1	1	13975254	rs3669485	−0.023	0.025	−0.020	0.061	−0.016	0.033
Eya1	1	14464945	rs3713198	−0.020	0.025	−0.020	0.061	−0.016	0.033
Trpa1	1	14667237	rs13475734	0.017	0.055	0.019	0.083	0.016	0.044
Trpa1	1	14668678	rs3723784	0.013	0.063	0.019	0.083	0.016	0.044
Gm19430	1	35090486	rs3657255	−0.015	0.048	−0.005	0.592	−0.004	0.548
Exosc3	4	45329692	rs4224463	−0.012	0.042	−0.020	0.040	−0.017	0.060
Dcaf10	4	45336647	rs6313392	−0.013	0.042	−0.020	0.040	−0.017	0.060
Shb	4	45488873	rs3665393	0.011	0.050	0.020	0.061	0.017	0.055
Shb	4	45531929	rs3668228	−0.009	0.041	−0.021	0.047	−0.017	0.055
Gm12608	4	89126034	rs13477833	−0.012	0.043	−0.013	0.132	−0.011	0.121
Epb4.1	4	131555056	CEL-4 130248229	0.009	0.073	0.018	0.047	0.015	0.068
Cdk14	5	4805395	rs3666313	0.009	0.065	0.020	0.050	0.017	0.037
Cdk14	5	4858914	rs6190354	−0.010	0.065	−0.020	0.050	−0.017	0.037
Frmd4b	6	97234200	rs3023082	−0.018	0.013	−0.020	0.052	−0.017	0.035
Csmd1	8	16859147	rs13479624	−0.015	0.047	−0.019	0.052	−0.016	0.050
Atg5	10	44026225	rs13480601	−0.009	0.069	−0.018	0.038	−0.015	0.036
Gas7	11	67464648	rs13481080	−0.008	0.048	−0.018	0.069	−0.015	0.072
Usp43	11	67705918	rs6262977	0.008	0.048	0.018	0.069	0.015	0.072

^*Computed using the multi-split method.

6.2 Application to rheumatoid arthritis data

Rheumatoid arthritis (RA) is a complex human disorder with a prevalence ranging from around 0.8% in Caucasians to 10% in some native American groups [1]. Its risk is generally higher in females than in males. Some studies have identified smoking as a risk factor. Genetic factors underlying RA have been mapped to the HLA region on 6p21 [12], PTPN22 locus at 1p13 [2], and CTLA4 locus at 2q33 [13]. Other potential loci include 6q (TNFAIP3), 9p13 (CCL21), 10p15 (PRKCQ), and 20q13 (CD40), which seem to have weaker effects [1].

GAW 16 RA data is from the North American Rheumatoid Arthritis Consortium (NARAC). It is the initial batch of whole genome association data for the NARAC cases (N=868) and controls (N=1,194) after removing duplicated and contaminated samples. After quality control and removing SNPs with low minor allele frequencies, there are 475,672 SNPs over 22 autosomes, of which 31,670 are on chromosome 6.

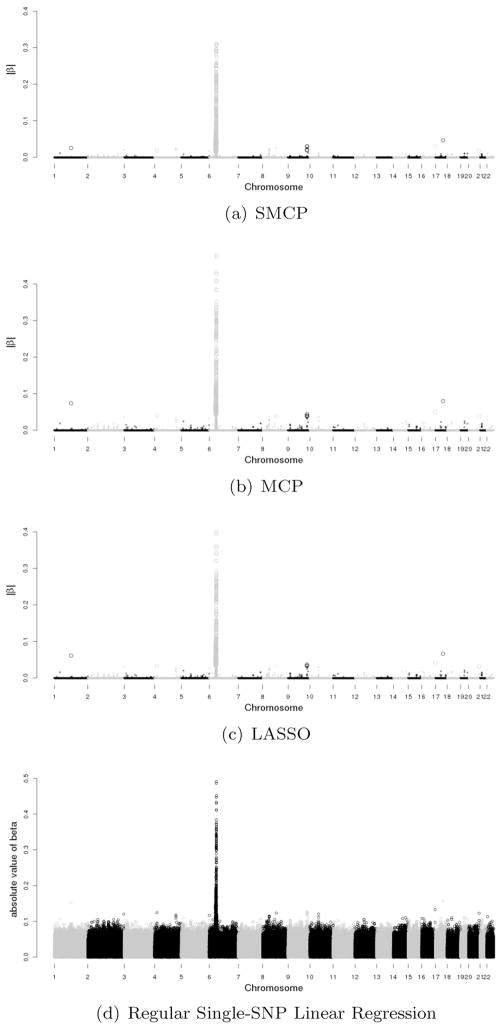
By using different predetermined numbers of SNPs, we find that 800 SNPs are appropriate for this dataset. For SMCP, the tuning parameter τ is 1.861 with η = 0.05. p-values of the selected SNPs are computed using the multi-split method. The majority of SNPs (539 out of 800) selected by SMCP are on chromosome 6, 293 of which are significant with p-values smaller than 0.05. For LASSO, the tuning parameter τ is 0.091. There are 537 SNPs selected on chromosome 6, and 280 of them are significant with p-values less than 0.05. MCP selects the same set of SNPs as LASSO. The estimates of βs obtained from SMCP, MCP, LASSO and regular single-SNP linear regression analysis are presented in Fig. 3. In Fig. 3, the large dots are SNPs with significant estimates, and small dots are for insignificant SNPs. The difference between LASSO and MCP lies in the magnitude of estimates, as MCP may be unbiased under a proper choice of γ, but LASSO is always biased. The two sets of SNPs selected by SMCP and LASSO on chromosome 6 are both in the region of HLA-DRB1 gene that has been found to be associated with RA [12].

Figure 3.

Genome-wide plot of |β| estimates for RA data. (Large dots for significant estimates and small dots for in-significant estimates in SMCP, MCP and LASSO.)

There are SNPs on other chromosomes that are significant (Table 3). Particularly, association with rheumatoid arthritis at SNP rs2476601 in gene PTPN22 has been reported previously [2]. Other noteworthy SNPs include SNP rs512244 in RAB28 region, 4 SNPs in TRAF1 region, SNP rs12926841 in CA5A region, SNP rs3213728 in RNF126P1 region, and SNP rs1182531 in PHACTR3 region. On chromosome 9, 4 SNPs in the region of TRAF1 gene are identified by SMCP and LASSO. One can see from Fig. 3 that MCP produces larger estimates than LASSO, but the SMCP estimates are smaller than those from LASSO. This is caused by the (side) shrinkage effect of the proposed smoothing penalty. In terms of model selection, SMCP tends to select more adjacent SNPs that are in high LD.

Table 3.

Significant SNPs (p-value <= 0.05) selected by the SMCP method on chromosomes other than chromosome 6 for rheumatoid arthritis dataset

Gene	Chr	Position	SNP name	SMCP		MCP		LASSO
				Estimates	p-value*	Estimates	p-value*	Estimates	p-value*
PTPN22	1	114089610	rs2476601	−0.026	6e-05	−0.074	2.0–05	−0.061	2.3e-05
RAB28	4	12775151	rs512244	0.019	0.024	0.040	0.025	0.033	0.021
LOC392232	8	73406911	rs346617	0.026	0.074	0.039	0.045	0.032	0.051
TRAF1	9	120720054	rs1953126	−0.021	0.025	−0.037	0.045	−0.031	0.053
TRAF1	9	120732452	rs881375	−0.030	0.014	−0.040	0.029	−0.033	0.016
TRAF1	9	120769793	rs3761847	0.029	0.014	0.040	0.027	0.033	0.027
TRAF1	9	120785936	rs2900180	−0.019	0.008	−0.044	0.013	−0.037	0.006
CA5A	16	86505516	rs12926841	−0.031	0.002	−0.042	0.002	−0.042	0.002
RNF126P1	17	52478747	rs3213728	0.046	8e-06	0.066	1.4e-06	0.066	1.4e-06
PHACTR3	20	57826397	rs1182531	0.018	0.025	0.032	0.021	0.032	0.021

^*Computed using the multi-split method.

7. DISCUSSION

Penalization is a modern variable selection approach developed to handle “large p, small n” problems. Application of this approach to GWAS is highly anticipated. Compared to traditional GWAS analysis where one SNP is analyzed at a time, penalized methods are able to handle a large collection of SNPs at the same time. In this article, we have proposed a novel SMCP penalty and introduced a penalized regression method suitable for GWAS. A salient feature of this method is that it takes into account the LD among SNPs in order to reduce the randomness often seen in the traditional single SNP analysis. We have developed a coordinate descent algorithm to implement the proposed method. Also, we have applied a multi-split method to compute p-values of selected SNPs.

The proposed SMCP method is different from the fused LASSO. The penalty function for fused LASSO can be written as

$${\lambda }_1\sum _{j=1}^p\mid {\beta }_j\mid +{\lambda }_2\sum _{j=1}^{p-1}\mid {\beta }_{j+1}-{\beta }_j\mid .$$

One apparent difference between SMCP and fused LASSO is in the second penalty term. The SMCP uses the square of the difference of absolute values. In comparison, the fused LASSO uses the absolute value of the difference. Therefore, SMCP is not affected by the choice of reference allele for genotype scoring. But the fused LASSO requires specification of reference alleles for all markers. Second, SMCP explicitly incorporates a measure of LD of adjacent SNPs to only encourage smoothness of the effects of those with high LD. This feature of the penalty is particularly suitable for GWAS. Third, SMCP is computationally efficient as it has an explicit solution when updating β_j in the coordinate descent algorithm. In comparison, no such explicit solution exists for fused LASSO. Its computation is not as efficient as SMCP even using the method proposed by [5]. A referee pointed out that the fusion penalty (absolute value of difference) can be used in the second penalty term. Although we did not think this is appropriate in the current setting, we agree it would be interesting to compare the findings of the SMCP and those of the fused LASSO (or fused MCP). However, a systematic comparison is beyond the scope of this paper. The biggest obstacle is the computational burden in implementing the fused Lasso with a large number of SNP markers.

A thorny issue in handling a large number of SNPs simultaneously is computation. We have used several measures to tackle this issue. We have introduced explicit expressions for implementing the coordinate descent algorithm. This algorithm is stable and efficient in our simulation studies and data examples. For a dichotomous phenotype, we have showed that a marginal quadratic loss function yields a correct estimate of the effect of a SNP. Two important advantages in using the marginal loss (4) as opposed to a joint loss are its convenience in computing over genome and capability of handling missing genotypes, a phenomenon common with high-throughput genotype data. As expression (5) indicates, only c_j needs to be updated for each iteration. Thus, there is no need to read all the data on 22 chromosomes in a computer. The inner products between standardized phenotypes and genotypes are all needed. It makes computing for all SNPs over genome possible. Second, the joint loss function does not allow any missing genotypes. Missing genotypes have to be imputed upfront, incurring extra computation time and uncertainty in imputed genotypes. In contrast, the marginal loss function (4) is not impeded by missing genotypes.

Compared with LASSO and MCP, the proposed SMCP is able to incorporate the consecutive absolute difference into the penalty. Simulation studies show that the SMCP method is superior to LASSO and MCP in terms of the number of true positives and false negative rate.

We have focused on quantitative and dichotomous phenotypes. For dichotomous phenotype, we show that it is reasonable to use a marginal quadratic loss. We expect that covariates and environmental factors, including those derived from principal components analysis based on marker data for adjusting population stratification, can be incorporated in SMCP analysis. Specifically, we can consider a loss function that includes the effects of SNPs and covariate effects based on an appropriate working regression model, then use the SMCP penalty on the coefficients of SNPs. The coordinate descent algorithm for SMCP and the multi-split method for assessing statistical significance can be used in such settings with some modifications.

APPENDIX A. APPENDIX SECTION

A.1 Accommodating case-control data with logistic regression

To accomandate the properties of case-control data, we use the marginal logistic regression with the proposed SMCP penalty.

$$L_n(\mathit{\beta })=-\sum _{j=1}^p\frac{1}{n_j}\sum _{i=1}^{n_j}(y_{ij}\text{log}{p}_{ij}+(1-y_{ij})\text{log}{p}_{ij})+\sum _{j=1}^p\rho (\mid {\beta }_j\mid ;\lambda ,\gamma )+\frac{1}{2}{\lambda }_2\sum _{j=1}^{p-1}{\zeta }_j{(\mid {\beta }_{j+1}\mid -\mid {\beta }_j\mid )}^2,$$ (9)

where $p_{ij}=\frac{e^{{\beta }_{0j}+x_{ij}{\beta }_j}}{1+e^{{\beta }_{0j}+x_{ij}{\beta }_j}}$, (t; λ, γ) is defined in Section 2. Then, quadratic approximation can be applied piecewise to index j by using following equations.

$$\begin{array}{l}{z}_{ij}={\widehat{\beta }}_{0j}+x_{ij}{\beta }_j+\frac{y_{ij}-{\stackrel{\sim }{p}}_{ij}}{{\stackrel{\sim }{p}}_{ij}(1-{\stackrel{\sim }{p}}_{ij})},\\ w_{ij}={\stackrel{\sim }{p}}_{ij}(1-{\stackrel{\sim }{p}}_{ij}).\end{array}$$

The new objective function after quadratic approximation is given as follows.

$$L_n(\mathit{\beta })=\sum _{j=1}^p\frac{1}{2n_j}\sum _{i=1}^{n_j}{w}_{ij}{(z_{ij}-{\widehat{\beta }}_{0j}-x_{ij}{\beta }_j)}^2+\sum _{j=1}^p\rho (\mid {\beta }_j\mid ;\lambda ,\gamma )+\frac{1}{2}{\lambda }_2\sum _{j=1}^{p-1}{\zeta }_j{(\mid {\beta }_{j+1}\mid -\mid {\beta }_j\mid )}^2,$$ (10)

β ₀ can be omitted for linear model by centering the response variable, but it must be included in the model for logistic regression. β₀s can be fitted marginal logistic regression and then fixed in objective function (10). ζ_j s are defined the same as in Section 2. Then algorithm implemented in marginal linear regression with the SMCP penalty can be used to solve the marginal logistic regression with the SMCP penalty.

A.2 Application to rheumatoid arthritis data

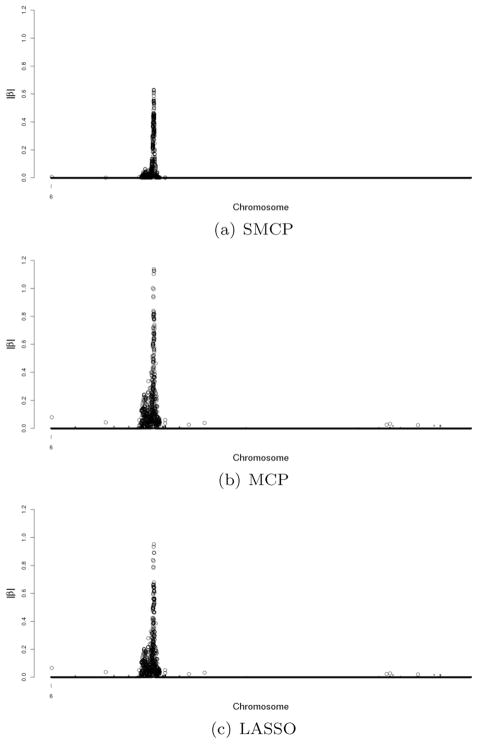
Due to the computational burden, we conduct the analysis for rheumatoid arthritis data only on chromosome 6 by marginal logistic regression. The plots of estimates by the SMCP, the MCP and the LASSO methods are presented in Fig. 4 and their significance estimates are large dots. By cross-sectional comparison with the results in Section 6.2, we found that there are 559 overlapping SNPs by the SMCP metho, in which 293 SNPs are significant. There are 535 overlapping SNPs by the MCP method, in which 293 SNPs are significant. while the LASSO method identifies the same set of SNPs. From simulation result and analysis results in Section 5, we see that despite that the logistic regression is a more natural choice for case-control studies, marginal linear regression can capture the pattern of SNPs’ effect in GWAS. Furthermore, the computational burden prohibit us from conducting genome-wide scan by using marginal logistic regression, but it is possible to conduct it by marginal linear regression.

Figure 4.

Genome-wide plot of |β| estimates for RA data on chromosome 6 by marginal logistic loss function.

Table 4.

List of SNPs selected by the SMCP, the MCP and the LASSO method for a simulated data set with quantitative trait. Recall that the 31 disease-associated SNPs are 2287 – 2298 and 2300 – 2318

SNP	SMCP		MCP		LASSO		Regression
	|β̂|	p-value*	|β̂|	p-value*	|β̂|	p-value*	|β̂|	p-value**
1866			−0.011	1.000	−0.005	1.000	−0.211	1.2E-04
2144	−3.6E-04	1.000	−0.044	0.031	−0.019	0.056	−0.227	3.3E-05
2167			−0.038	0.034	−0.017	0.090	−0.225	4.1E-05
2171	−0.029	0.168	−0.096	1.000	−0.043	1.000	−0.253	3.6E-06
2173	−0.026	0.112	−0.115	1.000	−0.051	1.000	−0.262	1.6E-06
2178	0.001	1.000	0.043	0.015	0.019	0.078	0.227	3.3E-05
2209			0.005	0.080	0.002	0.097	0.208	1.5E-04
2212			0.002	0.080	0.001	0.098	0.207	1.6E-04
2235			0.027	0.050	0.012	0.040	0.219	6.4E-05
2240	0.042	0.013	0.162	0.008	0.072	0.004	0.286	1.5E-07
2241	0.037	0.241	0.038	0.031	0.017	0.030	0.225	4.1E-05
2242	0.052	0.019	0.139	0.012	0.062	0.005	0.274	5.0E-07
2243	0.035	0.193	0.069	1.000	0.031	1.000	0.240	1.2E-05
2269	−0.065	0.015	−0.167	0.014	−0.074	0.005	−0.288	1.2E-07
2270	0.059	0.034	0.097	0.032	0.043	0.021	0.254	3.5E-06
2271	−0.038	0.059	−0.121	0.024	−0.054	0.024	−0.265	1.1E-06
2272	−0.009	0.950	−0.007	0.057	−0.003	0.095	−0.210	1.3E-04
2275			−0.029	1.000	−0.013	1.000	−0.220	6.0E-05
2279	−0.081	0.002	−0.237	1.000	−0.105	1.000	−0.322	2.7E-09
2281	−0.016	0.413	−0.080	1.000	−0.036	1.000	−0.245	7.2E-06
2284	−0.048	0.011	−0.159	0.007	−0.071	0.006	−0.284	1.8E-07
2285	0.039	0.470					0.205	1.9E-04
2286	−0.183	3.0E-04	−0.265	1.000	−0.118	1.000	−0.336	5.1E-10
2287	0.274	3.3E-04	0.271	3.1E-04	0.120	0.001	0.339	3.5E-10
2288	0.287	3.3E-04	0.277	2.7E-04	0.123	0.001	0.342	2.4E-10
2289	−0.352	6.0E-05	−0.412	3.2E-05	−0.183	8.1E-05	−0.409	2.0E-14
2290	0.428	3.1E-11	0.841	1.000	0.374	1.000	0.619	1.6E-34
2291	−0.037	0.187					−0.159	0.004
2293	0.201	4.9E-07	0.524	6.3E-07	0.233	5.1E-06	0.463	1.7E-18
2294	0.190	0.001	0.294	1.1E-04	0.131	0.001	0.351	8.2E-11
2295	−0.121	4.6E-04	−0.252	1.6E-04	−0.112	0.001	−0.330	1.1E-09
2296	0.035	1.000					0.159	0.004
2297	−0.015	0.211	−0.077	0.064	−0.034	0.031	−0.244	8.4E-06
2299	0.054	1.000					0.033	5.5E-01
2300	0.716	1.8E-15	0.643	2.3E-16	0.456	7.2E-15	0.711	4.0E-48
2301	−0.789	2.2E-19	−0.706	8.2E-19	−0.520	1.6E-17	−0.781	7.4E-62
2302	0.718	2.7E-12	0.913	1.4E-13	0.406	1.3E-12	0.655	2.6E-39
2303	−0.401	0.089					−0.191	5.1E-04
2304	−0.615	4.4E-17	−0.681	5.9E-18	−0.494	3.3E-18	−0.753	6.3E-56
2305	−0.531	8.5E-10	−0.762	1.7E-10	−0.339	1.2E-09	−0.580	9.0E-30
2306	0.384	0.290					0.175	0.002
2307	−0.406	1.5E-06	−0.559	1.000	−0.249	1.000	−0.481	6.1E-20
2308	0.237	0.114					0.195	3.8E-04
2309	0.359	6.9E-09	0.695	1.8E-10	0.309	7.3E-10	0.547	3.5E-26
2310	−0.291	3.5E-05	−0.452	1.000	−0.201	1.000	−0.428	8.4E-16
2312	0.153	4.7E-04	0.331	1.000	0.147	1.000	0.369	7.2E-12
2313	0.146	0.092	0.047	1.000	0.021	1.000	0.229	2.9E-05
2314	−0.276	6.6E-05	−0.368	8.8E-05	−0.164	4.1E-05	−0.387	5.4E-13
2315	0.296	6.6E-05	0.368	8.8E-05	0.164	4.1E-05	0.387	5.4E-13
2316	−0.322	3.4E-07	−0.597	1.88E-07	−0.265	1.21E-07	−0.499	1.5E-21
2317	−0.260	0.005	−0.181	0.003	−0.081	0.002	−0.295	5.8E-08
2318	0.228	0.003	0.236	1.000	0.105	1.000	0.322	2.8E-09
2320	0.014	0.735	0.065	0.009	0.029	0.015	0.238	1.4E-05
2321	−0.012	0.992	−0.055	0.009	−0.024	0.018	−0.233	2.1E-05
2337	−0.087	0.002	−0.317	1.000	−0.141	1.000	−0.362	1.8E-11
2363			−0.024	0.047	−0.011	0.054	−0.218	7.1E-05
2371	−0.023	0.035	−0.124	0.023	−0.055	0.005	−0.267	1.0E-06

^*Computed using the multi-split method.

^**Single SNP analysis, not corrected for multiple testing.

^***Empty cells stand for SNPs that are not identified from the model.

Table 5.

List of SNPs selected by the SMCP and the LASSO method for a simulated data set with binary trait. The analysis is based on marginal negative log-likelihood loss. Recall that the 31 disease-associated SNPs are 2287–2298 and 2300–2318

SNP	SMCP		MCP		LASSO		Regression
	|β̂|	p-value*	|β̂|	p-value*	|β̂|	p-value*	|β̂|	p-value**
366			−0.009	1.000	−0.004	1.000	−0.071	0.004
368	−0.001	1.000	−0.045	1.000	−0.020	1.000	−0.075	0.002
506	−0.002	1.000	−0.103	1.000	−0.043	1.000	−0.081	0.001
656	0.001	1.000	0.056	1.000	0.025	1.000	0.077	0.002
932			0.001	1.000	0.001	1.000	0.071	0.005
948			0.020	1.000	0.009	1.000	0.073	0.004
1047			0.009	1.000	0.004	1.000	0.071	0.004
1476			−0.003	1.000	−0.001	1.000	−0.071	0.005
1477			0.025	1.000	0.011	1.000	0.073	0.003
1478			−0.011	1.000	−0.005	1.000	−0.072	0.004
1678	−0.001	1.000	−0.033	1.000	−0.015	1.000	−0.074	0.003
1978	−0.008	1.000	−0.195	0.788	−0.083	0.788	−0.091	2.6E-04
1980	−3.8E-05	1.000	−0.028	1.000	−0.012	1.000	−0.073	0.003
1990	0.005	1.000	0.068	1.000	0.030	1.000	0.078	0.002
2048	0.001	1.000	0.039	1.000	0.016	1.000	0.074	0.003
2283	0.002	1.000					0.060	0.017
2284	−0.030	1.000	−0.108	1.000	−0.047	1.000	−0.082	0.001
2285	0.034	1.000					0.060	0.016
2286	−0.144	0.015	−0.436	0.026	−0.180	0.026	−0.113	4.9E-06
2287	0.150	0.425	0.168	0.720	0.072	0.720	0.088	3.9E-04
2288	0.151	0.354	0.187	0.615	0.080	0.615	0.090	2.9E-04
2289	−0.152	0.218	−0.192	1.000	−0.077	1.000	−0.089	3.6E-04
2290	0.152	1.0E-04	0.751	8.1E-05	0.313	8.1E-05	0.144	4.2E-09
2291	−0.034	1.000					−0.054	0.031
2292	−0.018	1.000					−0.006	0.820
2293	0.065	0.014	0.444	0.013	0.187	0.013	0.116	2.8E-06
2294	0.067	0.126	0.268	0.191	0.117	0.191	0.099	6.2E-05
2295	−0.048	0.629	−0.167	1.000	−0.072	1.000	−0.088	3.9E-04
2296	0.030	1.000					0.061	0.014
2299	−0.097	1.000					−0.021	0.399
2300	0.275	2.0E-04	0.553	0.002	0.238	0.002	0.128	0.000
2301	−0.307	2.3E-06	−0.887	2.3E-06	−0.438	2.3E-06	−0.170	2.4E-12
2302	0.294	1.9E-04	0.684	3.1E-04	0.278	3.1E-04	0.136	3.0E-08
2303	−0.211	1.000					−0.048	0.053
2304	−0.206	1.1E-05	−0.876	1.1E-05	−0.371	1.1E-05	−0.157	1.4E-10
2305	−0.176	0.003	−0.490	0.008	−0.196	0.008	−0.118	1.9E-06
2306	0.131	1.000					0.020	0.421
2307	−0.076	1.000	−0.003	1.000	−0.001	1.000	−0.071	0.005
2308	0.041	1.000					0.053	0.034
2309	0.053	0.117	0.313	0.134	0.130	0.134	0.102	3.7E-05
2310	−0.040	1.000	−0.148	1.000	−0.061	1.000	−0.085	0.001
2316	−0.005	0.753	−0.216	0.591	−0.086	0.591	−0.091	2.4E-04
2329			0.003	1.000	0.001	1.000	0.071	0.005
2337	−0.016	0.328	−0.299	0.253	−0.113	0.253	−0.097	9.8E-05
2360	−0.002	1.000	−0.055	1.000	−0.024	1.000	−0.076	0.002
2362			−0.028	1.000	−0.012	1.000	−0.073	0.003
2461	0.001	1.000	0.049	1.000	0.020	1.000	0.075	0.003
2550	0.009	1.000					0.068	0.007
2551	0.038	0.460	0.269	0.514	0.100	0.514	0.093	1.7E-04
2552	−0.033	1.000	−0.134	1.000	−0.057	1.000	−0.085	0.001
2553	0.029	1.000	0.146	1.000	0.062	1.000	0.086	0.001
2554	−0.015	1.000					−0.056	0.024
2912	0.001	1.000	0.031	1.000	0.014	1.000	0.074	0.003
3140	0.002	1.000	0.066	1.000	0.028	1.000	0.077	0.002
3329	0.015	1.000	0.117	1.000	0.050	1.000	0.083	0.001
3388	0.001	1.000	0.045	1.000	0.020	1.000	0.075	0.002
3620	0.001	1.000	0.053	1.000	0.023	1.000	0.076	0.002
4018	0.006	0.576	0.243	0.598	0.096	0.598	0.094	1.5E-04
4078	0.002	1.000	0.059	1.000	0.026	1.000	0.077	0.002
4745			−0.007	1.000	−0.003	1.000	−0.071	0.004
4877			0.007	1.000	0.003	1.000	0.071	0.004

^*Computed using the multi-split method.

^**Single SNP analysis, not corrected for multiple testing.

^***Empty cells stand for SNPs that are not identified from the model.

Table 6.

List of SNPs selected by the SMCP and the LASSO method for a simulated data set with binary trait. The analysis is based on marginal least-square loss. Recall that the 31 disease-associated SNPs are 2287–2298 and 2300–2318

SNP	SMCP		MCP		LASSO		Regression
	|β̂|	p-value*	|β̂|	p-value*	|β̂|	p-value*	|β̂|	p-value**
366			−0.002	1.000	−0.002	1.000	−0.071	0.004
368	−0.002	1.000	−0.012	1.000	−0.010	1.000	−0.075	0.002
506	−0.005	1.000	−0.025	1.000	−0.021	1.000	−0.081	0.001
656	0.002	1.000	0.015	1.000	0.012	1.000	0.077	0.002
932			3.4E-04	1.000	2.9E-04	1.000	0.071	0.005
948	0.001	1.000	0.005	1.000	0.004	1.000	0.073	0.004
1047			0.002	1.000	0.002	1.000	0.071	0.004
1476	0.000	1.000	−0.001	1.000	−0.001	1.000	−0.071	0.005
1477	0.001	1.000	0.006	1.000	0.005	1.000	0.073	0.003
1478	−0.001	1.000	−0.003	1.000	−0.002	1.000	−0.072	0.004
1678	−0.002	1.000	−0.009	1.000	−0.007	1.000	−0.074	0.003
1978	−0.013	0.240	−0.049	0.230	−0.041	0.230	−0.091	2.6E-04
1980	−0.001	1.000	−0.007	1.000	−0.006	1.000	−0.073	0.003
1990	0.008	1.000	0.018	1.000	0.015	1.000	0.078	0.002
2048	0.003	1.000	0.009	1.000	0.008	1.000	0.074	0.003
2284	−0.009	1.000	−0.028	1.000	−0.023	1.000	−0.082	0.001
2285	0.005	1.000					0.060	0.016
2286	−0.076	0.006	−0.102	0.006	−0.085	0.006	−0.113	4.9E-06
2287	0.049	0.250	0.043	0.442	0.036	0.442	0.088	3.9E-04
2288	0.051	0.222	0.047	0.282	0.039	0.282	0.090	2.9E-04
2289	−0.060	0.206	−0.044	0.328	−0.037	0.328	−0.089	3.6E-04
2290	0.093	0.001	0.177	0.001	0.147	0.001	0.144	4.2E-09
2291	−0.003	1.000					−0.054	0.031
2293	0.051	0.028	0.109	0.028	0.091	0.028	0.116	2.8E-06
2294	0.049	0.153	0.069	0.259	0.058	0.259	0.099	6.2E-05
2295	−0.028	0.187	−0.042	0.500	−0.035	0.500	−0.088	3.9E-04
2296	0.007	1.000					0.061	0.014
2300	0.122	0.009	0.138	0.009	0.115	0.009	0.128	2.1E-07
2301	−0.148	4.2E-05	−0.240	4.2E-05	−0.200	4.2E-05	−0.170	2.4E-12
2302	0.126	0.003	0.158	0.003	0.131	0.003	0.136	3.0E-08
2303	−0.040	0.707					−0.048	0.053
2304	−0.090	0.001	−0.207	0.001	−0.172	0.001	−0.157	1.4E-10
2305	−0.060	0.027	−0.113	0.027	−0.095	0.027	−0.118	1.9E-06
2306	0.007	1.000					0.020	0.421
2307	−0.001	1.000	−0.001	1.000	−0.001	1.000	−0.071	0.005
2309	0.030	0.081	0.076	0.081	0.064	0.081	0.102	3.7E-05
2310	−0.024	0.313	−0.035	0.689	−0.029	0.689	−0.085	0.001
2316	−0.010	0.299	−0.050	0.214	−0.041	0.214	−0.091	2.4E-04
2329			0.001	1.000	0.001	1.000	0.071	0.005
2337	−0.022	0.238	−0.063	0.238	−0.052	0.238	−0.097	9.8E-05
2360	−0.005	1.000	−0.014	1.000	−0.012	1.000	−0.076	0.002
2362	−0.002	1.000	−0.007	1.000	−0.006	1.000	−0.073	0.003
2461	0.002	1.000	0.011	1.000	0.010	1.000	0.075	0.003
2550	0.003	1.000					0.068	0.007
2551	0.031	0.172	0.055	0.172	0.046	0.172	0.093	1.7E-04
2552	−0.022	0.639	−0.034	1.000	−0.028	1.000	−0.085	0.001
2553	0.018	0.768	0.037	0.902	0.031	0.902	0.086	0.001
2912	0.003	1.000	0.008	1.000	0.007	1.000	0.074	0.003
3140	0.004	1.000	0.016	1.000	0.014	1.000	0.077	0.002
3329	0.016	1.000	0.029	1.000	0.024	1.000	0.083	0.001
3388	0.003	1.000	0.012	1.000	0.010	1.000	0.075	0.002
3620	0.002	1.000	0.013	1.000	0.011	1.000	0.076	0.002
4018	0.011	0.124	0.057	0.124	0.047	0.124	0.094	1.5E-04
4078	0.004	1.000	0.015	1.000	0.013	1.000	0.077	0.002
4745			−0.002	1.000	−0.001	1.000	−0.071	0.004
4877			0.002	1.000	0.002	1.000	0.071	0.004

^*Computed using the multi-split method.

^**Single SNP analysis, not corrected for multiple testing.

^***Empty cells stand for SNPs that are not identified from the model.

A.3 Application to dominant model with heterogeneous stock mice data

The proposed approach can be implemented to dominant and recessive models as well as additive model described in Section 2 to Section 6. We choose predetermined number to be 400 for the SMCP, the MCP and the LASSO methods. The multi-split method is used to evaluate the significance of the selected SNPs. The manhattan plots for all three methods are shown in Fig. 5. The large dots stand for SNPs with significant multi-split p-values while small dots for insignificant SNPs.

Figure 5.

Genome-wide plot of |β| estimates for heterogeneous stock mice data by dominant genetic model.