Visualizing Simulated Electrical Fields from Electroencephalography and Transcranial Electric Brain Stimulation: A Comparative Evaluation

Abstract

Electrical activity of neuronal populations is a crucial aspect of brain activity. This activity is not measured directly but recorded as electrical potential changes using head surface electrodes (electroencephalogram - EEG). Head surface electrodes can also be deployed to inject electrical currents in order to modulate brain activity (transcranial electric stimulation techniques) for therapeutic and neuroscientific purposes. In electroencephalography and noninvasive electric brain stimulation, electrical fields mediate between electrical signal sources and regions of interest (ROI). These fields can be very complicated in structure, and are influenced in a complex way by the conductivity profile of the human head. Visualization techniques play a central role to grasp the nature of those fields because such techniques allow for an effective conveyance of complex data and enable quick qualitative and quantitative assessments. The examination of volume conduction effects of particular head model parameterizations (e.g., skull thickness and layering), of brain anomalies (e.g., holes in the skull, tumors), location and extent of active brain areas (e.g., high concentrations of current densities) and around current injecting electrodes can be investigated using visualization. Here, we evaluate a number of widely used visualization techniques, based on either the potential distribution or on the current-flow. In particular, we focus on the extractability of quantitative and qualitative information from the obtained images, their effective integration of anatomical context information, and their interaction. We present illustrative examples from clinically and neuroscientifically relevant cases and discuss the pros and cons of the various visualization techniques.

1. Introduction

In this work, we show the value of several, common visualization methods using three well chosen and neuroscientifically relevant examples where electrical fields play a significant role. We are convinced that visualization can help to gain deeper insights into volume conduction phenomena. Those phenomena are often only statistically describable, and, at best, investigated by standard visualization techniques. Further, we want to contribute with this work to approach an answer to the question: “What aspects of visualization are helpful regarding electrical fields in neuroscientific research?”.

We structured our work in sections as following. First, we introduce noninvasive neuroscientific techniques (electroencephalography (EEG) and transcranial direct current stimulation (tDCS)) that are relevant in this work and discuss visualization in this context. In the current work, tDCS was chosen exemplarily as a representative of a family of electric brain stimulation techniques, like transcranial alternating current stimulation (tACS), transcranial random noise stimulation (tRNS), transcranial electrical stimulation (TES) (Paulus, 2011; Ruffini et al., 2013) that employ scalp surface electrodes to inject electric currents. Second, we identify three generic criteria to evaluate visualization techniques in neuroscience, introduce common visualization techniques and explain their basic working principles. Third, we describe three clinically relevant examples to evaluate visualization methods. Fourth, we present visualization results and discuss the findings. Fifth, we conclude our work and summarize general advantages and disadvantages of standard visualization techniques.

1.1. Electroencephalography (EEG)

Noninvasive mapping of neuronal activity is important for a better understanding of human brain function. In clinical practice, for example, the mapping is essential for the diagnosis of neurodegenerative diseases and the identification of epileptogenic brain tissue (Rullmann et al., 2009). Electroencephalography (EEG) is a noninvasive technique that is directly sensitive to the electrical activity of neuronal populations, and therefore well suited to observe normal and pathological brain function in humans. Recording electrodes are placed on the head surface and pick up potential differences caused by Ohmic return currents, which are driven by electromotive forces in and around active neuronal areas. Electric flow fields mediate between those neural sources and the measured EEG. These fields are embedded in a very complicated volume conductor, the human head, which features many different structures of varying electrical properties (conductivities). Both the prediction of measurements from known sources (forward problem) and the estimation of the source locations from measurements (source reconstruction) involve modeling these fields. The accuracy and precision of these estimations depend on the accuracy of the head modeling, which, in the most general case, requires a voxelwise description of inhomogeneous and anisotropic conductivity values as well as a reasonable sampling of the tissue boundaries. For more information concerning head modeling and source reconstruction (Wendel et al., 2009).

In order to gain insights into the complicated relationship between neural activity and measured EEG, visualization of electrical fields is of great value. It allows assessing, in one glance, which features of the head exercise a large influence and therefore need to be modeled in greater detail. Visualization can also help to assess the effect of certain modeling errors and simplifications. Moreover, it can show, in a very demonstrative fashion, how pathological anomalies, such as holes in the skull, influence the way EEG reflects brain activity. One important prerequisite for field visualization is that the electrical field is explicitly computed within the three-dimensional head volume, using, for example, the finite element or the finite difference method (Bertrand, 1991; Dannhauer et al., 2011; Fuchs et al., 2007; Hallez et al., 2008; Marin et al., 1998; Rullmann et al., 2009; Schimpf et al., 2002; van den Broek et al., 1998; Wolters, 2003).

1.2. Transcranial direct current stimulation (tDCS)

Transcranial direct current stimulation (tDCS) is a noninvasive technique to modulate neural brain activity (e.g., Lozano and Hallett, 2013; Meideiros et al., 2012; Nitsche et al., 2008a; Utz et al., 2010) by injecting low amplitude direct currents through surface electrodes. tDCS has been known for over a century, but has recently been rediscovered as a promising tool to support a wide range of clinical applications (Boggio et al., 2006; Brunoni et al., 2012; Flöel, 2014; Kuo et al., 2014; Nitsche and Paulus, 2009; Schjetnan et al., 2013). Moreover, it has been successfully applied in basic and cognitive neuroscience research (e.g., Kalu et al., 2012; Wirth et al., 2011). In this technique, frequently, large rectangular patch electrodes are used (normally 25 – 35 cm², e.g., Nitsche et al., 2008b) in experimental settings and placed according to accepted EEG standards (e.g., 10 – 20). In some rare cases also smaller electrodes are employed in experiments (Caparelli-Daquer et al., 2012; Edwards et al., 2013). To study the impact of modeling tDCS for experimental settings, electrical current density is one of the main parameters to determine physiological effects for brain and other head tissues. Visualization of tDCS simulations (e.g., as current density plots, Wagner et al., 2014) can be helpful for assessing those effects as well as for understanding the way particular brain areas are stimulated depending on electrode montage and design, head geometry (e.g., skull thickness), and other factors.

1.3. Visualization of electrical fields

In general, when considering head modeling in EEG/MEG/tDCS analysis, the significance of certain modeling issues or particular features in the biological tissues (e.g., holes in the skull) are mostly assessed by visualizing and quantifying their final consequences, such as changes in surface potentials or mislocalization of dipolar sources (e.g., Dannhauer et al., 2011). These consequences are, however, mediated by the electric flow field in the head. Hence, visualizing the direct effects of above mentioned features in models or real head anatomy in terms of current flows and electrical potentials throughout the head might provide more direct insight into the nature of that relationship.

Generally, the literature on volume current visualization regarding EEG and tDCS (Berger, 1933; Nunez, 1981; Sharbrough et al., 1991) is relatively scarce. Often, visualization of electrical currents is based on simple voxelwise current density visualizations represented graphically as cones, arrows (Salvador et al., 2010; Shahid et al., 2013; Wagner et al., 2014), or as current density magnitudes using colormaps (Shahid et al., 2013; Wagner et al., 2014). Visualizations with more advanced techniques, such as streamlines, are rare in the EEG- (e.g., Wolters et al., 2006) or tDCS-related literature (e.g., Im et al., 2008; Park et al., 2011; Sadleir et al., 2012). Characterization of visualization methods for local or global examples to evaluate visualization methods and applicability for certain tasks and domains has not yet been analyzed sufficiently. Wolters et al. (2006) (for EEG) as well as Bangera et al. (2010) (for tDCS) demonstrated the impact of white matter anisotropy and highly conducting cerebrospinal fluid (CSF) onto volume currents by computing streamlines using line integral convolution (LIC, Cabral and Leedom, 1993). Very closely related to this paper is the work (Tricoche et al., 2008), where several advanced vector field methods are shown in the context of bioelectric fields for EEG. In most existing publications, volume current visualization is not the main focus, and visualization procedures are not used systematically to investigate the effect of features in real biological tissue (e.g., skull holes), assumptions in volume conductor models (e.g., modeling the CSF or not, taking into account anisotropy), or experimental settings (e.g., electrode montages). Such studies might help to better understand effects that otherwise can be assessed only by their final results, i.e., simulated sensor readings or source localization results (e.g., Dannhauer et al., 2011, 2013; Lanfer et al., 2012).

Visualization of electrical flow fields in three dimensions can be based on either the scalar electrical potential or on the vector-valued current flow. In both cases, several principal techniques are available (see Section 2). The aim of this work is to demonstrate not only the advantages of certain methods, but also their drawbacks, as the applicability of these methods differ for each case, domain, and desired analysis. To achieve this goal, we will define a set of concise criteria for the usefulness of visualization techniques in the context of neuroscience and apply these to the evaluation of the presented algorithms.

2. Visualization Algorithms

In the last decade, visualization made a big step towards interactive and visually appealing methods, fuelled by the rapid development of affordable graphics hardware and computing devices. These developments made advanced visualization available also to neuroscience. It is important to stress that the scientific benefit of using visualization techniques is not just a matter of “pretty images”, but lies in the extent to which these methods actually improve the perception, exploration, and interpretation of scientific results. Here, we identify three criteria that convey whether and to what extent a visualization technique is useful to a neuroscientist.

1. Comparability - The images produced by one method need to be comparable in a quantitative way over a series of subjects or time series. Colormaps play an especially important role in this context.

2. Anatomical Context - Anatomy plays an important role for exploring and navigating through the data. Without this structural context, visualized functional data loses its anatomical embedding.

3. Interactivity - Interactivity represents the interaction of the user with the data and its visualization. Interactivity depends on the speed with which visual feedback to a user action can be produced. Due to the large amount of data and the required detail of visualization, hardware and software limits can be quickly exceeded.

In this section, we briefly present standard visualization techniques in the light of the above criteria and describe our particular implementations, which are available in OpenWalnut (Eichelbaum et al., 2013b).

2.1. Slice View

The simplest, yet essential way of visualizing volume data is based on mostly orthogonally oriented slices cutting the data domain, often in axial, coronal, and sagittal directions. These slices in three-dimensional space are used to merge multiple colormaps representing anatomy as well as functional data. This way, comparability in a multi-subject or time-dependent context is ensured and navigation through complicated scenarios is greatly facilitated. It is important to note in this context that an essential prerequisite of comparability is proper image registration (e.g., Lohmann et al., 2001; Smith et al., 2004).

2.2. Isosurfaces

In the context of bioelectric fields and their exploration, isosurfaces can help to gain insight into the propagation of the field through head tissues in conjunction with anatomical structures. Isosurfaces can be computed from scalar potential fields, such as electrical potentials. They describe a surface in the field, where the values are equal to a userdefined, so-called isovalue. This concept allows visualization of value distributions inside the three-dimensional data field. Isosurfaces derived from electrical fields are normally used to understand the propagation of the field in a volume.

Many methods are currently available to create isosurface renderings. Most commonly known is the marching cubes algorithm (Lorensen and Cline, 1987; Nielson and Hamann, 1991). The marching cubes algorithm works on the cell grid, which can be seen as the dual grid of the original voxel grid. Each cell is defined by eight neighboring voxels, forming the cell’s corners. The algorithm classifies each corner of each cube according to whether the value is smaller or larger than the desired isovalue. This way, the algorithm can check whether a part of the isosurface cuts the cube. If this is the case, marching cubes draw this surface part, depending on the inside-outside-configuration of each corner of the current cube. However, the native marching cubes algorithm might be too slow to fulfill the interactivity criterion. Therefore, many optimizations have been developed. These optimized methods make use of additional data structures to speed up mesh creation in marching cubes. Well known examples are octrees (Wilhelms and Van Gelder, 1992), interval trees (Cignoni et al., 1997), and a technique called span-space optimization (Livnat et al., 1996). By now, many approaches for isosurface rendering are available that exploit the calculation power of modern graphics processing units (GPU) and create isosurface renderings directly by ray-casting on the GPU (Knoll et al., 2009a,b; Wald et al., 2005).

Here, we use a ray-casting-based approach in order to ensure interactive frame rates and thereby allow direct modification of the isovalue with surface adaptation in real time. The underlying principle is to render the bounding box geometry (the so-called proxy geometry) representing the data volume. On this proxy geometry, ray-casting is performed for each rendered pixel on the three-dimensional data domain, which is stored as a three-dimensional memory block. In other words, a ray is shot into the data volume for each pixel. If the ray hits the surface with the desired isovalue, the algorithm stops for the particular pixel and further lighting and coloring can be applied.

2.3. Direct Volume Rendering

Another important visualization technique is direct volume rendering (DVR), which is able to reveal features in a three-dimensional context and makes them spatially more perceivable. To achieve the volume rendering, the algorithm first needs a transfer function, which assigns a color and a transparency to each voxel of the dataset. Given this, the DVR algorithm sends a virtual ray for each pixel on screen into the data volume. Along each ray, the colors of each intersected voxel are composited using the transparencies, provided by the transfer function. This process finally defines the pixel’s color on screen. An extensive description of this technique and its possible optimizations can be found in literature (e.g., Engel et al., 2006). Due to its ability to show whole volumes of interest, the DVR technique is widely used for visualizing three-dimensional imaging data, such as MRT and CT images.

One of the greatest challenges of DVR is the transfer function design process, which can be complicated, even for experienced users. Therefore, many automatic and semi-automatic transfer function techniques have been developed (e.g., Maciejewski et al., 2009). In this paper, however, we use manually selected transfer functions.

2.4. Streamlines and Explorative Tools

In flow visualization, streamlines play an important role in visualizing directional information. Basically, the streamline describes the trajectory of a particle within a vector field and can be calculated by specifying seed points. From each of those seed points, the vector field values are used to move one step towards the vector direction. This is done in an iterative fashion for each new point until a certain stop-criterion is reached. Usually, advanced step and error estimation techniques are used to achieve numerically accurate streamlines. For a more comprehensive overview, see Granger (1995).

In the current work, we calculate streamlines using a fifth-order Runge-Kutta approach (as in Dormand and Prince, 1980) with 100,000 random seed points in the entire volume. For validation, we compare results from different runs with randomly initialized seed points. Other seeding schemes, such as spherical seeding around the source, yield similar results in our case because of the properties of the electric flow field, where all paths of the field start and end at field singularities.

For the streamline rendering, we used a combination of quad-strip-based tubes (Merhof et al., 2006) and illuminated lines (Mallo et al., 2005) with proper ambient shading (Eichelbaum et al., 2013a) for improved perception of structure. The idea is to render camera-oriented quad-strips instead of line-strips to emulate tubular streamlines. The illusion of a continuous tube can be achieved by adding a quadratic intensity gradient perpendicular to the tangential direction. This approach creates the effect of having cylindrical tubes at each line segment that also reduces computational complexity while having a realistic visual appearance. We combined this approach with per-pixel illumination, which creates an additional cue of line orientation in space. Furthermore, we used directional standard coloring, where the absolute components of tangent vectors are interpreted as red-green-blue (RGB) color triples (red: left-right, green: back-front; blue: bottom-top). This coloring is common in medical visualization and helps users to grasp the local orientation of the line in space.

2.4.1. Streamline Selection and Clipping

Dense streamlines generate an unwanted occlusion problem. Selective rendering of streamlines is a common way to overcome this problem. Basically, there are two options: selection and clipping. Selection is a tool that allows removing whole streamlines, which match a certain criterion. This criterion can be defined either automatically or manually. A commonly known selection mechanism involves dynamic queries using multiple regions of interest (ROI, see Akers et al., 2004), which were originally developed for the exploration of white matter pathways in the human brain, where it is possible to logically combine several cuboid regions in order to select white matter pathways. The query describes spatial features, such as “x is in region of interest” and “x is not in region of interest”. This way, a very fine-grained selection of streamlines can, in principle, be accomplished. However, in many cases a complex combination of several ROIs would be needed to get the desired result. Unlike automatic selection methods, ROI-based approaches can potentially be combined with general or patient-specific knowledge about anatomical structures and abnormalities. Thereby, the user can directly explore electric fields for particular anatomical features.

In contrast to selection, clipping removes all occluding parts of a rendered scene to allow direct sight onto otherwise occluded parts of the data. This process is usually accomplished with clipping planes, which can be placed and oriented arbitrarily and cut the space into two half-spaces, one visible and one invisible. Alternatively, it is possible to use anatomical structures as clipping surfaces, such as the cortical or inner bone surface. Clipping surfaces are typically used whenever no useful selection criteria can be defined or too many streamlines occlude the interesting, inner, part of the ROI.

2.4.2. Local Opacity and Coloring

As pointed out above, visualization of all streamlines makes it impossible to understand the complete structure of the electrical field due to occlusion. By using transparency, the occluded parts of the streamlines can also help to attain a more volumetric impression. This technique allows rendering of all streamlines at the same time, which clarifies the three-dimensional structure of the field. Similar to direct volume rendering, a transfer function is needed to map each point on a streamline to its color and transparency values. Again, the design of these transfer functions can be time consuming and application specific. Basically, we found two transfer functions very beneficial for our applications. Firstly, the curvature of the field can be mapped to transparency in a suitable way. Curvature models the angle between two consecutive tangents on the streamline (Weinkauf and Theisel, 2002). Using these coloring schemes produces a volumetric impression of the streamlines and emphasizes areas with many local changes (high curvature). Secondly, interesting results can be obtained by using transfer functions, which incorporate anatomical information. In particular, portions of streamlines are highlighted by coloring if they are located within certain anatomical structures of interest, such as the skull or a target region for tDCS.

2.5. Line Integral Convolution

Line integral convolution (LIC, Cabral and Leedom, 1993; Stalling and Hege, 1995) is one of the most widely used techniques in flow visualization. LIC uses a three-dimensional vector field of a flow to create Schlieren-like (i.e., having a streaky, directional texture) patterns on a given surface. The direction that is depicted by the Schlieren-like patterns will always be orthogonal to the direction of isolines, making LIC represent the directions of the largest change in the field.

To generate a LIC rendering, one has to define a two-dimensional domain (i.e., a surface) within the vector field. On this surface, the LIC algorithm initializes random points, yielding a white noise texture. The term “texture” hereby refers to the two- or three-dimensional memory block on a graphics card, which can be used for mapping surface structure to the currently rendered geometry. The LIC algorithm then starts a streamline at each texel (texture pixel) until each texel is either the seed point of a streamline or is intersected by another streamline. With a streamline given on each texel, the LIC renderer smears the original white-noise texture along each streamline using a rectangular smoothing filter. For a more detailed description, please refer to the literature (Cabral and Leedom, 1993; Stalling and Hege, 1995).

Unfortunately, the originally proposed LIC approach can be computationally expensive, which is undesirable for most interactive applications. For highest performance in terms of interactivity, we implemented the LIC approach on the GPU. The technique we employed is similar to other image-space-based LIC techniques (Grabner and Laramee, 2005; Laramee et al., 2003, 2004) and provides the interactive performance needed for exploring the data, which is not possible with standard implementations. Another advantage of this approach is the ability to map LIC textures to arbitrary surfaces without losing performance. In order to compute the Schlieren-effect on the GPU, the vector field is projected to screen space, and so is the initial noise texture on a surface. In the following step, the projected surface and vector field are smeared directly, by using several steps of Euler integration for each pixel. In other words, the GPU-based LIC algorithm does not compute whole streamlines, but uses only fragments of the streamlines. This implementation creates a similar effect as the classical LIC, but is computationally less expensive. A main drawback of LIC is its intrinsic two-dimensionality. In three-dimensional space, LIC-like methods would have to deal with occlusion, which might be possible to solve to a certain degree using transparency (Grabner and Laramee, 2005).

3. Application Cases

In the following section we will describe three neuroscientifically relevant applications for electrical field visualization in the human head. The first two examples deal with the electrical modeling of the human skull in terms of volume conduction. The skull, with its very low conductivity, is the major obstacle for Ohmic currents on their way between sources and EEG electrodes. Hence, the correct modeling of the skull is of major importance for EEG-based source reconstruction (e.g., Dannhauer et al., 2011) and also for tDCS forward modeling (e.g., Datta et al., 2010; Suh et al., 2012; Wagner et al., 2014). Visualizing the influence that different aspects of skull modeling have on the electric flow field can provide important insights into the relationship between neural activity and EEG readings, as well as elucidate the impact of errors and simplifications on modeling accuracy (e.g., Wagner et al., 2014). Here, we will first visualize the effect of a hole in the skull, for example due to injury or surgery. For this purpose, we use a finite element model of a human head (Lanfer et al., 2012). In the second case, we investigate how the intact skull can be modeled with various levels of detail (Dannhauer et al., 2011). Skull modeling has also been of general interest in recent tDCS literature (e.g., Datta et al., 2010; Rampersad et al., 2013). For all simulated volume currents, in the first to examples (EEG), the Saint Venant source model (linear basis functions, transfer matrix approach, Rullmann et al., 2009; Dannhauer et al., 2011) was used, which is implemented in SimBio/NeuroFEM toolbox (Delevoper-Group-SimBio, 2009). The third application evaluates the visualization of electrical currents based on an electrode placement common in tDCS settings. The forward solution for tDCS was computed using software implemented in the SCIRun package (Dannhauer et al., 2012).

3.1. Modeling a Hole in the Skull

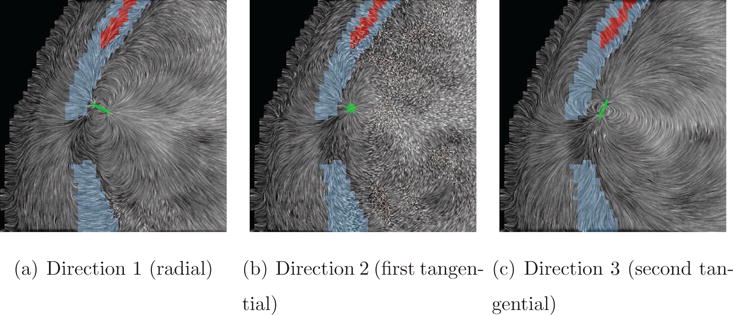
In clinical practice, EEG is a widely used tool to investigate and monitor brain function. It can be utilized, for example, in the treatment of epileptic patients in order to investigate and localize epileptic seizures (Rullmann et al., 2009). The treatment of those patients often involves surgery, where epileptogenic and tumorous brain tissue is removed. In many cases, several surgeries have to be performed to finally remove all epileptogenic tissues, leading to significant differences in volume conduction due to the removed tissue and remaining skull holes. It is still not entirely clear how the EEG generated by differently oriented and positioned electrical current sources is affected by skull holes in their vicinity. Therefore, we use all the previously described visualization techniques (previous section) to investigate local and global changes of volume conduction in the presence of a skull hole (denoted Skull-Hole-Model). The impact of the skull hole is evaluated with regard to the direction to which a source near the hole is pointing (Direction 1: perpendicular to skull surface; Direction 2 and Direction 3: tangential). Instead of placing the current source directly underneath the hole, we chose the slightly more interesting case in which the dipole is placed near the hole such that one of the two tangential directions (Direction 3) has a larger component pointing towards the hole than the other one. It is well known that the direction of a current source has a major impact on scalp potential distributions - in fact, it is more important than the location of the source. If source directions are known (cortical surface constraint, Lin et al., 2006) from anatomy, e.g., derived from MRI, the solution space can be reduced to improve source localization. Visualization can make a contribution to better constraint dipole locations in source localization problems.

The Skull-Hole-Model (Lanfer et al., 2012) comprises 10 tissue types with different isotropic conductivities: scalp, muscle, fat, soft tissue (e.g., eyes), soft bone, hard bone, air, cerebrospinal fluid, gray matter, and white matter. All generated field differences are computed by subtracting the electrical field of the Skull-Hole-Model from that of the reference model (without hole).

3.2. Modeling the layered structure of the skull

In general, head modeling involves certain simplifications. These simplifications are motivated by the need to keep calculations tractable and by the limited availability of information, for example, on tissue conductivities. The skull comprises three layers of different conductivities: two outer layers of hard bone and, sandwiched between them (Sadleir and Argibay, 2007), a layer of soft bone (not always present, see Figure 1). This fact can be accounted for by different models (for more details, see Dannhauer et al., 2011). Here we explore the following possibilities: (i) modeling three layers of bone, using measured conductivity values from the literature (Akhtari et al., 2002); (ii) assuming a single homogeneous isotropic conductivity using a standard value from the literature (σ_{hard/soft bone} = 0.0042 S/m); (iii) assuming a single homogeneous isotropic conductivity, determined by fitting an optimal isotropic conductivity estimate to the three-layer model (σ_{hard/soft bone} = 0.01245 S/m) using a bisection method within the range of hard (σ_{hard bone} = 0.0064 S/m) and soft bone (σ_{soft bone} = 0.0268 S/m) conductivity (see more details in Dannhauer et al. (2011) and review subject 3, IH model). The terms soft and hard skull bone are also known in the literature as spongy and compact bone (e.g. in Dannhauer et al., 2011). The skull modeling using an isotropic conductivity of σ_{hard/soft bone} = 0.0042 S/m has been common practice for decades. Dannhauer and colleagues (Dannhauer et al., 2011), in accordance with earlier work (Oostendorp et al., 2000), could show that a value of 0.01 S/m is more appropriate. Since 0.0042 S/m still appears sporadically in default settings in EEG (e.g., Li and Wen, 2008) and older software packages for source localization, we compared its effect in a qualitative manner. The rest of the head, both inside and outside the skull, was modeled as homogeneous compartments (skin: 0.43 S/m, brain: 0.33 S/m). For this model (referred to as the 3-Layer-Model), we demonstrate the use of the LIC and streamline approaches.

Figure 1. Visualization of skull bone plates from MRI.

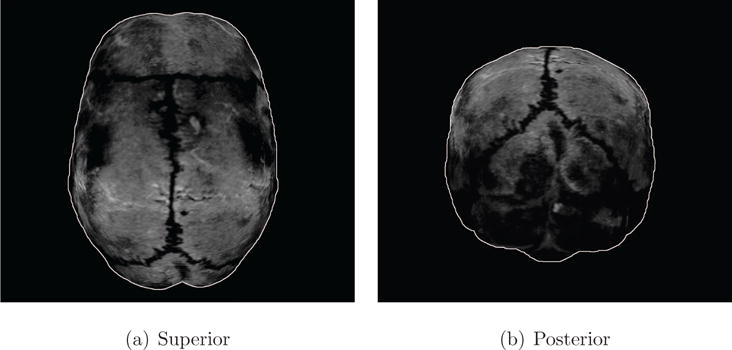
Human skull bone tissues, 2 mm below the skull surface based on a T1-weighted magnetic resonance image is shown here. The coronal, sagittal, and lambdoidal sutures appear darker (zig-zag-pattern). The sutures join skull bone plates together. The figure highlights soft bone tissues (brighter areas in figure) within skull plates that are separated by sutures. A white outline is added to clearly show the object boundaries.

3.3. Stimulating of brain tissue using tDCS

Up to this point it has not been well understood how experimentally applied tDCS stimulation affects tissues of the human head. In consequence, the exact impact of electrode montages, parameterization of electrical stimulation, and volume conductor properties in tDCS is still subject to research (for more details see below). In clinical environments stimulation parameters are often based on examples taken from the literature and might not be always ideal for individual subjects (Minhas et al., 2012; Datta et al., 2012). Furthermore, information from literature is limited to certain stimulation setups and therefore new experimental protocols are difficult to establish without having knowledge of their impact on head tissues. Visualization of simulation results can make a real contribution to help to understand general effects of tDCS to the human head and especially to brain tissues.

In order to evaluate the implemented visualization algorithms we performed tDCS simulations using a realistic head model. The model is composed of 8 tissues (skin, skull, cerebrospinal fluid (CSF), gray matter, white matter, eyes, internal air, electrode material), which were derived from a multimodal integration approach. Skin, skull, and internal air were derived from a computed tomography (CT) data set (GE CT Scanner, General Electrics, Fairfield, United States; 1 mm isotropic voxel resolution). Gray and white matter as well as eyeballs were derived from a MRI data set (1 mm isotropic voxel resolution) acquired with a 1.5 T Magnetom Symphony (Siemens Healthcare). We used the tool BrainK (Li, 2007) to combine the data acquired from different imaging modalities in order to integrate them into the tissue segmentation. An automated procedure implemented in BrainK was used to extract and, if necessary, manually correct, the different tissue segmentations. Furthermore, the tissues, such as eyeball, etc., could be extracted based on the available MRI contrast and modeled as homogeneous segmentation masks. Two patch electrodes (surface area: 50×50 mm, 5 mm height) were placed on the head using a C3-Fp3 (10–20 system) electrode montage to target the primary and secondary motor cortex. Based on the tissue segmentation, a tetrahedral mesh (43.7 million elements, 7.7 million element nodes) was generated using a novel meshing package (cleaver V1.5.4, Bronson et al., 2012) that preserves conformal mesh boundaries and guarantees a certain mesh quality (dihedral angles 4.7–159.1). Isotropic conductivity tensors (Dannhauer et al., 2012) were assigned to each of the tetrahedral elements depending on tissue type: skin (0.43 S/m, Dannhauer et al., 2011), skull (0.01 S/m, Dannhauer et al., 2011), cerebrospinal fluid (CSF, 1.79 S/m, Baumann et al., 1997), gray matter (0.33 S/m, Dannhauer et al., 2011), white matter (0.142 S/m, Haueisen et al., 2002), eyes (0.4 S/m, Datta et al., 2011), internal air (1e – 15 S/m, Datta et al., 2011), electrode material (1.4 S/m, Datta et al., 2011). A stiffness matrix was computed for the resulting FEM model using the SCIRun environment (Dannhauer et al., 2012). For the two current injecting patch electrodes, the electrical boundary conditions were considered using the complete electrode model (Somersalo et al., 1992; Polydorides and Lionheart, 2002) considering an electrode-skin impedance of 5 kΩ ⋅ m².

To study the effects of volume conductor modeling for EEG and tDCS stimulation, we performed careful simulations. Our modeling efforts naturally contain modeling simplifications (e.g., no white matter anisotropic conductivity modeling) with respect to realistic conditions. However, we believe that our head models capture important features of volume conduction, and therefore, results as well as the drawn conclusions are helpful to understand better specific effects in EEG and tDCS. Experimential validation in clinical settings is still an indispensable issue. Only a few studies in the literature have focused primarily on experimental validation of current injection. In an early animal study, Hayes (1950) investigated current injection in vivo using anaesthetised spider monkeys, injected 58 mA through surface electrodes and measured voltages at intracerebral probe sites. The author was able to estimate different tissue resistivities (scalp, skull, brain) to investigate their effects on the current flow through the monkey’s head. To obtain results for human physiology, Rush and Driscoll (1968) used data from an electrolytic tank that contained a half-skull structure with attached surface point electrodes. Currents were injected throughout the surface electrodes at different locations and electrical potentials were measured, its attenuation was depicted with respect to the skull center and resistivities were estimated. For a human volume conductor model, and finite tDCS electrodes, Datta and colleagues (2013) validated their simulations with experimental electrode readings (errors for potentials between 5–20%) conducted using a whole head electrode array and low amplitude current injection (1 mA). Besides empirical evidence supporting the effects of tDCS-like technologies in a broad range of medical applications (see above for more details) in human, there are numerous studies investigating cortical excitability and activity alterations induced via tDCS (for more details see e.g. Nitsche et al., 2008a; Staag and Nitsche, 2011; Nitsche and Paulus, 2011; Brunoni et al., 2012; Meideiros et al., 2012; Paulus et al., 2012; Brunoni et al., 2011). For example, Caparelli-Daquer and colleagues (2012) as well as Edwards and colleagues (2013) used event-related potentials (EEG) to prove the ability of focal stimulation of the motor cortex using tDCS.

The used volume conductor models in the current work, 3-Layer-Model and Skull-Hole-Model (Dannhauer et al., 2011; Lanfer et al., 2012), are based on segmentations from structural MRI contrasts similar to many studies in the literature (e.g., Dannhauer et al., 2012, 2013; Datta et al., 2010, 2011, 2012, 2013; Hallez et al., 2008; Im et al., 2008; Lew et al., 2013; Minhas et al., 2012; Rullmann et al., 2009; Sadleir et al., 2012; Wagner et al., 2014; Wolters et al., 2006). However, the head model used for tDCS in this work represent a more novel type that incorporates multimodal imagaing data (MRI, CT) for more realistic modeling of scalp, skull (Montes-Restrepo et al., 2014) and internal air cavities. It also features a more advanced current injection formulation (complete electrode model, Somersalo et al., 1992) that is frequently used in electrical impedance tomography (Polydorides and Lionheart, 2002). For all three applications cases, the volume conductor models were parameterized with respect to tissue conductivities (see above for more details) widely applied in recent literature.

4. Results and Discussion

We have applied the methods from Section 2 to all three application cases. In this section, we evaluate and review the usefulness of the visualization methods for the chosen applications with respect to the three criteria described above: comparability, anatomical context, and interactivity (see Section 2).

4.1. Surfaces and Direct Volume Rendering

4.1.1. Isosurfaces

We applied the interactive isosurface ray-tracer to the Skull-Hole-Model data and visualized the scalar electrical potential as the difference between modeling approaches. Figure 2 shows isosurfaces (red for +0.2 μV; blue for −0.2 μV) generated from a source located near the skull hole, in difference to the reference model without hole. The rendered isosurfaces represent the boundary of a spatial domain, where the absolute potential difference between the models exceeds a value of 0.2 μV. These rendering clearly show that the skull-hole influences the electrical field only near the hole itself. Note that, while the visualization of an isosurface of the potential difference is useful, as it renders a volume within which significant differences occur, isosurfaces of the potentials in either condition are far less useful, as the potential value depends on a reference (so, one would render a volume, where the potential is close to the one at the reference electrode).

Figure 2. Isosurface renderings for Skull-Hole-Model.

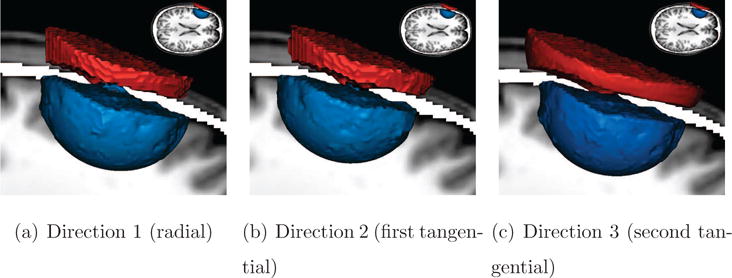
These isosurfaces show, for each source direction, the potential differences (red for +0.2 μV; blue for −0.2 μV) between the Skull-Hole-Model and the reference model. For the positions and orientations of the dipoles, see Figure 12. These surfaces denote the border between the volume with an absolute difference of more than 0.2 μV on the inside and less than 0.2 μV on the outside. Directly comparing the colormaps of the reference field and the skull-hole fields does not allow a quantitative rating of differences between the two fields. Using the difference field instead unveils the structural difference caused by the skull-hole very explicitly. The images demonstrate that the influence of the skull hole is different (more wide-spread) for the second tangential source orientation (Direction 3). It is clearly shown that the skull-hole only influences the area around the hole and that the difference of reference model and Skull-Hole-Model on the remaining field is rather low.

Comparability

In general, isosurfaces allow a high degree of comparability, and proper lighting can support a direct comparison of local shape and structure. Additionally, colormaps are useful in order to give cues about the surface potential or current density magnitude, which in turn increases comparability. Note that comparability is ensured only if the range of the values in all data sets is the same. Thus, normalization might be needed.

Anatomical Context

The isosurface approach has some significant advantages with respect to its anatomical embedding. First, isosurfaces can be rendered in combination with other objects, such as slices or surfaces. Second, isosurfaces can be combined with anatomical information, e.g., from magnetic resonance imaging (MRI). Naturally, anatomical context can help to increase comparability. However, combining anatomy and colors could also create confusing renderings, if too much information is combined into one color. A possible solution to overcome this problem is to use orthogonal slices for anatomy, as shown in Figure 2.

Interactivity

Since the isosurface renderer is implemented on the GPU, the interaction with surface renderings and surface modifications can be done without a significant loss of performance. For example, the modification of isovalues allows for a direct real-time exploration of the potential field and its propagation inside the head, just by pulling a slider.

Skull-Hole-Model

Isosurfaces used to render electrical fields and differences between electrical fields can help to interactively explore these fields. In Figure 2, the electrical field difference between the Skull-Hole-Model and its reference model (same, but without hole) for all three source orientations is rendered. It can be seen that all three source orientations lead to similar difference renderings. With closer inspection, the radial direction (Direction 1) and the first tangential source orientation (Direction 2) have a more similar appearance than the second tangential direction (Direction 3). It appears the second tangential direction (Direction 3) is more influenced by the presence of the skull hole. This is expected, as this direction is pointing towards the center of the hole. With the help of LIC, this can be shown more clearly, as done in section 4.3.

3-Layer-Model

For the 3-Layer-Model, isosurfaces are not very useful since model differences are diverse and inhomogeneously distributed in the skull. Hence, it was difficult to define meaningful surfaces based on isovalues for this particular application.

tDCS

In Figure 3, the current density magnitude is depicted (without isosurface truncation) on orthogonal slices cutting through all materials modeled in the volume conductor for the tDCS example. It can be seen that the highest current density magnitudes seem to be located on the electrode sponge-scalp interface (e.g., Song et al., 2011). Further, the impact of high conducting CSF can be clearly seen with higher current density magnitudes values close to the injecting electrodes. The current density magnitude is almost zero in the air-filled cavities and small in the skull tissue. Furthermore, in Figure 4, the current density magnitude is mapped onto material surfaces: scalp, skull, and brain. The visualization clearly shows the impact of the different conductive materials on the current density. As also implied in Figure 3, the increased current densities are concentrated around the edges of the electrode sponge, with the highest values near the corners. The current density on the skull surface is only slightly smeared out since the skin is just 2–3 mm thick and skin resistance is not very high compared to other materials (skull, air). However, the current density on the brain surface is very broadly distributed due to the low conductivity of skull tissue and the high conductivity of CSF. Another important point to mention here is the window-function used to map a certain current density magnitude interval to a color intensity interval. In Figure 4, the values on each tissue are mapped to the full white-red interval using a different window for each tissue. This windowing is motivated by the rapidly decreasing maximum magnitude when moving from the head surface towards the brain. Without the windowing, the color mapping on the brain would be nearly white.

Figure 3. Current density magnitude plot for tDCS example on cutting plane.

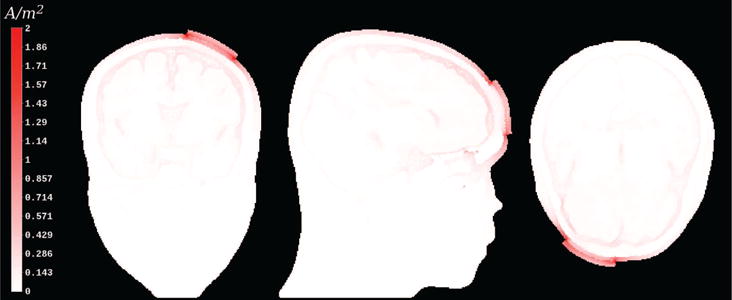
An coronal, sagittal, and axial view of the volume conductor, where current density magnitudes (white-to-red colormap) are mapped. High current density concentrations are present at the electrode sponge-scalp boundaries as well as in CSF. Although the current density around the electrode sponge-scalp boundaries was maximally up to 4.2 A/m², we have chosen a windowing interval of [0,2] A/m². This way, we are able to show the rapidly decreasing current density in vicinity of the sponge-scalp boundaries, which, otherwise, would not be seen as their value would be mapped to a nearly white color.

Figure 4. Current density magnitude plot for tDCS example on material boundaries.

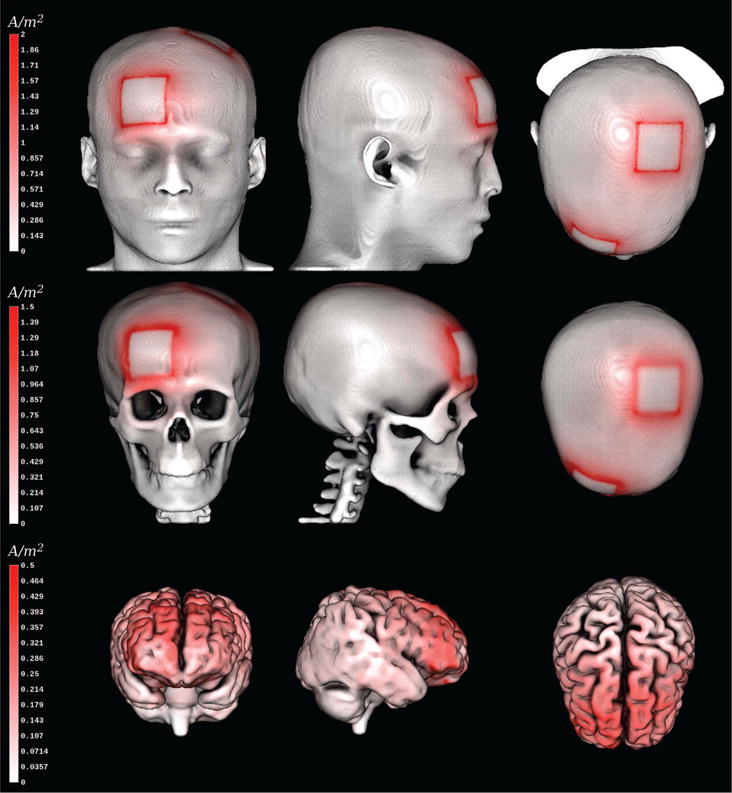
Current density magnitude (white-to-red colormap) computed for a standard tDCS electrode setting displayed on tissue boundaries: scalp ([0, 2] A/m²), skull ([0, 1.5] A/m²), and brain surface ([0, 0.5] A/m²). We have used different windowing intervals for each tissue boundary to cope with the rapidly decreasing current density. This way, we avoid that the maxima on the skin influence the coloring on inner tissues. It can be seen that the conductivity profile of the modeled materials has different effects on the current density distribution.

4.1.2. Direct Volume Rendering

Similar to isosurface renderings, we applied a red-blue colormap to denote positive and negative potential differences for the Skull-Hole-Model. Figure 5 depicts a volume rendering, with a specific transfer function. This transfer function was designed to specifically emphasize the gradient of the potential difference outside the skull hole, rather than its absolute values. For this purpose, we stippled the positive part of the transfer function to map the positive potential difference to alternating colors (red and yellow in this case). The negative part is a fading blue, to show the negative potential difference inside the skull. This is conceptually similar to isolines, but has the advantage of also providing information on the spatial extend of a certain value interval within the data.

Figure 5. Direct Volume Rendering (DVR) for Skull-Hole-Model.

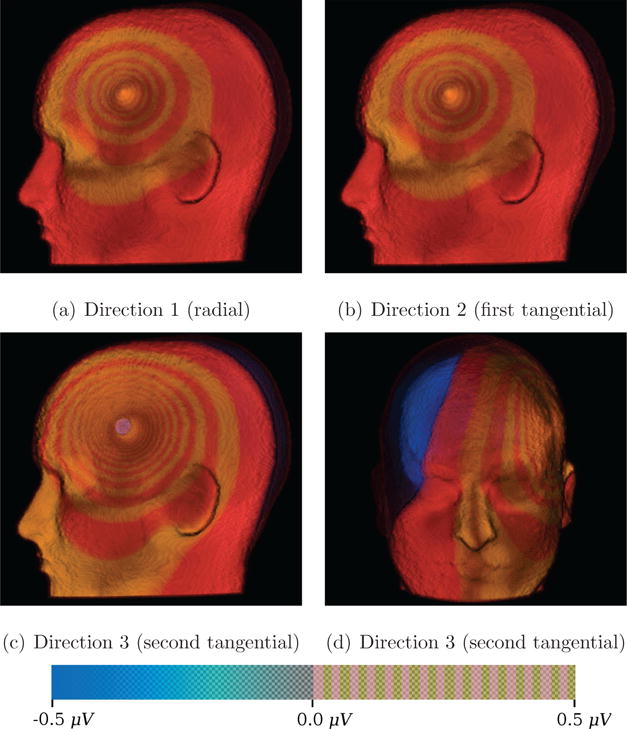
DVR for the potential difference fields for each source orientation in the Skull-Hole-Model. As Figure 2 indicated, the skull hole has the strongest influence on the field simulated from the second tangential direction. The used transfer-function shows the spreading potential difference between the Skull-Hole-Model data and the corresponding reference field. The transfer function maps negative potential differences to blue and positive differences up to 0.5 μV to a color pattern switching from red to yellow every 0.033 μV. This way, the spreading structure can be visualized in an intuitive way using direct volume rendering and is conceptually similar to isolines but has the advantage of also showing the spatial extend of intervals. For the positions and orientations of the dipoles, see Figure 12.

Comparability

Similar to isosurfaces, DVR provides high comparability, if transfer function and data range stay the same over all data-sets. Transfer functions, which were designed to unveil certain features or value distributions in the data, can provide a particularly high degree of comparability (e.g., Figure 5). However, unlike isosurfaces, DVR suffers from a lack of clear and crisp surfaces. Local illumination can additionally help to create surface-like effects, which influence the colormap. Overlap and high transparency in the transfer function further complicate comparisons over multiple renderings as they falsify the coloring of certain features or structures.

Anatomical Context

The combination of DVR and anatomical structures is a difficult problem. The additional use of orthogonal slices with anatomical colormaps is a difficult task as well. Figure 5 shows a feature-enhancing transfer function, where the shape of the head happens to be reflected quite well by the shape of the potential field.

Interactivity

Modern GPU implementations of DVR are able to perform high-quality volume renderings in real time with interactive transfer function design. The interactive modification of transfer functions with an easy-to-use interface is important to allow neuroscientists to explore data sets with different parameters quickly and intuitively.

Skull-Hole-Model

In Figure 5, a DVR of electrical field differences is shown for all three source orientations. To emphasize specific changes of positive potential differences, the transfer function includes an alternating red-yellow colormap (see Figure 5). For the negative potential differences, the transfer function uses a blue-transparency fading. It can be seen that positive potential differences are present in outer parts of the head (mainly in skin tissue). The negative range of the potential differences is primarily present inside the skull (in the brain tissues), whereas the biggest differences are close to the skull hole. In comparison to isosurfaces, we obtain similar results. DVR results for Directions 1 and 2 appear similar in contrast to Direction 3. Even though Direction 1 and Direction 2 look similar, there are potential differences, mainly in the brain tissue. It is also apparent that the potential gradients point radially towards the center of the hole, but their strengths are modified by the head shape and clearly differ for Direction 3 as compared to the other two directions. Another interesting finding is visualized by the different spatial frequencies of the circular structure. This pattern is different for Direction 1 and Direction 2 as compared to Direction 3, which has a much higher spatial frequency. This frequency indicates that the potential differences in Direction 3 increase much faster around the skull hole. The higher spatial frequency also proves that for this particular source orientation, the skull hole has the biggest effect. This information could not be conveyed by just one isosurface. DVR provides a simple way to represent multiple value ranges, which spatially overlap.

3-Layer-Model

Similar to using isosurfaces, it is difficult to gain any benefits and new insights into volume conduction from using DVR for the 3-Layer-Model due to the very local effect, confined to the skull compartment. It is hard to model a proper transfer function, which would be able to provide the needed resolution for seeing local details without the inherent occlusion.

tDCS

Also for the chosen tDCS example, it appeared difficult to design a proper transfer function to highlight the mostly local effects. The situation is further complicated by the fact that similar ranges of current density magnitude values are present in skin and CSF tissue, which would lead to significant occlusion effects.

4.2. Streamlines and Explorative Tools

In this section, we explore streamlines and streamline rendering methods in all three application cases. We calculated streamlines for all model variants. If not stated otherwise, the streamlines are colored according to their local tangent direction.

Comparability

A quantitative comparison between several streamlines is not reasonably possible. In Figures 6 and 7, global differences in streamlines generated from different models can be judged subjectively by the user. The user can directly compare density, orientation, and also number of streamlines among several images. For a comparison, it is important to provide the same coloring and value ranges for colormaps throughout the models.

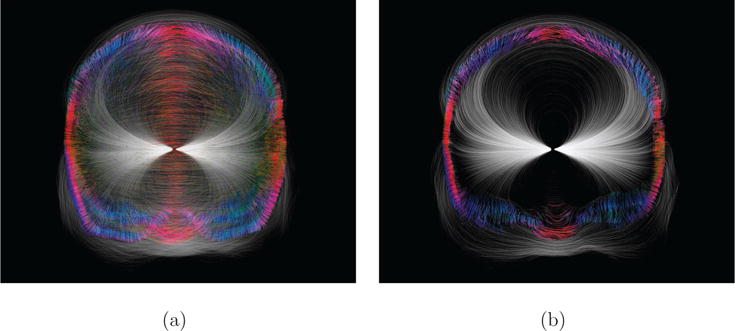
Figure 6. Streamlines depict the electrical flow field in the Skull-Hole-Model.

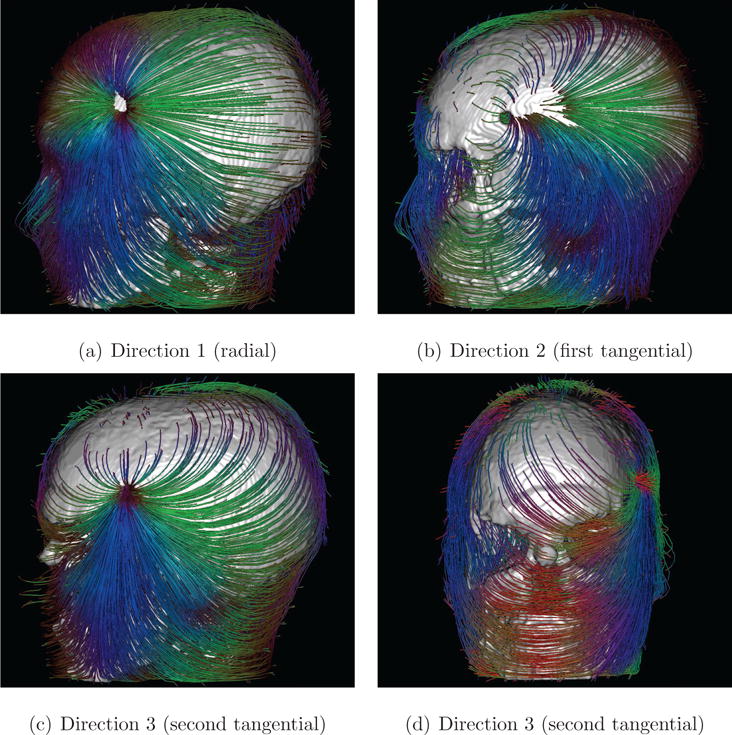
The skull mask, including the hole, has been added to provide anatomical context. As already seen in Figures 2 and 5, the influence of the skull hole seems to be nearly identical for source orientations Direction 1 and Direction 2. With the second tangentially oriented source (Direction 3), the field leaves the skull through the hole and enters it again through the eyes and foramen magnum due to the higher conductivity there. The streamlines use tangential coloring. This coloring can make the local orientation of each point of the streamline in three dimensions more visible, without the need to rotate the scene. For the positions and orientations of the dipoles, see Figure 12.

Figure 7. Streamlines depict differences of the electrical flow fields.

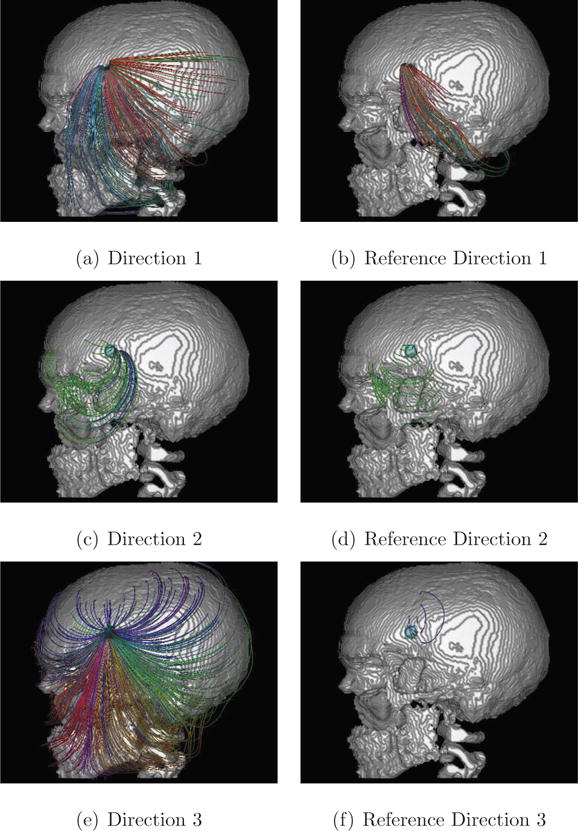
Direct comparison of the tangentially colored streamlines computed for each source orientation and both models: reference model (without hole) and Skull-Hole-Model. The skull hole is the region of interest (cyan ROI box covering the hole). The usage of the ROI box ensures that only streamlines are depicted, which are running through the skull hole (also for the reference case without the hole!). Unlike Figure 6, this figure shows that the field of the radial source is also influenced by the skull hole. However, Direction 3 is by far most strongly influenced, which can also be seen in direct volume rendering results (Figure 5). In comparison to the previously described methods, this technique offers a detailed view. For the positions and orientations of the dipoles, see Figure 12.

Anatomical Context

Embedding of anatomical context with streamlines can be a problem. In very dense areas near the source (or in deeper brain regions), occlusion becomes a serious problem and can prohibit the direct sight to anatomy. This problem can be solved to a certain degree by utilizing clipping surfaces or transparency, such as in Figures 8 and 9.

Figure 8. Clipping planes used for streamlines with anatomical context (Skull-Hole-Model).

A clipping plane placed through the radially oriented source in the Skull-Hole-Model. With such a clipping plane (or a combination of planes), it is possible to select a certain fraction of the streamlines. Part (a) shows a top view of the applied clipping plane. As the isosurface prohibits the direct view onto the dipole, it is often more useful to combine interactive selection tools with orthogonal anatomy slices for orientation. In (b), such an axial slice helps to improve orientation and allows an unhindered view to the dipole. For the positions and orientations of the dipoles, see Figure 12.

Figure 9. Perception of streamlines in 3D (Skull-Hole-Model).

Electrical flow field of the Skull-Hole-Model in combination with transparency and a curvature-based transfer-function. The transparency, which is defined by the line curvature at each point, highlights the shape of the electric field deeper inside the brain. Curvature is a common measure to describe how much a streamline deviates from being straight. In the left image (a), no anatomy is provided, rendering spatial relations difficult to see. Due to the missing depth cue, these types of renderings are useful only if the viewer interacts with the scene, allowing perception of spatial relations and structure of the field inside the head. The right image (b) uses stereoscopic (anaglyph three dimensional) rendering to add a spatial cue and, thus, allows perceiving the spatial relation of the field structures towards a given anatomical cue. For the positions and orientations of the dipoles, see Figure 12.

Interactivity

The streamline calculation process itself cannot be performed in real time. However, rendering large numbers of pre-computed streamlines is possible in real time. The selection and coloring using transfer functions can also be done interactively, which is required for efficient exploration of the data, with the possibility to display details on demand.

Skull-Hole-Model

In Figure 6, the streamline tracking results are shown for all three source orientations. Further, all streamlines outside the skull (mainly in skin tissue) are running more or less tangentially to the skin surface. For different source orientations, the impact of the skull hole is very different. For Direction 3, the impact of the skull hole is most apparent since a huge number of streamlines are passing through it. This result is quite interesting, because Direction 3 is a tangentially-oriented source, which, however, has a relatively large component pointing towards the center of the hole. The source is located slightly superior and anterior to the skull hole (see radially oriented Direction 1 for reference). Furthermore, besides the impact of the skull hole, some other effects are visible. First, the high tissue conductivity of the eyes evidently diverts some of the streamlines (i.e., electrical currents) and makes them pass through the natural skull openings (e.g., for optical nerves) at these locations. Second, a similar behavior is apparent at the foramen magnum. This behavior is generally expected at locations where the skull is not closed or a conductivity bridge (through low-conductance skull tissue) can be established, for example by surgery holes, sutures, etc.

tDCS

Figure 10 displays streamline tracking results in relation to the brain surface. The depicted streamlines indicate that electrical currents enter the skull tissue radially close to the injecting electrodes. As in the Skull-Hole-Model, the streamlines are strongly bent when flowing through a natural skull opening (foramen magnum).

Figure 10. Streamlines through volume conductor.

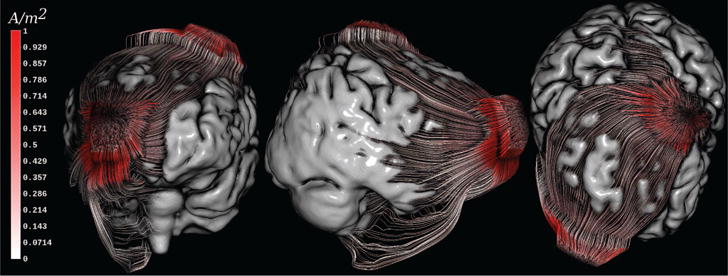
Streamlines show results of a tDCS simulation with respect to the brain surface while using a colormap to encode current density magnitude (white-to-red colormap, [0, 1] A/m²).

4.2.1. Streamline Selection and Clipping

Skull-Hole-Model

In Figure 7, the particular effect of the skull hole was investigated by visualizing streamlines running through the hole (or the site of the hole for the reference model). A ROI box was used that approximately covers the hole (shown in cyan), thus selecting only streamlines that actually pass through the hole. For comparison, the streamlines for the reference model regarding the same source orientation are depicted. It can be seen that, for all three source directions (Direction 1, Direction 2, and Direction 3), there appears to be a clear difference in volume conduction. With respect to the absence of the skull hole, the number of the outgoing streamlines in the reference model is much smaller. Again, the biggest difference between the models can be seen for Direction 3. In Figure 8, another selection tool, the clipping plane approach, is shown. With such a clipping plane or a combination of planes, it is possible to select a certain fraction of the streamlines. In combination with anatomical slices, interesting areas, e.g., the source singularity, can be investigated more precisely.

tDCS

In tDCS, the streamline algorithm always creates streamlines starting and ending at the injecting electrodes, independently from where the seed points were placed. This means that a ROI box covering the motor area underneath the anodal electrode (C3) selects the majority of streamlines running through the target brain tissue (motor cortex) as shown in in Figure 10. The advantage of using the selection tool is to exclude those streamlines, which run through the skin and, thus, would otherwise occlude the view onto the much more interesting streamlines through the target region. All in all, the tDCS and the Skull-Hole-Model share the same advantages and disadvantages for the respective methods. In both examples, streamlines are adequate for showing the global structure of the electrical field, but are limited when it comes to local details.

4.2.2. Local Opacity and Coloring

Skull-Hole-Model

In Figure 9, a curvature-based transfer function in combination with the streamline approach is shown. The curvature-based rendering accentuates areas with high streamline curvature, which correspond to tissue conductivity jumps or gradients based on large differences in potentials of adjacent nodes. This rendering makes it possible to see interesting details (such as the mainly affected streamlines) inside the model without the need of explicitly selecting them. It is important to note that the full benefit of this technique is only achieved in combination with modern display techniques, such as interactivity (the user can turn around the object in real time) and 3D display using modern display devices (see Figure 9(b)).

3-Layer-Model

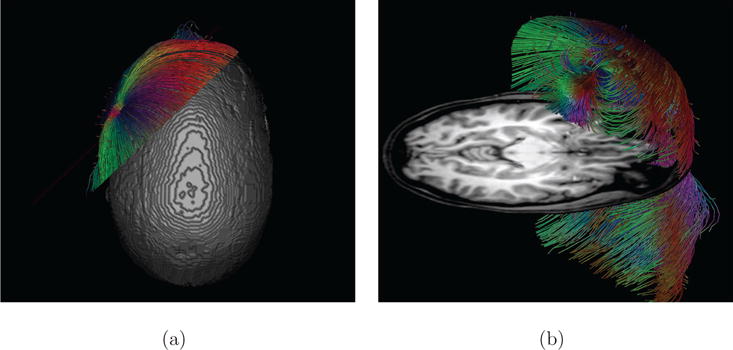
Figure 11 shows a streamline rendering of a source located in the human thalamus. Since all areas inside the skull are modeled isotropically (with a brain conductivity of σ_brain = 0.33 S/m), the streamlines are smooth (due to the absence of conductivity jumps). However, the skull is modeled inhomogeneously (Dannhauer et al., 2011) with much lower conductivities for soft and hard bone, as compared to isotropic skin and brain conductivity. Therefore, the streamlines, being representations of the electrical currents, are bent at boundaries between tissues.

Figure 11. Perception of streamlines in 3D (3-Layer-Model).

Coronal view of the 3-Layer-Model, where a source is placed near the thalamus. The streamlines were made opaque inside the skull and slightly transparent elsewhere. The color of each streamline inside the skull reflects its local direction (tangential coloring). Due to the coloring inside the skull, the field lines clearly undergo different degrees of diversion, depending on the angle at which they enter the skull: (a) volumetric rendering of all streamlines, (b) rendering of streamlines within a slab (thickness 10 mm) around a coronal slice passing through the thalamus, which removes the occlusion problem and unveils the streamline structure inside the slab.

tDCS

In Figure 10, generated streamlines are colored with current density magnitudes using a white to red colormap. Clearly, the corners of the electrode sponges touching the skin surface have the highest current densities. The current densities inside the skull are significantly smaller compared to the skin. However, current densities magnitudes appear to be higher in CSF even though they are more distant from current injecting sites most likely because of the high conductivity (σ_CSF = 1.79 S/m) of CSF compared to surrounding materials. Similar to the Skull-Hole example, a curvature-based coloring of the streamlines would be possible. This coloring could help to find conductivity bridges indicating problems that have been overlooked during tissue segmentation.

4.3. Line Integral Convolution

We applied LIC to all three application cases (see Figures 12, 13 and 14) on orthogonally oriented slices. A skull mask was used as a colormap for the Skull-Hole-Model (see Figure 12). Furthermore, we combined tissue masks (from tissue segmentation) as an additional colormap for the different bone layer models (see Figure 13) and tDCS-Model (see Figure 14).

Figure 12. Line Integral Convolution (LIC) for Skull-Hole-Model.

LIC images on a coronal slice through the hole combined with the electric fields for all three source orientations in the Skull-Hole-Model. Small differences in current flow between the source orientations can be seen. However, a direct quantitative comparison is not reasonably possible with LIC. The green bar in each image indicates the source orientation and position. The soft bone tissue is colored in red, the hard bone tissue in blue, and the remaining head tissues in gray.

Figure 13. Line Integral Convolution (LIC) for the 1- and 3-Layer-Model.

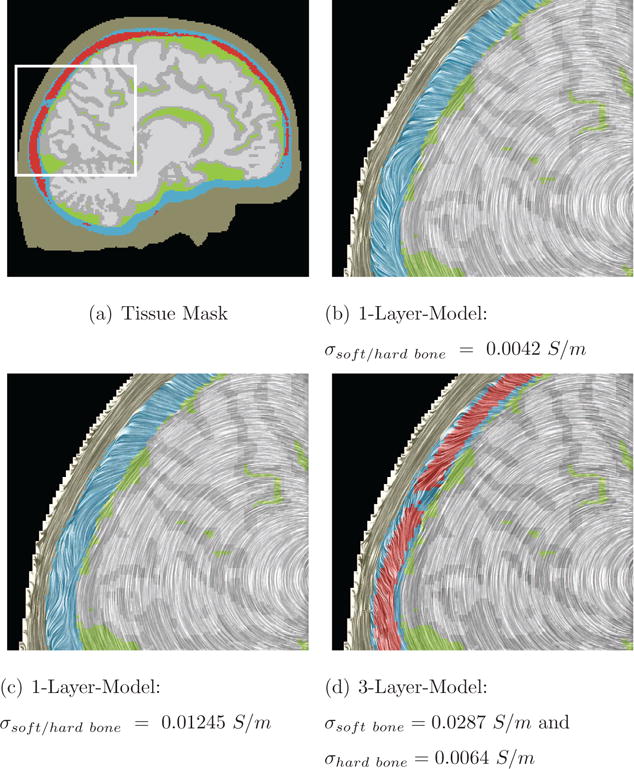
In (a), the different tissue types are visualized (skin in beige, CSF in green, gray matter in gray, white matter in light-gray, hard bone in blue, and soft bone tissue red). CSF, gray and white matter are modeled electrically using an isotropic conductivity of 0.33 S/m. The zoomed images use LIC to show the influence of the occipital fontanel regarding the electric flow field, for different values and bone conductivity models. The source is located in the thalamus for the 3-Layer-Model. (c) shows the best matching isotropic model, which seems to be a good approximation of the 3-Layer-Model (d).

Figure 14. Line Integral Convolution (LIC) on cutting plane.

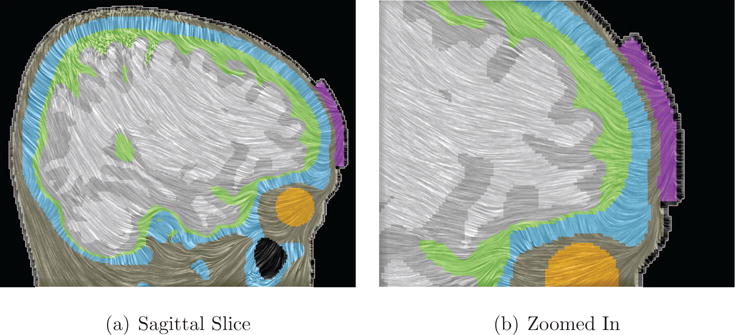
LIC images mapped on a sagittal slice (right panel: zoomed) through volume conductor shows results of a tDCS simulation in combination with a colored background based on tissue labels. The different tissue types are visualized using a colormap similar to the one in Figure 13: skin in beige, CSF in green, gray matter in gray, white matter in light-gray, skull in blue, the eyeball in yellow, and the tDCS electrode sponge in purple.

Comparability

LIC provides a global overview of the electrical field as well as specific local details. Both aspects can be compared between models and to other visualization techniques. Unlike color mapping, quantitative comparisons with LIC are not reasonably possible - only the local direction of the current flow can be inspected qualitatively. In combination with colormaps, comparability can be enhanced, since colormaps allow the combination of the flow direction with other details (such as the strength of local potential changes). In terms of visibility, the contrast between colormaps and LIC may be a limiting factor. Moreover, LIC textures modify color intensities, which can lead to misinterpretation of the colormap. Again, similar to the other methods, it is important to make sure that the same algorithm parameters are used throughout the whole series for comparison.

Anatomical Context

As mentioned above, a combination of colormaps with LIC is possible (although not without limitations). Another option is to use geometric information derived from anatomical data (isosurfaces) for LIC. The LIC effect is then applied to the surface serving as an anatomical cue and can easily be combined with orthogonal slices showing the anatomy.

Interactivity

Usually, the standard LIC implementation is too slow for interactive modification and exploration. In contrast, our GPU-based approach does allow rendering at interactive frame-rates.

Skull-Hole-Model

In Figure 12, LIC textures are shown on a coronal slice, for a source near the skull hole (see mask), for the three current directions (Direction 1, Direction 2, Direction 3). It can be seen in all three LIC images that some currents flow through the skull hole. However, as mentioned above, this effect cannot be quantified. The seemingly “noisy” parts of the texture indicate flow directions perpendicular to the depicted slice.

3-Layer-Model

Figure 13 shows LIC results for the different ways of skull modeling. The figure shows the area around the occipital suture, whereas the only difference between Figures 13(b)–13(d) is the applied conductivity profile of the skull. In Figure 13(b), the skull is modeled with the traditionally used isotropic conductivity (σ_{hard/soft bone} = 0.0042 S/m). In Dannhauer et al. (2011), we showed that the isotropic conductivity must be much higher in a realistic setting (Figure 13(c)). For that model, the isotropic conductivity was fitted (see section 3.2) for more details) to the 3-Layer-Model, yielding an isotropic value of σ_{hard/soft bone} = 0.01245 S/m. In Figure 13(d), the LIC result for the reference model is shown. The reference model uses experimentally measured conductivities for soft (red) and hard bone (blue). Soft and hard bone distribution was estimated by skull segmentation based on a T1-weighted MR image. The LIC approach allows detailed insight into flow features and structures inside the differently modeled bones and emphasizes their difference. It can be seen that Figures 13(c) and 13(d) are much more similar than Figures 13(b) and 13(d). Furthermore, LIC streamlines that are, due to the presence of soft bone, diverted tangentially with respect to the skull surface, can be clearly identified (Figure 13(d) compared to Figure 13(c)). For more details about the approximation of the three-layered skull structure using a global isotropic conductivity model please refer to Dannhauer et al. (2011).

tDCS

Figure 14 depicts streamlines of a sagittal slice passing through the frontal electrode (Fp2) combined with a colormap helping to perceive material boundaries. Similar to Figure 13 and more detailed as in Figure 10 the dominance of a radially-oriented electrical currents is strikingly apparent.

Wagner and colleagues (2014) investigated the impact of homogeneous and inhomogeneous skull modeling for tDCS in which they varied conductivity ratios of soft and hard bone within ranges that were experimentally determined as described in Akhtari and colleagues (2002). They depicted the results as cones having normalized length. Based on their visualizations they concluded that currents mainly flow radially through isotropically modeled skull tissue. Their investigations contained inhomogeneous skull models in which they stepwise increased the hard-to-soft bone conductivity ratio (nominally soft bone conductivity) from averaged (Akhtari et al., 2002) to ratios that led to mainly tangential current flow within soft bone structures. They claimed that for higher hard-to-soft bone conductivity ratios their chosen target regions were significantly affected by those changes depending their location. Additionally, they used similar cone plots to investigate changes in current flow direction in the case of including CSF, differentiating between brain tissues (gray and white matter) in the volume conductor model and using color maps to point out the impact of white matter conductivity anisotropy. Our results confirm the results reported by Wagner and colleagues (2014) for tDCS but also for EEG as shown in figure 13 and 14, respectively.

5. Conclusion

In the previous sections, we have highlighted advantages and disadvantages of several standard visualization techniques exemplarily for three interesting models regarding the influence of the human skull and tDCS stimulation on bioelectric field simulations. We used visualization methods to create an intuitive understanding of volume conduction effects, which otherwise can be described only in a rather unintuitive way by numerical measures (e.g., Dannhauer et al., 2011). Most importantly, we assessed all algorithms in all examples with respect to clearly defined criteria: (1) the quantitative comparability between data sets, (2) the possibility to provide anatomical context, and (3) the feasibility of interactive use. In particular, the latter point is often underestimated in the written literature with its unavoidably static images. The possibility to interactively change parameters or turn the image around in three dimensions can often provide more insight than very sophisticated renderings trying to pack as much information as possible into static images.

Isosurfaces and Direct Volume Renderings provide a quick overview of the data and the influence of anatomical structures on the field propagation. These methods were especially fruitful for the visualization of global features of the field in the Skull-Hole-Model. The local features of the 3-Layer-Model could not be sufficiently captured. In the chosen tDCS example, isosurfaces were especially helpful to visualize the current density magnitude on anatomical structures. Unfortunately, DVR suffers from the problem of complicated and time-consuming designs of useful transfer functions and hence is the subject of further research.

The visualization using streamlines provides more detail on the structure of the actual electrical field, especially the influence of the skull hole and current flow properties in tDCS stimulation, which can be seen very clearly together with filter and selection tools. The selection mechanisms allow for simple exploration and comparison of the field in conjunction with anatomy and model-specific regions. As with DVR and Isosurfaces, the prime benefit of this method is the exploration of features within a global scope. For the 3-Layer-Model, local effects are hard to interpret with streamlines as the interesting areas are small and cluttered inside the skull tissue. The same is true for the tDCS example, where dense streamlines occlude the more interesting, local stream features in certain tissue types. Selection mechanisms can help to filter out uninteresting streamlines to avoid intense visual clutter.

Finally, LIC proved ideal for exploring the interesting local details in the 3-Layer-Model and tDCS. It provides a qualitative explanation for local effects of different skull models and their statistically measured similarities and dissimilarities. Unfortunately, quantification is difficult with LIC. Especially for the Skull-Hole-Model and tDCS, the combination of LIC with colormaps is difficult, as LIC directly influences the brightness of the underlying colormap, which can lead to misinterpretation. LIC is an interesting option, as it provides local details otherwise invisible with streamlines. Its limitation to surfaces and slices prohibits the fast volumetric perception of the field. Volumetric LIC (3D-LIC) methods could help if a proper importance-function could be defined, which might be difficult and very application dependent.

Altogether, visualization provides a tremendous insight into volume conduction and helps us to understand the underlying models and the influence of their parameters. Visualization allows us to qualitatively explain features in bioelectric fields, even if they are only indirectly detectable using quantitative error measures. A myriad of visualization techniques is available, all with their own benefits and drawbacks. The selection of the proper method mainly depends on the specific application and the kind of features that need to be explored. In addition, neuroscience and other life sciences have very specific visualization requirements. Besides the three main requirements postulated in this work (comparability, context, and interactivity), acceptance of a method mainly depends upon its ability to reveal information and to allow its intuitive interpretation. We found that an interactive, intuitive, and adapted tool is often more important than nice-looking images, created with methods that require multiple parameters. The latter often lead to error-prone methods, requiring a great deal of manual fine-tuning. Even if they provide subjectively impressive images, they do not necessarily transport the needed information. Table 1 gives an overview on the general advantages and disadvantages of the methods used in this paper. The actual value of a method heavily depends on the domain and the features to investigate.

Table 1.

Comparison of the general advantages and disadvantages of the shown visualization methods.

Pro	Contra
Isosurfaces
Insights into spatial distribution of scalar fields. Easy embedding of anatomical context.	Only shows a part of volumetric structure (choose isovalue properly; consider meaning of “volume” and “distance” in renderings). Prone to noise and sampling artifacts.
Most useful in the context of selectively showing global features and behavior.
Direct Volume Rendering (DVR)
Insights into spatial structure and distribution of scalar fields in the entire volume. Avoids occlusion problems.	Transfer function (TF) design is very domain- and case-specific. Anatomical context is hard to embed.
Most useful in the context of catching multiple, global features in the entire volume.
Streamlines
Insights into directional structures at globally in 3D	Occlusion problem (partially solvable by transfer functions and line filters).
Most useful in the context of grasping major directional structures in 3D.
Line Integral Convolution (LIC)
Insight into directional structures locally (focus on details). Good qualitative comparison among multiple images.	Only depicts directional information; quantification difficult. Combination with colormaps can lead to misinterpretation.
Most useful in the context of analyzing local and small-scale directional structures.

Future directions of this type of application-specific visualization research should involve experimental and clinical validation. In this context, other neuroscientific techniques and aspects of volume conduction might be interesting to explore such as induced neuronal activity by transcranial magnetic stimulation (TMS), reconstruction of current flow measured by intracranial EEG (iEEG), and modeling the specific volume conductor properties, e.g., skull modeling in children (Lew et al. (2013)). In general, we aim at more application specific techniques, including automated transfer function design and estimation of parameters from the data (rather than asking the user for them).

Highlights.

• We apply visualization techniques on electrical fields from EEG and tDCS

• We demonstrate how to utilize these techniques to gain insight into the data

• We evaluate each method against comparability, anatomical context and interactivity

• We have shown that each visualization method has its pros and cons in our data