Abstract
A large-scale computational model of the hippocampus should consider plasticity at different time scales in order to capture the non-stationary information processing behavior of the hippocampus more accurately. This paper presents a computational model that describes hippocampal long-term potentiation/depression (LTP/LTD) and short-term plasticity implemented in the NEURON simulation environment. The LTP/LTD component is based on spike-timing-dependent plasticity (STDP). The short-term plasticity component modifies a previously defined deterministic model at a population synapse level to a probabilistic model that can be implemented at a single synapse level. The plasticity mechanisms are validated and incorporated into a large-scale model of the entorhinal cortex projection to the dentate gyrus. Computational expense of the added plasticity was also evaluated and shown to increase simulation time by less than a factor of two. This model can be easily included in future large-scale hippocampal simulations to investigate the effects of LTP/LTD and short-term plasticity in conjunction with other biological considerations on system function.
I. Introduction
As computational capability increases over time, large-scale models of neural systems can be made that incorporate increasing amounts of detail. With careful incorporation of more details into simulations, simulated brain region activity can give approximations to the information processing properties in real brain regions in diseased and healthy states. The hippocampus represents an ideal candidate for large-scale simulation because it has been so well studied and because of its importance in memory and high-level cognition.
In order to represent the information processing behavior of the hippocampus in a large-scale simulation, considerations to accurately reflect cellular morphology, biophysics, connectivity, and non-stationary behavior must be made. Refer to Hendrickson et al. in these proceedings [1] for a general framework of how all these factors will be initially addressed and Yu et al. in these proceedings [2] for an initial incorporation of realistic connectivity. This paper will focus on the preliminary implementation of non-stationary behavior in a hippocampal large-scale simulation with consideration of plasticity. Plasticity does not represent the only non-stationarity in the hippocampus (other examples include disease or development related non-stationarities); however, studying plasticity can provide insights into the activity-dependent information processing characteristics of the hippocampus. The goal of this study is to produce a mechanism which describes long-term potentiation/depression (LTP/LTD) and short-term plasticity that can be used in subsequent large-scale modeling studies. In order to produce such a model, appropriate rules for each type of plasticity are selected, proper functions of the rules are verified in simulations, and the computational expense is analyzed.
Activity dependent changes in synaptic weight due to LTP/LTD are widely believed to be integral in learning and memory formation. While the exact relationship between neural activity patterns and LTP/LTD is not completely understood, there is evidence that the relative timing of presynaptic and postsynaptic spiking influences potentiation and depression. As defined by spike-timing-dependent plasticity (STDP), if a presynaptic spike precedes a postsynaptic spike, there is potentiation, while conversely, if a postsynaptic spike precedes a presynaptic spike, there is depression [3]. Furthermore, the magnitude of the potentiation/depression increases with a shorter time interval between the presynaptic and postsynaptic spikes. STDP will be used as a first implementation of LTP/LTD.
Short-term plasticity describes how the vesicle release probability of a single synapse is increased or decreased due to presynaptic spiking temporal patterns on the time scale of tens of milliseconds to seconds [4]. Most current models of populations of neurons consider graded synaptic transmission with each presynaptic event. It is believed, however, that for each individual cortical synapse, presynaptic signal transmission is binary, with either vesicles released or not according to a vesicle release probability. This probabilistic release could have a large impact on how signals are integrated and processed between neural populations. In order to include short-term plasticity in a large-scale model that incorporates probabilistic release, current deterministic models of short-term plasticity can be modified.
One important difference to note between LTP/LTD and short-term plasticity as considered in this paper is how they modulate synaptic transmission. The mechanism for short-term plasticity is presynaptic and affects the vesicle release probability, while LTP/LTD modulates the amplitude of the postsynaptic conductance spike triggered by each vesicle release (see diagram in Figure 1).
Fig 1.
Diagram of short-term plasticity and STDP implementation. Short-term plasticity determines the vesicle release probability based on the presynaptic spike train timing. For each presynaptic spike, vesicle release either occurs or not based on the vesicle release probability. With each vesicle release, there is a momentary increase in synaptic conductance. STDP determines the magnitude of the increase in synaptic conductance based on the relative timing of vesicle release and postsynaptic spiking.
II. Methods
All plasticity learning rules and large-scale simulations will be implemented in the NEURON simulation environment [5].
A. STDP Implementation
The weight of each synapse, w, is defined by the peak increase in synaptic conductance after each vesicle release event. In the STDP rule implemented [6], as defined in Equations (1), (2), and (3), w is bounded between wmin and
| (1) |
A is a variable that captures the fluctuation in synaptic weight caused by pre/postsynaptic spike pairings according to the following STDP learning rules:
| (2) |
| (3) |
The parameters p and d can be tuned to values between zero and one in order to scale the magnitude of potentiation or depression for each pre/postsynaptic spike pairing. The interspike interval affects the potentiation and depression magnitude with the time constants of τp = 17ms and τd = 34ms respectively.
In this implementation of STDP, there is an immediate onset of change for each synaptic. This enables the effects of the STDP learning rule to be analyzed for simulations of seconds of activity instead of simulations of minutes or hours.
The validity of other STDP rules that calculate the postsynaptic spiking at the soma have been challenged because they do not account for the fact that LTP/LTD can be induced when there is only dendritic spiking and no somatic spiking [7]. The STDP rule presented here, however, measures the postsynaptic spiking in the dendrite where the synapse is located, and therefore can incorporate the effects of local dendritic spiking.
The proper functioning of the STDP learning rule in the large-scale model was validated by running a simulation of a single dentate gyrus (DG) granule cell with a physiologically realistic dendritic morphology and 3000 individual synapses. Each synapse received an independent Poisson input train, and the weight fluctuations of a synapse were analyzed with respect to the presynaptic and postsynaptic spike pairings.
B. Short-term Plasticity Implementation
The short-term plasticity rule proposed by Dittman et al. [8] was modified from a deterministic, synapse population level rule into a probabilistic, individual synapse rule. In the deterministic model, the excitatory postsynaptic current (EPSC) is mediated by a facilitation variable, F, and a depression variable, D. The magnitude of each EPSC is proportional to F times D. In the deterministic model, F increases and D decreases with each presynaptic action potential. In an individual synapse, mechanisms for short-term facilitation are activated with each presynaptic spike and rely on influx of presynaptic calcium. Therefore, F should increase with each presynaptic event as in the deterministic model. Factors for depression, however, such as vesicle depletion, are activated with each vesicle release, which means that for an individual synapse, D should only decrease when vesicles are released. The deterministic model, therefore, needed to be modified so that the same population performance is achieved when D decreases only with each probabilistic release. Equation (4) shows the dynamics of the D variable in the deterministic model [8].
| (4) |
Equations (5), (6), and (7) show the changes made in order to implement and test synapse level, probabilistic release. Refer to table 1 for a summary of the different variables used.
| (5) |
| (6) |
| (7) |
TABLE I.
Model Parameters
| F | Facilitation variable; ratio of sites activated by a stimulus |
| D | Deterministic Depression variable; ratio of sites that are release ready |
| DP | Probabilistic Depression variable |
| DPi | Probabilistic depression variable for each release site |
| t0 | Times of each presynaptic spike |
| Reli | Timing of vesicle release for each release site |
| NT | Total number of release sites |
| RD | Recovery rate of depression variable |
| U | Uniform random distribution sample |
For validation, the probabilistic and the deterministic model variable values were computed and compared for trains of consecutive presynaptic events at varying physiologically representative frequencies of 10–80Hz. Model parameters were chosen that correspond to hippocampal synapses [8].
C. Large-Scale Plasticity Computational Expense
The computational expense of incorporating plasticity into a large-scale model must be analyzed to ensure that it is not prohibitive on running simulations. In order to do so, the run times of a large-scale model of the DG granule cell population receiving inputs from the entorhinal cortex (EC) will be modeled with and without plasticities. The large-scale model used will have one tenth of the total rat physiological neural population (11,000 EC cells and 100,000 DG granule cells). Each granule cell will also explicitly model a realistic dendritic morphology. Furthermore, approximations of realistic connectivity and topography of the cells will be implemented. Refer to Hendrickson et al. [1] for additional details of the large-scale model. Each simulation was run on 400 processors at a time.
III. Results
A. Spike-timing-dependent Plasticity Validation
A simulation was performed for a single granule cell with 3000 explicitly modeled synapses. Each synapse incorporated the short-term plasticity and STDP rules described in the previous section. The inputs for each synapse were independent, random, Poisson trains with a frequency of 5 Hz. The traces of synaptic conductance and postsynaptic membrane potential for a single synapse are shown in Figure 2. The first presynaptic spike occurs after a postsynaptic spike which should cause the synaptic weight to decrease according to the STDP learning rule. This decrease in synaptic weight is shown in the simulation when the peak magnitude of the next conductance spike is diminished. Conversely, the proper functioning of the potentiation component of the STDP rule can be seen when the second presynaptic spike occurs right before a postsynaptic spike and the subsequent weight is increased.
Fig. 2.
STDP function in a single synapse during a simulation. The vertical dotted line in the bottom plot indicates the timing of presynaptic events.
B. Short-term Plasticity Validation
Validation of the probabilistic short-term plasticity equations were performed by simulating a population of 5000 individual synapses and comparing their average output to the output of the deterministic model for input spike trains of different frequencies. A visualization of the difference in dynamics caused by using the probabilistic versus the deterministic rule can be seen by comparing their respective D traces during a simulation. An individual probabilistic DPi trace varies significantly from the deterministic model D trace; however, the average of the probabilistic DPi traces did produce a qualitatively similar signal to the deterministic D trace at tested presynaptic input frequencies of 10–80Hz. See Figure 3 for an example of D traces with a 20Hz stimulus train.
Fig. 3.
Traces of D variable with 20 Hz stimulus for 10 consecutive presynaptic events.
Another comparison made for validation purposes is between the normalized EPSC amplitude in calculations with the deterministic and probabilistic models. Deterministic and probabilistic normalized EPSC values, EPSCD and EPSCP respectively, are calculated as in equations (8) and (9), where F1 is the initial release probability.
| (8) |
| (9) |
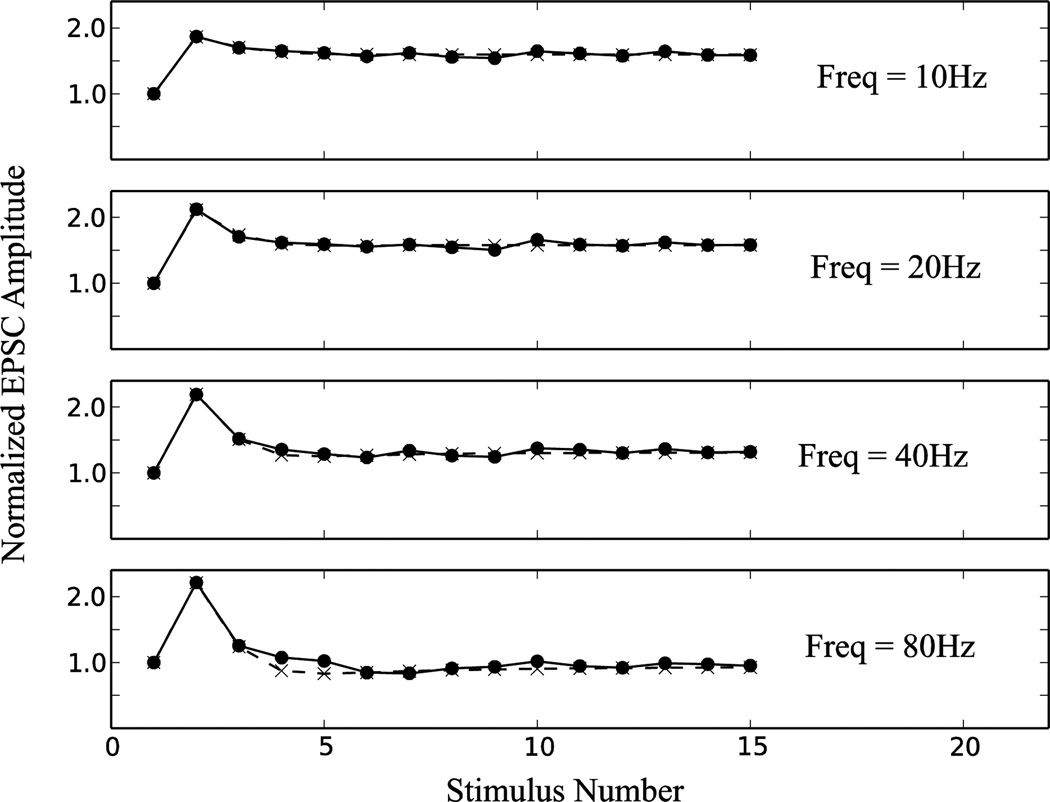
The similarity in EPSC amplitude at frequencies of 10–80Hz is shown in Figure 4.
Fig. 4.
Normalized EPSC amplitude comparison between deterministic model (dashed line) and probabilistic model (solid line).
C. Computational Penalty of Plasticity in Large-Scale Implementation
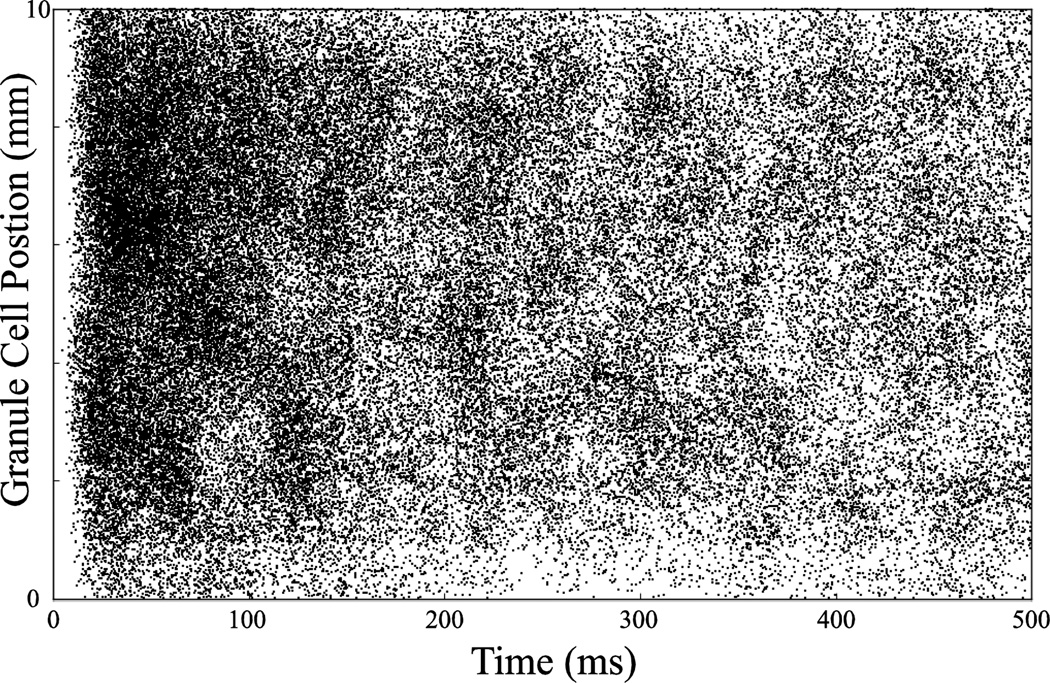
The computation time was compared for large-scale simulations with and without synaptic plasticity. A sample output of a large-scale simulation is shown in Figure 5. Figure 6 shows the different run times between two simulations with and without plasticity. The computational time increase due to the plasticity rules is 64%.
Fig. 5.
Example raster plot of spiking activity of large-scale simulation. Granule cell position refers to position along septotemporal axis of the DG.
Fig. 6.
Simulation time with 100,000 DG granule cells, 11,000 EC cells, ~3000 synapses per granule cell, 200ms simulated biological time.
IV. Discussion
The simulations presented indicate the suitability of using the described plasticity rules for large-scale model implementation. For the STDP model, change of weights in the simulation represented weight changes that would be expected with a STDP rule. For short-term plasticity, the similarities in performance between the aggregate of probabilistic single synapses and the deterministic model indicate that the proposed model can be implemented at the single synapse. Furthermore, the inclusion of synaptic plasticity increased simulation computational time by a factor of less than two, which will allow plasticity to be included in any future large-scale simulations without changing the order of magnitude of simulation time. Because the plasticity models were implemented in the NEURON simulation environment, they can easily be incorporated into future large-scale models of the hippocampus.
Future work includes adding other forms of plasticity, such as augmentation and homeostasis into one NEURON mechanism. With such a model, investigations can be made into how information processing in the hippocampus is affected by all different types of plasticity. Furthermore, the affects of plasticity can be studied in conjunction with other biological mechanisms and processes.
Acknowledgment
Computation for the work described in this paper was supported by the University of Southern California Center for High-Performance Computing and Communications (www.usc.edu/hpcc)
Contributor Information
Brian S. Robinson, Email: bsrobins@usc.edu.
Gene J. Yu, Email: geneyu@usc.edu.
Phillip J. Hendrickson, Email: phendric@usc.edu.
Dong Song, Email: dsong@usc.edu.
Theodore W. Berger, Email: berger@bmsr.usc.edu.
References
- 1.Hendrickson PJ, Yu GJ, Robinson BS, Song D, Berger TW. Toward a Large-Scale Biologically Realistic Model of the Hippocampus; 34th Annual International Conference of the IEEE EMBS; 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yu GJ, Robinson BS, Hendrickson PJ, Song D, Berger TW. Implementation of a Topographically Constrained Connectivity for a Large-Scale Biologically Realistic Model of the Hippocampus; 34th Annual International Conference of the IEEE EMBS; 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Caporale N, Dan Y. Spike timing-dependent plasticity: a Hebbian learning rule. Annual review of neuroscience. 2008 Jan.31:25–46. doi: 10.1146/annurev.neuro.31.060407.125639. [DOI] [PubMed] [Google Scholar]
- 4.Fioravante D, Regehr WG. Short-term forms of presynaptic plasticity. Current opinion in neurobiology. 2011 Apr.21(2):269–274. doi: 10.1016/j.conb.2011.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hines ML, Carnevale NT. The NEURON simulation environment. Neural computation. 1997 Aug.9(6):1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- 6.Cutsuridis V, Cobb S, Graham BP. Encoding and retrieval in a model of the hippocampal CA1 microcircuit. Hippocampus. 2010 Mar.20(3):423–446. doi: 10.1002/hipo.20661. [DOI] [PubMed] [Google Scholar]
- 7.Kampa BM, Letzkus JJ, Stuart GJ. Dendritic mechanisms controlling spike-timing-dependent synaptic plasticity. Trends in neurosciences. 2007 Sep.30(9):456–463. doi: 10.1016/j.tins.2007.06.010. [DOI] [PubMed] [Google Scholar]
- 8.Dittman JS, Kreitzer AC, Regehr WG. Interplay between facilitation, depression, and residual calcium at three presynaptic terminals. Journal of Neuroscience. 2000 Feb.20(4):1374–1385. doi: 10.1523/JNEUROSCI.20-04-01374.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]