Examining Moderation Analyses in Propensity Score Methods: Application to Depression and Substance Use

Abstract

Objective

This study provides guidance on how propensity score methods can be combined with moderation analyses (i.e., effect modification) to examine subgroup differences in potential causal effects in non-experimental studies. As a motivating example, we focus on how depression may affect subsequent substance use differently for men and women.

Method

Using data from a longitudinal community cohort study (N=952) of urban African Americans with assessments in childhood, adolescence, young adulthood and midlife, we estimate the influence of depression by young adulthood on substance use outcomes in midlife, and whether that influence varies by gender. We illustrate and compare five different techniques for estimating subgroup effects using propensity score methods, including separate propensity score models and matching for men and women, a joint propensity score model for men and women with matching separately and together by gender, and a joint male/female propensity score model that includes theoretically important gender interactions with matching separately and together by gender.

Results

Analyses showed that estimating separate models for men and women yielded the best balance and, therefore, is a preferred technique when subgroup analyses are of interest, at least in this data. Results also showed substance use consequences of depression but no significant gender differences.

Conclusions

It is critical to prespecify subgroup effects before the estimation of propensity scores and to check balance within subgroups regardless of the type of propensity score model used. Results also suggest that depression may affect multiple substance use outcomes in midlife for both men and women relatively equally.

There has been growing interest in identifying differential effects of mental health conditions or of treatment options. Gender, in particular, has been proposed to play an important role in understanding different risk factors and consequences of mental health conditions, and in tailoring treatments for men and women to increase impact (Dwight-Johnson, Sherbourne, Liao, & Wells, 2000; Gorman, 2006; Kornstein, 1997; Nolen-Hoeksema, 2004; Reinherz, Giaconia, Carmola Hauf, Wasserman & Paradis, 2000; Weisman & Olfson, 1995). As interest in effect modification by gender has grown, at the same time propensity score methods have emerged as a key tool for estimating causal effects in non-experimental studies (see Stuart, 2010). In many instances, randomized controlled trials, the gold standard for testing causal relationships, are not ethical or feasible; propensity score methods have shown to be useful in those cases. However, it is unclear how to combine effect modification with propensity scores as this topic has received little attention in the methodological literature. For instance, the presence of a depressive disorder cannot be randomized to individuals; thus to answer questions about potential differential effects of depression for men and women, we are in need of ways to combine moderation analysis with advanced causal methods, such as propensity scores. This paper provides an overview of the different methods by which propensity score methods can be combined with moderation analyses in order to estimate subgroup differences in potential causal effects in non-experimental data. We apply these techniques to an investigation of gender differences in substance use consequences of depression using data from a longitudinal community cohort study.

Gender Differences in Consequences of Depression

Gender differences in the consequences of mental health conditions have garnered significant attention. Studies have long shown gender differences in the prevalence, etiology, comorbidity, and clinical course of mental disorders (Brady & Randall, 1999, Kessler, McGonagle, Swartz, Blazer & Nelson, 1993; Kessler, McGonagle, Zhao, Nelson, Hughes, Eshleman, Wittchen & Kendler, 1994). Recently, it has been proposed that the consequences of mental health conditions also may differ for men and women as a result of different coping styles (e.g., Angst, Gamma, Gastpar, Lepine, Mendlewicz, & Tylee, 2002).

Despite increasing evidence of gender differences in consequences of mental health disorders, it is not always clear how to analyze gender differences in these non-experimental settings. Research shows an increasing number of studies finding outcomes that are specific to only one gender, stronger in one gender, or opposite in direction for men and women. Pertaining to the motivating example for this study, the influence of depression on the development and maintenance of substance use and disorders, the effect may vary for men and women (Husky, Mazure, Paliwal, & McKee, 2008; Lau-Barraco, Skewes, & Stasiewicz, 2009). It may be that depression only affects substance use among women, is more influential (i.e., stronger) among women compared to men, or that depression may even be protective against substance use for one gender. Failure to properly consider the role of gender in studying the consequences of mental health disorders can lead to erroneous conclusions with regards to men, women or both genders.

Etiologic theories concerning the comorbidity of depression and substance use often focus on drinking or drug use to self-medicate or cope with affective symptoms (Khantzian, 1985; Khantzian, 1990; Khantzian, 1997). Results of several studies lend support to the self-medication hypothesis for depression, finding higher rates of substance use, abuse, and dependence among the depressed than the non-depressed (Bolton, Robinson, & Sareen, 2009; Swendsen, Tennen, & Carney, 2000). Further, the onset of depression has been found to typically precede the onset of substance use disorders (Abraham & Fava, 1999), and those with major depression are more likely to use substances when experiencing depressed mood (Weiss et al., 1992). However, studies assessing causal relationships between depression and substance use, beyond establishing the important criteria of association and temporal ordering, are lacking. Moreover, few studies examining whether depression increases the risk of substance use have focused on potential gender differences in associations despite some preliminary evidence of stronger comorbid associations between depression and substance use among women compared to men (Hartka et al., 1991; Husky, et al., 2008; Kessler, et al., 1997; Ross, 1995).

In this study, we demonstrate how propensity score methods can be combined with subgroup analyses to investigate whether major depressive disorder increases the risk for later substance use and substance use disorders among men and/or women. Since depression cannot be randomly assigned through an experimental design, in attempting to estimate potential causal effects of depression on substance use, it is desirable to replicate an experimental design as closely as possible. Propensity scores have become an increasingly popular statistical technique in psychology over the past decade for this purpose (Haviland, Nagin, & Rosenbaum, 2007; Steiner, Cook, Shadish, & Clark, 2010; Stuart, 2010). It is often applied in situations in which a randomized experiment is not possible, such as when estimating the consequences of any treatment or exposure that cannot easily be randomly assigned, such as mental health disorders.

Propensity Score Methods Overview

We begin by providing some background information on propensity score methods for readers who are less familiar with this analytic technique. Propensity score methods attempt to replicate the properties of a randomized experiment by equating individuals on observed background characteristics (Rosenbaum & Rubin, 1983). In our case, we are interested in estimating the potential effect of a condition (depression), which clearly cannot be randomized, on an outcome (substance use). Propensity score methods help make those with the condition (e.g., depressed individuals) look similar to those without the condition (e.g., non-depressed individuals) on observed background characteristics, to isolate the effects of the condition on outcomes, separate from any other differences (confounding.) When comparing depressed and non-depressed individuals, ideally the depressed and non-depressed individuals would be similar on everything except depression – thus they should be of similar racial/ethnic background, age, socioeconomic status, genetic vulnerability, have similar family environments, etc.; propensity score methods, as described here, can help accomplish this.

Propensity score methods and the common approach of regression adjustment for covariates both rely on an assumption that there are no unmeasured confounders: that there are no unobserved differences between treatment groups, given the characteristics we observe (termed “ignorability” by Rosenbaum and Rubin, 1983 and sometimes referred to as “unconfoundedness”). (See Liu, Kuramoto, and Stuart (2013) for methods to assess sensitivity to this crucial assumption.) However, propensity score methods have an advantage over standard regression adjustment in that they are less reliant on model misspecification and more directly identify situations that would involve extrapolation from one treatment group to another (Drake, 1993; Ho et al., 2007; Rubin & Thomas, 2000). When the treatment and comparison groups do not have overlapping covariate distributions, standard regression adjustment will simply extrapolate from one group to another, without even necessarily identifying the problem. In contrast, common propensity score diagnostics will identify when extrapolation would be required, and will try to balance the data to reduce the need for such extrapolation. Multiple papers have shown propensity score methods to better estimate causal effects than traditional regression adjustment for covariates (Dehejia & Wahba, 1999; Ho et al., 2007; Stuart, 2010).

Combining Propensity Scores and Moderation Analyses

Psychologists have long been interested in moderation analyses (e.g., Aiken & West, 1991), and propensity score methods have been gaining attention in the psychological sciences (Thoemmes & Kim, 2011). However, little work has examined how to best combine propensity score methods with moderation analyses. One of the only studies to directly address this issue was conducted by Rassen and colleagues (2012), which tested whether a propensity score estimated for the full cohort could be validly applied to subgroups, in the context of a pharmacoepidemiological study. Rassen et al.’s study compared differences in treatment effect estimates for subgroup analyses adjusted by full cohort propensity scores versus subgroup-specific propensity scores. They concluded from their empirical and simulation studies that it was not ideal to use a propensity score estimated in the full cohort for subgroup analyses, but that estimates from both approaches were quite similar when subgroup sizes exceeded 1000 patients and with more common outcome events. As Rassen and colleagues (2012) remind us, propensity score theory predicts that a correctly specified propensity score estimated in a full cohort should remain valid within subgroups, assuming that the score correctly reflects the underlying propensity and that the cohort and subgroups are of sufficient size (Rosenbaum & Rubin, 1983). In practice, though, it is unclear how to ensure these conditions are met, particularly whether we have the true propensity score model. In a comment on Rassen et al. (2012), Marcus and Gibbons (2012) point out that particularly important considerations are that it may be difficult to correctly specify propensity scores for a full cohort in smaller samples or when the true propensity score model (i.e., the process that determines treatment status) differs substantially across subgroups (Marcus & Gibbons, 2012), for example if different factors lead to depression in men compared to women. Other concerns include whether the propensity score approach needs to be conducted (and assessed) within each subgroup or across subgroups and what the implications are for ignoring the subgroups in the propensity score process.

In order to make valid inferences about potential causal effects of depression on substance use, it is critical to isolate the impact of depression from that of confounding variables. Previous work by our research group and others found that the risk factors for depression, substance use, and their comorbidity differ somewhat by gender (Green, Fothergill, Robertson, Zebrak, Banda & Ensminger, 2013; Green, Zebrak, Fothergill, Robertson, & Ensminger, 2012; Fothergill, Ensminger, Green, & Robertson, & Juon, 2009), suggesting the importance of considering gender in the propensity score process.

In the present study, we test five approaches for combining propensity score methods with subgroup analyses. For simplicity, in all approaches we utilize full matching (Hansen, 2004; Rosenbaum, 1991), which we demonstrated previously to be particularly effective at reducing bias due to observed confounders (Stuart & Green, 2008). In these five approaches, we vary the way in which the propensity scores are estimated (Step 1) and whether the matching is done separately by gender (Step 2). See Harder, Stuart, and Anthony (2010) for more discussion of these two separate steps.

For Step 1, estimating the propensity score, we test three approaches. The first approach runs the propensity score estimation separately for men and women. We use the same set of covariates for men and women (though this is not required). This flexible approach likely yields the best propensity score model for each gender, but it can be hard to implement if there are multiple subgroups of interest, and, as discussed later, makes it harder to pool men and women in the matching process. The second approach uses a single propensity score model, without any special consideration of gender. This is arguably the easiest and least restrictive approach, but it ignores interest in differential effects by gender and therefore, its validity is not clear. The third approach can be thought of as a compromise between the first two approaches: One propensity score model is fit, but with theoretically important gender interactions. In our motivating example, these gender interactions are based on literature suggesting that risk factors for depression and substance use vary for men and women (Doherty, Green, Reisinger & Ensminger, 2008; Green et al., 2012; Green et al., 2013; Reinherz et al., 2000). In this example, we include seven gender interactions in estimating the propensity score model; however, the choice of the number of gender interactions is at the discretion of the researcher, as no guidelines exist as to the most appropriate number. Note that if all possible gender interactions are included, this is the same as the first approach described (i.e., separate male/female propensity score models).¹

Step 2 involves how those propensity scores are then used. The two options we explore are (1) full matching within gender (i.e., exact matching on gender, only matching men with men and women with women), and (2) full matching across gender (i.e., allowing men and women to be matched with each other). Although the three estimation procedures and two matching procedures could lead to three times two, or six total, procedures, we illustrate only five approaches. We exclude the approach that would estimate the propensity scores separately for men and women and then allow men and women to be matched with each other, since in that case the resulting propensity scores would not be comparable across groups (e.g., a “0.2” in men would not mean the same thing as a “0.2” in women). This is not a problem when matching within gender, but would be problematic with matching across gender. Thus, the five approaches we consider are:

1. estimating the propensity score separately for men and women and then matching within gender (“stratified approach”),

2. estimating a joint propensity score (with the subgroups of interest included as predictors) and matching without consideration of gender (“joint approach”),

3. estimating a joint propensity score and exact matching on gender (“joint model, separate matching”),

4. estimating a joint propensity score with gender interactions and matching without consideration of gender (“interaction approach”), and

5. estimating a joint propensity score with gender interactions and exact matching on gender (“interaction model, separate matching”).

Our specific research questions of interest are as follows. First, of the different strategies for combining subgroup analyses with propensity score matching, which is most valid as judged by which produces the greatest balance (the most similarity) between the depressed and non-depressed groups? Second, do the different strategies for combining propensity scores with subgroup analyses yield different substantive conclusions?

Methods

Study Design

Data from this study come from the Woodlawn Study, a longitudinal study of urban African Americans followed from age six to age 42 with assessments in childhood (age 6, N=1242), adolescence (age 16, N=705), young adulthood (age 32, N=952) and midlife (age 42, N=833). This community cohort study began in 1966 and included all but 13 families with first grade students in one of the 13 public or parochial schools in the neighborhood of Woodlawn (one of 76 defined community areas of Chicago). At the time the study began, Woodlawn was characterized by overcrowding, single-mother households, and poverty; however, there was also some diversity within the community with some blocks having high rates of home ownership and high levels of employment and education (Council for Community Services, 1975).

Data has been collected from teachers, mothers, individuals themselves, school records, crime records, and death records over time. The initial population included 1,242 individuals. The current analyses are based on those who participated in the young adult follow-up (N=952), which included 496 women and 456 men. At all stages of research, informed consent has been obtained from participants and/or their mother/guardian. The University of Maryland and the Johns Hopkins Bloomberg School of Public Health Institutional Review Boards approved the conduct of this study. Additional details on the Woodlawn Study, including detailed attrition analyses, are available elsewhere (Crum et al., 2006; Ensminger, Juon & Fothergill, 2002; Green, Doherty, Zebrak, & Ensminger, 2011; Kellam, Branch, Agrawal, & Ensminger, 1975).

Measures

Independent Variable

The exposure of interest is lifetime major depressive disorder by age 32. Depression was assessed at the young adult interview by a module from the Michigan version of the Composite International Diagnostic Interview (CIDI-UM) to diagnose lifetime major depressive disorder according to the Diagnostic and Statistical Manual (DSM-III-R) criteria (Kessler, McGonagle, Swartz, Blazer, & Nelson, 1993). Fifteen percent of males and 16% of females met lifetime criteria for major depressive disorder.

Dependent Variables

Substance use and disorders were assessed at the midlife interview (age 42). Adult interviews assessed abuse and dependence of alcohol, marijuana, cocaine, heroin, analgesics, inhalants, hallucinogens, barbiturates, tranquilizers, stimulants, and sedatives. Six outcomes were considered. These included meeting criteria for alcohol abuse within the past 10 years, meeting criteria for alcohol dependence within the past 10 years, heavy drinking (five or more drinks on drinking days) in the past 10 years, meeting criteria for drug abuse within the past 10 years, meeting criteria for drug dependence within the past 10 years and being a current smoker. Substance use diagnoses were based on DSM IV criteria and obtained via a module modeled after the CIDI modules developed for the National Comorbidity Survey (Kessler et al., 1994).

Matching Variables

In our attempt to equate depressed individuals with non-depressed individuals on observed background characteristics, we included 24 variables from childhood (age six) and adolescence (age 16) in the propensity score model. These included maternal history of depressed mood, SES indicators (poverty, female headed household, mother’s years of schooling), low birth weight, IQ, behavioral problems in first grade (shyness, aggression, conduct problems) as rated by the first grade teacher, reading scores, maternal school aspirations, family discipline in terms of harsh punishment in childhood, parental supervision regarding substance use in adolescence, family conflict in adolescence, adolescent depressive symptoms and angry symptoms, adolescent school attachment, adolescent delinquency, maternal substance use, and adolescent substance use onset (smoking, hard liquor, marijuana). These variables were selected because of their relationship with depression and/or substance use or their statistical association with potential unobserved variables that may be predictive of depression and/or substance use. They are based on the social fields of the Life Course Social Fields Perspective, which has long guided the Woodlawn Study (Kellam et al., 1975), as well as previous empirical findings (e.g., Green et al., 2013; Green et al., 2012; Fothergill et al., 2009).

Analytic Plan

The first step in the analysis involved estimating the propensity score using the three approaches described above. In the “interactions model” we included seven theoretically important interactions between gender and (1) aggressive behavior, (2) childhood poverty, (3) adolescent poverty, (4) female-headed household, (5) mother’s education, (6) maternal school aspirations, and (7) parental supervision regarding substance use. When estimating propensity scores, missing data on childhood and adolescent matching variables were accounted for through mean imputation, and a missing data indicator was included in the propensity score model if greater than 10% of individuals had missing values for a given variable (Haviland et al., 2008). All three approaches used logistic regression to estimate the propensity scores. For each logistic regression, depression was the dependent variable and the matching variables (e.g., maternal history of depressed mood, first grade behavioral problems, family conflict) served as predictors. The propensity scores themselves were then obtained as the predicted probabilities from each model, calculated for each individual. These propensity scores, which vary from zero to one, represent the probability of being depressed based on the observed covariates included in the logistic regression model.

Full matching using the propensity scores followed the propensity score estimation (Hansen, 2004; Rosenbaum, 1991; Stuart & Green, 2008), either matching within or across gender. Full matching uses all individuals in the data by forming a series of matched sets based on the propensity score, where each set has at least one exposed individual (i.e., depressed) and at least one comparison (i.e., non-depressed) individual. Matched sets are formed in an optimal way in that exposed individuals who have many comparison individuals with similar propensity scores will be grouped with many comparison individuals, whereas exposed individuals with few similar comparison individuals will be grouped with relatively fewer comparison individuals. The ratio of exposed to comparison individuals in each set depends on the relative number of exposed and comparison individuals with similar propensity scores, and the algorithm minimizes the sum of the differences in propensity scores between all pairs of exposed and comparison individuals within each matched set. As demonstrated in Stuart and Green (2008), we use the full matching sets to form weights, which are then used in the outcome analyses. Exposed individuals are assigned a weight of one while comparison individuals received a weight proportional to the number of exposed individuals divided by the number of comparison individuals in their set; this serves to weight the comparison individuals to look like the group of exposed individuals. The sum of the comparison individuals' weights is scaled to equal the total number of comparison individuals. These weights are used in the calculation of balance measures and in the outcome regression models, as described next. The matching was conducted in the MatchIt Program for R (Ho, Imai, King & Stuart, 2007).

After each approach, and separately for each gender, we examined balance (covariate similarity) across exposed and comparison groups using the standardized difference (see Austin and Mamdani, 2006), a quantity similar to effect size or Cohen’s d, calculated for each covariate. To calculate the standardized differences for each covariate after full matching we used the weights created by full matching to calculate the weighted difference in means between two groups (e.g., depressed women and non-depressed women), divided by the gender-specific standard deviation in the original depressed group (Rubin, 2001). If the matching was successful at reducing covariate differences between exposed and comparison groups the standardized differences calculated using the full matching weights would be smaller (in absolute value) than those in the original data (without the full matching weights). This balance diagnostic also allowed us to compare balance directly across the five approaches since all of the balance measures were on the same standard deviation metric. We assessed balance within gender as achieving this balance was critical to the validity of the causal conclusion regarding effect modification by gender.

After propensity score matching, we employed multiple imputation to reduce bias due to differential attrition by depression status (Rubin, 1987). (Analyses were based on those with observed depression status in young adulthood, and above we described how we handled missing covariate values in the propensity score estimation; thus, outcomes were the only variable needing imputation). We thus imputed missing values for outcome variables only multiple times using reasonable predictions, creating multiple datasets with complete data. We created 40 multiple imputations as recommended by Graham, Olchowski, and Gilreath (2007) to maximize study power and account for uncertainty in the imputed values. Using the mim command in Stata, we ran the outcome logistic regression analyses separately in each imputed dataset, and then the results were automatically combined by the software using the standard combining rules (Rubin, 1987). The estimates generated account for within and between imputation uncertainty, resulting in correct standard error estimates and coverage rates.

After the creation of weights using full matching and the imputation of outcomes we used logistic regression analyses to estimate the effects of interest. For each weighted logistic regression analysis, the independent variable was the binary indicator of meeting depression criteria by young adulthood. The dependent variable was one of the binary substance use indicators (i.e., midlife alcohol abuse, alcohol dependence, heavy drinking, drug abuse, drug dependence, and smoking). The interaction of gender and depression, as well as gender, was included in the logistic regressions to determine whether the consequences of depression vary across genders. No other covariates were added to simplify the models and enable us to report marginal effects. We compare the five propensity score methods described above to the traditional covariate-adjusted regression model (i.e., unweighted multivariate logistic regression controlling for all matching variables). Outcome models were fit in Stata 11 SE using the iweight option.

Results

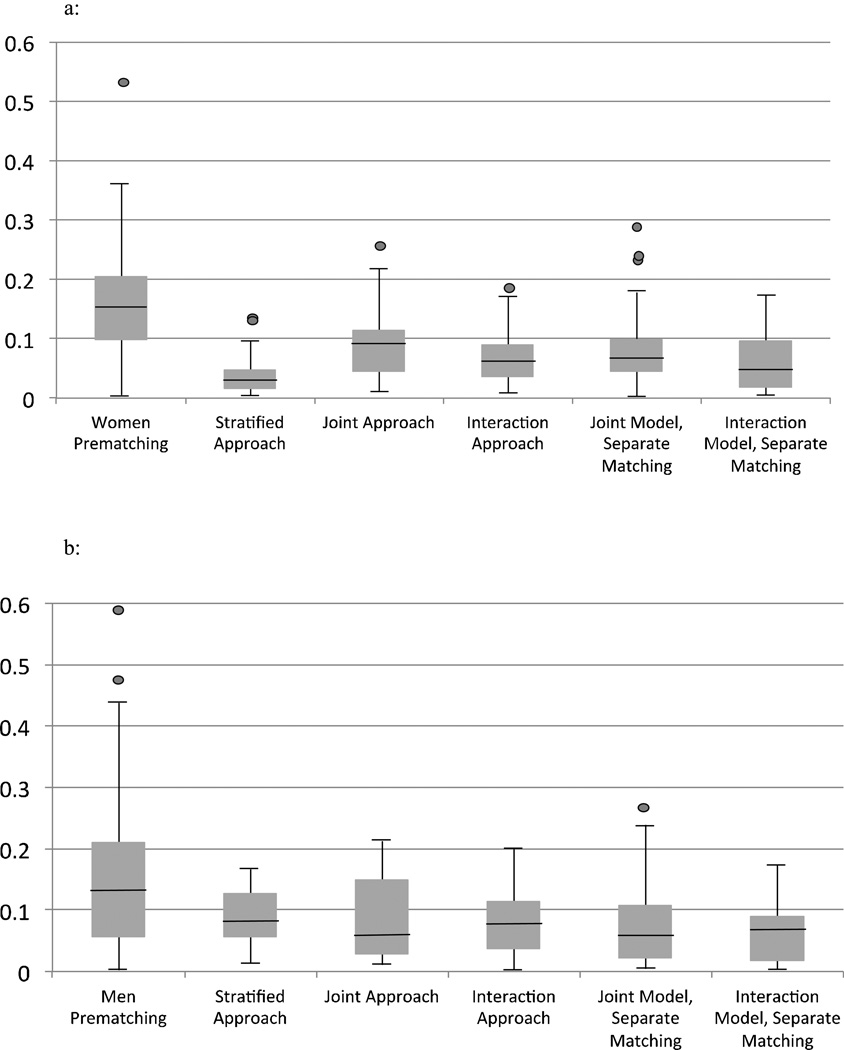
Figure 1a displays the distribution of the absolute standardized differences for the original data before matching and for each of the five propensity score methods for women. As can be seen in this figure, we were able to achieve the best overall balance with the “stratified approach;” this approach yields the lowest mean absolute standardized difference (see Table 2a) as well as a small spread of standardized differences. The absolute standardized difference decreased in 23 of the 24 variables compared to the original sample of women, and all but two were below the conventional standard of 0.10 (all were less than 0.15), which represents acceptable balance (Stuart et al., 2009). The two approaches that included gender interactions (“interaction approach” and “interaction model, separate matching”) also showed significant reductions in the standardized differences for women after matching, with all absolute standardized differences less than 0.20 and the vast majority less than 0.10. The two joint approaches (i.e., the approaches that ignored our interest in subgroups) performed the worst. In the “joint approach,” 10 absolute standardized differences were greater than 0.10 and one was greater than 0.20. For the “joint model, separate matching,” six absolute standardized differences were greater than 0.10 and three were greater than 0.20.

Figure 1.

a: Balance for Women: Boxplots of Absolute Standardized Differences

b: Balance for Men: Boxplots of Absolute Standardized Differences

Note: PS=Propensity Score. Standardized difference (SD) is the weighted difference in means between the depressed and non-depressed individuals, divided by the gender-specific standard deviation in the original depressed group. Boxplots are of the SDs for each covariate as shown in Table 2.

Table 2.

a: Comparison of Absolute Standardized Differences (SDs) Before and After Matching: Women (N=496)
Variable	Women Before PS Methods	Stratified Approach	Joint Approach	Interaction Approach	Joint Model, Separate Matching	Interaction Model, Separate Matching
Propensity Score	0.807*	0.008	0.139	0.094	0.043	0.016
Maternal Depression Time 1	0.005	0.041	0.011	0.042	0.015	0.021
Maternal Depression Time 2	0.138	0.016	0.064	0.086	0.059	0.015
Intelligence Quotient (IQ)	0.151	0.013	0.114	0.052	0.295	0.054
Shy Behavior	0.178	0.021	0.142	0.086	0.054	0.064
Aggressive Behavior	0.262	0.034	0.096	0.106	0.092	0.050
Conduct Problems	0.215	0.120	0.045	0.066	0.068	0.045
Reading Ability	0.015	0.088	0.039	0.102	0.223	0.133
Childhood Poverty Status	0.057	0.022	0.261	0.067	0.237	0.018
Adolescent Poverty Status	0.076	0.063	0.013	0.071	0.158	0.014
Female Headed Household	0.173	0.033	0.085	0.026	0.076	0.043
Mother's Years of Schooling	0.100	0.061	0.039	0.018	0.034	0.053
Maternal School Aspirations	0.176	0.007	0.093	0.061	0.055	0.097
Harsh Punishment	0.185	0.016	0.022	0.019	0.041	0.122
Low Birth Weight	0.100	0.015	0.100	0.115	0.075	0.033
Adolescent Depressive   Feelings	0.204	0.005	0.100	0.071	0.090	0.140
Adolescent Angry Feelings	0.307	0.096	0.171	0.112	0.008	0.070
School Bonds	0.168	0.048	0.150	0.090	0.046	0.069
Parental Supervision	0.122	0.117	0.105	0.021	0.050	0.103
Family Conflict	0.524	0.029	0.123	0.009	0.099	0.010
Adolescent Delinquency	0.329	0.025	0.079	0.032	0.058	0.173
Maternal Substance Use	0.030	0.024	0.108	0.191	0.137	0.114
Adolescent Hard Liquor Use	0.099	0.013	0.104	0.043	0.077	0.007
Adolescent Marijuana Use	0.096	0.025	0.065	0.060	0.003	0.005
Adolescent Smoking	0.145	0.028	0.026	0.036	0.102	0.053
Mean Absolute (Abs) SD	0.186	0.039	0.092	0.067	0.088	0.061
# of Abs SDs that Decreased	n/a	23	20	20	19	22

b: Comparison of Absolute Standardized Differences (SDs) Before and After Matching: Men (N=456)
Variable	Men Before PS Methods	Stratified Approach	Joint Approach	Interaction Approach	Joint Model, Separate Matching	Interaction Model, Separate Matching
Propensity Score	0.599	0.059	0.063	0.034	0.005	0.005
Maternal Depression Time 1	0.003	0.130	0.036	0.027	0.056	0.063
Maternal Depression Time 2	0.068	0.057	0.076	0.096	0.064	0.102
Intelligence Quotient (IQ)	0.032	0.086	0.148	0.080	0.196	0.090
Shy Behavior	0.045	0.167	0.213	0.057	0.108	0.017
Aggressive Behavior	0.058	0.134	0.185	0.038	0.059	0.031
Conduct Problems	0.040	0.126	0.147	0.012	0.021	0.061
Reading Ability	0.253	0.017	0.018	0.108	0.143	0.071
Childhood Poverty Status	0.471	0.014	0.111	0.063	0.267	0.015
Adolescent Poverty Status	0.210	0.089	0.026	0.044	0.139	0.088
Female Headed Household	0.306	0.114	0.149	0.002	0.091	0.067
Mother's Years of Schooling	0.079	0.082	0.206	0.096	0.011	0.007
Maternal School Aspirations	0.106	0.024	0.021	0.114	0.036	0.135
Harsh Punishment	0.265	0.001	0.022	0.044	0.072	0.007
Low Birth Weight	0.028	0.092	0.032	0.012	0.031	0.088
Adolescent Depressive   Feelings	0.197	0.095	0.080	0.074	0.013	0.106
Adolescent Angry Feelings	0.207	0.126	0.012	0.118	0.009	0.011
School Bonds	0.112	0.031	0.129	0.166	0.174	0.172
Parental Supervision	0.071	0.002	0.030	0.079	0.084	0.048
Family Conflict	0.236	0.031	0.161	0.193	0.053	0.145
Adolescent Delinquency	0.204	0.098	0.039	0.114	0.050	0.079
Maternal Substance Use	0.132	0.075	0.176	0.012	0.111	0.081
Adolescent Hard Liquor Use	0.017	0.035	0.028	0.199	0.083	0.084
Adolescent Marijuana Use	0.138	0.049	0.040	0.040	0.018	0.004
Adolescent Smoking	0.153	0.071	0.028	0.181	0.005	0.111
Mean Absolute (Abs) SD	0.161	0.042	0.087	0.080	0.076	0.068
# of Abs SDs that Decreased	n/a	17	14	15	17	17

Note: PS=Propensity Score. Bolded font indicates SDs whose absolute value decreased in comparison with the original sample.

^*This outlier is omitted from Figure 1a to assist in readability.

As shown in Figure 1b, for men, we also achieved the best balance in the “stratified approach.” This approach had the lowest mean absolute standardized difference (see Table 2b). While the absolute standardized differences were greater than 0.10 for five covariates when using this approach, all were less than 0.20, and the absolute standardized difference decreased for 16 out of 24 observed covariates after matching (see Table 2b). Table 2b also shows that both approaches with gender interactions for men achieved acceptable balance with all standardized differences less than 0.20 and the majority less than 0.10. Neither of the joint approaches had the consistently low standardized differences as the “stratified approach.” Both joint approaches had at least one standardized difference greater than 0.20.

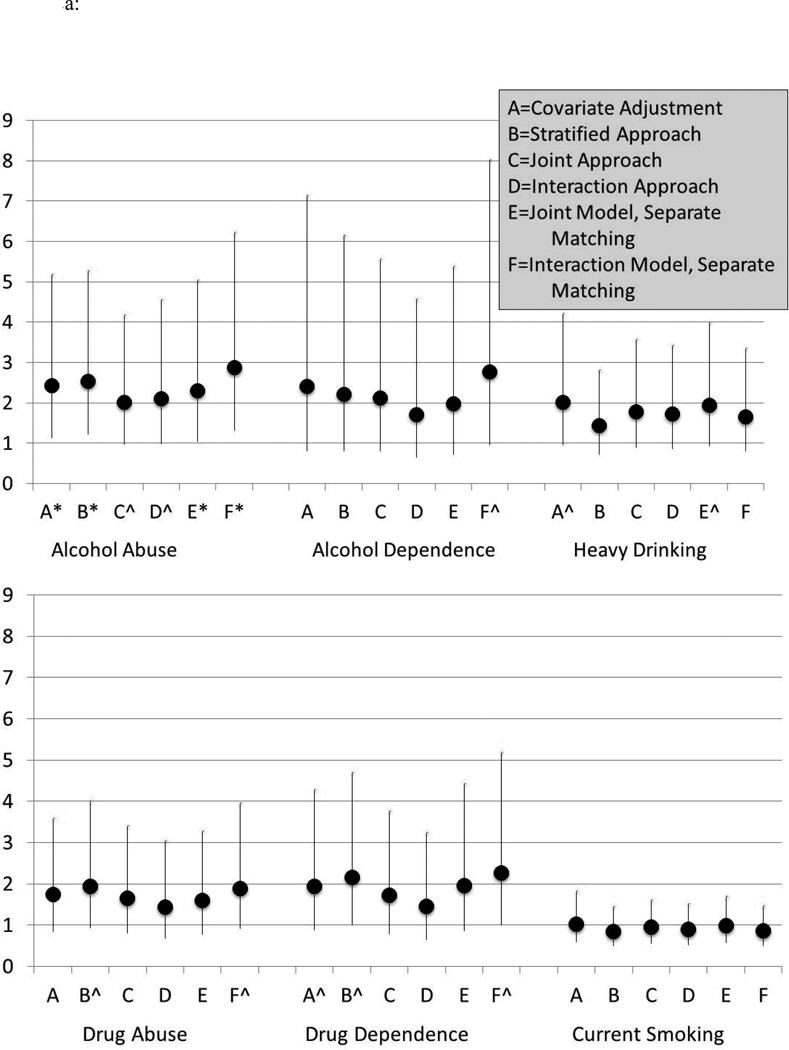
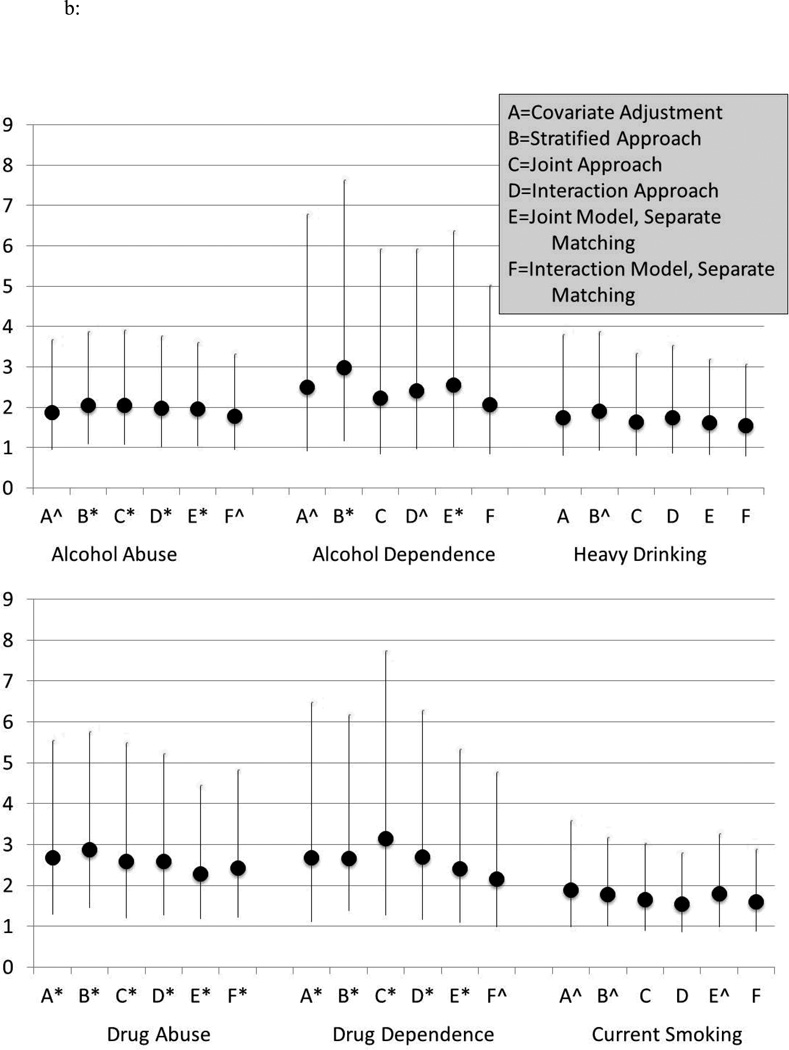
Next, we examined impact estimates for each of the approaches for six different substance use outcomes for women (Figure 2a) and men (Figure 2b) separately. We compare the five propensity score approaches with that from a traditional regression with covariate adjustment. We find similarity in estimates across the six approaches for both men and women. For example, for women’s alcohol abuse, odds ratios ranged from 2.01 (p=0.06) for the “joint approach” to 2.87 (p<0.01) for the “interaction model, separate matching.” For four of the approaches, the association of depression by young adulthood with midlife alcohol abuse for women was statistically significant at p<0.05. For the other two approaches (those that matched across gender), it was marginally statistically significant (p=0.06 for both the “joint approach” and the “interaction approach”). For men’s alcohol abuse, odds ratios ranged from 1.78 (p=0.07) for the “interaction model, separate matching” to 2.05 (p=0.03) for the “stratified approach.” We found associations statistically significant at the p<0.05 level in four of the approaches and marginally significant in two approaches (p=0.07 with covariate adjustment and in the “interaction model, separate matching”). This pattern is somewhat consistent across the other five substance use outcomes whereby the estimates are relatively similar but the statistical significance varies. Thus, our conclusion about whether depression by young adulthood potentially affects alcohol abuse in midlife varies somewhat, but not tremendously, depending on our analytic approach. The most consistently strong associations are for men’s midlife drug abuse and drug dependence as potential consequences of depression.

Figure 2.

a: Comparison of Outcome Estimates for Women across Analytic Methods: Odds Ratios and Confidence Intervals for the Impact of Depression on Substance Use Outcomes

b: Comparison of Outcome Estimates for Men across Analytic Methods: Odds Ratios and Confidence Intervals for the Impact of Depression on Substance Use Outcomes

Note: *p<0.05, ^p<0.10

Overall, we did not find evidence of effect modification; the gender by depression interaction term did not achieve statistical significance in any of the approaches, suggesting that consequences did not vary for men and women. As shown in Figure 2, the odds ratios for men and women were highly comparable for all of the substance use outcomes, with the exception of smoking in which there appeared to be an elevated risk for men but not women. (This interaction term was marginally significant (p=0.06) in the “stratified approach” and non-significant in all other approaches.)

Discussion

In estimating the effect of a treatment, exposure, or condition, researchers are often interested in whether the effect is consistent across different populations or subgroups, such as gender, racial or socioeconomic groups. This is particularly true given recent interest in personalized medicine and treatment effect heterogeneity (Hamburg & Collins, 2010; Kravitz, Duan, & Braslow, 2004; Ng, Murray, Levy & Venter, 2009). Despite these interests, most studies examining subgroup differences in a treatment effects using propensity score methods pay little attention to the interest in subgroups when choosing the most appropriate propensity score approach. In this article, we demonstrate various options for combining propensity score analyses with investigation of effect modification. The most important conclusion is that it is necessary to think about subgroup effects before estimating the propensity score; just as subgroup analyses should be prespecified in randomized experiments, similar prespecification and consideration should be done in non-experimental studies. The conventional propensity score approaches that ignore interest in subgroup specific estimates performed the poorest in terms of creating balance between the depressed and non-depressed individuals within each gender. Creating balance between the exposed and non-exposed is the goal of propensity score methods and thus, the approach that creates that best balance (judged in this study through standardized differences) is the approach that allows for stronger inferences regarding causality. Thus, we suggest deciding in advance of choosing a propensity score approach if there is a substantive interest in effect modification as this should guide the selection of the propensity score approach.

Perhaps not surprisingly, our study found the best balance is achieved for each gender when the propensity score approach is done separately by gender. (We note that our simple approach could be even further tailored for each gender by including different covariates or interaction terms). Overall, propensity score estimation and matching separately within subgroups is the recommended approach when possible. However, this subgroup specific approach is most viable when there are a minimal number of subgroups of interest and when subgroups are of an adequate size to allow matching within each subgroup. An additional advantage of subgroup specific approaches is that it is easier to compare balance between the exposed and non-exposed within subgroups. This balance checking within subgroups is more cumbersome with propensity score models that match across subgroups as this diagnostic is not typically part of propensity score program output. We calculated the gender-specific standardized differences by hand for the two propensity score models with matching across gender. When subgroup-specific effects are of interest it is important to check balance within subgroups even if the propensity score procedure is done across subgroups.

In cases where it is not practical or feasible to estimate subgroup specific propensity scores, we found that both propensity score models with numerous gender interactions also performed relatively well, regardless of whether the matching was done separately by gender. This may be a particularly attractive option when there are numerous subgroups and estimating subgroup specific propensity scores, and doing the matching separately for each subgroup, is prohibitive. Thus, it was encouraging that the gender interaction approach with matching across genders seemed to perform as well as the gender interaction approach with matching within gender, as within subgroup matching is not always feasible. It is typically relatively easy in most propensity score programs to incorporate interaction terms, even a large number of them, into the propensity score model. However, the success of this approach in achieving balance is dependent on the number and the choice of interactions, and we recommend being generous in choosing the number to include, relying on previous work and theory to guide selection.

We found little difference in the magnitude of impact estimates across approaches though there was variability in statistical significance, and thus potential variability in conclusions drawn had only one approach been applied. We have greatest confidence in the results from the stratified approach since this achieved the best balance within gender. Although in this motivating example we find similar results from traditional regression adjustment and the propensity score methods, that will not always be the case, and researchers should have more confidence in the propensity score-adjusted results, as they provide better covariate adjustment and less reliance on correct outcome model specification.

Substantively, we found evidence that having a diagnosis of major depression by young adulthood seemed to increase the risk of multiple substance use outcomes for both men and women, providing support for the self-medication hypothesis, particularly for alcohol abuse for women and substance abuse and dependence for men. This study adds to accumulating evidence that self-medicating depression can lead to negative outcomes (Bolton, Robinson, & Sareen, 2009; Crum et al., 2013). Understanding the role of depression as a risk factor for later life substance use and problems among African Americans is critical for reducing health disparities in substance use, as previous work shows that African Americans are more likely than Whites populations to develop substance use problems in midlife (French, Finkbiner, & Duhamel, 2002).

We found little evidence of gender differences in the substance use consequences of depression, suggesting the importance of this issue for both men and women. The only evidence of a potential gender difference was with regards to smoking. We found that depressed men (not women) had an increased risk of smoking in midlife, although the gender interaction term was not statistically significant. This finding is in contrast with the literature that has found a greater association between depression and smoking behavior in a national sample of women compared to men (Husky, Mazure, Paliwal, & McKerr, 2008). Thus, more research is necessary to identify the robustness of this finding for African Americans.

It is important to acknowledge the limitations of this work. First, we used balance as the measure of success of an approach. We feel that this is an appropriate strategy, since this is what researchers will be able to assess in real data analyses. However, future work should do in depth simulation studies to assess the bias in outcome effect estimates (i.e., how much the effect estimate varies from the true effect), rather than using balance as a proxy. Second, a limitation of all propensity score methods is the potential for unobserved confounding. We believe that we have matched on a sufficient set of variables (feasible because of the extensive longitudinal data available on the Woodlawn sample) but future work should conduct analyses of sensitivity to unobserved confounders (e.g., Liu et al., 2013).

In this paper we explored five different approaches for estimating subgroup specific treatment effects when using propensity score methods in non-experimental studies. In this example, the approach used yielded varying performance in terms of the covariate balance within subgroups, and we stress the importance of checking balance within subgroups when subgroup-specific treatment effects will be estimated. We hope this article will encourage researchers who are applying these techniques to carefully consider the best methodology to answer their research questions and apply these techniques appropriately.

Table 1.

Sample Characteristics (N=952)

	Women (N=496)	Men (N=456)
Exposure Variable (age 32)
Depression Diagnosis	16.1%	15.1%
Midlife Outcomes (age 42)
Alcohol Abuse past 10 years	13.7%	33.2%
Alcohol Dependence past 10 years	6.5%	11.2%
Heavy Drinking past 10 years	12.0%	23.7%
Drug Abuse past 10 years	14.5%	20.4%
Drug Dependence past 10 years	11.8%	13.1%
Current Smoking	39.3%	50.9%