Detecting differential protein expression in large-scale population proteomics

Abstract

Motivation: Mass spectrometry (MS)-based high-throughput quantitative proteomics shows great potential in large-scale clinical biomarker studies, identifying and quantifying thousands of proteins in biological samples. However, there are unique challenges in analyzing the quantitative proteomics data. One issue is that the quantification of a given peptide is often missing in a subset of the experiments, especially for less abundant peptides. Another issue is that different MS experiments of the same study have significantly varying numbers of peptides quantified, which can result in more missing peptide abundances in an experiment that has a smaller total number of quantified peptides. To detect as many biomarker proteins as possible, it is necessary to develop bioinformatics methods that appropriately handle these challenges.

Results: We propose a Significance Analysis for Large-scale Proteomics Studies (SALPS) that handles missing peptide intensity values caused by the two mechanisms mentioned above. Our model has a robust performance in both simulated data and proteomics data from a large clinical study. Because varying patients’ sample qualities and deviating instrument performances are not avoidable for clinical studies performed over the course of several years, we believe that our approach will be useful to analyze large-scale clinical proteomics data.

Availability and Implementation: R codes for SALPS are available at http://www.stanford.edu/%7eclairesr/software.html.

Contact: wenzhong.xiao@mgh.harvard.edu

Supplementary information: Supplementary materials are available at Bioinformatics online.

1 INTRODUCTION

Mass spectrometry (MS) in large-scale clinical studies provides new insights into how disease affects our bodies at the molecular level (Altelaar et al., 2013; Paczesny et al., 2010), identifying and quantifying thousands of proteins in patients’ samples. Even though MS is a powerful tool in biomedical research, it is subject to white noise, chemical noise and stochastic variation, needing robust and sophisticated bioinformatics algorithms (Nesvizhskii, 2010; Ryu, 2014). One of the challenges in analyzing MS data is the absence of peptide abundance in a subset of the measurements. Peptides are often not observed because of their low intensities. And this intensity-dependent missing trend can introduce bias into downstream analyses when it is ignored. Wang et al. (2006) suggested a normalization procedure using the top-L ordered statistics of peptide intensities in each sample (L is a user-defined threshold) and proposed an imputation approach. Karpievitch et al. (2009) modeled the random missing mechanism and the peptide intensity-dependent missing mechanism assuming that instrument detection thresholds vary from one peptide to the other. Wang et al. (2012) carried out an intensity-based analysis and a presence/absence analysis separately and controlled their false discovery rates. In Wang et al. (2012), they argued that logistic regressions were not adequate to analyze presence/absence data when all intensity values were missing for one group. However, it is not a problem of the logistic regression, but rather a problem of the test statistics in the logistic regression. In the situation when all or almost all peptide abundances are missing, Wald tests overestimate P-values of the significant tests, but log-likelihood ratio tests do work reliably (Hauck and Donner, 1977). Thus, using a mixture model approach with proper test statistics instead of fitting two models separately may be better.

Another challenge in the MS data analysis is that experiments sometimes have different total numbers of quantified peptides. This phenomenon is often observed in MS studies (Wang et al., 2006) and is inevitable for large-scale clinical studies because the studies are often performed over the course of several years. The quality of patient samples varies because of their different storage time and the performance of the instrument(s) changes due to the tuning of the MS instruments or the degradation of the liquid chromatography (LC) columns over time. Varying total numbers of quantified peptides result in unequal numbers of missing peptide values across experiments. An experiment with a smaller total number of quantified peptides has more missing peptide abundances. For example, let us assume that Experiment A produced 4000 quantified peptides and Experiment B produced only 2000 quantified peptides because the quality of biological sample B was not as good as A. Then, Experiment B has 2000 missing peptide intensities compared with Experiment A. Now, to investigate this missing mechanism further, assume that one peptide named X is present in Experiment A, but absent in Experiment B. Another peptide named Y is present in both experiments. The reason why peptide X is absent in Experiment B but present in Experiment A can be one of the following: (i) peptide X is less abundant in Experiment B than in Experiment A (intensity-dependent missing mechanism); (ii) peptide X is not abundant enough to be in the top 2000 quantified peptides (total quantification-dependent missing mechanism); or (iii) peptide X is missing at random. Here, the total quantification-dependent missing mechanism should not be confused with the intensity-based missing mechanism. The total quantification-dependent missing mechanism implies that peptide X may be less abundant than peptide Y that is listed in the top 2000 quantified peptides of Experiment B. However, such missing values are not informative because we are not comparing peptide X with peptide Y (at least not in this article), but comparing the abundances of the peptide X between the Experiment A and B. Thus, it would introduce bias if we blindly use the censored approach proposed previously, assuming the missing values are caused by the lower abundance of peptide X in Experiment B compared with Experiment A. Karpievitch et al. (2009) and Wang et al. (2012) did not deal with the issue of total quantification-dependent missing values.

Figure 1 demonstrates a peptide expression profile with the intensity-dependent missing values and the total quantification-dependent missing values. A colored cell represents observed peptide abundance, while a white cell represents missing peptide abundance. Two different colors—blue and red—represent two sample groups (i.e. controls versus patients). The missing values in part A of Figure 1 are only from the intensity-dependent missing mechanism. The missing values in part B result from both the intensity- and total quantification-dependent missing mechanisms. Because the missing values resulting from the varying total quantification are not informative, one way to deal with these missing values is to remove them.

Fig. 1.

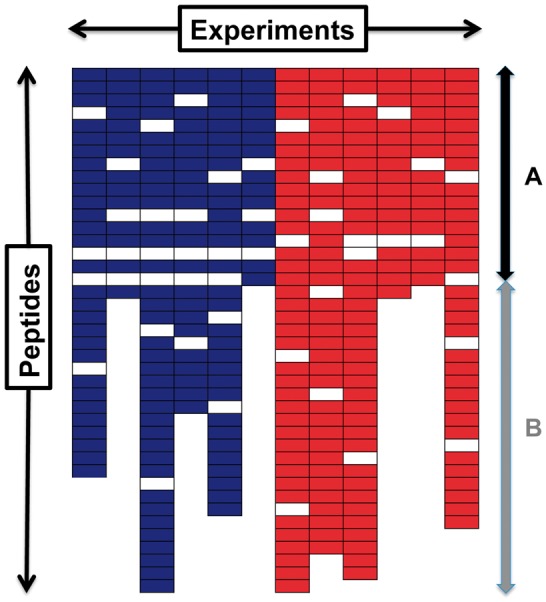
An example of the peptide experiment profile measured in a MS proteomics study. The rows and columns of this profile represent peptides and experiments, respectively. Different colors imply different groups (i.e. control versus patients). A colored cell represents the abundance of a peptide observed, while a white cell represents a missing observation of peptide abundance. The missing values in part A are only from the intensity-dependent missing mechanism, and in part B from both the intensity- and total quantification-dependent missing mechanisms

In this article, we propose a Significance Analysis for Large-scale Proteomics Studies (SALPS) that filters the total-quantification-dependent missing values and makes use of the intensity-dependent missing values. Using simulated data, we show how SALPS performs with the missing values generated from the two mechanisms. Finally, we demonstrate our model performance using proteomics data of human blood monocytes in a large-scale clinical study of trauma patients.

2 METHOD

2.1 Definitions

Here we define the terms frequently used in this article. A peptide is a short chain of amino acids or a substring of a protein; thus, multiple peptide sequences observed in an experiment can come from the same protein. In a typical high-throughput proteomics study, the levels of the peptides are quantified by the peak intensities in the LC-MS spectra. Because one peptide eluted over time, the peptide intensity was a sum of peak intensities of multiple LC/MS spectra. A quantified peptide was a peptide with non-zero peptide intensity in a given experiment. One peptide with the same sequence could have multiple charge states (i.e. 2, 3 or 4). One could either combine all charge states of the same peptide and use it as one peptide intensity or treat the peptide with different charge states as different peptides and used them as separate peptide intensities. In our data analysis, we used the latter approach.

2.2 Significance Analysis for Large-scale Proteomics Studies

Censored regression with filtering

This section describes how we used intensity-dependent missing values using a censored regression and how we filtered quantification-dependent missing values. Our censored regression was a mixture of two models: a probit regression that modeled presences/absences of peptide intensities and a linear regression that modeled peptide intensities. For each protein, a censored regression was constructed as the following:

$$\begin{array}{l}{y}_{ijl}=\{\begin{array}{cc}\mu +P_i+G_j+{\mathrm{ϵ}}_{ijl}& \text{if}{m}_{ijl}=0,\\ 0& \text{if}{m}_{ijl}=1,\end{array}\\ {\mathrm{ϵ}}_{ijl}\sim N(0,{\sigma }^2),\\ \\ m_{ijl}\sim Bernoulli(p_{ij})\\ p_{ij}=\Phi (\mu \prime +P{\prime }_i+G{\prime }_j),& \end{array}$$ (1)

where $i=1,\mathrm{...},m$ was the index of a peptide, j = 1, 2 was the index of a group and $l=1,\mathrm{...},n_j$ was the index of a biological replicate within a group. y_ijl represented a log-transformed intensity of peptide i measured in biological replicate l of study group j. y_ijl was positive when m_ijl = 0. ${\sigma }^2$ represented the variance of y given covariates. m_ijl represented an indicator variable—whether a peptide quantification was absent ($=1$) or not ($=0$). p_ij was a probability of missing peptide quantification. Φ was the standard cumulative normal distribution. $\mu \prime$ estimated a proportion of peptide intensities that were absent at random. We also adjusted the differences in the intensity values and missing rates between peptides by adding P_i and $P{\prime }_i$ terms. It was known that even though peptides from the same protein had the same abundance in a biological sample, their peak intensities and missing rates varied because of their different ionization efficiencies and detectibilities (Tang et al., 2006). Thus, it was necessary to adjust these differences.

Equation (1) contained peptide terms and group terms for both the linear regression part and the probit regression part. Here, we let ${\beta }_g=G_2-G_1$ and ${\gamma }_g=G{\prime }_2-G{\prime }_1$ for a convenience. Then, a positive value of ${\beta }_g$ implied that a protein of interest was more abundant in Group 2 compared with Group 1. A negative value of ${\gamma }_g$ implied that the protein had less missing values in Group 2 compared with Group 1. Thus, ${\beta }_g$ and ${\gamma }_g$ had opposite signs in the ideal case.

Before constructing the final censored regressions and testing for the differential proteins, we removed the total quantification-dependent missing values by determining the filtering threshold such that high proportions of ${\beta }_g$ and ${\gamma }_g$ had opposite signs. Graphically, it attempted to remove the vertical white spaces in part B in Figure 1. First, we obtained a median value of observed intensities from all experiments for each peptide. According to these median peptide intensities, we assigned ranks to the peptides in a descending order. Then, we let k_il be a ratio between the rank of peptide i and the total number of quantified peptides in Experiment l. For instance, if peptide i was ranked in ${2000}^{th}$ place and Experiment l had 1000 quantified peptides, then its k value would be $2(=\frac{2000}{1000})$. Next, we fit the model (1) after filtering the missing values with various thresholds of k scores. (We expressed the threshold of k’s as k_th.) We measured the percentage of ${\beta }_g$ and ${\gamma }_g$ having opposite signs with various k_th values in {1, 1.5, 2, 2.5, …}. Then, we chose the k_th that produced the largest percentage of ${\beta }_g{\gamma }_g<0$ and filtered all missing values with their k values greater than k_th.

After filtering the total quantification-dependent missing values, we were left with the intensity-dependent missing values and constructed the final model (1). The likelihood of this model was the following:

$$L={\displaystyle \prod _{ijl}{[(1-p_{ij})\sigma \varphi (\sigma (y_{ijl}-{\nu }_{ij}))]}^{1-m_{ijl}}}{[p_{ij}]}^{m_{ijl}},$$ (2)

where ${\nu }_{ij}=\mu +P_i+G_j$.

Maximum likelihood estimates of parameters were same as the linear regression and probit regression. Thus, we estimated these parameters using a standard package of linear regression and probit regression in R. This model reduced to a probit regression when all peptide intensity values in one group were missing, while it reduced to a linear regression when all peptides intensity values were present. This model was similar to a lognormal Hurdle regression commonly used in economics (Wooldridge, 2010).

Hypothesis testings

We used a bootstrap approach to detect proteins whose abundances or missing rates were different between Group 1 and 2. The null hypothesis of interest was $H_0:G_1=G_2=G{\prime }_1=G{\prime }_2=0$. We let our test statistics $-2\lambda =-2(log(L_0)-log(L))$ where L₀ was a likelihood for the model without group terms for both linear regression and logistic regression parts. Then, we constructed a null distribution of $-2\lambda$ by permuting subject group labels and estimated P-values based on the null distribution. To correct multiple testing errors, q-values were computed for each protein using Storey (2002). An alternative way to estimate P-values is to use the likelihood-ratio test assuming that $-2\lambda$ under the null has chi-square distribution. However, the bootstrap gave more accurate q-values than likelihood ratio tests (See Supplementary Materials), and thus, we used the bootstrap approach to test H₀.

As mentioned previously, for detected differential proteins with small q-values, it is ideal to have ${\beta }_g{\gamma }_g<0$. But, we can sometimes have proteins with ${\beta }_g{\gamma }_g>0$. In other words, in the ideal situation, if the peptides from Protein X were more abundant in Group 2 than 1, then the intensities of these peptides were supposed to be more frequently present in Group 2. However, sometimes, these peptides can appear less frequently in Group 2, but the difference in these frequencies between two groups was not significant. This would be more evident when ${\gamma }_g$ was close to zero. For example, in the situation when Protein X was actually more abundant in Group 2 than 1, two of 100 peptides intensities were missing for Group 2, and one of 100 peptides intensities was missing for Group 1. Then, Group 1 had smaller missing rate for Protein X, but the difference in the missing rates between two groups was negligible.

Thus, we further tested two null hypotheses, $H_{0G}:G_1=G_2=0$ and $H_{0G\prime }:G{\prime }_1=G{\prime }_2=0$ noting that ${\beta }_g=G_2-G_1=0$ and ${\gamma }_g=G{\prime }_2-G{\prime }_1=0$. We restricted these tests to the differential proteins with q-values $<q_{th}$ (i.e. q_th = 0.01) and with ${\beta }_g{\gamma }_g>0$. Because it was not plausible to use bootstrap for these tests, we used likelihood ratio tests. By taking a sign of either ${\beta }_g$ or ${\gamma }_g$ (not both) with a smaller P-value, we determined whether a protein of interest is more or less abundant in Group 1 than 2.

2.3 Datasets

Simulated data

We generated several simulated datasets that were aimed to reflect real MS data. The different simulated datasets contained various proportions of total quantification- and intensity-dependent missing values. Details of simulation procedures and parameters were shown in the Supplementary Materials. In brief, peptide intensities were generated from the linear regression part of (1). Concerning the missing mechanisms, we had three parameters of interest, τ₁, τ₂ and b. τ₁ represented the magnitude of association between mean peptide intensities and missing rates (${\tau }_1\in (0,1]$). A larger τ₁ indicated a stronger association between peptide intensities and peptide missing rates in the data. τ₂ ranged in (0,1] and represented the magnitude of association between k values and missing rates. The values of b were the probabilities that missing values were generated from the total quantification-dependent missing mechanism. A higher b value would produce a larger portion of part B in Figure 1.

Monocyte proteomics data of trauma patients

The data were generated by the National Institutes of Health large-scale collaborative program, Inflammation and Host Response to Injury Consortium. The study was reviewed and approved by the institutional review boards at each participating site. Blood monocyte samples of 147 trauma patients were collected within 12 h after the injury. Among 141 patients, 77 patients had complicated recovery and 64 patients had uncomplicated recovery (Xiao et al., 2011). Our interest was to find the proteins whose abundances were different between these two recovery groups.

Samples were prepared using ¹⁸O-labeled universal reference-based approach described in Qian et al. (2010) and analyzed by MS. Each experiment contained peptides from a pool sample and from an individual patient sample. Peptides from the pool sample were labeled with ¹⁸O and used as universal standards. (We will call peptides from the pool sample as heavy-labeled peptides and peptides from the individual patient sample as light-labeled peptides.) Both heavy- and light-labeled peptides were identified and quantified at false discovery rate 1%, and homogeneous proteins were grouped by MaxQuant (Version 1.4.1.2) (Cox and Mann, 2008). The light-labeled peptide abundances were normalized by their paired heavy-labeled peptide abundances. These normalized light-labeled peptide abundances were used for SALPS.

3 RESULTS

3.1 Simulation results

SALPS had good performances in detecting differential proteins. Here, we compared SALPS with two alternative approaches. One approach was to omit missing data and to carry the linear regression on the remaining data. This is known as the complete case analysis. Here, we denote it as LinearC. The variants of the complete case data analysis were often used in the proteomics (Oberg et al., 2008; Radulovic et al., 2004; Ryu et al., 2008; Wang et al., 2003). The other approach was the linear regression with imputation (denoted as LinearI). It is a simple approach that handles intensity-dependent missing data. In this approach, we obtained the minimum observed peptide intensity for each peptide and replaced missing values of the corresponding peptide with this minimum value.

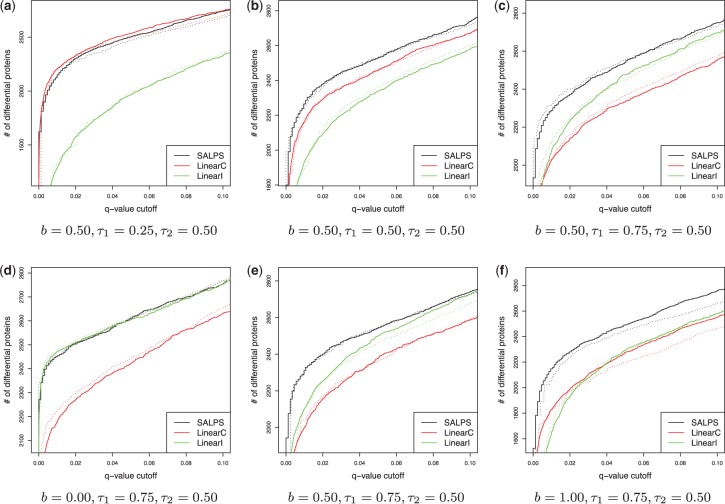
As shown in Figure 2, SALPS identified more differential proteins than LinearC and LinearI in most of the parameter space, (τ₁, τ₂, b). The only exception was when there was a relatively weak association between peptide intensities and missing values (a smaller value of τ₁). In this case, SALPS performed slightly worse than LinearC (Fig. 2a). But, the difference in the number of differential proteins at q < 0.01 was 3.8% on average (See Supplementary Materials). While SALPS performed the best or very close to the best, the performances of LinearC and LinearI fluctuated. Fixing parameters, $b(=0.50)$ and ${\tau }_2(=0.50)$, LinearC performed better than LinearI for a smaller value of τ₁ (Fig. 2a and b). For a bigger value of τ₁, LinearI performed better (Fig. 2c). This was expected because LinearI does not perform well when missing rate of peptide intensities does not reflect the peptide intensities much.

Fig. 2.

Simulation results showing the number of differentially expressed proteins versus q-value at varying parameter values of (b, τ₁). b was the probability that missing values were generated from the total quantification-dependent missing mechanism. τ₁ was the magnitude of association between mean peptide intensities and missing rates. τ₂ was the magnitude of association between k values and missing rates (${\tau }_2=0.50$). The solid lines were based on the estimated q-values, while the dotted lines were based on the actual q-values

We also investigated the relationship between the model performances and the proportion of part B (represented by b) in Figure 1. Again, our model performed the best or close to the best as the parameter, b, varies. However, as the proportion of part B increased (bigger b value), LinearC performed better than LinearI (Fig. 2f). As the proportion of part B decreased, LinearI performed better (Fig. 2d and e). This implies that the missing values have valuable information when experiments have similar total numbers of quantified peptides and that it is better to remove missing values when experiments have different total numbers of quantified peptides. SALPS also performed well with varying τ₂. More simulations with varying τ₂ values were also found in the Supplementary Materials.

In addition, we compare the performance of Karpievitch et al. (2009) and Wang et al. (2012) in the simulated datasets. Wang et al. (2012) performed better than Karpievitch et al. (2009), but not as good as LinearI, LinearC and SALPS (Supplementary Figure 5S). For example, in the simulation dataset, where $b=0.50,{\tau }_1=0.75,{\tau }_2=0.50$, the numbers of truly differentially expressed proteins detected by LinearI and LinearC are >75% of the true differential proteins detected by SALPS, but this percentage reduced to <50% for Karpievitch et al. (2009) and Wang et al. (2012).

Because in the simulated data, the true set of differential proteins was known, we computed the actual q-values based on the number of proteins that were falsely classified as differential proteins. Our q-values based on the bootstrap-based tests were close to the actual q-values (Fig. 2). The dotted lines in Figure 2 represented the actual q-values given the number of significant proteins. The dotted lines of SALPS were close to their estimated (solid) lines.

At estimated q < 0.01, ∼99% of differential proteins detected were from the true set of differential proteins for all three approaches. When $b=0.50,{\tau }_1=0.75,{\tau }_2=0.50$, SALPS detected 2273 proteins from the true set of differential proteins (q < 0.01). At the same q-value threshold, LinearC and LinearI detected 2007 and 2060 proteins from the true set, respectively. A total of 1760 proteins were detected by all three approaches.

3.2 Monocyte proteomics data results

SALPS performed well in the monocyte proteomics data of trauma patients. Using this dataset, we were interested in identifying proteins of which the abundance was different between two patients groups (uncomplicated versus complicated recovery patients). SALPS detected 78 differential proteins at q < 0.0001 and 107 differential proteins at q < 0.01. These proteins were known to be associated with inflammatory response, immunological disease and organismal abnormalities. For examples, matrix metalloproteinase 8 (MMP8) was detected as significant by only SALPS. Matrix metalloproteinses were well known to be important in various inflammatory diseases (Lagente and Boichot, 2008). Specifically, Quintero et al. (2010) had shown that MMP8 in monocytes reduced acute lung inflammation and injury in mice. In our proteomics data of monocytes from patients, MMP8 was more abundant in patients of uncomplicated recovery than complicated recovery, which aligned well with the anti-inflammatory role of MMP8. Besides, damage-specific binding protein (DDB1) was not detected as significant by LinearC, but by SALPS and LinearI. In our monocytes proteomics data, the complicated recovery patients had more DDB1 proteins in their monocytes than the uncomplicated patients within 12 h after the injury. This could indicate that complicated recovery patients needed more DDB1 proteins for DNA repair (Dualan et al., 1995). However, as part of the cullin4-DDB1 E3 ubiquitin ligase complex, multiple studies had shown that DDB1 was essential for viruses to escape from innate immune sensing (Andrejeva et al., 2002; Laguette et al., 2014; Leupin et al., 2003; Precious et al., 2005). Further studies are needed to discern the functional impact of differentially expressed DDB1 in trauma patients.

In terms of the number of differential proteins, the performance of SALPS was better than the traditional approaches (Fig. 3). Our approach detected ∼25 and 300% more differential proteins than LinearI and LinearC, respectively (q < 0.01). Over 96 and 90% of differential proteins detected by LinearC and LinearI were also detected by SALPS at the same q threshold. LinearI worked well in this dataset identifying more differential proteins than LinearC. In contrast, when we applied these algorithms to another dataset, while SALPS still performed the best, LinearC performed better than LinearI (see Supplementary Materials). The algorithms of Karpievitch et al. (2009) and Wang et al. (2012) did not converge when applied to the monocyte proteomics data.

Fig. 3.

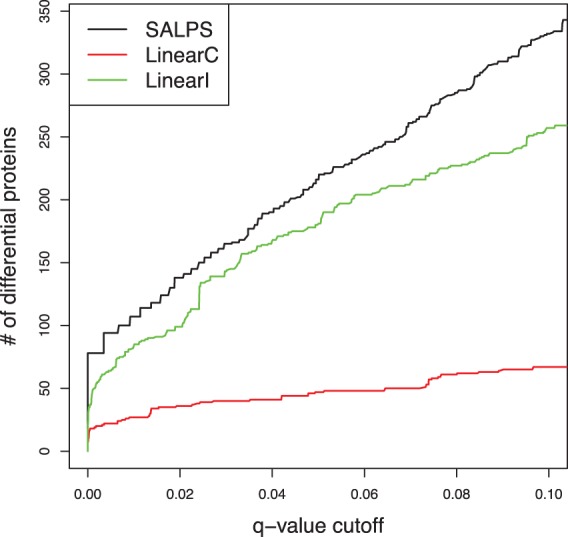
Monocytes proteomics results of trauma patients. Shown are the number of proteins detected as differentially expressed between patients with uncomplicated and complicated recovery

The percentage of ${\beta }_{g_B}{\gamma }_{g_B}<0$ was 81.31% at q < 0.01. For the rest of proteins with ${\beta }_{g_B}{\gamma }_{g_B}>0$, testing $H_{0\beta }$ and $H_{0\gamma }$ determined whether the proteins were more abundant (or had less missing rate) in the complicated recovery patients than the complicated recovery patients.

4 DISCUSSION AND CONCLUSION

We developed a SALPS and demonstrated its performance. As shown in our simulation studies (Fig. 2), it was important to recognize the different causes of peptide missing values and to handle them appropriately. Our model was flexible enough to handle missing values from different sources.

There are a few things we want to mention about our proposed approach. First, we used a (log)normal distribution in the linear regression part. However, one can use a truncated normal distribution in place of the normal distribution. This model would be the truncated normal hurdle model (Wooldridge, 2010). Second, we used the percentage of opposite signs between ${\beta }_{g_B}$ and ${\gamma }_{g_B}$ to determine the filtering threshold (k_th). One can also use a rank correlation between group covariates in linear regression and probit regression and chose k_th that gives the smallest rank correlation. Third, SALPS estimates more parameters than the traditional approaches (e.g. 2 p parameters were estimated in SALPS versus p parameters in LinearI and LinearC), thus demands larger sample sizes.

Nowadays, large-scale proteomics studies have become increasingly important in biomedical research. Such a study can provide a large-scale assessment of the relationship between proteomics and clinical outcomes. Potential protein biomarkers can be used to further develop diagnostic and therapeutic targets. To detect as many potential protein biomarkers as possible with high confidence, it is important to use the appropriate bioinformatics algorithm. The development of SALPS was motivated by analyzing an ongoing multicenter clinical study to examine the proteomic response to severe injury in blood leukocytes, which currently includes MS analysis of >2100 samples of isolated monocytes, T cells and neutrophils from trauma patients. We believe that SALPS can provide the valuable information in such large-scale population proteomics studies.