Abstract
Joint modeling of survival and longitudinal data has been studied extensively in the recent literature. The likelihood approach is one of the most popular estimation methods employed within the joint modeling framework. Typically, the parameters are estimated using maximum likelihood, with computation performed by the expectation maximization (EM) algorithm. However, one drawback of this approach is that standard error (SE) estimates are not automatically produced when using the EM algorithm. Many different procedures have been proposed to obtain the asymptotic covariance matrix for the parameters when the number of parameters is typically small. In the joint modeling context, however, there may be an infinite-dimensional parameter, the baseline hazard function, which greatly complicates the problem, so that the existing methods cannot be readily applied. The profile likelihood and the bootstrap methods overcome the difficulty to some extent; however, they can be computationally intensive. In this paper, we propose two new methods for SE estimation using the EM algorithm that allow for more efficient computation of the SE of a subset of parametric components in a semiparametric or high-dimensional parametric model. The precision and computation time are evaluated through a thorough simulation study. We conclude with an application of our SE estimation method to analyze an HIV clinical trial dataset.
Keywords: EM algorithm, HIV clinical trial, Numerical differentiation, Observed information matrix, Profile likelihood, Semiparametric joint modeling
1. Introduction
In biomedical studies, it has become increasingly common to record key longitudinal measurements up to a possibly censored time-to-event (or survival time) along with additional relevant covariates. A classical example in this context is an HIV clinical trial with the CD4 counts being the key longitudinal measurements. Researchers’ interests are usually 2-fold: (1) to model the pattern of change of the longitudinal process and (2) to characterize the relationship between the survival process, the longitudinal process, and any additional covariate. Unfortunately, the longitudinal process is subject to informative dropout; moreover, the longitudinal responses are only collected intermittently and may involve measurement error. Joint modeling approaches that model the event time and longitudinal process jointly have been effective in overcoming the difficulties and studied extensively in the recent literature. Tsiatis and Davidian (2004) provide an overview of the joint modeling literature in this context.
In early joint modeling literature, the survival times were modeled parametrically; later papers suggested approximating the baseline hazard by piecewise constant functions or spline-based methods, and both are implemented in the R package “JM” (Rizopoulos, 2010). Both approaches are examples of the method of sieves (Hsieh and others, 2013). In this paper, we focus on an even more flexible model for the survival times, the Cox proportional hazards model, where the baseline hazard is left completely unspecified. This leads to a semiparametric model which can be used to guide the choice of a parametric model. One caveat with the Cox model under the joint modeling setting is that partial likelihood is no longer feasible. Instead, a non-parametric maximum likelihood approach was pioneered by Wulfsohn and Tsiatis (1997), who derived an expectation maximization (EM) algorithm for parameter estimation. Zeng and Cai (2005a) proved consistency and asymptotic normality of the maximum likelihood estimate (MLE) but no explicit form for the asymptotic covariance matrix is available. This raises the question of how to estimate the standard errors (SEs), i.e. the standard deviations, of the parameter estimates. Several approaches, such as the bootstrap (Efron, 1994) and the profile likelihood (PL) (Murphy and van der Vaart, 2000) approach, have been proposed in the literature but their performance has not been examined systematically. The goal of this paper is to address the important issue of SE estimation in the joint modeling setting and, where necessary, to provide new solutions.
Two key factors contribute to the difficulty of SE estimation for the semiparametric joint modeling. The first is that the likelihood function typically involves integrals that cannot be computed analytically. The second is the presence of the non-parametric baseline hazard function employed. As a result, direct maximization of the likelihood function is unstable and the EM algorithm is utilized to provide computational stability. Since first appearing in the statistical literature in Dempster and others (1977), the EM algorithm has become a popular tool for computing MLEs for multi-level and missing data models. The celebrated property of monotone convergence in the observed-data log-likelihood endows the algorithm with a high degree of numerical stability. However, one drawback of the EM algorithm is that the SE estimates of the parameters are not automatically produced, thus requiring additional procedures to enable practical inference.
The first major contribution to SE estimation using the EM algorithm came from Louis (1982). The approach therein uses a formula for computing the observed information matrix in terms of the complete and missing information matrices. However, the missing information requires calculating the conditional expectation of the outer product of the complete-data score vector, an inherently problem-specific task that can require much computational effort as discussed in Meng and Rubin (1991). To address these deficiencies, many alternative EM-based procedures have been proposed to estimate SEs. Key references include Meilijson (1989), Meng and Rubin (1991), and Jamshidian and Jennrich (2000). The overwhelming majority of applications using these methods have been restricted to parametric settings where the number of parameters is typically small, and, to our best knowledge, none explicitly address SE estimation for semiparametric or high-dimensional models. The SEM algorithm proposed by Meng and Rubin (1991) turns out to be poorly suited to joint modeling applications since it requires very accurate MLEs for all parameters and the E-step in the joint modeling context cannot be computed in closed form. Thus, SEM can be numerically unstable, as addressed in Jamshidian and Jennrich (2000).
In this paper, we build from the core ideas of the FDM/REM/FDS/RES methods introduced in Jamshidian and Jennrich (2000). The basic approach of the FDM/REM algorithms is to numerically differentiate the EM update operator using either forward difference (FDM) or Richardson extrapolation (REM). The FDS/RES methods instead proceed by numerically differentiating the Fisher score vector, again using either forward differencing (FDS) or Richardson extrapolation (RES). Applying these algorithms directly in our joint modeling context is typically infeasible due to the dimensionality of the baseline hazard function. Therefore, we propose a novel profile technique to profile out the nuisance parameter so that the methods can be comfortably implemented in a semiparametric or high-dimensional joint modeling setting.
In general, semiparametric settings two main techniques have been studied for SE estimation, namely the bootstrap (Efron, 1994) and the PL approach (Murphy and van der Vaart, 2000). Numerical performance of the methods in the joint modeling setting has been verified in Tseng and others (2005) and Zeng and Cai (2005b), respectively. However, both of these two approaches have limitations. The bootstrap approach is computationally intensive and the PL approach, based on an approximation to the second derivative of the PL function (see (3.2)), could be sensitive to the increment chosen when performing the numerical differentiation. Hence, a second goal in this paper is to determine which SE estimation methods provide the best trade-off between reliably providing precise SE estimates and computational efficiency.
The remainder of the article is structured as follows. The basic semiparametric joint modeling framework and notation are introduced in Section 2. In Section 3, we explain the idea of each SE estimation method and the corresponding implementation details for the semiparametric setting. A simulation study is provided in Section 4 to facilitate the comparison of all the aforementioned methods and a substantive data analysis (HIV clinical trial data) follows. Finally, in Section 5, we present conclusions, recommendations, and possible extensions. Some technical details of the algorithms are deferred to the Appendix of supplementary material available at Biostatistics online.
2. Semiparametric joint modeling of survival and longitudinal processes
In the semiparametric joint modeling framework, continuous longitudinal outcomes are commonly modeled by linear mixed-effects models and survival times are assumed to follow a proportional hazards model (Cox, 1972). The model in Wulfsohn and Tsiatis (1997) assumes that the fixed and random effects in the linear mixed-effects model share the same covariates and the entire longitudinal trajectory is involved in the survival model. Here, we adopt a more flexible model.
Let 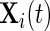 ,
, 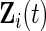 be vectors of the observed covariates that are assumed to be either time-independent or time-dependent. Typically
be vectors of the observed covariates that are assumed to be either time-independent or time-dependent. Typically 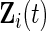 is a subvector of
is a subvector of 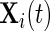 but this is not required. Let
but this is not required. Let 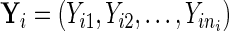 denote the longitudinal process that is modeled as
denote the longitudinal process that is modeled as
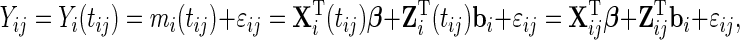 |
(2.1) |
with 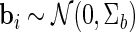 and
and 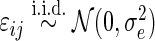 . The survival time
. The survival time 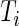 is subject to right censoring by
is subject to right censoring by 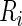 so that the observed data are
so that the observed data are 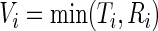 and
and 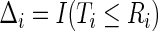 . The survival process can be modeled as
. The survival process can be modeled as
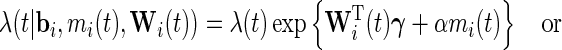 |
(2.2) |
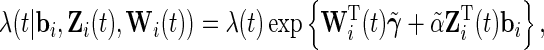 |
(2.3) |
where 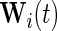 is also a vector of the observed covariates and
is also a vector of the observed covariates and 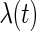 is the baseline hazard function and is left completely unspecified. In (2.2), the error-free longitudinal process serves as a covariate in the survival model. Model (2.3) is a reparameterization of (2.2) where up to a scale factor, the survival model only shares the same random effects with the longitudinal trajectory but possibly different fixed effects. Model (2.3) is computationally simpler since
is the baseline hazard function and is left completely unspecified. In (2.2), the error-free longitudinal process serves as a covariate in the survival model. Model (2.3) is a reparameterization of (2.2) where up to a scale factor, the survival model only shares the same random effects with the longitudinal trajectory but possibly different fixed effects. Model (2.3) is computationally simpler since 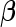 is not involved in the survival model, while (2.2) has more explanatory power for characterizing the effect of the longitudinal process on the survival time. For the following derivations, we focus on model (2.2) and the corresponding derivations based on model (2.3) follow similarly.
is not involved in the survival model, while (2.2) has more explanatory power for characterizing the effect of the longitudinal process on the survival time. For the following derivations, we focus on model (2.2) and the corresponding derivations based on model (2.3) follow similarly.
The observed and complete data are denoted by 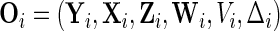 and
and 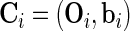 , respectively. Let
, respectively. Let 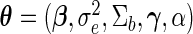 (a vector of length
(a vector of length 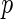 ) denote the finite-dimensional parameter and
) denote the finite-dimensional parameter and 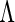 the cumulative baseline hazard function, and
the cumulative baseline hazard function, and 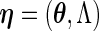 . Generally,
. Generally, 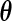 is the parameter of interest and
is the parameter of interest and 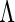 is considered a nuisance parameter. The observed- and complete-data likelihood functions are
is considered a nuisance parameter. The observed- and complete-data likelihood functions are
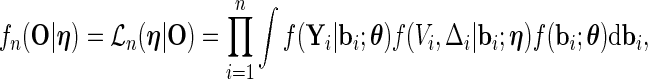 |
(2.4) |
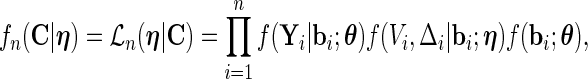 |
(2.5) |
where
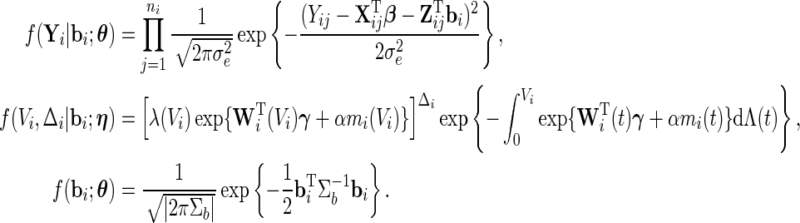 |
In light of the possibly multi-dimensional integral, direct maximization of (2.4) is quite difficult. Fortunately, the EM algorithm is ideally suited to this context and is thus employed to obtain the MLE. Numerical integration techniques such as Laplace approximation, Gaussian quadrature, and Monte Carlo methods can be applied in the E-step to evaluate the conditional expectations. In our setting, Gauss–Hermite quadrature is preferred due to its precision and computational speed. The likelihood approach results in non-parametric MLEs (Kiefer and Wolfowitz, 1956) 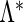 for
for 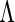 , which is a function with positive jumps only at the observed survival times. Hence, the dimension of
, which is a function with positive jumps only at the observed survival times. Hence, the dimension of 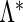 equals
equals 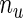 , the number of unique uncensored event times. Details of the EM algorithm and the asymptotic properties of the MLEs are provided in Zeng and Cai (2005a) and so we omit them and focus on the SE estimation methods. We further introduce the following notation for better illustration. During the E-step, we calculate
, the number of unique uncensored event times. Details of the EM algorithm and the asymptotic properties of the MLEs are provided in Zeng and Cai (2005a) and so we omit them and focus on the SE estimation methods. We further introduce the following notation for better illustration. During the E-step, we calculate
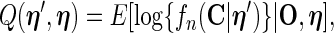 |
(2.6) |
and in the M-step, 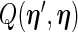 is maximized as a function of
is maximized as a function of 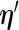 given
given 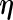 . The EM update operator
. The EM update operator 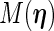 can be expressed as
can be expressed as
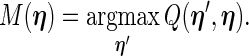 |
(2.7) |
3. SE estimation
3.1. Existing methods the PL and the bootstrap
the PL and the bootstrap
The PL method proposed by Murphy and van der Vaart (1999) and (2000) obtains the variance estimate for 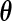 at
at 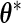 (the MLE for
(the MLE for 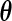 ) by taking the second derivative of the PL function:
) by taking the second derivative of the PL function:
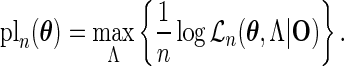 |
(3.1) |
Let 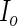 be the observed-data information matrix for
be the observed-data information matrix for 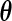 at
at 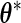 ; then
; then
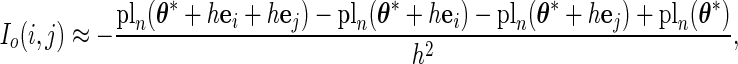 |
(3.2) |
where 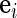 is the
is the 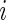 th coordinate vector and
th coordinate vector and 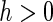 is the increment used to numerically obtain the second-order derivative. It is important to note that the choice of
is the increment used to numerically obtain the second-order derivative. It is important to note that the choice of 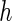 is subjective, with Murphy and van der Vaart (1999) suggesting
is subjective, with Murphy and van der Vaart (1999) suggesting 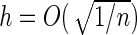 .
.
In contrast, the bootstrap SE estimation method is based on the idea of resampling full observational units. The observed data are denoted by 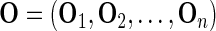 and the number of bootstrap samples by
and the number of bootstrap samples by 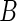 . For
. For 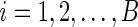 , sample with replacement from
, sample with replacement from 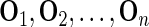 to form a new observed dataset
to form a new observed dataset 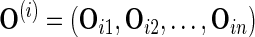 and obtain the corresponding parameter estimate
and obtain the corresponding parameter estimate 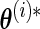 through the EM algorithm. The full covariance matrix and elementwise SE estimates of the parameters are then given by the analogous sample quantities for
through the EM algorithm. The full covariance matrix and elementwise SE estimates of the parameters are then given by the analogous sample quantities for 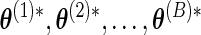 .
.
3.2. PFDM and PREM the FDM and REM algorithms with a profile technique
the FDM and REM algorithms with a profile technique
The FDM and REM algorithms introduced by Jamshidian and Jennrich (2000) are built on ideas first presented in the SEM algorithm of Meng and Rubin (1991). These methods are all based on differentiation of the EM update operator (2.7) and seek to relate it to the asymptotic covariance matrix. The FDM and REM algorithms avoid the outer layer of iterations required by the SEM algorithm by directly calculating the first derivative of the EM operator using two different numerical differentiation techniques. Each type of differentiation method, forward difference (FD) and Richardson extrapolation (RE), leads to its own corresponding SE estimation algorithm (FDM and REM, respectively).
If the FDM and REM algorithms are applied directly to the entire MLE vector 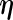 at
at 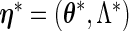 , then the resulting derivative of the EM operator
, then the resulting derivative of the EM operator 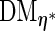 would be a
would be a 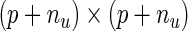 matrix with the
matrix with the 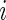 th row calculated using either FD
th row calculated using either FD
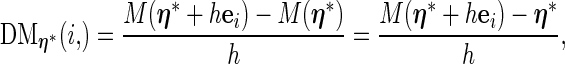 |
(3.3) |
or RE
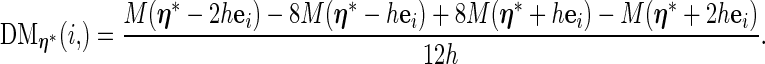 |
(3.4) |
Since 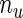 (number of unique uncensored event times) is usually large, this makes the computation of
(number of unique uncensored event times) is usually large, this makes the computation of 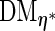 slow despite the fact that our interest is only in the finite-dimensional parameter
slow despite the fact that our interest is only in the finite-dimensional parameter 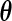 . Moreover, although computing the derivative with respect to
. Moreover, although computing the derivative with respect to 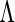 is numerically feasible due to discretization, differentiation with respect to an infinite-dimensional parameter is not suitably defined. Therefore, we now propose a new profile modification to the standard FDM and REM algorithms. In place of (3.3) and (3.4), our method instead evaluates
is numerically feasible due to discretization, differentiation with respect to an infinite-dimensional parameter is not suitably defined. Therefore, we now propose a new profile modification to the standard FDM and REM algorithms. In place of (3.3) and (3.4), our method instead evaluates 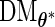 (a
(a 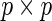 matrix), the derivative of the EM update operator with respect to
matrix), the derivative of the EM update operator with respect to 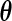 only. Let
only. Let
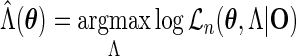 |
(3.5) |
be the estimate of 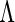 given
given 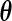 . The derivative of the EM operator at the MLE,
. The derivative of the EM operator at the MLE, 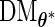 , can be obtained through the following algorithm. For illustration purposes, we present the algorithm using Richardson extrapolation [PREM (differentiate the EM update operator using Richardson extrapolation with a profile technique)]. The corresponding PFDM (differentiate the EM update operator using forward difference with a profile technique) algorithm follows similarly.
, can be obtained through the following algorithm. For illustration purposes, we present the algorithm using Richardson extrapolation [PREM (differentiate the EM update operator using Richardson extrapolation with a profile technique)]. The corresponding PFDM (differentiate the EM update operator using forward difference with a profile technique) algorithm follows similarly.
Let
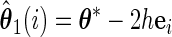 ,
, 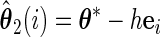 ,
, 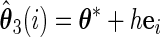 , and
, and 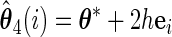 , obtain
, obtain 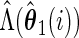 ,
, 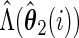 ,
, 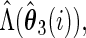 and
and 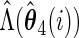 .
.For
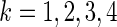 , treat
, treat 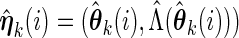 as the current estimate and run one iteration of the EM algorithm to obtain the updated estimate
as the current estimate and run one iteration of the EM algorithm to obtain the updated estimate 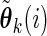 for
for 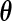 .
.- Calculate the
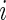 th row of
th row of 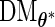 :
:
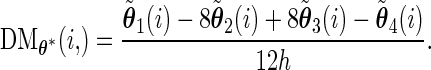
- The asymptotic covariance matrix can be obtained by the identity (Meng and Rubin, 160 1991):
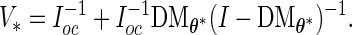
(3.6) If
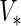 is symmetric, set
is symmetric, set 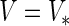 . Otherwise, symmetrize the matrix :
. Otherwise, symmetrize the matrix : 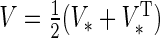 .
.
Note that in step 4, 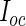 is the conditional expectation of the complete-data information matrix given the observed data evaluated at the MLE
is the conditional expectation of the complete-data information matrix given the observed data evaluated at the MLE 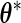 . We refer the reader to Appendix A.1 of supplementary material available at Biostatistics online for technical details about the computation of
. We refer the reader to Appendix A.1 of supplementary material available at Biostatistics online for technical details about the computation of 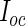 .
.
3.3. PFDS and PRES: the FDS and RES algorithms with a profile technique
The central idea of the FDS and RES algorithms of Jamshidian and Jennrich (2000) was first noted in Meilijson (1989). The key idea is that the observed-data information matrix 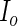 can be approximated by numerical differentiation of the Fisher score vector defined by (3.7). Let
can be approximated by numerical differentiation of the Fisher score vector defined by (3.7). Let 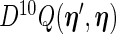 denote the first derivative of
denote the first derivative of 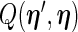 , defined by (2.6), as a function of its first argument
, defined by (2.6), as a function of its first argument 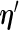 , i.e.
, i.e. 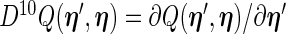 . The Fisher score vector is then defined as
. The Fisher score vector is then defined as
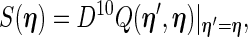 |
(3.7) |
and 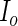 can be obtained by numerically differentiating
can be obtained by numerically differentiating 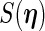 using forward difference (FDS) or Richardson extrapolation (RES). Differentiating the entire parameter vector is again unnecessary and so a profile technique can be used to speed up the algorithm. The profile version of the
using forward difference (FDS) or Richardson extrapolation (RES). Differentiating the entire parameter vector is again unnecessary and so a profile technique can be used to speed up the algorithm. The profile version of the 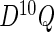 function,
function, 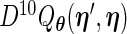 , and the profile Fisher score vector
, and the profile Fisher score vector 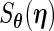 are given in Appendix A.2 of supplementary material available at Biostatistics online. Detailed steps for the PRES (differentiate the Fisher score using Richardson extrapolation with a profile technique) algorithm are [PFDS (differentiate the Fisher score using forward difference with a profile technique) similar].
are given in Appendix A.2 of supplementary material available at Biostatistics online. Detailed steps for the PRES (differentiate the Fisher score using Richardson extrapolation with a profile technique) algorithm are [PFDS (differentiate the Fisher score using forward difference with a profile technique) similar].
Same as the PREM algorithm.
For
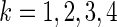 , let
, let 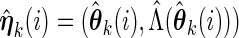 and evaluate
and evaluate 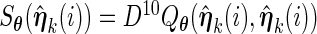 .
.- Calculate the
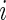 th row of
th row of 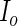 :
:
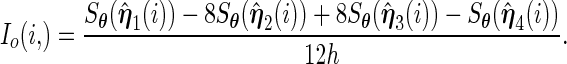
(3.8) Symmetrize
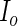 as in the PREM algorithm and let
as in the PREM algorithm and let 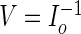 .
.
3.4. Comparison of the methods: implementation considerations
Each of the methods presented for obtaining SE estimates under joint modeling has its implementation trade-offs. In this section, we compare their implementation and computational difficulties as a precursor to the simulation study results of Section 4.1.
Out of all the methods, the bootstrap is the simplest to implement, requiring only trivial additional code beyond the code for the EM algorithm. Despite its simplicity, however, the bootstrap requires running the full EM algorithm for each bootstrap dataset. When the time to fit a single dataset is substantial, this can either severely limit the bootstrap sample size, or necessitate the use of parallel/batch computing for the bootstrap datasets. In addition, depending on the computational stability and implementation details of the EM algorithm used, convergence problems may arise for a subset of the bootstrap samples. It is also worth noting that multi-modality of the observed-data likelihood would be highly problematic for the bootstrap procedure, although in practice we have not found it to be a problem in our joint modeling context.
For the PL method, we need to compute 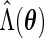 when fixing
when fixing 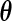 (3.5). Unfortunately,
(3.5). Unfortunately, 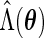 cannot be calculated via direct maximization. Therefore, in addition to the original EM algorithm for parameter estimation, another EM algorithm is required to obtain
cannot be calculated via direct maximization. Therefore, in addition to the original EM algorithm for parameter estimation, another EM algorithm is required to obtain 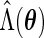 . This algorithm, abbreviated PEME (Partial Expectation, Maximization and Evaluation), was presented in Zeng and Cai (2005b). With the PEME algorithm, we can apply (3.2) to obtain the observed-data information matrix
. This algorithm, abbreviated PEME (Partial Expectation, Maximization and Evaluation), was presented in Zeng and Cai (2005b). With the PEME algorithm, we can apply (3.2) to obtain the observed-data information matrix 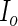 , a
, a 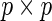 symmetric matrix. Hence, we need to compute
symmetric matrix. Hence, we need to compute 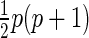 entries of
entries of 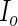 and the calculation of each entry requires evaluating
and the calculation of each entry requires evaluating 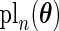 (3.1) at different
(3.1) at different 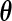 's.
's.
For the PFDM and PREM methods, we also need the PEME algorithm since a profile technique is proposed in their applications. Moreover, code for computing 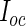 (defined in Section 3.2) is required. Fortunately,
(defined in Section 3.2) is required. Fortunately, 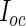 is only calculated once and these methods actually save computation time compared with the PL method due to how the
is only calculated once and these methods actually save computation time compared with the PL method due to how the 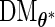 matrix is evaluated. As shown by (3.3) and (3.4),
matrix is evaluated. As shown by (3.3) and (3.4), 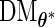 can be evaluated row by row rather than entry by entry. Note that, despite the saving in computation time,
can be evaluated row by row rather than entry by entry. Note that, despite the saving in computation time, 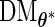 may not be symmetric, which would lead to asymmetry in our target covariance matrix as indicated by (3.6). This is a result of numerical approximation used to compute
may not be symmetric, which would lead to asymmetry in our target covariance matrix as indicated by (3.6). This is a result of numerical approximation used to compute 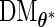 , and is the reason why a symmetrization step is added in step 4 of Section 3.2.
, and is the reason why a symmetrization step is added in step 4 of Section 3.2.
Finally, for the PFDS and PRES methods, again the PEME algorithm is required. Furthermore, these methods need the code for the Fisher score vector 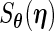 . Then
. Then 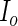 can be obtained row by row instead of entry by entry as shown by (3.8). This row vectorization makes the PFDS and PRES methods much faster than the PL method.
can be obtained row by row instead of entry by entry as shown by (3.8). This row vectorization makes the PFDS and PRES methods much faster than the PL method.
Table 1 summarizes the above discussion. We want to point out explicitly that, unlike that bootstrap method, the PL, PFDM, PREM, PFDS, and PRES methods all utilize numerical differentiation which introduces numerical error. As a result, these methods are not guaranteed to provide positive-definite covariance matrix estimates. In particular, it is possible for the diagonal entries of the resulting covariance matrix to be negative. In contrast, the bootstrap is subject to resampling error but has the advantage of ensuring a non-negative-definite full covariance matrix.
Table 1.
Summary of the SE estimation methods
| Method | Calculate | Calculate | Evaluate | Computation |
|---|---|---|---|---|
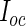 |
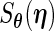 |
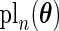 |
demand | |
| PFDM/PREM | 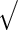 |
 |
 |
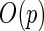 |
| PFDS/PRES |  |
 |
 |
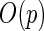 |
| Profile Lik. | 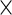 |
 |
 |
 |
| Bootstrap | 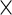 |
 |
 |
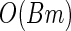 |
p is the length of the finite-dimensional parameter θ; B is the number of Bootstrap samples; m is the average number of iterations for the EM algorithm to converge.
4. Simulation study and substantive data application
4.1. Simulation study
Consider two time-independent covariates 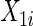 and
and 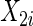 (
(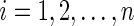 ):
): 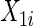 is a binary covariate from
is a binary covariate from 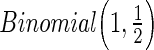 ;
; 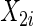 is a continuous covariate from
is a continuous covariate from 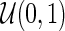 . The longitudinal model is
. The longitudinal model is
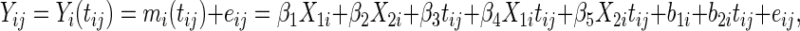 |
with 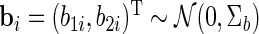 ,
, 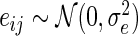 and
and 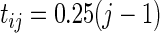 for
for 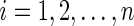 . The hazard function for the survival time is
. The hazard function for the survival time is
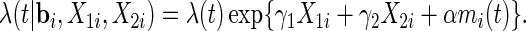 |
The true values of the parameters are chosen as below. Case II is considered in addition to Case I to explore the effect of magnified measurement error to the SE estimation methods.
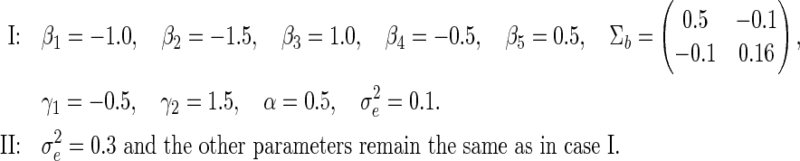 |
The true baseline hazard function is given below, which starts high and gradually decreases, then stays at a certain level for some period of time, and finally goes up:
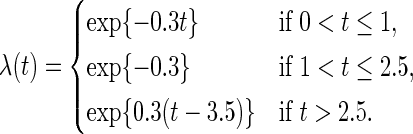 |
The censoring time is from the exponential distribution with mean 2.5 which yields a censoring proportion of approximately 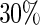 and the average number of longitudinal measurements is 3.5 per subject. The simulation is repeated 500 times with sample size
and the average number of longitudinal measurements is 3.5 per subject. The simulation is repeated 500 times with sample size 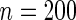 and the results are shown in Table 2. The “MCSE” column in Table 2, which are the empirical SEs (Monte Carlo SE) of the parameter estimates from the 500 simulations, serves as the benchmark of comparison with the SE estimation methods. The SE estimates corresponding to different choices of
and the results are shown in Table 2. The “MCSE” column in Table 2, which are the empirical SEs (Monte Carlo SE) of the parameter estimates from the 500 simulations, serves as the benchmark of comparison with the SE estimation methods. The SE estimates corresponding to different choices of 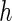 's from all SE estimation methods are reported (for case I). Owing to limited space, the results for
's from all SE estimation methods are reported (for case I). Owing to limited space, the results for 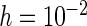 and
and 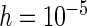 are presented, while additional results for
are presented, while additional results for 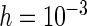 ,
, 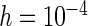 and those for case II are available in supplementary material available at Biostatistics online (Tables 1 and 2). The purpose of choosing different
and those for case II are available in supplementary material available at Biostatistics online (Tables 1 and 2). The purpose of choosing different 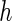 's is to illustrate the effect of the choice of
's is to illustrate the effect of the choice of 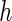 on the SE estimation procedures. Moreover, the bootstrap method is implemented with
on the SE estimation procedures. Moreover, the bootstrap method is implemented with 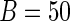 and
and 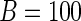 bootstrap samples. As illustrated in Table 2, the computation time for the bootstrap greatly exceeds that of the other methods, and we restrict to
bootstrap samples. As illustrated in Table 2, the computation time for the bootstrap greatly exceeds that of the other methods, and we restrict to 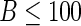 to ensure comparability and avoid prohibitive runtimes. For case I, we construct the
to ensure comparability and avoid prohibitive runtimes. For case I, we construct the 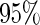 confidence intervals using the corresponding SE estimates and present the empirical coverage of each method in Figure 1. Another simulation setting where the longitudinal and survival processes only share the same random effects (as stated by (2.3)) is presented in Appendix A.3 of supplementary material available at Biostatistics online.
confidence intervals using the corresponding SE estimates and present the empirical coverage of each method in Figure 1. Another simulation setting where the longitudinal and survival processes only share the same random effects (as stated by (2.3)) is presented in Appendix A.3 of supplementary material available at Biostatistics online.
Table 2.
Parameter and SE estimates for case I in Section 4.1
 |
Mean | MCSE | PFDM 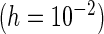
|
PREM 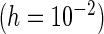
|
PFDS 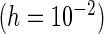
|
PRES 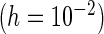
|
PL 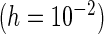
|
Bootstrap 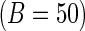
|
|---|---|---|---|---|---|---|---|---|
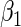 |
 0.99922 0.99922 |
0.09939 | 0.09675 | 0.09529 | 0.09527 | 0.09527 | 0.09528 | 0.09532 |
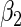 |
 1.50637 1.50637 |
0.11760 | 0.12278 | 0.11908 | 0.11826 | 0.11821 | 0.11821 | 0.11947 |
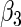 |
1.00145 | 0.12354 | 0.12251 | 0.12007 | 0.11979 | 0.11968 | 0.11990 | 0.12266 |
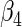 |
 0.50416 0.50416 |
0.10917 | 0.11591 | 0.11498 | 0.11487 | 0.11482 | 0.11490 | 0.11753 |
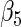 |
0.49678 | 0.18441 | 0.17368 | 0.18310 | 0.18312 | 0.18311 | 0.18318 | 0.18727 |
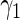 |
 0.49800 0.49800 |
0.24130 | 0.24637 | 0.24144 | 0.23871 | 0.23849 | 0.23784 | 0.24470 |
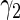 |
1.54721 | 0.37139 | 0.36045 | 0.35430 | 0.35327 | 0.35264 | 0.35208 | 0.36223 |
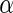 |
0.51229 | 0.13989 | 0.13208 | 0.13595 | 0.13561 | 0.13585 | 0.13508 | 0.14017 |
| N. | Posit. | 243 | 500 | 500 | 500 | 500 | 500 | |
| C. | Time | 56 | 213 | 35 | 131 | 178 | 4702 |
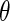 |
Mean | MCSE | PFDM 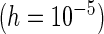
|
PREM 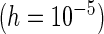
|
PFDS 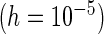
|
PRES 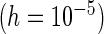
|
PL 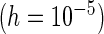
|
Bootstrap 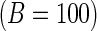
|
|---|---|---|---|---|---|---|---|---|
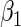 |
 0.99922 0.99922 |
0.09939 | 0.09426 | 0.09529 | 0.09507 | 0.09527 | 0.09524 | 0.09471 |
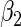 |
 1.50637 1.50637 |
0.11760 | 0.11236 | 0.11908 | 0.10917 | 0.11821 | 0.11796 | 0.11881 |
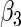 |
1.00145 | 0.12354 | 0.11999 | 0.12008 | 0.11065 | 0.11968 | 0.11963 | 0.12294 |
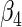 |
 0.50416 0.50416 |
0.10917 | 0.11640 | 0.11498 | 0.11360 | 0.11482 | 0.11476 | 0.11820 |
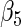 |
0.49678 | 0.18441 | 0.19045 | 0.18310 | 0.17709 | 0.18311 | 0.18073 | 0.18778 |
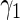 |
 0.49800 0.49800 |
0.24130 | 0.20927 | 0.24144 | 0.16850 | 0.23849 | 0.16789 | 0.24645 |
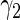 |
1.54721 | 0.37139 | 0.31366 | 0.35430 | 0.20435 | 0.35264 | 0.20523 | 0.36383 |
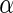 |
0.51229 | 0.13989 | 0.10381 | 0.13594 | 0.08203 | 0.13585 | 0.08213 | 0.14048 |
| N. | Posit. | 500 | 500 | 490 | 500 | 499 | 500 | |
| C. | Time | 56 | 213 | 35 | 131 | 178 | 9175 |
“Mean” and “MCSE”, empirical means and SEs of the parameter estimates from the 500 simulations; “PFDM/PREM”, numerically differentiate the EM update operator with forward difference/Richardson extrapolation; “PFDS/PRES”, numerically differentiate the Fisher score vector with forward difference/Richardson extrapolation; “PL”, profile likelihood method; “N. Posit.” row, number of positive variance estimates out of the 500 simulations for each method; “C. Time” row, average computation time (in seconds) for each method.
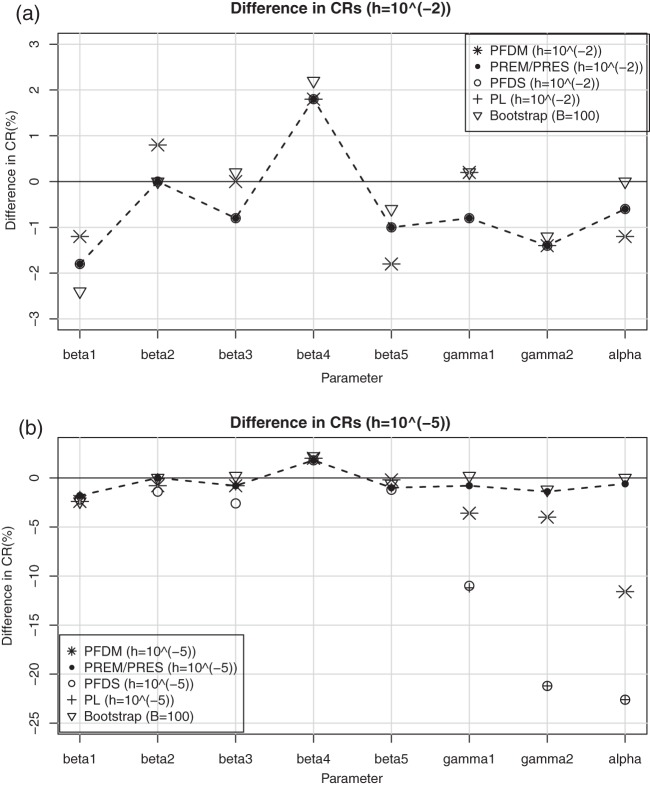
Fig. 1.
The CRs of the 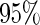 confidence interval (obtained using the SE estimates from each method) minus
confidence interval (obtained using the SE estimates from each method) minus 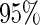 for case I with (a)
for case I with (a) 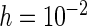 ; (b)
; (b) 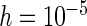 . The dashed lines connect the points for PREM/PRES methods. Note that some of the points are overlapping.
. The dashed lines connect the points for PREM/PRES methods. Note that some of the points are overlapping.
4.2. Discussion of the simulation results
Comparing the results of case II with those of case I, we observe that raising the measurement error increases the empirical SE (“MCSE”) of all the parameters, as expected. Moreover, with greater measurement error, the EM algorithm takes longer to converge (on average, it takes 45.50 steps in case II while only 28.47 steps in case I).
From Table 2 and Tables 1 and 2 of supplementary material available at Biostatistics online, we observe that, by and large, the new approaches (PFDM/PREM, PFDS/PRES) yield comparable SE estimates with the PL method. In the following, we discuss the performance of the methods in detail. First, for the choice of numerical differentiation approach, although RE is about four times slower than the FD, it is more stable in two aspects: (1) methods using RE are more likely to produce positive variance estimates as the “N. Posit.” rows (number of positive variance estimates out of the 500 simulations) show, especially when the measurement error is large and 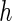 is small; (2) methods using RE are less sensitive to the choice of
is small; (2) methods using RE are less sensitive to the choice of 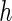 (comparing the results from “
(comparing the results from “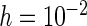 ” with those from “
” with those from “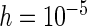 ”). Therefore, our profile methods using RE are typically preferred for the stability of the SE estimates, despite a slight sacrifice in computation time.
”). Therefore, our profile methods using RE are typically preferred for the stability of the SE estimates, despite a slight sacrifice in computation time.
Second, for the choice between PREM and PRES, although they yield almost identical results, PRES is in general preferred since numerically differentiating the Fisher score vector rather than the EM operator is more straightforward and it avoids the problem of PREM that the error would be magnified when the EM algorithm is slow. From the perspective of writing computer code, PRES is also preferred. PRES only requires code for the Fisher score vector which relates to the first derivative of the complete-data log-likelihood, while PREM requires code for 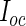 , which relates to the second derivative of the complete-data log-likelihood.
, which relates to the second derivative of the complete-data log-likelihood.
Third, the choice between PRES and PL is considered. The PL method appears to be more sensitive to the choice of 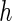 and may lead to negative or underestimation of the SE when
and may lead to negative or underestimation of the SE when 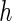 is small (by comparing the “PL
is small (by comparing the “PL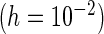 ” and “PL
” and “PL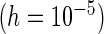 ” results), particularly for the survival regression parameters (
” results), particularly for the survival regression parameters (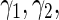 and
and 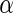 ). Moreover, PRES is computationally faster than PL, particularly when the sample size of the data or the number of parameters grows larger. Hence, PRES is also considered to outperform PL.
). Moreover, PRES is computationally faster than PL, particularly when the sample size of the data or the number of parameters grows larger. Hence, PRES is also considered to outperform PL.
To be complete, results from the bootstrap method are also provided. The computation time of the bootstrap method for case II is much longer than that for case I, e.g. for 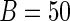 , the average computation time for case I is 4702 s while that for case II is 8456 s. The reason is that the EM algorithm converges slower under greater measurement error. Therefore, the bootstrap procedure suffers from an unappealing property that the computation time depends on the convergence speed of the EM algorithm. Moreover, the results of the additional simulation study (Table 3 of supplementary material available at Biostatistics online) show that the Bootstrap method seems to overestimate the SEs of the survival regression parameters (
, the average computation time for case I is 4702 s while that for case II is 8456 s. The reason is that the EM algorithm converges slower under greater measurement error. Therefore, the bootstrap procedure suffers from an unappealing property that the computation time depends on the convergence speed of the EM algorithm. Moreover, the results of the additional simulation study (Table 3 of supplementary material available at Biostatistics online) show that the Bootstrap method seems to overestimate the SEs of the survival regression parameters (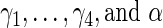 ). This is possibly due to the bootstrap resampling (with replacement) scheme which leads to resampled covariates that have slightly smaller variations than the original covariates and hence slightly larger SE estimates. A similar phenomenon was observed in Hsieh and others (2006) and explained on p. 1041. The key explanation, like in standard experimental designs, is that a design with larger variations leads to better precision in the estimation of regression coefficients. We would like to make an additional remark which is not displayed explicitly in the tables that a subset of the bootstrap samples were subject to convergence problems. For case I, the convergence problem is negligible, while for case II, 1.6% (averaging over the 500 simulations) of the bootstrap samples fail to converge.
). This is possibly due to the bootstrap resampling (with replacement) scheme which leads to resampled covariates that have slightly smaller variations than the original covariates and hence slightly larger SE estimates. A similar phenomenon was observed in Hsieh and others (2006) and explained on p. 1041. The key explanation, like in standard experimental designs, is that a design with larger variations leads to better precision in the estimation of regression coefficients. We would like to make an additional remark which is not displayed explicitly in the tables that a subset of the bootstrap samples were subject to convergence problems. For case I, the convergence problem is negligible, while for case II, 1.6% (averaging over the 500 simulations) of the bootstrap samples fail to converge.
Table 3.
Results for the HIV clinical trial data analysis
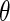 |
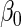 |
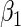 |
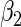 |
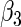 |
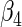 |
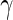 |
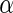 |
|---|---|---|---|---|---|---|---|
| Est. value | 2.5210 |
 0.0582 0.0582 |
0.0013 | 0.0251 |
 0.0016 0.0016 |
0.5137 |
 1.0631 1.0631 |
| Est. SE | 0.04315 | 0.00992 | 0.00074 | 0.01323 | 0.00096 | 0.18059 | 0.11531 |
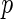 -value -value |
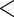 0.0001 0.0001 |
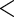 0.0001 0.0001 |
0.0640 | 0.0580 | 0.0862 | 0.0044 |
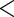 0.0001 0.0001 |
“Est. SE” are the estimated SEs obtained using the PRES method with 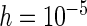 .
.
In terms of coverage properties, the performance of all the SE estimation methods are illustrated in (a) and (b) of Figure 1. PREM and PRES are again shown to provide more accurate SE estimates and are more stable under different choices of 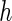 since they display smaller differences in coverage ratios (CRs) to the theoretical true value than the other methods. As a result, we would generally recommend the PRES method as the best choice for the purpose of SE estimation.
since they display smaller differences in coverage ratios (CRs) to the theoretical true value than the other methods. As a result, we would generally recommend the PRES method as the best choice for the purpose of SE estimation.
4.3. HIV clinical trial data analysis
To verify that the recommended PRES method can be applied practically, we now present a substantive data example. This set of HIV clinical trial data is originated from Goldman and others (1996) and has been analyzed by Rizopoulos (2010) as an illustrative example. The clinical trial was called a ddI/ddC study, which is aimed to compare the clinical efficacy and safety of two drugs, namely ddI (didanosine) and ddC (zalcitabine), in HIV-infected patients intolerant or failing ZDV (zidovudine) therapy. There were 467 patients enrolled in the study with 230 of them randomized to receive ddI and 237 to ddC. The average follow-up time was 15.6 months and CD4 lymphocyte counts were recorded at study entry and at the 2-, 6-, 12-, and 18-month visits (measurements may be missing due to patients’ condition). By the end of the study, 279 patients had not experienced death, resulting in approximately 60% right censoring.
Figure 2 displays the cross-sectional mean curves of 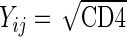 (a square root transformation is put on the CD4 counts due to its right skewness) for the ddI and ddC treatment groups. Based on the patterns shown in the figure, a quadratic trend over time is included in our model for
(a square root transformation is put on the CD4 counts due to its right skewness) for the ddI and ddC treatment groups. Based on the patterns shown in the figure, a quadratic trend over time is included in our model for 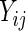 , while Rizopoulos (2010) assumed a linear trend. We also fitted the linear trend for
, while Rizopoulos (2010) assumed a linear trend. We also fitted the linear trend for 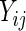 with the model and results provided in supplementary material available at Biostatistics online. Moreover, Rizopoulos (2010) opted for approximating
with the model and results provided in supplementary material available at Biostatistics online. Moreover, Rizopoulos (2010) opted for approximating 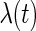 with a piecewise constant function due to the underestimation problem of the SEs if
with a piecewise constant function due to the underestimation problem of the SEs if 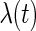 is left completely unspecified. Since our methodology can handle this case, we opt for the semiparametric model. Now, after proposing the new SE estimation approaches, we can readily apply the PRES method to obtain the SE estimates. The fitted model is
is left completely unspecified. Since our methodology can handle this case, we opt for the semiparametric model. Now, after proposing the new SE estimation approaches, we can readily apply the PRES method to obtain the SE estimates. The fitted model is
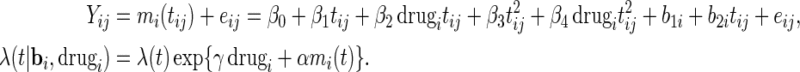 |
The results are provided in Table 3. The 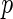 -value for
-value for 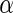 is very small (
is very small (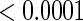 ) which suggests that the CD4 lymphocyte count is an important covariate in the survival model. Moreover, the treatment effect on the CD4 counts seems to be moderately significant since the
) which suggests that the CD4 lymphocyte count is an important covariate in the survival model. Moreover, the treatment effect on the CD4 counts seems to be moderately significant since the 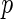 -value for
-value for 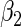 and
and 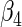 are
are 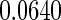 and
and 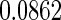 , respectively. This point differs from Rizopoulos (2010), where the treatment had little effect on the CD4 counts. Therefore, according to our results, the CD4 counts satisfy the first two criteria to be an adequate surrogate marker. However, with the CD4 counts in the survival model, the treatment effect is still statistically significant (the
, respectively. This point differs from Rizopoulos (2010), where the treatment had little effect on the CD4 counts. Therefore, according to our results, the CD4 counts satisfy the first two criteria to be an adequate surrogate marker. However, with the CD4 counts in the survival model, the treatment effect is still statistically significant (the 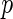 -value of
-value of 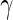 is
is 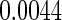 ). Hence, we conclude that the CD4 count is not a useful surrogate marker for these patients.
). Hence, we conclude that the CD4 count is not a useful surrogate marker for these patients.
Fig. 2.
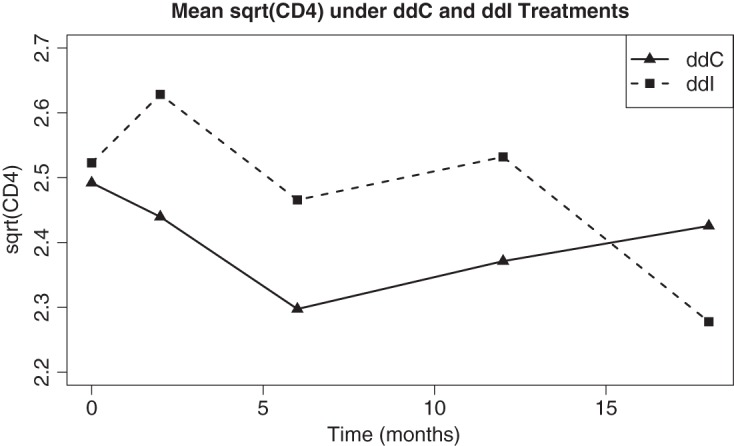
Time plot that displays the cross-sectional mean curves of sqrt(CD4) for the ddC and ddI treatment groups.
5. Discussion and conclusion
In this paper, we have proposed two new SE estimation methods when using the EM algorithm in a semiparametric joint modeling setting by applying a profile technique to overcome the challenges of high-dimensional parameters brought upon by the non-parametric component. The performance of these methods is examined systematically through simulation studies. Simulation results verify that these methods produce accurate SE estimates and the PRES method is recommended as the best choice. We hope that the ability to rapidly obtain reliable SE estimates with high- or infinite-dimensional hazard functions can expand the types of models applied in practice. The HIV clinical trial data analysis shows that the PRES method also performs well when analyzing a realistically sized substantive dataset.
Finally, we would like to make a concluding remark that the efficient procedures introduced to obtain SE estimates are applicable whenever the EM algorithm is used and a high- or infinite-dimensional nuisance parameter presents. Although the proposed methods are illustrated through our joint modeling setting in this paper, their applications are potentially quite broad. For instance, they can be implemented in settings with a more complicated censoring scheme or in models other than the Cox model for survival time or linear mixed-effects models for longitudinal measurements. Even more generally, the same ideas can be extended beyond the joint survival-longitudinal modeling context. While we have focused on the SE estimation of the finite dimensional parameter, our approach could be employed to the cumulative baseline hazard at a computational cost.
6. Software
The simulation studies and substantive data analysis are implemented in R. Software in the form of R code is available online as supplementary material.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
The research of Jane-Ling Wang was supported by the National Science Foundation (DMS-09006813) and the National Institutes of Health (1R01 AG025218-01A2). The research of Cong Xu is supported by the same NIH grant.
Supplementary Material
Acknowledgements
The authors appreciate the comments and suggestions from the editor, associate editor, and the reviewers, which are really helpful for the presentation of the paper. Conflict of Interest: None declared.
References
- Cox D. R. Regression models and life tables (with discussion) Journal of the Royal Statistical Society, Series B. 1972;34:187–220. [Google Scholar]
- Dempster A. P., Laird N. M., Rubin D. B. Maximum likelihood from incomplete data via the EM algorithm (with discussion) Journal of the Royal Statistical Society, Series B. 1977;39:1–38. [Google Scholar]
- Efron B. Missing data, imputation, and the bootstrap. Journal of the American Statistical Association. 1994;89:463–475. [Google Scholar]
- Goldman A. I., Carlin B. P., Crane L. R., Launer C., Korvick J. A., Deyton L., Abrams D. I. Response of CD4 lymphocytes and clinical consequences of treatment using ddI or ddC in patients with advanced HIV infection. Journal of Acquired Immune Deficiency Syndromes. 1996;11(2):161–169. doi: 10.1097/00042560-199602010-00007. [DOI] [PubMed] [Google Scholar]
- Hsieh F., Ding J., Wang J. L. Method of sieves to jointly model survival and longitudinal data. Statistica Sinica. 2013;23:1181–1213. [Google Scholar]
- Hsieh F., Tseng Y. K., Wang J. L. Joint modeling of survival and longitudinal data: likelihood approach revisited. Biometrics. 2006;62:1037–1043. doi: 10.1111/j.1541-0420.2006.00570.x. [DOI] [PubMed] [Google Scholar]
- Jamshidian M., Jennrich R. I. Standard errors for EM estimation. Journal of the Royal Statistical Society, Series B. 2000;62:257–270. [Google Scholar]
- Kiefer J., Wolfowitz J. Consistency of the maximum likelihood estimator in the presence of infinitely many nuisance parameters. Annals of Mathematical Statistics. 1956;27:887–906. [Google Scholar]
- Louis T. A. Finding the observed information matrix when using the EM algorithm. Journal of the Royal Statistical Society, Series B. 1982;44:226–233. [Google Scholar]
- Meilijson I. A fast improvement to the EM algorithm on its own terms. Journal of the Royal Statistical Society, Series B. 1989;51:127–138. [Google Scholar]
- Meng X. L., Rubin D. B. Using EM to obtain asymptotic variance-covariance matrices: the SEM algorithm. Journal of the American Statistical Association. 1991;86:899–909. [Google Scholar]
- Murphy S. A., van der Vaart A. W. Observed information in semi-parametric models. Bernoulli. 1999;5:381–412. [Google Scholar]
- Murphy S. A., van der Vaart A. W. On the profile likelihood. Journal of the American Statistical Association. 2000;95:449–465. [Google Scholar]
- Rizopoulos D. JM: an R package for the joint modelling of longitudinal and time-to-event data. Journal of Statistical Software. 2010;35:1–33. [Google Scholar]
- Tseng Y. K., Hsieh F., Wang J. L. Joing modeling of accelerated failure time and longitudinal data. Biometrika. 2005;92:587–603. [Google Scholar]
- Tsiatis A. A., Davidian M. Joint modeling of longitudinal and time-to-event data: an overview. Statistica Sinica. 2004;14:809–834. [Google Scholar]
- Wulfsohn M. S., Tsiatis A. A. A joint model for survival and longitudinal data measured with error. Biometrics. 1997;53:330–339. [PubMed] [Google Scholar]
- Zeng D., Cai J. Asymptotic results for maximum likelihood estimators in joint analysis of repeated measurements and survival time. Annals of Statistics. 2005a;33:2132–2163. [Google Scholar]
- Zeng D., Cai J. Simultaneous modeling of survival and longitudinal data with an application to repeated quality of life measures. Lifetime Data Analysis. 2005b;11:151–174. doi: 10.1007/s10985-004-0381-0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.