Abstract
Missing values in covariates of regression models are a pervasive problem in empirical research. Popular approaches for analyzing partially observed datasets include complete case analysis (CCA), multiple imputation (MI), and inverse probability weighting (IPW). In the case of missing covariate values, these methods (as typically implemented) are valid under different missingness assumptions. In particular, CCA is valid under missing not at random (MNAR) mechanisms in which missingness in a covariate depends on the value of that covariate, but is conditionally independent of outcome. In this paper, we argue that in some settings such an assumption is more plausible than the missing at random assumption underpinning most implementations of MI and IPW. When the former assumption holds, although CCA gives consistent estimates, it does not make use of all observed information. We therefore propose an augmented CCA approach which makes the same conditional independence assumption for missingness as CCA, but which improves efficiency through specification of an additional model for the probability of missingness, given the fully observed variables. The new method is evaluated using simulations and illustrated through application to data on reported alcohol consumption and blood pressure from the US National Health and Nutrition Examination Survey, in which data are likely MNAR independent of outcome.
Keywords: Complete case analysis, Missing covariates, Missing not at random, Multiple imputation
1. Introduction
Missing data in covariates of regression models are a common problem in epidemiological and clinical studies. Three commonly applied approaches for analyzing datasets with missing covariates are complete case analysis (CCA), multiple imputation (MI), and inverse probability weighting (IPW). As typically implemented, each make different assumptions about various aspects of either the data or the mechanism causing missingness.
CCA has the advantage of being simple to apply, and is usually the default method in statistical packages. It is well known that CCA gives valid inferences when data are missing completely at random. Perhaps less widely appreciated is the fact that CCA gives valid inferences provided that the probability of being a complete case is independent of the outcome in the model of interest, conditional on the model's covariates (Little and Rubin, 2002). In particular, CCA is valid under missing not at random (MNAR) mechanisms in which missingness in a covariate is dependent on the value of that covariate, but is conditionally independent of outcome (White and Carlin, 2010). However, even when this assumption holds, it does not make full use of the observed information, since observed data from the incomplete cases are discarded.
MI involves creating multiple imputed values for each missing value, creating a number of imputed datasets. Each imputed dataset is analyzed separately, and their estimates combined using rules developed by Rubin (1987). If data are missing at random (MAR) and the imputation model is correctly specified, MI gives valid inferences, and is generally more efficient than CCA since it uses the observed data from incomplete cases and potentially also from auxiliary variables which are not involved in the model of interest. This had led to MI being widely advocated and used in applications (Sterne and others, 2009).
IPW is also typically implemented assuming MAR. IPW avoids the necessity to model the distribution of the partially observed variables, and instead relies on a model for the missingness mechanism (Seaman and White, 2011). However, IPW is difficult to implement with non-monotone missingness, and is usually less efficient than MI. In recent years, doubly robust MAR estimators have been proposed which attempt to improve upon the efficiency of IPW, and which also give additional robustness to model mis-specification (Carpenter and others, 2006; Tsiatis, 2006).
In this article, we argue that in some settings an MNAR missingness mechanism under which CCA is valid is more plausible than an MAR mechanism which is required for validity of a conventional MI or IPW analysis. In such settings, it may therefore be preferable from the perspective of bias to use CCA. However, as previously noted, CCA is inefficient because it fails to draw on the information available in those subjects with some data missing. To address this, we develop an augmented CCA estimation method which can improve upon the efficiency of CCA, through specification of an additional model for the probability of missingness given the fully observed variables.
In Section 2, we argue why the CCA assumption may in some settings be more plausible than MAR, and propose an estimation method which makes this assumption but which draws on the information available from incomplete cases. We explore the performance of the proposed method in simulations in Section 3. In Section 4, we illustrate the method using alcohol and blood pressure data from the US National Health and Nutrition Examination Survey (NHANES), and give some concluding comments in Section 5.
2. Improving upon the efficiency of CCA
Consider a study where an outcome 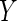 and covariates
and covariates
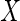 and
and  are intended to
be collected for a random sample of independent subjects. Either of
are intended to
be collected for a random sample of independent subjects. Either of
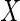 and
and  (or both) may
be vector valued. We assume throughout that the following conditional mean model
holds:
(or both) may
be vector valued. We assume throughout that the following conditional mean model
holds:
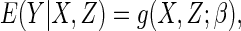 |
(2.1) |
where the function 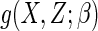 is a known smooth
function of
is a known smooth
function of 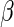 , a finite-dimensional
parameter to be estimated, with true value
, a finite-dimensional
parameter to be estimated, with true value 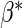 .
Conditional mean models include familiar models such as linear and logistic
regression.
.
Conditional mean models include familiar models such as linear and logistic
regression.
2.1. Missingness assumptions
We assume that  and
and
 are fully observed, while the
covariate
are fully observed, while the
covariate 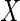 is partially observed. In the
case where
is partially observed. In the
case where 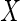 is vector valued, we assume
that for a given subject either all elements of
is vector valued, we assume
that for a given subject either all elements of 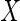 are
observed or all elements are missing (see Section 5 for discussion on extensions
to more complex missingness patterns). We let
are
observed or all elements are missing (see Section 5 for discussion on extensions
to more complex missingness patterns). We let  denote
whether
denote
whether 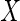 is observed
(
is observed
( ) or missing
(
) or missing
(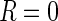 ). Within this setup, the MAR
assumption, upon which most MI and IPW methods rely, is that
). Within this setup, the MAR
assumption, upon which most MI and IPW methods rely, is that
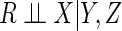 .
In contrast, CCA provides consistent parameter estimates and valid inferences if
missingness is independent of outcome conditional on covariates, i.e.
.
In contrast, CCA provides consistent parameter estimates and valid inferences if
missingness is independent of outcome conditional on covariates, i.e.
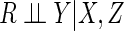 .
This condition encompasses both certain MAR mechanisms, whereby
.
This condition encompasses both certain MAR mechanisms, whereby
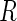 depends on the fully observed
covariates
depends on the fully observed
covariates  , but given this is independent
of
, but given this is independent
of 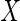 and
and 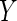 , and
certain MNAR mechanisms, whereby
, and
certain MNAR mechanisms, whereby 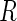 depends on
depends on
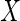 (and possibly
(and possibly
 ), but given this, is
independent of
), but given this, is
independent of 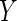 . Unfortunately, as
discussed by White and Carlin
(2010), it is usually impossible to distinguish on the basis of the
observed data which, if either, missingness assumption is appropriate. In
Appendix A of supplementary material available at Biostatistics
online, we show that there exist exceptions whereby the
assumption that
. Unfortunately, as
discussed by White and Carlin
(2010), it is usually impossible to distinguish on the basis of the
observed data which, if either, missingness assumption is appropriate. In
Appendix A of supplementary material available at Biostatistics
online, we show that there exist exceptions whereby the
assumption that 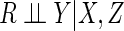 may be testable on the basis of the observed data. However, generally our
contextual knowledge must guide us as to which, if either, is plausible.
may be testable on the basis of the observed data. However, generally our
contextual knowledge must guide us as to which, if either, is plausible.
For some questions (and variables), it may be deemed likely from contextual
knowledge and experience that propensity to respond to the question is at least
partly determined by the value of that variable, such that missingness is not at
random. Examples include surveys in which participants are asked about their
income, with those with low or high income generally considered less likely to
respond (Little and Zhang, 2011). In
Section 4, we consider data on alcohol consumption and blood pressure from
NHANES, in which we argue missingness in alcohol consumption is likely to depend
largely on alcohol consumption itself, and given consumption (and other
covariates), be independent of blood pressure level. As we describe in further
detail in Appendix B of supplementary material available at Biostatistics
online, in other settings the assumption that
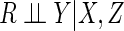 may be plausible if the covariate
may be plausible if the covariate 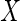 is measured much earlier in
time than the outcome
is measured much earlier in
time than the outcome 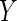 . Thus, sometimes the
assumption that
. Thus, sometimes the
assumption that  may be plausible, while the MAR assumption that
may be plausible, while the MAR assumption that 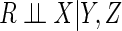 will
not be.
will
not be.
2.2. Estimation with full data
Before considering estimation with partially observed 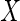 , we first
consider estimation in the absence of missing data. Let
, we first
consider estimation in the absence of missing data. Let
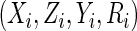 ,
,
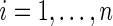 denote an
i.i.d. sample of
denote an
i.i.d. sample of  subjects. All regular and
asymptotically linear estimators of the parameter
subjects. All regular and
asymptotically linear estimators of the parameter 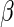 indexing the conditional mean model of interest (equation (2.1)) can be expressed (up
to asymptotic equivalence) as the solution
indexing the conditional mean model of interest (equation (2.1)) can be expressed (up
to asymptotic equivalence) as the solution 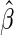 to an estimating equation of the form
to an estimating equation of the form
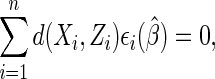 |
(2.2) |
where  is a vector-valued
function of
is a vector-valued
function of  with dimension that of
with dimension that of
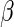 , and
, and
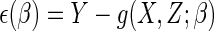 (Rotnitzky and Robins, 1997).
That estimating
(Rotnitzky and Robins, 1997).
That estimating 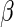 by solving such an
estimating equation results in a consistent estimator follows from the fact that
the expectation of the estimating function
by solving such an
estimating equation results in a consistent estimator follows from the fact that
the expectation of the estimating function 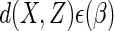 is zero
when evaluated at the true value
is zero
when evaluated at the true value 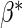 . The efficiency of
the estimator depends on the choice of the function
. The efficiency of
the estimator depends on the choice of the function  , with
the optimal choice being given by
, with
the optimal choice being given by 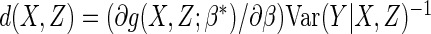 .
.
2.3. Estimation with partially observed 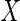
Now suppose that 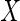 is partially observed, with
is partially observed, with
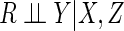 .
As described previously, under this assumption CCA gives valid inferences, but
fails to draw on the observed information in the incomplete cases. In Appendix C
of supplementary material available at Biostatistics
online, we show that if a fully parametric model
.
As described previously, under this assumption CCA gives valid inferences, but
fails to draw on the observed information in the incomplete cases. In Appendix C
of supplementary material available at Biostatistics
online, we show that if a fully parametric model
 is assumed
(rather than the conditional mean model of (2.1)), without making further assumptions all
regular and asymptotically linear estimators of
is assumed
(rather than the conditional mean model of (2.1)), without making further assumptions all
regular and asymptotically linear estimators of 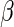 only
use information from the complete cases. It follows that we must make additional
assumptions in order to extract information from the incomplete cases.
only
use information from the complete cases. It follows that we must make additional
assumptions in order to extract information from the incomplete cases.
One route to gaining efficiency over CCA is to take a fully parametric approach,
which involves specifying parametric models for 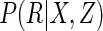 , for
, for
 , and for
, and for
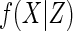 , or a semi-parametric
approach as in Rotnitzky and Robins
(1997), based only (in additional to the conditional mean model of
interest) on a parametric model for
, or a semi-parametric
approach as in Rotnitzky and Robins
(1997), based only (in additional to the conditional mean model of
interest) on a parametric model for 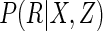 . These are somewhat
unappealing because the validity of resulting inferences will depend on the
correct specification of these models. In particular, since a model for
. These are somewhat
unappealing because the validity of resulting inferences will depend on the
correct specification of these models. In particular, since a model for
 cannot be directly
estimated using the observed data (whenever
cannot be directly
estimated using the observed data (whenever 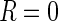 ,
,
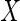 is missing), ensuring that this
model is correctly specified would be difficult.
is missing), ensuring that this
model is correctly specified would be difficult.
Instead, we consider estimation of 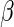 given specification of
a model
given specification of
a model 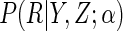 , indexed by
parameter
, indexed by
parameter 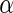 , for
, for
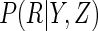 . Note that, under
our assumptions, this is not a model for the underlying missingness mechanism
. Note that, under
our assumptions, this is not a model for the underlying missingness mechanism
 . However, since the
model
. However, since the
model 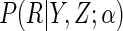 only involves
fully observed variables (unlike a model for the underlying missingness
mechanism), estimation of
only involves
fully observed variables (unlike a model for the underlying missingness
mechanism), estimation of  is standard, e.g. by
maximum likelihood (ML). Specifically, we assume that the following logistic
model holds:
is standard, e.g. by
maximum likelihood (ML). Specifically, we assume that the following logistic
model holds:
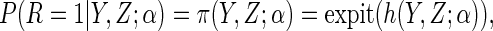 |
(2.3) |
where 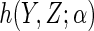 is a known
function, linear in
is a known
function, linear in  , and
, and
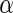 is a
finite-dimensional parameter with true value
is a
finite-dimensional parameter with true value 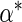 .
.
Suppose for the moment that the true value of  ,
,
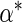 is known. Letting
is known. Letting
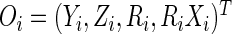 denote the data observed from subject
denote the data observed from subject 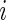 , it is then easily verified
that the (infeasible) estimator
, it is then easily verified
that the (infeasible) estimator 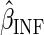 which solves the estimating equation
which solves the estimating equation
 |
(2.4) |
where
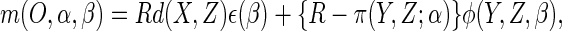 |
(2.5) |
and where  and
and
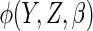 are
arbitrary functions with dimension the same as
are
arbitrary functions with dimension the same as 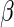 , is
consistent and asymptotically normal. The first part is identical to the CCA
estimating function, which has mean zero (at
, is
consistent and asymptotically normal. The first part is identical to the CCA
estimating function, which has mean zero (at 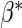 )
when
)
when 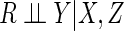 .
The second part, to which both subjects with
.
The second part, to which both subjects with 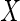 observed
and those with
observed
and those with  missing contribute, has
mean zero provided that the model for
missing contribute, has
mean zero provided that the model for  is correctly
specified, since then
is correctly
specified, since then 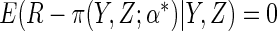 .
.
In practice, 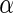 must be estimated. We
assume that
must be estimated. We
assume that 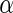 is estimated by its
MLE, which is the value
is estimated by its
MLE, which is the value 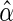 solving the
likelihood score equations
solving the
likelihood score equations
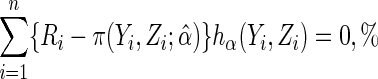 |
with  .
The parameter
.
The parameter 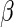 of interest can then
be estimated by solving the estimating equation (2.4), replacing the unknown
of interest can then
be estimated by solving the estimating equation (2.4), replacing the unknown
 by its MLE
by its MLE
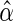 , i.e. by
solving
, i.e. by
solving
 |
(2.6) |
In Appendix D.1 of supplementary material available at Biostatistics
online, we show that under suitable regularity conditions, this
augmented complete case (ACC) estimator 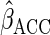 is
consistent and asymptotically normal, with influence function
is
consistent and asymptotically normal, with influence function
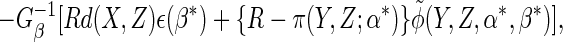 |
(2.7) |
where
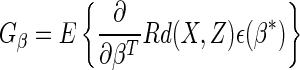 |
(2.8) |
and
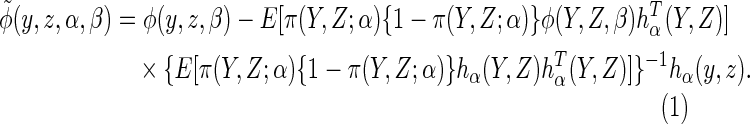 |
(2.9) |
The asymptotic variance of 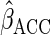 is equal to
is equal to 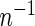 times the variance of
the influence function (as given by (2.7)), and this can be estimated using (2.8) and (2.9), replacing expectations
and variances by their empirical counterparts, and
times the variance of
the influence function (as given by (2.7)), and this can be estimated using (2.8) and (2.9), replacing expectations
and variances by their empirical counterparts, and 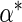 and
and 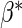 by their
corresponding sample estimates.
by their
corresponding sample estimates.
The choices of the functions  and
and
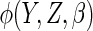 affect the
efficiency of
affect the
efficiency of 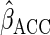 .
For simplicity, we consider how to choose
.
For simplicity, we consider how to choose 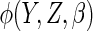 in order to
minimize the variance of
in order to
minimize the variance of 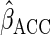 for a given choice of
for a given choice of  (e.g. the choice we
would use with full data). In Appendix D.2 of supplementary material available at Biostatistics
online, we show that the optimal function
(e.g. the choice we
would use with full data). In Appendix D.2 of supplementary material available at Biostatistics
online, we show that the optimal function
 is given by
is given by
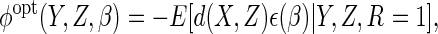 |
(2.10) |
which in particular improves upon the efficiency of CCA, which
is obtained by choosing  . We let
. We let
 denote the estimator which uses
denote the estimator which uses 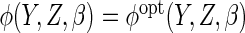 .
.
2.4. Implementation
The optimal choice 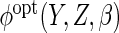 depends on aspects of the data generating mechanism about which we have not made
assumptions. We consider two approaches for estimating
depends on aspects of the data generating mechanism about which we have not made
assumptions. We consider two approaches for estimating 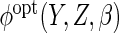 .
.
The first is to posit a parametric working model 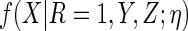 and calculate
the expectations required in
and calculate
the expectations required in 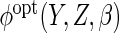 .
We denote the resulting estimator by
.
We denote the resulting estimator by 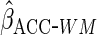 .
Note that while mis-specification of this working model will affect the
efficiency of the estimator, it will not affect its consistency. This also means
that, by Newey and McFadden (1994,
Theorem 6.2), estimation of
.
Note that while mis-specification of this working model will affect the
efficiency of the estimator, it will not affect its consistency. This also means
that, by Newey and McFadden (1994,
Theorem 6.2), estimation of 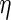 can be ignored when
calculating variance estimates, and that the estimator in which
can be ignored when
calculating variance estimates, and that the estimator in which
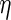 is estimated will have
the same asymptotic efficiency as the estimator which uses the probability limit
value
is estimated will have
the same asymptotic efficiency as the estimator which uses the probability limit
value 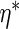 . If the working
model is correctly specified,
. If the working
model is correctly specified, 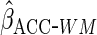 will thus have the same efficiency as
will thus have the same efficiency as 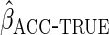 .
In our simulations and illustrative example, we estimate
.
In our simulations and illustrative example, we estimate
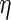 by ML in the complete
cases and calculate the expectations involved in
by ML in the complete
cases and calculate the expectations involved in 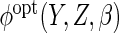 by
Monte-Carlo integration. This involves generating
by
Monte-Carlo integration. This involves generating 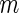 improper
imputations from the implied distribution
improper
imputations from the implied distribution  for
each subject, and approximating the required expectations by their empirical
means based on these imputations. Inferences may be anti-conservative if a small
value of
for
each subject, and approximating the required expectations by their empirical
means based on these imputations. Inferences may be anti-conservative if a small
value of 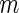 is used, although we did not
find this to be the case in simulations (see Section 3).
is used, although we did not
find this to be the case in simulations (see Section 3).
If the posited working model 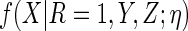 is
mis-specified, there is no guarantee that
is
mis-specified, there is no guarantee that  will improve upon the efficiency of CCA. In Appendix D.3 of supplementary material available at Biostatistics
online, we give details of a modified estimator
will improve upon the efficiency of CCA. In Appendix D.3 of supplementary material available at Biostatistics
online, we give details of a modified estimator
 which, for a given choice of
which, for a given choice of 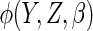 (or working
model used to estimate
(or working
model used to estimate 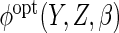 ),
ensures that estimates are at least as efficient as CCA. We denote the
corresponding estimator which uses a parametric working model to estimate
),
ensures that estimates are at least as efficient as CCA. We denote the
corresponding estimator which uses a parametric working model to estimate
 by
by 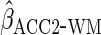 .
.
The second approach we consider is non-parametric estimation of
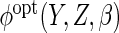 using kernel regression. Following similar approaches used in the MAR context
(Qi and others,
2005), we estimate
using kernel regression. Following similar approaches used in the MAR context
(Qi and others,
2005), we estimate 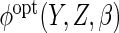 using the Nadaraya–Watson estimator. Letting
using the Nadaraya–Watson estimator. Letting 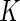 denote a
kernel function, this is given by
denote a
kernel function, this is given by
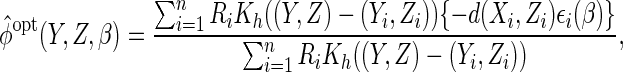 |
where 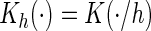 and
and
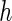 denotes a vector of bandwidths.
To avoid having to calculate
denotes a vector of bandwidths.
To avoid having to calculate 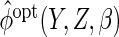 repeatedly when solving the estimating equations, one can instead use
repeatedly when solving the estimating equations, one can instead use
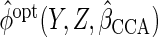 ,
where
,
where 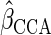 denotes the CCA estimator. In Appendix E of supplementary material available at Biostatistics
online, we show that under suitable regularity conditions, the
resulting estimator, denoted by
denotes the CCA estimator. In Appendix E of supplementary material available at Biostatistics
online, we show that under suitable regularity conditions, the
resulting estimator, denoted by  ,
has the same asymptotic distribution as
,
has the same asymptotic distribution as 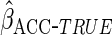 .
This means in particular that, as in the case of a parametric working model,
kernel estimation of
.
This means in particular that, as in the case of a parametric working model,
kernel estimation of 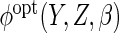 can be ignored for the purposes of variance estimation. Letting
can be ignored for the purposes of variance estimation. Letting
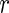 denote the number of continuous
components in
denote the number of continuous
components in 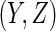 , the bandwidth
conditions of Appendix E of supplementary material available at Biostatistics
online can be satisfied by choosing
, the bandwidth
conditions of Appendix E of supplementary material available at Biostatistics
online can be satisfied by choosing 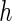 to be of
order
to be of
order  , for some integer
, for some integer
 with
with 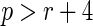 and
and
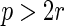 .
.
In the special case of a linear conditional mean model, 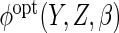 depends only on
depends only on 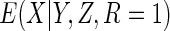 and
and
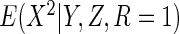 , and so in
the simulation study and illustrative analysis we also implement an estimator
, and so in
the simulation study and illustrative analysis we also implement an estimator
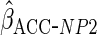 in which
in which 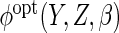 is estimated using the Nadaraya–Watson estimates of
is estimated using the Nadaraya–Watson estimates of
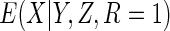 and
and
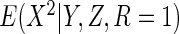 .
.
3. Simulations
In this section, we present simulation results to examine the performance of the
proposed estimator for a linear conditional mean model, and compare it to CCA, MI
(assuming MAR), and an IPW CCA (assuming MAR) estimator. The simulation setup is
described in detail in Appendix F of supplementary material available at Biostatistics
online. In brief, for 1000 datasets of size 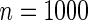 , the
observation indicator
, the
observation indicator 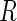 was simulated with
was simulated with
 and covariates
and covariates
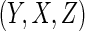 were then generated from a
trivariate normal distribution conditional on
were then generated from a
trivariate normal distribution conditional on 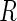 , such that
, such that
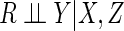 . The
setup meant that
. The
setup meant that  was a logistic regression
with
was a logistic regression
with 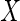 and
and  as covariates
and that
as covariates
and that 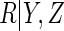 was a logistic regression with
was a logistic regression with
 and
and 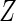 as linear
covariates. The conditional mean model of interest was
as linear
covariates. The conditional mean model of interest was
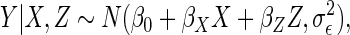 |
with  ,
,
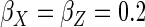 , and
the coefficient of determination
, and
the coefficient of determination 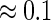 . We present results
for the following estimators:
. We present results
for the following estimators:
CCA;
MI, assuming MAR: estimates based on 10 (proper) MIs of
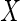 , assuming a normal
linear regression imputation model for
, assuming a normal
linear regression imputation model for 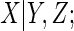
IPW MAR: the standard IPW CCA estimator assuming MAR, using weights found from a logistic regression model with
 and
and
 included as linear
covariates;
included as linear
covariates;- ACC estimator, assuming a logistic regression model for
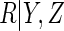 :
: 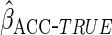 using the true
using the true 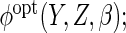
 with
with 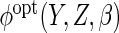 estimated using Monte-Carlo integration (10 imputations)
based on a parametric working model (normal linear
regression for
estimated using Monte-Carlo integration (10 imputations)
based on a parametric working model (normal linear
regression for  ,
with
,
with 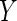 and
and
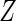 as
covariates);
as
covariates);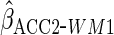 ,
using the working model of
,
using the working model of 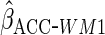 ;
;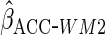 with
with  estimated using Monte-Carlo integration but with a
mis-specified working model (normal linear regression with
estimated using Monte-Carlo integration but with a
mis-specified working model (normal linear regression with
 and
and
 as
covariates);
as
covariates);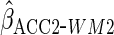 using the working model of
using the working model of  ;
;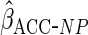 and
and 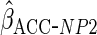 ,
using a normal kernel, assuming independence, and with
,
using a normal kernel, assuming independence, and with
 where
where 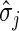 denotes the sample standard deviation of the
denotes the sample standard deviation of the
 th
conditioning variable in the subset where
th
conditioning variable in the subset where
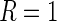 and
and
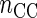 denotes the number of complete cases.
denotes the number of complete cases.
Table 1 shows the simulation results,
based on 1000 simulations for each scenario. CCA was unbiased for all scenarios, as
expected. Both MI and IPW assuming MAR were biased for 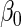 , but
had little bias for
, but
had little bias for 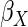 and
and
 . These findings are
consistent with the analytical results of Appendix G of supplementary material available at Biostatistics
online, where we derive analytical expressions for the bias of MI
assuming MAR for a simpler parametric linear regression model setting without
. These findings are
consistent with the analytical results of Appendix G of supplementary material available at Biostatistics
online, where we derive analytical expressions for the bias of MI
assuming MAR for a simpler parametric linear regression model setting without
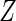 .
.
Table 1.
Mean 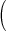 SD
SD of
estimates over
of
estimates over 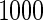 simulations
simulations
| Estimator | 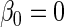 |
 |
 |
|---|---|---|---|
| CCA |
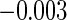 (0.062)
(0.062) |
0.200 (0.044) | 0.199 (0.044) |
| MI |
 (0.052)
(0.052) |
0.202 (0.044) | 0.200 (0.034) |
| IPW |
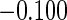 (0.054)
(0.054) |
0.202 (0.045) | 0.198 (0.044) |
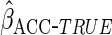 |
 0.003
(0.061) 0.003
(0.061) |
0.200 (0.043) | 0.200 (0.034) |
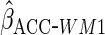 |
 0.003
(0.062) 0.003
(0.062) |
0.201 (0.045) | 0.200 (0.034) |
 |
 0.001
(0.062) 0.001
(0.062) |
0.200 (0.044) | 0.200 (0.034) |
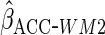 |
 0.001
(0.064) 0.001
(0.064) |
0.198 (0.047) | 0.201 (0.034) |
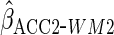 |
 0.001
(0.062) 0.001
(0.062) |
0.199 (0.044) | 0.200 (0.034) |
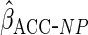 |
 0.006
(0.064) 0.006
(0.064) |
0.202 (0.047) | 0.195 (0.058) |
 |
 0.001
(0.061) 0.001
(0.061) |
0.199 (0.043) | 0.201 (0.034) |
Estimates from CCA, MI assuming MAR, IPW CCA assuming MAR,
and ACC analysis for various choices of 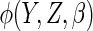 (see
text for details).
(see
text for details).
The ACC estimator was unbiased for all choices of 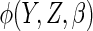 ,
as expected from the asymptotic theory. Using the true optimal
,
as expected from the asymptotic theory. Using the true optimal
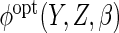 (
(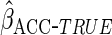 )
resulted in efficiency gain for
)
resulted in efficiency gain for 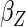 compared to CCA, but
estimates of
compared to CCA, but
estimates of  and
and
 had similar efficiency
to CCA. Using a correctly specified working model (
had similar efficiency
to CCA. Using a correctly specified working model ( )
resulted in identical efficiency to
)
resulted in identical efficiency to 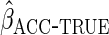 ,
in agreement with the asymptotic theory, which states that in our setting there is
no cost (asymptotically) to estimating the working model parameters. Since the
working model was correct here, as expected the estimator
,
in agreement with the asymptotic theory, which states that in our setting there is
no cost (asymptotically) to estimating the working model parameters. Since the
working model was correct here, as expected the estimator 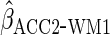 had identical efficiency to
had identical efficiency to 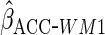 .
.
Using a mis-specified working model ( )
led to estimates of
)
led to estimates of 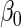 and
and
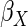 which were less
efficient than CCA, although as predicted from theory estimates remained unbiased.
With this mis-specified working model, as predicted, use of
which were less
efficient than CCA, although as predicted from theory estimates remained unbiased.
With this mis-specified working model, as predicted, use of
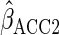 ensured that efficiency was at least as good as CCA (in fact
ensured that efficiency was at least as good as CCA (in fact
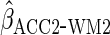 had the same efficiency as the optimal estimator).
had the same efficiency as the optimal estimator).
The non-parametric estimator 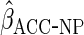 was less efficient, with estimates in fact more variable than CCA. However, the
estimator
was less efficient, with estimates in fact more variable than CCA. However, the
estimator 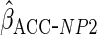 ,
which estimated
,
which estimated 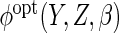 using non-parametric estimates of
using non-parametric estimates of 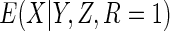 and
and
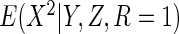 , attained the
same efficiency as
, attained the
same efficiency as 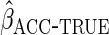 .
.
Table 2 shows the empirical coverage of
the nominal 95% confidence intervals for the various ACC estimators, found
using the sandwich estimator described in Section 2.3. Coverage was close to the
nominal 95% level for all choices of 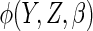 .
.
Table 2.
Coverage of 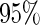 confidence
intervals for ACC analyses
confidence
intervals for ACC analyses from
from
 simulations
simulations
| Estimator | 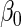 |
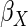 |
 |
|---|---|---|---|
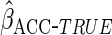 |
94.2 | 94.8 | 94.9 |
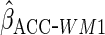 |
94.2 | 93.5 | 94.8 |
 |
93.9 | 94.1 | 93.8 |
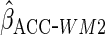 |
93.4 | 95.7 | 95.1 |
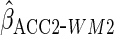 |
94.0 | 94.5 | 94.8 |
 |
95.3 | 95.4 | 95.2 |
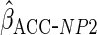 |
93.5 | 93.0 | 94.6 |
4. Application to nhanes
To illustrate the proposed method, we consider data on alcohol consumption and
systolic blood pressure (SBP) from the 2003–2004 NHANES. We focus on the
dependence of SBP on the reported average number of alcoholic drinks consumed per
day on days where the participant drank alcohol (obtained via a questionnaire)
(“no. drinks”), with adjustment for age and body mass index (BMI). Data
are available for  men, for whom
men, for whom
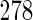 are missing SBP and
are missing SBP and
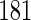 are missing BMI. As argued by
Little and Zhang (2011), it is
plausible that missingness in SBP and BMI is completely at random due to missed
visits, and therefore excluding these participants ought not to introduce bias.
Amongst the remaining
are missing BMI. As argued by
Little and Zhang (2011), it is
plausible that missingness in SBP and BMI is completely at random due to missed
visits, and therefore excluding these participants ought not to introduce bias.
Amongst the remaining  participants,
participants,
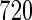 (34.1%) have the alcohol
variable missing. It is a priori plausible that missingness in the
alcohol variable is primarily dependent on the value of the alcohol variable (i.e.
MNAR), and given this, and age and BMI, is independent of SBP. Consequently, CCA is
expected to give valid inferences, while the MAR assumption likely does not
hold.
(34.1%) have the alcohol
variable missing. It is a priori plausible that missingness in the
alcohol variable is primarily dependent on the value of the alcohol variable (i.e.
MNAR), and given this, and age and BMI, is independent of SBP. Consequently, CCA is
expected to give valid inferences, while the MAR assumption likely does not
hold.
A logistic regression model was fitted relating whether the alcohol variable was
observed, with age, BMI, and SBP (linear and quadratic terms) as covariates (Table
3). There was strong evidence that
age was associated with missingness, with increasing age associated with reduced
odds of responding. Increasing BMI was independently associated with reduced odds of
responding to the alcohol question. Lastly, there was evidence (joint test
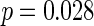 ) that SBP was independently
associated with the probability of missingness, with reduced odds of responding to
the question for those with low or high SBP, relative to those with average SBP.
Assuming that increasing levels of reported alcohol assumption is independently
associated with increased SBP (see CCA results below), this finding is consistent
with the probability that the alcohol variable is missing being elevated for those
with either low or high alcohol consumption.
) that SBP was independently
associated with the probability of missingness, with reduced odds of responding to
the question for those with low or high SBP, relative to those with average SBP.
Assuming that increasing levels of reported alcohol assumption is independently
associated with increased SBP (see CCA results below), this finding is consistent
with the probability that the alcohol variable is missing being elevated for those
with either low or high alcohol consumption.
Table 3.
Estimated adjusted odds ratios  CIs
CIs relating response
to the alcohol question to age
relating response
to the alcohol question to age BMI and SBP in
NHANES
BMI and SBP in
NHANES
| ariable | Odds ratio (95% CI) |
 -value -value |
|---|---|---|
| Age (decades above 50) | 0.763 (0.723, 0.805) |
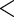 0.001 0.001 |
BMI (kg/m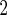 ) ) |
0.978 (0.961, 0.996) | 0.019 |
| SBP (per 10 mmHg above 125) | 1.08 (1.01, 1.16) | 0.020 |
SBP (per
10 mmHg above 125) (per
10 mmHg above 125)
|
0.979 (0.963, 0.996) | 0.015 |
We fitted a linear regression model (using ordinary least squares and sandwich
standard errors to allow for non-constant variance) for SBP with age (linear and
quadratic effects), BMI, and 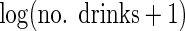 as
covariates. The number of alcoholic drinks variable was entered using a (natural)
log transformation so that the few participants with very large values did not have
undue influence on parameter estimates and because preliminary analyses suggested a
multiplicative effect of number of drinks fitted the data better. Table 4 shows the CCA estimates, which
assuming missingness in the alcohol variable is independent of SBP, conditional on
age, BMI, and reported average number of alcoholic drinks per day, are unbiased.
There was strong evidence that, as expected, increasing age is associated with
increased SBP, with some suggestion of a non-linear effect. Increasing BMI was
associated with increasing SBP, and there was evidence that increasing reported
alcohol consumption is associated with increasing SBP.
as
covariates. The number of alcoholic drinks variable was entered using a (natural)
log transformation so that the few participants with very large values did not have
undue influence on parameter estimates and because preliminary analyses suggested a
multiplicative effect of number of drinks fitted the data better. Table 4 shows the CCA estimates, which
assuming missingness in the alcohol variable is independent of SBP, conditional on
age, BMI, and reported average number of alcoholic drinks per day, are unbiased.
There was strong evidence that, as expected, increasing age is associated with
increased SBP, with some suggestion of a non-linear effect. Increasing BMI was
associated with increasing SBP, and there was evidence that increasing reported
alcohol consumption is associated with increasing SBP.
Table 4.
Estimates of conditional mean model parameters relating SBP
 mmHg
mmHg
 centered at
centered at
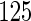 mmHg
mmHg to
age
to
age BMI
BMI and reported
average number of alcoholic drinks consumed per day in
NHANES
and reported
average number of alcoholic drinks consumed per day in
NHANES
| Variable |
|||||
|---|---|---|---|---|---|
| Estimator | Constant | No. of drinks
|
BMI (kg/m ) ) |
Age (decades above 50) | Age (decades
above 50) (decades
above 50)
|
| CCA |
 1.93
(0.80) 1.93
(0.80) |
1.27 (0.58) | 0.41 (0.080) | 3.94 (0.26) | 0.26 (0.14) |
| MI |
 2.36
(0.81) 2.36
(0.81) |
1.51 (0.65) | 0.32 (0.070) | 3.88 (0.21) | 0.30 (0.12) |
| IPW |
 2.07
(0.85) 2.07
(0.85) |
1.50 (0.67) | 0.36 (0.092) | 3.95 (0.24) | 0.21 (0.16) |
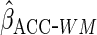 |
 2.21
(0.76) 2.21
(0.76) |
1.40 (0.59) | 0.39 (0.066) | 3.90 (0.24) | 0.32 (0.11) |
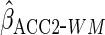 |
 2.02
(0.75) 2.02
(0.75) |
1.21 (0.58) | 0.39 (0.065) | 3.88 (0.24) | 0.31 (0.11) |
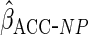 |
 1.90
(0.94) 1.90
(0.94) |
1.37 (0.67) | 0.43 (0.107) | 3.97 (0.31) | 0.22 (0.21) |
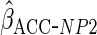 |
 2.03
(0.72) 2.03
(0.72) |
1.20 (0.53) | 0.39 (0.066) | 3.87 (0.23) | 0.32 (0.11) |
Estimates from CCA, MI assuming MAR, IPW CCA assuming MAR,
and ACC analysis using four different choices for
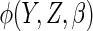 (see text for details).
(see text for details).
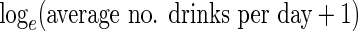 .
.
Next we estimated the conditional mean model parameters assuming missingness in the alcohol variable was MAR, first using MI. The alcohol variable on its original scale was imputed 200 times using a negative binomial regression model with covariates age (linear and quadratic), BMI (linear and quadratic), and SBP (linear and quadratic). Standard errors were obtained using Rubin's rules, but using the sandwich estimator of variance when estimating within-imputation variances. Consistency of MI here relies on the MAR assumption holding and the imputation model being correctly specified. The resulting estimates were fairly similar to CCA, although the coefficient of BMI was somewhat lower, the coefficient of the alcohol variable was somewhat higher, and the estimated constant was lower than that from CCA. Standard errors were smaller than those from CCA for the effects of BMI and age.
Since consistency of MI relies on the imputation model being correctly specified, we also used complete case IPW, with weights calculated using the previously described logistic regression model. Sandwich standard errors were found by stacking the estimating equation used to estimate the parameters of this logistic regression with the IPW complete case estimating equations. The estimated linear age effect was similar to that from CCA, but the estimated quadratic effect was smaller. The estimated coefficient of BMI was slightly smaller than from CCA, and the estimated constant was closer to that from CCA than the MI estimate. The estimated coefficient of the alcohol variable was almost identical to the MI estimate. As is typical, the (sandwich) standard errors for IPW CCA were larger than those for CCA (except for the linear age coefficient).
Lastly, we used the proposed ACC estimator, using the logistic model shown in Table
3 for 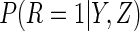 . We
first used
. We
first used 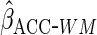 ,
with the parametric working model identical to that used to impute the alcohol
variable in MI (i.e. negative binomial regression imputation). This gave estimates
with smaller standard errors than CCA, and also lower than MI. The estimated
constant and effect of alcohol were both in between the corresponding CCA and MI
estimates. The estimated BMI effect was close to that from CCA, and the estimated
age effects were similar to those from CCA. Using
,
with the parametric working model identical to that used to impute the alcohol
variable in MI (i.e. negative binomial regression imputation). This gave estimates
with smaller standard errors than CCA, and also lower than MI. The estimated
constant and effect of alcohol were both in between the corresponding CCA and MI
estimates. The estimated BMI effect was close to that from CCA, and the estimated
age effects were similar to those from CCA. Using 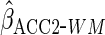 led to an estimated constant closer to that from CCA and an estimated effect of
alcohol which was smaller than from CCA. Standard errors were very slightly smaller
than from
led to an estimated constant closer to that from CCA and an estimated effect of
alcohol which was smaller than from CCA. Standard errors were very slightly smaller
than from  .
The non-parametric estimator
.
The non-parametric estimator 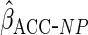 gave estimates with much larger standard errors, whereas
gave estimates with much larger standard errors, whereas 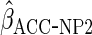 gave estimates with standard errors smaller than those from
gave estimates with standard errors smaller than those from
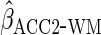 .
.
Overall inferences from the methods were fairly similar. Nevertheless, standard errors were smallest from the proposed ACC estimator(s), and in particular were smaller than CCA for the effects of the fully observed covariates. There is the suggestion that the estimated effect of the alcohol variable was larger when assuming MAR compared with assuming missingness conditionally independent of outcome. Unlike in the simulations, there was no apparent substantial bias in the estimated constant from the methods which assumed MAR.
5. Discussion
In some settings, contextual knowledge will suggest that missingness in a covariate, such as income, is driven primarily by the value of the covariate itself, such that data are MNAR. In prospective studies, missingness in covariates measured at study entry may often plausibly be affected by the covariates themselves (and hence again MNAR), and given these, be independent of the (future) outcome. In these settings, an analysis based on the MAR assumption, such as most implementations of MI and IPW, will lead to asymptotically biased estimates and invalid inferences. For a linear conditional mean model, the analytical results of Appendix G of supplementary material available at Biostatistics online and simulation analyses suggest that the biases may be moderately large for the intercept parameter, but are sometimes modest for the parameters corresponding to covariate effects. However, there likely exist MNAR scenarios in which CCA is unbiased but MAR estimators of covariate effects are biased to a larger extent.
In contrast, if missingness is conditionally independent of outcome, which includes a particular class of MNAR mechanisms, CCA is unbiased but does not make use of all of the observed information. Our proposed augmented CCA estimator improves upon the efficiency of CCA, by relying on a parametric model for how missingness is associated with fully observed covariates and outcome. While one may argue whether it is appropriate to increase precision by relying on additional models, we note that this is also the case for other missing data methods. Furthermore, standard model selection techniques can be used since this model only involves fully observed variables. Given the assumption that missingness is independent of outcome given covariates, CCA and our proposed augmented CCA estimator are both consistent, provided the missingness model used in the latter is correctly specified.
Consistent with the findings of others (e.g. White and Carlin, 2010), in both our simulations and data analysis, while efficiency gain is possible for the coefficients of fully observed covariates, neither MI nor ACC gave improved efficiency for the covariate which was partially observed. This emphasizes the point that, in the absence of auxiliary variables or external information, the gain in efficiency (for both MI and ACC) is achieved through utilizing the observed information in incomplete cases. This implies that in studies where missingness only occurs in the exposure of interest, there is little efficiency to be gained for the exposure effect through using an estimation method which utilizes the incomplete cases.
For the proposed estimator, we have considered estimating the optimal augmentation
function 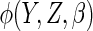 either using a
parametric working model or non-parametric kernel regression methods. For the
latter, we found that direct non-parametric estimation of the optimal augmentation
function lead to estimates with high variability, and in fact efficiency worse than
CCA. In contrast, non-parametric estimation of the first two moments of the
partially observed covariate, which is sufficient in the case of a linear
conditional mean model, gave estimates with efficiency essentially identical to that
obtained using the true optimal augmentation function. Further work is thus
warranted regarding how to best non-parametrically estimate the optimal augmentation
function directly for conditional mean models which are not linear.
either using a
parametric working model or non-parametric kernel regression methods. For the
latter, we found that direct non-parametric estimation of the optimal augmentation
function lead to estimates with high variability, and in fact efficiency worse than
CCA. In contrast, non-parametric estimation of the first two moments of the
partially observed covariate, which is sufficient in the case of a linear
conditional mean model, gave estimates with efficiency essentially identical to that
obtained using the true optimal augmentation function. Further work is thus
warranted regarding how to best non-parametrically estimate the optimal augmentation
function directly for conditional mean models which are not linear.
The data analyst who adopts the assumption 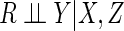 should be aware of the fact that the observed data may sometimes carry evidence to
refute it (see Appendix A of supplementary material available at Biostatistics
online). This can be a concern in settings where the outcome is
continuous,but the covariates are discrete with few levels (see, e.g. Vansteelandt, 2009 for an example where
failure to study the testability of missing data assumptions lead to a severely
biased analysis); however, we tend not to worry about it in more realistic settings
where the power to refute the assumption will typically be very low. Further, the
data analyst should consider whether their postulated model for
should be aware of the fact that the observed data may sometimes carry evidence to
refute it (see Appendix A of supplementary material available at Biostatistics
online). This can be a concern in settings where the outcome is
continuous,but the covariates are discrete with few levels (see, e.g. Vansteelandt, 2009 for an example where
failure to study the testability of missing data assumptions lead to a severely
biased analysis); however, we tend not to worry about it in more realistic settings
where the power to refute the assumption will typically be very low. Further, the
data analyst should consider whether their postulated model for
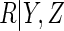 is compatible with the
restrictions imposed by the missing data assumption
is compatible with the
restrictions imposed by the missing data assumption 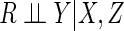 together
with the conditional mean model; careful checking of the missingness model is
therefore recommended.
together
with the conditional mean model; careful checking of the missingness model is
therefore recommended.
Throughout, we have restricted our development to the case of a single partially
observed covariate or vector of covariates. However, we believe the approach may be
extendable to more general patterns of missingness, including non-monotone patterns,
and describe how this could be done for the case of two partially observed variables
in Appendix H of supplementary material available at Biostatistics
online. An advantage of such an approach would be that the
missingness assumption 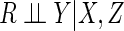 , where
, where
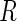 is a vector of missingness
indicators, is easier to interpret than MAR when missingness is non-monotone (Robins and Gill, 1997).
is a vector of missingness
indicators, is easier to interpret than MAR when missingness is non-monotone (Robins and Gill, 1997).
Lastly, we note that in the case of data MAR, so-called doubly robust estimators are available, which remain consistent so long as either the model for missingness or the imputation type model is correct (Tsiatis, 2006). The ACC estimator developed here does not possess such a doubly robust property, and it is indeed unclear whether such estimators exist under the assumptions considered here.
6. Software
A Stata program implementing 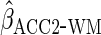 for conditional linear mean models is available for free download by typing
“net from http://missingdata.lshtm.ac.uk/stata” into Stata's command
window and selecting “augcca”.
for conditional linear mean models is available for free download by typing
“net from http://missingdata.lshtm.ac.uk/stata” into Stata's command
window and selecting “augcca”.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
This work was supported by UK Economic and Social Research Council [RES-189-25-0103 to J.W.B. and J.R.C.] and Medical Research Councils [G0900724 to J.W.B., J.R.C., and K.T., and MR/K02180X/1 to J.W.B.]. This work was also supported by the Interuniversity Attraction Poles Programme [P7/06 to SV]. Funding to pay the Open Access publication charges for this article was provided by the UK Medical Research Council.
Supplementary Material
Acknowledgements
Conflict of Interest: None declared.
References
- Carpenter J. R., Kenward M. G., Vansteelandt S. A comparison of multiple imputation and inverse probability weighting for analyses with missing data. Journal of the Royal Statistical Society, Series A (Statistics in Society) 2006;169:571–584. [Google Scholar]
- Little R. J. A., Rubin D. B. Statistical Analysis with Missing Data. Chichester: Wiley; 2002. 2nd edition. [Google Scholar]
- Little R. J., Zhang N. Subsample ignorable likelihood for regression analysis with missing data. Journal of the Royal Statistical Society. 2011;60:591–605. [Google Scholar]
- Newey W. K., McFadden D. Large sample estimation and hypothesis testing. In: Engle R. F., McFadden D. L., editors. Handbook of Econometrics. 1994. pp. 2111–2245. Elsevier B.V.: [Google Scholar]
- Qi L., Wang C. Y., Prentice R. L. Weighted estimators for proportional hazards regression with missing covariates. Journal of the American Statistical Association. 2005;100:1250–1263. [Google Scholar]
- Robins J. M., Gill R. D. Non-response models for the analysis of non-monotone ignorable missing data. Statistics in Medicine. 1997;16:39–56. doi: 10.1002/(sici)1097-0258(19970115)16:1<39::aid-sim535>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- Rotnitzky A., Robins J. M. Analysis of semi-parametric regression models with nonignorable nonresponse. Statistics in Medicine. 1997;16:81–102. doi: 10.1002/(sici)1097-0258(19970115)16:1<81::aid-sim473>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- Rubin D. B. Multiple Imputation for Nonresponse in Surveys. New York: Wiley; 1987. [Google Scholar]
- Seaman S. R., White I. R. Review of inverse probability weighting for dealing with missing data. Statistical Methods in Medical Research. 2011;22:278–295. doi: 10.1177/0962280210395740. [DOI] [PubMed] [Google Scholar]
- Sterne J. A. C., White I. R., Carlin J. B., Spratt M., Royston P., Kenward M. G., Wood A. M., Carpenter J. R. Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls. British Medical Journal. 2009;339:157–160. doi: 10.1136/bmj.b2393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsiatis A. A. Semiparametric Theory and Missing Data. New York: Springer; 2006. [Google Scholar]
- Vansteelandt S. Discussion on identifiability and estimation of causal effects in randomized trials with noncompliance and completely non-ignorable missing-data. Biometrics. 2009;65:686–689. doi: 10.1111/j.1541-0420.2008.01120.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White I. R., Carlin J. B. Bias and efficiency of multiple imputation compared with complete-case analysis for missing covariate values. Statistics in Medicine. 2010;28:2920–2931. doi: 10.1002/sim.3944. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


