Information transfer and behavioural inertia in starling flocks

Abstract

Collective decision-making in biological systems requires all individuals in the group to go through a behavioural change of state. During this transition fast and robust transfer of information is essential to prevent cohesion loss. The mechanism by which natural groups achieve such robustness, though, is not clear. Here we present an experimental study of starling flocks performing collective turns. We find that information about direction changes propagates across the flock with a linear dispersion law and negligible attenuation, hence minimizing group decoherence. These results contrast starkly with current models of collective motion, which predict diffusive transport of information. Building on spontaneous symmetry breaking and conservation laws arguments, we formulate a new theory that correctly reproduces linear and undamped propagation. Essential to the new framework is the inclusion of the birds’ behavioural inertia. The new theory not only explains the data, but also predicts that information transfer must be faster the stronger the group’s orientational order, a prediction accurately verified by the data. Our results suggest that swift decision-making may be the adaptive drive for the strong behavioural polarization observed in many living groups.

Consider a flock of starlings under direct threat from a peregrine falcon. To dodge the attack, the group constantly changes direction of motion. Each such change, however, puts the flock in a vulnerable condition, which the predator is ready to exploit. The slightest uncertainty in turning may decrease cohesion, or even split the flock and push some birds astray, leaving them easy prey of the falcon. Keeping cohesion during collective decision-making is a general issue in social species, for which living in group is a matter of fitness [1-3]. Irrespective of the consensus mechanism leading to the decision, its actual execution cannot be instantaneous, as a certain amount of time is needed to propagate the decision throughout the group. During this time, cohesion is strained by the mismatch between individuals who have already changed behavioural state and those who have not yet done so. The mechanism by which the information is transferred from individual to individual has therefore a significant impact on collective decision-making [4-8].

In the footsteps of the seminal work by Pomeroy and Heppner [9], we study here natural flocks of starlings (Sturnus vulgaris) performing collective turns in the field (Movie 1). By using a 3-cameras setup (see Methods and [10]), we reconstruct the full 3d trajectory of each bird in the flock (Fig. 1 and Movie 2). For each pair of birds, i and j, we calculate their mutual turning delay, τ_ij, defined as the amount of time by which bird j turns before (τ_ij > 0) or after (τ_ij < 0) bird i (Fig. 1-d,e). By using the delays τ_ij we rank all birds in the flock according to their turning order, that is we find the first to turn, the second, and so on. Each bird i is thus labelled by its rank, r_i, and by its absolute turning time, t_i, that is the delay of i with respect to the top bird in the rank (Methods). We can then plot the rank r_i of each bird as a function of its absolute turning time t_i, thus obtaining the ranking curve, r(t) in Fig. 2-a (see also SI-Fig. S3).

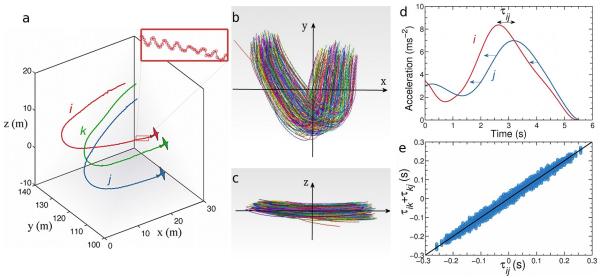
FIG. 1. Birds trajectories and turning delays.

a, Reconstructed 3d trajectories of three birds belonging to a flock performing a collective turn. Inset: zig-zag due to wing flapping. b, c, Trajectories of all N = 176 birds in a flock. Each trajectory lies approximately on a plane. d, The radial acceleration of a turning bird displays a maximum as a function of time. This is in fact our very definition of a turn. Given two birds, i and j, we define the mutual turning delay τ_ij as the time we have to shift the full curve of the radial acceleration a_j(t) to maximally overlap it with a_i(t) (Methods). e, In the absence of experimental noise we must have, τ_ik + τ_kj = τ_ij: if i turns 20ms before k, and k turns 15ms before j, then i turns 35ms before j. Due to noise, time ordering will not hold strictly, but we still want it to be correct on average for τ_ij to make biological sense. We consider all triplets of birds and plot τ_ik + τ_kj vs. τ_ij. The data fall on the identity line with relatively small spread, confirming the temporal consistency of the turning delays (see also Methods and SI-Fig. S2).

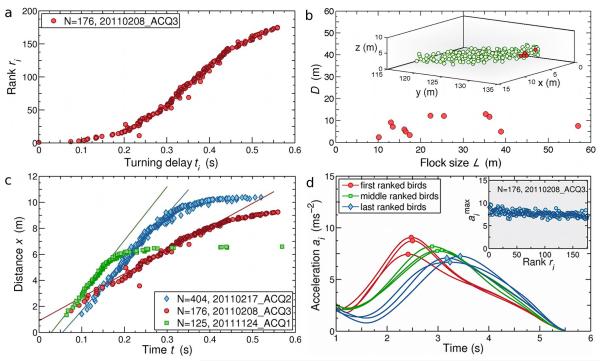
FIG. 2. Propagation of the turn across the flock.

a, The rank r of each bird, i.e. its order in the turning sequence, is plotted vs its absolute turning delay t, i.e. the delay with respect to the first bird to turn (ranking curves for all turning events are presented in Supplementary Information Fig. S3). b, The maximum mutual distance D between the top 5 birds in the rank does not increase with the linear size of the flock, L, hence indicating that the first birds to turn are actually close to each other in space. The result does not change if we use a different number of top birds, as long as this number is much smaller than the flock’s size. Inset: the actual position of the top 5 birds (red) within a real flock. c, The distance x traveled by the information in a time t is proportional to the radius of the sphere containing the first r(t) birds in the rank, namely x(t) = [r(t)/ρ]^1/3. The speed of propagation, c_s, is the slope of the linear regime of x(t) for early and intermediate times (black lines are linear fits - see Supplementary Information, Appendix A for later time saturation). d, The intensity of the peak of the radial acceleration, a^max, (solid symbols) decreases very weakly in passing from the first to the last turning birds. In the inset, we plot $a_i^{\max }$ vs the rank r_i for each bird. Hence, information propagates through the flock with negligible attenuation.

We find that the top birds in the rank, namely the first birds to turn, are physically close to each other (Fig. 2-b). Hence, the decision to turn has a spatially localized origin and it then propagates across the group through a bird-to-bird (‘social’) transfer of information [11]. The alternative view, namely that the turn is caused by an external stimulus hitting all birds at the same time, would imply an independent response of each bird and thus a spatially unstructured distribution of the delay times, while we always find a clear spatial modulation of the delays (Movie 2). Our aim is to understand what is the mechanism through which information propagates from its local origin to the rest of the flock.

From the ranking curve we can calculate the dispersion law, namely how much distance x the information travels in a time t. We are in three dimensions and the turn has a localized origin, hence x(t) is equal to the radius of the sphere containing the first r(t) birds in the rank, namely x(t) = [r(t)/ρ]^1/3, where ρ is the density of the flock. The most important feature of the curve x(t) (Fig. 2-c) is that there is a clear linear regime for early and intermediate times (before border effects kick in - see SI-Appendix A). We conclude that the distance traveled by the information grows linearly with time, x(t) = c_st. The parameter c_s is the speed of propagation of the directional information; its value is in the range 20–40 ms⁻¹. These values of c_s are high: the decision to turn can sweep through a flock of 400 birds in little more than half a second. We stress that x(t) is the distance traveled by the information in the flock’s reference frame: this transport is not the mere effect of the flock’s absolute motion, but rather a genuine transfer of information within the flock. Note also that the flocks’ speed v₀ is in the range 7–12 ms⁻¹ and that we find no correlation between c_s and v₀.

Although always large, c_s varies significantly across different flocks (Fig. 2-c and SI-Table S1). It therefore seems that some flocks manage faster information transfer than others. If we model the flock as a simple fluid, where small density fluctuations transport sound waves, we may naively expect this variability of c_s to disappear by rescaling it with the flock’s density, as it would be the case for ordinary sound [12]. However, the density rescaling does not work. In fact, what propagates during the turn are fluctuations of orientation, not of density, of which we find no significant fluctuations. We shall see later on that the variability of c_s has an entirely different explanation.

Acceleration data show another interesting result: the information to turn propagates across the flock with negligible attenuation (Fig. 2-d). Flocks are large, the information to turn dynamically reaches all birds through a lot of intermediate passages, so that a substantial level of damping could be expected. Yet it is not so. Both sub-linear propagation and attenuation would result into a physical spread of the flock, and eventually into its disruption. On the contrary, the linear and fast propagation that we find, together with the low damping of the signal, are key factors in preserving flock’s cohesion. What is the theoretical mechanism at the basis of this phenomenon?

Virtually all theoretical descriptions of collective motion are based on alignment dynamics: each individual tends to keep its direction of motion as close as possible to that of its neighbours [12-17],

$${\mathbf{v}}_i(t+1)={\mathbf{v}}_i\left(t\right)+J\sum _{j\in i}{\mathbf{v}}_j\left(t\right)$$ (1)

where the vector v_i is the velocity of bird i and the sum extends over all neighbours j of i (be they metric or topological [18, 19]). We have disregarded noise/temperature, which is inessential for what follows; we will just assume that the alignment strength J is large, so that we are in the deeply ordered phase (as natural flocks are [17]). In continuous time, the update rule (1) is equivalent to the equation,

$$\frac{d{\mathbf{v}}_i}{dt}=-\frac{\partial H}{\partial {\mathbf{v}}_i},H=-J\sum _{\langle ij\rangle }{\mathbf{v}}_i\cdot {\mathbf{v}}_j$$ (2)

Hence, each bird changes its velocity following a social force, ${\mathbf{F}}_{\mathrm{s}}^i=-\partial H∕\partial {\mathbf{v}}_i$, produced by its neighbours. We stress that we are not studying eqs.(1-2) for the sake of realism, but because we want to understand the mathematical consequences of the alignment term. To do so we need the simplest equation containing such term. Adding more realistic ingredients would not alter the mathematical effects of alignment.

To simplify the algebra we exploit the fact that the trajectories of birds during a turn lie approximately on a plane (Fig. 1-b,c and Movie 2). This allows us to use a two-dimensional order parameter, ${\mathbf{v}}_i=(v_i^x,v_i^y)=v_0{e}^{i{\phi }_i}$, where the phase φ_i is the angle between the direction of motion of i and that of the flock (in SI-Appendix G we describe the more general 3d case). We make the assumption - justified by the data - that v₀ is constant during the turn and the same for all birds. In the highly ordered regime the velocities v_i differ little from the flock’s one, so that φ_i << 1. We can thus expand the Hamiltonian and obtain,

$$H=\frac{J}{2}\sum _{\langle ij\rangle }{({\phi }_i-{\phi }_j)}^2=\frac{1}{2}{a}^{2}J\int \frac{d^{3}x}{a^3}{[\nabla \phi (x,t\left)\right]}^2$$ (3)

where a is the average nearest neighbours distance and a term $v_0^2$ has been reabsorbed into J. The equation of motion associated to Hamiltonian (3) is,

$$\frac{\partial \phi }{\partial t}=-\frac{\delta H}{\delta \phi }=a^{2}J{\nabla }^2\phi$$ (4)

Relation (4) is a diffusion equation for the phase φ, with dispersion law ω ~ ik². This theoretical prediction has two consequences, both in sharp contrast with the empirical data: i) Information travels sub-linearly, $x\sim \sqrt{t}$, at variance with the linear propagation we find in turning flocks. A speed of propagation c_s cannot even be defined. ii) The frequency is purely imaginary, meaning that this is an overdamped, non-propagating mode, in stark disagreement with the undamped propagation we observe in flocks.

The theory just described has two problems. First, it seems to be missing a conservation law. Hamiltonian (2) is invariant under a global gauge symmetry, namely a uniform rotation of the velocities v_i(φ_i → φ_i + δφ), encoding the fact that all directions of flight are equivalent. Through Noether’s theorem, a symmetry implies in general a conservation law, of which, however, there is no trace in equation (4). A hidden conservation may heavily affect the dispersion law, because the excitation of a conserved field cannot be relaxed locally, but it must be transported away. Second, equation (4) completely neglects behavioural inertia, as the social force, F_s = aJ∇²φ, controls directly $\stackrel{.}{\phi }$, rather than $\ddot{\phi }$. This is odd. Imagine that the interaction with the neighbours requires bird i to perform a U-turn in one time step. This behaviour is allowed by (4), although it is clearly unreasonable.

Missing conservation law and neglected inertia are two sides of the same coin. When a generalized coordinate (like φ) parametrizes a symmetry of the interaction, its canonically conjugated momentum (let us call it s_z) is conserved [20]. However, if the inertial term containing the momentum is neglected, namely if the overdamped approximation is done, the conservation law is lost and a purely dissipative equation like (4) is obtained. This is the case with the previous theory. For a turning flock, however, there is no justification for the overdamped approximation. We can therefore cure both problems by adding a new kinetic term, $s_z^2∕2\chi$, where s_z is the momentum canonically conjugated to φ, and χ is the generalized moment of inertia. We therefore propose the novel Hamiltonian,

$$H=\int \frac{d^{3}x}{a^3}\left\{\frac{1}{2}{a}^{2}J{[\nabla \phi (x,t\left)\right]}^2+\frac{s_z^2(x,t)}{2\chi }\right\}$$ (5)

The momentum s_z is defined as the local generator of the rotations around the z axis parametrized by the phase φ, so that (s_z, φ) are generalized action-angle canonical variables. It can be shown that s_z is the intrinsic spin of the bird, equivalent to the inverse radius of curvature of its trajectory (SI-Appendix B), whereas χ is the behavioural resistance (inertia) of a bird to change its instantaneous radius of curvature when a social force is exerted by its neighbours (SI-Appendix C). The canonical equations of motion generated by (5) are,

$$\frac{\partial \phi }{\partial t}=\frac{\delta H}{\delta s_z}=\frac{s_z}{\chi };\frac{\partial s_z}{\partial t}=-\frac{\delta H}{\delta \phi }=a^{2}J{\nabla }^2\phi$$ (6)

The crucial consequence of the symmetry is that the r.h.s of the second equation of motion is in fact a divergence, ∇² φ = ∇ · ∇ φ, so that we can rewrite this relation as a continuity equation for the spin s_z(x, t),

$$\frac{\partial s_z}{\partial t}-\nabla \cdot {\mathbf{j}}_z=0$$ (7)

with conserved current j_z(x, t) = a² J∇ φ(x, t). We stress that j_z is not a mass, nor a momentum current. What is transported by j_z is spin, in the form of fluctuations of the phase φ, not of the density. This transport of spin, and therefore of curvature, is what actually gives rise to the collective turn.

Equation (7) is the conservation law generated by the rotational symmetry, which was missing in the previous theory. Imagine that a strong misalignment among a subgroup of birds forms in a certain position of the flock. This causes a local excess of curvature, and thus an excitation of the field s_z(x, t). Conservation law (7) states that such excitation cannot be locally dissipated out, but it must be transported away. This mechanism gives rise to a propagating mode, namely to an undamped spin wave [26]. Indeed, by taking the second derivative with respect to time in (6) we obtain,

$$\frac{{\partial }^2\phi }{\partial t^2}-c_s^2{\nabla }^2\phi =0,c_s^2=a^{2}J∕\chi$$ (8)

Relation (8) is D’Alembert’s equation, describing waves propagating with speed c_s and no damping. Its dispersion relation is linear, ω = c_sk, which in terms of the distance x traveled by the information in a time t, reads, x = c_st. This is precisely the linear and undamped propagation law that we find in turning flocks.

The rotation of the velocity vectors parametrized by φ corresponds to an equal radius turn, i.e. a turn in which all birds have the same radius of curvature and where trajectories cross. This is exactly the way adopted by real flocks to turn (see Fig. 1 and Supplementary Movie 2) and it has a clear biological motivation: it keeps the speed v₀ constant throughout the flock. Equal radius turning was first experimentally discovered in [9], and later confirmed in [21]. On the other hand, the rotation of the position vectors parametrized by the orbital angle θ of 2d polar coordinates corresponds to a parallel path turn, typical of rigid bodies (see Appendix B). In this kind of turn, paths do not cross and different points have different radii of curvature. Parallel path turning does not occur in flocks, as it would require a significant increase of speed of birds on the outer side of the turn.

We note that, although the dynamical equation (8) is different from (4), the static properties of the field φ(x, t) (for example, the equal time correlations studied in [17]), are the same as those described by Hamiltonian (3). In particular, the Nambu-Goldstone mode (or zero mode) emerging from the continuous symmetry breaking of the phase φ [22, 23] is also responsible for the emergence of long-range (scale-free) velocity correlations causally connecting very distant parts of the flock. Such correlations have indeed been experimentally observed in starling flocks [24].

When formulated in terms of velocities and positions, as in equation (2), the theory is certainly not Hamiltonian: the acceleration, $\stackrel{.}{v}$, is equal to the social force, but this force is the derivative of H with respect to the velocity v, rather than with respect to the position, x. Indeed, flocks are highly dissipative and forced systems. If, however, we assume that the net effect of all these nonconservative factors (air drag, self-propulsion, etc) is to enforce a constant speed, |v_i| = v₀, we can describe the system through an effective variable that automatically satisfies this constraint. This effective variable is the phase, φ. By working with the phase, we can disregard the complications related to how the constant speed constraint is achieved and simply focus on the symmetry properties of the theory, similarly to what one would do in uniform circular motion. By reinstating the kinetic term associated to the phase one obtains a new effective Hamiltonian, where φ is the generalized coordinate and s_z is its conjugated momentum. Therefore, although the theory is non-Hamiltonian in the (x, v) variables, it becomes so in the (φ, s_z) canonical variables.

Equations (5-7) belong to the universality class of Model F in the Halperin and Hohenberg classification of dynamical critical phenomena [25, 26]. Matsubara and Matsuda showed in [27] that Model F is mathematically equivalent to a lattice-gas model for superfluid helium. In this context, the propagating fluctuations of the quantum phase φ are called second-sound, while the alignment coupling constant, J, is called stiffness [25, 26, 28]. Linear and undamped propagation (as opposed to diffusive propagation) is nestled into the identical mathematical structure of these apparently very different systems: i) existence of a continuous symmetry; ii) spontaneous symmetry breaking, due to the emergence of a nonzero order parameter; iii) coupling of the phase, φ, to the conserved generator of the symmetry, the spin s_z. Because of universality, irrespective of the physical and biological details, these three elements alone generate the dissipationless propagating mode described by (8).

The novel theory not only provides an explanation for the linear and undamped propagation of information that we observe, but it also makes a quantitative prediction that makes sense of the otherwise unexplained variability of c_s from flock to flock. In contrast with standard sound, which travels over density fluctuations and whose speed depends on density and pressure, the propagating speed of the phase fluctuations depends on the strength J of the alignment between the spins, $c_s^2=a^{2}J∕\chi$. Although we have no direct experimental access to the coupling J, we can experimentally determine the polarization, Φ(J), which is a function of the coupling. The polarization is defined as, $\Phi =\mid (1∕N){\sum }_i{\mathbf{v}}_i∕v_i\mid$, and it measures the overall degree of alignment in the flock. In the limit of small phase fluctuations (which is verified in flocks [17]), the alignment coupling constant and the polarization are connected by the equation (see Appendix D for proof),

$$\Phi (J,\beta )=1-\frac{1}{\beta J}$$ (9)

where 1/β is the temperature, i.e. the noise level in the system. This equation simply states that the polarization goes to 1 either in the zero noise limit β → ∞ (perfect alignment), or in the case of infinitely strong alignment, J → ∞. By inverting (9) we finally get an expression for the speed of information transfer in turning flocks,

$$c_s=\frac{1}{\sqrt{\beta \chi }}\frac{a}{\sqrt{1-\Phi }}$$ (10)

Equation (10) states that, at fixed noise level β, the speed of propagation of the turn across a given flock must be larger the larger the degree of alignment Φ in that flock. We report c_s/a vs. $1∕\sqrt{1-\Phi }$ for all analyzed flocks in Fig. 3. Data show a clear linear dependence, in agreement with equation (10). The square root behaviour reproduced by the data is nontrivial: the polarization is a dimensionless quantity, hence the functional dependence of c_s on Φ cannot be worked out by mere dimensional analysis.

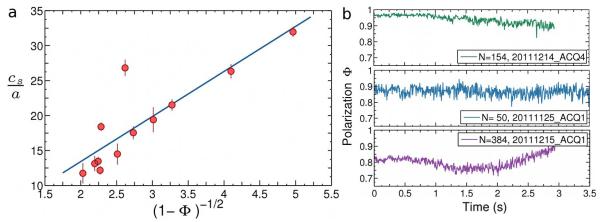
FIG. 3. Prediction of the new theory.

a, The new theory predicts that the rescaled speed of propagation of the turn, c_s = a, must be a linear function of $1∕\sqrt{1-\Phi }$, where Φ is the polarization. The prediction is verified by the empirical data (P-value: P = 3.1 × 10⁻⁴; correlation coefficient: R² = 0.74). Each point is a different turning flock. Error bars on c_s are obtained from its variability under changing the linear fitting regime of x(t). c_s/a has the dimensions of sec⁻¹. The slope of this line is equal to $1∕\sqrt{\beta \chi }$ - equation (10). b, Polarization as a function of time in three different turning flocks. The value of Φ reported in panel a corresponds to the time average over the entire duration of the turn.

Linear and undamped flow of information in collective motion, and its prediction eq.(10), have never been discovered before. Some forms of inertia have been considered in previous models [29-32], but in a very different way than the one discussed here, as inertial terms were not coupled to the conservation of spin generated by the gauge symmetry. Standard inertia, either linear (coupled to linear momentum) or rotational (coupled to orbital angular momentum), does not generate equations (8) and (10). Similarly, in a perfect fluid setup (with the velocity potential playing the role of φ), the conserved currents would be mass and momentum, which would produce standard first sound. Even in the state-of-the-art hydrodynamic theories of active matter [12, 33], conservation laws do not regard the spin current, so that in the flock’s reference frame phase fluctuations unrelated to density fluctuations display very limited propagation.

The link between speed of propagation of the information, c_s, and behavioural polarization, Φ, is not an evolutionary trait; it is simply the mathematical consequence of the gauge symmetry. However, the specific level of polarization of a flock is not fixed by math, nor by symmetry, but by adaptive factors. In many social species polarization is very large [4, 5, 17]. Global order is indeed the most conspicuous trait of collective behaviour. However, were the only concern of a bird not to bump into its neighbours, such a large polarization would be difficult to justify. Flocks are rather diluted systems, with packing fraction lower than 0.01 [21]. Yet these same flocks are very ordered: the alignment strength, J, is very large and the polarization Φ is close to 1. Why is that?

We believe equation (10) may be one of the reasons behind this phenomenon. In collective decision-making swift transfer of information is beneficial to the cohesion of the group. In the case of turns this is obvious: during the turn the wavefront divides the flock into two groups of birds with different directions of motion. Such misalignment causes a spatial spread of the flock, with loss of cohesion. The slower the speed c_s of the wavefront, the more severe this loss. It is reasonable to believe that this is a general mechanism for moving biological groups. Every collective decision drives the group through a momentary lapse of cohesion, due to the transient coexistence of different behavioural states. The link (10) between high behavioural polarization and fast propagation of the information suggests that keeping this lapse to a minimum, therefore achieving a fast and robust collective decision, may be the adaptive drive for the high degree of order observed in many living groups.

METHODS

Experiments

European starlings spend the winter in Rome, where they populate several roosting sites. Data were collected at the site of Piazza dei Cinquecento, between November 2010 and December 2012. To acquire the video sequences we use the trifocal method described in [10]. We employ three cameras IDT-M5 with monochromatic CMOS sensor with resolution 2288 × 1728 pixels, shooting at 170hz. Lenses used are Schneider Xenoplan 28mm f/2.0. Typical exposure parameters are: aperture between f/2.8 and f/8; exposure time between 700 and 3500 ms. Intrinsic camera parameters are calibrated every two weeks in the lab using a set of 50 images of a planar target. The accuracy of the 3d apparatus is regularly tested using laser-metered artificial targets. Flocks are typically at 80–130m from the cameras. The error on the relative distance between two neighbouring birds is ~ 0.1m. The recorded events have a time duration between 2 and 13 seconds. The data-set consists of 12 distinct flocking events, each one including one collective turn.

Tracking

Segmentation is performed using the method described in [10]. To assign stereoscopic links, i.e. to match birds across the three images, we use global optimization using a cost function based on the trifocal constraint [34]. To assign temporal links we first determine the optimal rotoscale-translation to predict the position of each bird in the next frame. We then link birds from one frame to the next one in a redundant way, i.e. when in doubt we use multifurcation. We percolate the full set of temporal links though the entire sequence and build the graph of all possible 2d paths in the image space of each camera. The three sets of 2d paths are then matched via a global assignment, based on a cost function proportional to the number of stereoscopic links between each triplet of 2d paths. To avoid exponential explosion of the number of paths, the temporal sequence is recursively divided into shorter time intervals over which global optimization can be handled [35]. All global optimizations are performed using linear programming [36]. Our method produces very low time fragmentation: 90% of the reconstructed trajectories last more than 90% of the duration of the event. We tested the method against synthetic data: the comparison with this ground-truth data fully confirms the reliability of the tracking algorithm. All details of the tracking can be found in [35].

Filtering

Filtering of the time-discrete trajectories is necessary for two reasons: i) to reduce experimental noise; ii) to eliminate wing-flapping, whose frequency for starlings is ω_flap = 10hz. By sampling at 170hz we are fully exposed to the trajectories zig-zag (see inset in Fig.1a), which would completely dominate acceleration. To cut this high frequency mode we a use 2nd order lowpass digital Butterworth filter on the velocities, typically with a cutoff frequency ω_flap/30. Accelerations obtained in this way (see Fig.1d) capture the low frequency corresponding to the turn. Our final results are robust against changes of the cutoff frequency.

Turning delay

We define the turning delay τ_ij of bird i with respect to bird j as the time by which we have to shift the radial acceleration a_j(t) with respect to a_i(t) to maximally overlap them. More precisely, we define the following normalized correlation (or overlap) function,

$$G_{ij}\left(\tau \right)=\frac{\langle {\mathbf{a}}_i\left(t\right)\cdot {\mathbf{a}}_j(t-\tau )\rangle -\langle {\mathbf{a}}_i\left(t\right)\rangle \cdot \langle {\mathbf{a}}_j(t-\tau )\rangle }{{\sigma }_i{\sigma }_j}$$

where 〈·〉 indicates a time average,

$$\langle {\mathbf{a}}_i\left(t\right)\cdot {\mathbf{a}}_j(t-\tau )\rangle \equiv \int dt{\mathbf{a}}_i\left(t\right)\cdot {\mathbf{a}}_j(t-\tau ),$$ (11)

and ${\sigma }_i=\sqrt{(\langle {\mathbf{a}}_i{\left(t\right)}^2\rangle -{\langle {\mathbf{a}}_i\left(t\right)\rangle }^2)}$, is the fluctuation of a_i(t) during the turn. Given this definition, the time shift τ_ij corresponds to the value of τ where G_ij(τ) reaches its maximum (examples of the function G_ij are reported in SI-Fig. S1). τ_ij > 0 means that j turns before i, and vice versa. In absence of noise time ordering requires that τ_ij = τ_ik + τ_kj, for each triplet i, j, k. We check robustness of this relation with respect to noise in all our flocks and find a relatively small spread of the data along the identity line (SI-Fig. S2). The quality of our consistency test can be fully appreciated when we compare turning with non-turning flocks. If there is no turn, τ_ij is just a random number, so temporal consistency is strongly violated and the test gives quite a different result (SI-Fig. S2, lowest-right panel).

Ranking

Noise introduces some violations of the time ordering; hence, we are in a similar case as sport ranking, where player i may win over k, k may win over j, but i may lose to j, introducing some frustration. For every bird i, we say that i ‘wins’ over j if τ_ij < 0, in which case we set w_ij = 1; conversely, i ‘loses’ to j if τ_ij > 0, in which case we set w_ij = −1. We then define the total score of i as, ${\varphi }_i={\sum }_{j\ne i}{w}_{ij}$. Given that we are in a round-robin tournament, it is convenient to rank the birds according to the scores ϕ_i [37]. Thanks to the low violation of the time ordering, this score ranking gives very small frustration (defined as the number of cases in which i ranks higher than j, but i has lost to j). More refined rankings can be obtained by using probabilistic methods [37]. In our case, these methods decrease only marginally the frustration.

Absolute turning time

The absolute turning time t_i for each bird i is the delay with respect to the top bird in the ranking, i.e. the first to turn (t_top = 0, r_top = 1). To reduce the statistical error on t_i, introduced by time ordering violations, we define t_i using the mutual delay τ_ij with respect to all birds j higher ranked than i,

$$t_i=\frac{1}{r_i-1}\sum _{r_j<r_i}(t_j+{\tau }_{ij}),r_i>1$$ (12)

If there were no time ordering violations, we would simply have t_i = τ_i,top. In the presence of noise, though, definition (12) is a more robust estimate of t_i. By plotting r_i vs. t_i for all birds in the flock, we obtain the ranking curve, r(t), which is reported for several of our flocks in SI-Fig. S3 together with the propagation curve, x(t) = [r(t)/ρ]^1/3.