Abstract
Objective
To identify local meteorological drivers of dengue fever in French Guiana, we applied an original data mining method to the available epidemiological and climatic data. Through this work, we also assessed the contribution of the data mining method to the understanding of factors associated with the dissemination of infectious diseases and their spatiotemporal spread.
Methods
We applied contextual sequential pattern extraction techniques to epidemiological and meteorological data to identify the most significant climatic factors for dengue fever, and we investigated the relevance of the extracted patterns for the early warning of dengue outbreaks in French Guiana.
Results
The maximum temperature, minimum relative humidity, global brilliance, and cumulative rainfall were identified as determinants of dengue outbreaks, and the precise intervals of their values and variations were quantified according to the epidemiologic context. The strongest significant correlations were observed between dengue incidence and meteorological drivers after a 4–6-week lag.
Discussion
We demonstrated the use of contextual sequential patterns to better understand the determinants of the spatiotemporal spread of dengue fever in French Guiana. Future work should integrate additional variables and explore the notion of neighborhood for extracting sequential patterns.
Conclusions
Dengue fever remains a major public health issue in French Guiana. The development of new methods to identify such specific characteristics becomes crucial in order to better understand and control spatiotemporal transmission.
Keywords: Dengue fever, Data Mining, Meteorological factors, Infectious diseases, Epidemiologic surveillance, French Guiana
Introduction
Dengue virus, which is most commonly acquired through the bite of an Aedes aegypti mosquito, is the most important arthropod-borne viral disease affecting humans.1 The increasing number of cases is associated with the expanding geographic range and the increasing intensity of transmission in affected areas.2 3 Recent estimates indicate 390 million infections per year worldwide, of which 96 million dengue infections per year are manifested.4 This virus has four serotypes—DENV-1, DENV-2, DENV-3, and DENV-4—although the existence of a fifth serotype has been discussed.5 The clinical forms of each serotype include asymptomatic infection, influenza-like illness, and severe forms— for example, fatal dengue hemorrhagic fever (DHF), dengue shock syndrome, encephalitis, and hepatitis. Even though several dengue vaccines are being developed,6 no vaccine or curative treatment is currently available. Prevention strategies are limited to vector control, and treatment strategies are limited to supportive care to avoid shock syndrome.7
In Latin American and Caribbean countries, the reintroduction and dissemination of A aegypti were observed in the 1970s after a reduction in vector control interventions that had been initiated in the 1960s. Since then, regular outbreaks have occurred on a 3–5-year cycle, and there has been an increase in severe forms of dengue, particularly DHF.8 In French Guiana, France's overseas territory in South America with 230 000 inhabitants, the epidemiology of dengue evolved from an endemo-epidemic to a hyper-endemic state.9 Five major epidemics linked to the circulation of one or two predominant serotypes have occurred over the last 10 years. These outbreaks usually last for 6–12 months and may affect nearly 10% of the population.
With the increasing frequency of epidemics and the resulting health, social, and economic impacts of dengue,10 the surveillance, control, and prevention of dengue have become social, political, and public health challenges that require specific preparedness activities.11 One key element of an effective preparedness plan is the capacity to understand and predict the occurrence of dengue epidemics.
Epidemic dynamics are driven by complex interactions between intrinsic factors associated with human host demographics, vectors, and viruses, which drive multiannual dynamics, as well as extrinsic drivers, such as climate patterns, that potentially drive annual seasonality.
Previous investigators have created descriptive and predictive dengue models using various input variables,12–14 including climate data,15 16 vector characteristics,17 18 circulating viral serotypes, the immune status of the host population,15 or demographic data.19 20 Even if the different studies in various affected areas do not always yield the same results, climatic variability is postulated to be one of the most important determinants of dengue epidemics; therefore, many studies have highlighted the influence of meteorological conditions on dengue incidence.21 The increase in temperature has been associated with dengue in Thailand,22 Indonesia,23 24 Singapore,25 Mexico,26 Puerto Rico,27 New Caledonia,28 Guadeloupe,29 and Sri Lanka.30 An increase in humidity and high mosquito density increased the transmission rate of dengue fever in southern Taiwan.31 The abundance of predominant vectors is partly regulated by rainfall, which provides breeding sites and simulates egg hatching.32–36
However, dengue patterns are dependent on the study area and are often characterized by non-linear dynamics, multi-annual oscillation, and irregular fluctuations in incidence; these factors complicate the understanding, detection, and prediction of both temporal and spatial transmission.
Data mining (ie, discovering useful, valid, unexpected, and understandable knowledge using databases) has been recognized as a promising new area for database research.37 This area can be defined as efficiently discovering interesting information in large databases using statistical methods, database management techniques, and artificial intelligence.
Among the different data mining techniques, sequential pattern extraction38 has received increased attention in recent years and has a wide range of applications in various areas, including finance, marketing, insurance, medical research, and sensor data. Traditional sequential pattern mining aims to extract sets of items that are commonly associated over time. However, this approach has rarely been applied to assess the spatiotemporal factors associated with infectious disease transmission.20
The development of infectious disease surveillance in French Guiana in combination with technological advances in information systems offers new possibilities for applying data mining methods in future analyses.
We concentrated our efforts on applying sequential pattern mining to an epidemiological and meteorological dataset to identify potential drivers of dengue fever outbreaks. We used contextual sequential patterns, which extend the concept of traditional sequential patterns and were recently introduced by Rabatel et al39 to identify relationships. By considering the fact that a pattern is associated with one specific epidemiological or spatial context, the experts can then adapt their strategy depending on specific situations.
In this paper, we focus on the descriptive component, using different ‘epidemiological contexts’ to consider the impact of the interrelationships between dengue fever and climatic factors on specific epidemiologic figures. Our contribution is described in terms of methodology, epidemiological findings, and surveillance implications.
Material and methods
Settings
French Guiana is located in South America between the Tropic of Cancer and the equator (4°00 north latitude and 53°00 west longitude); it is found between Brazil and Surinam. Its climate is typically tropical: hot and humid, with little variation in seasonal temperatures, heavy rainfall in the wet season from January to June, and low rainfall in the dry season from July to December. The relative humidity is high and varies between 80% and 90% according to the season. Primary health delivery differs according to location: in the coastal area, primary healthcare is delivered by 85 general practitioners (GPs), whereas further inland, care is provided by 17 public healthcare centers.40
Epidemiological dataset
Epidemiologic data on dengue fever were obtained for the period from 2006 to 2011 from the multi-source surveillance system of the Regional Epidemiology Unit of the Institut de Veille Sanitaire (InVS).40
Weekly numbers of biologically confirmed cases (BCCs), stratified according to the municipality of residence, were obtained from the laboratory surveillance system. This surveillance system, which collects individual information (including the patient's sex and age, area of residence, date of onset, date of blood sample, and results) from the seven laboratories located in the coastal area, was authorized by the French Data Protection Agency (CNIL, N°1213498). In accordance with the CNIL, all of the data used in this study were aggregated so that they could not be associated with any specific individual.
The following criteria were used to define BCCs: virus isolation, viral RNA detection by reverse transcription-PCR (RT-PCR), detection of secreted NS1 protein, or a serological test based on an immunoglobulin M (IgM)-capture ELISA (MAC-ELISA).41 The dengue serotype data were identified for some of the BCCs (approximately 30% of the cases) by the National Reference Center (NRC) based at the Institut Pasteur in French Guiana (IPG).
Clinical case (CC) surveillance was set up from a sentinel network composed of 30 voluntary GPs located in the municipalities of the coastal area (representing approximately 35% of the GPs’ total activity) and health centers located inland.40 A CC was defined as a fever (≥38°C) with no evidence of other etiology and associated with one or more non-specific symptoms, including headache, myalgia, arthralgia, and/or retro-orbital aches. The weekly number of CCs from 2006 to 2011 was included in the dataset.
For an outbreak in a given territory, we calculated the cumulative number of incident BCCs of dengue (BCCi) and the clinical dengue incidence (CCi) per week per 1000 residents. In the calculations, we assumed that the population of a territory was constant throughout a given year.
Weekly variation rates were calculated from the average of the four previous weeks for biological cases and CCs; 10th and 20th percentiles were used to classify the number of cases and the rates in 5 or 10 groups of similar size.
Meteorological dataset
Climatic records were obtained from Meteo France. Daily climate data, including cumulative rainfall (RR in mm), minimum and maximum temperatures (TN and TX in °C), sunstroke averages (INST in hours), wind strength at 10 meters (FXI in km/h), minimum and maximum relative humidity (UN and UX in %), and global brilliance (GLOT in KWh/m2/day), were collected from six meteorological stations (Cayenne, Kourou, Maripasoula, Matoury, Saint-Laurent, and Saint-Georges). From these daily data, weekly means were calculated throughout the study period. There were no missing values during this time period.
Weekly variation rates were calculated from the average of the four previous weeks for all of the meteorological indicators; 10th and 20th percentiles were used to classify the indicators and the rates in 5 or 10 groups of similar size.
Statistical analysis
The bivariate analyses were conducted using Stata V.12.42 The relationships between the epidemiological and meteorological data from 2006 to 2011 were studied at the national level of French Guiana and at different time scales using a Spearman rank correlation method. A p value <0.05 indicated statistical significance. On a weekly level, time-lagged correlation analyses (with a lag of 1–12 weeks) were performed on the time series of the weekly means of the meteorological variables and dengue incidence rates. Epidemic and non-epidemic years were compared to identify suitable meteorological patterns for dengue epidemics.
Contextual sequential pattern mining
The methodology involved three steps:
Step 1: The spatiotemporal resolution and the epidemiological contexts were defined.
Step 2: The sequence preprocessing module transformed the raw data into sequences of events.
Step 3: The sequential patterns extraction module extracted frequent sequences of events for each context.
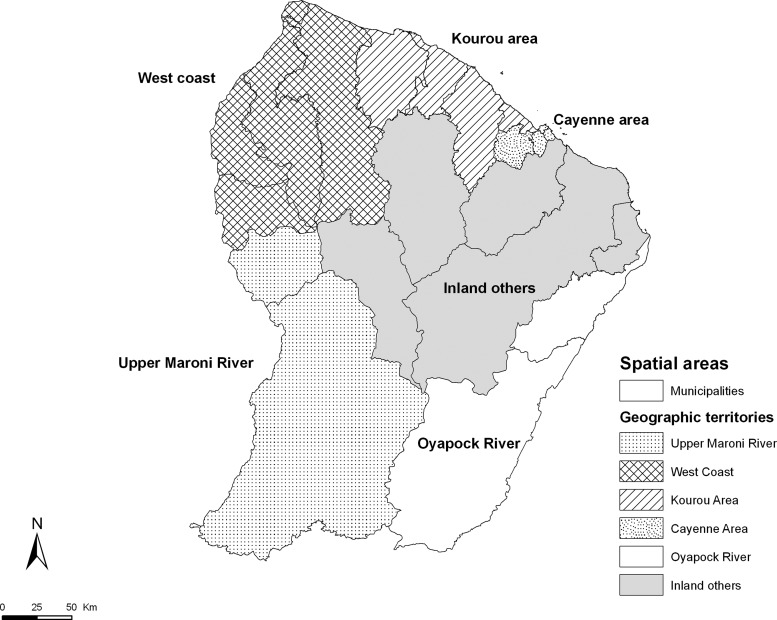
For the analyses performed after step 1, all the variables needed to fit the same spatiotemporal scale. A weekly temporal scale was used because weekly dengue surveillance data were available. The spatial distribution was based on homogeneous territories in terms of geographic distance and the movements of the population. Territories that consisted of several neighboring municipalities (figure 1) were established in collaboration with a local expert committee composed of epidemiologists, biologists, clinicians, entomologists, and specialists involved in the control and prevention of vector-borne diseases.40
Figure 1.
Spatial distribution of geographic territories for the dengue fever analysis, French Guiana, 2006–2011.
Five distinct epidemiological stages were defined by the expert committee40:
Stage 1: Sporadic transmission.
Stage 2: Presence of dengue fever clusters in some areas.
Stage 3: Pre-alert epidemic (when alert thresholds for CCs and BCCs are exceeded in the two following weeks).
Stage 4: Confirmation of the epidemic (when thresholds are exceeded in the 2 weeks following the pre-alert epidemic).
Stage 5: End of the epidemic.
For the subsequent analyses, five epidemiological phases were defined according to the different stages:
Pre-epidemic (4 weeks preceding stage 3).
Beginning of the epidemic (the first 4 weeks of stage 3).
Ascending phase (from the 5th week following stage 3 to 4 weeks preceding the epidemic peak).
Epidemic peak (from 3 weeks before to 3 weeks after the peak).
Descending phase (the end of the epidemic).
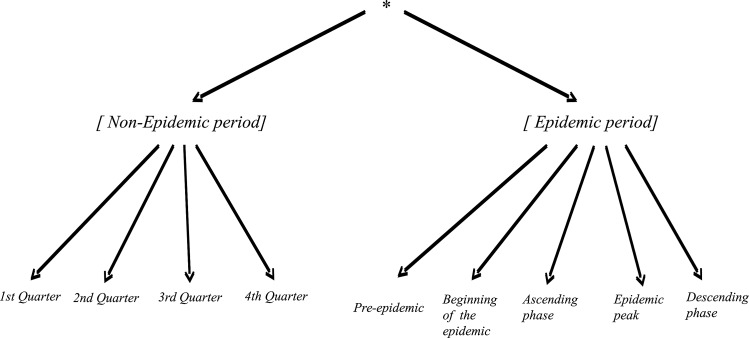
For each territory, the raw data included weekly epidemiological and meteorological data (table 1). For each week, the number of CCs and BCCs were known as well as the positivity rates of the blood samples, the values of local meteorological indicators, and the variation in the epidemiological and meteorological indicators. We defined contextual dimensions using either the epidemic or non-epidemic periods. We used 3-month periods (ie, quarter years) for the non-epidemic periods, and we used the epidemiological phases for the epidemic periods. We defined ‘epidemic’ or ‘non-epidemic’ weeks as general contexts, and the ‘pre-epidemic’ or ‘1st quarter of the year’ periods were denoted as minimal contexts in alignment with the hierarchies depicted in figure 2.
Table 1.
Example of raw data, dengue fever, French Guiana, 2006–2011
| Territory | Week | General context | Minimal context | BCC variation (%) | TX (°C) | TX. variation (%) | RR (mm) |
|---|---|---|---|---|---|---|---|
| T1 | W2009/i−4 | Non-epidemic | 2nd quarter | (−17; 0) | (32.0–33.1) | (−2; 0) | (85–158) |
| W2009/i−3 | Non-epidemic | 2nd quarter | (−17; 0) | (30.3–31.2) | <−3 | (32–85) | |
| – | – | – | – | – | – | – | |
| W2009/i−1 | Non-epidemic | Pre-epidemic | (33; 80) | (30.3–31.2) | (−2; 0) | (158–327) | |
| W2009/i | Epidemic | Beginning | >80 | <30.3 | (−2; −10) | (158–327) | |
| W2009/i + 1 | Epidemic | Epidemic | >80 | (30.3–31.2) | (−2; 0) | (85–158) | |
| – | – | Beginning | – | – | – | – | |
| W2009/i + 4 | Epidemic | Epidemic | (0; 33) | (31.2–32.0) | (0; 2) | (32–85) | |
| – | |||||||
| Epidemic peak | |||||||
| T2 | W2010/i−4 | Non-epidemic | 2nd quarter | (−17; 0) | >33.1 | (−2; 0) | (32–85) |
| W2010/i−3 | Non-epidemic | 2nd quarter | (−17; 0) | (30.3–31.2) | <−3 | (32–85) | |
| – | – | – | – | – | – | – | |
| W2010/i−1 | Non-epidemic | Pre-epidemic | (33; 80) | (31.2–32.0) | (−2; −10) | (158–327) | |
| W2010/i | Epidemic | Beginning | >80 | <30.3 | (−2; −10 | (85–158) | |
| W2010/i + 1 | Epidemic | Epidemic | (33; 80) | (30.3–31.2) | (−2; 0) | (85–158) | |
| – | – | Begin epidemic | – | – | – | – | |
| W2010/i + 4 | Epidemic | – | (−17; 0) | (30.3–31.2) | (0; 2) | <32 | |
| Descending phase |
BCC, biologically confirmed case; RR, cumulative rainfall; TX, maximum temperature.
Figure 2.
Hierarchies of the epidemic and non-epidemic periods of dengue fever, French Guiana, 2006–2011.
Each weekly value associated with a territory was called an item (eg, a maximum temperature variation of <−3% meant that the temperature decreased more than 3% compared to the previous 4 weeks). An itemset it1 = (i1…in) is a non-ordered set of items (eg, events that occurred during the same week). For example, a maximum temperature of 32.0–33.1°C, a maximum temperature variation of <−3%, and a cumulative rainfall of 85–158 mm is an itemset that indicates that for the designated week, the maximum temperature was between 32°C and 33.1°C, the maximum temperature decreased more than 3%, and the rainfall was between 85 and 158 mm.
The second step consisted of transforming the raw data into sequences of events. The aim of this step was to build sequences by ordering the itemsets according to the week of their appearance during the periods of interest for the epidemiology of dengue.
The sequence St1=‘(maximum temperature variation (<−3%), rainfall variation (>157%)) (number of clinical dengue cases variation >33%)’ means that in territory T1, an increase in dengue cases >33% was preceded by maximum temperature decreases greater than 3% and associated with an increase in rainfall >157%. In step 2, we generated a sequence of events for territory 1 (see table 2).
Table 2.
Sequence of events for territory 1 for dengue fever, French Guiana, 2006–2011
| Territory | Context | Associated event sequences |
|---|---|---|
| T1 | Inter-epidemic | (e2 e3 e5)(e1)(e4) |
| Inter-epidemic | (e5)(e2)(e4) | |
| Pre-epidemic | (e2 e5)(e1 e2)(e3 e4) | |
| Epidemic | (e3 e5)(e3)(e4) |
Bold values are those selected in the extracted pattern cited in the example on the previous page.
We introduced constraints in this step to focus on more specific patterns that matched the specified domain constraints defined by the epidemiological and meteorological experts.
A constraint is a list of regular expressions, exp, separated by time intervalsj. An example of a constraint is (exp1)[time1](exp2)[time2]:::[timek-1](expk), with k as the length of the constraint. For example, let Pc be a constraint and a time unit corresponding to a week, where Pc=(UN) [1–3](CC). In other words, we extract all frequent patterns with a length of 2 (ie, the number of itemsets) where the characteristic humidity (UN) in the first itemset lasts for an interval of 1–3 weeks as well as the number of CC. Table 2 provides some valid patterns according to this constraint.
The objective of step 3 was to build sequential patterns. Support for a pattern was obtained from the data sequences defined in step 1. For example (see table 2), the pattern P ‘(e2 e5)(e1)(e4)’ was included in two data sequences for zone T1. Thus, support(P)=2/4.
To obtain the most frequent patterns, we used the PrefixSpan algorithm,43 which extracts all the frequent sequential patterns according to the constraints defined. We only select patterns of size 1–3 with temporal intervals of 1–2 weeks between two itemsets. We also focus on patterns with at least one item related to the number of dengue cases in the given time interval. Support was calculated for all the minimal contexts of all the frequent patterns extracted. We considered that a pattern must have a support greater than 0.5 to be considered as a frequent pattern in a given minimal context.
The difference between the support of the pattern obtained in a context and the second highest support obtained in other contexts was calculated to provide a ‘c-specificity’ score to quantify the extent to which the pattern was specific to that context.39 The sequential pattern extraction algorithms were applied using Weka Data Mining software.44
Results
Overall dengue incidence
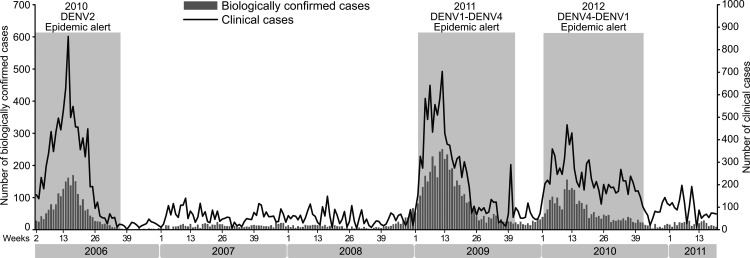
From the beginning of 2006 to April 2011, 39 587 CCs and 11 133 BCCs were recorded in French Guiana. The national activity levels were strongly influenced by outbreak periods (figure 3). As shown in figure 3, three major outbreaks occurred during the study period. The average duration of these epidemics varied from 38 to 41 weeks.
Figure 3.
Weekly number of biologically confirmed and clinical cases of dengue fever and outbreak periods, French Guiana, January 2006–April 2011.
Bivariate statistical analysis
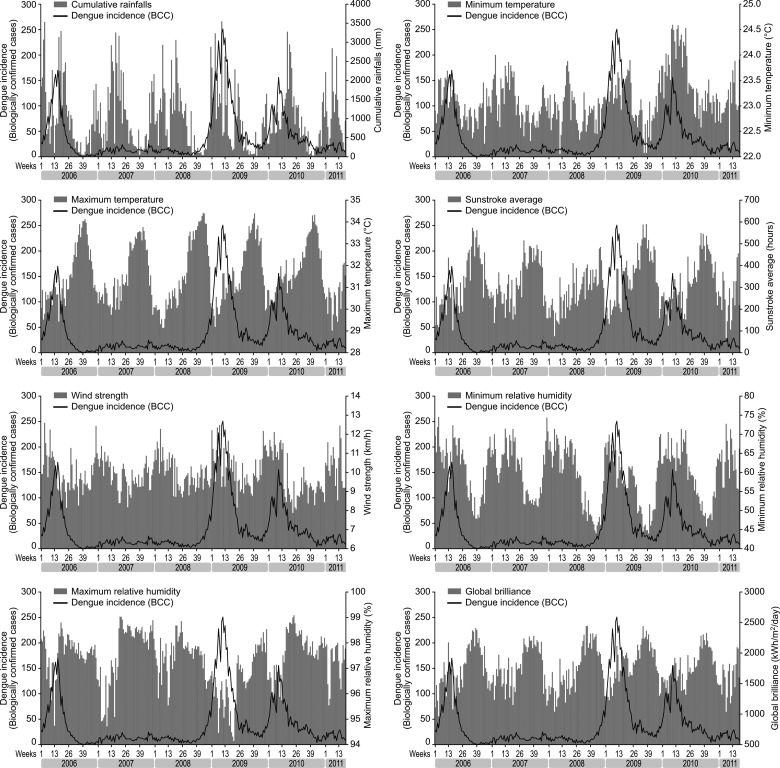
During the study period, we found statistically significant positive correlations between dengue incidence and meteorological variables during the epidemic years for each family of variables (table 3, figure 4). The maximum correlation rates were obtained after a 4–6-week lag during the epidemic years.
Table 3.
Correlations between meteorological variables and dengue incidence
| Non-epidemic years | Epidemic years | ||||||
|---|---|---|---|---|---|---|---|
| Lag2wk | Lag3wk | Lag2wk | Lag3wk | Lag4wk | Lag6wk | Lag8wk | |
| RR | 0.06 | 0.01 | 0.485*** | 0.498*** | 0.509*** | 0.498*** | 0.375*** |
| −0.214* | 0.275* | 0.456*** | 0.465*** | 0.486*** | 0.474*** | 0.384*** | |
| TN | 0.105 | 0.171 | 0.501*** | 0.515*** | 0.516*** | 0.483*** | 0.436*** |
| −0.041 | 0.04 | 0.521*** | 0.522*** | 0.528*** | 0.487*** | 0.428*** | |
| TX | −0.206* | −0.18* | −0.678*** | −0.702*** | −0.716*** | −0.646*** | −0.502*** |
| 0.144 | 0.191* | −0.693*** | −0.703*** | −0.721*** | −0.670*** | −0.549 | |
| INST | −0.167 | −0.098 | −0.591*** | −0.632*** | −0.649*** | −0.634*** | −0.538*** |
| 0.152 | 0.221* | −0.573*** | −0.598*** | −0.620*** | −0.607*** | −0.538*** | |
| FXI | 0.284** | 0.204* | 0.338*** | 0.378*** | 0.405*** | 0.435*** | 0.431*** |
| 0.025 | 0.009 | 0.397*** | 0.411*** | 0.441*** | 0.481*** | 0.475*** | |
| UN | 0.191* | 0.114 | 0.563*** | 0.584*** | 0.611*** | 0.568* | 0.454*** |
| −0.200* | −0.262* | 0.519*** | 0.535** | 0.556*** | 0.514*** | 0.405*** | |
| UX | −0.252** | −0.218* | −0.269** | −0.268** | −0.260** | −0.234** | −0.192* |
| −0.197* | −0.226** | −0.496*** | −0.490*** | −0.479*** | −0.482 | −0.457*** | |
| GLOT | −0.230*** | −0.166** | −0.527*** | −0.580*** | −0.622*** | −0.626*** | −0.562*** |
| 0.067 | 0.186* | −0.502*** | −0.540*** | −0.582*** | −0.600*** | −0.543*** | |
Spearman's rank correlation test (r, significance score of p value).
The first row represents correlation between the meteorological variable and clinical cases (CC) incidence. The second row represents correlation with biologically confirmed cases (BCC) incidence.
Significance score: *p<10−2, **p<10−3, ***p<10−4.
FXI, wind strength; GLOT, global brilliance; INST, sunstroke average; Lag2wk, lag 2 weeks; RR, cumulative rainfall; TN/TX, minimum and maximum temperature; UN/UX, minimum and maximum relative humidity.
Figure 4.
Weekly incidence of dengue fever (biologically confirmed cases, BCC) in French Guiana from April 2006 to April 2011 compared to crude meteorological variables for the same period: (A) cumulative rainfall; (B) minimum temperature; (C) maximum temperature; (D) sunstroke average; (E) wind strength; (F) minimum relative humidity; (G) maximum relative humidity; (H) global brilliance.
Contextual sequential patterns extraction
The extracted sequential patterns showed temporal associations between local weather conditions, the evolution of dengue incidence, and time periods in the various territories of French Guiana.
Regardless of their position in the extracted sequential patterns, the meteorological variables were considered to have a relevant association; for example, an item included in an extracted pattern was considered to be associated with an epidemiological context whether it was in the 1st, 2nd, or 3rd itemset.
Outside epidemic periods, the 1st quarter of each year was characterized by minimum relative humidity greater than the median class (63–68%) (table 4). Low levels of incidence were frequently observed during this quarter, which was also marked by an increase in the number of clinical and BCCs without a high c-specificity score considering the evolution of the number of cases during outbreaks. This period was also marked by an increase in rainfall that was frequently associated with the appearance of the 1st isolated clusters. The different epidemics in the study period all began during the 1st quarter of their respective years.
Table 4.
Non-epidemic contextual sequential patterns
| Minimal context | Non-epidemic associated sequential patterns | Support | C-specificity |
|---|---|---|---|
| 1st quarter (non-epidemic period) | (UN (63–68%)) (RR (85–158 mm)) | 0.72 | 0.22 |
| (UN (63–68%)) (TX<30°C) | 0.67 | 0.57 | |
| (UN (63–68%)) (UN>68%) | 0.64 | 0.17 | |
| (UN (63–68%)) (Var_CC>33%) | 0.64 | 0.14 | |
| (UN (63–68%)) (RR (158–327 mm)) | 0.57 | 0.09 | |
| (UN (63–68%)) (Var_BCC>33%) | 0.64 | 0.07 | |
| 2nd quarter (non-epidemic period) | (Var_TX>2%) (UN>68%) | 0.59 | 0.19 |
| (Var_TX>2%; Var_UN>7%) | 0.74 | 0.19 | |
| (Var_TX>2%; BCC (0;2)) | 0.74 | 0.09 | |
| (TX (30.3–31.2°C)) | 0.89 | 0.08 | |
| (Var_TX>2%) (TN (23.2–23.8°C)) | 0.63 | 0.08 | |
| (Var_TX>2%) (Var_FXI<7%) | 0.63 | 0.08 | |
| 3rd quarter (non-epidemic period) | (Var_TX>2%) (RR<32 mm) | 0.87 | 0.42 |
| (FXI<8.7 km/h) | 0.65 | 0.14 | |
| (Var_TX (0.7%; 1.9%)) | 0.94 | 0.13 | |
| (Var_UN<−6%) | 0.97 | 0.12 | |
| (CC=0) | 0.87 | 0.11 | |
| (TN (22.4–22.8°C)) | 0.74 | 0.11 | |
| 4th quarter (non-epidemic period) | (TX>33.1°C)) (Var_TX (−2–0%)) | 0.85 | 0.59 |
| (TX>33.1°C)) (TX (32.0–33.1°C)) | 0.76 | 0.56 | |
| (TX>33.1°C)) (Var_UN>7%) | 0.82 | 0.53 | |
| (TX>33.1°C)) (Var_BCC (−17–0%)) | 0.79 | 0.27 | |
| (TX>33.1°C)) | 0.94 | 0.16 | |
| (TX>33.1°C) RR<32 mm) | 0.82 | 0.11 |
BCC, biologically confirmed case; CC, clinical case; RR, cumulative rainfall; TN/TX, minimum and maximum temperature; UN/UX, minimum and maximum relative humidity.
The 2nd and 3rd quarters were frequently associated with an increase in maximum temperatures, a decrease in the minimum relative humidity, and low levels of dengue incidence. The 4th quarter was marked by high maximum temperatures and low levels of rainfall. All of these results were compatible with the occurrence of the dry season. No specific evolution of dengue incidence was observed during this period.
Considering the fact that epidemic-period contexts were defined according to the epidemiological phases, items related to dengue incidence were frequently found in the epidemiological patterns (table 5). Nevertheless, our findings related to these items were compatible with the epidemiological phases defined by the local vector-borne disease expert committee.
Table 5.
Epidemic contextual sequential patterns
| Minimal context | Epidemic associated sequential patterns | Support | C-specificity |
|---|---|---|---|
| Pre-epidemic (4-week period) | (Var_TX°(−2% to −10%), CCi<1‰, BCCi<0.3‰) (CCi<1‰, BCCi<0.3‰) | 0.57 | 0.57 |
| (Var_UN (2–7%), CCi<1‰, BCCi<0,3‰) | 0.67 | 0.52 | |
| (CCi<1‰, BCCi<0.3‰, Var_GLOT (−11% to −50%)) (CCi<1‰, BCCi<0.3‰) | 0.57 | 0.57 | |
| (Var_TX°(−2% to −10%), CCi<1‰, BCCi<0.3‰) | 0.62 | 0.48 | |
| (CCi<1‰, BCCi<0.3‰) (Var_BCC>40%, CCi<1‰, BCCi<0.3‰) | 0.57 | 0.48 | |
| (Var_UX (0.1–0.4%) CCi<1‰, BCCi<0.3‰)) | 0.57 | 0.43 | |
| (Var_UN>7%, CCi<1‰, CCi<1‰) | 0.57 | 0.38 | |
| (Var_BCC>40%, CCi<1‰, BCCi<0.3‰) (CCi<1‰, BCCi<0.3‰) | 0.57 | 0.38 | |
| Beginning of epidemic (4-week period) | (Var_BCC>40%) (BCCi (0.3–1.9‰)) | 0.76 | 0.56 |
| (BCCi (0.3–1.9‰)) (BCCi (0.3–1.9‰)) | 0.86 | 0.51 | |
| (BCCi (0.3–1.9‰)) (Var_UX (0.1%; 0.4%))> | 0.71 | 0.46 | |
| (Var_BCC>40%) (RR (158–327 mm)) | 0.67 | 0.18 | |
| (Var_BCC>40%) (Var_CC (0–33%) | 0.81 | 0.16 | |
| (Var_BCC>40%) (Var_UN (7–40%)) | 0.67 | 0.09 | |
| (Var_BCC>40%) (UN (62–67%)) | 0.57 | 0.05 | |
| (Var_GLOT>12%) | 0.62 | 0.02 | |
| (Var_BCC>40%) (Var_UX (0.1–0.4%)) | 0.62 | 0.01 | |
| (UX<96%) | 0.57 | 0.01 | |
| Epidemic peak (7-week period) | (BCC>8) (TX (30.3°; 31.2°), BCC>8) | 0.6 | 0.25 |
| (BCCi (1.8‰; 4.3‰)) (BCCi (1.8‰; 4.3‰)) | 0.6 | 0.17 | |
| (UN (62–67%)) (BCC>8) | 0.65 | 0.10 | |
| (Var_BCC (1–40%)) | 0.8 | 0.04 | |
| (Var_GLOT>(3–12%))) | 0.65 | 0.04 | |
| Descendant phase | (Var_BCC<−33%) (Var_UN (2–7%)) | 0.85 | 0.30 |
| (Var_BCC<−33%) (Var_TX (0%)) | 0.85 | 0.30 | |
| (Var_BCC<−33%) (Var_BCC<−33%) | 0.90 | 0.23 | |
| (Var_CC (−4–0%)) | 0.70 | 0.21 | |
| (Var_BCC<−33%) (Var_TX>2%)> | 0.85 | 0.20 |
BCC, biologically confirmed case; CC, clinical case; GLOT, global brilliance; RR, cumulative rainfall; TX, maximum temperature; UN/UX, minimum and maximum relative humidity.
The pre-epidemic periods were associated with a decrease in the maximum temperature (2–10% from the mean of the previous 4 weeks), a decrease in global brilliance (11–50%), and an increase in the minimum relative humidity (2–10%).
The beginning of an outbreak was frequently associated with a 4-week lag during which there was a strong increase in the minimum relative humidity (>40%), a decrease in the maximum temperature (−2 to 10%) (after a peak observed 1 or 2 months before the start of the epidemic), high levels of cumulative rainfall (158 –327 mm), and a very slight increase in the maximum relative humidity. Similar to the pre-epidemic phase, a decrease in global brilliance was associated with the beginnings of the epidemics.
Importantly, epidemiological items included in the sequential patterns of the first two epidemic-period contexts suggested a premature evolution of the BCCs compared to the increase in CCs before the ascending phase of the epidemic. Dengue incidence-related items were frequently found in the sequential patterns extracted from the epidemic period contexts.
Except for the increase in global brilliance (between 62% and 67%) at the pre-epidemic peak, the evolution of specific weather conditions was not included in the sequential patterns that were associated with the phases surrounding the epidemic peak, where a predominance of the cumulative incidence occurred.
Discussion
Sequential pattern mining is an important method that has been widely used by the data mining community in many different types of applications. In this paper, we have presented the critical steps of a data-mining project which will allow better understanding and prediction of temporal dynamics of dengue fever in French Guiana. In particular, we applied an algorithm for contextual sequential pattern extraction to identify the most important climatic factors related to dengue fever in French Guiana.
Our results suggest that the local climate has major effects on the occurrence of dengue epidemics in French Guiana and well known climatic factors were found as determinants in outbreak occurrence.
The correlation rates obtained from the clinical dengue incidence rates were compatible with the rates obtained from biologically confirmed dengue cases. The maximum correlation rates were obtained after a 4–6-week lag during the epidemic years. These findings are compatible with mosquito biology and the viral transmission cycle.
Maximum temperature, minimum relative humidity, global brilliance, and cumulative rainfall were identified as determinants of dengue epidemics, and the intervals of their values were quantified. For instance, the level of cumulative rainfall was frequently associated with the beginning of outbreaks (RR 158–327 mm), suggesting that dengue epidemics are associated with a rainfall level that was relatively high but not too extreme (which would destroy breeding sites via a ‘washing effect’).
The approach we developed helped us to explore the dataset by bringing various descriptive and analytical results together. The contextual analysis allowed us to make comparisons between temporal or spatial subgroups by identifying the most discriminating categories and anticipating possible classifications or typologies for situations. Compared with traditional models, such an approach is particularly useful for two main reasons: it can provide relevant insights that account for various temporal intervals and spatial units, and it is quite appropriate for comparing situations that can constrain analysts to multiply stratified analyses with traditional methods. The situations observed in French Guiana were particularly heterogeneous in space (ie, a small amount of the population lives in the Amazonian land area where the presence of vectors is low, and the urban coastal area is home to 90% of the population) and time (ie, different seasons); thus, they were well suited to contextual approaches.
Another advantage is that the approach allows the simultaneous analysis of associations between many outcomes and various explanatory variables. For instance, we studied the associations between meteorological variables and CCs and BCCs while also exploring reactivity and the evolution of one indicator versus the others.
However, our study has several limitations. First, well-known factors that were not included in our dataset may have contributed to the epidemic dynamics in the different territories. We did not include any direct measurements of vector behavior as input variables; for example, mosquito prevalence, vector behavior, the presence of potential or confirmed breeding sites, or the prevalence of the dengue virus in the vector. Although this information is particularly important for estimating the transmission risk of vector-borne diseases, it requires intensive financial, laboratory, and technical resources that are usually not available in routine practice in the territory and for long time periods.
Other factors that can play a key role in transmission, such as environmental characteristics, social and demographic indicators, or the immune status of host populations, could not be explored in our study because the data were unavailable or not available in a temporal and spatial format. In the absence of seroprevalence data, future studies need to consider the population age distribution and human movement patterns to approximate the role of the immune status of the population. An older and thus more immune population reduces the probability of a vector feeding on a susceptible or infectious person, both of which drive transmission.
Second, the defined contexts were based on temporal periods and did not allow for the identification of possible spatial differences between the climatic drivers of dengue in the various territories.
Future work should integrate additional variables and create new contexts. Remote sensing data are currently being collected and may provide very useful information about environmental factors, such as types of habitats and types of areas (city centers, spontaneous settlements, road borders, collective buildings, individual houses with gardens, etc). Future studies should also include geographic areas as contexts to estimate the existing differences between the various regions of French Guiana. The results will help to target the territories in which the predictive models could be implemented to anticipate the risk of transmission of dengue fever. Creating hierarchies between the various contexts will enable researchers to estimate the contributions of the spatial or temporal units and consequently differentiate the most relevant contexts for developing predictive models. Among other possible future developments, we plan to take into account the notion of neighborhood in the extraction of the sequential patterns. A new method recently described by Alatavista et al45 highlighted an extension of sequential patterns, called new spatio-sequential patterns, for analyzing the evolution of areas considering their neighboring environment. Furthermore, the extraction could be used with the aim of determining the geographic clustering in French Guiana to identify the relevant spatial units for characterizing, monitoring, and predicting the local transmission of dengue. Accurate prediction of dengue outbreaks may lead to useful public health interventions. The final aim of our research project will be the development of predictive tools that allow for spatial identification of specific high risk areas whilst taking into account the temporal dynamics of dengue transmission.
Conclusion
Dengue remains a major public health issue in French Guiana. Our findings highlight the utility of the data mining approach to analyze disease surveillance data on a temporal and a spatial scale in relation to climatic, social, and environmental variables. Despite the heightened awareness among health authorities of the importance of dengue prevention and vector control, various challenges still exist to better understand and accurately predict dengue epidemics. Better understanding of dengue epidemics is necessary for public health interventions to mitigate the effect of these outbreaks, particularly in areas where resources are limited and where the medical infrastructure may become overwhelmed by significant epidemics.
Acknowledgments
We are grateful to all of the collaborators involved in the surveillance system monitored by the Regional Epidemiology Unit. We wish to thank Dr Alain Bouix and Dr Stanley Caroll, coordinators of the GP's sentinel network; all the biological laboratories; Dr Dominique Rousset and Dr Séverine Matheus, virologists at the National Reference Center based at the Institut Pasteur in French Guiana; Dr Felix Djossou and Christelle Prince from the Infectious Tropical Disease Unit of the Hospital Center of Cayenne; and Dr Muriel Ville, who coordinates the Health Centers, for their help in the epidemiologic and virology data collection. We wish to thank Philippe Palany, Jean-Louis Maridet, and Christian Brevignon from Meteo France for their help with the meteorological data collection. We thank Laurel Zmolek-Smith from the University of Iowa for linguistic support.
Footnotes
Contributors: CF conducted the study, performed data analysis, and drafted the manuscript. MF performed data mining analysis. VA contributed to the collection, classification, and interpretation of epidemiologic data. SB and MT contributed to the conception and design of the study and helped to draft the manuscript. PQ and J-CD contributed to the epidemiologic interpretation of the results of the study and helped to draft the manuscript. All authors read and approved the final manuscript.
Competing interests: None.
Provenance and peer review: Not commissioned; externally peer reviewed.
References
- 1.Gubler DJ. The global emergency/resurgence of arboviral diseases as public health problems. Arch Med Res 2002;334:330–42 [DOI] [PubMed] [Google Scholar]
- 2.Guzman MG, Halstead SB, Artsob H, et al. Dengue: a continuing global threat. Nat Rev Microbiol 2010;8(Suppl):S7–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.WHO. Dengue and severe dengue. Fact Sheet No. 117, 2013 Geneva: World Health Organisation. http://www.who.int/mediacentre/factsheets/fs117/en/ [Google Scholar]
- 4.Bhatt S, Gething PW, Brady OJ, et al. The global distribution of dengue. Nature 2013;496:504–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Normile D. Tropical medicine. Surprising new dengue virus throws a spanner in disease control efforts. Science 2013;342:415. [DOI] [PubMed] [Google Scholar]
- 6.Guy B, Saville M, Lang J. Development of Sanofi Pasteur tetravalent dengue vaccine. Hum Vaccin 2010;6:696–705 [DOI] [PubMed] [Google Scholar]
- 7.Beatty ME, Stone A, Fitzsimons D, et al. Best practices in dengue surveillance: a report from the Asia-Pacific and Americas Dengue Prevention Boards. Plos Negl Trop Dis 2010;4:e890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Halstead SB. Dengue in the Americas and Southeast Asia: do they differ? Rev Panam Salud Publica 2006;20:407–15 [DOI] [PubMed] [Google Scholar]
- 9.Quenel P, Dussart P, Marrama L, et al. Contributions de la recherche virologique, clinique, épidémiologique, socio comportementale et en modélisation mathématique au contrôle de la dengue dans les DFA. Bulletin de Veille Sanitaire 2009;3:1–16 [Google Scholar]
- 10.Torres JR, Castro J. The health and economic impact of dengue in Latin America. Cad Saude Publica 2007;22(Suppl 1):S23–31 [DOI] [PubMed] [Google Scholar]
- 11.IMS Dengue. Cire Antilles-Guyane: integrated management strategy for dengue prevention and control in the Caribbean subregion. Bull de Veille Sanit Antilles Guyane 2009;8:2–15 http://www.invs.sante.fr/publications/bvs/antilles_guyane/2009/bvs_ag_2009_08.pdf [Google Scholar]
- 12.Focks DA, Haile DG, Daniels E, et al. Dynamic life table model for Aedes aegypti (Diptera: Culicidae): analysis of the literature and model development. J Med Entomol 1993;30:1003–17 [DOI] [PubMed] [Google Scholar]
- 13.Focks DA, Daniels E, Haile DG, et al. A simulation model of the epidemiology of urban dengue fever: literature analysis, model development, preliminary validation, and samples of simulation results. Am J Trop Med Hyg 1995;53:489–506 [DOI] [PubMed] [Google Scholar]
- 14.Racloz V, Ramsey R, Tong S, et al. Surveillance of dengue fever virus: a review of epidemiological models and early warning systems. PLoS Negl Trop Dis 2012;6:e1648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Barbazan P, Yoksan S, Gonzalez JP. Dengue hemorrhagic fever epidemiology in Thailand: description and forecasting of epidemics. Microbes Infect 2002;4:699–705 [DOI] [PubMed] [Google Scholar]
- 16.Otero M, Solari HG. Stochastic eco-epidemiological model of dengue disease transmission by Aedes aegypti mosquito. Math Biosci 2010;223:32–46 [DOI] [PubMed] [Google Scholar]
- 17.Bartley LM, Donnelly CA, Garnett GP. The seasonal pattern of dengue in endemic areas: mathematical models of mechanisms. Trans R Soc Trop Med Hyg 2002;96:387–97 [DOI] [PubMed] [Google Scholar]
- 18.Wearing HJ, Rohani P. Ecological and immunological determinants of dengue epidemics. Proc Natl Acad Sci USA 2006;103:11802–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Esteva L, Vargas C. A model for dengue disease with variable human population. J Math Biol 1999;38:220–40 [DOI] [PubMed] [Google Scholar]
- 20.Buczak AL, Koshute PT, Babin SM, et al. A data-driven epidemiological prediction method for dengue outbreaks using local and remote sensing data. BMC Med Inform Decis Mak 2012;12:124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Halstead SB. Dengue virus-mosquito interactions. Ann Rev Entomol 2008;53:273–91 [DOI] [PubMed] [Google Scholar]
- 22.Focks D, Alexander N, Villegas E. Multicountry study of Aedes aegypti pupal productivity survey methodology: findings and recommendations. Dengue Bull WHO 2007;31:192–200 [Google Scholar]
- 23.Arcari P, Tapper N, Pfueller S. Regional variability in relationships between climate and dengue/DHF in Indonesia. Singap J Trop Geogr 2007;28:251–72 [Google Scholar]
- 24.Bangs M, Larasati R, Corwin A, et al. Climatic factors associated with epidemic dengue in Palembang, Indonesia: implications of short-term meteorological events on virus transmission. Southeast Asian J Trop Med Public Health 2006;37:1103–16 [PubMed] [Google Scholar]
- 25.Burattini M, Chen M, Chow A, et al. Modelling the control strategies against dengue in Singapore. Epidemiol Infect 2007;136:309–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chowell G, Sanchez F. Climate-based descriptive models of dengue fever: the 2002 epidemic in Colima, Mexico. J Environ Health 2006;68:40–4 [PubMed] [Google Scholar]
- 27.Keating J. An investigation into the cyclical incidence of dengue fever. Soc Sci Med 2001;53:1587–97 [DOI] [PubMed] [Google Scholar]
- 28.Descloux E, Mangeas M, Menkes CE, et al. Climate-based models for understanding and forecasting dengue epidemics. PLoS Negl Trop Dis 2012;6:e1470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gharbi M, Quenel P, Gustave J, et al. Time series analysis of dengue incidence in Guadeloupe, French West Indies: forecasting models using climate variables as predictors. BMC Infect Dis 2011;11:166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Goto K, Kumarendran B, Mettananda S, et al. Analysis of effects of meteorological factors on dengue incidence in Sri Lanka using time series data. PLoS ONE 2013;8:e63717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chen SC, Liao CM, Chio CP, et al. Lagged temperature effect with mosquito transmission potential explains dengue variability in southern Taiwan: insights from a statistical analysis. Sci Total Environ 2010;408:4069–75 [DOI] [PubMed] [Google Scholar]
- 32.Corwin A, Larasati R, Bangs M, et al. Epidemic dengue transmission in southern Sumatra, Indonesia. Trans R Soc Trop Med Hyg 2001;95:257–65 [DOI] [PubMed] [Google Scholar]
- 33.Chadee D, Shivnauth B, Rawlins S, et al. Climate, mosquito indices and the epidemiology of dengue fever in Trinidad (2002–2004). Ann Trop Med Parasitol 2007;101:69–77 [DOI] [PubMed] [Google Scholar]
- 34.Barrera R, Delgado N, Jiménez M, et al. Stratification of a city with hyperendemic dengue hemorrhagic fever. Rev Panam Salud Publica 2000;8:225–33 [DOI] [PubMed] [Google Scholar]
- 35.Depradine C, Lovell E. Climatological variables and the incidence of Dengue fever in Barbados. Int J Environ Health Res 2004;14:429–41 [DOI] [PubMed] [Google Scholar]
- 36.Nakhapakorn K, Tripathi NK. An information value based analysis of physical and climatic factors affecting dengue fever and dengue haemorrhagic fever incidence. Int J Health Geogr 2005;4:13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fayyad U, Piatetsky-Shapiro G, Smyth P, Uthurusamy R, eds. Advances in knowledge discovery and data mining. AAAI/MIT Press, 1996 [Google Scholar]
- 38.Agrawal R, Srikant R. Mining sequential patterns. In: Yu PS, Chen ASP, eds. Eleventh International Conference on Data Engineering; IEEE Computer Society Press, 1995 [Google Scholar]
- 39.Rabatel J, Bringay S, Poncelet P. Contextual Sequential Pattern Mining. In: IEEE. 2010 IEEE International Conference on Data Mining Workshops 2010:981–8 [Google Scholar]
- 40.Flamand C, Quenel P, Ardillon V, et al. The epidemiologic surveillance of dengue fever in French Guiana: when achievements trigger higher goals. Stud Health Technol Inform 2011;169:629–33 [PubMed] [Google Scholar]
- 41.Dussart P, Petit L, Labeau B, et al. Evaluation of two commercial tests for the diagnosis of acute dengue virus infection using NS1 antigen detection in human serum. PLoS Negl Trop Dis 2008;2:e280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.StataCorp. Stata statistical software: release 12. College Station, TX: StataCorp LP, 2011 [Google Scholar]
- 43.Pei J, Han J, Mortazavi-Asl B, et al. Mining sequential patterns by pattern-growth: the PrefixSpan approach. IEEE Trans Knowledge Data Eng 2004; 16–11:1424–40 [Google Scholar]
- 44.Hall M, Eibe F, Holmes G, et al. The WEKA data mining software: an update. SIGKDD Explorations. 2009;11:10–18 [Google Scholar]
- 45.Salas HA, Bringay S, Flouvat F, et al. The pattern next door: Towards spatio-sequential pattern discovery. 16th PAKDD, 2012