Ancient dates or accelerated rates? Morphological clocks and the antiquity of placental mammals

Abstract

Analyses of a comprehensive morphological character matrix of mammals using ‘relaxed’ clock models (which simultaneously estimate topology, divergence dates and evolutionary rates), either alone or in combination with an 8.5 kb nuclear sequence dataset, retrieve implausibly ancient, Late Jurassic–Early Cretaceous estimates for the initial diversification of Placentalia (crown-group Eutheria). These dates are much older than all recent molecular and palaeontological estimates. They are recovered using two very different clock models, and regardless of whether the tree topology is freely estimated or constrained using scaffolds to match the current consensus placental phylogeny. This raises the possibility that divergence dates have been overestimated in previous analyses that have applied such clock models to morphological and total evidence datasets. Enforcing additional age constraints on selected internal divergences results in only a slight reduction of the age of Placentalia. Constraining Placentalia to less than 93.8 Ma, congruent with recent molecular estimates, does not require major changes in morphological or molecular evolutionary rates. Even constraining Placentalia to less than 66 Ma to match the ‘explosive’ palaeontological model results in only a 10- to 20-fold increase in maximum evolutionary rate for morphology, and fivefold for molecules. The large discrepancies between clock- and fossil-based estimates for divergence dates might therefore be attributable to relatively small changes in evolutionary rates through time, although other explanations (such as overly simplistic models of morphological evolution) need to be investigated. Conversely, dates inferred using relaxed clock models (especially with discrete morphological data and MrBayes) should be treated cautiously, as relatively minor deviations in rate patterns can generate large effects on estimated divergence dates.

1. Introduction

Approximately 94% of modern mammal species are members of the clade Placentalia (crown-group Eutheria). The timing of the origin and early diversification of placentals has been the focus of intensive research, yet remains controversial [1–5]. Palaeontological studies typically place the origin and early diversification of Placentalia at, or at most slightly before, the Cretaceous–Palaeogene (K–Pg) boundary at 66 Ma [2,6–8]. This conclusion is based on the age of oldest known definitive placentals, all of which are Palaeocene or younger [1,2,6–8]. This palaeontological evidence is the basis for the ‘explosive’ model of placental origins [9], which proposes that Placentalia diversified from a single lineage in the aftermath of the K–Pg mass extinction event [10]. Obviously, the discovery of a single unequivocal placental fossil prior to the K–Pg boundary would overturn the strict ‘explosive’ model. However, despite intensive collecting and enormous improvements in our knowledge of Mesozoic mammals in recent years [11–13], definitive pre-Palaeocene placentals have still not been identified [2,7,8,14]; a few putative Mesozoic records of placentals have been reported, but they are from the latest Cretaceous [15,16], and they remain controversial [2,16,17].

Molecular estimates of the deepest divergences within Placentalia, by contrast, are usually considerably older. The development of ‘relaxed’ clock models [18] that allow molecular evolutionary rates to vary across branches has somewhat reduced the discrepancy with the fossil record [4,5]. However, recent molecular studies typically place the origin of Placentalia in the Middle-to-Late Cretaceous and indicate that several divergences (including those between most extant orders) occurred well before the K–Pg boundary [3–5,19]. These results most closely approximate the ‘long-fuse’ model of placental origins [9]. They are consistent with the Cretaceous Terrestrial Revolution [20] playing a role in promoting the initial, interordinal diversification of placentals [3,4], with subsequent diversification within the modern orders occurring after the K–Pg extinction event [3–5,19].

Molecular estimates of divergence times must be calibrated to calculate absolute (rather than relative) dates, and these calibrations are usually based on fossil evidence. However, identifying fossils suitable for calibration purposes is often difficult, particularly as their affinities have often not been tested using quantitative phylogenetic analysis [21]. Different researchers may elect to use different calibrations, and each calibration can be modelled in various ways (e.g. as a point estimate or as a range with hard or soft bounds); both choices can result in very different estimates of divergence dates [19,22,23]. There is also increasing evidence that molecular rates of evolution within mammals may exhibit extreme patterns of rate heterogeneity that cannot be fully accommodated by current relaxed clock models [24–26].

The recent generalization of relaxed clock models to encompass discrete morphological character data and tip calibrations [27,28] provides an alternative avenue for inferring divergence times. These methods simultaneously consider both character and temporal information in terminal taxa to co-estimate phylogeny, divergence dates and evolutionary rates. To date, such ‘morphological clock’ models have been used mainly in the context of total evidence (TE) analyses that combine morphological and molecular data [27–31]. However, they can also be applied to purely morphological datasets [32,33]. Morphological clock analyses have a number of potentially appealing features. First, they do not assume that the actual age of a clade is necessarily close to the age of its oldest member: the age of a clade could be estimated to substantially pre-date its oldest member if that taxon is highly apomorphic relative to the inferred most recent common ancestor of the clade. Second, because phylogeny and divergence times are calculated simultaneously, fossil taxa do not need to be assigned a priori to particular nodes as they are in typical molecular clock analyses; instead, their phylogenetic relationships are estimated directly during the analysis. Finally, morphological clock analyses simultaneously calculate the amount of evolutionary change and divergence times, and therefore automatically calculate rates of morphological evolution. Rates of discrete morphological character evolution are increasingly being used in macroevolutionary studies [34–36]. However, these studies have instead typically inferred divergence dates by first constructing undated parsimony-based trees and then minimizing ghost lineages, which may result in very short branches and therefore very high estimated rates [36].

Despite these attributes, the use of morphological clock models is still in its infancy, and their performance relative to other methods for inferring divergence times is only beginning to be tested (but see [32,33]). A critical assessment of their performance is therefore warranted. The timing of the origin and early diversification of Placentalia is well studied yet remains controversial, and so represents an excellent case study for such an assessment.

Here, we apply two very different relaxed clock models—the independent gamma rates (IGR) model [28,37] and the Thorne–Kishino (TK) model [38]—to a large morphological character matrix (102 taxa, 421 discrete characters) that includes at least one representative of every extant placental order plus a diverse range of other Mesozoic and Coenozoic eutherians. All analyses used MrBayes v. 3.2 [39]. We also carry out TE analyses by combining the morphological data with 8.5 kb of nuclear sequence data for the 14 extant placentals present in our morphological matrix. As all of these morphological and TE analyses infer divergence dates deep in the Mesozoic, we then constrain the origin of Placentalia to post-date the K–Pg boundary (66 Ma), and thus generate quantitative estimates for rates of evolution required to accommodate the ‘explosive’ model of placental origins. We also investigate the effect of constraining the origin of Placentalia to be no older than 93.8 Ma, to match the estimated 95% maximum upper bound for this node from a recent molecular dating study [5].

2. Material and methods

(a). Phylogenetic definitions and assumptions

We follow a crown-clade definition for Placentalia, with Eutheria referring to the total clade of Placentalia [2]. In the context of our analyses, Placentalia is the least inclusive clade that includes all extant placentals present in our morphological character matrix, whereas Eutheria is the most inclusive clade that excludes our outgroup taxa, namely the metatherians (Deltatheridium, Mayulestes and Pucadelphys) and the non-therian cladotherians (Nanolestes, Peramus and Vincelestes).

(b). Morphological character matrix

We created the most taxon-rich morphological character matrix of Eutheria (plus six outgroup taxa; see above) currently available by combining matrices from five existing studies [8,11,40–42], which represent differently modified versions of a previously published matrix focused on eutherian relationships [7] (see the electronic supplementary material, §1, for details). The final matrix comprises 102 taxa and 421 characters.

(c). Molecular sequence data

We combined sequence data from six nuclear protein-coding genes for the 14 extant placentals present in our morphological matrix (see the electronic supplementary material, §1, for details). The final alignment was 8.5 kb.

(d). Topological constraints

One set of analyses of the matrix was performed without any topological constraints. However, these resulted in topologies with a number of conflicts with the current consensus view of placental phylogeny. We therefore ran additional analyses which enforced nine a priori topological constraints within Placentalia (see the electronic supplementary material, §3), resulting in topologies that are more consistent with the current phylogenetic consensus [43]. We focus on analyses with these topological constraints, with and without various age constraints; however, the topologically unconstrained analyses gave similar divergence times and evolutionary rates (see the electronic supplementary material, §7).

(e). Taxon ages

Our clock analyses required that each terminal taxon was assigned an age. A full justification for the age of each taxon is given in the electronic supplementary material, §2.

(f). Node age constraints

We investigated the effect of three different node age constraint schemes (see the electronic supplementary material, §4). All node age constraints were specified as hard uniform priors, and so simply provided maximum and minimum bounds. (1) In the first, only the age of the root node was constrained, to between 161.001 and 199.6 Ma. The minimum bound is marginally older than the maximum age (161 Ma) of the oldest fossil taxon in our matrix, Juramaia, whereas the maximum bound is based on the maximum probable age of the well-preserved ?Sinemurian mammaliforms Hadrocodium, Sinoconodon and Morganucodon, all of which fall well outside Cladotheria in published phylogenetic analyses [11–13]. (2) In the second, we added 16 plausible but conservative age constraints on internal nodes, based on the fossil record; of these, 14 are within Placentalia. (3) In the third, we constrained the age of Placentalia to be less than 93.8 Ma; this represents the older limit (95% confidence interval) of the age of Placentalia based on extensive DNA data [5], and so investigates the impact of enforcing a younger, molecular-based estimate for the age of the crown radiation of eutherians. (4) The fourth was similar to (3), except that we constrained the age of Placentalia even further to be less than 66 Ma, ensuring the crown radiation of eutherians post-dates the K–Pg boundary, and thus enforcing the ‘explosive’ model.

(g). Models and phylogenetic analyses

For the morphological characters, the Mk model [44] was employed; this simple stochastic model is the most commonly used model for analysing discrete morphological data. Bayes factors favoured use of the gamma parameter for accommodating rate variation across characters (BF = 539.9). The ‘coding = inf’ command was used to correct for undersampling of invariant and autapomorphic characters (see the electronic supplementary material, §5). We investigated two different relaxed clock models: the IGR model (which assumes no phylogenetic autocorrelation of rates) and the TK model (which assumes autocorrelation). Bayes factors (see the electronic supplementary material, §5) strongly favoured the IGR model over both the TK model (BF = 616.8) and the strict clock model (BF = 354.9), but we investigated both relaxed clock models. For our analyses of the TE dataset, the above Mk model was implemented for the morphological partition, while for the sequence partition, an appropriate partitioning scheme and associated models for the sequence data were determined using PartitionFinder [45]. Analyses were run using MrBayes v. 3.2 [40]; all MCMC run settings and tests for stationarity are discussed in the electronic supplementary material, §5, and included in the MrBayes data files.

(h). Rates of evolution

The majority rule consensus tree produced by MrBayes v. 3.2 for each analysis includes estimates of the (relative) evolutionary rate for each branch: mean, median and 95% highest posterior density (HPD) interval. Rate estimates exhibited strongly positively skewed distributions, and so the median rather than mean evolutionary rate was used for subsequent analyses and discussion. These relative rates were converted into absolute rates in changes/site/Ma by multiplying by the median overall clock rate (given in the .pstat file output by MrBayes) for each analysis, and then into median absolute rates in percentage change/Ma by multiplying by 100. For the morphological rates, we only examined internal branches within the ingroup (i.e. Eutheria). Terminal branches were excluded, because the paucity of autapomorphies in the matrix means that rates along these branches might be underestimated (even with the above correction implemented in MrBayes). When looking at rates of molecular evolution from the TE analyses, we only examined branches that were within Placentalia and that included at least one extant descendant represented by sequence data, because molecular rates along entirely extinct branches cannot be robustly estimated. However, because autapomorphies are properly sampled with molecular sequence data, we included rates on terminal branches leading to extant taxa.

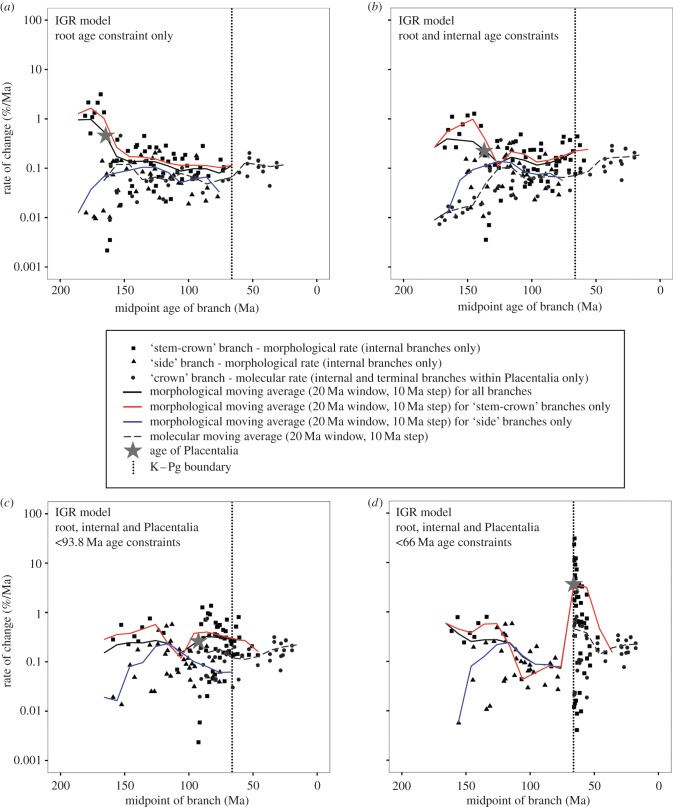
To visualize variation in the rate of evolution through time, plots of median rate (%/Ma) against age of branch (Ma) were created, using the midpoint age of each branch. For both morphological and molecular rates, a moving average (the mean of all the median branch rates) with a 20 Ma wide sliding window and 10 Ma step was calculated for all branches. For the morphological rates, moving averages using the same sliding window and step size were also calculated for ‘stem-crown’ and ‘side’ branches separately. In each case, the moving average was started at 206 Ma, so that one window (76–56 Ma) was centred at the K–Pg boundary (66 Ma).

3. Results

When only the age of the root mode was constrained, point estimates for the age of Placentalia were 136.2 Ma with the TK model (95% HPD interval: 118.6–151.2 Ma) and 163.7 Ma with the IGR model (95% HPD interval: 146.9–181.3 Ma) for the morphology-only analyses (table 1). For the TE analyses, use of the IGR model with topological constraints resulted in an estimate of 164.5 Ma (95% HPD interval: 150.1–180.1) for the age of Placentalia (figure 1a and table 1), almost identical to the equivalent morphology-only analysis (analyses of the TE matrix with the TK model failed to converge despite multiple different attempts). The retrieved dates suggest that 45–53 placental lineages (composite 95% HPD interval: 31–56) cross the K–Pg boundary (figure 1a and table 1).

Table 1.

Summary of estimates for the age of Placentalia and the number of placental lineages crossing the K–Pg boundary with different datasets, clock models and assumptions. Values in italic represent point estimates, while values in brackets represent 95% HPD intervals. All analyses enforced nine topological constraints within Placentalia to match the current consensus phylogeny.

dataset	morph	morph	TEa	morph	morph	TE	morph	morph	TE	morph	morph	TEb
clock model	TK	IGR	IGR	TK	IGR	IGR	TK	IGR	IGR	TK	IGR	IGR
node age constraints	root only	root only	root only	root and internal	root and internal	root and internal	root, internal and Placentalia <93.8 Ma	root, internal and Placentalia <93.8 Ma	root, internal and Placentalia <93.8 Ma	root, internal and Placentalia <66 Ma	root, internal and Placentalia <66 Ma	root, internal and Placentalia <66.0 Ma
age of Placentalia (Ma)	136.2 (118.6–151.2)	163.7 (146.9–181.3)	164.5 (150.1–180.1)	121.7 (108.6–134.5)	141.5 (127.6–158.1)	137.0 (124.0–151.7)	92.9 (90.5–93.8)	93.0 (90.6–93.8)	92.2 (90.2–93.8)	66.0 (65.9–66.0)	65.9 (65.5–66.0)	65.9 (65.6–66.0)
number of placental lineages crossing KPg boundary	45 (31–50)	53 (36–56)	49 (35–52)	37 (27–46)	40 (28–46)	40 (28–46)	30 (23–37)	35 (24–46)	34 (22–46)	1	1	1

^aShown in figure 1a.

^bShown in figure 1b.

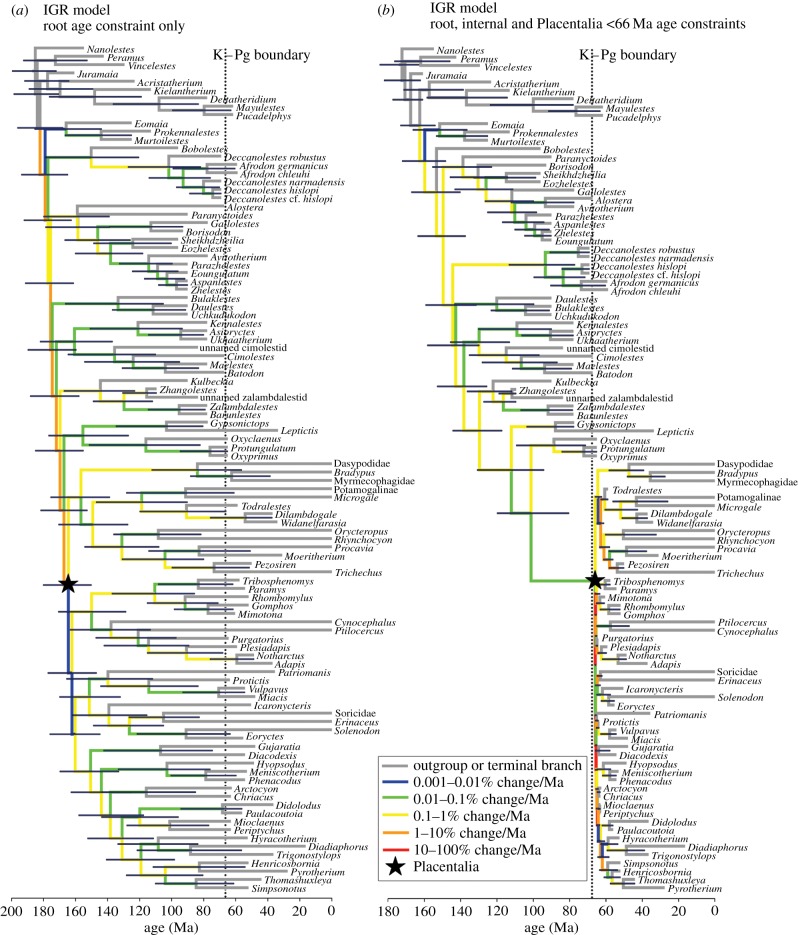
Figure 1.

‘TE clock’ phylogenies of eutherian mammals using the IGR relaxed clock model and with the age of Placentalia (crown-group Eutheria) either unconstrained or constrained to less than 66 Ma. Both phylogenies are majority rule consensuses with all compatible partitions of post-burnin trees from Bayesian analysis (using MrBayes v. 3.2) of a 102 taxon TE matrix comprising 421 morphological characters and 8.5 kb of sequence data from six nuclear genes (ADRA2B, BRCA1, GHR, IRBP, RAG1 and VWF). The analyses assumed IGR relaxed clock model (with separate clocks fitted to the morphological and molecular partitions), and enforced nine topological constraints based on the current consensus of placental phylogeny. Branches are coloured according to their estimated median rate of morphological evolution. Blue bars at nodes represent 95% HPD intervals. The vertical dotted line marks the K–Pg boundary (66 Ma), and the black star marks the point estimate for the origin of Placentalia (see table 1). (a) Only the age of the root node was constrained (to between 160.75 and 199.6 Ma; see main text). (b) The ages of the root node and selected internal divergences were constrained, and the age of Placentalia (crown-group Eutheria) was constrained to less than 66 Ma (see main text and the electronic supplementary material).

Both clock models give very ancient (Late Jurassic or Early Cretaceous) divergence dates for Placentalia and its major subclades. Perhaps most surprisingly, the 95% HPD intervals of these analyses are considerably older than most molecular estimates, failing to overlap the confidence intervals of recent studies [3–5] (see the electronic supplementary material, §7). These analyses also retrieve ages of numerous subclades within Placentalia that significantly pre-date all recent molecular and palaeontological estimates (see the electronic supplementary material, §7). Age estimates for the morphological matrix under the IGR and TK models were very strongly correlated (R² > 0.8; 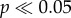), with the IGR model giving slightly older estimates for most nodes (see the electronic supplementary material, §7). Interestingly, the morphological and TE dates are also significantly correlated with the molecular dates of dos Reis et al. [5] (R² = 0.37–0.45; p = 0.01–0.02), even though the latter are much younger.

Enforcing age constraints for selected nodes within Placentalia, but leaving the latter unconstrained, slightly reduced the age estimates for Placentalia (table 1): for the morphological matrix, from 136.2 to 121.7 Ma (95% HPD interval: 108.6–134.5 Ma) with the TK model, and from 163.7 to 141.5 Ma (95% HPD interval: 127.6–158.1 Ma) with the IGR model; for the TE matrix, from 164.5 to 137.0 Ma (95% HPD interval: 124.0–151.7 Ma) with the IGR model. However, these remain older than recent molecular and (especially) palaeontological estimates for the age of Placentalia (see the electronic supplementary material, §7). As a result, even with internal constraints enforced, 37 (95% HPD interval = 27–46) placental lineages are estimated to have crossed the K–Pg boundary under the TK model with the morphological matrix, and 40 (95% HPD interval = 28–46) under the IGR model with the morphological and TE matrices (table 1). These dates are also significantly correlated (R² = 0.42–0.45; p = 0.009–0.02) with molecular dates [5].

Enforcing Placentalia to be less than 93.8 Ma, broadly congruent with recent molecular divergence estimates [5], resulted in the estimated age abutting relatively tightly against this constraint: for the morphological matrix, 92.9 Ma (95% HPD interval: 90.5–93.8 Ma) under the TK model and 93.0 Ma (95% HPD interval: 90.6–93.8 Ma) under the IGR model (table 1); for the TE matrix, 92.2 Ma (95% HPD interval: 90.2–93.8 Ma) under the IGR model. In these analyses, 30–35 (95% HPD: 22–46) placental lineages are inferred to cross the K–Pg boundary. These dates are significantly correlated (R² = 0.37–0.41, p = 0.01–0.02) with molecular dates [5].

Finally, enforcing the age of Placentalia to be less than 66 Ma necessarily resulted in only a single lineage crossing the K–Pg boundary, and the age estimate of Placentalia predictably abutted very tightly against this constraint: for the morphological matrix, 66.0 Ma (95% HPD interval: 65.9–66.0 Ma) under the TK model and 65.9 Ma (95% HPD interval: 65.5–66.0 Ma) under the IGR model (table 1); for the TE matrix, 65.9 Ma (95% HPD interval: 65.6–66.0 Ma) under the IGR model (figure 1b and table 1). It also resulted in a relatively long branch leading to Placentalia: for the morphological matrix, 31.7 Ma under the TK model and 34.8 Ma under the IGR model; for the TE matrix, 35.3 Ma under the IGR model (figure 1b). This is possibly because stretching a single branch to accommodate this severe constraint is less ‘costly’ than stretching and compressing multiple branches outside Placentalia. For both the morphological and TE analyses with the Placentalia less than 66 Ma constraint, the resultant dates were not significantly correlated (R² = 0.12–0.23; p > 0.05) with molecular dates [5], because many basal divergences within Placentalia are compressed into approximately the same time slice.

Rates of evolution (evaluated only for internal branches within Eutheria for morphology and for internal and terminal branches within Placentalia for the molecular sequence data; see above) exhibited several striking patterns (figure 2; electronic supplementary material, §7). Morphological rate heterogeneity was much greater under the IGR model than under the TK model for all analyses (see electronic supplementary material, §7): with only the age of the root constrained, median morphological rates across different branches of the tree under the IGR model spanned a range of approximately 1299× (minimum = 0.0087%/Ma; maximum = 11.34%/Ma), whereas under the TK model they spanned a range of only approximately 10× (minimum = 0.12%/Ma; maximum = 1.12%/Ma). Similarly high variance under the IGR model was retrieved in analyses of a hymenopteran insect dataset [29]. Plots of rate against time revealed no clear evidence of elevated rates being concentrated in branches near the K–Pg boundary (figure 2a,b); indeed, under both the IGR and TK models, rates are highest on branches closer to the root (figure 2a,b), which accordingly are compressed in time—a similar result was found by Ronquist et al. [28] in their analysis of hymenopterans. Perhaps unsurprisingly, molecular rates in these analyses (all under the IGR model; see above) show much less heterogeneity; median rates across different branches spanned a range of approximately 51× both when only the age of the root was constrained and when the ages of selected internal divergences within Placentalia were also constrained (figure 2a,b; electronic supplementary material, §7).

Figure 2.

Rates of morphological and molecular evolution of eutherian mammals through time with the IGR relaxed clock model and with different temporal constraints. Median rate of evolution (y-axis) against time (x-axis) is plotted for four different analyses, which vary in the use of different age constraints: (a) root age constraint only; (b) root and internal constraints; (c) root, internal and Placentalia less than 93.8 Ma constraints; (d) root, internal and Placentalia less than 66 Ma constraints. Note that the y-axis employs a log-scale. Black squares represent morphological rates along ‘stem-crown’ branches, black triangles represent morphological rates along ‘side’ branches and grey circles represent molecular rates along branches within Placentalia (see main text). The black trendline represents a moving average (20 Ma window, 10 Ma step size) for morphological rates for all branches, whereas the red and blue trendlines represent equivalent moving averages for ‘stem-crown’ and ‘side’ branches, respectively. The grey dashed line represents an equivalent moving average for molecular rates (branches within Placentalia only). The vertical dotted line marks the K–Pg boundary, and the grey star marks the point estimate for the origin of Placentalia in each analysis.

Strikingly, enforcing Placentalia to be less than 93.8 Ma (broadly consistent with recent molecular estimates [5]) resulted in only very slight changes in evolutionary rates compared with the corresponding analysis with only a root age constraint (figure 2a,c; electronic supplementary material, §7). For the morphology-only matrix and the TK model, maximum evolutionary rate was 1.93%/Ma (compared with 1.29%/Ma when the age of Placentalia was unconstrained), and the span of rates across different branches remained similar (approx. 14× with Placentalia less than 93.8 Ma; 12× with the age of Placentalia unconstrained). More surprisingly, with the morphology-only matrix and the IGR model, maximum morphological rate was lower when Placentalia was less than 93.8 Ma than when its age was left unconstrained (4.22%/Ma versus 7.14%/Ma), and rate variation across branches was also lower (approx. 661× versus approx. 984×). Finally, for the TE analyses with the IGR model, maximum rate was largely unchanged for morphology (1.37%/Ma versus 1.27%/Ma) but doubled for sequence data (0.76% Ma⁻¹ versus 0.37% Ma⁻¹).

Finally, constraining the age of Placentalia to be less than 66 Ma predictably resulted in high evolutionary rates, especially along the deepest branches within Placentalia (figure 2c,d; electronic supplementary material, §7), by compressing large amounts of morphological and molecular evolutionary change into the Early Palaeogene. With the morphology-only matrix and the IGR model, the highest morphological rate on any branch was 129%/Ma, and rates across different branches spanned a range of approximately 15 265× (minimum = 0.0085%/Ma; maximum = 129%/Ma), which in both cases is approximately 10× greater than in the corresponding unconstrained analysis (11.34% Ma⁻¹ and approx. 1299×, respectively), whereas the lowest rate remains unchanged (approx. 0.008%/Ma in both analyses). With the morphology-only matrix and the TK model, the highest morphological rate on any branch was 15.26%/Ma, and rates spanned a range of approximately 118×, which again is approximately 10× greater the corresponding unconstrained analysis (max rate 1.12%/Ma, span 10×), whereas the lowest rate remains similar (0.13%/Ma versus 0.12%/Ma). In the TE analysis (with IGR model), maximum morphological rates were substantially higher compared with the equivalent TE analysis without age constraints (30.84%/Ma versus 3.15%/Ma), and also showed much more rate variation across branches (span approx. 7566× versus approx. 1456×). Molecular rates showed similar trends in maximum rates (2.54%/Ma versus 0.46%/Ma) and rate variation across branches (span approx. 137× versus approx. 51×).

4. Discussion

The IGR and TK clock models used here entail very different assumptions: the IGR model assumes rates in adjacent branches are uncorrelated and permits huge amounts of rate variability, whereas the TK model employed assumes rates in adjacent branches are autocorrelated and favours less rate variability. Despite these differences, both models produced concordant results in several areas. Both models support a Late Jurassic or Early Cretaceous age of Placentalia, more than twice as old as the earliest definitive fossil placentals (table 1; see the electronic supplementary material, §7). Such ancient dates are implausible given the known mammalian fossil record (but see [46]). They require either: (i) extremely low preservation rates of fossil placentals during the Mesozoic, but not for the Coenozoic [47]; (ii) biogeographically unlikely ‘Garden of Eden’ hypotheses, in which Placentalia originated and began to diversify only in regions for which the Mesozoic mammalian fossil record is especially poor (such as Australia, India or Antarctica [48,49]); or (iii) that the earliest crown placentals lack apomorphies that allow them to be identified as unequivocal members of Placentalia [1]. The last possibility is perhaps the most likely, given the dearth of obvious apomorphies characterizing the four placental superorders [1]. However, our analyses also place numerous subsequent divergences within Placentalia well before the K–Pg boundary (see the electronic supplementary material, §7); several of these involve clades with distinctive apomorphies, Glires [2,6,50] and Paenungulata [2,51,52]. We thus prefer an alternative explanation, namely that the models employed here are overestimating divergence times within Placentalia, and presumably also within Eutheria as a whole.

In common with another relaxed clock study of morphological and molecular data in MrBayes [34], the analyses without any temporal constraints (apart from root age) reconstruct the fastest rates nearest the root node. This was unexpected, because in both studies the inclusiveness of the clade analysed was randomly determined (by the choice of outgroups), rather than chosen to reflect (for instance) a major adaptive breakthrough. The fast basal rates also disappear (or become slower) when plausible internal age constraints are applied. These results are consistent with the models in MrBayes overestimating the age (length) of branches further up in the tree, thus chronologically compressing basal branches and resulting in higher estimated rates in this part of the tree.

The morphological data exhibited extreme rate heterogeneity, either when analysed alone or in combination with molecular data. Rate heterogeneity per se does not seem to be the cause of the ancient dates: the IGR model always inferred much greater rate variability across branches than did the TK model, but typically recovered estimates that were only slightly older (approx. 10%; see the electronic supplementary material, §7). Another possible factor is the undersampling of autapomorphies in the matrix; as a result, terminal branch lengths may be underestimated, and conversely internal branch lengths may be overestimated, which may result in inflated age estimates for certain nodes. However, the analyses presented here implemented a correction for this ascertainment bias. Furthermore, heuristically adding different numbers of ‘dummy’ autapomorphies had relatively little effect on morphological clock divergence estimates in another study [33].

A recent paper which used the MrBayes IGR model to calculate divergence dates within Mammalia based on a TE dataset similarly recovered extremely ancient dates for several mammal divergences [30]. The estimated age of Placentalia in this study was somewhat younger than our results—102.7 Ma (95% HPD interval = 96.0–107.5 Ma)—and the origin of most placental orders was near or after the K–Pg boundary [30]. However, this pattern is probably due to the use of multiple strong priors, specifically 65 internal age constraints (most within Placentalia) based on a recent molecular analysis [4]. Other studies that have used TE dating have also found that many nodes were estimated to be considerably older than indicated by the fossil record (e.g. [28,31]). Such deep inferred divergences should be treated with caution, given the evidence presented here that the IGR and TK clock models can give implausibly ancient node age estimates when using temporal information provided by fossils.

The pattern of inferred rate variation across the tree exhibits consistent patterns, regardless of the model used. In the analysis with a temporal constraint only on the root, fast internal branches are dispersed across the tree, with a tendency for rates to be higher near the root (figure 2a,b; see above). Another pattern is a preponderance of chronologically long branches (undergoing extensive change) basally within Placentalia (figure 1a), which thus has a deep inferred age (figures 1a and 2a,b, and table 1). When Placentalia is constrained to be less than 66 Ma, the morphological and molecular changes on these branches are compressed into much shorter time intervals, resulting in elevated rates (figures 1b and 2c,d). Enforcing Placentalia to be younger than 66 Ma results in an approximately 10–20× increase in the fastest morphological branch rate (figures 1b and 2d; electronic supplementary material, §7), and an approximately 5× increase in the fastest molecular branch rate, with a concentration of fast rates shortly after the K–Pg boundary, corresponding to the deepest branches within Placentalia (figures 1b and 2c–d; electronic supplementary material, §7). Whether or not this increase is plausible is difficult to ascertain, given the paucity of similar studies. It is concordant with the suggestion that a single-order-of-magnitude increase in the rate of nuclear DNA sequence evolution is sufficient to reduce the age of Placentalia to fit the ‘explosive’ (less than 66 Ma) model [53]; however, it has been argued that such accelerated molecular rates are implausibly fast for mammals [54].

Another recent study, using a different program (BEAST), different relaxed clock model (uncorrelated lognormal) and different clade (arthropods), retrieved a similar pattern [29]: analysis of an extensive morphological and molecular dataset retrieved an implausibly ancient age for pan-arthropods (approx. 940 Ma) when this node was left unconstrained; however, constraining pan-arthropods to a reasonable age (e.g. approx. 558 Ma) resulted in only an approximately sixfold increase in both maximum molecular rate (0.175%/Ma versus 0.029%/Ma) and maximum morphological rate (1.295%/Ma versus 0.235%/Ma).

It should be noted that our study and other published TE and morphological clock studies [28–30,32,33] have all employed a very simple substitution model for discrete morphological data, namely the Mk model [44], which has some limitations (see the electronic supplementary material, §5). More realistic substitution models for morphology might dramatically reduce the inferred dates and make them more compatible with the molecular and fossil evidence.

5. Conclusion

Morphological and TE analyses yield an ancient origin of placental mammals (approx. 150 Ma) that strongly conflicts with both recent molecular clock analyses and the fossil record, and is probably too old. However, only very slight changes in morphological and molecular rates are required to reduce the age to less than 93.8 Ma, broadly in line with recent molecular clock analyses [5]. Furthermore, it only takes a 10- to 20-fold increase in maximal rates of morphological evolution and a fivefold increase in rates of molecular evolution to reconcile the phenotypic disparity of Early Palaeogene placentals, and the genetic disparity of extant placentals, with a post-K–Pg origin [5]. Thus, the morphological and molecular dataset analysed here, though seemingly implying an unrealistically old origin of placentals, cannot rule out substantially later origins—perhaps even a post-K–Pg radiation. This result is perhaps less surprising when one realizes (for instance) that a 10-fold elevation in morphological rates, sustained for approximately 6 Ma across the Early Palaeogene, would generate approximately 60 Ma ‘worth’ of morphological change that could seriously mislead relaxed clock analyses (e.g. resulting in an estimated age of 120 Ma rather than 66 Ma for Placentalia). Thus, relatively minor temporal changes in evolutionary dynamics could seriously compromise relaxed clock model estimates of divergence dates, whether these use morphology, molecules or both [26,29,53,55]. In particular, given that rate heterogeneity in morphological datasets is higher and less understood, dates dependent on morphological clocks (whether in exclusively morphological analyses, or as part of TE analyses) should be treated especially cautiously. It is true that preservation artefacts can cause the fossil record to seriously mislead, but this study suggests that ‘rate artefacts’ can greatly compromise clock models. It is thus important to compare the performance of clock models for morphology employed in MrBayes with different models employed in other packages [33,36], and also with results from ghost lineage approaches which entail opposite assumptions [40–43]. Reconciling palaeontological and molecular divergence dates remains a major challenge for many groups, including mammals; the solution should involve consideration of both the vagaries of the fossil record and the sensitivities of clock models.

Funding statement

Financial support for this research has been provided by the Australian Research Council via Discovery Early Career Researcher Award No. DE120100957 (to R.M.D.B.) and Linkage grant no. LP100100339 (to M.S.Y.L.).