Why climate change will invariably alter selection pressures on phenology

Abstract

The seasonal timing of lifecycle events is closely linked to individual fitness and hence, maladaptation in phenological traits may impact population dynamics. However, few studies have analysed whether and why climate change will alter selection pressures and hence possibly induce maladaptation in phenology. To fill this gap, we here use a theoretical modelling approach. In our models, the phenologies of consumer and resource are (potentially) environmentally sensitive and depend on two different but correlated environmental variables. Fitness of the consumer depends on the phenological match with the resource. Because we explicitly model the dependence of the phenologies on environmental variables, we can test how differential (heterogeneous) versus equal (homogeneous) rates of change in the environmental variables affect selection on consumer phenology. As expected, under heterogeneous change, phenotypic plasticity is insufficient and thus selection on consumer phenology arises. However, even homogeneous change leads to directional selection on consumer phenology. This is because the consumer reaction norm has historically evolved to be flatter than the resource reaction norm, owing to time lags and imperfect cue reliability. Climate change will therefore lead to increased selection on consumer phenology across a broad range of situations.

1. Introduction

Phenology, the seasonal timing of lifecycle events, has important fitness consequences in seasonal environments as there is generally only a limited period of favourable conditions for carrying out seasonal activities such as reproduction, migration or hibernation [1–11]. These favourable conditions could be set by weather, for example, arriving too early at the breeding grounds when conditions are still harsh [12], or by the phenology of other species [3,13]. For example, many prey species show a distinct seasonal peak in their abundance, on which predators depend for energy-demanding activities such as breeding [9,14]. Similarly, herbivores may depend on certain phases of plant growth when plant nutritional value is highest [15,16]. As the timing of these favourable conditions is directly or indirectly determined by climatic variables, which show substantial year-to-year variation in timing, phenological traits are generally phenotypically plastic in response to these climatic variables.

Synchronizing a phenological trait with timing of the favourable environmental conditions (i.e. the optimal timing) often requires advance ‘preparations’. For example, there can be considerable temporal gaps between the onset of reproduction and when offspring needs have to be matched with favourable conditions, as the length of the incubation period in birds or the gestation period in mammals can be substantial. In our model system, for example, great tits (the consumer) have to start laying their clutch at a time when most caterpillars (the resource) have not even hatched from their eggs, because laying a clutch of 8–10 eggs and incubating it takes about three weeks and hence environmental conditions (here ambient temperature) determining great tit and caterpillar phenology are different. Also spatial gaps may play a role, for instance in long-distance migratory species, which have to rely on cues in one environment (e.g. the wintering area) and/or along the migration route to time their arrival in another environment (e.g. the breeding area) to coincide with optimal conditions there. Consequently, the ‘decision’ that determines the phenological trait has to be based on different environmental conditions than the conditions that determine the optimal timing, i.e. individuals have to respond to certain ‘cues’ that are correlated with, but not identical to, the environmental conditions that determine the optimal time.

As many phenological traits are either directly or indirectly related to ambient temperature, the rising temperatures owing to climate change have caused widespread advancements in phenology [17,18]. For example, flowering time and leafing date in plants, end of hibernation in mammals, emergence time from diapause in insects and timing of breeding and migration in birds and fishes have substantially advanced over the past decades, with the shifts typically more pronounced at higher latitudes and lower trophic levels [19,20]. Differential shifts across trophic levels could be caused by interacting species experiencing effectively different rates of climate change (e.g. if consumer phenology and resource phenology are sensitive to cues during different time windows and climate change is temporally heterogeneous), or by differential intrinsic sensitivity. Regardless of the causes, such differential shifts will disrupt the existing synchrony or partial synchrony between trophic levels [3,15,21]. As synchrony between trophic levels generally affects individual fitness, disrupting this synchrony, i.e. a mismatch between trophic levels, probably leads to selection on the phenology of the involved species [13]. Here, we clarify the role of both mechanisms, differential shifts in environmental variables affecting trophic levels or differential intrinsic environmental sensitivities and show how current reaction norms can still become suboptimal even if interacting species effectively experience the same rate of climate change.

Because climate change is heterogeneous in space and time [22], it is likely that the variables affecting consumer and resource phenologies change at different rates and it has been argued that this should lead to selection on the phenological reaction norm of the consumer [23]. However, what is much less well appreciated is that identical changes in these environments can also lead to selection, as we will clarify with our model. McNamara et al. [24] explored fitness consequences of environmental change on phenotypically plastic phenological traits and showed how these consequences can be decomposed into a component resulting from changes in the predictive power of phenological cues, and a component owing to mismatch between observed timing (which may have been optimal prior to environmental change) and the optimal timing under the new conditions. We here use a similar conceptual approach but explicitly model the dependence of optimal phenology (as indexed by resource phenology) on an environmental variable, which is distinct from the ‘cue environment’ that determines consumer phenology. This allows us to directly assess the consequences of different (heterogeneous) or equal (homogeneous) rates of changes in the environments affecting optimal and realized phenology and thereby directly link our model to variables affected by climate change (e.g. local temperatures or rainfall). Based on simple theoretical considerations we show that, provided there is stabilizing selection around an optimum, then the vast majority of climate change scenarios will change patterns of directional selection on consumer phenology and thus climate change invariably leads to selection on reaction norms for phenological traits. We present additional evidence for this from a simulation model, which was parametrized based on the exceptionally well-understood consumer–resource system of great tits and their nestling food source, caterpillars.

2. The analytical model

Consider a consumer (species 1) that must match its phenology to the phenology of its resource (species 2). However, the consumer and resource must determine their phenologies using two different but correlated environmental cues, E₁ and E₂, respectively. An example might be a great tit that must use the early season temperature (E₁) to determine when to initiate breeding such that peak nestling food requirements coincide with the peak in caterpillar abundance as determined by late-season temperature E₂ approximately four weeks later (cf. figure 1). Although this is conceptually different from assuming a time lag between trait development and selection on the trait [25–27], it is functionally identical in that the cue environment (E₁) does not predict the selective environment (E₂) perfectly. Phenology of consumer and resource was described by linear reaction norms with E₁ and E₂, respectively, as independent environmental variables. We here assumed that the timing of resource phenology equals the optimal timing for the consumer. However, the model can also easily accommodate situations where the optimal timing for the consumer is earlier or later than resource phenology by a constant amount [28,29] by incorporating an ‘offset’ into equation (2.1) and this would not affect the results.

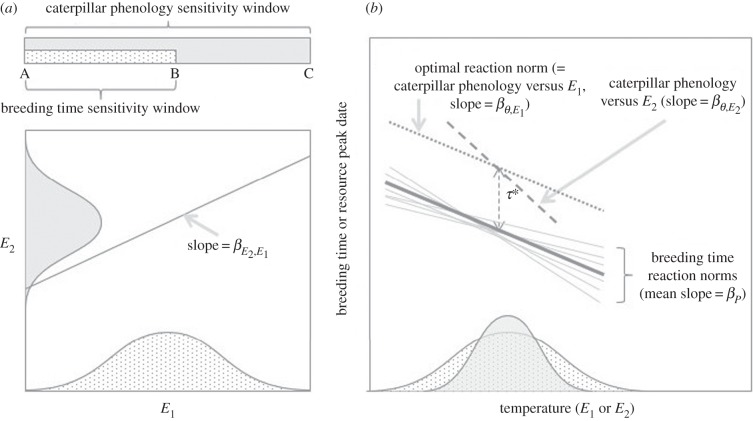
Figure 1.

Schematic of resource and consumer reaction norms using the great tit–caterpillar system as an example. (a) Great tit breeding time and caterpillar phenology respond to temperatures E₁ (shaded light grey) and E₂ (shaded darker grey), respectively. E₁ is measured over an earlier and shorter period (A–B, hence showing a larger variation as indicated by the wider distribution), whereas E₂ is measured over a longer period (A–C). (b) Linear relationships between great tit breeding time and E₁ (solid line, slope = β_P) and between caterpillar phenology and E₂ (dashed line, 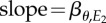). The thick solid line indicates the population-average reaction norm and the thin grey lines indicate individual-specific reaction norms. The optimal reaction norm slope with respect to E₁ (dotted line) is equal to the resource reaction norm slope 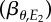multiplied by the slope of E₂ versus E₁ 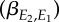. Ignoring the existing mismatch between bird and caterpillar phenology (see Discussion), the initial difference in elevation between the reaction norm elevations, τ*, is set to approximately 30 days, so that food demands and availability coincide.

The reaction norm of the resource θ is dependent upon its environmental variable E₂ and was modelled as

2.1

where 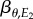is a regression coefficient, μ_θ the mean phenology of the resource and 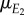the mean of the environmental variable E₂. The consumer's optimal reaction norm will be equivalent to the optimal phenotype θ as a function of the environment E₁, the ‘cue’ environment, and can be derived as follows [24]:

The two environments are correlated and, so a regression of E₂ against E₁ is

2.2

where 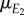is the mean of the environmental variable E₂, 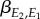a regression coefficient and 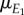the mean of environmental variable E₁.

Therefore, substituting equation (2.1) into equation (2.2) yields

2.3

As illustrated in figure 1a, the regression coefficient of E₁ against E₂ is

2.4

where ρ is the correlation between E₁ and E₂ 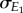and and 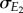 are the standard deviations in E₁ and E₂, respectively. Substituting equation (2.4) into equation (2.3) gives

2.5

which shows that the slope of the optimal consumer phenotype is a function of the resource reaction norm slope 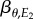, the correlation between E₁ and E₂ (i.e. ρ), and the ratio of their standard deviations 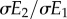. Assuming equal variances in E₁ and E₂, for the sake of simplicity, this means that the consumer reaction norm slope will always be shallower than the resource reaction norm, unless the correlation between E₁ and E₂ is perfect (in that case, the slopes would be equal). As a consequence of this, consumer phenology will change less than resource phenology for the same change in the respective environmental variables (cf. figure 1).

This shallower slope of the consumer reaction norm has two consequences for the phenological synchrony between consumer and resource phenology. In a stable environment, synchrony will vary with E₁: taking our great tit–caterpillar system (see ‘The simulation model’ section for a detailed description) as an example, the birds (consumers) will be too late in relation to the caterpillars (resource) in warm springs, whereas the birds will be too early in cold springs (figure 1b). On average, however, the birds will match the caterpillars, assuming a symmetric temperature distribution. In a changing environment, however, this differential sensitivity will lead to the consumer becoming systematically mismatched with the resource, even when the environments affecting consumer and resource (E₁ and E₂) change at the same rate. To illustrate this again with our great tit–caterpillar system, for a 1°C increase in the temperatures affecting the phenologies of birds and caterpillars, the birds will advance their phenology by about 3 days, whereas the caterpillars will advance their phenology by about 6 days, i.e. twice as much.

Selection upon the consumer's reaction norm occurs when it deviates from the optimal reaction norm. We assumed that consumer phenology was optimally adapted prior to the onset of climate change and θ(E₂) = θ(E₁). With climate change therefore, directional selection will continue to be absent only if consumer and optimal phenology change at the same rate, which is to say

2.6

Denoting the rates of changes in the cue environments 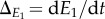and 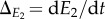 and substituting in equation (2.1) and equation (2.3) gives

2.7

Directional selection will be absent if and only if the linear change in the environment affecting resource phenology (E₂) is equal to the linear change in the environment affecting consumer phenology (E₁) times the correlation between these environments times the ratio of their standard deviations. As such a narrow set of conditions will rarely be met, the majority of environmental change scenarios involving linear changes in the mean will lead to directional selection on consumer phenology.

3. The simulation model

We constructed an individual-based simulation model that was based on our great tit–caterpillar consumer–resource system as a template. Great tits (Parus major) are small passerine birds that rely on caterpillars as a food source on which to raise their offspring [9,30]. These caterpillars develop during spring and their biomass peaks around mid-May. To maximize their reproductive success, great tits strive to synchronize the nestling period with this peak in food abundance, and to achieve this, they need to initiate egg-laying about four weeks earlier. Consequently, the birds cannot use the temperatures that determine caterpillar growth as a cue to time egg-laying. Figure 1a illustrates schematically the different reaction norms of resource and consumer using the great tit–caterpillar system as an example. Great tit breeding time correlates best with mean temperature from 16 March to 20 April [31], making this the likely cue environment E₁. Caterpillar phenology responds to mean temperature from 8 March to 17 May (E₂) [9]. Figure 1b shows the linear relationships between great tit breeding time and E₁ (slope = β_P) and between caterpillar phenology and E₂ (dashed line, 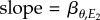). The thick black line indicates the population-average reaction norm for breeding time and the thin grey lines indicate individual-specific reaction norms that differ in elevation and slope.

We used an individual-based model to simulate evolution of consumer reaction norms. In contrast to the phenology of caterpillars (i.e. the resource), which could not evolve in the model, the reaction norm of great tits (i.e. the consumer) could evolve. The consumer reaction norm was modelled assuming a linear function, with the elevation and slope parameters considered as two separate traits that were each affected by additive genetic variation and residual variation.

Individuals were tracked throughout their ‘lifetime’ and their trait values, reproductive success and survival recorded. At the beginning of each simulation run, a consumer base population was set up with genotypic values for elevation and slope drawn randomly from a multivariate normal distribution with variances and covariance given by the additive genetic (co)variances. Then, 100 ‘years’ were simulated, which consisted of the following steps: (i) temperatures affecting resource and consumer phenology were drawn from a multivariate normal distribution defined by the (co)variation in temperatures; (ii) random mating occurs; (iii) phenotypes of resource and consumers are predicted from these temperatures using the corresponding reaction norms; (iv) offspring are produced depending on the mismatch between the maternal phenotype and resource phenology; the maternal phenotype was used to determine the pair's reproductive success, because in great tits, our model system, males do not affect their females' egg-laying dates [32]; (v) offspring genotypic values for reaction norm elevation and slope are calculated as mid-parent value plus segregation error [33]; and (vi) random adult mortality occurs at a set rate: to keep population numbers constant, recruitment rate of offspring is adjusted according to the number of surviving adults, which results in a constant population size over time. The breeding population in the next year will consist of surviving adults and recruiting offspring. Space was assumed to be homogeneous and was not modelled explicitly. One thousand simulation runs of each scenario were performed.

Because we were interested in evolution (i.e. the response to selection) but also selection itself, we first tracked annual mean genotypic values of reaction norm elevation and slope and, second, calculated annual selection differentials on these parameters.

We parametrized our model with values from our long-term studies on great tits and the seasonal biomass peak of caterpillars [9,31,34,35]. We explored a range of scenarios of linear environmental change with differential increases in the temperatures affecting consumer phenology (E₁) and temperatures affecting resource phenology (E₂). The increase in both E₂ and E₁ varied from no increase to an increase of 0.06°C per year, which corresponds to an ‘extreme’ scenario. However, the observed increases in E₂ in our great tit study area are similar to this rate of increase [35]. Such a differential temperature increase can be expected under climate change, although the ratio will probably vary regionally and be hard to predict a priori [22]. See the electronic supplementary material for a more detailed description of the simulation model (electronic supplementary material, S1) and its code (electronic supplementary material, S2).

4. Results

As our analytical model showed, selection on consumer phenology will be absent only if the change in the environment affecting resource phenology (E₂) is equal to the change in the environment affecting consumer phenology (E₁) times the correlation between these environments times the ratio of their standard deviations (figure 2). In other words, selection will be absent when the relationship between E₁ and E₂ is not changed by environmental change. A stronger increase in the temperature affecting the resource (E₂) than the consumer (E₁), i.e. all parameter combinations above the 1 : 1 diagonal in figure 2, always led to directional selection on elevation and slope. Under these circumstances, resource phenology advances at a faster rate than consumer phenology which leads to phenological mismatch and hence selection. Additionally, an equal increase in the temperatures affecting resource and consumer phenology (i.e. values along the 1 : 1 diagonal), or even stronger increases in E₁ than E₂ (see lower right corner), mostly led to directional selection on elevation and slope. In our ‘model system’, standard deviations in E₁ and E₂ are 1.20 and 0.95, respectively, and ρ is 0.57. Hence, we expect no directional selection only for ratios of increases in E₂ over E₁ of 0.45, i.e. considerably stronger increases in E₁ than E₂ (see ‘ridge’ in figure 2).

Figure 2.

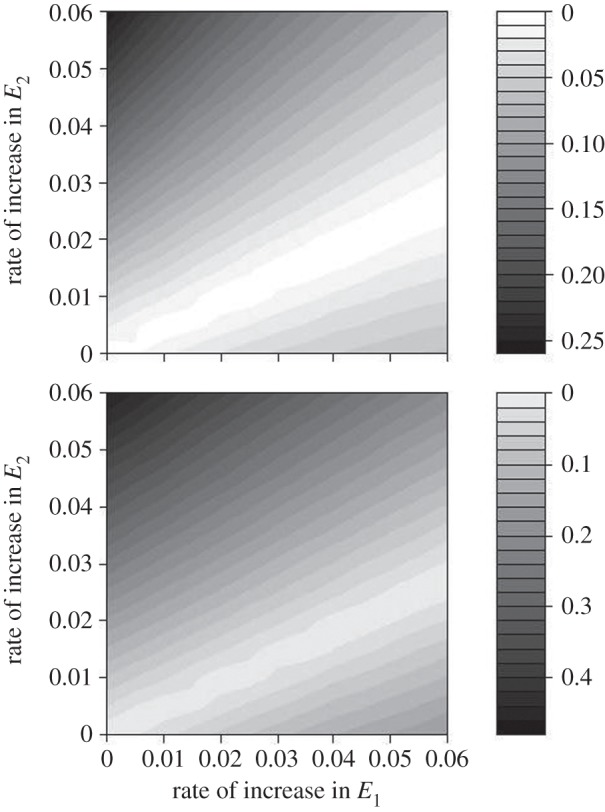
(a) Selection on reaction norm elevation and (b) slope. Absolute standardized selection differentials (average annual values, calculated over a 100 year period) are plotted against the rates of increases in consumer temperatures (E₁) and resource temperatures (E₂). Note that in the figure only the strength of the selection is indicated but not the direction. Above the ‘ridge of no selection’ selection favoured earlier phenology (i.e. a lower intercept) and a steeper reaction norm while below this ridge selection favoured later phenology and a shallower slope. Note also that in the area below the ridge of no selection (i.e. with selection for later phenology relative to that expressed) the optimal consumer phenology would still advance driven by a plastic response to the increase in E₁; in other words, selection would oppose the direction of the plastic component of trait change. The increases in resource and consumer temperatures varied from no increase to an increase of 0.06°C per year. Most combinations of differential increases in E₁ and E₂ lead to directional selection on both the elevation and the slope of the reaction norm.

Detailed results from our simulation model on changes in phenology, selection and genotypic value of reaction norm elevation and slope for four scenarios of temperature increases are illustrated in the electronic supplementary material, figures S1–S4.

5. Discussion

If the environments determining the phenologies of consumer and resource change at different linear rates, one might ‘intuitively’ expect that this leads to selection on the phenology of the consumer, because the relationship between cue and selective environment has changed. Conversely, if they change at the same rate, one might intuitively expect no resulting directional selection. We here clarified why neither of these need be the case. The key point is that the optimal consumer reaction norm will typically be shallower than the resource reaction norm. The optimal consumer and resource reaction norm slopes will only be identical if the standard deviations of the temperatures affecting consumer and resource (E₁ and E₂) are equal and their correlation equals one (cf. equation (2.4)). Alternatively, the ratio of the standard deviations needs to be the inverse of the correlation. This is obviously a fairly restricted set of conditions and consequently consumer and resource reaction norms will typically differ.

On the one hand, a consequence of these differing reaction norm slopes is that even equal rates of changes in the environments (i.e. homogeneous environmental change) affecting consumer and resource phenology will lead to directional selection on consumer phenology. On the other hand, unequal rates of environmental change in these environments (i.e. heterogeneous environmental change) could result in no directional selection if the very restricted condition of equation (2.5) is satisfied.

These findings are confirmed and illustrated by the results from our simulation model. Heterogeneous environmental change with a stronger increase in the temperatures affecting the resource (E₂) would lead to selection on both elevation and slope of the reaction norm. In our simulations based on parameters from our great tit–caterpillar study system and within a time frame of ca 50 generations, the magnitude of this selection is substantial, when compared with the median standardized linear selection differential in Kingsolver et al. [36] of 0.08 (figure 2). Even stronger increases in E₁ than in E₂ can lead to selection on consumer phenology (cf. figure 2 for parameter combinations below the 1 : 1 diagonal), as in our ‘model system’, caterpillar phenology (the resource) advances by about six days for a 1°C increase in temperature, whereas the phenology of the great tits, the consumer, advances only about 3 days for the same temperature increase. No or weak directional selection on the consumer reaction norm is expected only for a very restricted combination of the rates of increase in E₁ and E₂, the variation in E₁ and E₂, and their (detrended) correlation (cf. equation (2.5)), resulting in the narrow ‘ridge’ of no selection in figure 2.

In our scenarios of climate change, we assumed that E₁ and E₂ would increase linearly and that their variances would not change. A nonlinear change in E₁ and E₂ would also lead to selection on consumer phenology, except for the short period when the ‘ridge’ of no selection is crossed by the nonlinearly increasing temperatures. Changes in the (co)variances of E₁ and E₂ would lead to selection on the consumer reaction norm slope unless these changes would be exactly counterbalanced by changes in the means (see equation (2.5)). While it is theoretically possible that E₁ and E₂ would change in their means, variances and correlation in such a way that no selection on consumer phenology would result, it seems unlikely as the fairly restricted conditions of equation (2.5) would need to be met.

One reason why one might expect intuitively that different rates of increases in E₁ and E₂ would lead to selection is because such differential increases in two variables will alter the correlation between them and hence how one can be used as ‘cue’ for the other. We would however like to note here that our correlation parameter ρ is the ‘residual’ correlation between the detrended variables, i.e. their residuals after correcting for temporal trends, which means that it will remain constant, even if the ‘realized’ correlation between the variables changing at different rates changes.

An important assumption of our model was that phenology of consumer and resource are affected by different environmental variables. While some types of behavioural plasticity may be more or less instantaneously expressed, the fitness consequences of the plastic response are unlikely to be instantaneously realized. In most cases, time lags are expected both between cue perception and trait expression, and between trait expression and the fitness consequences of trait expression being realized. The longer the time lags and the more temporally variable the environment, the lower the expected correlation between cue and selective environment and hence the flatter the optimal reaction norm [37,38]. In the extreme case of very low correlations (and/or if intrinsic costs to plasticity are high), environmental canalization or bet-hedging strategies might be selectively favoured over plasticity [39]. In the case of phenological traits, cue and selective environment are rarely identical, as these traits typically require some preparation, for example, accumulation of body reserves for breeding, migration or hibernation, or have to be initiated at entirely different locations, as in individuals migrating from wintering areas to far removed breeding areas. As a consequence, the phenological reaction norm of consumers will generally be shallower than that of the resource.

Another important assumption of our modelling work was that deviating from the optimal reaction norm (in both elevation and slope) carries a fitness cost for the consumer, which seems to be common in phenological traits [1–11]. Furthermore, even if the correlation between E₁ and E₂ was so low (prior to the onset of climate change) that the consumer reaction norm would be so shallow that it would effectively be zero, increases in E₂ would still cause a mismatch and selection on consumer phenology [16]. We also assumed that the match between consumer and resource phenology was the only ecological factor affecting individual fitness. Other selection pressures might additionally be important and these might shift the optimal timing for the consumer to a later or earlier time than the timing of the resource phenology. For example, if early breeding carries fitness costs, the optimal breeding time might be later than the peak of resource abundance [29] or if there was (strong) competition for breeding territories the optimal arrival time for migratory species might be earlier than expected from resource phenology [28]. However, such scenarios would only lead to an ‘offset’ between optimal timing for the consumer and resource phenology and any changes in E₁ and E₂ would still lead to selection on consumer phenology.

When modelling extinction risk caused by selection on phenotypically plastic traits, Chevin et al. [40] demonstrated that the difference between the slopes of the optimal phenotype as a function of the environment and the actual phenotype as a function of the environment (i.e. the observed reaction norm) is important for population persistence. In their model, however, both actual and optimal phenotypes were assumed to be affected by the same environmental variable. In our case, the slope of caterpillar phenology against the great tit's temperature cue (E₁) is very similar to the observed great tit reaction norm (−2.99 versus −3.11; note that the optimal reaction norm of −2.99 lies within the 95% confidence interval (−2.42, −3.80) of the great tit reaction norm slope). One might hence expect that climate change should not have led to strong mismatch and selection in our population, given that these slopes are so similar. The key thing to realize, however, is that the caterpillars are sensitive to temperatures in a different period (E₂) and that the slope of caterpillar phenology versus E₂ is steeper than the slope of great tit phenology versus E₁. This explains the observed changes in selection [9,34] and those we predict here. Consequently, explicitly modelling the dependency of resource and consumer phenotypes on different environmental variables can considerably affect conclusions about effects of environmental change. It is also noted that whether E₁ and E₂ are two different but correlated environmental variables or the same environmental variable ‘measured’ at different time points leads to the same outcomes, because two measurements of the same variable taken at different time points (or over different periods) will generally be positively but not perfectly correlated.

Phenotypically plastic traits can obviously respond to more than one environmental variable, for example, seasonal timing of breeding in passerines depends on both ambient temperature and day length [41,42]. Assuming in our model that consumer phenology depends on more than one environmental variable would only make equation (2.5) more complex and hence lead to an even more restricted set of conditions that lead to no selection on consumer phenology.

Based on theoretical arguments and a simulation model, we have shown here that environmental change will invariably lead to selection on phenotypically plastic traits, simply because the environment that determines the trait value and the environment that determines the optimal phenotype will (very) rarely be identical or perfectly correlated. In contrast to our great tit study population in the Hoge Veluwe (the Netherlands) where climate change has led to intensified selection for earlier breeding time, increasing temperatures did not lead to increased selection on breeding time in the great tit population in Wytham Wood (UK) [43], which would indicate that the phenologies of birds and caterpillars advanced at the same rate. We showed here that an equal advance of resource and consumer phenology is possible if equation (2.5) applies. This can be achieved in several ways depending on the correlation between the temperatures affecting birds and caterpillars and the variation in these temperatures. To understand why climate change has not led to increased mistiming in this population, it would be necessary to carefully estimate these parameters for the Wytham Wood population.

Although advancements in the phenology of many taxa across a broad geographical range have been reported [19], in the vast majority of cases, the collected data could be analysed only at the population level, rather than also at the individual level, simply because individual identity was not recorded. For example, recording how many individuals initiated breeding at given dates in several years allows assessment of whether breeding time changed across years at the population level. It however does not allow inferences to be made regarding selection on breeding time, because this would require individual fitness to be recorded and related to individual breeding time. Out of more than 1000 studies on advancements in avian phenology, for example, only 21 had data at the individual level (reviewed in [44]). Reviews in plants, freshwater insects and mammals found similar ratios of population-level versus individual-level studies [45–47]. Consequently, there are very few studies that could have analysed climate change induced selection and even fewer that actually analysed it.

‘Evolutionary rescue’, the process by which adaptation to novel environmental conditions ensures population survival, depends crucially on the additive genetic variation of the traits under selection [48,49]. We hence need reliable estimates of genetic variation in elevation and slope of reaction norms, and their possible covariation, to be able to assess possible extinction risks caused from selection by environmental change. Many quantitative genetic studies estimated heritabilities of life-history traits, which are likely to be affected by climate change, and found moderate heritabilities of these traits [50]. Although most, if not all, of these traits are phenotypically plastic, the vast majority of studies in natural populations ignored this and—by removing year-to-year variation in the analyses—only analysed reaction norm elevations. While there is hence evidence that reaction norm elevations are genetically variable and could respond to selection, we have virtually no information about genetic variation in reaction norm slopes, at least in natural populations [51]. This limits our ability to assess the potential for ‘evolutionary rescue’ from environmental change, which is crucial because, as we have shown here, climate change will lead to selection on phenology, and thus an evolutionary response is needed.

Data accessibility

Not applicable as in this article no original data were analysed.

Funding statement

M.E.V. was supported by an NWO-VICI grant. T.E.R. is currently supported by the Beaufort Marine Research Award: fish population genetics, Irish Government NDP (2007–2014) administered by the Marine Institute.