Fossil evidence for key innovations in the evolution of insect diversity

Abstract

Explaining the taxonomic richness of the insects, comprising over half of all described species, is a major challenge in evolutionary biology. Previously, several evolutionary novelties (key innovations) have been posited to contribute to that richness, including the insect bauplan, wings, wing folding and complete metamorphosis, but evidence over their relative importance and modes of action is sparse and equivocal. Here, a new dataset on the first and last occurrences of fossil hexapod (insects and close relatives) families is used to show that basal families of winged insects (Palaeoptera, e.g. dragonflies) show higher origination and extinction rates in the fossil record than basal wingless groups (Apterygota, e.g. silverfish). Origination and extinction rates were maintained at levels similar to Palaeoptera in the more derived Polyneoptera (e.g. cockroaches) and Paraneoptera (e.g. true bugs), but extinction rates subsequently reduced in the very rich group of insects with complete metamorphosis (Holometabola, e.g. beetles). Holometabola show evidence of a recent slow-down in their high net diversification rate, whereas other winged taxa continue to diversify at constant but low rates. These data suggest that wings and complete metamorphosis have had the most effect on family-level insect macroevolution, and point to specific mechanisms by which they have influenced insect diversity through time.

1. Introduction

Why some groups of organism are very speciose, while others are species-poor, is a problem that has fascinated evolutionary biologists ever since Darwin [1–3]. The insects, with over half of all described species [4,5], have long stood out as a very speciose group whose richness requires explanation [6]. Of the many hypotheses proposed to explain this richness, some of the most prominent include the origin of novel phenotypic characters known as key innovations [7]. Here, we use a new dataset on the fossil record of the hexapods (insects and their six-legged relatives such as springtails) to assess the relative importance of, and mechanisms underlying, several putative key innovations.

Macroevolutionary approaches to understanding current standing diversity require data on the past history of life, which comes from two complementary sources of information [8]. The neontological approach uses phylogenies of extant taxa to infer changes in past processes [9]. The palaeontological approach uses information from the fossil record [10]. Phylogenies of extant taxa allow one to study processes at the species level and in the absence of a fossil record, but inferences about speciation and extinction rates are problematic (e.g. [11]). Fossils, although often studied at taxonomic levels above the species, and though prone to sampling biases [12], provide direct evidence about the timing of changes in rate, as well as extinctions [13].

Ultimate causes of macroevolutionary change can include extrinsic factors such as environmental change [14,15], as well as intrinsic ones such as evolutionary novelties [16]. Key innovations are novel phenotypic characters such as morphologies, behaviours or developmental strategies that enhance species richness [8,17], seen through an increase in net diversification rate. The underlying macroevolutionary process could be an increase in speciation, decrease in extinction or some combination of changes in both. Three general ecological mechanisms have been proposed to explain the macroevolutionary effects of key innovations [8], corresponding to changes in three macroevolutionary parameters [7]: (i) escape from competition into a new adaptive zone, thus changing the carrying capacity of taxa in the environment; (ii) decreasing the probability of extinction; and (iii) ecological or reproductive specialization, thus increasing the speciation rate. For neontological studies, explicit data supporting these macroevolutionary parameters may be lacking because they work with the net outcome rather than the underlying origination and extinction rates, making it hard to tease the different underlying parameters apart. By contrast, fossil studies are intrinsically better able to provide data on these different macroevolutionary parameters, thus aiding inference of the mechanism.

Four progressive evolutionary steps have traditionally been recognized in the evolutionary history of the hexapods, based on the sequence in which they appear in the fossil record [18,19] and phylogenies (e.g. [20]) (figure 1). These are the evolution of the insect bauplan in wingless insects, wings, wing folding and complete metamorphosis (figure 1). Evidence that acquisition of these features increased net diversification rates and are therefore key innovations, has largely come from sister-group species-richness comparisons across orders [21,22], suggesting that shifts in net diversification rate occurred at or after the origin of wings. However, the results of these studies are sensitive to phylogenetic uncertainties [22], give no indication of which macroevolutionary parameters may have changed [21] and may be biased by the low phylogenetic resolution and simple macroevolutionary models employed (e.g. [11]). Fossil studies have been rare, but Yang [23] used Lyellian survival analysis on family-level data [24] to suggest that extinction rates do not differ between Holometabola and Paraneoptera, and hence that differences in origination rates probably account for the larger increase in families in Holometabola. However, Yang only considered this single key innovation, and the dataset on which his study was based is now considerably dated. Since 1994 there have been major changes to insect taxonomy (e.g. [25]), the estimated ages of deposits (e.g. [26]), about 400 additional insect families are known from the fossil record [27] and 21% of the families in Labandeira [24] have since been synonymized.

Figure 1.

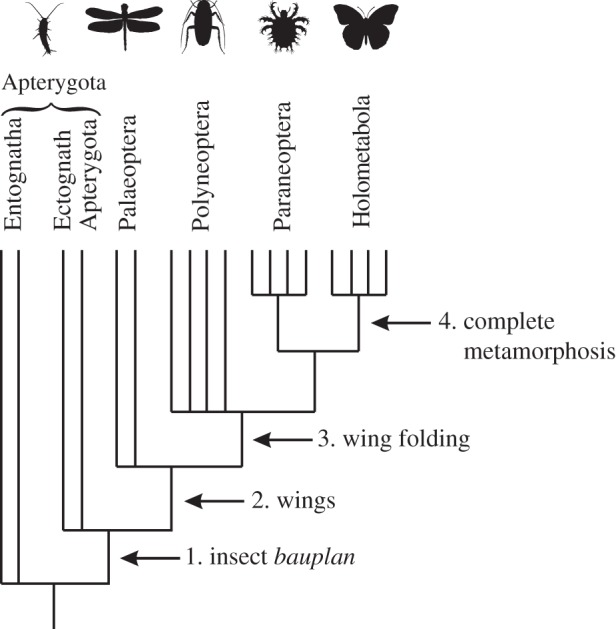
Four putative hexapod key innovations, together with the taxa defined by them [7].

Here, we use a new compilation of the first and last occurrences of fossil hexapod families to test for the effects of potential key innovations, by seeking tell-tale significant differences in the rates of origination, extinction and accumulation of taxa across major morphological groupings (figure 1). Specifically, we test for the effect of the insect bauplan by comparing non-insect Entognatha (e.g. springtails) with ectognathan Apterygota (e.g. silverfish); for the effect of wings by comparing primitively wingless hexapods (Apterygota) with the primitive winged Palaeoptera (e.g. dragonflies); for the effect of wing folding by comparing Palaeoptera (which cannot fold their wings) with Polyneoptera (e.g. cockroaches, which can); and we test for complete metamorphosis by comparing Holometabola (e.g. beetles, with metamorphosis) with their sister group Paraneoptera (e.g. true bugs, without metamorphosis) (figure 1). We examine the shape of the temporal accumulation of taxa across the different groups, and associations between richness and rates within and across taxa, to test for constraints on richness, and whether certain key innovations might have elevated diversification rates.

2. Material and methods

(a). Data collection

Starting with the dataset of Ross & Jarzembowski [28], searches were made of the published literature to the end of 2009 for the earliest and latest occurrence (stage resolution) of each fossil family of Hexapoda. Families were classified into higher taxa following the widely adopted Eur-American scheme [5], with some differences owing to recent revisions (see the electronic supplementary material). Where there was disagreement over the taxonomic status of a specimen or family, a consensus approach was taken. The timescale of Ogg et al. [29] was adopted to date stages.

(b). Data analysis

Adjacent geological stages were aggregated to form time bins of approximately equal length (mean, s.d. 9.87 ± 3.1 Myr) (see the electronic supplementary material). Per capita origination and extinction rates were estimated using Foote's [30] metrics 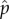and which help control for variation in interval duration and sampling intensity because they are instantaneous rates and ignore single-interval taxa which are more susceptible to sampling bias. As the rates time series are highly right skewed (electronic supplementary material, figure S2) and log-transformation does not normalize their distribution, they were compared across taxonomic groups using non-parametric Friedman tests. Because the time series began at different intervals for different groups, tests were implemented pairwise so as not to discard data unnecessarily and to reduce type 1 errors (false positives), tests were limited to the most essential hypotheses. Because there are so few families of Apterygota, comparisons between Entogatha and Ectognatha lacked power and were not pursued beyond these initial basic analyses, which failed to show any significant differences between them (see Results).

Diversification models were investigated using nonlinear least-squares regressions on the clade richness data through time, with time coded relative to the present (i.e. negative numbers becoming less negative through time). Linear, exponential, logistic and Gompertz models were fitted using the nls() function from the nlrwr package, and the preferred model for each clade identified by comparison of Akaike information criterion with correction for small sample sizes (AICc) values [31,32] using the akaike.weight() function in the qpcR package in R ([33]; electronic supplementary material]). For Palaeoptera and Polyneoptera, logistic and Gompertz model runs failed to converge on a solution. Examination of terminated model runs showed selection for an ever-increasing (and unrealistically large) value of the richness asymptote. The fitted values resembled exponential or linear growth, with little sign of a richness asymptote in the data, while the AICc scores were relatively high, indicating that the assumption of a richness asymptote was inappropriate. For these cases, model runs were terminated after 500 iterations and output for illustrative purposes, noted where appropriate in table 1.

Table 1.

Competing nonlinear least-squares models for clade diversification, with AICc scores. (Parameters: linear a, b; logistic/Gompertz a, b and c; exponential y0, b; NULL intercept only. Parameter significance levels: *p < 0.05; **p < 0.01; ***p < 0.001. Note that significance may be inflated owing to autocorrelation in the time series.)

model	par 1	par 2	par 3	AICc	ΔAICc	AICc weight	R2
Apterygota
logistic	17.087***	5.757***	0.053***	143.64	0.00	0.74	0.9139
Gompertz	17.363***	0.009	0.040***	145.70	2.06	0.26	0.9083
exponential	22.111***	104.115***	—	157.41	13.77	0.00	0.8593
linear	16.013***	0.057***	—	179.92	36.28	0.00	0.7217
NULL	7.000***	—	—	219.86	76.22	0.00	—
Palaeoptera
exponential	40.277***	307.667***	—	255.23	0.00	0.69	0.3097
lineara	35.998***	0.067**	—	257.78	2.55	0.19	0.2544
Gompertza	22040	6.497	2.82 × 10−4	260.26	5.02	0.06	0.2533
logistic	1405	−3.737	0.002	260.40	5.17	0.05	0.2500
NULL	25.364***	—	—	265.195	9.96	0.00	—
Polyneoptera
exponential	52.049***	496.706**	—	260.73	0.00	0.47	0.2817
linear	50.136***	0.073**	—	261.38	0.64	0.34	0.2675
logistica	169.5	−0.880	0.002	263.66	2.93	0.11	0.2707
Gompertza	6414	4.903	2.882 × 10−4	264.20	3.46	0.08	0.2588
NULL	38.52***	—	—	269.38	8.65	0.00	—
Paraneoptera
Gompertz	1210.72	2.147	0.997***	221.82	0.00	0.60	0.9647
exponential	149.643***	133.714***	—	223.93	2.10	0.21	0.9591
logistic	331.46	29.69	103.58***	224.06	2.24	0.19	0.9620
linear	124.714***	0.434***	—	236.49	14.67	0.00	0.9386
NULL	60.097***	—	—	320.72	98.90	0.00	—
Holometabola
Gompertz	745.8***	0.522**	0.993***	301.46	0.00	0.95	0.9739
logistic	519.148***	−95.47***	59.354***	307.41	5.95	0.05	0.9686
linear	411.201***	1.525***	—	324.40	22.93	0.00	0.9423
exponential	508.75***	116.8***	—	324.73	23.27	0.00	0.9417
NULL	176.44***	—	—	413.68	112.22	0.00	—

^aModel run terminated and output after 500 iterations due to non-convergence (see Material and methods for explanation).

Associations between richness, origination and extinction in the time series for different groups were investigated using bivariate correlation of the first differences. First differencing is a simple detrender that removes short-term autocorrelation, long-term patterns and the spurious correlations that may derive from them, as well as removing random walk effects. Significance was assessed using bootstrapping of the test statistic to reduce the necessary underlying assumptions about the data.

3. Results

(a). Origination and extinction rates

Instantaneous per capita family origination and extinction rates [30] are mostly low but with occasional high values, mostly restricted to the early half of the record (figure 2). Unsurprisingly, origination rates are generally higher than extinction rates in all morphological groups (figure 2; electronic supplementary material, table S1). Through time, however, there is heterogeneity in the difference between these rates. There are intervals when extinction rates temporarily outweigh origination rates, most notably during the Permian (299–251 Myr ago) in Palaeoptera and Polyneoptera, but not in Holometabola (figure 2), and Upper Triassic (229–200 Myr ago) in Polyneoptera. Episodes when origination rates are much higher than extinction rates include the Pennsylvanian (318–299 Myr ago), Lower Triassic (251–246 Myr ago), Barremian (130–125 Myr ago) and Eocene (56–34 Myr ago) (figure 2 and the electronic supplementary material). Both rates are higher for Palaeoptera than Apterygota (Friedman tests, p < 0.0001). However, origination rates do not differ significantly between Palaeoptera and Polyneoptera, or Paraneoptera and Holometabola (figure 2; electronic supplementary material, table S2 and figure S1). Extinction rates do not differ significantly between Palaeoptera and Polyneoptera (figure 2; electronic supplementary material, table S2 and figure S1), but are significantly lower in Holometabola than Paraneoptera (Friedman test, p = 0.041). The median net diversification rate is highest in Holometabola and lowest in Apterygota and differs significantly between them (Friedman test, p = 0.02), but not between other groups (figure 2; electronic supplementary material, table S2).

Figure 2.

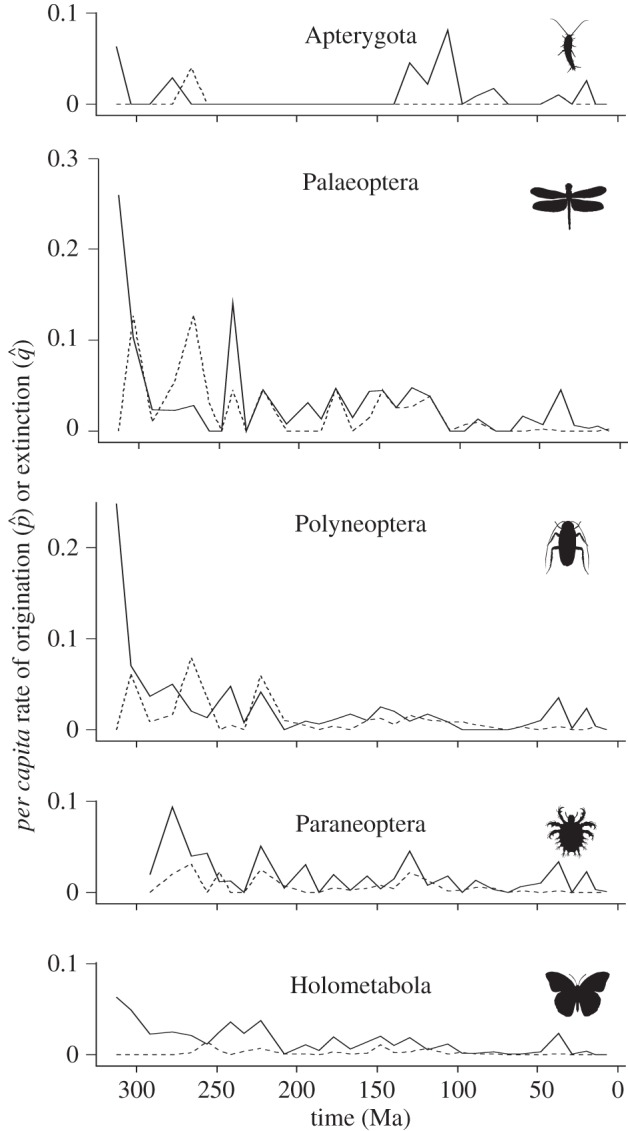
Family-level origination (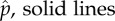) and extinction rates (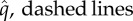) through time in the five major groups of hexapods.

(b). Rates of family accumulation and correlations among time series

The best-fit diversification model varies by clade: logistic for Apterygota, exponential for Palaeoptera and Polyneoptera, and Gompertz for Paraneoptera and Holometabola (figure 3), although for Paraneoptera the exponential and logistic models are only marginally worse, as is the linear model for Polyneoptera (see table 1). This indicates a decrease in the rate of accumulation of taxa in the more derived and richer Paraneoptera and Holometabola (most strongly in the latter) towards the present, with the more-basal Palaeoptera and Polyneoptera showing no slow-down in diversification despite an overall slow rate of taxon accumulation (figure 3). There is also a strong preference for a logistic growth model for Apterygota, indicating a low current rate of diversification.

Figure 3.

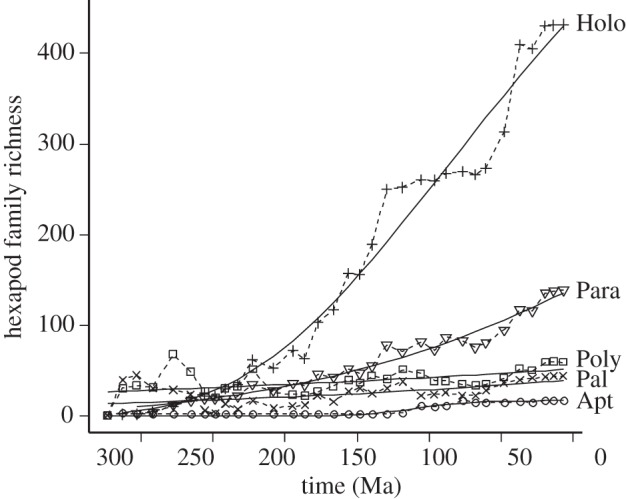
Accumulation of hexapod families through time in the major groups. The thick lines show the fitted values of different models. Apt (circles), Apterygota (logistic model); Pal (Xs), Palaeoptera (exponential model); Poly (squares), Polyneoptera (exponential model); Para (triangles), Paraneoptera (Gompertz model); Holo (+s), Holometabola (Gompertz model). Relative support for these models can be seen in table 1.

The first differences in log richness were most highly correlated between Paraneoptera and Holometabola (r = 0.848, n = 29, p < 0.001), and between Palaeoptera and Polyneoptera (r = 0.623, n = 29, p < 0.01), reflecting similar short-term richness trajectories in those pairs of taxa (figure 3). First differences in richness were negatively correlated with future (1 interval step) origination in Palaeoptera (r = −0.627, n = 28, p < 0.001), Polyneoptera (r = −0.540, n = 28, p < 0.05), Paraneoptera (r = −0.657, n = 28, p < 0.001) and Holometabola (r = −0.548, n = 28, p < 0.001). However, there was no significant relationship between the first differences in extinction rate and future origination rate except in Palaeoptera, where it was negative (r = −0.505, n = 28, p < 0.01). There were significant positive relationships between (first differences in) Holometabola richness and Polyneoptera extinction (r = 0.651, n = 29, p < 0.001) and Palaeoptera extinction (r = 0.556, n = 29, p < 0.05), while first differences in Holometabola richness are also negatively correlated with future richness in Polyneoptera (r = −0.549, n = 28, p < 0.05) and Palaeoptera (r = −0.569, n = 28, p < 0.01).

4. Discussion

Net rates of diversification vary across taxa [21] but are also highly heritable in the hexapods [34]. These facts, long casually observed, have suggested that key evolutionary changes have been responsible for generating much of the richness in this very diverse group, and four such evolutionary innovations have held centre stage [18,19]: the insect bauplan [35], wings [36], wing folding [21] and complete metamorphosis [23]. Here, we have reported evidence that both fossil family origination and extinction rates increased in groups that have wings but not the other key innovations, while insects with complete metamorphosis have lower extinction rates than their sister group without this innovation. There is evidence from the most derived groups that the rate at which described richness accumulates has slowed through their history, with taxonomic replacement evident between Palaeozoic and post-Palaeozoic faunas. These results suggest specific modes by which taxonomic richness has been generated by key innovations in the hexapods.

The contrast between the rates of origination and extinction in Palaeoptera and Apterygota, taken at face value, suggests that the origin of wings, in-of-itself, led to large macroevolutionary changes, a fact that has long been suspected [36], although the phylogenetic evidence for this is equivocal since the richness of Palaeopteran orders is not very much greater than that of some apterygote orders [21]. Previous authors have suggested that dispersal via wings could not only lower rates of extinction (e.g. [37]), for example via increased immigration rates within metapopulations, but also raise speciation rates via dispersal to isolated habitat patches [7]. Our data indicate that winged insects had both increased speciation and extinction rates. Many Palaeozoic Palaeoptera families did not survive into the Mesozoic (figure 2), suggesting that the Permo-Triassic (P–T) extinction is one reason for the high extinction rates in this group, although extinction rates also remained high after the P–T boundary (figure 2). Prima facie, this suggests that susceptibility to extinction has tempered the evolutionary potential of basal winged insects. It is debateable, on the strength of this evidence, whether wings should be regarded as a key innovation in of themselves, as the difference between the speciation and extinction rates is not significantly greater than Apterygota, and family richness, like species richness, is not particularly enhanced (figure 3).

The other potential key innovation highlighted by our results is complete metamorphosis. A decline in extinction in Holometabola was previously proposed by Ross et al. [38] who considered Holometabola less susceptible to mass extinction than other groups. However, another fossil analysis [23] suggested that origination rates have increased in Holometabola and suggested that extinction rates are unchanged. Our results suggest that the difference between the origination and extinction rate has widened in more derived groups, despite origination rates generally declining. There are a number of differences between our analyses and Yang's [23] including the underlying data, the rate metrics used and the analytical approaches. In all these characteristics, we consider our analysis to be an improvement: the data take account of more recent discoveries (including 400 more families); we use more robust rate metrics (estimated per capita rates ignoring single-interval taxa); we use statistical approaches that take account of repeated measures; we assess origination and extinction directly and in ways that account for the whole of the time series available (as opposed to Lyellian survival analysis which mainly reflects the latter part of the time series). How extinction rates might be lowered by metamorphosis has been little discussed: metamorphosis might allow greater buffering from environmental variability in the protected pupal stage [38], faster development, higher population sizes and reduced intraspecific competition between adult and offspring. All are plausible and testable contributors [5].

The richness time series of the different taxa appear prima facie consistent with the macroevolutionary changes described above. Over the majority of the time series, richness is highest in the derived Holometabola and lowest in the basal Apterygota (figure 2; electronic supplementary material, figure S4). Palaeozoic richness was dominated by Palaeoptera and Polyneoptera, which gave way to the more derived groups Paraneoptera and Holometabola (see also [39]), with lower extinction rates. This reflects a more general tendency in the fossil record for high turnover groups to dominate the earlier record [40]. The first differences in the time series confirm that these pairs of taxa (Palaeoptera and Polyneoptera; Paraneoptera and Holometabola) show very similar short-term trajectories. Only Holometabola and Apterygota show clear evidence of a slow-down in the rate of addition of taxa (figure 3 and table 1), although with Apterygota, it is difficult to say if this is simply owing to the paucity of data from the fossil record. Palaeoptera and Polyneoptera best fit exponential or linear models of diversification, implying that limits to family richness, if there are any, have not yet been met by these groups. By contrast, the Holometabola only show signs of possible limits to richness after attaining considerably higher richness than the less derived Palaeoptera and Polyneoptera, limits that are apparently not yet fully attained. The Paraneoptera show signs of a slow-down with a preferred Gompertz growth model, but the evidence for this is not much better than that for an exponential model (table 1). These patterns of richness through time provide equivocal support for the idea of new adaptive zones [17]: Holometabola have attained richnesses far above those ever achieved by the other taxa, but there is not strong evidence that the richness has been constrained by carrying capacity limits in Paraneoptera, Palaeoptera or Polyneoptera. The latter clades therefore conform to other terrestrial studies showing exponential clade growth (e.g. [41–44]), whereas the others conform to a pattern that may be more common in marine taxa (but see [45]). While increases in richness tend to be associated with decreases in future origination, which in the marine record has been interpreted as density-dependent cladogenesis [13], in insects it probably simply reflects the episodic nature of origination in the record [5], an interpretation supported by the lack of a predicted positive relationship between current extinction and future origination [13]. The associations between increases in Holometabola richness and current extinction and future reductions in richness in Polyneoptera and Palaeoptera may suggest that the latter faunas have been negatively affected by the rise of more derived faunas.

Our data provide no support for the idea that the basic or primitive insect bauplan is a key innovation, in common with previous phylogenetic tests [21,22]. Zeh et al. [35] made the case for modification to the egg and egg-laying apparatus in apterygote insects as a key innovation, though as with wings, the low diversity of basal groups with this innovation suggests that it is insufficient for generating high diversity, though perhaps necessary. There is also little support for wing folding, and in fact Polyneoptera show a marginally non-significant decline in origination rates relative to Palaeoptera (electronic supplementary material, table S2), as well as a quite similar richness. It is however likely that the diversity of Holometabola is in some way contingent [16] on this innovation given the richness of species, such as beetles, that depend on it.

Recently, analyses of fossil richness and rates have paid much attention to the effect of sampling bias through time as an explanation for patterns (e.g. [12,44–46]). As our analyses focus on variability across groups rather than through time, and because it is doubtful that even standardized subsampling of occurrence data could eliminate the taphonomic biases that probably accrue across time intervals in hexapods, this issue is less important than an alternative one; that sampling may be biased owing to uneven preservation potential of different taxa. However, Labandeira & Sepkoski [39] tested variation in preservation potential across orders by observing the correlation between the number of extant families per order and the number fossilized in the latest Tertiary. They found a very high correlation in which the only outlying order was Lepidoptera, suggesting little support for such bias at the scale of this analysis. Standardized estimates of richness through time would probably depress the apparent growth of clades near the present [46], but are unlikely to affect the rank order of richness across the major taxa considered here.

Our analyses suggest a new model of insect macroevolution; that of a major up-shift in both family-level origination rates and extinction rates (but not net diversification rate) with the origin of wings, giving rise to a group of families vulnerable to extinction. This was followed by a decline in extinction rates in Holometabola, allowing richness to rise towards an apparent limit that has never been attained by the other groups. In this latter respect, Holometabola conform to the classical notion of an adaptive radiation [17]. The mechanism of change, through a reduction in subclade extinction rate [17], has also been suggested as an explanation for the radiation of the angiosperms [47]. By contrast, there is little evidence from the fossil record that wing folding or the insect bauplan were sufficient to alter insect family macroevolution, although they may have been necessary. The different extinction propensities of taxa shown here may also imply differing resistance to anthropogenic extinction, and hence contribute to debate on the vulnerability of extant insects to environmental change [7]. In the future, better-resolved phylogenetic studies may allow additional tests of the importance of metamorphosis and there is a need to elucidate the ecological or life-history determinants of the proximate macroevolutionary forces suggested above.

Data accessibility

Data presented in this paper are available as an electronic supplementary material.

Funding statement

D.B.N. was supported by a NERC studentship, National Museums Scotland and The Natural History Museum, London.