Abstract
Background
Validated risk equations are currently recommended to assess individuals to determine those at ‘high risk’ of cardiovascular disease (CVD). However, there is no longer a risk ‘equation of choice’.
Aim
This study examined the differences between four commonly-used CVD risk equations.
Design and setting
Cross-sectional analysis of individuals who participated in a workplace-based risk assessment in Carmarthenshire, south Wales.
Method
Analysis of 790 individuals (474 females, 316 males) with no prior diagnosis of CVD or diabetes. Ten-year CVD risk was predicted by entering the relevant variables into the QRISK2, Framingham Lipids, Framingham BMI, and JBS2 risk equations.
Results
The Framingham BMI and JBS2 risk equations predicted a higher absolute risk than the QRISK2 and Framingham Lipids equations, and CVD risk increased concomitantly with age irrespective of which risk equation was adopted. Only a small proportion of females (0–2.1%) were predicted to be at high risk of developing CVD using any of the risk algorithms. The proportion of males predicted at high risk ranged from 5.4% (QRISK2) to 20.3% (JBS2). After age stratification, few differences between isolated risk factors were observed in males, although a greater proportion of males aged ≥50 years were predicted to be at ‘high risk’ independent of risk equation used.
Conclusions
Different risk equations can influence the predicted 10-year CVD risk of individuals. More males were predicted at ‘high risk’ using the JBS2 or Framingham BMI equations. Consideration should also be given to the number of isolated risk factors, especially in younger adults when evaluating CVD risk.
Keywords: cardiovascular diseases, decision support techniques, prevention and control, primary care, risk
INTRODUCTION
Cardiovascular disease (CVD) remains the leading cause of mortality in the UK, with the latest statistics documenting that almost one-third of all deaths are currently attributed to the condition.1 Current UK government guidelines implemented through the National Institute for Health and Care Excellence (NICE) advocate risk assessment of individuals aged 40–74 years to identify those at ‘high risk’ (≥20% 10-year risk of developing CVD).2 Early identification of individuals at elevated risk is essential so that lifestyle modification or pharmacological interventions can be prescribed to alleviate the risk of disease.3 It is recommended that validated equations should be used to assess CVD risk and up until February 2010, the Framingham Risk Equation4 was the ‘equation of choice’ before this endorsement was withdrawn.2 The amended NICE guidelines now encourage healthcare professionals to use the cardiovascular risk equation that they feel most appropriate.2,5
Previous research has highlighted differences in false-positive rates (at a 20% threshold) between six widely cited CVD risk algorithms,6 despite these differences the screening performance of the six was similar. It was concluded that age remains the most dominant predictor in CVD events despite individual risk factors being present.6 This observation is somewhat surprising, especially as 80% of all premature coronary heart disease in males can be attributed to the combination of smoking, hypertension, and high levels of total cholesterol (>5.2 mmol/l).7 In further terms of CVD risk factors, there is evidence that a multifactorial strategy treating glycaemic control, lipid profiles, and blood pressure together through either medication or behavioural therapy has been shown to be highly effective in reducing cardiovascular mortality compared with conventional treatment.8
Statin therapy is recommended as part of the management strategy for primary prevention of CVD for adults at high risk of developing CVD.2,9 Treatment should be initiated with simvastatin (40 mg) in those adults who have a ≥20% 10-year risk of developing CVD.2 Therefore, any differences between predicted risk equations could have a number of implications for the correct treatment of individuals (such as either over- or underprescribing statins as a primary treatment) and the associated costs of medications.
How this fits in
Up until February 2010 the ‘equation of choice’ of NICE to determine cardiovascular disease (CVD) risk was the Framingham Risk Equation, with the guidance now encouraging healthcare professionals to adopt the equation that they deem ‘most appropriate’. This research compares four commonly-used CVD risk equations in the UK and examines the number of individuals predicted at ‘high risk’. The JBS2 and Framingham BMI equations predicted a higher proportion of individuals at ‘high risk’ of CVD than the Framingham Lipids or QRISK2 algorithms. Furthermore, despite changes in absolute risk prediction after age stratification in all of the equations, there are few differences between isolated risk factors.
This study primarily compared four commonly-used CVD risk equations when the same individual dataset was applied, and examined if isolated risk factors translated to ‘high risk’ of CVD.
METHOD
Study population
All participants in this study were employees of either the local health board or steel workers within the Welsh region of Carmarthenshire who had received a CVD risk assessment as part of the established Prosiect Sir Gâr workplace-based initiative.10 The initiative was introduced in 2009 and data collection for this study took place between 2009 and 2012. All current employees aged >40 years (if white), or >25 years (if South Asian) with no prior diagnosis of CVD or diabetes were invited to participate in the project. In total, 790 employees accepted the invitation of a health assessment, of which 474 were females and 316 males.
Baseline measurements and risk prediction equations
According to a standard operational policy (SOP), all recruited individuals attended a standardised health assessment appointment with an occupational health nurse which lasted 30–40 minutes. During the session, demographic (date of birth, sex, and postcode of residence) and anthropometric (body mass and height) data were collected. Systolic and diastolic blood pressure, pulse rate and rhythm, smoking status, and family and medical histories were also recorded. Blood samples were also collected via capillary puncture and analysed immediately for total cholesterol (TC), high-density-lipoprotein cholesterol (HDL) and triglycerides (Cholestech LDX® System, Alere Inc., Orlando, FL). Ten-year predicted CVD risk was calculated by entering the relevant variables into the QRISK2,11 Framingham Lipids,12 Framingham BMI,12 and the Joint British Societies 2 (JBS213) risk equations.
Data analysis
The focus of analysis within this study was to compare four validated and routinely used CVD risk equations. Within the analysis, samples were stratified by age. Statistical analysis was performed using SPSS software (version 19) with significance set at P<0.05. Normality of data was assessed by a one-sample Kolmogorov-Smirnov test. Homogeneity of variance was determined by Levene’s statistic and one-way analysis of variance (ANOVA) with post-hoc Bonferroni or Tamhane’s T2 correction factor used to locate any differences within groups. χ2 analysis with α set at 0.05 was performed to analyse discrete data variables. Diastolic blood pressure data are represented as mean ± standard deviation. Body mass index (BMI), systolic blood pressure, triglyceride concentrations, QRISK2, Framingham Lipids, and Framingham BMI scores did not have a normal distribution. These datasets were consequently log transformed for analysis and represented as the geometric mean and approximate standard deviation. Age, TC:HDL ratio, and JBS2 scores did not have a normal distribution after log transformation and these data are represented as median and interquartile range. Kruskal–Wallis and Mann-Whitney tests were used to analyse JBS2 data.
RESULTS
All age baseline analysis
Table 1 shows the baseline risk characteristics and predicted all age 10-year CVD risk of the two sex cohorts. Although no statistical comparisons were made between the sexes, the table clearly illustrates a number of interesting observations. Despite the two cohorts being of similar age, BMI values, systolic and diastolic blood pressure readings, lipid profiles (TC:HDL ratio), triglyceride concentrations, and 10-year predicted CVD risk in each of the equations are all greater in the male cohort compared with the females. There was also a greater proportion of male individuals who reported being current smokers and who were presently prescribed antihypertensive medication. Furthermore, in each of the sex cohorts the all-age predicted CVD risk value was different dependent on which risk equation was adopted.
Table 1.
Baseline risk characteristics of female and male cohorts
| Risk variable | Females (n = 474) | Males (n = 316) |
|---|---|---|
| Age, years a | 49 (44–54) | 49 (44–53) |
| BMI, kg/m2b | 26.6 ± 1.9 | 28.1 ± 1.7 |
| Systolic blood pressure, mmHg b | 125 ± 6 | 128 ± 5 |
| Diastolic blood pressure, mmHg | 82 ± 9 | 84 ± 9 |
| Total cholesterol: HDL ratio a | 3.2 (2.7–4.0) | 4.4 (3.6–5.7) |
| Triglycerides, mmol/l b,c | 1.24 ± 0.27 | 1.87 ± 0.47 |
| Family history of cardiovascular disease | 98 (20.7) | 66 (20.9) |
| Current smoker | 46 (9.7) | 52 (16.5) |
| Prescribed antihypertensive medication | 24 (5.1) | 26 (8.2) |
| QRISK2, % b | 2.3 ± 0.9 | 5.8 ± 1.9 |
| Framingham Lipids, % b | 2.6 ± 0.7 | 8.2 ± 2.1 |
| Framingham BMI, % b | 4.8 ± 1.2 | 10.7 ± 2.4 |
| JBS2, % a | 5 (2–8) | 11 (7–17) |
Data expressed as means ± SD with discrete data represented as numbers with percentage of sex in brackets.
Data not normally distributed after log transformation, median and interquartile range reported.
Log transformed data, geometric mean and approximate standard deviation reported.
Triglyceride data only available for some individuals (females n = 437, males n = 251). BMI = body mass index. HDL = high-density lipoprotein. JBS2 = Joint British Societies 2.
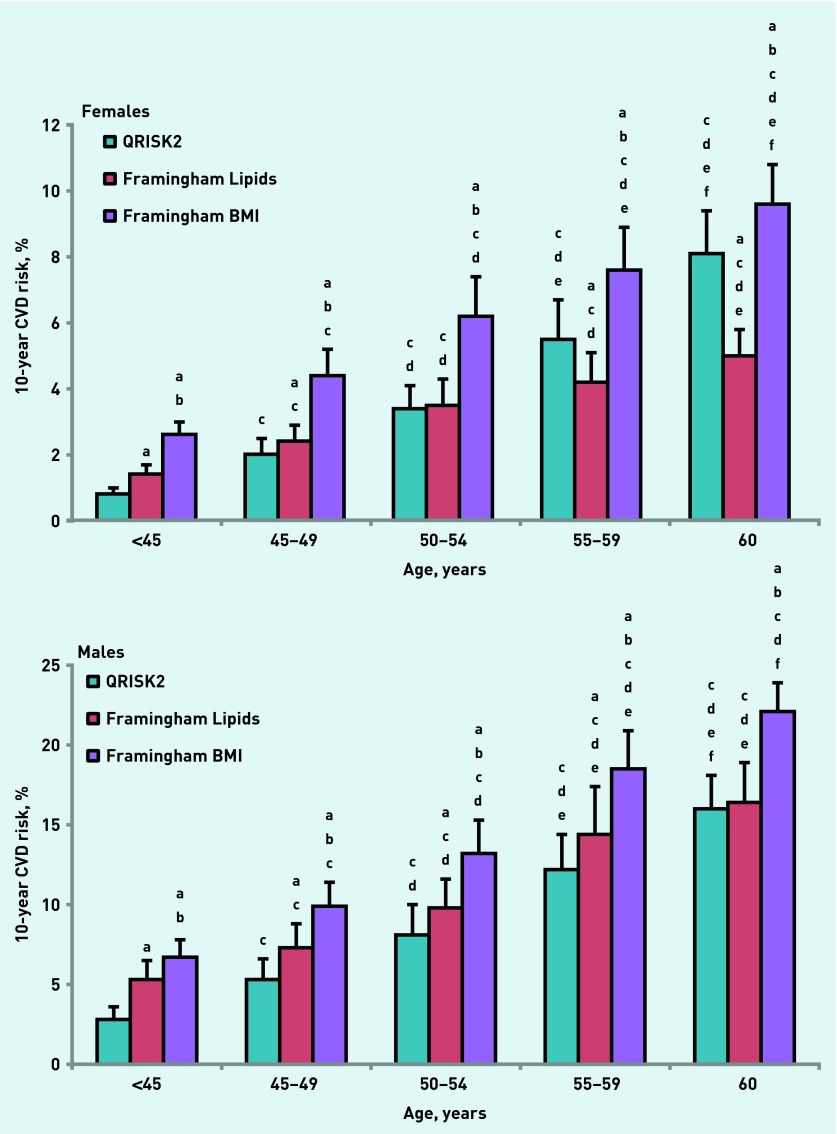
Ten-year CVD risk prediction after age stratification
Table 2 and Figure 1 illustrate the 10-year predicted CVD risk for QRISK2, Framingham Lipids, Framingham BMI (Figure 1), and JBS2 (Table 3) after age stratification of the data into five predetermined age ranges (<45 years, 45–49 years, 50–54 years, 55–59 years, and ≥60 years). Figure 1 demonstrates that predicted 10-year CVD risk increased concomitantly with age in each of the risk equations for both sexes. Female predicted risk increased from 0.8±0.2% to 8.1±1.3% (QRISK2), 1.4±0.3% to 5.0±0.8% (Framingham Lipids), and 2.6±0.4% to 9.6±1.2% (Framingham BMI). In the male cohort, CVD risk estimation increased from 2.8±0.8% to 16.0±2.1% (QRISK2), from 5.3±1.2% to 16.4±2.5% (Framingham Lipids), and from 6.7±1.1% to 22.1±1.8% (Framingham BMI). In addition, at each age range, the Framingham BMI risk equation predicted individuals to be at a higher risk than either the QRISK2 or Framingham Lipids algorithms. In the male cohort the Framingham Lipid equation also predicted individuals at a higher risk than QRISK2 up until 60 years old. Of interest, in the female cohort, in the two youngest age ranges (<45 years and 45–49 years), Framingham Lipids estimated risk to be higher than QRISK2; however, in the latter two age ranges (55–59 years and ≥60 years) this relationship was reversed. In Table 3, the JBS2 median and interquartile ranges are displayed. The female predicted risk again increased concomitantly with age from 2% (1–3%) to 8.5% (7–14%) and the male cohort predicted risk increased from 7% (4–11%) to the peak value of 20% (12–25%) in the 55–59 years age range.
Table 2.
Proportion of individuals categorised by risk category (low [<10%], intermediate [10–19.9%], or high [≥20%]) after prediction by different CVD risk equations
| QRISK2 | Framingham Lipids | Framingham BMI | JBS2 | ||
|---|---|---|---|---|---|
| Females (n = 474) | Low risk, n (%) | 455 (96.0) | 463 (97.7) | 423 (89.2) a,b | 390 (82.3) a,b,c |
| Intermediate risk, n (%) | 17 (3.6) | 11 (2.3) | 48 (10.2) a,b | 74 (15.6) a,b,c | |
| High risk, n (%) | 2 (0.4) | 0 (0.0) | 3 (0.6) | 10 (2.1) a,b | |
|
| |||||
| Males (n = 316) | Low risk, n (%) | 226 (71.5) | 201 (63.6) a | 147 (46.5) a,b | 23 (38.9) a,b |
| Intermediate risk, n (%) | 73 (23.1) | 89 (28.2) | 126 (39.9) a,b | 129 (40.8) a,b | |
| High risk, n (%) | 17 (5.4) | 26 (8.2) | 43 (13.6) a,b | 64 (20.3) a,b,c | |
Data represented as numbers with percentage of sex in brackets.
Denotes difference from QRISK2 (P<0.05).
Denotes difference from Framingham Lipids (P<0.05).
Denotes difference from Framingham BMI (P<0.05). BMI = body mass index. JBS2 = Joint British Societies 2.
Figure 1.
Changes in predicted 10-year CVD risk after age stratification after adoption of QRISK2, Framingham Lipids, and Framingham BMI risk equations. The graphs illustrate female and male cohorts. adenotes difference from QRISK2 (P<0.05). b denotes difference from Framingham Lipids (P<0.05). c denotes difference from <45-year age group (P<0.05). d denotes difference from 45–49-year age group (P<0.05). e denotes difference from 50–54-year age group (P<0.05). f denotes difference from 55–59-year age group (P<0.05).
Table 3.
Changes in risk score predicted by JBS2 equation after age stratification
|
Age group, years
|
|||||
|---|---|---|---|---|---|
| <45 | 45–49 | 50–54 | 55–59 | ≥60 | |
| Females (n = 474) | 2 (1–3) | 4 (3–6) a | 7 (4–9) a,b | 8 (5–12) a,b,c | 8.5 (7–14)a,b,c |
| Males (n = 316) | 7 (4–11) | 10 (7–14) a | 14.5 (10–19) a,b | 20 (12–25) a,b,c | 19 (14–24) a,b,c |
Data represented as median and interquartile range.
Denotes difference from < 45 years (P<0.05).
Denotes difference from 45–49 years (P<0.05).
Denotes difference from 50–54 years (P<0.05). JBS2 = Joint British Societies 2.
Individuals predicted at different risk classifications
Table 2 illustrates individuals categorised by low, intermediate, or high 10-year CVD risk after adoption of the four different equations. The number of women predicted at high risk was relatively low irrespective of which risk equation was adopted. The JBS2 equation predicted the greatest number of females at high risk (10 individuals), but this still only equated to 2.1% of the female cohort. Of note, no females were predicted to be at high risk when the Framingham Lipids risk score was used. However, the Framingham BMI and JBS2 tools resulted in a greater number of females at intermediate risk and fewer at low risk than either QRISK2 or Framingham Lipids. The JBS2 equation also predicted more females at intermediate risk and fewer at low risk than the Framingham BMI. Within the male cohort, the same relationship was observed, with the Framingham BMI and JBS2 equations predicting more males at intermediate and fewer at lower risk than the two other equations. The QRISK2 algorithm predicted the greatest number of males at low risk and this proportion was significantly lower than the three other algorithms. Unlike the female cohort, the differences between numbers of male individuals predicted at high risk are clearly apparent. The male JBS2 discrepancies in high risk prediction are most prominent, with 1 in 5 males categorised at high risk compared with 1 in 20, 1 in 12, and 1 in 8 using QRISK2, Framingham Lipids, and Framingham BMI, respectively.
Analysis of isolated risk factors and ‘high risk’ individuals after age stratification
Table 4 details the examination of isolated risk factors and amount of individuals predicted to be at ‘high risk’ of 10-year CVD after age stratification, which further uncovered a number of interesting observations. In the female cohort, there was a greater prevalence of females with high concentrations of total cholesterol from age ≥50 years; however, this was not reflected in a larger proportion of females observed to have dyslipidaemia. In all age groups except those aged <45 years, over one in five females were found to have systolic hypertension; however, only the JBS2 risk equation predicted any differences between ‘high risk’ females in the latter two age groups (55–59 years and ≥60 years). In the male cohort, the only differences between isolated risk factors were observed in a greater prevalence of systolic hypertension after age 55 years, and in high total cholesterol concentrations in the 55–59 years compared with the 50–54 years group. Despite very few differences between isolated risk factors, a higher proportion of males were predicted to be at ‘high risk’ of CVD in older age groups (50–54 years, 55–59 years, ≥60 years) in each of the four risk equations, except those aged 50–54 years for Framingham Lipids.
Table 4.
The prevalence of isolated risk factors and proportion of individuals categorised as ‘high risk’ after age stratification
| Females (n = 474) | <45 years n = 126 | 45–49 years n = 132 | 50–54 years n = 110 | 55–59 years n = 72 | ≥ 60 years n = 34 |
|
| |||||
| Body mass index ≥30 kg/m2 | 27 (21.4) | 38 (28.8) | 33 (30.0) | 11 (15.3) b,c | 7 (20.6) |
| Body mass index 25–29.9 kg/m2 | 44 (34.9) | 45 (34.1) | 43 (39.1) | 29 (40.3) | 14 (41.2) |
| Total cholesterol ≥5.20 mmol/l | 22 (17.5) | 35 (26.5) | 44 (40.0) a,b | 33 (45.8) a,b | 16 (47.1) a,b |
| TC:HDL ratio ≥6 | 0 (0.0) | 4 (3.0) a | 4 (3.6) a | 3 (4.2) a | 1 (2.9) |
| Systolic blood pressure ≥140 mmHg | 7 (5.6) | 29 (22.0) a | 29 (26.4) a | 18 (25.0) a | 8 (23.5) a |
| Diastolic blood pressure ≥90 mmHg | 18 (14.3) | 28 (21.2) | 23 (20.9) | 10 (13.9) | 6 (17.6) |
| Current smoker | 12 (9.5) | 14 (10.6) | 12 (10.9) | 5 (6.9) | 3 (8.8) |
| QRISK2 ≥20% | 0 (0.0) | 0 (0.0) | 0 (0.0) | 2 (2.8) | 0 (0.0) |
| Framingham Lipids ≥20% | 0 (0.0) | 0 (0.0) | 0 (0.0) | 0 (0.0) | 0 (0.0) |
| Framingham BMI ≥20% | 0 (0.0) | 1 (0.8) | 0 (0.0) | 2 (2.8) | 0 (0.0) |
| JBS2 ≥20% | 0 (0.0) | 1 (0.8) | 2 (1.8) | 4 (5.6) a,b | 3 (8.8) a,b |
|
| |||||
| Males (n = 316) | <45 years n = 89 | 45–49 years n = 98 | 50–54 years n = 68 | 55–59 years n = 42 | ≥ 60 years n = 19 |
|
| |||||
| Body mass index ≥30 kg/m2 | 27 (30.3) | 32 (32.7) | 21 (30.9) | 15 (35.7) | 8 (42.1) |
| Body mass index 25–29.9 kg/m2 | 41 (46.1) | 50 (51.0) | 36 (52.9) | 19 (45.2) | 8 (42.1) |
| Total cholesterol ≥5.20 mmol/l | 33 (37.1) | 40 (40.8) | 21 (30.9) | 23 (54.8)c | 7 (36.8) |
| TC:HDL ratio ≥6 | 22 (24.7) | 17 (17.3) | 14 (20.6) | 13 (31.0) | 3 (15.8) |
| Systolic blood pressure ≥140 mmHg | 11 (12.4) | 20 (20.4) | 11 (16.2) | 16 (38.1) a,b,c | 9 (47.4) a,b,c |
| Diastolic blood pressure ≥90 mmHg | 25 (28.1) | 33 (33.7) | 22 (32.4) | 13 (31.0) | 5 (26.3) |
| Current smoker | 20 (22.5) | 15 (15.3) | 8 (11.8) | 7 (16.7) | 2 (10.5) |
| QRISK2 ≥20% | 0 (0.0) | 2 (2.0) | 6 (8.8) a,b | 5 (11.9) a,b | 4 (21.1) a,b |
| Framingham Lipids ≥20% | 1 (1.1) | 4 (4.1) | 4 (5.9) | 12 (28.6) a,b,c | 5 (26.3) a,b,c |
| Framingham BMI ≥20% | 0 (0.0) | 6 (6.1) a | 10 (14.7) a | 14 (33.3) a,b,c | 13 (68.4) a,b,c,d |
| JBS2 ≥20% | 8 (9.0) | 10 (10.2) | 16 (23.5) a,b | 21 (50.0) a,b,c | 9 (47.4) a,b,c |
Data are represented as numbers and proportion of age group in brackets.
Denotes difference from <45-year age group (P<0.05).
Denotes difference from 45–49-year age group (P<0.05).
Denotes difference from 50–54-year age group (P<0.05).
Denotes difference from 55–59-year age group (P<0.05).
DISCUSSION
Summary
This study compared CVD risk prediction when the same dataset was applied to four commonly-used risk equations. The main finding from this investigation is that adoption of the JBS2 or Framingham BMI equations predicts more individuals at absolute risk and ‘high risk’ than either QRISK2 or Framingham Lipids. This observation was more evident in male prediction using either the Framingham BMI or JBS2 risk equations, where 13.6% and 20.3% of males, respectively, were predicted to be at high risk of CVD compared with only 8.2% (Framingham BMI) and 5.4% (QRISK2). Up to a four-times greater cost would be associated with statin prescription, therefore, if the Framingham BMI or JBS2 risk equations were used instead of QRISK2. In addition, more males were predicted to be at ‘high risk’ of CVD in the older age groups despite very few differences between the prevalence of isolated risk factors. It appears that age remains more important than isolated risk factors when determining those individuals at ‘high risk’, irrespective of which risk equation is adopted.
Strengths and limitations
One of the strengths of this research is that the study population is based on an undiagnosed cohort, representative of the working demographic in Carmarthenshire, south Wales. If not for the Prosiect Sir Gâr initiative, these data would not be routinely available. All of the risk engines in this study accounted for sex, age, and systolic blood pressure, with all but the Framingham BMI equation incorporating the TC:HDL ratio. It was feasible, therefore, to make comparisons between the four prediction tools. The Framingham BMI equation requires the fewest clinical measurements of the four equations compared with only systolic blood pressure incorporated into the prediction algorithm. Another merit to the Framingham BMI is that a number of CVD risk factors, such as elevated non-HDL cholesterol, reduced HDL cholesterol, and hypertension, are influenced by obesity,14 and, furthermore, obesity is an independent risk factor for fatal coronary events.15 It is acknowledged that there are other risk equations available that may have been pertinent to this dataset. For example, the Scottish ASSIGN16 prediction model or the SCORE17 equation based on a European population could have been relevant to the study population. One of the advantages of the ASSIGN model is the inclusion of social deprivation; however, this deprivation is based on Scottish postcodes and would not be applicable to the present Welsh dataset, which is why the QRISK2 model was chosen instead which also incorporates social deprivation. The risk equations chosen for comparison in this study also account for non-fatal CVD unlike the SCORE equation, which is why this risk equation was not chosen for analysis. The only other limitation to this research could be that the cohort used may possibly be perceived as small; however, even in this cohort, differences were uncovered when making comparisons between the CVD risk algorithms.
Comparison with existing literature
Validation studies predicting absolute risk have reported that the NICE version of the Framingham Equation can overestimate risk by up to 5% in males, and shows poor calibration with females in comparison with QRISK2.18 It is unsurprising, therefore, that differences were also observed between numbers of individuals in different risk categories. In terms of absolute risk, however, only a 2.5% higher estimation was observed when comparing Framingham Lipids and QRISK2 in males. Comparisons between males using QRISK2 and Framingham BMI resulted in a 5% higher prediction in the latter risk equation, which may suggest some reliance on lipid profiles in more accurate CVD risk estimation, although the average male JBS2 median value is also 5% greater than the QRISK2 score and the Framingham BMI and JBS2 female average risk estimates are double that of QRISK2. An interesting observation is that, in relative terms, the older risk engines predicted risk to be higher than the more recent or updated equations. Healthcare professionals should account for this when determining which equation they deem ‘most appropriate’. Despite these observations, however, research has reported that six cardiovascular risk algorithms performed equally well in terms of screening performance even when differences were witnessed in false-positive rates between the equations.6 Three of these risk equations (QRISK2, Framingham General Cardiovascular Risk Profile [Framingham Lipids and Framingham BMI]) analysed in that research were adopted in this study, further justifying their selection. It appears that all the risk equations adopted in the present study have their own individual merits for selection; however, the reported better accuracy of absolute risk in the QRISK2 model after independent validation18 may enhance this risk equation for prioritisation in this Welsh population.
Implications for research and practice
From the observations in this study and the strong evidence of better accuracy, the QRISK2 model should be recommended for use in primary care in the Welsh population in terms of primary prevention of CVD. The added benefit to the QRISK2 model is that it is updated annually with the latest available routinely collected data from England and Wales. The variations in estimation of absolute risk could lead to ‘overtreatment’, where individuals are treated when their risk is substantially lower and vice versa. In both these scenarios there is a financial implication, be it by an increase in emergency admissions for individuals who believed they were at ‘low’ or ‘intermediate’ risk, or through statin treatments that are not required. One of the disadvantages of CVD risk prediction models is that the most heavily weighted variable in their algorithms is age,6,19 which explains how an increase in predicted CVD risk concomitant with age was observed with all the risk algorithms despite very small differences between the prevalence of isolated risk factors.
The shortcoming to this approach is that younger individuals (males <50 years, females <65 years) with a number of risk factors for developing CVD may not reach the thresholds required to be prescribed medication to reduce their risk.20 This is an important consideration in males as premature coronary heart disease is primarily caused by the combination of systolic hypertension, high concentrations of total cholesterol, and smoking.7 The other limitation to the heavy weighting for age is that older individuals with a single risk factor for CVD would score above the thresholds and be recommended for pharmacological intervention. It could be argued that management of isolated risk factors, rather than treatment initiated at an absolute predicted risk value, is more important. It will be interesting in time to observe whether the emergence of ‘lifetime’ risk models such as the QIntervention and the in-development JBS3 risk equations will improve CVD prediction and primary treatment. Unlike some type 2 diabetes prediction models that include other lifestyle factors, such as physical activity 21,22 and/or dietary habits,21 CVD equations only account for smoking. If included in CVD risk prediction, such factors would provide the opportunity for more relevant advice to be provided to individuals for lifestyle changes that could reduce CVD risk.
Acknowledgments
The Prosiect Sir Gâr Group is: Kerry Morgan, Chris Cottrell, Vanessa Davies, Liz Newbury-Davies, Michael Thomas, Enzo M Di Battista, Lesley Street, Fiona Judd, Cindy Evans, Jo James, Claire Jones, Carolyn Williams, Susan Smith, James Thornton, Sally P Williams, Rhys Williams, Sam Rice, Jeffrey W Stephens, and Meurig Williams.
Funding
This work was part-funded by the European Social Fund (ESF) through the European Union’s Convergence programme administered by the Welsh Government. Prosiect Sir Gâr received funding contributions from TATA, Hywel Dda Health Board (Diabetes Charitable Fund and Carmarthenshire Charitable Fund), Carmarthenshire County Council, and the following pharmaceutical companies; Takada, Lilly, Sanofi-Aventus, Boehringer-Ingelheim, Pfizer, and AstraZeneca.
Ethical approval
This study was approved by Dyfed Powys local research ethics committee (reference number: 11/WA/0101).
Provenance
Freely submitted; externally peer reviewed.
Competing interests
The authors have declared no competing interests.
Discuss this article
Contribute and read comments about this article: bjgp.org.uk/letters
REFERENCES
- 1.Scarborough P, Bhatnagar P, Wickramasinghe K, et al. Coronary Heart Disease Statistics 2010 edition. 2010 http://www.bhf.org.uk/publications/view-publication.aspx?ps=1001546 (accessed 7 Aug 2014) [Google Scholar]
- 2.National Institute for Health and Care Excellence Lipid modification, Cardiovascular risk assessment and the modification of blood lipids for the primary and secondary prevention of cardiovascular disease. 2008. NICE guidelines [CG67], http://www.nice.org.uk/guidance/cg67/chapter/guidance (accessed 12 Sep 2014) [PubMed]
- 3.Stephens JW, Ambler G, Vallance P, et al. Cardiovascular risk and diabetes. Are the methods of risk prediction satisfactory? Eur J Cardiovasc Prev Rehabil. 2004;11:521–528. doi: 10.1097/01.hjr.0000136418.47640.bc. [DOI] [PubMed] [Google Scholar]
- 4.Anderson KM, Odell PM, Wilson PW, et al. Cardiovascular disease risk profiles. Am Heart J. 1991;121:293–298. doi: 10.1016/0002-8703(91)90861-b. [DOI] [PubMed] [Google Scholar]
- 5.Mayor S. Doctors can decide which tool to use to assess heart risk. BMJ. 2010;340:c1774. [Google Scholar]
- 6.Simmonds MC, Wald NJ. Risk estimation versus screening performance: a comparison of six risk algorithms for cardiovascular disease. J Med Screen. 2012;19:201–205. doi: 10.1258/jms.2012.012076. [DOI] [PubMed] [Google Scholar]
- 7.Emberson JR, Whincup PH, Morris RW, et al. Re-assessing the contribution of serum total cholesterol, blood pressure and cigarette smoking to the aetiology of coronary heart disease: impact of regression dilution bias. Eur Heart J. 2003;24:1719–1726. doi: 10.1016/s0195-668x(03)00471-8. [DOI] [PubMed] [Google Scholar]
- 8.Gæde P, Lund-Andersen H, Parving H-H, et al. Effect of a multifactorial intervention on mortality in type 2 diabetes. N Engl J Med. 2008;358:580–591. doi: 10.1056/NEJMoa0706245. [DOI] [PubMed] [Google Scholar]
- 9.National Institute for Health and Care Excellence Statins for the prevention of cardiovascular events. 2006. NICE technology appraisals [TA94], http://www.nice.org.uk/nicemedia/live/11564/33151/33151.pdf (accessed 12 Sep 2014)
- 10.Gray BJ, Bracken RM, Thomas M, et al. ‘Prosiect Sir Gâr’: Workplace-based cardiovascular disease and diabetes risk assessments. Occup Med (Lond) 2014 doi: 10.1093/occmed/kqu103. in press. [DOI] [PubMed] [Google Scholar]
- 11.Hippisley-Cox J, Coupland C, Vinogradova Y, et al. Predicting cardiovascular risk in England and Wales: prospective derivation and validation of QRISK2. BMJ. 2008;336:1475–1482. doi: 10.1136/bmj.39609.449676.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.D’Agostino RB, Vasan RS, Pencina MJ, et al. General cardiovascular risk profile for use in primary care: the Framingham Heart Study. Circulation. 2008;117:743–753. doi: 10.1161/CIRCULATIONAHA.107.699579. [DOI] [PubMed] [Google Scholar]
- 13.Wood D, Wray R, Poulter N, et al. JBS 2: Joint British Societies’ guidelines on prevention of cardiovascular disease in clinical practice. Heart. 2005;91(Suppl V):v1–v52. doi: 10.1136/hrt.2005.079988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Whitlock G, Lewington S, Sherliker P, et al. Body-mass index and cause-specific mortality in 900 000 adults: collaborative analyses of 57 prospective studies. Lancet. 2009;373:1083–1096. doi: 10.1016/S0140-6736(09)60318-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Logue J, Murray HM, Welsh P, et al. Obesity is associated with fatal coronary heart disease independently of traditional risk factors and deprivation. Heart. 2011;97:564–568. doi: 10.1136/hrt.2010.211201. [DOI] [PubMed] [Google Scholar]
- 16.Woodward M, Brindle P, Tunstall-Pedoe H. Adding social deprivation and family history to cardiovascular risk assessment: the ASSIGN score from the Scottish Heart Health Extended Cohort (SHHEC) Heart. 2007;93:172–176. doi: 10.1136/hrt.2006.108167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Conroy RM, Pyörälä K, Fitzgerald AP, et al. Estimation of ten-year risk of fatal cardiovascular disease in Europe: the SCORE project. Eur Heart J. 2003;24:987–1003. doi: 10.1016/s0195-668x(03)00114-3. [DOI] [PubMed] [Google Scholar]
- 18.Collins GS, Altman DG. Predicting the 10 year risk of cardiovascular disease in the United Kingdom: independent and external validation of an updated version of QRISK2. BMJ. 2012;344:e4181. doi: 10.1136/bmj.e4181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Abd TT, Blaha MJ, Blumenthal RS, Joshi PH. Cardiovascular disease risk prediction — integration into clinical practice. Curr Cardiovasc Risk Rep. 2013;7:346–353. [Google Scholar]
- 20.Cavanaugh-Hussey MW, Berry JD, Lloyd-Jones DM. Who exceeds ATP-III risk thresholds? Systematic examination of the effect of varying age and risk factor levels in the ATP-III risk assessment tool. Prev Med. 2008;47:619–623. doi: 10.1016/j.ypmed.2008.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bang H, Edwards AM, Bomback AS, et al. Development and validation of a patient self-assessment score for diabetes risk. Ann Intern Med. 2009;151:775–783. doi: 10.1059/0003-4819-151-11-200912010-00005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lindström J, Tuomilehto J. The Diabetes Risk Score: A practical tool to predict type 2 diabetes risk. Diabetes Care. 2003;26:725–731. doi: 10.2337/diacare.26.3.725. [DOI] [PubMed] [Google Scholar]