A Phenomenological One-Parameter Equation of State for Osmotic Pressures of PEG and Other Neutral Flexible Polymers in Good Solvents

Abstract

We present a phenomenological one-parameter scaling equation of state that accurately represents osmotic pressures of neutral flexible polymers in good solvents from the dilute through the semidilute regime. The equation comprises a sum of scaled van’t Hoff and des Cloizeaux terms including a fitted parameter α, the “crossover index”, which encapsulates all chemical specificity and determines the relevant prefactors. Strikingly different values of α are found for the two very different systems poly(ethyleneglycol)/water (PEG) and poly(α-methylstyrene)/toluene (PAMS). α-dependent rescaling collapses both data sets to a simple one-parameter scaling function. The fact that the anomalous system PEG/water and the canonical system PAMS/toluene can both be described by the same equation of state attests to the robustness of the polymer-scaling concepts introduced by de Gennes.

Introduction

Osmotic pressure was one of the first applications of scaling analysis¹ to the description of polymer properties in solution. P.-G. de Gennes,² by use of scaling arguments, was able to simplify des Cloizeaux’s derivation of the osmotic pressure of semidilute solutions.³ The analysis was based on a momentous discovery made by de Gennes a few years earlier⁴ concerning an analogy between long polymers and magnetic systems close to a second-order phase transition. He assumed that the ideal van’t Hoff osmotic pressure and the des Cloizeaux scaling form of the osmotic pressure, which he presumed to have a power-law dependence on concentration, were the same order of magnitude at the crossover between the dilute and semidilute regimes. This ansatz led immediately to the now-famous “9/4 law” for the semidilute osmotic pressure. de Gennes found this expression consistent with available data on osmotic pressure of polystyrene in carbon disulfide. His detailed proof of the scaling hypothesis, however, relied on a comprehensive theoretical analysis of the polymer concentration dependence of the correlation length, which had been measured experimentally by neutron scattering.²

Here we show that the osmotic pressure of aqueous solutions of poly(ethyleneglycol) (PEG, also known as poly(ethyleneoxide), PEO), a polymer of biological interest⁵ with often-noted anomalous physical properties,^6,7 surprisingly conforms to a scaling equation of state. We propose a simple form for this equation based on additive contributions from the ideal van’t Hoff and des Cloizeaux limiting behaviors. By this method, we show that the PEG data collapse precisely onto the scaling equations of state of other neutral polymers in good solvents, such as poly(α-methylstyrene) (PAMS) in toluene. The complete scaling form of the PEG osmotic pressure parsimoniously unifies all available experimental data that, until now, required time-consuming, extensive, and complicated fittings.⁸ This economy of description is particularly valuable in the context of the osmotic-stress method. To quantify macromolecular interactions,⁹ protein conformational transitions,¹⁰ DNA condensation and collapse,¹¹ as well as DNA packing in geneplexes¹² and in simple viruses,¹³ the osmotic method of probing the thermodynamics of macromolecular solutions relies heavily on the PEG osmotic equation of state.

Results

J. H. van’t Hoff, in a major advance of solution thermodynamics, discovered a “deep-seated analogy—indeed, almost an identity—between solutions and gases” that enabled him to formulate a universal limiting law for osmotic pressures of dilute solutions.¹⁴ The surprising correspondence between solutions and gases suggested that osmotic pressure, like other colligative properties such as vapor-pressure lowering and freezing-point depression, should depend only on the concentration of solute molecules and not on their chemical nature.

van’t Hoff’s law applies directly to dilute solutions of polymers. This well-known limiting expression for osmotic pressure Π_vH is

$${\mathrm{\Pi }}_{\mathrm{vH}}=\mathit{RTc}=\mathit{RT}\left(\frac{C}{M_{\mathrm{p}}}\right)=\frac{\mathit{RT}}{M_{\mathrm{m}}}\left(\frac{C}{N}\right)$$ (1)

where R is the universal gas constant, T is temperature, c is polymer molar concentration, C is polymer mass concentration, M_p is polymer molecular weight, M_m is monomer molecular weight, and N is the number of monomers in a polymer chain.¹⁵ The van’t Hoff expression for infinitely dilute solutions is usually extended to finite concentrations by a virial expansion.^1,16

J. des Cloizeaux, in a seminal contribution to modern polymer physics,³ extended the notion of universality to the semidilute regime in which polymer coils interpenetrate. The surprising feature of his analysis is that in this regime the osmotic pressure of a polymer solution depends only on monomer concentration, not on the concentration or length of the polymer chains, and not on the chemical nature of the polymers or monomers. des Cloizeaux’s result was later incorporated into a full scaling description of polymers.^1,3,16–19 The des Cloizeaux ~C^9/4 limiting form for polymer osmotic pressure Π_dC in the semidilute regime is^1,3,16

$${\mathrm{\Pi }}_{\mathrm{dC}}=\mathrm{\alpha }{\mathrm{\Pi }}_{\mathrm{vH}}{\left(\frac{C}{C^{\ast }}\right)}^{5/4}=\mathrm{\alpha }\frac{\mathit{RT}}{M_{\mathrm{m}}}\left(\frac{C}{N}\right){\left(\frac{C}{C^{\ast }}\right)}^{5/4}$$ (2)

where C* is a characteristic N-dependent polymer concentration associated with the crossover between the dilute and semidilute regimes and α is an undetermined numerical prefactor. C* traditionally is taken as a semiquantitatively defined polymer overlap concentration,^1,16 i.e., $C^{\ast }~N^{-4/5}/\overline{V}$, where $\overline{V}$ is the polymer partial specific volume.²⁰

Up through the semidilute regime, the osmotic pressure can be written symbolically as Π = (Π_vH → Π_dC), where the arrow means “goes from one limiting form to the other”.

It has been suggested previously that the asymptotic van’t Hoff and des Cloizeaux expressions might be combined to produce a universal equation of state. However, such an ansatz has not been quantitatively investigated, tested, and assessed. The treatment of most relevance to the present work is that of Rubinstein and Colby,¹⁷ who focus on scaling behavior. They propose a sum of two limiting terms, use approximate numerical C* values obtained from independent light-scattering measurements,²¹ and achieve a near fit to data in the des Cloizeaux regime. Our treatment uses a similar equation but focuses on empirical evaluation of prefactors. It does not use ancillary C* data, contains only one numerical parameter, and produces an excellent fit over the whole data range including the crossover region. Earlier, des Cloizeaux and Noda²² proposed a universal function with no free parameters which they evaluated approximately in the asymptotic regimes. Ohta and Oono²³ derived a complicated one-parameter equation of state by renormalization group methods that should be valid in both limits as well as in the crossover regime. Freed²⁴ using renormalization group theory subsequently derived a more general integral equation with no adjustable parameters, but which could not be evaluated analytically. Schulz and Stockmayer²⁵ presented a complicated equation of state based on previous work by Knoll et al.²⁶ Krasilnikov and Bezrukov²⁷ proposed a nonscaling equation of state related to ours. Ramos et al.²⁸ suggested a crossover function with two undetermined prefactors unrelated to our parametrization.

To cast eqs 1 and 2 into a unified scaling form, we formally transform the independent variable C to (C/C*) using the identity C/N ≡ (C/C*) (C*/N). The two limiting forms of the osmotic pressure then assume the form:

$$\mathrm{\Pi }{N}^{9/5}=\frac{\mathit{RT}}{M_{\mathrm{m}}\overline{V}}\left[\right(\frac{C}{C^{\ast }})\to \mathrm{\alpha }{\left(\frac{C}{C^{\ast }}\right)}^{9/4}]$$ (3)

Thus, for a given system of neutral flexible polymers in good solvent comprising polymers of various sizes N at various concentrations C, we expect a plot of ΠN^9/5 vs C/C* to collapse the low and high osmotic-pressure data simultaneously to the limiting expressions in eq 3.

We examine osmotic-pressure data for two very different systems of neutral flexible polymers in good solvents: poly-(ethyleneglycol) (PEG) in water and poly(α-methylstyrene) (PAMS) in toluene. PEG consists of –CH₂–CH₂–O chains having both hydrophilic and hydrophobic character. At room temperature, PEG hydrogen-bonds to water and is highly water soluble. Because of strong and complicated water-mediated monomer–monomer interactions,^6,29 PEG does not seem a likely candidate to conform to a universal polymer equation of state over the whole range of its concentrations. Osmotic pressures of PEG/water, covering a wide range of sizes and concentrations, have been measured extensively by Rand et al.³⁰ PAMS consists of –C–CH₂ chains with a methyl group and benzene ring attached to the α carbon. It is insoluble in water but dissolves in toluene, a good solvent. Osmotic pressures of PAMS/toluene have been measured accurately and extensively by Noda et al.²¹ over wide ranges of size and concentration. For neutral flexible polymers in good solvents, these high-quality measurements have become the canonical set of Π data, widely referenced and displayed in many books on polymer physics.^17,18 There is virtually no chemical similarity between the systems PEG/water and PAMS/toluene.

Figure 1 shows the raw Π data for both systems. The high-C PAMS data are independent of N, as predicted by eq 2.

Figure 1.

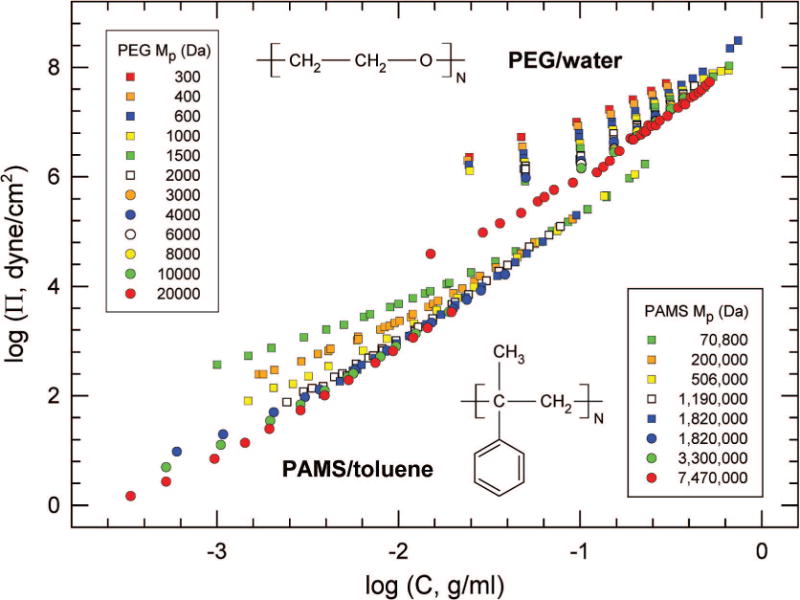
Osmotic-pressure data for PEG/water³⁰ (top) and PAMS/toluene²¹ (bottom). The M_p values for 12 molecular weight PEG and 7 PAMS polymers are shown in the upper and lower legends, respectively. PEG data are at 20 °C, PAMS at 25 °C. PEG concentrations were converted from weight % to g/mL using partial specific volume $\overline{V}=0.825\mathrm{mL}/\mathrm{g}$.³¹ PAMS data were obtained by osmometry (squares) or light scattering (circles). Light-scattering data were integrated by use of eq 4.

To plot the data in the scaling form of eq 3, we define $C_N^{\ast }\equiv N^{-4/5}/\overline{V}$; i.e., $C_N^{\ast }$ is the N-dependent scaled part of C* exclusive of its unspecified prefactor. Figure 2 shows plots of ΠN^9/5 vs $C/C_N^{\ast }$. The collapse of data predicted by eq 3 is evident. All PEG data collapse to a master curve, as do all PAMS data.

Figure 2.

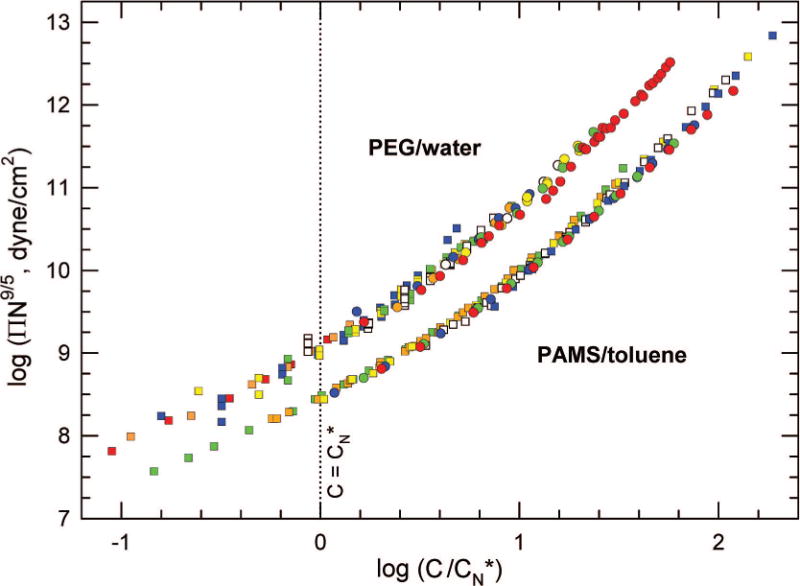
ΠN^9/5 vs $C/C_N^{\ast }$ scaling and data collapse. The data are the same as those in Figure 1. PEG: M_m = 44 Da. PAMS: M_m = 118 Da. For PAMS/toluene, $\overline{V}=0.873\mathrm{mL}/\mathrm{g}$.³²

Data collapses have been demonstrated before. Noda et al.,²¹ in a famous plot, show a data collapse for PAMS/toluene plotted as ΠM_p/(CRT) vs C/C*, where C* values are determined from experimental measurements of 〈R_g²〉 and assumed prefactors. They demonstrate an equation of state based on a second-order virial expansion for C/C* < 1 and another based on a des Cloizeaux expression for C/C* > 1. These equations fit the collapsed data in their respective regimes, crossing near C/C* ≅ 1. However, the fits deviate from the data near the crossover and do not provide a continuous equation of state encompassing both regimes.

The data collapse of eq 3, shown in Figure 2, suggests a simple scaling fitting function. We test a linear combination of Π_vH and Π_dC constructed from eq 3 by replacing the imprecisely defined C* with the precisely defined $C_N^{\ast }$, replacing “→” with “+”, and using α as a single fitting parameter. Thus, we seek to fit the data for each polymer/solvent system by the one-parameter non-virial interpolation function:

$$\mathrm{\Pi }{N}^{9/5}=\frac{\mathit{RT}}{M_{\mathrm{m}}\overline{V}}\left[\right(\frac{C}{C_N^{\ast }})+\mathrm{\alpha }{\left(\frac{C}{C_N^{\ast }}\right)}^{9/4}]$$ (4)

We call α the “crossover index”. Figure 3 shows fits of eq 4 to the collapsed data for both polymers. The fits are excellent. Decompositions of the fits into their van’t Hoff and des Cloizeaux components identify a “crossover concentration” for each polymer system, defined as the concentration where Π_vH = Π_dC, i.e., at $C/C_N^{\ast }={\mathrm{\alpha }}^{-4/5}$. The crossover concentrations and α values for the two systems are significantly different.

Figure 3.

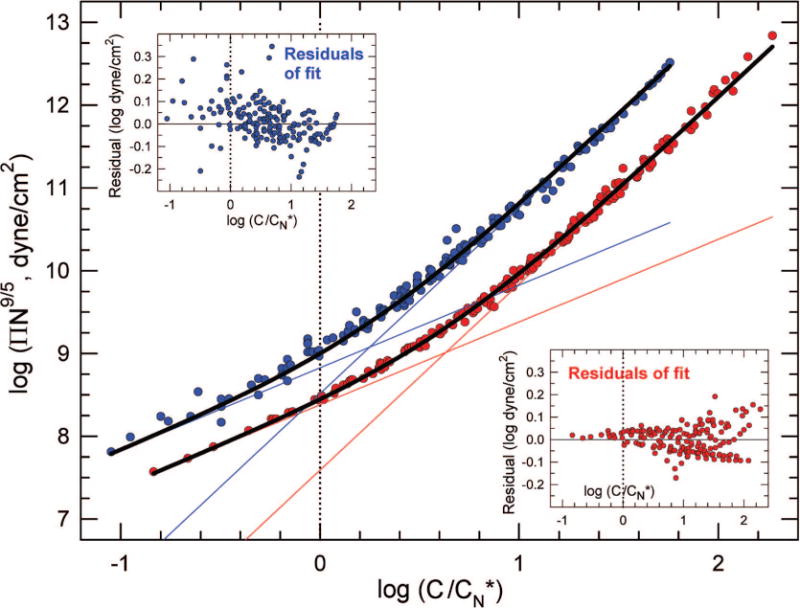
Fits, residuals, and crossover concentrations. Same data and axes as those in Figure 2. Blue (upper dataset) refers to PEG/water, red (lower dataset) to PAMS/toluene. Heavy black lines are logarithmic fits of eq 4. Fitted values of α are α_PEG = 0.49 ± 0.01 (r² = 0.9926) and α_PAMS = 0.162 ± 0.002 (r² = 0.9972). Residuals are small with no systematic deviations (some smoothing results from integration of PAMS light-scattering data). Straight lines are van’t Hoff and des Cloizeaux components of the fits. “Crossover concentrations” are where the van’t Hoff and des Cloizeaux lines cross. $C/C_N^{\ast }$ values at crossover are PEG: 1.78 ± 0.03 and PAMS: 4.29 ± 0.05.³⁴

It is noteworthy that neither crossover occurs at $C/C_N^{\ast }=1$; i.e., $C_N^{\ast }$ is not the crossover concentration, as it lacks the correct prefactor.³³ We define a new quantity $C^{\#}\equiv C_N^{\ast }$ multiplied by a prefactor chosen to produce crossover at C/C^# = 1, whence $C^{\#}={\mathrm{\alpha }}^{-4/5}{C}_N^{\ast }={\mathrm{\alpha }}^{-4/5}{N}^{-4/5}/\overline{V}$. Thus, for osmotic pressures, we replace the semiquantitative overlap concentration C* with the quantitative crossover concentration C^# by assigning α^−4/5 as a $C_N^{\ast }$ prefactor. We note C^#, via α, is different for each polymer/solvent system.

By use of C^#, the collapsed data and fits for PEG/water and PAMS/toluene can be compared. Normalizing the osmotic pressure as $\tilde{\mathrm{\Pi }}\equiv \mathrm{\Pi }/(\mathit{RT}/M_{\mathrm{m}}\overline{V})$, eq 4 takes the simple form:

$$\tilde{\mathrm{\Pi }}{N}^{9/5}{\mathrm{\alpha }}^{4/5}=\left(\frac{C}{C^{\#}}\right)+{\left(\frac{C}{C^{\#}}\right)}^{9/4}$$ (5)

All explicit α dependence factors out of the right side of the equation; there are no undetermined prefactors. $\tilde{\mathrm{\Pi }}’\mathrm{s}$ for the two systems differ solely by their values of α, i.e., α_PEG = 0.49 and α_PAMS = 0.162.

We plot $\tilde{\mathrm{\Pi }}{N}^{9/5}{\mathrm{\alpha }}^{4/5}$ vs C/C^# for both PEG and PAMS in Figure 4. The two datasets now collapse onto a single curve. When superimposed on this curve, eq 5 is seen to provide a simple and accurate one-parameter scaling equation of state for the osmotic pressures of these two highly dissimilar polymer/solvent systems.

Figure 4.

$\tilde{\mathrm{\Pi }}{N}^{9/5}{\mathrm{\alpha }}^{4/5}$ vs C/C^# scaling of the data in Figure 3. The heavy black line is the function eq 5, where $C^{\#}={\mathrm{\alpha }}^{-4/5}{N}^{-4/5}/\overline{V}$ and the α’s are determined by the fits in Figure 3. The data and equations of state for the two systems coincide.

Equation 5 provides an accurate representation of the crossover region. The crossover width is independent of C^# and α. By use of an extrapolated-tangent method, the crossover region can be shown to extend 8/(5 ln 10) log units to either side of log(C/C^#) = 0. The van’t Hoff domain is C ≲ 0.2C^#, and the des Cloizeaux domain is C ≳ 5C^#. The crossover extends over a 25-fold range of C, or 1.4 units of log(C/C^#).

Discussion

Our ansatz for the scaling form of the equation of state tidily collapses the data for both polymers onto a universal curve. For each system, all chemical specificities appear in only one parameter, the crossover index α. Decomposition of the fit for each system unambiguously defines a crossover concentration, expressible in terms of α. Alpha is necessary to ensure accuracy in the high-concentration limit. It encapsulates a number of physical properties: microscopic structure, Flory radius, monomer size and volume,²⁰ and strength and range of interactions. Although the PEG monomer size (~3.5–7.2 Å)³⁵ is less than that of PAMS (~7.2 Å),³⁶ the complicated polymer–solvent interactions for PEG/water^6,29 lead to larger α, higher interaction strength,³⁷ hence a lower crossover concentration (cf. Figure 3), compared to PAMS/toluene. The interaction strength of PEG/water is 4.4 times that of PAMS/toluene.³⁷

Equation 5 depends crucially on the scaling exponents, T, M_m, $\overline{V}$, N, and α. The system is highly constrained. Systematic error in any of these quantities would prevent the total collapse of data. Our ansatz is validated by the fact that α is found to be approximately independent of N.³⁸ The double-limit formalism precludes use of the virial expansion. The heuristic simple sum of van’t Hoff and des Cloizeaux terms with a fitted des Cloizeaux prefactor is accurate over the whole data range, including the crossover region. It coincides almost exactly with the much more complicated equation of state proposed by Ohta and Oono²³ on the basis of renormalization group analysis. Our parameter α is related to an adjustable proportionality constant in the Ohta-Oono formalism.⁴⁰

Because the proposed phenomenological equation of state contains only one parameter, a single Π measurement in the semidilute regime in principle suffices to determine the entire equation of state for each system of neutral flexible polymers in good solvent, thus yielding Π’s for polymers of all sizes at all concentrations. By reducing all specificity of each polymer/solvent system to one number, the scaling equation of state provides exquisite economy of description. It enables efficient use of osmotic-stress methods, permits new analysis of polymer channel-permeation measurements,^27,41 and allows quantitative interpretation of surface-brush scaling phenomena.⁴² The analytic expression Π(α) provides an analytic expression for the chemical potential μ(α) by simple integration, and allows Π determinations by analytic integration of light-scattering data, as done in Figure 1. Future applications include measurements of the temperature, salt, and solvent-quality dependences of α as well as Π studies of flexible, screened polyelectrolytes. The effect of polydispersity on the fitted value of α is expected to be minimal. Ohta and Oono²³ tested the effects of very broad distributions on their renormalization group formalism and concluded that “the polydispersity effect is very small”.

In conclusion, we present a detailed, explicit demonstration of the validity and robustness of the polymer-scaling universality hypothesis. Despite its unusual physical and biological properties that might suggest otherwise, the system PEG/water follows precisely the same polymer-scaling laws as does PAMS/toluene. We demonstrate that (1) proper scaling collapses extensive osmotic-pressure data encompassing the dilute and semidilute regimes for two vastly different polymer/solvent systems onto a single universal curve, accurately described by a continuous function of a single parameter; (2) this parameter, which we name the “crossover index”, is analytically related to a precisely defined “crossover concentration”, which replaces the prefactorless overlap concentration for osmotic-pressure scaling; (3) all physical and chemical specificity for each polymer/solvent system and all relevant prefactors are encapsulated in the crossover index; (4) the crossover region between the van’t Hoff and des Cloizeaux regimes has a universal shape with quantifiable boundaries.⁴³

Finally, it is intellectually pleasing to note that both terms in the proposed equation of state stem from deep-seated analogies between different areas of physics: the van’t Hoff term from the analogy between solutions and gases, and the des Cloizeaux term from the analogy between polymers and magnetic systems close to their second-order phase transition, as first noted and described by P.-G. de Gennes.