A C++ Template Library for Efficient Forward-Time Population Genetic Simulation of Large Populations

Abstract

fwdpp is a C++ library of routines intended to facilitate the development of forward-time simulations under arbitrary mutation and fitness models. The library design provides a combination of speed, low memory overhead, and modeling flexibility not currently available from other forward simulation tools. The library is particularly useful when the simulation of large populations is required, as programs implemented using the library are much more efficient than other available forward simulation programs.

THE past several years have seen an increased interest in simulating populations forward in time (Peng et al. 2007; Carvajal-Rodríguez 2008; Chadeau-Hyam et al. 2008; Hernandez 2008; Neuenschwander et al. 2008; Padhukasahasram et al. 2008; Peng and Amos 2008; Peng and Liu 2010; Pinelli et al. 2012; Messer 2013; Kessner and Novembre 2014) to understand models with natural selection at multiple linked sites that cannot be easily treated using coalescent approaches. Compared to coalescent simulations, forward-time simulations are extremely computationally intensive, and several early efforts may not be efficient enough for in-depth simulation studies (reviewed in Messer 2013). More recently, two programs, sfs_code (Hernandez 2008) and SLiM (Messer 2013) have been introduced and demonstrated to be efficient enough (both in runtime and in memory requirements) to obtain large numbers of replicates, at least for the case of simulating relatively small populations. Both of these programs are similar in spirit to the widely used coalescent simulation program ms (Hudson 2002) in that they attempt to provide a single interface to simulating a vast number of possible demographic scenarios while also allowing for multiple selected mutations, which is not possible on a coalescent framework. The intent of both programs is to allow efficient forward simulation of regions with large scaled mutation and recombination rates (θ = 4Nμ and ρ = 4Nr, respectively, where N is the number of diploids, μ is the mutation rate per gamete per generation, and r is the recombination rate per diploid per generation) by simulating a relatively small N and relatively large μ and r (also see Hoggart et al. 2007; Chadeau-Hyam et al. 2008, for another example of a similar strategy). This “small N” strategy allows a sample of size n ≪ N to be taken from the population to study the effects of complex models of natural selection and demography on patterns of variation in large chromosomal regions. Messer (2013) has recently shown that his program SLiM is faster than sfs_code for such applications and requires less memory. However, both programs are efficient enough such that either could be used for the purpose of investigating the properties of relatively small samples.

The modern era of population genomics involving large samples (1000 Genomes Project Consortium et al. 2012, 2012; Cao et al. 2011; Mackay et al. 2012; Pool et al. 2012) and very large association studies in human genetics (Burton et al. 2007) demonstrates a need for efficient simulation methods for relatively large population sizes. For example, simulating current human genome-wide association studies with thousands of individuals would require simulating a population much larger than the number of cases plus controls. Further, the simulation of complex genotype-to-phenotype relationships will require parameters such as random effects on phenotype and fitness (not currently implemented in SLiM or in sfs_code) such that heritability is less than one (see Neuenschwander et al. 2008; Peng and Amos 2008; Pinelli et al. 2012; Thornton et al. 2013; Kessner and Novembre 2014, for existing examples of such simulations).

In this article I present fwdpp, which is a C++ library for facilitating the implementation of forward-time population genetic simulations. Rather than attempt to provide a general program capable of simulating a wide array of models under standard modeling assumptions akin to ms, SLiM, or sfs_code, fwdpp instead abstracts the fundamental operations required for implementing a forward simulation under custom models. An early version of the code base behind fwdpp has already been used successfully to simulate a novel disease model in a large population that would not be possible with existing forward simulations (Thornton et al. 2013) and to simulate “evolve and resequence” experiments such as in Burke et al. (2010; Baldwin-Brown et al. 2014). Since the publication of those articles, the library code has been improved in many ways, reducing runtimes by more than a factor of 2. fwdpp provides a generic interface to procedures such as sampling gametes proportional to their marginal fitnesses, mutation, recombination, and migration. The use of advanced C++ techniques involving code templates allows a library user to rapidly develop novel forward simulations under any mutation model or fitness model (including disease models as discussed above). The library is compatible with another widely used C++ library for population genetic analysis [libsequence (Thornton 2003)] and contains functions for generating output compatible with existing programs based on libsequence for calculating summary statistics. Further, the runtime performance of programs implemented using fwdpp compares quite favorably to SLiM for the small N case described above. However, for the case of large N, fwdpp results in programs with significantly smaller runtimes and memory requirements then either SLiM or sfs_code, allowing for very efficient simulation of samples taken from large populations for the purposes of modeling population genomic data sets or large case/control studies.

Sampling Algorithm

The library supports two sampling algorithms for forward simulation. The first of these is an individual-based method, where N diploids are represented. Descendants are generated by sampling parents proportionally to their fitnesses, followed by mutating and recombining the parental gametes. Below, I show that the individual-based method results in the fastest runtime for models involving natural selection. Therefore, for most applications, the individual-based sampling functions should be considered the default choice for developing custom simulations.

The second algorithm is gamete based. In this algorithm, no diploids are represented. Rather, in any generation t, there are g_t gametes, each with 0 < x < 2N copies present in the population. To generate the next generation, the expected frequency of each gamete in the next generation is obtained using the formula

$${p^{\prime }}_i=\frac{p_i{w}_i}{\overline{w}},$$

where ${p^{\prime }}_i$ is the expected frequency of the ith gamete in the next generation, p_i is its current frequency $\left(x/2N\right),$ and $w_i={\displaystyle {\sum }_{j=1}^{j=g_t}{P}_{ij}{w}_{ij}}/p_i$ is the marginal fitness of the gamete over all possible diploid genotypes (P_ij) containing the ith gamete (Crow and Kimura 1971, p. 179). The expected frequencies of each gametes are used in one round of multinomial sampling to obtain the number of copies of each gamete in the next generation. Although slower than the individual-based sampler for models with selected mutations, the gamete-based sampler reflects the original code base of fwdpp, previously used in Thornton et al. (2013) and Baldwin-Brown et al. (2014). This code provides only one additional function to the library user and requires fewer data structures (as no container of diploids is needed). It is therefore kept in the library both for backward compatibility with previous projects and for the possibility of future performance improvements.

Library Design

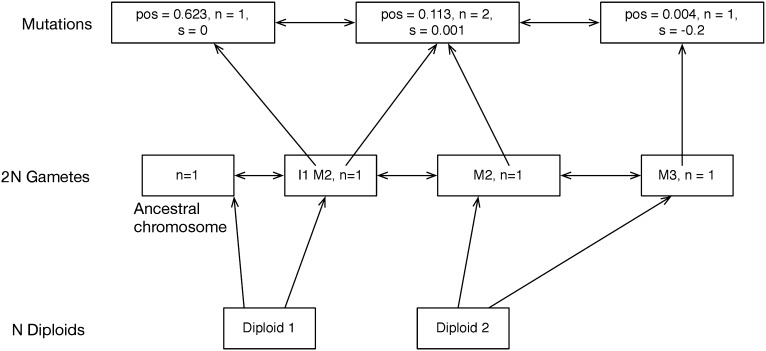
The intent of the library is to provide generic routines for mutation, recombination, migration, and sampling of gametes proportionally to their fitnesses in a finite population of N diploids. The library does this in a memory-efficient manner by defining a small number of simple data types. First, there are mutations. The simplest mutation type is represented by a position and an integer representing its count in the population (0 ≤ n ≤ 2N). Second, there are gametes, which are containers of pointers to mutations. Finally, in individual-based simulations, there are diploids, which are pairs of pointers to gametes. The schema relating these data structures is shown in Figure 1. The details of the relations between data types in individual-based simulation are shown in supporting information, Figure S1. This pointer-based structure is perhaps obvious, but it has several advantages. First, it replaces copying of data with copying of pointers, which is both faster and much more memory efficient. Second, because each pointer is unique, we can ask whether two gametes carry the same mutation by asking whether they contain the same pointers, with no need to query the actual position, etc., of the mutation object pointed to. Finally, storing pointers to neutral and nonneutral mutations in separate containers typically speeds up the calculation of fitness because most models of interest will involve a relatively small proportion of selected mutations compared to the total amount of variation in the population.

Figure 1.

Major data structures used by the simulation library for individual-based simulation. Mutations are stored in a doubly linked list. Within the list, each mutation occupies a unique place in memory accessible via a C++ pointer. The pointers to the three mutations are labeled M1, M2, and M3. Gametes are containers of pointers, meaning that the data for any specific mutation are stored only once and may be accessed via the pointers contained by gametes bearing that mutation. The “gamete pool” of a population is also stored in a doubly linked list. The entire population is thus represented by three data structures: a list of mutations, a list of gametes containing pointers into the mutation list, and a vector of diploids.

Library users create their own custom data types primarily by extending fwdpp’s built-in mutation type by creating a new mutation type that inherits from the built-in type (described above) and adding the new required data. For example, selection coefficients, origination and fixation times, etc., may be tracked by a custom mutation type (Figure S1). The gamete type is then a simple function of the custom mutation type and the container in which these mutations are stored (Figure S1).

These user-defined data types are passed to functions implementing the various sampling algorithms required for the simulation. Because the library cannot know ahead of time what the “rules” of the simulation are, library algorithms are implemented in terms of templates, which may be thought of as skeleton code for a particular algorithm. In other words, a template function could be implemented in terms of type “T”, which could be an integer, a floating-point number, or a custom data type as decided by the programmer using the function. The substitution of specific types for the place holders (and related error checking) is performed by the compiler. In standard C++, templates are used to implement algorithms on data stored in containers [such as sorting (Josuttis 1999, pp. 94–101)]. The behavior of these algorithms may be modified by custom policies (Josuttis 1999, pp. 119–134). For example, a sorting order may be affected by a policy. Similarly, users of fwdpp provide policies specifying the biology of the population at each stage of the life cycle. An example of a policy function would be the mutation model. A mutation model policy must specify the position and initial frequency of a new mutation along with any other data such as selection coefficients, dominance, etc. Many of the most commonly used policies for standard population genetic models (multiplicative fitness, how mutation containers are updated after sampling, etc.) are provided by the library. A typical custom policy typically involves little new code, and the example programs distributed with the library demonstrate this point. The library also comes with additional documentation detailing the concept of policies in standard C++ and how that concept is applied in fwdpp and what the minimal requirements are for each type of policy (mutation, migration, and fitness being the three most important). The ability to extend the built-in mutation and gamete types and combine them with custom policies facilitates the implementation of algorithms for simulation under arbitrary models. As the library has developed, I have found that it has evolved to a point where the balance between inheritance (the ability to build custom types from existing types, such as mutations) and template-based data types and functions is such that new models may be implemented with relatively little new code being written.

Library Features

The library contains several features to facilitate writing efficient simulations. As of library version 0.2.0, these features are supported for both the gamete- and individual- based portions of fwdpp and include the following:

1. The ability to initialize a population from the output of a coalescent simulation stored in the format of the program ms (Hudson 2002). Either this input may come from an external file or the coalescent simulation could be run internally to the program, for example using the routines in libsequence (Thornton 2003). The routines are compatible with coalescent simulation output stored in binary format files, using routines in libsequence version ≥1.7.8.

2. Samples from the population may be obtained in ms format.

3. The ability to copy the containers of mutations and gametes into new containers. The result of the copy operation is an exact copy of the population that can be evolved independently. Applications include simulating replicated experimental evolution (Baldwin-Brown et al. 2014) or conditioning simulation results on a desired event, such as the fate of a particular mutation, and repeatedly restoring and evolving the population until the desired outcome is reached via naive rejection sampling.

4. The population may be written to a file in a compact binary format. This binary output may then be used as input for later simulation. Applications of this feature include storing populations simulated to equilibrium for later evolution under more complex models and/or storing the state of the population during the course of a long-running simulation such that it may be restarted from that point in the case of unexpected interruptions.

Library Dependencies

The code in fwdpp uses the C-language GNU Scientific Library (GSL) (http://www.gnu.org/software/gsl/) for random number generation. The boost libraries (http://www.boost.org) are used extensively throughout the code. Finally, libsequence (Thornton 2003) was used to implement the input and output in ms format described in the previous section. All three of these libraries must be installed on a user’s system and be accessible to the system’s C++ compiler.

Documentation and Example Programs

The library functions are documented using the doxygen system (http://www.doxygen.org). The documentation includes a tutorial on writing custom mutation and fitness functions. The library also contains several example programs whose complete source codes are available in the documentation. The simplest of these programs are diploid and diploid_ind, which use the gamete- and individual-based methods, respectively, to simulate a population of N diploids with mutation, recombination, and drift and output a sample of size 0 < n ≪ 2N in the same format as ms (Hudson 2002). The remaining example programs add complexity to the simulations and document the differences with respect to these programs. All of the example programs model mutations according to the infinitely many sites model (Kimura 1969) with both the mutation and recombination rates being uniform along the sequence. (Nonuniform recombination rates are trivial to implement via custom policies returning positions along the desired genetic map of the simulated region.) In practice, I expect that future programs developed using fwdpp will use the individual-based sampler due to its speed in models with selection (see below). Many of the examples are implemented using both the gamete- and individual-based sampling methods. The names of source code files and binaries for the latter have the suffix “_ind” added to them to highlight the difference.

The complete library documentation and example code are distributed with the source code (see Availability below). All of the performance results described below are based on the example programs.

Availability

fwdpp is released under the GNU General Public License (GPL) (http://www.gnu.org/licenses/gpl.html). The primary web page for all software from the author is http://www.molpopgen.org/software/, where links to the main fwdpp page may be found. The source code is currently distributed from https://github.com/molpopgen/fwdpp.

Performance

Performance under the constant-sized Wright–Fisher model without selection was evaluated using the University of California, Irvine, High-Performance Computing Cluster, which consists of dozens of 64-core nodes, mainly with AMD Opteron 6274 processors. An entire queue of three such nodes was reserved for performance testing, ensuring that no disk-intensive processes were running alongside the simulations and degrading their performance. All code was compiled using the GNU Compiler Collection (GCC) suite (http://gcc.gnu.org), version 4.7.2. Programs based on fwdpp depended on boost version 0.5.3 (http://www.boost.org), libsequence version 1.7.8 (http://www.molpopgen.org), and the GSL (http://gnu.org/software/gsl) version 1.16. The GSL version 1.16 was also used to compile SLiM (Messer 2013). The software versions used for all results were fwdpp version 0.2.0, SLiM version 1.7, and sfs_code version 2013-07-25. For all simulations, sfs_code was run with the infinitely many-sites mutation option.

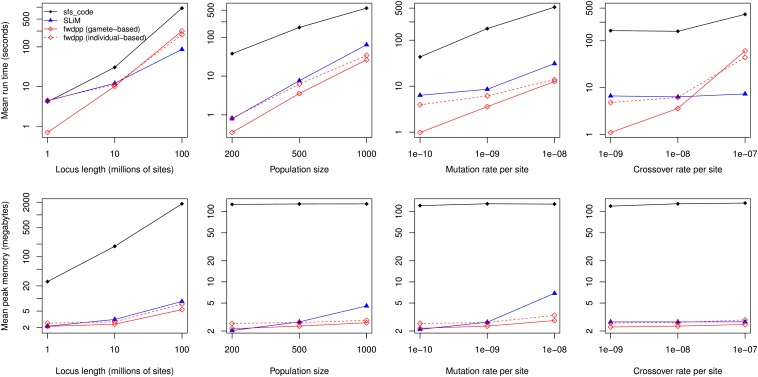
Figure 2 shows the average runtimes and memory requirements of sfs_code (Hernandez 2008), SLiM (Messer 2013), and fwdpp over a variety of parameter values where the population size, N, is small (≤1000). For nearly all parameter combinations, SLiM and fwdpp are much faster than sfs_code and require less memory. When the total amount of recombination gets very large (the locus length gets very long and/or the recombination rate gets large), fwdpp is slower than SLiM but still several times faster than sfs_code. Holding the population size and recombination rate constant, fwdpp is faster than SLiM as either the population size increases or the mutation rate increases (two center columns of Figure 2). Although Figure 2 suggests very large relative differences in performance, it is important to note that the absolute runtimes are still rather short for all three programs.

Figure 2.

Performance comparison for the case of small population size (N). Shown are the means of runtime and of peak memory use for sfs_code, SLiM, and a program written using fwdpp. Note that the y-axis is on a log scale. The results are based on 100 simulations with the following base parameter values: diploid population size N = 500, locus length L = 5 × 10⁶ bp, mutation rate per site μ_bp = 1 × 10⁻⁹, and recombination rate per diploid per site r_bp = 1 × 10⁻⁸. (Both SLiM and sfs_code parameterize per-generation rates as per base pair.) All simulations were run for 10N generations. For each column, one of the four parameters was varied while the remainder were kept at their base values. For the leftmost column, sfs_code was run with 100 loci of length L/100 for all L > 10⁶. Simulations implemented using fwdpp do not explicitly model sites and instead are implemented in terms of the usual scaled mutation and recombination rates θ = 4NLμ_bp and ρ = 4NLr_bp, respectively.

As N becomes larger, fwdpp becomes much faster than either sfs_code or SLiM (Figure 3). For populations as large as N = 50,000 diploids and θ = ρ = 100, fwdpp and sfs_code are comparable in performance and both are substantially faster than SLiM as N increases. For θ = ρ = 500, fwdpp is orders of magnitude faster than either SLiM or sfs_code.

Figure 3.

Performance comparison for the case of large population size (N). Shown are the means of runtime and of peak memory use for sfs_code, SLiM, and a program written using fwdpp. Note that the y-axis is on a log scale. The left column is for the case of θ = ρ = 100 and the right column shows θ = ρ = 500 (θ and ρ refer to the scaled mutation and recombination rates, respectively, for the entire region). The results are based on 100 replicates of each simulation engine for each value of N and each replicate was evolved for 10N generations. Missing data points occurred when a particular simulation did not complete any replicates within 7 days, at which point the task was set for automatic termination. For SLiM and sfs_code, the locus length simulated was L = 10⁵ bp and the per-site mutation and recombination rates were chosen to obtain the desired θ and ρ for the entire region.

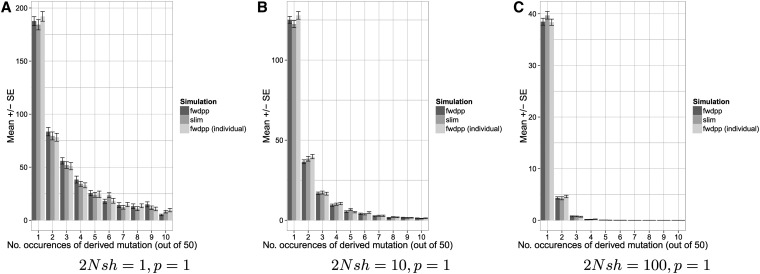
The results in Figure 2 and Figure 3 consider only neutral mutations. However, coalescent simulations (Hudson 2002; Chen et al. 2009) should generally be the preferred choice for neutral models because such simulations will typically be much faster than even the fastest forward simulation. For forward simulations, both the strength of selection and the proportion of selected mutations in the population will affect performance. Figure 4 compares the runtimes and peak memory usage of fwdpp and SLiM for the simple case of selection against codominant mutations with a fixed effect on fitness and multiplicative fitness across sites. Further, comparison to SLiM seems relevant because it is an efficient and relatively easy way to use a program that is likely to be widely used for population-genetic simulations of models with selection. Because SLiM and the example programs written using fwdpp scale fitness differently (1, 1 + sh, 1 + s and 1, 1 + sh, 1 + 2s, respectively, for the three genotypes), I chose s and h for each program such that the strength of selection on the three genotypes was the same. The population size was set to N = 10⁴ diploids and the total mutation rate was chosen such that 2Nμ = 200. The recombination rate was set to 0, and p, the proportion of newly arising mutations that are deleterious, was set to 0.1, 0.5, or 1. For each value of p, 100 replicates were simulated for 10N generations. As p increases and selection gets weaker (2Nsh gets smaller), fwdpp’s gamete-based algorithm gets slower (Figure 4). The case of 2Nsh = 1 and P = 0.5 or 1 is particularly pathological for fwdpp. However, this parameter combination models a situation where 50% or 100% of newly arising mutations are deleterious with $sh=-1/2N,$ and thus selection and drift are comparable in their effects on levels of variation. In practice, many models of interest will incorporate a distribution of selection coefficients such that this particular case should be viewed as extreme. For SLiM, the parameters have the opposite effect on performance; slim slows down as selection gets stronger and there are fewer selected mutations in the population. However, with the exception of the pathological case of a large proportion of weakly selected mutations, SLiM and fwdpp’s gamete-based sampling scheme showed similar mean runtimes overall, suggesting that both are capable of efficiently simulating large regions with a substantial fraction of selected mutations and when selection is a stronger force than drift. For all parameters shown in Figure 4, fwdpp’s individual-based sampling method is much more uniform in average runtime, typically outperforming both SLiM and fwdpp’s gamete-based method. As seen in Figure 2 and Figure 3 above for the case of neutral models, fwdpp uses much less memory than SLiM for models with selection (Figure 4). Finally, Figure 5 shows that SLiM and the two sampling algorithms of fwdpp result in nearly identical deleterious mutation frequencies for the models shown in Figure 4, implying that all three methods are of similar accuracy for multisite models with selection. The results in Figure 4 strongly argue that the individual-based sampling routines of fwdpp should be preferred for models involving natural selection.

Figure 4.

Performance comparison between SLiM, fwdpp’s gamete-based sampling scheme, and fwdpp’s individual-based scheme for models involving both neutral and codominant deleterious alleles. All results are based on 100 replicates with N = 10⁴ and 10N generations of evolution simulated per replicate. The total mutation rate was chosen such that 2Nμ = 200 and the proportion of newly arising deleterious mutations was varied. The three different panels represent three different strengths of selection against heterozygotes (2Nsh = 1, 10, or 100).

Figure 5.

(A–C) Site frequency spectra for models with codominant deleterious alleles. Plots are based on a sample of size n = 50 taken from the simulations in Figure 4 where the proportion of newly arising deleterious mutations (p) was 1.

Applications

In this section, I compare the output of programs written using the gamete-based sampler in fwdpp to both theoretical predictions and the output of well-validated coalescent simulations. Each of the models below is implemented in an example program distributed with the fwdpp code. For results based on forward simulations, the population size was N = 10⁴ diploids and the sample size taken at the end of the simulation was n = 50 (from each population in the case of multipopulation models). All summary statistics were calculated using routines from libsequence (Thornton 2003). For all neutral models, the coalescent simulation program used was ms (Hudson 2002). The neutral mutation rate and the recombination rate are per region and the region is assumed to be autosomal. These assumptions result in the scaled mutation rate θ = 4Nμ, where μ is the mutation rate to neutral mutations per gamete per generation, and the scaled recombination rate ρ = 4Nr, where r is the probability of crossing over per diploid per generation within the region. All simulation results are based on 1000 replicates each of forward and coalescent simulation.

The equilibrium Wright–Fisher model

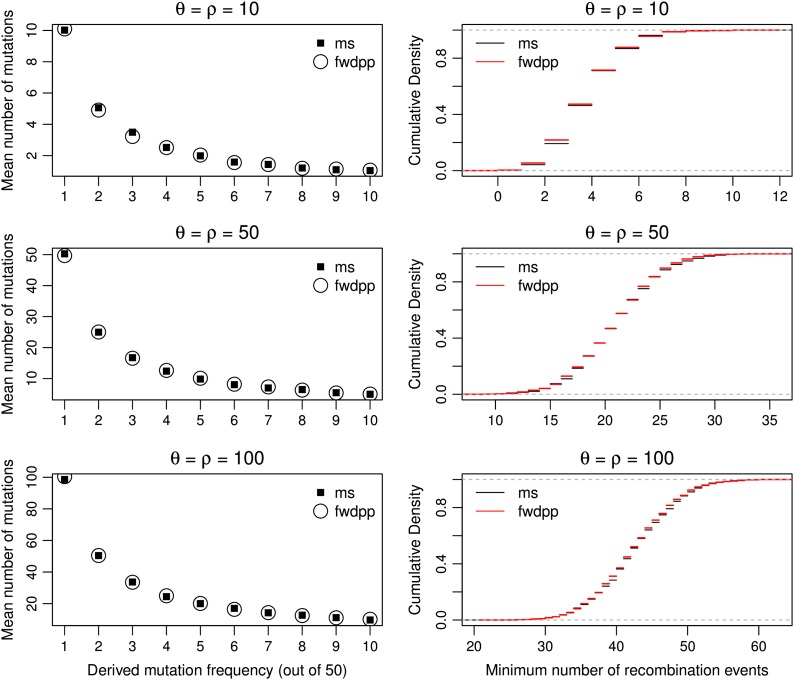
We first consider the standard Wright–Fisher model of a constant population and no selection. I performed simulations for each of three parameter values (θ = ρ = 10, 50, and 100). Figure 6 shows the first 10 bins of the site frequency spectrum and the distribution of the minimum number of recombination events (Hudson and Kaplan 1985) obtained using both simulation methods. The forward simulation and the coalescent simulation gave identical results (to within Monte Carlo error) in all cases, and there were no significant differences in the distributions of these statistics (Kolmogorov–Smirnov tests, all P > 0.05). All of the results below are based on the gamete-based portion of fwdpp as it is more efficient for models without selection.

Figure 6.

The average site frequency spectrum (left column) and the distribution of the minimum number of recombination events [Hudson and Kaplan 1985 (right column)] are compared between fwdpp and the coalescent simulation program ms (Hudson 2002). All results are based on 1000 simulated replicates. The forward simulation involved a diploid population of size N = 10⁴ evolving with mutation and recombination occurring at rates θ and ρ, respectively, for 10N generations. All summary statistics are based on a sample of size n = 50 and were calculated using libsequence (Thornton 2003).

Population split followed by equilibrium migration

I simulated the demographic model shown in Figure 7A, using a forward simulation implemented with fwdpp. The model in Figure 7A is equivalent to the following command using the coalescent simulation program ms (Hudson 2002):ms 100 1000 -t 50 -r 50 1000 -I 2 50 50 1 -ej 0.025 2 1 -em 0.025 1 2 0.

Figure 7.

Distributions of genetic variation between populations simulated under a model of recent divergence with migration. (A) A population split followed by symmetric migration. An ancestral population of size N = 10⁴ diploids was evolved for 10N generations with mutation rate θ = 50 and recombination rate ρ = 50. The ancestral population was then split into two equal-sized daughter populations of size 10⁴ (thus resulting in a population split with no bottleneck). The two populations were evolved for another 1000 generations with symmetric migration at rate 4Nm = 1. B–D compare results based on 1000 replicates of forward simulation using fwdpp and 1000 replicates of the coalescent simulation ms (Hudson 2002). (B) The distribution of F_ST (Hudson et al. 1992). (C) The distribution of the total number of private polymorphisms. (D) The distribution of the number of polymorphisms shared between the two populations.

Figure 7, B–D, compares the distributions of several summaries of within- and between-population variation. The forward and coalescent simulations are in excellent agreement, and no significant differences in the distribution of these summary statistics exist (Kolmogorov–Smirnov test, all P > 0.05).

Discussion

I have described fwdpp, which is a C++ template library designed to help implement efficient forward-time simulations of large populations. The library’s performance compares favorably to other existing simulation engines and has the additional advantage of allowing novel models to be rapidly implemented. I expect fwdpp to be of particular use when very large samples with selected mutations must be simulated, such as case/control samples or large population-genomic data sets. The library is under active development and future releases will likely both improve performance as well as add new features.

Importantly, users of forward simulations should appreciate that there may be no single software solution that is ideal for all purposes. For example, users wishing to evaluate the population-genetic properties of relatively small samples (say n ≤ 100) under standard population genetic fitness models would perhaps be better served by SLiM or sfs_code, as such scenarios can be simulated effectively with either program in a reasonable time (Figure 2 and Messer 2013) by keeping the population size (N) small. Further, SLiM and sfs_code already implement a variety of relevant demographic models such as migration and changing population size. The intent of fwdpp is to offer a combination of modeling flexibility and speed not currently found in existing forward simulation programs and to provide a library interface to that flexibility. There are several scenarios where fwdpp may be the preferred tool. First, for models requiring large N and selection, fwdpp may be the fastest algorithm (Figure 3 and Figure 4). Second, when nonstandard fitness models and/or phenotype-to-fitness relationships are required (such as in Thornton et al. 2013), fwdpp provides a flexible system for implementing such models while also allowing for complex demographics, complementing existing efforts in this area (Neuenschwander et al. 2008; Peng and Amos 2008; Pinelli et al. 2012; Kessner and Novembre 2014). Finally, fwdpp is likely to be useful when the user needs to maximize runtime efficiency for a particular demographic scenario and does not require the flexibility of a more general program.