Genetic Dissection of a Genomic Region with Pleiotropic Effects on Domestication Traits in Maize Reveals Multiple Linked QTL

Abstract

The domesticated crop maize and its wild progenitor, teosinte, have been used in numerous experiments to investigate the nature of divergent morphologies. This study examines a poorly understood region on the fifth chromosome of maize associated with a number of traits under selection during domestication, using a quantitative trait locus (QTL) mapping population specific to the fifth chromosome. In contrast with other major domestication loci in maize where large-effect, highly pleiotropic, single genes are responsible for phenotypic effects, our study found the region on chromosome five fractionates into multiple-QTL regions, none with singularly large effects. The smallest 1.5-LOD support interval for a QTL contained 54 genes, one of which was a MADS MIKC^C transcription factor, a family of proteins implicated in many developmental programs. We also used simulated trait data sets to investigate the power of our mapping population to identify QTL for which there is a single underlying causal gene. This analysis showed that while QTL for traits controlled by single genes can be accurately mapped, our population design can detect no more than ∼4.5 QTL per trait even when there are 100 causal genes. Thus when a trait is controlled by ≥5 genes in the simulated data, the number of detected QTL can represent a simplification of the underlying causative factors. Our results show how a QTL region with effects on several domestication traits may be due to multiple linked QTL of small effect as opposed to a single gene with large and pleiotropic effects.

IN evolutionary biology, quantitative trait locus (QTL) mapping has been used with great success to define the genetic architecture controlling morphological differences between species. These QTL mapping experiments have identified many QTL with large effects in animal (White et al. 2012; Alem et al. 2013; Miller et al. 2014) and plant systems (Paterson et al. 1991; Xiong et al. 1999; Wills and Burke 2007; Shannon 2012). Often these experiments identify QTL clusters in a small number of genomic regions, suggesting an underlying genetic architecture of single pleiotropic genes or several closely linked genes (Cai and Morishima 2002; Peng et al. 2003; Doebley 2004; Gyenis et al. 2007; Miller et al. 2014). QTL effects have been successfully mapped to single large-effect pleiotropic genes in many species (Frary et al. 2000; Wang et al. 2005; Konishi et al. 2006; Li et al. 2006; Simons et al. 2006; Cong et al. 2008; Studer et al. 2011). However, these large-effect genes explain only a portion of the divergence between species, leaving a considerable amount of phenotypic differences unexplained.

Domesticated crop plants and maize in particular provide a well-suited system in which to study the evolution of new morphologies for a number of reasons. First, maize (Zea mays spp. mays) and its wild progenitor teosinte (Z. mays spp. parviglumis) differ for a suite of traits commonly seen in domesticated crop pairs. Collectively, these differences are known as domestication syndrome and include reduced lateral branching, loss of natural seed dispersal, and gigantism of vegetative and reproductive tissues (Pickersgill 2007; Allaby et al. 2008). Second, intense artificial selection for desirable agronomic traits leaves a signature of selection (reduced nucleotide diversity), allowing for identification of putative targets of artificial selection in selective sweeps (Wright et al. 2005). Third, maize domestication took place in the last 10,000 years and surviving wild progenitor populations serve as reasonable surrogates for the ancestor (Doebley et al. 2006). In addition, maize and teosinte are interfertile, allowing for the use of genetic techniques and crosses to dissect the genetic architecture underlying divergent traits (Doebley and Stec 1991; Briggs et al. 2007). Finally, researchers studying maize have the advantage of a powerful tool in the reference maize genome sequence, providing the ability to anchor genetic markers to physical positions, annotate candidate genes, and characterize important genomic features (Schnable et al. 2009).

Previous work in maize and its wild progenitor suggests the genes responsible for phenotypic change are scattered throughout the genome, but with several concentrations of genes (QTL) controlling large portions of the phenotypic differences (Doebley 2004; Shannon 2012). To date, three large-effect pleiotropic genes have been mapped to these genomic regions of large phenotypic importance. The short arm of chromosome one is home to grassy tillers1 (gt1), which influences tillering (Whipple et al. 2011) and is largely responsible for the concentration of seed into a single large ear (Wills et al. 2013). The gene teosinte branched1 (tb1) is found on the long arm of chromosome one and has a large pleiotropic impact on plant and inflorescence branching (Doebley et al. 1997; Studer et al. 2011). Finally, the gene teosinte glume architecture1 (tga1) liberates the kernel from its stony fruit case in teosinte (Wang et al. 2005).

While early studies identified tb1 as the gene responsible for much of the phenotypic effect on the long arm of chromosome one (Clark et al. 2006), a more recent study has identified at least two additional loci upstream of tb1 with significant effects on phenotype (Studer and Doebley 2011). These loci influence the expression of tb1-like phenotypes in both additive and epistatic ways. The nearest of these loci was only 5 cM away from tb1 itself and also had an effect specific to ear traits, leaving plant architecture traits such as tillering unaffected. This suggests secondary factors to major-effect genes can be closely linked and can also mediate tissue-specific effects. Similarly, the work identifying gt1 also found evidence of a secondary factor located downstream of the identified causative region that slightly increases prolificacy (the number of ears) in plants carrying the teosinte allele (Wills et al. 2013).

One of the six genomic regions of large pleiotropic effect identified in maize is on chromosome five where the genetic architecture underlying phenotypic effects is largely unknown (Doebley 2004). Previous work has found a number of domestication QTL on chromosome five for culm diameter, kernel row number, ear diameter, disarticulation, and pedicellate spikelet length (Doebley and Stec 1991; Doebley 2004; Briggs et al. 2007). A more recent experiment confirms QTL for these traits on chromosome five, some of which (kernel row number, ear diameter, and disarticulation) had particularly large effect and LOD score (Shannon 2012). While these previous mapping experiments found significant QTL for domestication traits on chromosome five, they could not determine whether this region contained a major QTL with pleiotropic effects on several traits or multiple linked QTL.

In this article, we undertook a QTL mapping study to better characterize the effect of chromosome five on domestication traits. This experiment utilized a population of nearly isogenic recombinant inbred lines (NIRILs) that allowed for concentration of informative crossover events in the region of interest (chromosome five) and replicated block experiments to improve trait estimates. Both of these characteristics increase the mapping power specifically on chromosome five in comparison with a standard F₂ mapping population. Our study detected QTL at multiple locations on the fifth chromosome, none of which have singularly large effect. This suggests that unlike other regions of the maize genome with single large-effect genes (Wang et al. 2005; Studer et al. 2011; Wills et al. 2013), chromosome five houses several linked factors influencing phenotype. We also performed a simulation study to gauge the power and precision of our mapping population. This analysis indicates that for some traits the genetic architecture could be more complex than observed with empirical data.

Materials and Methods

Plant material, genotypes, and phenotypes

We conducted a QTL mapping experiment to investigate the genetic architecture of domestication traits on maize chromosome five, using a collection of NIRILs in the summers of 2009 and 2010. The experimental population was built by introgressing the majority of the short arm and part of the long arm of chromosome five from a teosinte (Iltis and Cochrane collection 81) into the maize inbred W22 by six generations of backcrossing. RFLP markers (Supporting Information, Table S1) were used during this process to follow the desired genomic segment and eliminate teosinte segments at other known domestication QTL identified in a previous study (Doebley and Stec 1993). The extensive backcrossing in tandem with tracking and eliminating teosinte segments from specific regions of the genome allowed the experiment to be focused on the segregating teosinte introgression on chromosome five. Five BC₆ individuals heterozygous for the target segment on chromosome five were selfed to produce five BC₆S₁ families. The families were then selfed for five additional generations to give an experimental BC₆S₆ population of 259 highly homozygous NIRILs, which carried a collection of teosinte fifth-chromosome introgressions in an isogenic W22 background.

Genomic DNA was extracted with a standard CTAB protocol from tissue collected from an average of 15 individuals from each NIRIL in the summer of 2009. A collection of 25 insertion/deletion and microsatellite markers (Table S2) was genotyped across the fifth-chromosome introgression, using standard PCR and gel electrophoresis methods. In total, there were 443 observed recombination breakpoints among the NIRILs or ∼1.7 events per line. The range of recombination breakpoints went from 0 to 6 with the majority of lines (51.7%) having either 0 or a single recombination event. The numbers of lines with numbers of breakpoints in parentheses are as follows: 56 (0 breakpoints), 78 (1 breakpoint), 49 (2 breakpoints), 48 (3 breakpoints), 19 (4 breakpoints), 7 (5 breakpoints), and 2 (6 breakpoints).

Phenotype data were collected for the experimental NIRILs in three replicated blocks, two in the summer of 2009 and one in 2010, grown at the West Madison Agricultural Research Station in Madison, Wisconsin. Blocks consisted of the 259 NIRILs planted in randomized plots of 10 or 12 plants each in 2009 and 2010, respectively. Five plants from each plot were assessed for 13 phenotypes (Table 1) representing a number of plant and inflorescence phenotypic differences between teosinte and maize. Plant traits included plant height, days to pollen shed, the amount of tillering, length of the primary lateral branch, prolificacy, and culm diameter. Inflorescence traits measured in the female inflorescence (ear) were kernels per rank, kernel row number, ear diameter, ear length, and percentage of staminate spikelets. Several traits from the male inflorescence or tassel were also measured and include the pedicellate spikelet length and tassel branch number. Genotype and phenotype data are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.7sq67.

Table 1. NIRIL phenotyped traits, descriptions, approximate distribution, between-year Pearson correlation coefficients, and Pearson P-values.

Trait	Description	Distribution	Pearson coefficient	Pearson P-value
CULM	Diameter of culm	Normal	0.688	<0.0001
DTP	Days to pollen shed	Normal	0.668	<0.0001
EARD	Ear diameter	Bimodal	0.907	<0.0001
EARL	Ear length	Normal	0.409	<0.0001
KPR	Kernels per rank	Bimodal	0.698	<0.0001
KRN	Kernel row no.	Bimodal	0.718	<0.0001
LBLH	Primary lateral branch length	Normal	0.519	<0.0001
PLHT	Plant height	Normal	0.652	<0.0001
PROL	Prolificacy, ears on lateral branch	Exponential	0.422	<0.0001
SPLH	Spikelet length	Normal	NA	NA
STAM	% staminate spikelets	Exponential	0.321	<0.0001
TBN	Tassel branch no.	Normal	0.691	<0.0001
TILL	Tillering index	Exponential	0.346	<0.0001

NA, not applicable.

Mixed models and heritability

We estimated the NIRIL phenotype for all traits by fitting a linear mixed model. Fixed effects consisted of NIRIL, NIRIL family, and position within block, while block and year were used as random effects. The following model was fitted with the MIXED procedure in SAS (Littell et al. 1996) as an initial scope:

$$\begin{array}{l}{Y}_{ijklmno}=\mu +a_i(f_j)+f_j+b_k+c_l(b_k)+d_m(b_k)\\ +\hspace{0.17em}{c}_l(b_k):d_m(b_k)+t_n+e_{ijklmn}+g_{ijklmno}.\end{array}$$

In this model, $Y_{ijklmno}$ is the individual trait value, μ is the overall mean, $f_j$ is the family effect, $a_i(f_j)$ is line nested in family, $b_k$ is random block effect, $c_l(b_k)$ and $d_m(b_k)$are horizontal and vertical positions in the field nested in block, respectively, $t_n$ is the year, $e_{ijklmn}$ is the experimental error (between plots), and finally $g_{ijklmno}$ is within-plot sampling error. Each model term was tested for significance on a trait-by-trait basis with t-tests for fixed effects and likelihood-ratio tests with 1 d.f. for random effects. Likelihood-ratio and t-tests with P-values >0.05 were deemed not significant and the corresponding terms were removed from the model. While the initial scope of the model included a random block and year effect, none of the random effects were found to be significant. Following definition of appropriate models for the studied traits (Table 2), least-squares means for each trait were calculated and used for QTL mapping.

Table 2. Final models selected for the 13 NIRIL phenotypes.

Trait	Model
CULM	Line(family) + family + x(plot) + y(plot)
DTP	Line(family) + family + x(plot) + y(plot) + x:y(plot)
EARD	Line(family) + family + x(plot) + y(plot) + x:y(plot)
EARL	Line(family) + family + x(plot) + y(plot) + x:y(plot)
KPR	Line(family) + family + x(plot) + y(plot) + x:y(plot)
KRN	Line(family) + family + x(plot)
LBLH	Line(family) + family + x(plot) + y(plot) + x:y(plot)
PLHT	Line(family) + family + x(plot) + y(plot)
PROL	Line(family) + family + x(plot)
SPLH	Line(family) + family + x
STAM	Line(family) + family + x(plot) + y(plot) + x:y(plot)
TBN	Line(family) + family + x(plot) + y(plot) + x:y(plot)
TILL	Line(family) + family + y(plot)

Broad-sense heritabilities on a plot means basis (H²) were calculated for each of the traits. The variance components needed for this calculation were found using a linear mixed model with plot means as the dependent variable and plot and line as random independent variables. Variance components for the line or genotypic component (${\sigma }_{\text{g}}^2$), the plot (${\sigma }_{\text{p}}^2$), and the residual variance due to environment (${\sigma }_{\text{e}}^2$) were extracted and the following equation was used to calculate H²:

$$H^2=\frac{{\sigma }_{\text{g}}^2}{{\sigma }_{\text{g}}^2+{\sigma }_{\text{e}}^2}.$$

The plot variance (${\sigma }_{\text{p}}^2$) was calculated in the model as a known source of variation in phenotype. Since this plot variance is known, it does not contribute to unaccounted for environmental variation as seen by the residual variance (${\sigma }_{\text{e}}^2$) and was not used to calculate heritability.

QTL mapping

We mapped QTL using a model-based approach in R/qtl (Broman et al. 2003; Broman and Sen 2009) with phenotype, represented by least-squares means and 25 genetic markers for the NIRILs. The introgression on the fifth chromosome started as a heterozygous segment in the BC₆ generation and segregates as an S₆ population. Consequently, we analyzed the population as a BC₀S₆ in R/qtl. Genotypes were first used to produce a genetic map for the teosinte segment introgression, using the Kosambi mapping function (Kosambi 1944), with a 0.0001 genotyping error rate as implemented in R/qtl. Genetic marker order was initially found by BLAST to the AGPv2 genome and confirmed using the ripple function in R/qtl with a 5-marker window. Significant LOD score thresholds were determined for each trait with a 5% cutoff based on 10,000 permutations of the data.

QTL models for each phenotype were determined by scanning for potential QTL, using the Haley–Knott regression method and testing for QTL significance one by one. Definition of QTL models was accomplished by first scanning for QTL with the R/qtl function scanone to find an initial QTL position with a LOD score greater than the 5% cutoff calculated by permutations. Next, we scanned for additional QTL, using the addqtl function. If this secondary QTL scan detected a QTL that exceeded the 5% LOD score cutoff defined by permutations, it was added to the model and QTL positions were refined using the R/qtl function refineqtl. QTL were added to the model using this cycle of (1) scanning for additional QTL, (2) adding significant QTL to the model, and (3) refining QTL positions until no more significant QTL could be added. Once all significant QTL were added, pairwise interactions between QTL were tested using the addint function of R/qtl. Significant pairwise interactions (F-test, P < 0.05) were added to the model one by one until no more significant interactions were detected. After the model was finalized, each QTL in the final QTL model was tested for significance with drop-one ANOVA analysis.

Simulation experiment

To explore the theoretical maximum number of detectable QTL possible in this study, we used a custom R script (File S1) to map QTL in simulated trait data sets where causative genes were randomly chosen from the genes in the teosinte introgressed region. Simulated traits were made for 1–15 causative genes, then 20–50 genes by 5’s, and then 75 and 100 causative genes for a total of 24 different causative gene set sizes. The 25 genotyped markers in our 259 NIRILs were used to assign genotype probabilities to the 2576 total genes in the introgressed segment of chromosome five based on the genotype of flanking markers. These genotype probabilities were assigned based on physical proximity to the two flanking markers, assuming physical distance was proportional to genetic distance so that a gene closely linked to a given marker had a high probability of sharing that marker genotype. When consecutive markers had identical genotypes, this method resulted in all genes between them matching the flanking genotypes.

Phenotypic trait values are based on both the underlying genetic contributions of genes and random environmental noise, which together define the heritability of a trait. The genetic values in the simulated data were set as follows. For each simulated data set, the randomly chosen causative genes were assigned a genotype based on the previously derived genotype probabilities and two effect types: equal and random gamma distributed (α = 1.36 and β = 1) (Orr 1998). The effect types for each gene were given a positive, zero, or negative value, depending on whether the assigned genotype was homozygous maize, heterozygous, or homozygous teosinte, respectively. Thus, each simulated causative gene had two numeric values (one for equal and one for gamma-distributed effects) representing the magnitude and direction of effect on the trait. The total genetic contribution to NIRIL phenotype was then found by simply summing the gene values (equal and gamma effects kept separate) for all simulated causative genes.

Environmental noise was added to the summed NIRIL genetic phenotype values by taking random draws from a normal distribution with variance equal to the additional variance needed to reach the desired level of heritability. Two levels of heritability were simulated (67% and 90%) to mimic the heritabilities of two actual traits, the moderately heritable culm diameter and highly heritable ear diameter. Heritability of the simulated traits was required to be within 2.5% of the desired heritability; otherwise the normal distribution was resampled. This process resulted in each set of simulated causative genes having four states for the NIRILs: equal effect 67% H², equal effect 90% H², gamma effect 67% H², and gamma effect 90% H².

We simulated 24 causative gene set sizes with two effect types and two heritabilities for a total of 96 distinct simulated states. Each of these states was replicated 1000 times, resulting in 96,000 simulated sets of phenotypes for the 259 NIRILs. These phenotype values were then used with actual NIRIL genotypes to map QTL in the R/qtl software, using the same method as described in the previous section. Pairwise QTL interactions were not tested for in the simulated data sets because interactions were not part of the simulated conditions. Mapping of QTL for thousands of simulated traits could not be accomplished manually and consequently was done with a custom R script (File S1) that automated the addition of QTL and saved summary information, including QTL estimated effect, QTL position, LOD scores, and number of QTL.

Results

QTL mapping

Previous work has shown chromosome five to be home to several high-LOD score and large-effect size QTL for a number of inflorescence and plant architecture domestication traits (Doebley 2004; Shannon 2012). We undertook a high-resolution mapping experiment with a population of NIRILs with fifth-chromosome teosinte introgressions in a primarily W22 maize inbred background. In the summers of 2009 and 2010, the 259 NIRILs were grown in randomized plots arranged in three replicated blocks. Phenotype data for 13 traits were collected for five plants per plot. Spikelet length was collected only for a single block in the summer of 2010. We analyzed trait measurements from all three growth environments together in a single linear mixed model with block and year as random effects and position, NIRIL, and family as fixed explanatory variables. Least-squares means were estimated from the mixed models and later used for QTL mapping.

Least-squares mean histogram plots show several distribution types, including normal, bimodal, and exponential (Figure S1). NIRILs genotyped as 100% maize (29 lines) and 100% teosinte (27 lines) were used to determine whether traits behaved as expected, with the full teosinte introgression lines having more teosinte-like phenotypes. Several traits believed to not be primary targets of selection during domestication such as days to pollen shed and plant height appear to have little or no overall difference between NIRILs containing the maize and teosinte introgression, while traits that were the primary focus of selection during domestication including kernel row number (KRN) and ear diameter (EARD) have a substantial phenotypic difference between homozygous maize and teosinte NIRILs. For all domestication traits, we observed a difference (sometimes quite small) between the least-squares means for maize and teosinte NIRILs, consistent with the expected effect of domestication. Particularly large differences are seen for EARD and KRN traits, where the maize genotype is 17.3% and 14.8% larger than the teosinte genotype, respectively. Also of interest is the diameter of culm (CULM) trait, where the maize genotype was 6.5% larger than teosinte.

There was a balanced representation of maize and teosinte genotypes with a high degree of homozygosity in the QTL mapping population. Overall genotypes of the NIRILs were 48.3% maize, 48.2% teosinte, and 3.5% heterozygous. The NIRIL population included lines with teosinte introgressions across 162.24 Mbp, from position 6,985,619 to 169,231,037 on the maize reference genome (AGPv2). This introgression includes 74.47% of the ∼218-Mbp fifth chromosome. Of the 4503 fifth-chromosome genes in the Filtered Gene Set (version 5b), 411 genes on the tip of the small arm and 1516 genes on the long arm were not included in the teosinte introgressions used in this study. The genetic map generated in R/qtl was calculated to be 86.64 cM, giving an average megabase pair to centimorgan ratio of 1.873 Mbp/cM.

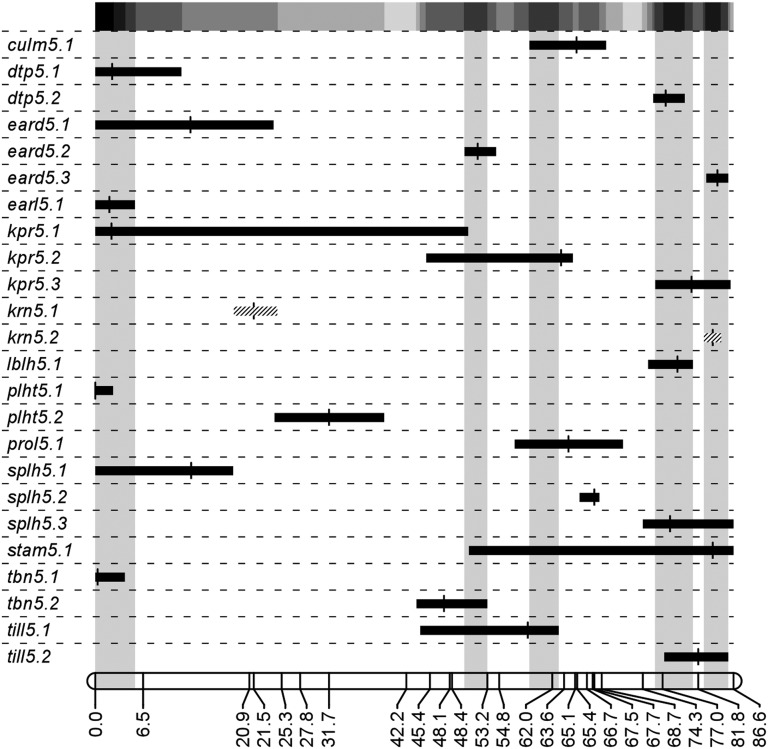
We analyzed 13 traits and identified 24 QTL (Figure 1, Table 3) with a broad range of LOD scores ranging from 2.70 [kernels per rank (KPR)] to 47.22 (KRN). A single epistatic interaction was detected between the two kernel row number QTL, suggesting epistasis is minimal. QTL 1.5-LOD support intervals ranged from 2.3 cM (KRN) to 50.6 cM (KPR) with an average value of ∼12.5 cM. Heritability on a plot mean basis (Table 3) for each trait varied with an average H² of 63% and range of 23% [prolificacy, ears on lateral branch (PROL)] to 90% (EARD). Five QTL clusters, defined as contiguous regions with five or more QTL 1.5-LOD support intervals, were found in the mapping region on chromosome five near 2, 51, 61, 70, and 84 cM (Figure 1). There is no clear single concentration of QTL, suggesting this genomic region lacks a single gene of large, pleiotropic effect and that multiple linked factors spread across the fifth chromosome are responsible for the previously identified influence of chromosome five on domestication traits.

Figure 1.

Cumulative plot of QTL detected in the mapping experiment. Molecular marker positions are shown in centimorgans at the bottom. QTL names consisting of an abbreviated trait name, chromosome number, and QTL number are located on the left side. The 1.5-LOD support intervals for QTL are indicated by horizontal bars and peak LOD scores by vertical lines. Hatched bars indicate interacting QTL while solid bars are noninteracting QTL. In total, 24 QTL were identified across the fifth chromosome with a variety of confidence interval sizes, maximum LOD scores, and effect sizes (Table 3). Five QTL clusters with contiguous regions of five or more QTL 1.5-LOD support intervals are indicated by gray shading. A grayscale heat map depicting number of QTL 1.5-LOD support intervals across the entire mapping interval from white (0) to black (8) is located at the top.

Table 3. Detected QTL for the T5S mapping population with LOD score, position, and heritability.

QTL	LOD	1.5-LOD SI	Peak location	% variation	% H2
culm5.1	13.5	58.9–69.3	65.3	21.30	66.50
dtp5.1	16.36	0.0–11.7	2.3	20.10	—
dtp5.2	18.76	75.7–80.0	77.4	23.60	—
dtp_model	28.93	—	—	40.10	67.30
eard5.1	3	0.0–24.2	12.9	1.70	—
eard5.2	17.99	50.1–54.4	51.9	11.70	—
eard5.3	33.76	82.9–85.9	84.4	25.60	—
eard_model	65.62	—	—	69.00	90.00
earl5.1	12.38	0.0–5.4	1.9	19.70	49.10
kpr5.1	2.7	0.0–50.6	2.2	3.00	—
kpr5.2	6.8	44.9–64.8	63.2	7.90	—
kpr5.3	4.11	76.0–86.2	80.9	4.60	—
kpr_model	27.41	—	—	38.50	72.70
krn5.1	6.22	18.8–24.7	21.5	4.80	—
krn5.2	47.22	82.6–84.9	83.8	53.40	—
krn5.1:2	3.32	—	—	2.50	—
krn_model	50.56	—	—	59.20	73.70
lblh5.1	24.61	75.0–81.1	79	35.30	53.50
plht5.1	7.64	0.0–2.4	0	11.30	—
plht5.2	2.89	24.3–39.2	31.7	4.10	—
plht_model	14.06	—	—	22.00	63.10
prol5.1	8.38	56.9–71.6	64.2	13.80	22.90
splh5.1	9.14	0.0–18.7	13	10.20	—
splh5.2	7.16	65.7–68.4	67.7	7.90	—
splh5.3	2.78	74.3–86.6	78	2.90	—
splh_model	30.6	—	—	41.80	88.30
stam5.1	6.5	50.7–86.6	83.8	10.90	25.90
tbn5.1	8.28	0.0–4.0	0.3	13.10	—
tbn5.2	4.6	43.6–53.2	47.3	7.10	—
tbn_model	10.46	—	—	16.90	69.90
till5.1	7.21	44.1–62.9	58.7	9.80	—
till5.2	3.22	77.2–85.9	81.8	4.20	—
till_model	18.61	—	—	28.10	34.30

SI, support interval.

Simulation experiment

We performed a simulation experiment to determine the power and precision of our mapping population. Using causative genes projected onto actual NIRIL genotypes, a total of 96 distinct simulated states in terms of number of genes (between 1 and 100), heritability (67% and 90%), and effect type (equal and gamma) were replicated 1000 times for a grand total of 96,000 simulated NIRIL trait data sets. Histograms of simulated traits with 90% heritability were clearly bimodal when one causative gene was simulated and progressively moved toward a normal distribution as more and more causative genes were simulated. In comparison, simulated traits with 67% heritability lack a clear bimodal distribution even when only a single causative gene was simulated and are approximately normal when 100 genes are simulated (Figure S2).

Since calculating significant LOD score thresholds via permutations for all 96,000 simulated trait data sets would have taken weeks of computation time, we first calculated LOD score cutoffs in the first 50 replicates of the 96 states. The average cutoff was lower for 90% heritability than for 67% heritability with no clear difference in threshold caused by the effect type of causative genes. Simulated phenotypes with few causative genes had a lower threshold on average with this effect more pronounced for the gamma-distributed effect type. The range of LOD score thresholds determined was quite narrow (2.37–2.59 for gamma-distributed and 2.38–2.60 for equal effects). Consequently, we chose the maximum of the 5% cutoffs found in the first 50 replicates of each of the 96 states as a conservative cutoff for mapping all simulated traits.

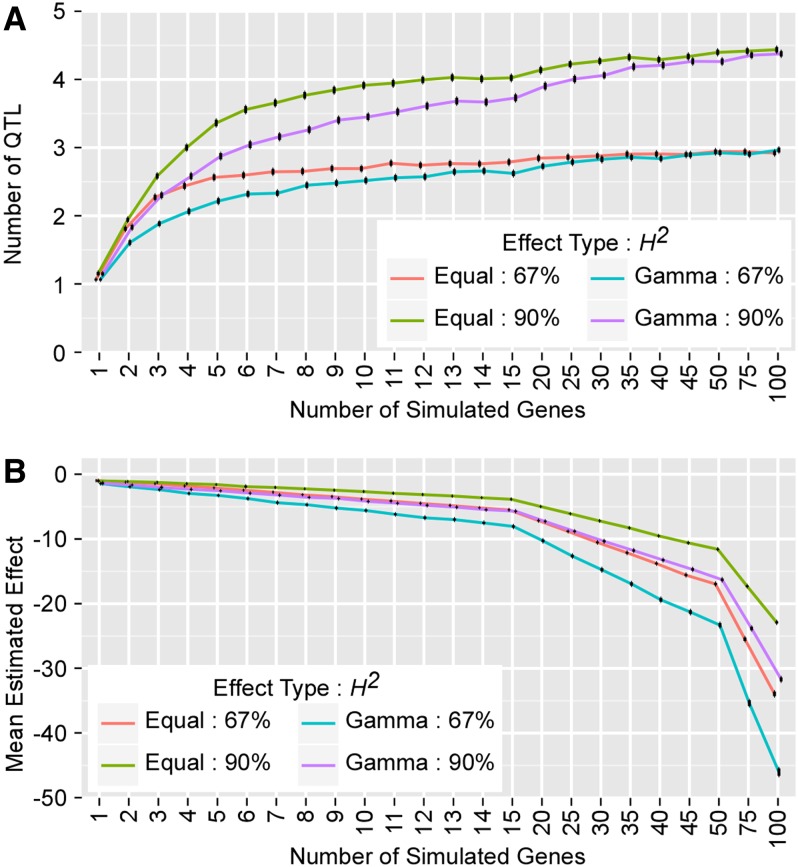
After simulated phenotypes were generated and significance thresholds were set, QTL were mapped using the 96,000 simulated data sets with actual genotypes for the NIRILs in this study. Increasing the number of simulated causative genes from 1 to 100 caused the mean number of detected QTL to rise from 1 to ∼4.5 or ∼3 for simulated traits with 90% or 67% heritability, respectively (Figure 2). Thus, heritability was an important factor in determination of the number of detectable QTL in our experiment. The simulated gamma effects, as opposed to equal effects, appeared to cause the maximum number of detectable QTL to be reached at a larger number of simulated causative genes, but there was no difference in the overall maximum number of QTL detected.

Figure 2.

The number of detected QTL and mean detected QTL effect size vs. number of simulated causative loci. Black lines indicate 95% confidence intervals. (A) Simulations consistently detect one QTL when a single causative gene is simulated, but when as few as three or four causative genes are simulated, we lose the ability to distinguish between genes. With high numbers of simulated causative genes, total QTL detected reach a ceiling of ∼4.5 QTL for simulated traits with 90% heritability and ∼3.0 for traits with 67% heritability. (B) The effects of unresolved genes are merged into the few large-effect QTL that are detected, consistent with the Beavis effect. This is seen in the negative correlation between mean estimated effect and number of causative genes.

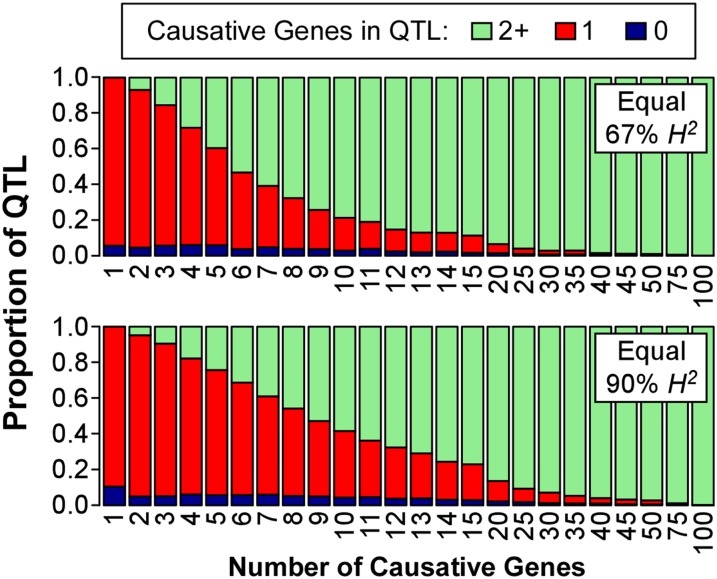
Our results show that QTL 1.5-LOD support intervals quickly become associated with multiple genes when many causative genes are simulated (Figure 3). In the case of five causative genes with equal effect and 67% heritability, the chance of a QTL support interval containing a single causative gene has already dropped to ∼50%. Similar patterns are seen for gamma-simulated phenotypes (Figure S3). This suggests that when making decisions about fine mapping of QTL, researchers would be well advised to consider factors such as trait heritability and the power of their mapping population to identify QTL support intervals that contain single genes.

Figure 3.

The proportion of detected QTL with zero, one, or more than one simulated causative genes in the 1.5-LOD support interval. High numbers of causative genes lead to detected QTL that contain multiple causative genes. There is a reasonable percentage of detected QTL in the simulations that contain a single causative gene when few (less than four) causative genes are simulated, but as the number of simulated causative genes increases we quickly lose the power to distinguish between closely linked causative genes and they become lumped into single detected QTL. Equal-effect simulations shown here are very similar to those seen for the gamma-distributed effects (Figure S3).

In our simulation experiment, increasing the number of causative genes also led to an increase in the average estimated effect size of detected QTL (Figure 2). We interpreted this as the effects of multiple underlying causative genes being combined into a single detected QTL with a cumulative effect, consistent with the Beavis effect where multiple small-effect loci are detected as single QTL of larger effect (Beavis 1998). On average, the total additive effect for each simulated phenotype should be the product of the total number of simulated causative genes and the average effect size. We found this expected relationship between number of detected QTL, average estimated additive effect of detected QTL, and expected total additive effect for both equal and gamma-distributed effects and both heritabilities.

Our mapping results using empirical, measured traits, found three QTL for a trait with heritability of 90% (ear diameter) and a single QTL for a trait with 67% heritability (culm diameter). Comparison of these results with the simulations shows that for simulated traits with 90% heritability, when three or more QTL are detected, there are likely to be anywhere from four to six underlying causative genes, making a 1:1 relationship between number of QTL and causative genes uncertain (Figure 2). In contrast to this result, simulated traits with heritability of 67% and a single causative gene averaged a single detected QTL that contained the causative gene 90–95% of the time. These observations have implications for future fine-mapping efforts to identify the causative gene underlying QTL.

Discussion

Previous studies in maize have found single genes underlying genomic regions of large effect on multiple domestication traits (Wang et al. 2005; Clark et al. 2006; Studer et al. 2011; Hung et al. 2012; Wills et al. 2013). This is in stark contrast to our work on chromosome five, where the previously observed large effect of chromosome five on several domestication traits in maize (Doebley 2004; Shannon 2012) is caused by multiple regions spread across the chromosome. This suggests the nature of genetic factors controlling domestication traits on chromosome five of maize is different from that of other large domestication loci in maize. Whether the situation of chromosome five in maize is unique in maize or crop plants is yet to be seen, but several loci identified in this study suggest that in addition to effectively acting on highly pleiotropic, large-effect single genes, the domestication process also has the capacity to work on several linked genes of variable effect to produce a chromosomal region of large QTL effect.

Although our results show that several regions on chromosome five contain QTL affecting different traits, this chromosomal region was initially defined as several tightly clustered QTL in F₂ crosses between teosinte and a small-eared primitive Mexican landrace (Doebley and Stec 1993). In contrast, our NIRIL population was developed from a cross of teosinte by a modern agronomic maize inbred and is expected to harbor domestication QTL as well as improvement QTL selected on during the past 9000 years since maize was domesticated. Thus, while results from this analysis suggest chromosome five houses a complex made of multiple linked factors, we cannot discount the possibility that a simpler genetic architecture would have been observed had we used a primitive maize landrace rather than the W22 maize inbred line.

One potential use of QTL mapping results is interrogation of the genes within QTL for likely candidates. The marker density in our experiment leads to most QTL 1.5-LOD support intervals containing hundreds of annotated genes. However, two QTL had a narrow confidence interval for which a relatively small number of genes fall within the 1.5-LOD support interval. These two QTL were krn5.2 and eard5.3, which colocalize to the same ∼2.3-cM region. When expanded to the nearest genetic markers, these QTL support intervals fell between umc1348 and um1966, which span a 4.81-cM region (2.654 Mbp) with 54 genes from the maize Filtered Gene Set (AGPv2). One interesting candidate that falls in this range is AC212823.4_FG003, which encodes a MADS box transcription factor previously cataloged as MADS-transcription factor 65 (mads65) in the GRASSIUS transcription factor database (Yilmaz et al. 2009). Initially identified in plants as important floral organ identity regulators (Schwarz-Sommer et al. 1990; Yanofsky et al. 1990), the MADS-box family of transcription factors has since been shown to be involved in a wide variety of developmental programs in various organs and stages of plant development (Smaczniak et al. 2012). This particular MADS-box gene has high sequence similarity to the rice gene OsMADS57, a type II MIKC^C MADS gene. The large subclass of MIKC^C MADS genes is quite diverse with members involved in floral specification, phase transition, and root development among other developmental functions (Smaczniak et al. 2012). This gene was also found to be selected during crop improvement by a recent study (Hufford et al. 2012) and has fairly high expression in many tissues as described in the maize gene expression atlas (Sekhon et al. 2011). All of these factors make AC212823.4_FG003 an attractive candidate in future studies to fine map the causative gene for kernel row number and ear diameter on chromosome five.

The limits of a QTL experiment in terms of power and resolution are important factors to consider when undertaking an experiment in any mapping population. To inform our QTL results with empirically measured traits, we explored the computational limits of the experimental mapping population, using simulated-trait data sets. In this experiment, we never detected more than eight QTL for any of the simulated conditions with heritability being the most important characteristic in determining number of detected QTL. As expected, when the number of underlying causative genes increased to a high level, we saw the effect of multiple causative genes being rolled into single detected QTL, consistent with the Beavis effect (Beavis 1998). If these polygenic QTL, which can have quite high LOD score and effect size, were chosen for fine mapping, we would be unlikely to find a single underlying causative polymorphism. Consequently, when considering QTL for fine-mapping purposes, researchers would be well advised to choose QTL from mapping populations with sufficient power to define QTL containing single causative genes. It is important to realize that the simulation results reflect the specific markers, genotypes, and mapping population used in this study. While some results are likely generally applicable to other QTL experiments, simulations using mapping population-specific parameters will provide the best insight into potential genetic architectures and information on population power and precision.

QTL mapping has been used to great effect to characterize the genomic regions controlling traits selected on during domestication in maize. These studies have shown that while genetic factors controlling domestication traits are spread throughout the genome, there are concentrated genomic regions where QTL for several domestication traits are in close proximity to each other (Doebley 2004; Shannon 2012). In this study, we use a QTL mapping population of NIRILs with teosinte introgressions specific to chromosome five to closely examine previously mapped QTL for a number of domestication traits. We confirmed QTL for these traits exist on chromosome five; however, in our population these QTL further fractionate into multiple QTL. This is in contrast to other genomic regions of large effect in maize where single pleiotropic genes were identified as the causative factor underlying genomic regions of large effect (Wang et al. 2005; Studer et al. 2011; Hung et al. 2012; Wills et al. 2013). The presence of multiple QTL in several locations on chromosome five suggests the existence of a linked complex of multiple genes controlling various aspects of domestication traits. This apparent complexity of the chromosome five locus is consistent with results from our simulation experiment, where we show that traits with multiple mapped QTL likely have a more complicated underlying genetic architecture than is indicated by the initial QTL mapping results.