Molecular Simulation of Water and Hydration Effects in Different Environments: Challenges and Developments for DFTB Based Models

Abstract

We discuss the description of water and hydration effects that employs an approximate density functional theory, DFTB3, in either a full QM or QM/MM framework. The goal is to explore, with the current formulation of DFTB3, the performance of this method for treating water in different chemical environments, the magnitude and nature of changes required to improve its performance, and factors that dictate its applicability to reactions in the condensed phase in a QM/MM framework. A relatively minor change (on the scale of k_BT) in the O–H repulsive potential is observed to substantially improve the structural properties of bulk water under ambient conditions; modest improvements are also seen in dynamic properties of bulk water. This simple change also improves the description of protonated water clusters, a solvated proton, and to a more limited degree, a solvated hydroxide. By comparing results from DFTB3 models that differ in the description of water, we confirm that proton transfer energetics are adequately described by the standard DFTB3/3OB model for meaningful mechanistic analyses. For QM/MM applications, a robust parametrization of QM-MM interactions requires an explicit consideration of condensed phase properties, for which an efficient sampling technique was developed recently and is reviewed here. The discussions help make clear the value and limitations of DFTB3 based simulations, as well as the developments needed to further improve the accuracy and transferability of the methodology.

Introduction

Water is arguably the most important molecule in life and physical sciences.^1,2 The importance of water to the structure, stability, dynamics, and function of biomolecules has been well documented for decades. For example, since hydrophobic interaction is a major driving force for the stability of proteins, the structure and dynamics of water near protein are essential to the folding/association of proteins^3,4 and dictate, at least in part, how small solutes influence biomolecular processes.^5,6 Being a highly polar and polarizable molecule, water is often found in the active site of enzymes for the stabilization of otherwise high-energy intermediates;^7,8 solvation of metal ions in the protein interior has been shown to make a significant contribution to the transport mechanism of these ions through ion channels and transporters,^9,10 and interfacial water molecules between proteins have also been demonstrated to facilitate interprotein electron transfers.¹¹ Another unique feature of the water molecule is its ability to relay the transfer of proton or “proton hole”¹² (hydroxide) through the celebrated Grotthus mechanism;^13,14 thus, water networks are commonly observed in proteins that mediate long-range proton transports.^1,15−18 These unique physical and chemical properties of water manifest themselves in processes that occur in nonbiological systems as well, such as reactions in aqueous solutions and at various interfaces. As a recent example, the water layer at the surface of a Pt electrode was suggested to exhibit hydrophobic characteristics,^19,20 which are expected to influence the composition and reactivity at the electrode/water interface.

This very incomplete list of properties and roles of water highlights why it is the most studied molecule by both experiments and theoretical means. For example, sophisticated spectroscopic techniques have been developed in recent years to analyze the structure and dynamics of water at various interfaces, the active site/surface of proteins, and also bulk water under different conditions (e.g., various phases of ice).²¹⁻²⁴ From a theoretical and simulation point of view, water, without any doubt, is the molecule for which the largest number of models have been developed;^25,26 these include quantum mechanical models,²⁷⁻³¹ classical force fields with various levels of treatment for many-body effects,^25,32−40 and statistical mechanical models in the framework of liquid state theories.^41,42 Some of the models have been developed for general purpose simulations, while others have been motivated with more specific applications, such as investigation of nonlinear spectroscopies.^43,44

In our own work, we have been focusing on developing methods for simulating water in different environments at two distinct levels and resolutions. One level is a semiempirical QM model⁴⁵ referred to as density-functional-tight-binding (DFTB),⁴⁶⁻⁴⁸ which allows one to routinely carry out the QM/MM type of simulations for condensed phase systems at a 1–10 ns time scale, making it a valuable complement to ab initio QM/MM methods⁴⁹⁻⁵² for problems that require extensive sampling. The other level is a coarse-grained (CG) model referred to as the big multipole water (BMW) model,⁵³ based on which we also developed CG models for amino acids and common lipids in the general framework of the MARTINI force field,⁵⁴ leading to the BMW-MARTINI model.⁵⁵ Clearly, CG models are required to extend the length and time scales of simulations to address questions of increasing complexity.⁵⁶⁻⁶⁰

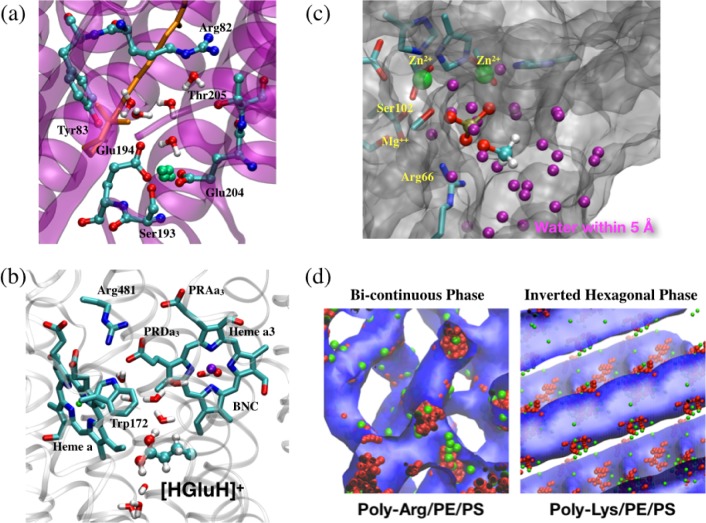
In Figure 1, we use several recent applications from our research to illustrate that calibrated semiempirical QM and CG models are uniquely valuable for a broad range of applications. For example, DFTB/MM simulations^{47,48,61−63} were used to probe the chemical nature of the proton storage group in bacteriorhodopsin (bR, Figure 1a)⁶⁴⁻⁶⁷ and the proton pumping mechanism in cytochrome c oxidase (CcO, Figure 1b).^68,69 In those applications, calibration of proton affinity for the key groups involved and conducting adequate sampling of local protein/water motions proved to be essential. More importantly, both examples implicated rather unusual chemical species: a pair of glutamates interacting strongly with nearby water in bR⁶⁵⁻⁶⁷ and a transiently doubly protonated glutamate in CcO.⁶⁹ Therefore, the use of a QM description for the region of interest was indispensable. Active site water molecules were found to play a major role in stabilizing these unusual species and therefore also needed to be treated at a QM level. The example of alkaline phosphatase (AP)^70,71 (Figure 1c) highlighted that some enzyme active sites are rather solvent accessible, especially those with a significant degree of catalytic promiscuity.⁷² A proper description of the level of hydration requires a careful treatment of QM/MM interactions; otherwise, spurious stabilization of certain intermediates can be observed.⁷³ Finally, the example in Figure 1d illustrated the need of CG simulations in the analysis of the phase behavior of complex materials (e.g., peptide/lipid mixtures),⁷⁴ which remain difficult to study using atomistic simulations.

Figure 1.

Examples that illustrate recent applications of DFTB3/MM and CG (BMW-MARTINI) models where the proper description of water proved essential: (a) the proton storage site in bacteriorhodopsin involves a proton delocalized between amino acid side chains that are solvated by active site water;⁶⁵⁻⁶⁷ (b) proton transfers in cytochrome c oxidase proceed through water wire and a neutral glutamate near a hydrophobic cavity;^69,75 (c) catalytic specificity and promiscuity in alkaline phosphatase are modulated in part by solvent molecules accessible to the active site;^70,71 (d) capturing the distinct phase behaviors of cationic peptide/lipid mixtures with coarse-grained simulations relies on a careful treatment of electrostatics and water.⁷⁴

Another topic we will not discuss extensively in this article but hope to highlight, nevertheless, concerns the sampling of hydration state, particularly the change of the level of hydration, when studying various water mediated processes in proteins and at interfaces. The importance of sampling water penetration coupled to events in the protein interior, such as deprotonation of a buried titratable group, has been emphasized by several authors.^76,77 A notable example concerns an internal cavity in the protein cytochrome c oxidase, for which our recent simulation study suggested that the change of the hydration state of this cavity is likely of major functional significance.⁷⁵ The importance of sampling hydration change at solid/liquid interfaces, however, has not been broadly emphasized. A recent example discussed by us⁷⁸ is the binding of small molecules at the interface between water and metal oxide (e.g., TiO₂). For the adsorbate to bind, the interfacial waters that occupy the potential binding site need to desorb. Due to the highly ionic nature of the metal oxide, however, the interfacial layer of water is strongly bound, making the desolvation of the binding site a rare event and therefore difficult to sample when it is not explicitly considered as part of the binding process. Both multidimensional PMF calculations and preliminary committor analysis⁷⁸ underscored the importance of explicitly including surface desolvation as part of the binding reaction coordinate.

Considering the rich literature on water, including in particular excellent recent reviews on the computational models for water,²⁵⁻²⁹ the goal of this work is not to review the current status of water simulations in general. Rather, motivated by the discussion above, we focus on several remaining challenges for modeling water or hydration effects in different environments using DFTB based QM or QM/MM simulations; this is worthwhile considering the promise of these methods for biological and materials applications.^{47,48,62,63,79} To avoid distraction, we will not discuss our ongoing developments of the BMW model, although it is tempting to imagine a QM/MM/BMW framework for multiscale simulations, since BMW treats electrostatic interactions carefully and therefore is uniquely suited for integration with QM/MM models. In the following, we first discuss the status, limitations, and ongoing improvements of DFTB in the context of modeling water in different protonation states. Next, we discuss recent developments related to the DFTB-MM interactions; these are essential to the establishment of a reliable QM/MM treatment of solvation effects in solution and protein active sites. Finally, we end with concluding remarks.

DFTB3: Toward a QM Model That Bridges Clusters and Bulk

General Background

One promising semiempirical method that has emerged in recent years is the density-functional-tight-binding (DFTB) method,⁴⁶ which has been thoroughly reviewed recently,^79,80 including by some of us.^47,48,81 Briefly, it is based on a Taylor expansion of the total electronic energy in the framework of density functional theory around a reference density, ρ₀. The reference density is usually taken to be the sum of (slightly modified) atomic densities; the original method truncates at the second order, and recent developments⁸¹⁻⁸⁴ extended the expansion to include terms up to the third order. The energy in DFTB is generally written in the following form:

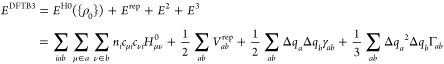1

The first two terms contain only first-order contributions in the density fluctuations and constitute the DFTB1 model, which is not appropriate for biological applications.^46,81 Including the third term, E², leads to the DFTB2 model (originally referred to as SCC-DFTB⁴⁶) which has been successfully applied to many biological problems.^62,63 DFTB2 has been tested extensively for reaction energies, geometries, and vibrational frequencies of large sets of organic molecules.^62,85,86 However, two rather systematic failures indicated a shortcoming of the computational model: the systematic underestimation of hydrogen bonding interactions and the accuracy for proton affinities. As discussed in detail previously,⁸¹⁻⁸³ the function γ_ab approximates the electron–electron interaction in the second-order terms in a way that lacks transferability across the periodic table. In particular, for interactions where hydrogen is involved, this approximation needs to be refined. A modified interaction term γ_ab^h was proposed,⁸¹ which seems to resolve these issues. Furthermore, for molecules where a net charge is highly localized, the description of the density within a minimal basis in the second-order terms is deficient. An extension to third order has led to a systematic improvement. In the first step, only the diagonal contributions to the third-order terms E³ were implemented,^81,82 resulting in the DFTB3-diag model which also uses the γ_ab interaction. Recently, the full third-order contributions were implemented,⁸³ and the model is called DFTB3. Note that DFTB has been augmented with a damped empirical 1/R⁶ term to address the dispersion interactions early on,⁸⁷ which are not included in the usual DFT-GGA functionals.

Most of the electronic contributions to the DFTB models are computed rather than fitted from DFT calculations,⁴⁷ while there are only several adjustable parameters that determine the reference density, basis sets, and thus accuracy of the results.^84,88E^rep in eq 1 is a sum of two-body potentials that are fitted with respect to reference data. Since E^rep depends only on the reference density, its form is in principle the same for DFTB1, DFTB2, or DFTB3. Indeed, the performance of DFTB3 using the repulsive potentials determined for DFTB2, referred to as “mio”, is surprisingly favorable.⁸³ However, a fitting at each level can improve the performance of the model; therefore, a new set of parameters has been developed especially for the DFTB3 model based on a list of organic molecules of general biological interest; this parameter set is called “3OB”. Thus, a full specification of a DFTB method has to indicate both the model and the parametrization, e.g., DFTB2/mio or DFTB3/3OB. For reference, we summarize the DFTB models discussed here in Table 1, although we will focus primarily on the DFTB3 models.

Table 1. DFTB Models Discussed in This Work.

nomenclature	third-order terms	parameterization	SRP?b	reference	applicability
DFTB2a	no	mio	no	(46)	general
DFTB3-diag	diagonal	mio	no	(81, 82)	improved proton affinity and H-bonding
DFTB3-diag+gaus	diagonal	mio	yes	(12)	improved proton transfer barrier
SCC-DFTBPR	diagonal	mio	yes	(89)	phosphate hydrolysis reaction
DFTB3	full	3OB	no	(84)	improved atomization energies for organic/biomolecules
DFTB3	full	3OBw	yes	this work	improved bulk water properties

^aReferred to as SCC-DFTB in previous literature.

^bWhether the model is designed as a specific reaction parameter (SRP) approach.

The DFTB models involve several approximations; therefore, not all molecular properties can be determined using one model/parametrization with high accuracy. Following the strategy of semiempirical models, we have introduced “specific reaction parameters” (SRPs) for specific purposes.⁹⁰ For example, with DFTB3-diag and “mio” parameters, proton transfer barriers and phosphate reaction energies were not well described. Accordingly, we have introduced SRPs that improved the performance for these special purposes, referred to as DFTB3-diag+gaus^12,82 and SCC-DFTBPR,⁸⁹ respectively (see Table 1). It was encouraging that, with the development of DFTB3/3OB,^84,88 a SRP is no longer necessary for many of those properties, although there remain several limitations for complex reactions such as phosphate hydrolysis,⁸⁸ indicating the necessity of continuing development of the DFTB model.

In the specific context of describing water mediated processes, DFTB3 and its earlier variants have been applied to many biological systems in which water participates in proton or proton hole transfers.^12,91−95 In these problems, proton (hole) transfer generally takes place via small clusters of water molecules in protein interiors, which are very different from bulk water. Hence, to reiterate our statement in ref (96), for most biological applications, benchmark calculations using small clusters are much more relevant than setting the behavior of an excess proton in bulk water as the reference; even more importantly, it is essential to calibrate the electrostatics of the active site by, for example, microscopic pK_a calculations of proton donor/acceptor groups.^{75,77,92,97,98} Nevertheless, considering that water is ubiquitous as a solvent, it is worthwhile to benchmark and improve the DFTB method for the description of bulk behaviors.^96,99−101 Ultimately, the power of a reliable QM model lies in its transferability among typical, if not all, environments of potential interest. Along this line, we mention here that there are several specifically parametrized semiempirical methods that have been tuned to work well for either water clusters¹⁰² or bulk under ambient conditions,^103,104 although their broad applicability to reactions in water remains to be tested.

For small neutral and protonated water clusters, DFTB3/3OB has been shown⁸⁴ to give generally adequate results in terms of the magnitude of total binding energy and relative energies of different conformers. However, several recent studies^96,99−101 have indicated the oversolvation tendency of all DFTB3 variants in bulk aqueous environments (e.g., see Table 2 and Figure 2), for neutral water as well as for a hydrated proton/hydroxide, which also likely leads to a higher density than 1 g/cm³ under ambient conditions. In these studies, detailed analyses^96,100 revealed that the oversolvation behavior is largely associated with water population in the “interstitial” sites around the central species, such as occupation of the faces of the coordination tetrahedron around a neutral water molecule or presence of water molecules in between the three H-bond-accepting water molecules around a central hydronium.

Table 2. Integrated First Peak, Denoted by n_O and n_H, of g_O–O and g_O–H, Respectively, of Neutral Bulk Water with Different DFTB Models.

	Exp.c	CPMD-HCTHa	DFTB2a	DFTB3-diagb	DFTB3/3OB	DFTB3/3OBw
nO	4.7	4.1	8.4	5.9	5.6	4.3
nH	1.7	1.9	1.7	1.8	1.8	1.9

^aReference (100).

^bReference (96).

^cReference (105).

Figure 2.

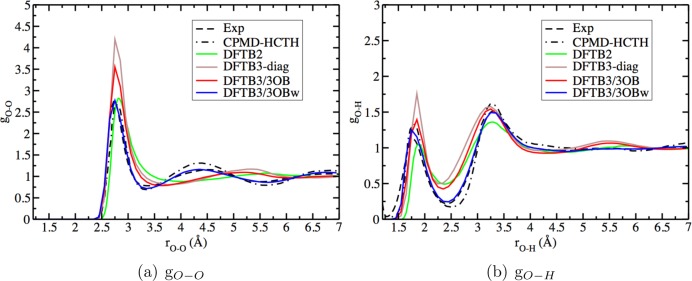
Comparison of neutral bulk water radial distribution functions from computations and experimental data.¹⁰⁵ The CPMD and DFTB2 results are from ref (100), while DFTB3-diag data is from ref (96).

There are several origins for the limited accuracy of DFTB3 for the description of water, especially for bulk properties. First of all, the charge fluctuations in DFTB3 are treated at the monopole level, while multipole terms are known to be essential to electrostatic interactions, such as the angular dependence of hydrogen bonding interactions;^106,107 due to electronic elements in DFTB3, however, the angular dependence of hydrogen bonding interactions appears to be properly described.¹⁰⁸ Second, with a minimal basis set, DFTB3 has limited electronic polarizability¹⁰⁹ and underestimated Pauli repulsion. For example, the dipole moment of water changes from ∼1.9 D in the gas phase to ∼2.4 D in the bulk (see the Supporting Information); the latter is comparable to the values for nonpolarizable water models, although larger values (∼3 D) were reported from DFT simulations of bulk water.¹¹⁰ The underestimation of Pauli repulsion is also reflected by the observation that internal rotational barriers are systematically too low with DFTB methods.⁴⁷ Third, the Pauli repulsion is treated with the reference density and explicit charge dependence of short-range interactions¹¹¹ is not included. In fact, considering these limitations, it is rather remarkable that DFTB3 works generally well for small to medium neutral and protonated water clusters; apparently, error cancellation is involved and not transferable to the bulk. Along this line, it is worth noting that York and co-workers developed a fragment based DFTB model that features multipolar interactions and Lennard-Jones potentials among water sites;^102,108 the model was found to give reliable results for water clusters and bulk water under ambient conditions, although a systematic analysis of its performance for water in different protonation states and environments remains to be carried out.

Reverse Monte Carlo (RMC) Optimization of the O–H Repulsive Potential in DFTB3/3OB for Neutral Bulk Water Solvation Structure

To improve the transferability of DFTB3 for water in different environments, one possible avenue is to systematically evaluate its performance for water clusters of different sizes and structures and compare various components of intermolecular interactions (e.g., two-body and three-body contributions) to those from high-level ab initio calculations.³⁸⁻⁴⁰ The three issues mentioned above can then be improved to minimize the difference between DFTB3 and ab initio components. Since improving these terms will have a major impact on the parameters in DFTB3, systematic reparamerization is required,¹¹² which may not be the most productive avenue for applications in the near future. Therefore, here we explore an alternative approach: since DFTB3 with the 3OB parametrization⁸⁴ already provides a rather encouraging description of hydrogen-bonding interactions, we hypothesize that it is possible to derive relatively minor modifications to the repulsive potential to improve the description of bulk water structure under ambient conditions; we focus on the repulsive potential because its computation is decoupled from the self-consistent solution of the charge fluctuations; thus, modification of the repulsive potential does not require reparameterization of the electronic parameters. The questions worth investigating are as follows: (i) At what intermolecular distance range are modifications necessary and what is the magnitude of the required changes? (ii) To what degree are modifications developed based on neutral bulk water structure transferable to other properties and water in other scenarios, such as water clusters of different protonation states and solvated proton/hydroxide?

Specifically, we adopt a reverse Monte Carlo (RMC)¹¹³ scheme (also known as iterative Boltzmann inversion¹¹⁴) based on eq 2 to tune the O–H repulsive potential for the 3OB^83,84 parametrization of DFTB3. (As the current manuscript was in preparation, Rothlisberger and co-workers reported an empirically adjusted DFTB2 (SCC-DFTB) model based on similar ideas,¹¹⁵ although many details differ from the current work.) In eq 2, g_OH^exp(r) denotes the target, experimental (although new experimental data became available recently,¹¹⁶ we have used the “standard” experimental result of Soper¹⁰⁵), OH radial distribution function (RDF), while V_OH(r) and g_OH⁽ⁱ⁾(r) indicate the repulsive potential and the calculated RDF in the ith iteration of RMC calculations; the calculated RDF is from NVT simulation following the same setup as in ref (96).

2

A comparison of the “3OB” and RMC-generated “3OBw” O–H repulsive potentials in Figure 3 shows that, upon RMC optimization, this potential becomes longer-ranged and more repulsive at O–H distances in the range 1.6–3.3 Å, thus affecting both the first and second solvation shells of a central water molecule. The magnitude of the modification is fairly modest and on the scale of k_BT for most ranges. Nevertheless, the collective effect of the change produces a very significant improvement in the bulk solvation structure. As shown in Figure 2, although only the O–H repulsive potential is modified, leaving the H–H and O–O repulsive potentials untouched, both O–O and O–H RDFs are substantially improved; the H–H RDF remains somewhat different from the experimental data (see the Supporting Information).

Figure 3.

Comparison of the original 3OB and RMC-generated (3OBw) O–H repulsive potentials.

Table 2 shows that, compared to other DFTB variants, DFTB3/3OBw leads to a much lower oxygen coordination number around a central water oxygen of 4.3, which is close to the experimental¹⁰⁵ and CPMD-HCTH¹⁰⁰ values of 4.7 and 4.1, respectively. Also, the spatial distribution function (SDF) plots of oxygen atoms about a central water O in Figure 4 show that the new parameters lead to a much sharper distribution of water molecules around another in the bulk, more closely resembling a tetrahedral coordination environment rather than an indiscriminate distribution.

Figure 4.

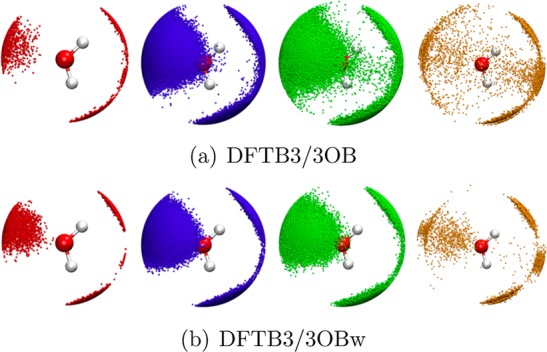
SDF of water O atoms about a central O in neutral bulk water with the different colors denoting different O–O distance ranges. Only SDF > 3 is shown. Red, 0.0 Å < r_O–O < 2.6 Å; blue, 2.6 Å < r_O–O < 2.8 Å; green, 2.8 Å < r_O–O < 3.0 Å; orange, 3.0 Å < r_O–O < 3.3 Å.

Transferability Test of the 3OBw Model

Other Properties of Bulk Water

The 3OBw model is established by considering only the structural properties of bulk water at ambient density. It is of interest to explore how other properties of bulk water are affected by the change of the repulsive potential. Although it is clear that the RMC scheme is state-dependent, it is also of interest to probe to what degree the modification applies to other thermodynamic conditions. In the following, we focus on the dynamic and spectroscopic observables of bulk water with 3OB and 3OBw models. In the Supporting Information, we discuss the temperature dependence of water with DFTB3 models and NPT simulations.

In Table 3, the diffusion coefficient of water calculated with different DFTB models is compared to CPMD and experimental values. The diffusion of water is rather similar for all three third-order variants, with the diffusion coefficient being almost twice larger than the experimental value. Compared to the second-order methods, the DFTB3 approaches represent a major improvement.

Table 3. Diffusion Coefficient (Ų/ps) of the Oxygen Atom in Neutral Bulk Water (D_H2O).

Exp.a	CPMD-HCTHb	DFTB2b	DFTB2-γh b	DFTB3-diagc	DFTB3/3OBd	DFTB3/3OBwd
0.23	0.10	1.11 ± 0.04	0.65 ± 0.02	0.38 ± 0.03	0.44 ± 0.04	0.38 ± 0.06

^aReferences (117 and 118).

^bReference (100).

^cReference (96).

^dComputed for a box of 128 water molecules under ambient conditions and experimental density with eight 45 ps trajectories for DFTB3/3OBw and six 40 ps trajectories for DFTB3/3OB.

We describe the orientational dynamics in liquid water by the second rank rotational time-correlation function of the O–H bond vector:

3

where û is a unit vector along the O–H bond and θ the angle between û at time “t” and at time 0. Figure 5 shows that DFTB3/3OB predicts C(t) for H₂O to decay faster than DFTB3/3OBw; the C(t)’s are computed by averaging independent NVE trajectories that sum to ∼300 ps. Table 4 shows the DFTB3/3OBw relaxation times to be lower than those from experiments and from the classical SPC/E water model. The inset in Figure 5 shows that, like the SPC/E water model, the DFTB3 models predict a very short librational response followed by an initial fast decay and then a long time exponential decay (the DFTB3 relaxation times are obtained by explicit integration of the correlation function until t = 2.5 ps and integration from 2.5 to 30 ps of the exponential fit to the part of the correlation function from 2.5 to 5 ps).

Figure 5.

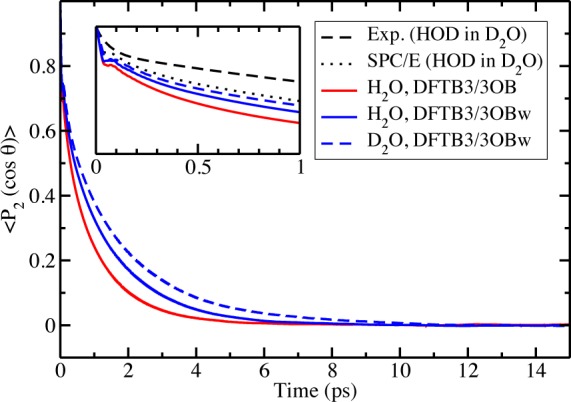
P₂ correlation function of the OH(/D) bond vector in light water (H₂O) and heavy water (D₂O). The experimental and SPC/E data for HOD in D₂O are from ref (119).

Table 4. Orientational Relaxation Time in ps from the P₂ Correlation Function (eq 3).

	Exp.	SPC	SPC/E	TIP3P	TIP4P	DFTB3/3OB	DFTB3/3OBw
H2O	1.7–2.6a	∼1.0c	1.6c	∼0.7c	∼1.2c	0.7 (1.3d)	1.0 (1.6d)
D2O	∼2.5b		1.94b				1.3 (2.1d)

^aReferences (120−123).

^bReference (124).

^cReference (125).

^dNumbers with parentheses are obtained with the alternative approach¹²⁶ of making an exponential fit of the long time decay part of C(t).

Figure 6 shows a comparison of calculated and experimental infrared spectra for bulk H₂O and D₂O, with the same sets of trajectories used to compute the P₂ correlation function. The calculated spectra are obtained by a Fourier transformation of the dipole autocorrelation function, followed by application of the quantum harmonic correction.¹²⁷ The peak at around 3500 cm^–1 for H₂O and that at ∼2500 cm^–1 for D₂O, which correspond to O–H and O–D stretching vibrations, respectively, agree well with the experimental sets (although a splitting of the peak, especially for D₂O, is observed). As expected, the frequencies are lower compared to corresponding gas-phase normal-mode frequencies (denoted by vertical lines). The calculated peaks corresponding to angle bending vibrations (in the 1000–2000 cm^–1 region) are red-shifted compared to the experimental peaks; the red-shift, however, is also present in the gas phase, as we noted earlier.¹²⁸ The peaks below 1000 cm^–1 correspond to librational motions and agree quite well with experiment. The shoulder at low (∼300–500 cm^–1) frequencies, which has been postulated to be seen in calculated spectra when polarization is accounted for in the simulation model,¹²⁹ is also seen in the calculated spectra. The relative intensities of the different peaks are also predicted quite well by DFTB3/3OB(w), especially for D₂O.

Figure 6.

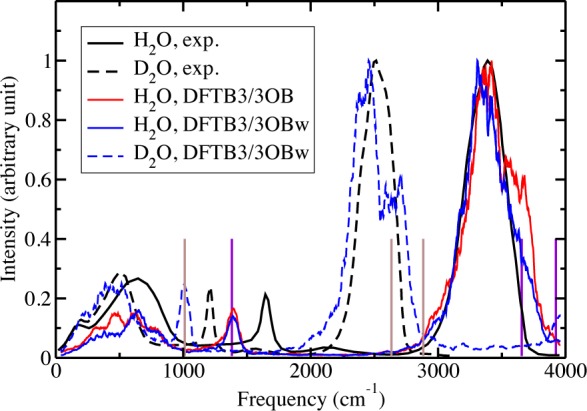
Infrared spectrum of light water (H₂O) and heavy water (D₂O). The experimental results for H₂O and D₂O are taken from refs (130) and (131), respectively. The vertical violet and brown lines denote the O–H/D bending and stretching frequencies in an isolated H₂O and D₂O molecule, respectively, with DFTB3/3OB (the frequencies are the same with DFTB3/3OBw) and are assigned arbitrary heights. All liquid-phase spectra are scaled so as to have a maximum intensity of 1.

Gas Phase Water Clusters with a Proton or Hydroxide

Concerning the structure and energetics of small protonated water clusters, we note that the RMC optimization above does not affect the O–H repulsive potential at O–H distances less than 1.6 Å (the distance range in which proton transfer barriers generally occur). Hence, proton transfer barriers with DFTB3/3OB and DFTB3/3OBw are very similar, and both show improvement over the previously tested DFTB3-diag+gaus variant⁹⁶ (see the Supporting Information for a discussion based on H⁺(H₂O)₂). In H⁺(H₂O)₆ and H⁺(H₂O)₂₂, DFTB3/3OB is able to provide a description of the Eigen–Zundel balance in low-energy isomers comparable to DFTB3-diag+gaus.⁹⁶ Compared to high-level MP2 calculations, DFTB3/3OB and DFTB3/3OBw give similar results for the relative energies of different conformers for H⁺(H₂O)₆, with the errors actually smaller with 3OB (see the Supporting Information). However, for the large cluster H⁺(H₂O)₂₂, where the oversolvation problem can start to affect the relative energies of the isomers, DFTB3/3OBw is seen to yield much lower errors in the relative energies (see Tables 5 and 6). For one of the two isomers (B and G) of H⁺(H₂O)₂₂ which have the excess proton in the interior of the cluster rather than on the surface, Figure 7 illustrates that DFTB3/3OBw removes “crowding” of water molecules around the hydronium. These results reflect a considerable degree of transferability of the 3OBw parameters optimized for the neutral bulk water solvation structure to systems with an excess proton; this is further confirmed by tests for a proton in bulk water (see below).

Table 5. Energies Relative to Isomer A (kcal/mol) and Zundel/Eigen Character of Low-Energy Isomers of H⁺(H₂O)₂₂^a.

isomer	RIMP2b			DFTB2			DFTB3-diag+gaus			DFTB3/3OB			DFTB3/3OBw
A	0.0	(E)	(E)	0.0	(Z)	(E-Z)	0.0	(E)	(E)	0.0	(E)	(E)	0.0	(E)	(E)
B	9.5	(E)	(E)	8.8	(Z)	(E-Z)	6.2	(E)	(E)	7.0	(E)	(E)	9.1	(E)	(E)
C	2.9	(E)	(E)	0.9	(Z)	(E-Z)	2.1	(E)	(E)	2.5	(E-Z)	(E)	2.5	(E-Z)	(E)
D	7.4	(E)	(E)	1.9	(Z)	(E-Z)	0.0	(E)	(E)	1.8	(E)	(E)	5.2	(E)	(E)
E	6.5	(E)	(E)	4.1	(Z)	(Z)	1.2	(E)	(E)	2.2	(E)	(E)	5.5	(E-Z)	(E)
F	5.3	(E)	(E)	2.6	(Z)	(Z)	3.3	(E)	(E)	1.5	(E)	(E)	1.8	(E)	(E)
G	9.8	(E-Z)	(E)	6.9	(Z)	(Z)	5.3	(E)	(E)	7.0	(E)	(E)	10.5	(E)	(E)
H	2.7	(E)	(E)	1.8	(E-Z)	(E)	–1.2	(E)	(E)	0.5	(E)	(E)	3.8	(E)	(E)
I	2.4	(E)	(E)	1.7	(Z)	(E)	–1.4	(E)	(E)	0.4	(E)	(E)	4.5	(E)	(E)
J	0.5	(E)	(E)	1.6	(E-Z)	(E)	1.0	(E)	(E)	1.1	(E)	(E)	0.9	(E)	(E)
K	12.0	(E)	(E)	8.0	(Z)	(E-Z)	6.6	(E)	(E)	7.8	(E)	(E)	9.8	(E)	(E)
L	3.4	(E)	(E)	4.5	(Z)	(E-Z)	3.3	(E)	(E)	3.3	(E)	(E)	4.0	(E)	(E)
M	6.8	(E)	(E)	3.9	(Z)	(Z)	4.5	(E)	(E)	5.2	(E-Z)	(E)	6.3	(E-Z)	(E)

^aIn the column for each method, the three subcolumns indicate the energy relative to isomer A, the Z/E/E-Z classification according to the criterion based on R_OO,¹³² and the Z/E/E-Z classification according to the criterion based on δ.¹⁰⁰

^bThe RIMP2 relative energies are from ref (133). The RIMP2 results therein were obtained by single-point calculations with the aug-cc-pVTZ basis set at B3LYP/6-31+G(d) optimized geometries. The Z/E/E-Z classification is based on the B3LYP/6-31+G(d) geometries.

Table 6. Summary of Results for H⁺(H₂O)₂₂^a.

	RIMP2b	DFTB2c	DFTB3-diag+gausc	DFTB3/3OB	DFTB3/3OBw
MAXE	0.0	–5.6	–7.5	–5.7	–3.6
RMSE	0.0	2.6	3.8	2.9	1.5
MUE	0.0	2.1	3.0	2.3	1.2
MSE	0.0	–1.7	–3.0	–2.2	–0.4
# of E isomers (def. 1)	13	0	13	11	10
# of E isomers (def. 2)	13	3	13	13	13

^aThe errors are in the energies of 13 low-lying isomers relative to that of isomer A (see Table 5) and are in kcal/mol. “E” denotes Eigen. Def. 1 denotes the criterion based on R_OO,¹³² while def. 2 denotes the criterion based on δ.¹⁰⁰

^bReference (133).

^cReference (96).

Figure 7.

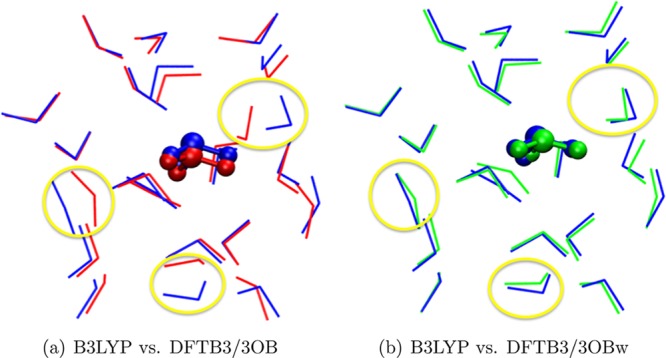
Isomer G of H⁺(H₂O)₂₂ optimized by different methods. Blue, B3LYP/6-31+G(d); red, DFTB3/3OB; green, DFTB3/3OBw. The yellow circles highlight the water molecules “crowding” around the central hydronium in the DFTB3/3OB optimized structure.

When finite temperature effects are considered, the Eigen–Zundel balance in protonated water clusters remains well described with the 3OBw parameters. An example studied in previous work is the “magic” cluster, H⁺(H₂O)₂₁. As shown in Figure S6 (Supporting Information), the results using DFTB3/3OBw compare well with DFTB3-diag+gaus, which was found⁹⁶ to be consistent with CPMD-BLYP studies.¹³⁴ By contrast, DFTB2 is qualitatively different, especially at temperatures higher than 150 K.

For the hydroxide–water clusters, both DFTB3/3OB and DFTB3/3OBw predict somewhat shorter O–O and O–H distances around the hydroxide ion in the small gas-phase clusters (H₂O)₂OH^– and (H₂O)₃OH^–, in addition to a very symmetric (H₂O)OH^– when compared to MP2/aug-cc-pVD(/T)Z (see the Supporting Information). For an isomer of (H₂O)₄OH^– with three water molecules H-bonded to the hydroxide ion and one water molecule in the “second solvation shell” of OH^–, while DFTB3/3OB optimization results in a collapse to an isomer with a tetra-coordinated OH^–, the DFTB3/3OBw optimized structure remains close to the MP2/aug-cc-pVDZ structure (Figure 8b). For both (H₂O)₄OH^– and (H₂O)₅OH^–, the relative energies of the two isomers investigated here are close at the levels of MP2/aug-cc-pVDZ and DFTB3/3OBw (see Table 7). By comparison, DFTB3/3OB overestimates the stabilization of isomer I of (H₂O)₅OH^– (see the Supporting Information for structures), which has a more highly coordinated OH^–. Therefore, the DFTB3/3OBw variant also improves the oversolvation of a hydroxide.

Figure 8.

Optimized structures of two isomers of (H₂O)₄OH^– with MP2/aug-cc-pVDZ (colored by atom type), DFTB3/3OB (colored in blue), and DFTB3/3OBw (colored in green). The starting structures are based on ref (135). The black dotted circle depicts the collapse of a tricoordinated OH^– structure to a tetra-coordinated OH^– structure with DFTB3/3OB.

Table 7. E_IsomerI – E_IsomerII for (H₂O)₄OH^– (Figure 8) and (H₂O)₅OH^– (See the Supporting Information for Structures).

	ΔE (kcal/mol)
	(H2O)4OH–	(H2O)5OH–
MP2/aug-cc-pVDZ	–4.4	0.1
DFTB3/3OB	–1.2	–1.8
DFTB3/3OBw	–4.5	–0.6

Excess Proton in the Bulk

The DFTB3/3OBw variant leads to an improved solvation structure around a proton in bulk water, compared to earlier variants of DFTB.⁹⁶ This is evident from Table 8 which shows that the integration of the first peak of different kinds of RDFs from DFTB3/3OBw leads to coordination numbers in good agreement with available EPSR, CPMD-HCTH, and MS-EVB3 data. Figure 9 further helps to illustrate the loss of oversolvation of the hydrated proton, with the first peak of the O₀–O RDF from DFTB3/3OBw almost completely comprised of the three nearest neighbors of the hydronium, in contrast to the situation with DFTB3/3OB. Parts a and b of Figure 10 show that, with the new parameters, the RDFs of water O atoms about the “hydronium” oxygen and hydrogen atoms, represented by g_O0–O and g_H0–O, respectively, have a better position for the first peak and a very distinct first minimum, in addition to much more pronounced second and third solvation shells for the O₀–O RDF, compared to other DFTB3 variants. The improved position of the first peak is also reflected in the better agreement between MP2/aug-cc-pVDZ and DFTB3/3OB for the position of the minima in the H₅O₂⁺ potential curves (see the Supporting Information), and in the absence of a split first peak in g_H0–O (unlike DFTB3-diag+gaus⁹⁶). The large improvement in the solvation structure is also reflected in other RDFs like g_O0–H, g_O1x–O, and g_O1yz–O, as illustrated in the Supporting Information.

Table 8. Integrated First Peak of Different RDFs Associated with an Excess Proton in Bulk Water.

	gO0–O	gO1x–O	gO1yz–O	gO0–H
EPSRa	2.1			10–12
CPMD-HCTHb	3.0	3.1	3.7
MS-EVB3c	3.0			10–12
DFTB3-diag+gausd	4.5	5.4	6.1	16
DFTB3/3OB	4.8	5.4	6.0	12.7
DFTB3/3OBw	3.3	4.2	4.3	11

^aReferences (136 and 137).

^bReference (100).

^cReference (138).

^dReference (96).

Figure 9.

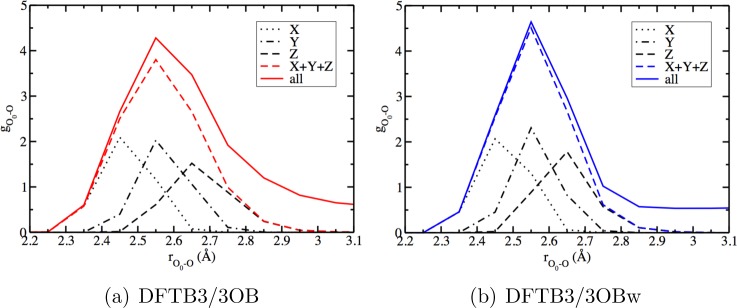
Decomposition of the first solvation peak of the O₀–O radial distribution function for bulk water with an excess proton (O₀ is the hydronium oxygen). The curves labeled X, Y, and Z represent the contributions of O_1x, O_1y, and O_1z, respectively. The curve labeled X+Y+Z represents the total contribution from these three atoms, and that labeled “all” represents the g(r) for all the water O atoms.

Figure 10.

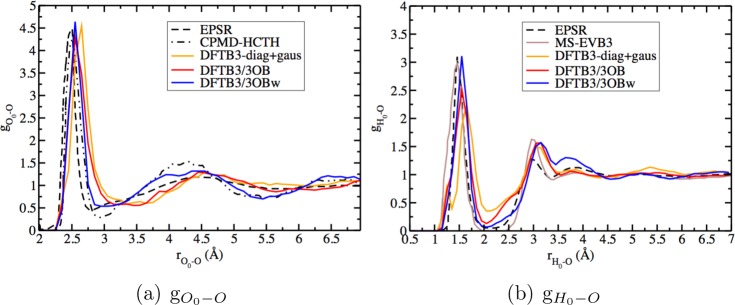
RDF of water O atoms around the hydronium O, denoted O₀, and around the hydronium hydrogen, denoted H₀. The EPSR, CPMD-HCTH, MS-EVB3, and DFTB3-diag+gaus data are from refs (136) and (137), ref (100), ref (138), and ref (96), respectively. For additional plots, see the Supporting Information.

In previous work,⁹⁶ we found that water molecules around the “hydronium” occupy so-called interstitial sites when DFTB3-diag+gaus is used. The SDFs from DFTB3/3OBw plotted in Figure 11 (see also the Supporting Information for the SDFs of water O atoms around the hydronium O) and compared to those from DFTB3/3OB reveal elimination of water population in the interstitial sites and hence a correct water distribution around the central “hydronium”.

Figure 11.

SDF of water O atoms around the hydronium H atoms (left, side view; right, top view) for a system comprised of an excess proton in bulk water. The different colors denote different H–O distance ranges. Only SDF > 3 is shown. Green, 0.0 Å < r_H0–O < 2.0 Å; blue, 2.0 Å < r_H0–O < 2.5 Å.

Compared to DFTB3-diag+gaus,⁹⁶ both DFTB3/3OB and DFTB3/3OBw provide a better description of the energetics of proton transfer in bulk water (Figure 12). Both of the 3OB variants predict the Zundel configuration to be the “transition state” and the Eigen configuration to be the “resting state” for the proton transfer, in agreement with CPMD-HCTH¹⁰⁰ and MS-EVB3.¹³⁸ While the proton transfer barrier is somewhat higher than that predicted by CPMD-HCTH¹⁰⁰ (more so with DFTB3/3OBw), previous (classical) MS-EVB2 and MS-EVB3¹³⁸ models also predict this barrier to be close to ∼1 kcal/mol.

Figure 12.

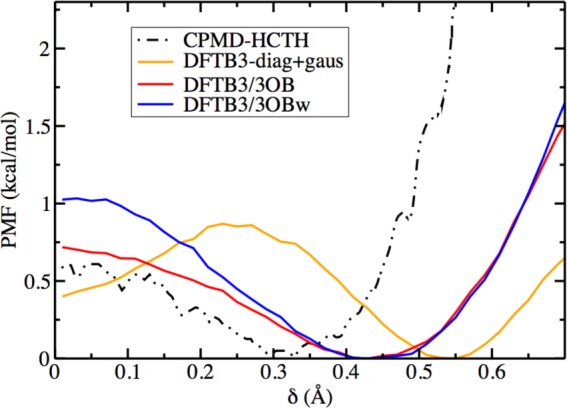
Potential of mean force for the transfer of an excess proton in bulk water. The reaction coordinate is δ = |r⃗_O0H – r⃗_O1xH|, where O₀ is the hydronium oxygen and O_1x is the “special pair” partner of O₀. δ ≤ 0.1 corresponds to the Zundel form, and δ ≥ 0.2 corresponds to the Eigen form. The CPMD-HCTH and DFTB3-diag+gaus data are from refs (100) and (96), respectively.

Hence, overall, the results in this section illustrate that the RMC-optimized 3OBw parameters, developed on the basis of the solvation structure of neutral bulk water, are fairly transferable to a system with an excess proton in the bulk, providing an encouraging description of both the solvation structure and the proton transfer energetics.

Excess Hydroxide in the Bulk

Choi et al.¹⁰¹ recently reported the performance of several variants of DFTB for the description of the solvation structure and dynamical properties of a hydroxide ion in bulk water. All investigated variants, including DFTB3/3OB, were found to predict OH^– to be oversolvated in the bulk. We find that DFTB3/3OBw can provide appreciable improvement in this oversolvation behavior. In the discussions below, to gain insight into the dynamical behavior of the hydroxide ion, we make use of a coordinate δ = min|r_O0H – r_OaH| (also employed in the relevant literature;^{101,139−141} note that this is different from δ defined in the section on proton in bulk water). Here, O_a is any water O atom which shares a hydrogen (H) with the hydroxide oxygen, O₀, such that the associated displacement coordinate δ is the smallest. Large values of δ imply configurations far from a proton transfer event, while low values are associated with configurations likely involved in proton transfer. Below, to be consistent with the literature,^139,140 we choose δ ≥ 0.5 and δ ≤ 0.1 to classify configurations far from and near a proton transfer event, respectively. The hydroxide hydrogen is designated H′.

As Figure 13 illustrates, compared to DFTB3/3OB, DFTB3/3OBw leads to a narrowing of the first peak of both g_O0–O and g_O0–H. Integration of the first peak of g_O0–O from DFTB3/3OBw leads to a value of 5.8 (Table 9), which, while still greater by 1 compared to CPMD-BLYP simulations,^139,140 is an improvement over the value of 6.9 from DFTB3/3OB. The first peak of g_O0−H also integrates to a value (4.9) higher by 1 compared to the CPMD-BLYP value of 3.9, but providing improvement over the DFTB3/3OB value of 5.6. Compared to results published by Choi et al.,¹⁰¹ DFTB3/3OBw performs better than all other variants (including DFTB2(-γ^h) which Choi et al. found to be better than/on par with DFTB3/3OB for these properties).

Figure 13.

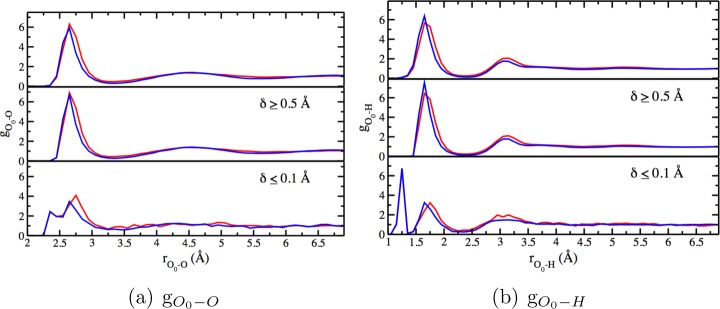
RDF (a) of water O atoms around the hydroxide O, denoted O₀, and (b) of water H atoms around O₀. The topmost panel in both parts a and b compares the RDFs obtained with DFTB3/3OB (in red) and DFTB3/3OBw (in blue), using all simulation data. The middle panels show the same comparison for configurations far from proton transfer events (large δ), while the bottom panels do so for configurations corresponding to the “transition state” of proton transfer (small δ).

Table 9. Integrated First Peak of Different RDFs Associated with a Hydroxide Ion in Bulk Water^a.

	gO0–O			gO0–H			gH′–O
	all	δ ≥ 0.5	δ ≤ 0.1	all	δ ≥ 0.5	δ ≤ 0.1	all	δ ≥ 0.5	δ ≤ 0.1
DFTB3/3OB	6.9	7.0	6.4	5.6	5.7	4.5	0.8	0.8	0.8
DFTB3/3OBw	5.8	5.9	5.4	4.9	5.0	4.0	0.7	0.7	0.7
CPMD-BLYP139,140	4.8			3.9			0.67

^aThe hydroxide oxygen is denoted as O₀, and its hydrogen, as H′.

The SDF of water O atoms about O₀ in Figure 14a (note that the SDF does not show the oxygen population H-bonding to the hydroxide hydrogen) reveals the presence of a H-bond donor population below the “expected” square planar arrangement of H-bond donors around O₀, thus overestimating the H-bond donor population by 1. Figure 14b shows greater oversolvation of hydroxide with DFTB3/3OB compared to DFTB3/3OBw (higher density of green spheres) in “interstitial” sites.

Figure 14.

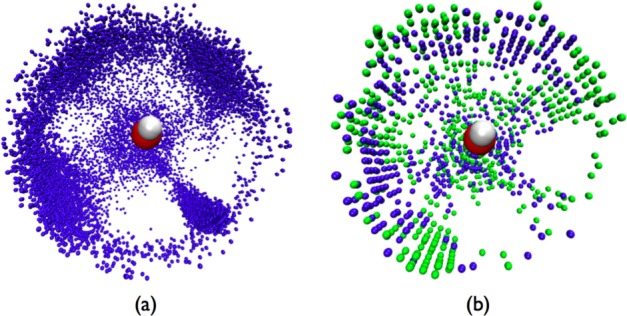
SDF of water O atoms around a hydroxide O solvated in bulk water: (a) SDF from DFTB3/3OBw; (b) a difference plot of the SDF from DFTB3/3OBw (in blue) and DFTB3/3OB (in green). In both cases, points with SDF > 3 and within 3 Å from the hydroxide O are shown (but, for clarity, excluding those within 2.5 Å from the hydroxide H). The reference coordinate frame is defined such that the hydroxide O is at the origin, the hydroxide ion is aligned with the z axis, and the hydroxide ion and its nearest H-bonding water H atom constitute the xz plane. For part a, a 0.1 Å bin-width along r and a 1° bin-width each along θ and ϕ are used. For part b, for clarity, a 0.2 Å bin-width along r and a 5° bin-width each along θ and ϕ are used.

The H-bond acceptor population around the hydroxide ion is also improved with DFTB3/3OBw, as reflected in the lowering of the first peak height (Figure S11, Supporting Information (top panel)) and a lower integrated first peak value compared to DFTB3/3OB (Table 9).

Concerning the dynamical behavior of the hydroxide ion, while it is clear from Table 9 that for both DFTB3/3OBw and DFTB3/3OB, in concert with proton transfer, a reduction of the H-bond donor population around the hydroxide ion takes place, it is less clear whether proton transfer is accompanied by a change in the H-bond acceptor population. While the middle and bottom panels of Figure S11 (Supporting Information) indicate a sharper first peak in the H′–O RDF accompanying proton transfer, the degeneration of the first peak into a broad plateau for large δ values observed in CPMD-BLYP simulations^139,140 is not observed even with DFTB3/3OBw. Figure S12 (Supporting Information) shows the proton transfer barrier with DFTB3/3OBw to be similar to that with DFTB3/3OB (although with a slight improvement in the position of the minimum), implying that the lowering in H-bond donor population by 0.5–0.7 with DFTB3/3OBw compared to DFTB3/3OB does not have an appreciable impact on the proton transfer barrier. Thus, the dynamical properties of solvated hydroxide described by DFTB3/3OBw are similar to those reported by Choi et al.¹⁰¹ using DFTB3/3OB.

Hence, while the 3OBw parameters yield appreciable improvement in the solvation structure around the hydroxide ion in bulk water compared to previous DFTB variants (besides improving the structure and energetics of gas-phase hydroxide clusters), the dynamical properties of the hydroxide ion and remaining deficiencies in the description of solvation structure still present a challenge which can guide further development of DFTB. This is a somewhat expected result in that treating hydroxide solvation likely requires a careful description of the charge dependence of Pauli repulsion, which is missing in the current formulation of DFTB and also not captured empirically in the RMC procedure based on neutral bulk water (the modification of the O–H repulsive potential occurs mainly at long range).

Proton Transfer Barrier in a Model Channel

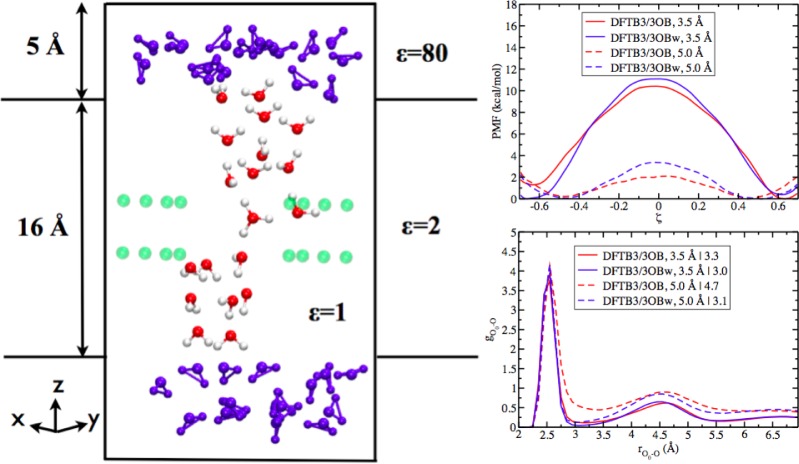
Having observed the difference between DFTB3/3OB and DFTB3/3OBw results for the hydration of excess proton, it is important to ask whether such a difference leads to any significant impact on the computed proton transfer energetics in biomolecules. To answer this question, we study the proton transfer in a simplified ion channel model that we established in previous work^142,143 (Figure 15, left); the advantage of using such a model system over more realistic biomolecular systems is that issues with QM/MM interactions^73,144 and sampling can be largely avoided, allowing us to directly assess the impact of different proton hydration in a confined environment. We study two model channels with a radius of 3.5 and 5 Å, respectively, to explore the magnitude of the effect with different degrees of confinement; these correspond to typical sizes of proton conducting channels found in biomolecules. The computational setup and simulation protocols for the proton transfer PMF along the collective ζ coordinate follow those reported in refs (142) and (143). Umbrella sampling involves 13 windows for each setup; the production run for each window is 500 ps for the wide channel and 800 ps for the narrow channel.

Figure 15.

Left: An illustration of the model channel. The “bulk” MM water molecules are shown in blue, while the QM water molecules are colored by atom type. The eight dipoles are shown in green. For the channel of radius 3.5 (5.0) Å, the (inner region) box edge-length along X and Y is 17.2 (20.4) Å. Each dipole is comprised of charges of +0.5e (+0.6e) and −0.5e (−0.6e) separated by 1.5 Å for the narrower (wider) channel, with the positive end pointing toward the channel. Top right: Proton transfer free energy profiles along ζ (two MM oxygen atoms fixed at (0, 0, 10) and (0, 0, −10) are used as the donor and acceptor for defining ζ. Bottom right: RDF of water O atoms about the “hydronium” O when it is near the center of the channel along z. The number after “|” in the legend results from integration of the first peak of the RDF.

As shown in Figure 15 (right top panel), the description of proton hydration has an impact on the computed barrier for the proton transport, and the magnitude of the effect varies depending on the degree of confinement. The levels of hydration of the proton when it is at the center of the channel (along ζ, see Figure 15, right bottom panel) differ with the 3OB and 3OBw models by 0.3 water molecules in the first solvation shell in the narrower channel model; the difference goes up to 1.6 water molecules in the wider channel model. Nevertheless, the difference in the PMF barriers between DFTB3/3OB and DFTB3/3OBw is on the order of 1–2 kcal/mol. Since this level of error in the energetics does not lead to any qualitative difference in most mechanistic analysis, we confirm that DFTB3/3OB is well suited for mechanistic analysis of proton transport in biomolecules.

Along this line, a recent study¹⁴⁵ analyzed the issue of proton oversolvation in a synthetic ion channel and concluded that the findings “called into question the applicability of the DFTB3 approach for proton transport in biomolecules”. Although the issue of proton oversolvation should certainly be resolved, our study here highlights that the key energetic properties for proton transport in biomolecules from DFTB3/MM simulations are meaningful for most purposes. The work of ref (145) compared proton dynamics in the channel at the time scale of 100 ps and observed a qualitative difference between DFTB3/MM and B(3)LYP/MM simulations. What ref (145) failed to point out, however, is that the local free energy minimum for the proton in the middle of the channel is separated from the mouth of the channel by a small barrier of merely 2 kcal/mol according to MS-EVB calculations.¹⁴⁶ Therefore, small differences in barrier heights from different calculations will lead to distinct proton dynamics at the 10–100 ps time scale. A more relevant comparison is the PMF profile, as we have done here for the model channel, and the results indicate that proton oversolvation likely has a limited impact on the proton transfer energetics for most purposes.

QM/MM Simulations Involving Water: Importance of the QM-MM Hamiltonian and Methods of Calibration

In most biological and many chemical applications, the bulk of the water environment can be treated at the classical level with only the site (solute) of interest treated at the QM level. The interface between the QM region and nearby MM atoms is expected to be important to the quantitative aspect of the simulation. In typical QM/MM implementations for biological applications,¹⁴⁷ the QM-MM interaction includes electrostatic and van der Waals contributions (we will not discuss QM/MM partition across covalent bonds here^147−150). The electrostatic component is usually described with one-electron Hamiltonians that involve the interaction between QM electrons and MM charge distributions, which, depending on the force field, may include point charges, permanent multipoles, and polarizabilities. The van der Waals interactions are usually taken to be decoupled from the determination of the QM wave function/density and described by the empirical Lennard-Jones expression,¹⁵¹ although more physical expressions like the Buckingham potential have been used;¹¹¹ a formulation of QM-MM van der Waals interactions that depend on the charge distribution of the QM region has also been developed.¹¹¹ In terms of empirical parameters, the simplest QM/MM implementation involves only the Lennard-Jones parameters for the QM atoms; several previous studies^144,151 have shown that the QM-MM van der Waals interactions may substantially perturb the structural properties of the MM atoms around the QM region (e.g., solvent distribution around the QM solute); the effect on energetic properties of typical interest, such as reduction potential, pK_a, and reaction energies, is, however, more modest (1–2 kcal/mol). For quantitative calculations, nevertheless, a careful parametrization of the QM van der Waals parameters is worthwhile.

Regarding the QM-MM electrostatics, there is no additional parameter in the most straightforward implementation. It has been recognized, however, that, when point charge MM models are used, it is beneficial to smear the MM charges to partially take the effect of charge penetration into consideration.^152,153 This protocol involves additional parameters such as the width of the smeared MM charges, which are usually described with Gaussian functions. Specifically for DFTB, we also recognized the importance of treating the QM-MM electrostatics more carefully, especially when the QM region is substantially charged. In the following sections, we first briefly review our recent development along this line and then discuss ways that QM-MM interactions can be calibrated, including a novel sampling protocol that can be particularly useful in this context.

QM-MM Electrostatics in DFTB/MM Simulations

The most physical way to describe QM-MM electrostatics should consider the finite size of the corresponding charge distributions, as in the Gaussian-blur approach.^152,153 Semiempirical methods⁴⁵ do not need to evaluate the additional core integrals between the electron density and the external point charges, but the idea of charge “blurring” was implemented already in their QM/MM extensions. For example, the pioneering QM/MM work by Field and co-workers evaluated the QM-MM electrostatics with the ⟨ss|ss⟩ electron integral¹⁵⁴ that takes the form of the Klopman–Ohno (KO) expression⁴⁵ for the two-center two-electron integral, ⟨μ_aν_a|λ_bσ_b⟩,

4

where the summations are over the multipole charges (Q_i’s) used to mimic atomic orbitals and d_i’s are parameters determined on the basis of the condition that as the distance R_ab approaches zero the expression reduces to known one-center two-electron integrals. For the interactions between two spherical charges (s orbitals), the d_i’s are nothing but the corresponding inverse chemical hardness values (1/U_i), which are fitted in semiempirical methods to reproduce certain molecular properties. Note that these inverse chemical hardness values represent on the one hand the electron–electron interaction and on the other hand the atomic size.^46,81 Also, the KO integral is very similar to the γ_ab function in the DFTB total energy expression, although the KO expression has a simpler functional form.

In semiempirical theory, ξ in eq 4 is set to equal unity, but to model the atomic size in QM/MM interactions, which is an effective blurring of the point charges, a scaling of ξ < 1 seems appropriate. In practice, several semiempirical QM/MM implementations have found different optimal values of ξ. In ref (154), ξ = 1 was chosen and U_j was set to zero when j indicates a MM atom. In other approaches, ξ was either optimized to roughly 0.1¹⁵⁵ or was set to zero.¹⁵⁶ In an early DFTB2/MM implementation,¹⁵⁷ we found that ξ = 0 leads to the best DFTB2/MM hydrogen bonding energies, and this value was also adapted in a subsequent DFTB2/MM implementation in CHARMM.⁶¹ This choice is related to the fact that DFTB2 underestimates hydrogen bonding energies systematically, and therefore an undamped 1/R scaling leads to improved interaction energies. However, the QM-QM, QM-MM, and MM-MM hydrogen bonding energies are then not well balanced. With DFTB3/3OB, hydrogen bonding energies are better treated,⁸⁴ and thus, a simple 1/R scaling is no longer appropriate.

Therefore, we recently explored using the KO expression to compute DFTB3-MM electrostatic interactions as follows:⁷³

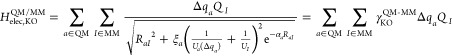5

in which ξ_a and α_a are element dependent parameters; together with the van der Waals parameters in the QM-MM Hamiltonian, there are four QM-MM parameters for each element type. For the Hubbard parameter of a MM atom (U_I), we simply took the computed value for an atom.⁸⁴ We note that, by including the charge dependence of the Hubbard parameters in DFTB3, the effective atomic size information is directly integrated into the SCF determination of the QM wave function/density. Due to the difference in physical origin, this does not replace the charge dependence of the QM-MM van der Waals interaction,¹¹¹ although it is an important step toward the reliable description of chemical reactions that involve a significant charge redistribution.

Calibration of QM-MM Hamiltonian: From Clusters to the Condensed Phase

To ensure transferability, we take the parameters to be element-dependent; thus, there are four parameters (ξ_a, α_a in eq 5 and the QM Lennard-Jones parameters) per element. Alternatively, we could make ξ element-independent as in previous semiempirical approaches,¹⁵⁵ and instead fit the Hubbard parameters for the MM atoms (U_I). What is the best approach to determine these parameters? In most previous studies,^144,151 parameters in the QM-MM Hamiltonian (e.g., the QM Lennard-Jones parameters) were empirically fitted on the basis of small molecule models, following the way that nonbonded parameters are fitted in empirical force fields.¹⁵⁸ For example, a MM water molecule is used as a probe to interact with a “solute” in different geometries, the QM-MM Hamiltonian is adjusted such that QM/MM results best match those from full QM calculations.

In our recent work,⁷³ we were concerned that these small solute–water systems were not representative of the solution environment. Therefore, an alternative strategy was followed in which larger clusters that included solutes interacting with multiple water molecules were studied; the structures were collected on the basis of DFTB/MM simulations of the solute in water. Test calculations indicated that including multiple water molecules was essential to a successful parametrization and including only pairwise models as in previous studies¹⁴⁴ did not capture the complexity of interactions in the condensed phase and therefore did not lead to as transferrable parameters. Calculations in ref (73) showed that this strategy led to a set of KO parameters that appeared to be rather transferrable for the SCC-DFTBPR⁸⁹ variant of DFTB; e.g., for 16 stable states and 24 transition states involved in 10 model phosphate hydrolysis reactions in RNA from the QCRNA database established by the York group,¹⁵⁹ which were not included in the fitting of the KO parameters, the mean unsigned errors (MUEs) were 3.5 and 4.8 kcal/mol for the stable and transition states, respectively, for the comparison of solute–water interaction between SCC-DFTBPR/MM and full SCC-DFTBPR calculations. We note that, due to the significant charges of these molecules, the total solute–water interactions are on the order of 100–200 kcal/mol; thus, a MUE of ∼4–5 kcal/mol is very satisfactory. For instance, by comparison, the MUEs for calculations that used the original (Coulombic) QM-MM model were 14.2 and 17.6 kcal/mol for the stable and transition states, respectively. The use of γ_KO^QM-MM in SCC-DFTBPR/MM simulations was essential in the study of several phosphate hydrolysis reactions in solution⁷³ and enzymes.⁷¹ For example, in our study⁷¹ of mono ester hydrolysis in alkaline phosphatase (AP), using the Coulombic QM-MM Hamiltonian led to significant overpolarization and thus instability in the simulations. With γ_KO, SCC-DFTBPR/MM simulations were much more stable; both structural and energetic properties of mono ester hydrolysis in two enzymes in the AP superfamily were consistent with available experimental data.

Despite these encouraging initial results, we note that the preliminary QM/MM-KO parameters were fitted on the basis of gas phase clusters rather than an authentic solution environment; moreover, the reference results were full SCC-DFTBPR calculations rather than high quality QM or experimental data. Therefore, a more robust protocol is to parametrize the QM-MM Hamiltonian based explicitly on condensed phase properties and experimental data; as an initial step, we use solvation free energies as the reference data, similar to force field developments.^106,158 To illustrate the promise of this protocol, we show the solvation free energies computed using several DFTB models with different QM-MM Hamiltonians for several neutral and charged small molecules. These calculations take advantage of the thermodynamic cycle in Figure 16, which has been adopted by several authors in the past,¹⁶⁰ most notably Gao¹⁶¹ and Warshel.¹⁶² The advantage of following this thermodynamic cycle is that the steps that require the most sampling are carried out with MM potential functions, while the most expensive QM/MM calculations are involved in the vertical processes only, which converge much faster due to the relatively small perturbation in solute–solvent interactions.

Figure 16.

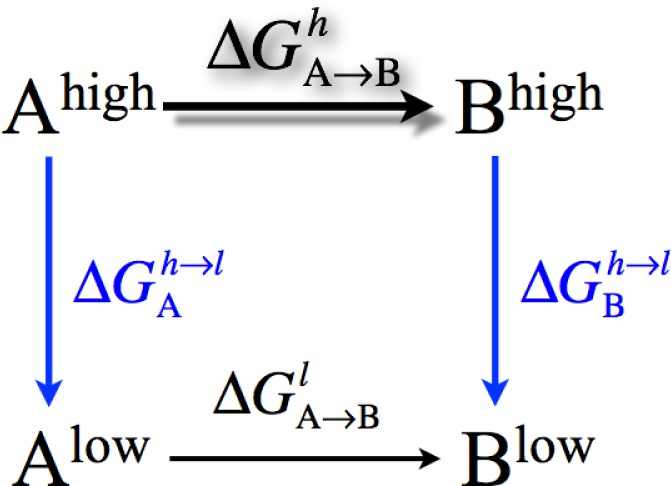
A general thermodynamic cycle used to compute the free energy change of a process (A → B) at different (high, low) levels of theory. For this work, the process corresponds to solvation and the high (low) level of theory corresponds to the treatment with a QM (MM) potential function. Thus, the high-level potential function is only used in simulations that involve the vertical processes: conversion of the solute from a MM to a QM description once in the gas phase and once in the solution phase.¹⁷¹

As shown in Table 10, the solvation free energies are modestly underestimated with the original DFTB2/MM model, when the QM atoms use van der Waals parameters from the CHARMM27 force field.¹⁵⁸ With DFTB3 as the QM model and otherwise the identical QM-MM Hamiltonian, the solvation free energies are typically overestimated, in agreement with the expectation based on the larger magnitudes of DFTB3 charges as discussed above. With the γ_KO^QM-MM parametrized in ref (73), SCC-DFTBPR/MM simulations lead to underestimated solvation free energies for charged solutes. Although the qualitative trend is expected since the KO expression (eq 5) damps QM-MM interactions, the magnitude of the effect is surprisingly large. As seen in Figure 17, the number of solvent molecules in the first solvation shell is smaller by ∼1 in the γ_KO based SCC-DFTBPR/MM simulations compared to either MM or DFTB/MM simulations using the Coulombic (1/R) QM-MM Hamiltonian.

Table 10. Relative Solvation Free Energy ΔΔG_gas→aq(MM → QM) (in kcal/mol) with Different QM and QM-MM Electrostatic Hamiltonians^a.

		DFTB2	SCC-DFTBPR	DFTB3/3OB
solute	MM ref. (Exp.)b	Coulomb	Klopman–Ohno (eq 5)c	Coulomb
H2O	–6.6 (−6.3)	+4.4		+1.7
CH3COOH	–4.5 (−6.7)	–0.1	–0.0 (+0.0)	–3.4
CH3COO–	–81.9 (−77.6/–80.7163)	+3.1	13.1 (15.3)	–5.4
CH3O–	–102.2 (−95.0)	+6.8	23.8 (24.9)	–3.9
H3PO4	–15.2 (−26.0)	–1.4	–3.9 (−3.8)	–8.8
H2PO4–	–80.8 (−76.0)	–1.7	10.1 (11.1)	–17.2

^aThe MM here is the CHARMM22 force field. The water molecules are treated with TIP3P. Unless specified otherwise, the QM atoms use the standard CHARMM van der Waals parameters.

^bThe “MM ref.” values are absolute solvation free energies computed following the standard protocol^163,164 with periodic boundary conditions; no correction related to the gas/liquid interface has been included.^165−167 Values in parentheses are experimental values from ref (168) for the first four solutes and from ref (169) for the phosphate species.

^cThe values in parentheses use the CHARMM van der Waals parameters for the QM atoms; those without parentheses use the van der Waals parameters optimized in ref (73).

Figure 17.

Oxygen–oxygen radial distribution functions (solid lines) for water near a charged QM solute (acetate or methoxide) in DFTB/MM simulations with different DFTB models and QM-MM electrostatic Hamiltonians; the integrated distribution functions are also shown as dotted lines.

Calculations of solute–solvent interactions using clusters collected from different windows confirm our previous observation⁷³ that γ_KO^QM-MM based SCC-DFTBPR/MM gives results very consistent with full SCC-DFTBPR and DFTB3, which give systematically weaker solute–solvent interactions than both full MM and 1/R based DFTB3/MM calculations (see Table S3 in the Supporting Information). Since the nonpolarizable TIP3P water model is overpolarized for the purpose of condensed phase applications, this observed trend for gas-phase clusters is not surprising. We defer a more detailed discussion to a separate work that reports the systematic parametrization of QM-MM Hamiltonian (including QM van der Waals parameters) for DFTB3. The purpose here is to illustrate that parametrizing the QM-MM Hamiltonian explicitly based on condensed phase properties is potentially very important. We note that, since the change of local solvation during a typical chemical reaction is unlikely very large, the errors in computed reaction free energies^71,73 due to the QM-MM Hamiltonian are not as large as those in the solvation free energies shown in Table 10. Nevertheless, adequately reproducing solvation free energies is clearly much more preferable than relying on error cancellation. Along this line, an equally important benchmark that also benefits from the thermodynamic cycle in Figure 16 is the calculation of QM/MM binding free energies of ligands to protein (enzyme) active sites. These will be reported elsewhere.

To facilitate the use of solvation/binding free energies in the parametrization and calibration of the QM-MM Hamiltonian, it is essential to maximize the efficiency of the MM ↔ QM/MM free energy perturbation simulations. When the MM and QM/MM potential functions have a good overlap in distribution, it is possible to use reweighing techniques based on, for example, a novel application of the Bennett acceptance ratio approach.¹⁷⁰ In general, however, it is difficult to predict the degree of overlap between the MM and QM/MM distributions, especially when the solute is flexible. Therefore, it is valuable to develop efficient free energy protocols that involve explicit sampling using the QM/MM potential function but without overwhelming computational cost.

Motivated by this consideration and other applications,⁷⁸ we have recently developed a novel sampling protocol referred to as the integrated Hamiltonian sampling (IHS).¹⁷¹ As explained in more detail in ref (171), in IHS, we introduce an effective potential (U_b(R)) whose canonical distribution is the integrated distributions of the intermediate and two-end states

6

where Ω(λ) is a weight function to be determined and U_λ takes the usual form (although other forms are also possible, like in free energy perturbations in general),

7

In the specific case of MM ↔ QM/MM free energy perturbation, U₀ and U₁ correspond to MM and QM/MM potential functions, respectively. In the more general applications, U₀ can be the potential function of a physical system while U₁ the potential function of a fictitious system introduced to enhance the sampling of U₀; e.g., specific torsional barriers or nonbonded interactions are reduced.

The key to the efficiency of IHS lies in the choice of the weight function Ω(λ). The aim is to weight the contributions from different intermediate Hamiltonians (potential functions) such that transition among them, including the end states, is facile. To this end, one criterion is to set the expectation value of the probability for the weighted intermediate states to be uniform

8

where ⟨···⟩_b is the ensemble average over the configurations sampled with the potential U_b (eq 6). Guided by this criterion, we have developed an efficient protocol to optimize the weight function (discretized as Ω(λ_i)) on the fly using a combination of the histogram flattening¹⁷² and weighted histogram¹⁷³ approaches. This automated protocol makes it rather straightforward to employ multiple end-state Hamiltonians to facilitate sampling along different chemical and conformational degrees of freedom. The IHS approach is closely related to several enhanced sampling techniques in the literature; its development was inspired by the integrated tempering approach of Gao,^174,175 and it has similar motivations to Hamiltonian replica exchange molecular dynamics (HREMD),^176,177 enveloping distribution sampling,¹⁷⁸ and λ-dynamics.¹⁷⁹ For more detailed discussions, see the original reference.¹⁷¹ We only point out here that IHS requires only one trajectory, and the computational cost is essentially independent of the number of intermediate Hamiltonians if simple interpolation between the end-state Hamiltonians (eq 7) is used. Therefore, the computational cost of IHS can be substantially reduced compared to HREMD, especially when the distributions of the end-state Hamiltonians do not overlap well and many intermediate states are required for efficient sampling. This feature is particularly desirable when expensive Hamiltonians such as (ab initio) QM/MM potentials are needed.

As an illustration of the convergence behavior of IHS, we show the convergence of the weight function for the MM ↔ QM conversion for an acetate ion in solution. As Figure 18 indicates, satisfactory convergence is reached essentially after about 50 ps. Simulations in ref (171) also indicate that the standard deviation of computed free energies is substantially smaller in IHS simulations when compared to regular free energy perturbation simulations of similar length (per λ window). It is also straightforward to compute properties for the end-states using trajectories from IHS simulations with proper reweighting.¹⁷¹ Therefore, we anticipate that, by combining efficient IHS and multistate reweighting techniques,¹⁸⁰ it is straightforward to automate optimization of QM-MM Hamiltonians based on solution properties.

Figure 18.

Convergence of weight functions (β^–1 ln Ω(λ_i)) for MM ↔ QM (DFTB2) perturbation of an acetate ion in the gas phase (top) and water (bottom), using the integrated Hamiltonian sampling (IHS).¹⁷¹ Solvent molecules are described by TIP3P. Cross points describe when the weights were updated, and blue, green, red, cyan, purple, and ochre lines represent λ = 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0, with U₀ and U₁ being QM/MM and MM Hamiltonians, respectively.

Concluding Remarks

The role of water in many chemical and biological processes is clearly beyond being merely a spectator solvent. Depending on the relevant length scale and specific role(s) of water in the problem of interest, different computational models are required. As a bulk solvent under ambient conditions, water is well treated by standard classical force fields because they were parametrized for this purpose. As the condition deviates from ambient conditions, however, the applicability of standard force field models is no longer obvious and careful tests need to be carried out to establish the appropriate model.¹⁸¹ In problems of biological relevance, examples include concentrated solutions, water in the interior of proteins and near the surface of nucleic acids. When water molecules are explicitly involved in the chemistry, such as proton transfers or proton-coupled electron transfers, they clearly need to be treated at a quantum mechanical level. In fact, a quantum mechanical treatment of many-body effects in water appears to be important even for nonreactive events such as ion diffusion; so far, it appears that only a quantum mechanical simulation is able to properly capture the temperature dependence of ion diffusion in water.¹⁸² This recent study again highlights the importance of and subtleties associated with many-body effects in condensed phase systems.

In this article, we have focused on our own studies of water using an approximate density functional theory, DFTB3, which is of interest because many applications require striking the proper balance between accuracy of the potential function and the degree of sampling. Our aim is not to argue that DFTB3 is already a reliable model for water that works under different conditions. Rather, our goal is to explore, with the current formulation of DFTB3, the performance of this method for treating water in different chemical environments, the magnitude and nature of changes required to improve its performance, and factors that dictate its applicability to reactions in the condensed phase with a QM/MM framework. This type of study helps establish both the value and limitations of the DFTB3 based simulations, and helps make clear the developments needed to further improve the accuracy and transferability of the methodology.

In previous studies, we and others found that DFTB3 generally gives encouraging results (e.g., low energy structures) for small water clusters, in both neutral and protonated forms. However, DFTB3 overpredicts the level of solvation of water and an excess proton in the bulk;^{96,99,100,145} there is also a significant tendency to oversolvate hydroxide even in gas phase clusters.¹⁰¹ Likely physical explanations for these limitations have been recognized⁴⁷ and are discussed in this article, which together with recent work of York and co-workers^102,108 highlight the potential importance of including multipole terms and a better treatment of Pauli repulsion in the next generation of DFTB models; the effect of dispersion, whose importance has been discussed for large water clusters^183,184 and bulk water simulations with DFT,^30,185 also needs to be analyzed with the empirical D3 model recently parametrized for DFTB3.¹⁸⁴ What we demonstrate here is that a relatively minor change (on the scale of k_BT) in the 3OB/O–H repulsive potential can substantially improve the description of bulk water structure under ambient conditions; several relevant dynamic properties and the infrared spectrum also show improvements. Moreover, this simple change has a considerable degree of transferability to protonated water clusters and solvated protons; it also improves the solvation of hydroxide, although further improvement of Pauli repulsion for charged species is needed to completely remove the oversolvation of hydroxide.

This simple but ad hoc correction based on the reverse Monte Carlo (RMC) scheme is by no means a satisfactory solution to the description of water in the DFTB framework. In fact, removal of oversolvation with the current RMC scheme is accomplished at the cost of reducing water–water interactions and therefore notably deteriorated heat of vaporization (see the Supporting Information), emphasizing the importance of further extending the DFTB3 model in a more systematic fashion as discussed above. Therefore, the 3OBw model should be applied with caution, especially in applications where there is a significant variation in water density (e.g., a liquid/vapor interface).

By comparing results using DFTB3 models that differ in the description of water, we are able to confirm that proton transfer energetics are adequately described by the standard DFTB3/3OB model for meaningful mechanistic analyses. This finding is consistent with the approach that we have been employing to calibrate the DFTB models over the years for proton transfer studies,^{12,63,92,186,187} i.e., focusing on proton affinities, pK_a values, and relative solvation free energies of different protonation states (including hydroxide¹²). Along this line, it is clear from the discussions here that a careful consideration of QM-MM interaction is also essential, and a robust parametrization requires an explicit consideration of condensed phase properties rather than gas phase clusters only. This requirement demands the development of efficient sampling algorithms, another technical issue that we have briefly touched upon in this article. The issue of sampling is particularly relevant in processes where the change of local hydration level plays a significant role, since such a change may be gated or be part of the kinetic bottleneck.^75,78

As a final reflection, we emphasize again that the accuracy and thus the applicability of any approximate method should be judged in the context of the problem of interest. For the analysis of complex problems, a major part of the challenge for any computational study is indeed to establish the required level of accuracy to properly answer the question. For instance, although an explicit consideration of nuclear quantum effects is not critical to many mechanistic studies at room temperature, it is essential for kinetic isotope effects^188,189 and potentially subtle spectroscopic features.^66,67 Therefore, it is essential to establish the most relevant benchmark calculations, such as pK_a calculations and solvation free energies for the discussion of proton transfers, while short-time behaviors sensitive to barriers of 1–2 kcal/mol¹⁴⁵ are often of more limited relevance. Another useful strategy is to cross-validate the computational results using methods with very different approximations, such as comparing QM/MM and continuum electrostatic models for pK_a predictions.⁷⁵ In the end, the ultimate goal is to establish a conceptual framework to guide the development of novel mechanistic hypotheses and to stimulate new experiments to evaluate them.

Biographies

Puja Goyal received a B.Sc. (2006) in Chemistry from Presidency College, Kolkata, India, an M.Sc. (2008) in Chemistry from the Indian Institute of Technology, Kharagpur, and a Ph.D. (2013) in Chemistry from the University of Wisconsin—Madison. Currently, she is a postdoctoral researcher at the University of Illinois at Urbana–Champaign.

Hu-Jun Qian received a B.S. (2002) in Polymer Materials and Engineering and a Ph.D (2007) in Physical Chemistry from Jilin University. He was a postdoctoral researcher at Technische Universität Darmstadt (2007–2009) and Nagoya University (2009–2011). He joined the faculty of Jilin University in 2011 as an Associate Professor in the State Key Laboratory of Theoretical and Computational Chemistry.

Stephan Irle received a Diploma in Chemistry (1992) from the University of Siegen in Germany and a Ph.D. (1997) in Chemistry from the University of Vienna. In 1998, he became Associate Scientist at the Cherry L. Emerson Center for Scientific Computation at Emory University in Atlanta, GA, USA. In 2006, he moved to Japan as an Associate Professor at Nagoya University, where he became a full Professor of Chemistry in 2011. Since 2013, he also holds an appointment as PI at the WPI-Institute for Transformative Bio-Molecules (ITbM).

Xiya Lu received her B.S. (2010) in Chemistry from Nankai University in China. Currently, she is a Ph.D. candidate in Chemistry at University of Wisconsin—Madison under the supervision of Professor Qiang Cui. Her thesis research focuses on the parameterization of DFTB3 and QM/MM free energy simulations in metalloenzymes.

Daniel Roston received a B.A. (2007) in Chemistry from Hamilton College and a Ph.D. (2013) in Chemistry from the University of Iowa. He is currently a post-doctoral researcher at the University of Wisconsin.

Toshifumi Mori received a B.S. (2005) from Kyoto University and an M.S. (2007) and a Ph.D. (2010) in Chemistry from the Graduate School of Science, Kyoto University. After being a postdoctoral researcher at Stanford University and University of Wisconsin—Madison, he became an Assistant Professor at the Institute of Molecular Science in 2013.

Marcus Elstner received his Diploma in Physics (1993) from Technical University of Berlin and Ph.D. from the University of Paderborn (1998). Following postdoctoral studies at Harvard University with Prof. Kaxiras, he was a Junior Professor in Paderborn. In 2006, he joined TU Braunschweig, and in 2009, he moved to Karlsruhe Institute of Technology as a Professor of Theoretical Chemical Biology.

Qiang Cui received a B.S. (1993) in Chemical Physics from the University of Science and Technology of China and a Ph.D. (1997) in Chemical Physics from Emory University, working with Professor Keiji Morokuma. Following postdoctoral studies at Harvard University with Professor Martin Karplus, in 2001, he joined University of Wisconsin—Madison, where he remained since as a Professor of Chemistry.

Supporting Information Available

Additional results for the performance of DFTB3/3OB vs DFTB3/3OBw for different gas phase and condensed phase systems are included. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^○ Department of Chemistry, University of Illinois at Urbana–Champaign, 505 South Mathews Avenue, Urbana, IL 61801.

Author Present Address

^∇ Institute for Molecular Science, Myodaiji, Okazaki, Aichi, 444-8585, Japan.

Author Contributions

^# Contributed equally.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States