Architecture of Polyglutamine-containing Fibrils from Time-resolved Fluorescence Decay

Background: Large polyglutamine-rich inclusions are hallmarks of CAG repeat pathologies.

Results: Sensitive time-resolved fluorescent decay measurements combined with Monte Carlo simulations reveal the architecture of polyglutamine amyloid fibrils.

Conclusion: Polyglutamine stretches are β-stranded in monomers and are organized into layered β-sheets with alternating N termini in amyloid fibrils.

Significance: This sensitive approach can be routinely used to characterize the effect of new amyloid therapeutics.

Abstract

The disease risk and age of onset of Huntington disease (HD) and nine other repeat disorders strongly depend on the expansion of CAG repeats encoding consecutive polyglutamines (polyQ) in the corresponding disease protein. PolyQ length-dependent misfolding and aggregation are the hallmarks of CAG pathologies. Despite intense effort, the overall structure of these aggregates remains poorly understood. Here, we used sensitive time-dependent fluorescent decay measurements to assess the architecture of mature fibrils of huntingtin (Htt) exon 1 implicated in HD pathology. Varying the position of the fluorescent labels in the Htt monomer with expanded 51Q (Htt51Q) and using structural models of putative fibril structures, we generated distance distributions between donors and acceptors covering all possible distances between the monomers or monomer dimensions within the polyQ amyloid fibril. Using Monte Carlo simulations, we systematically scanned all possible monomer conformations that fit the experimentally measured decay times. Monomers with four-stranded 51Q stretches organized into five-layered β-sheets with alternating N termini of the monomers perpendicular to the fibril axis gave the best fit to our data. Alternatively, the core structure of the polyQ fibrils might also be a zipper layer with antiparallel four-stranded stretches as this structure showed the next best fit. All other remaining arrangements are clearly excluded by the data. Furthermore, the assessed dimensions of the polyQ stretch of each monomer provide structural evidence for the observed polyQ length threshold in HD pathology. Our approach can be used to validate the effect of pharmacological substances that inhibit or alter amyloid growth and structure.

Introduction

Ten dominantly inherited neurodegenerative polyglutamine pathologies, including Huntington disease (HD),³ are linked to an expansion of the CAG repeat encoding a polyglutamine stretch (polyQ) in the disease protein, with a strong repeat length dependence of disease risk and age of onset (1). Large polyQ-rich inclusions are detected in patient brains, and cell and animal models suggest the involvement of polyQ aggregation in disease pathology (2). This is reinforced by the correlation between polyQ repeat length dependence and aggregation propensity (3). Aggregation is a multistep process (2), and the toxicity has been assigned to various intermediate aggregates (4–6). Mature end aggregates are considered rather benign, although when directed to the cell nucleus, they also exert a strong toxic effect (7). Pharmacological intervention aiming to inhibit aggregate formation has been shown to be beneficial in vivo (8). Thus, to develop drug design-based strategies to alter aggregation pathway and alleviate toxicity, knowledge of the structure and aggregate architecture is crucial. However, despite these efforts, the overall structure of various aggregates remains poorly understood.

Aggregates isolated post-mortem from HD patients or cell culture models, or grown in vitro, are β-sheet-enriched and share the typical cross-β diffraction pattern (9, 10). The cross-β pattern is a common feature of several amyloid aggregates (11); however, the core structure of aggregates of various diseases proteins differs significantly (12, 13). Although the β-sheet signature of the fibrils is indisputable, as evidenced by Fourier transform infrared spectroscopy, circular dichroism spectroscopy, and x-ray fiber diffraction (9, 10), evidence for the fibril architecture is rather contradictive. Various structures have been proposed, ranging from water-filled nanotube (9) and steric zipper arrangement with dry fibril core (14) to β-pseudohelix (15). Even the interpretations of the same x-ray fiber diffraction diagrams are inconsistent; Perutz et al. (9) suggested a water-filled cylindrical β-sheet structure for the polyQ fibrils, whereas Sikorski and Atkins (16), reanalyzing the diffraction pattern, concluded that β-sheets elongated in fibril growth direction and stacked on top of each other. Site-directed spin labeling and electron paramagnetic resonance spectroscopy show a lack of stacking of many residues in a parallel, in-register arrangement that is commonly found in other amyloids (17). Molecular dynamics simulations combined with docking experiments exclude some of the proposed monomer structures, e.g. α-helices or steric zipper, β-nanotube, and β-pseudohelix. NMR experiments, however, propose a steric zipper conformation for mature fibrils, where the individual monomers are stabilized via side-chain interactions (14). In addition, an innovative twist of two-dimensional Fourier transform infrared spectroscopy (18) and biochemical studies of β-sheet stabilizing motifs (19) proposes β-sheet-based structure as the most likely structure of the polyQ fibrils, although these studies do not reveal details on the molecular organization of the monomers, e.g. β-turns per monomer, orientation of neighboring monomers, and number of layers perpendicular to the fibril axis.

Here, we assess the architecture of polyQ fibrils using a distance-dependent energy transfer combined with Monte Carlo simulations. Typically, HD progression is accompanied by the aggregation of mutant huntingtin (Htt) and its N-terminal fragments composed of exon 1 (20, 21). Thus, we used Htt exon 1 with expanded polyQ length (here 51Q) to grow amyloid fibrils in vitro. By selective fluorophore labeling (donor or acceptor probes) of the polyQ monomers at various positions flanking the polyQ region, we measured the time-dependent fluorescent decay times of the donors. We developed a new algorithm for Monte Carlo simulations to capture time-resolved donor fluorescence decay and fit the experimental data to various models of fibril architecture. This approach allows for exact determination of distances between the monomers in addition to monomer dimensions in the fibrils. Our data suggest that polyQ monomers are organized in a five-layered β-sheet. Furthermore, each monomer consists of four strands with alternating N termini perpendicular to the fibril axis. The minimal length of the stable three-stranded polyQ region is 36 amino acids, which corresponds to the observed polyQ length threshold in HD pathologies.

EXPERIMENTAL PROCEDURES

Protein Expression and Purification

Htt exon 1 constructs with polyQ lengths of 25 or 51 were cloned in the pGEX6P vector and expressed in soluble form as GST fusions. All codons encoding Cys in GST were mutated to Ser to create a Cys-less GST fusion. Amino acids at positions 16, 69, or 111 in Htt exon 1 (the numbering is according to the primary sequence of Htt51Q) were mutated to Cys using a QuikChange protocol (Stratagene). All GST-tagged constructs were expressed in a soluble form in Escherichia coli BL21(DE3) in minimal medium containing 100 mg/liter ampicillin, induced at optical density ∼0.4 for 4 h at 30 °C by adding 400 μm isopropyl-1-thio-β-d-galactopyranoside, and affinity-purified to homogeneity using the GST tag as described previously (22). Purified proteins were flash-frozen in PBS (10 mm Na₂HPO₄, pH 7.3, 120 mm NaCl, 10% (v/v) glycerol, 1 mm EDTA, and 1 mm DTT).

Labeling and Aggregation

For fluorescent decay time measurements, 15 μm GST protein in PBS without glycerol was mixed with tris(2-carboxyethyl)phosphine and a 10-fold excess of the corresponding fluorescent dye, Alexa Fluor 488 maleimide or Alexa Fluor 594 maleimide. Samples were incubated for 5 h at 4 °C with slow vortexing at 80 rpm. Excess dye was removed with Bio-Spin P6 columns (Bio-Rad), and labeled protein was concentrated and washed in Amicon Ultra centrifugal filter devices (Millipore) with a cut-off size of 10 kDa until the ratio of dye and protein absorption remained constant. Labeling efficiency was calculated using the extinction coefficients of the protein and dyes at 280, 495, and 590 nm. Note that during the labeling and processing time, each construct remained soluble because of the GST tag.

Alexa Fluor 488-labeled (donor-labeled) and Alexa Fluor 594-labeled (acceptor-labeled) GST-tagged proteins were mixed in different ratios (from 20%:1.5% to 20%:20%), and the final concentration of each sample was adjusted to 4 μm with unlabeled protein. One unit of HRV protease (Mobitec) was added to each 100-μl reaction to remove the GST tag and induce aggregation. Aggregation proceeded to completion for 48 h at 30 °C with gentle agitation at 300 rpm. The labeled aggregates were collected by centrifugation at 21,000 × g for 30 min and washed several times with 1 ml of PBS to remove the soluble GST counterpart and non-aggregated Htt exon 1.

Fluorescent Decay Time Measurements

Fluorescent decay times were recorded on an FL920 spectrometer (Edinburgh Instruments) operated in a time-correlated single photon counting mode. A time window of 50 ns and 1024 channels were used in the measurements. Samples were excited at λ_ex = 450 nm using a SC-400-PP supercontinuum source (Fianum), and the emission was collected at λ_em = 525 nm using a polarizer set at magic angle position and a multichannel plate (Europhoton) as a detector. The repetition rate of the excitation light source was set to 10 MHz. The measurements were stopped upon 10,000 counts collected in the most prominent channel.

Quantum Yield and Förster Radius Determinations

The Förster radius R₀ was calculated according to

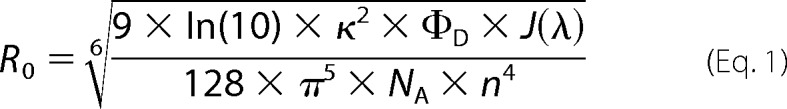where κ² accounts for the relative orientation between donor fluorescence and acceptor absorption transition dipole moments, Φ_D is the fluorescence quantum yield of the donor, J(λ) is the overlap integral of the donor emission and acceptor absorption spectra, N_A is the Avogadro constant, and n is the refractive index of the solution. Using a photoluminescence quantum yield measurement system (C9920, Hamamatsu Photonics), the quantum yield Φ_D for the Alexa Fluor 488-labeled Htt exon 1 monomer was determined to be 0.6.

The emission spectra of Alexa Fluor 488-labeled Htt exon 1 monomer and the excitation spectra of Alexa Fluor 594-labeled Htt exon 1 monomer were recorded on a QuantaMaster 40 (Photon Technology International), and Felix32 software was used to determine the Förster radius for the labeled monomer donor/acceptor pair. The relative orientation of the dye was assumed to be random and its movements much faster than the fluorescent decay times (κ² = 2/3). The refractive index of an infinitely diluted aqueous solution (n = 1.33) was used. The Förster radius R₀ was calculated to be 54 Å, which is in a good agreement with a previously determined Förster radius for the identical dye FRET pair in slightly different solvent conditions (23). The fluorescent decay time τ for the Alexa Fluor 488-labeled Htt exon I was determined using an algorithm written in our laboratory. The algorithm minimized the sum of the squared differences between the measured data and the theoretical fluorescent decay time function convoluted with the instrument response function. The fluorescent decay time τ was randomly varied by up to 10% in either direction in 100,000 iterations, and each result was accepted as a change in fluorescent decay time if it led to an improvement in the sum of squared differences. The resulting value was identical independent of what starting value was used, 0.01 ns or 100 ns.

The fluorescent decay time of the monomer (τ_M) is the reciprocal sum of the rate constants k_i of all possible processes leading to deactivation of excited dye.

The quantum yield of the donor-labeled monomer Φ_M can be expressed as the ratio of the fluorescence decay rate constant k_Fl,M to the sum of all deactivation rate constants.

The rate constant of fluorescence of donor-labeled monomers can therefore be calculated using,

Anisotropy measurements suggest little alteration of the solvent conditions, hence the difference between k_Fl,F and k_Fl,M should be close to zero.

where Φ_F is the quantum yield, and k_Fl,F and τ_F are the fluorescence rate constant and the fluorescence decay time of donor-labeled monomers in the fibril, respectively.

The quantum yield of the system can be corrected for increased quenching in fibrils by considering the change in the sum of all decay rates in Equation 3. Because the Förster radius, R₀, is dependent on the quantum yield, it was also adjusted for the labeled fibrils according to the donor fluorescent decay times in the fibrils for all different labeling positions.

Simulations of the Fluorescent Decay Times

The code for predicting the output of the fluorescence decay time experiments was written in Fortran90. The input files contain the dimension of the simulated space, its periodicity, the number of donors and acceptors, and their expected coordinates for each studied structure. The fibrils used in the simulations consisted of 7500 monomers, which were randomly assigned with donors and acceptors to represent the experimental constellation. The fibrils were periodic in their growth direction to avoid stochastically insignificant situations at the rare fibril ends.

Each donor was excited randomly with the probability

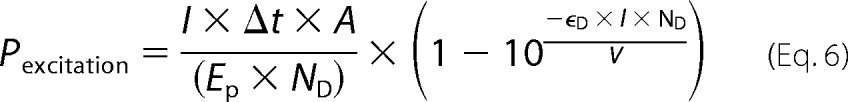where I is the irradiance, Δt is the time interval over which the excitation takes place, A is the surface area of light irradiation, ϵ_D is the extinction coefficient of the donor, l is the length of the excited volume in direction of the excitation beam, N_D is the number of donors in the observed volume V, and E_P is the energy of a photon with the excitation wavelength of 450 nm. To obtain sufficient signal, the low excitation probability was enhanced artificially to increase the speed of the simulations while ensuring that signals even from samples with the highest quenching rates were not altered by this adjustment. On average, 1 in 250 donors was excited in our simulations.

Because the distance of the dye to the α-carbon of the first or last glutamine can easily be 2 nm, in the experimental setup for simulation purposes, all dye positions were changed by that distance in a random direction for all the excited donors and nearby acceptors in a given excitation cycle. During the simulated 50 ns, the dye positions were assumed to remain constant. All distances to the acceptors within the relevant distance (2R₀ + 4 nm) were calculated for each excited donor.

Subsequently, the FRET rates k_T to all acceptors available to take up energy were added to the total sum of deactivation rates

where τ_F is the fluorescent decay time of the donor-labeled monomer within the fibril without any acceptor present and r is the distance to a given acceptor. As in the experiments, the 50-ns time frame was divided in 1024 equal intervals Δt. The probability of the donor being still excited after a given time interval was calculated, and a random number generator was used to deactivate the donor. The donor was therefore still excited with a probability.

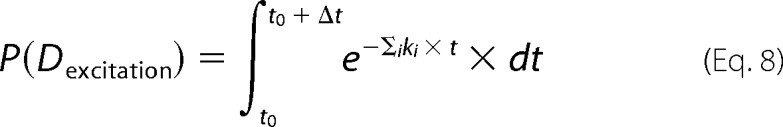If the donor was deactivated, the ratios of the rate constants were used to assign the probabilities to the deactivation mechanisms. If a photon was emitted, it was added to the total photon number at this time interval.

The possible bias due to restricted orientations of the excitable dyes and therefore time-dependent efficiencies of photon detection was found to be negligible by testing dye mobility in anisotropy measurements of fibrils labeled with donor only (see Fig. 2C). Subsequently, the acceptors excited in previous time steps, due to occurring transfers, were quenched according to their measured fluorescent decay times in the fibrils.

If an acceptor is excited (or deactivated), it is removed from (or added again to) the list of available acceptors for each excited donor in its proximity. All 1024 time intervals were simulated for each still excited donor or until no excited donor was left, after which the simulation was reset and a new subset of donors was randomly excited. 10,000 photons were collected in at least one of the 1024 time intervals.

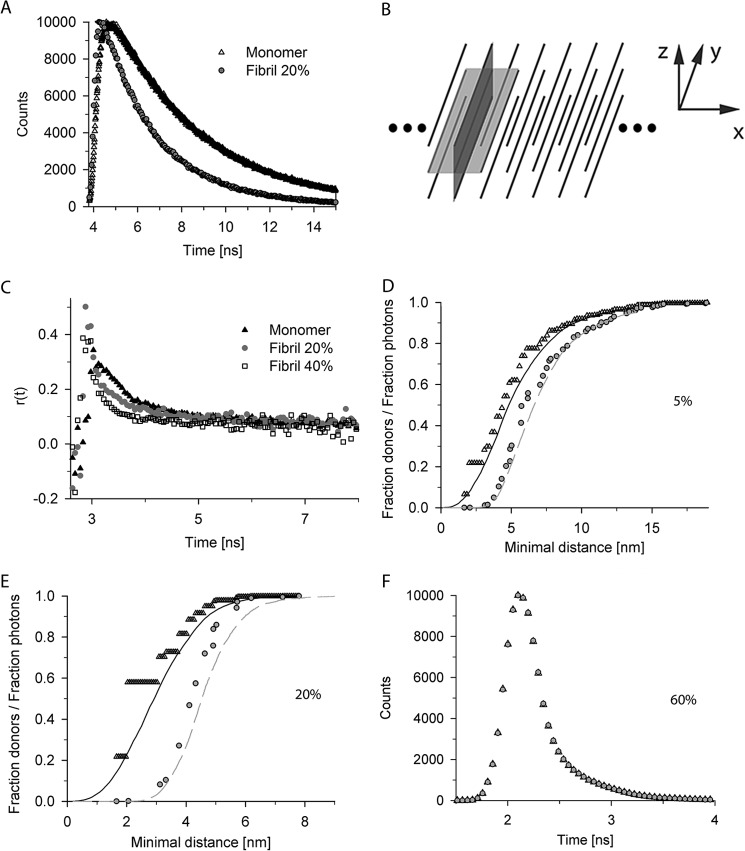
FIGURE 2.

Fluorescent time decay curves. A, the fluorescent time decay curves for monomer and aggregates differ. Typical fluorescent decay time curves for 20% donor-labeled P69C monomer and fibrils (Fibril 20%) are shown. B, general reference system for discussion of structural details: x axis denotes the fibril axis, y axis denotes the direction of the β-strands, and z axis denotes the direction of the monomer layers (by β-sheet) or monomers (by zipper) perpendicular to the fibril axis. β-Sheet according to Sikorski and Atkins (16) lies in the x/y-plane (light gray plane), and zipper structures according to Schneider et al. (14) are in the y/z-plane (dark gray plane). C, The mobility of the fluorescent dye is not restricted as revealed by anisotropy measurements for donor-labeled S16C monomer, fibrils containing 20% (Fibril 20%), or 40% (Fibril 40%) of donor-labeled S16C monomers. D–F, cumulative curves of distance distributions of donors to their closest acceptor for fixed (open black triangle) and flexible (black solid line) dye positions and the relative contribution of the photons derived from these donor fractions to the total signal in the first time interval in the simulations with fixed (gray filled circle) and flexible (gray dashed line) dye positions. The flexible dye positions were modeled with a 2-nm linker to additionally enhance the dye flexibility. The discrete values in two exemplary simulations of fibrils containing donor-labeled S16C monomer and 5% (D) or 20% (E) acceptor-labeled S16C are shown. F, impact of the photons derived from donors with acceptor in a very close proximity (<0.5R₀). Simulations are of 20% donor-labeled S16C und 60% acceptor-labeled S16C fibrils. There is negligible difference between convoluted simulations with (black open triangle) and without (gray filled circle) photons collected from donors with acceptors closer than the half of the Förster radius.

Analysis of the Fluorescent Decay Times

For comparison with the simulated data sets, the experimental data were convoluted with the corresponding instrument response function, and the fit was judged by two methods: (i) the absolute differences between the expected and measured amount of counts and (ii) the sum of the squares of the differences. To categorize different simulated structures, the simulations were separately and collectively judged with tests i and ii. Each test result was then judged in relation to the mean of all 0% acceptor samples within each set of labeling positions. The fibrils with 0% acceptor serve as a perfect standard to extract the distance between the experimental and simulated values because no errors can occur by wrongly predicted donor-acceptor distances or interactions. For test i, divergences from the 0% acceptor sample up to 5% were designated as good, up to 25% as acceptable fits and more than 25% as unacceptable fits. For test ii, those borders were 35 and 80%, respectively.

Electron Microscopy

Samples for electron microscopy were washed with pure water instead of PBS to avoid visual artifacts. Aggregates were loaded on freshly glow-discharged holey carbon grids (Quantifoil Micro Tools GmbH, Jena, Germany), covered with an additional self-made thin layer of continuous carbon, washed with deionized water, and negatively stained using 2% (w/v) uranyl acetate. Samples were imaged using either a 100-kV Philips CM100 transmission electron microscope equipped with a 1k F114 Fastscan camera (Tietz Video and Image Processing Systems) or a 120-kV Tecnai G2 Spirit microscope equipped with a 2k Eagle CCD camera (FEI) at a nominal magnification between 20,000× and 42,000×. For cryo-electron microscopy, samples were plunge-frozen in liquid ethane using a semi-automated Vitrobot plunger (FEI) and imaged using low dose conditions.

RESULTS

Choice of Positions to Introduce the Fluorophores and in Vitro Aggregation of Htt Exon 1 Mutants

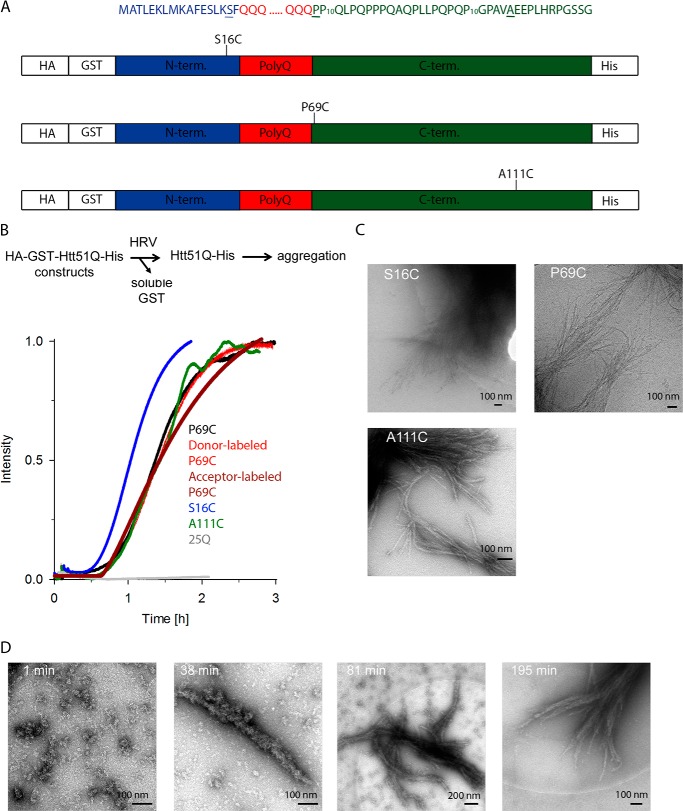
To assess the structure of native polyglutamine fibrils of Htt exon 1, the position of the mutation within the target sequence and fluorophore labeling should have minimal to no perturbation of Htt exon 1 aggregation behavior or fibril structure. PolyQ stretches (Fig. 1A) are invariant among the polyQ-containing proteins and are composed solely of consecutive glutamine repeats (1). A mutation within the polyQ stretch alters the length of the hairpins between the polyQ stretches (24, 25). Two consecutive polyproline (polyP) regions downstream of the polyQ stretch (Fig. 1A) influence the aggregation propensity of the polyQ stretch and stability of the polyQ fibrils (26). Thus, non-perturbing mutation is only possible at positions flanking the polyP stretches. Furthermore, the 17-amino acid-long N terminus of Htt exon (Fig. 1A) is crucial for the initial aggregation steps (27, 28); residues 4–12 have strong propensity to form α-helices and are involved in the formation of initial globular oligomers, and mutations within this region alter the aggregation pathway (27). The unprecedented complexity of how the HttQ primary sequence controls the aggregation behavior restricts the positions available for introducing cysteines and attaching dyes. Because we aimed at elucidating the conformation of the polyQ stretches within the mature amyloid fibrils, we have chosen two positions flanking this stretch, S16C upstream and P69C downstream of the polyQ region (Fig. 1A). Mutants were numbered according to the primary sequence of Htt exon 1 with a pathological polyQ length (Htt51Q). Furthermore, we introduced an additional mutation downstream of the polyP region (A111C) (Fig. 1A). This residue is far from the polyQ core, and when mixed with any other position of labeling flanking the polyQ stretch, it introduces longer distances into the system.

FIGURE 1.

Aggregation kinetics of Htt51Q mutants. A, schematic of the constructs used in this study. The amino acid sequences of the three regions of Htt exon 1, the 17-amino acid-long N terminus (blue), polyQ part (red), and C terminus (green), are color-coded as in the schematic. Residues mutated to Cys at which fluorescent labels were introduced are underlined, and their position relative to the polyQ stretch is designated on the schematics. Numbering is according to the primary sequence of Htt51Q. HA and His tags are used to monitor expression levels of the constructs. B, Cys mutations or fluorescent labeling did not alter the aggregation kinetics of Htt51Q. Aggregation is initiated by the addition of HRV protease, which recognizes the cleavage site downstream of the GST moiety as designated on the reaction schematic. Exemplary aggregation kinetics traces monitored by light scattering of unlabeled Htt51Q mutants and donor-labeled or acceptor-labeled P69C variant are shown. The variant with polyQ stretch below the pathological threshold, Htt25Q, did not aggregate (gray). C, cryo-EM images of end stage fibrils of different Htt51Q mutants. S16C and P69C fibrils were imaged at 48 h and A111C fibrils were imaged at 12 h of the aggregation time course. D, electron microscopy images (negative staining) of P69C at various time points in the aggregation time course.

Htt51Q and its point mutants are highly aggregation-prone; hence to express them in soluble form, they all were fused to Cys-less GST (Fig. 1A). An HRV protease cleavage site between the Cys-less GST and Htt51Q protein serves to release intact Htt exon 1 and initiate the aggregation reaction. The aggregation kinetics followed by static light scattering suggested that the Cys mutations did not significantly change the kinetics of fibril formation as compared with the Htt51Q (Fig. 1B). Only the S16C mutant exhibited slightly faster aggregation kinetics, likely due to the position of the mutation; Ser-16 resides in close proximity to the key intrinsic α-helical modulator sequence of Htt aggregation (27, 28).

A requirement for our measurements was a completed aggregation process to mature fibrils. The aggregation was completed after approximately 2 h for unlabeled and labeled mutants (Fig. 1B). Electron microscopy time series confirmed that the aggregation is also completed after ∼3 h with no further apparent growth of the fibrils (Fig. 1D). Notably, almost no single fibrils were detected, but rather large fibril bundles, which, if stably attached to each other, may interfere with the fluorescent decay time measurements and introduce FRET events originating from interfibrillar FRET pairs. Next, we applied cryo-electron microscopy to image the fibrils under more physiological conditions. Less compact bundles were observed in vitrified ice, indicating that the individual fibrils were not strongly attached to each other (Fig. 1C). The fibrils in negative stain tend to cluster due to drying on the grid or other typical negative stain artifacts.

Structural Insights into PolyQ Fibrils with Time-resolved Fluorescence Decay Measurements

To gain insight into the structure of Htt51Q fibrils, we measured the kinetics of donor fluorescence decay in fibrils composed of different ratios of donor- and acceptor-labeled monomers. The monomer labeling position was also varied in different combinations; donor-labeled P16C, P69C, or A111C was mixed in every possible combination with acceptor-labeled P16C, P69C, or A111C. In all fluorescence decay measurements and simulations, the fraction of donor-labeled monomers was held constant at 20%, while the amount of acceptor-labeled monomers was varied between 1.5 and 20%. Each construct was freshly labeled with a fluorophore as a GST-Htt51Q. Note that the Htt51Q remained soluble only as GST fusion during the labeling procedure. Thereafter the aggregation was initiated by adding HRV protease and allowed for completeness for 48 h. The soluble GST and traces of non-aggregated labeled Htt51Q monomers were removed by several washing steps of the mature fibrils. Thus, the signal in the time-resolved fluorescence decay measurements is solely from labeled aggregates.

Clearly, the time-resolved fluorescence decay traces differ for a monomer and mature fibril (Fig. 2, A and B). For each labeling position, the decay time of a donor-labeled monomer, or end-stage fibrils labeled only with the donor, served as a reference to set all relevant parameters for the simulation (e.g. quantum yields, Förster radii, donor deactivation rates). A requirement for time-resolved fluorescence decay measurements is high flexibility and random orientation of the fluorescent label. Anisotropy measurements revealed no mobility restrictions of the dye in the fibrils; the dye mobility in the fibrils was similar to the dye mobility in the soluble monomer (Fig. 2C). We next calculated the distance distributions from the fluorescence decay simulations (Fig. 2, D and E) and plotted the discrete cumulative values of the donor as a function of the minimal distance to their closest acceptor (Fig. 2, D and E). The highest quenching effect came from the closest acceptors, i.e. the fraction of photons and therefore the influence on the signal is the lowest for donors with close acceptors (Fig. 2, D and E). For higher acceptor amounts (compare Fig. 2E for 20% with Fig. 2D for 5% acceptor-labeled S16C fibrils), high frequencies of short range distances at which additional quantum mechanical effects, e.g. Dexter energy transfer, could be possible. However, the amount of photons collected by such donors was negligible even for higher acceptor concentrations. Thus, further alteration of their fluorescent decay times would not result in any significant change in the predicted photon distribution (Fig. 2F). Furthermore, although anisotropy measurements indicate a small degree of homo-FRET (29) (Fig. 2C), the distance ranges for such transfer (Fig. 2, D and E) indicate no significant alteration of the excited donor positions.

By mixing the donor- and acceptor-labeled monomers of each mutant (S16C, P69C or A111C), we covered every distance distribution between the labeling positions of the monomers assembled in a fibril. For the three possible combinations of S16C- or P69C-labeled monomers, the donor was largely quenched with much higher quenching effect at higher acceptor concentrations (Fig. 3A, example for P69C-S16C fibril), suggesting that the fluorophores are in a close proximity. Notably, the decay curves of S16C/S16C-labeled, S16C/P69C-labeled,or P69C/P69C-labeled (donor/acceptor) fibrils exhibited similar quenching patterns for the corresponding acceptor concentration so that we cannot extract any obvious information for N- to N-terminal or N- to C-terminal orientation of the monomers within the fibrils. In contrast, for fibrils of donor-labeled A111C and acceptor-labeled A111C (A111C/A111C) or in combination with other Htt51Q variants, the quenching effect on the donor fluorescence was very low, even at high acceptor concentrations (Fig. 3B). Thus, the two fluorophores were found rarely in a close proximity, suggesting high flexibility of this part of the molecule as observed before (17).

FIGURE 3.

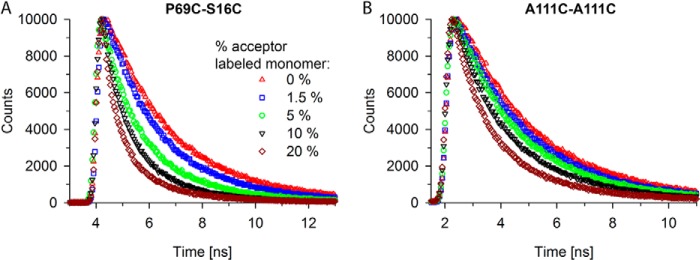
Time-resolved fluorescent decay time measurements of Htt51Q fibrils. A and B, two distinct exemplary measurements for fibrils of P69C-S16C (A) and A111C-A11C (B). A, fibrils contain 20% of P69C monomer labeled with the donor dye and increasing concentrations (from 1.5 to 20%) of S16C monomer labeled with the acceptor dye. B, fibrils contain 20% of A111C monomers labeled with the donor dye and increasing concentrations (from 1.5 to 20%) of A111C monomer labeled with the acceptor dye. The symbols in the legend of panel A apply to both panels. Note that the depicted two exemplary measurements illustrate the subtle but significant changes in the fluorescent decay time traces depending on the labeling position of the donor or acceptor dye.

Next, we fitted the curves with three decay times using the FAST software (Edinburgh Instruments). Fluorescence decay times shifted toward lower decay values, and the amplitude of the fastest fluorescence decay times increased at higher acceptor concentrations. The shift of the fluorescence decay times was partly counteracted by limiting the parameters of decay times for all curves to a single set. However, the fluorescence decay times did not randomly fluctuate around a defined value; instead, the persistent trend toward lower decay values suggests that the assumption for the existence of only three decay times insufficiently represents the system. Thus, structural information from the fluorescence decays can be extracted only when using a large number of parameters to fit the curves, which is beyond the potential of this method.

Simulation of Complex Fluorescence Decay Measurements

Generation of distances between the fluorophores based on the fluorescence decay curves was not possible with a simple set of parameters; thus, we decided to convert the fluorescence decay times into distances and structures by simulating different labeling variations and dye positions in possible structures described for polyQ aggregates. For this, we created detailed models of the fibril using various proposed structures (9, 14–16, 30), also including the distances between periodically present elements (e.g. the number of glutamines in each strand), the number of monomer layers, and the relative orientation of neighboring monomers. These additional parameters built a multidimensional parameter space, which we systematically scanned to extract parameter set(s) that best fit the experimental data. In all models, the distance parameters were restricted by the x-ray pattern observed by Perutz et al. (9). To scan the whole parameter space, we first performed elimination with fibrils composed of P69C-labeled monomer with both donor and acceptor. Structures predicted by the simulations to be drastically false were discarded in subsequent simulations with other mutants (Table 1). Structures with a high density of labeling positions showed the best performance in the simulations. For each set of labeling positions, fibrils composed of monomers with β-sheet (16) or zipper structures (14) showed a high label density. In contrast, the β-tube (9), α-helix (15), and β-pseudohelix structures (30) showed poor fits as monomer structure and were already excluded by this initial scanning procedure (Table 1).

TABLE 1.

Overview of the simulated distances by different orientations of donor- and acceptor-labeled monomer

All structures are ranked based on the value of sum of squares between the experimental time-resolved fluorescence decay and simulated curves. An interval up to 35% is considered a good fit (green), up to 80% are considered as reasonable (gray), and all values higher than 80% are considered as poor (red) (sum of squares column). Structures are specified according to their basic structural models with specification of the layers in z-direction and the amount of β-strands per monomer. The zipper structures are subdivided in classification with alternating or one-sided orientation of the N termini of each monomer along the z-axis. Color coding in the distances columns indicates the goodness of the fits: best (green, up to 5% deviation), reasonable (gray, up to 25% deviation), or poor (red, above 25% deviation).

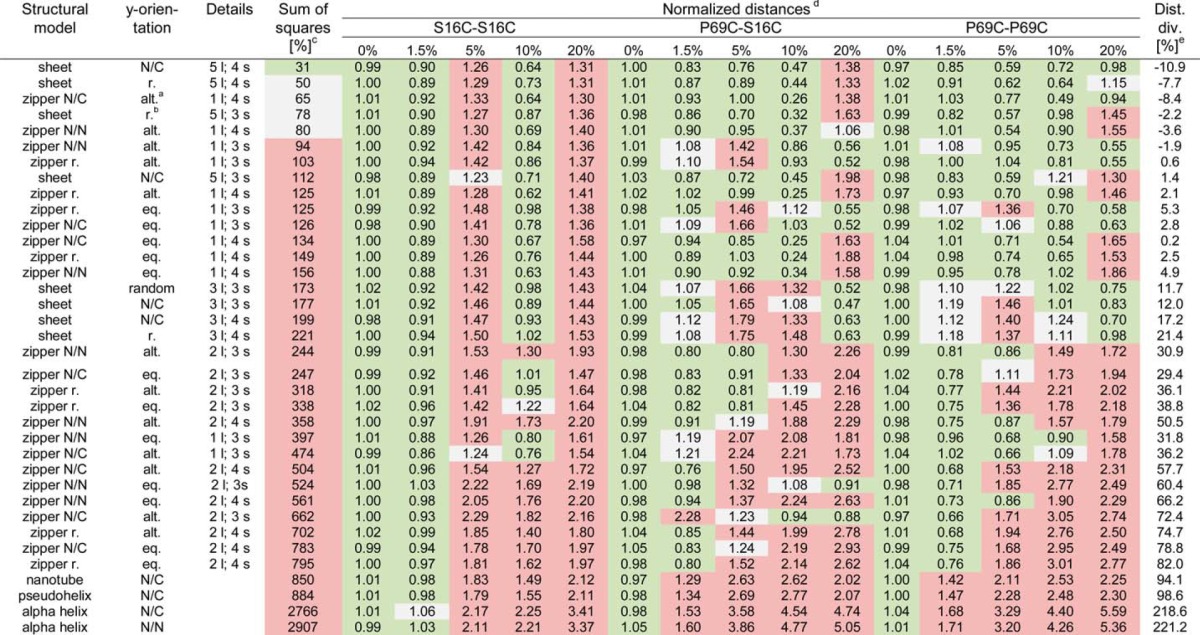
^a Abbreviations: alt., alternating; eq. or., equally oriented; r., random; N/N, N to N orientation; N/C, N to C orientation; l., layer; s., strands.

^b Note that β-sheet structures with random orientations of the N termini of monomers along the y axis are randomly oriented along the x axis, whereas β-sheet structures with alternating position of the N termini have fixed alignments along the x axis.

^c The average sum of squares values represents the excess (in percentage) of the sum of squares as compared with the averaged sum of squares for simulations of 0% acceptor for the given labeling position set.

^d Each value is the difference between simulated and experimental photon counts normalized to the averaged difference with 0% acceptor for the same labeling position.

^e Dist. div., distance divergence. For each simulated curve, we show the percentages by which the distance between predicted and measured photon amounts vary relative to the average of all fibrils without any acceptor.

The width of fibrils could accommodate up to 12 layers of β-sheet monomers stacked on top of each other. The width of the fibril was used to estimate the maximal glutamine length per turn (Fig. 1C). For 51Q this resulted in three to four strands, which corroborates the three-strand structure predicted from NMR measurements for a similar polyQ length (14). Considering the connecting turns, the average length of a strand is 10 glutamines, which corresponds to the minimal hairpin length of a monomeric nucleus that initiates polyQ aggregation (31). For the detailed simulations, in the case of β-sheet structure, the number of layers was restricted between three and five, suggested also as most reasonable by the initial simulations. Considering the initial steps of Htt exon 1 aggregation (27, 28), a continued assembly of N termini connecting two polyQ layers seemed very plausible. Thus, two layers of zippers on top of each other were considered for the zipper structure (Table 1).

The last parameter to simulate was the relative orientation of adjacent monomers. Although the options for the zipper structure were limited, the sheet structures allow many possible variations in the orientation of the neighboring monomer. We randomly simulated two orientations, although applying consistent rules for the neighboring monomers in x- and z-directions. In one set, the direction of the N termini of the monomers alternated at opposite sites across the fibril axis (Fig. 4 and Table 1). In the other set, the monomers had completely random orientation in x- and y-directions (Table 1). The possibility that two layers do not completely overlap but are rather shifted along the x axis was not considered. It should be noted that the orientation of the N termini of the monomer to its neighbor had only marginal influence on the outcome of the simulation.

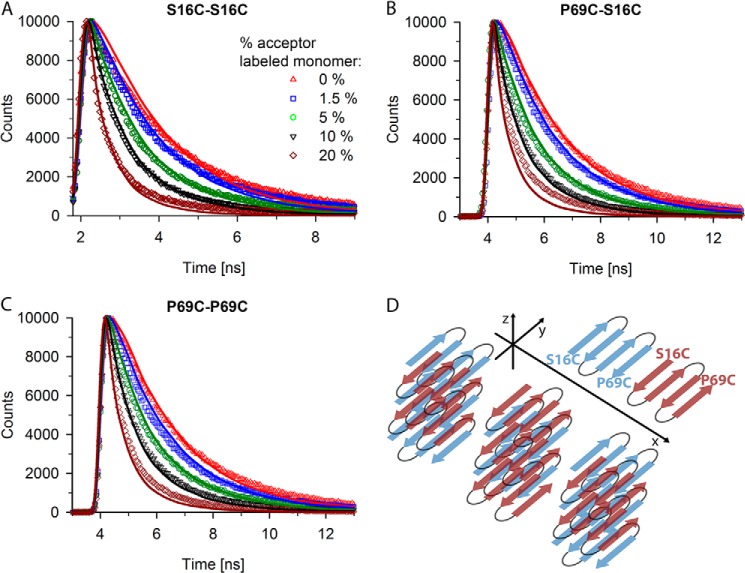
FIGURE 4.

Fluorescent decay curves fit well to five-layered β-sheet of four-stranded monomer. A–C, experimental (various symbols) and simulated (line) fluorescence decay curves for fibrils containing 20% S16C monomer labeled with donor dye and increasing concentrations (from 1.5 to 20%) of S16C monomer labeled with the acceptor dye (A), for fibrils containing 20% P69C monomer labeled with donor dye and increasing concentrations (from 1.5 to 20%) of S16C monomer labeled with the acceptor dye (B), and for fibrils containing 20% P69C monomer labeled with donor dye and increasing concentrations (from 1.5 to 20%) of P69C monomer labeled with the acceptor dye (C). The symbols in panel A represent the increase in the acceptor-labeled monomer and apply to all panels. D, the structural model used in simulations of A–C is composed of a five-layered β-sheet of monomers with alternating N-terminal orientation along the y axis but the same orientation along the x axis. Note that only the polyQ stretches and not the whole Htt exon 1 are presented; the polyQ stretch of each monomer adopts four β-strands. Two exemplary monomers are depicted with the position of the mutations flanking the polyQ stretch to illustrate the parallel orientation of a monomer to each neighbor in the β-sheet.

Fibrils with Five-layered β-Sheet of Four-stranded Monomers Fit the Fluorescence Decay Curves the Best

The initial simulations revealed two candidate structures, β-sheet and zipper, which best fit the parameters. To investigate detailed structural features and orientation of the Htt51Q monomers in the fibrils, we performed more detailed simulations using a Monte Carlo approach. Available algorithms to simulate FRET distances (32–34) are designed to evaluate static FRET measurements, but are not applicable for fluorescence decay measurements. Hence, we developed new code to simulate the time-resolved photon distributions and capture the dynamics of dye distributions in three-dimensional space. Within the multidimensional parameter space described above, we obtained two very distinct local minima for the parameter sets. According to the absolute differences between the expected and measured number of photon counts and the sum of the squares of differences (described under “Experimental Procedures”), the best prediction we obtained was for a β-sheet structure with four strands per monomer organized in five layers (Fig. 4, sum of squares relative to the average 0% acceptor-labeled fibril is +31%, Table 1). Every monomer is rotated by 180° to its neighbor respective to the fibril axis (x axis), resulting in a parallel intermolecular orientation (Fig. 4D). As a primary judgment method for the quality of a fit, we calculated the sum of squares for the distances between simulated and experimentally obtained photon counts and related them to the optimized 0% acceptor-labeled fibril. This is a valid standard because under ideal FRET behavior, no FRET events can be detected and minimal simulation discrepancies are expected. For the β-sheet structure, only the fluorescent decay time of fibrils made of 20% donor-labeled P69C and 20% acceptor-labeled S16C showed slight deviation from the prediction for this set (Fig. 4B). However, if the parameter describing the orientation of the monomer to each next neighbor was changed to a random orientation, the simulation fits similarly well the fluorescence decay curves (Table 1, relative sum of squares is 50%). Reduction of the number of strands from four to three within a monomer reduces the distances between the fluorophores of two consecutive monomers and the average donor-acceptor distance. Consequently, higher quenching rates were simulated that rendered the predictions suboptimal (Table 1, relative sum of squares is 112%). Furthermore, altering the number of the β-sheet layers along the z axis led to a more severe loss of quality in the predicted fluorescent decays (Table 1, relative sum of squares is 199%). Simultaneous changes of several parameters, such as orientation of the monomers or layering of β-sheets along z axis, did not result in good fits either (Table 1). By chance, a single fluorescent decay fit might be predicted well when changing more than one parameter, but for the 12 tested FRET systems, we did not observe any consistently good behavior.

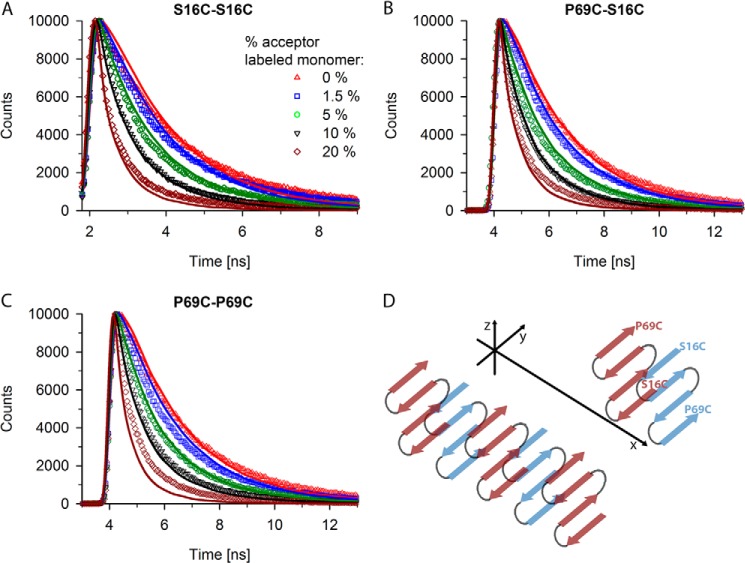
A thorough scan of the parameter space for possible zipper structures also resulted in considerably good fits, implying that this structure needs to also be considered. The best predicted zipper structure is a single layer of zippers with an antiparallel orientation of monomers in four glutamine strands. N termini occur in alternating orientation along the y axis and also alternating the side of the polyQ core along the z axis (Fig. 5D, Table 1). Up to 10% acceptor concentration, the predicted fluorescent decay curves fitted the measured data well (Fig. 5, A–C), but the fibrils labeled with 20% acceptor showed much worse predictions for the zipper structure than for the β-sheet (compare Fig. 4 and 5). Changing one parameter, e.g. alternating the position of the N termini along the z axis so that the N terminus of every next monomer is on the same site of the polyQ stretch of the previous monomer, resulted in slightly worse predictions except for donor-labeled P69C and 20% acceptor-labeled S16C fibrils (relative sum of squares is +65% as compared with 80%, Table 1). In contrast, a random orientation of the N termini along the z axis gave worse predictions (relative sum of squares is 125%, Table 1). Decreasing the number of β-strands per monomer from four to three increases the strand length and therefore the distance between the N termini of two monomers in opposite orientation (as seen from the y axis). This structure revealed lower quenching as compared with the four-strand zipper structure particularly for lower acceptor concentrations (relative sum of squares is 474%, Table 1). Allowing a second layer of zippers in z-direction also resulted in bad predictions of the fluorescent decay times regardless of the choice of all other parameters. The best predicted β-sheet structure has five layers of β-sheets, which is similar to a two-layered zipper structure with six strands. However, predictions of the five-layered β-sheet were by far the best. Thus, the algorithm can clearly discriminate structures with different monomer conformations but similar polyglutamine core structure, a problem of many other structural approaches. Similar to the β-sheet simulations, simultaneous changes of many parameters did not result in another satisfying minimum in the multidimensional parameter space.

FIGURE 5.

Fluorescent decay curves also fit reasonably to zipper structure. A–C, experimental (various symbols) and simulated (line) fluorescence decay curves for fibrils containing 20% S16C monomer labeled with donor dye and increasing concentrations (from 1.5 to 20%) of S16C monomer labeled with the acceptor dye (A), for fibrils containing 20% P69C monomer labeled with donor dye and increasing concentrations (from 1.5 to 20%) of S16C monomer labeled with the acceptor dye (B), and for fibrils containing 20% P69C monomer labeled with donor dye and increasing concentrations (from 1.5 to 20%) of P69C monomer labeled with the acceptor dye (C). The symbols in panel A represent the increase in the acceptor-labeled monomer and apply to all panels. D, schematic of an antiparallel zipper structure with four strands of the polyQ stretch, each layer perpendicular to fibril growth direction (x axis) and N termini aligned on one side. Note that only the polyQ stretches and not the whole Htt exon 1 are presented in panel D. Two exemplary monomers are depicted with the position of the mutations flanking the polyQ stretch to illustrate the antiparallel orientation of a monomer to each neighbor in the zipper.

DISCUSSION

In this study, we monitor FRET-induced changes in the fluorescence decay times of Htt51Q fibrils and combine them with Monte Carlo simulations to reveal the molecular architecture of the fibrils. The best structure that fits the experimental data is five-layered β-sheet with each monomer consisting of four strands. N termini alternate along the y axis, but monomer orientation is equal along the x axis (Fig. 4D). Although the five-layered β-sheet with four-stranded monomers in alternating orientation best fits the experimental data, the same structure with random orientation of the monomers also gave a reasonably good fit (Table 1). Htt exon I aggregation in vitro is initiated through interactions of the α-helical stretch N-terminal to polyQ (27, 28), supportive also for one-sided orientation of at least some N termini of the monomers.

Available structures of polyQ fibrils suggest multiple turns of the β-sheet within a monomer but do not reveal any information on the orientations of the monomers (16, 17). Unlike for other amyloid fibrils, the in-register signature of a polyQ fibril can be excluded (17). However, details on the monomer orientation, number of strands, and layers in z-direction are unknown. Using distances between fluorophores, we were able to restrict the structural heterogeneity and precisely define the most likely structure of the polyQ core and the orientation of the monomers to each other and to the fibril axis. The polyQ stretch (51Q) in each monomer forms four β-strands with ∼10 glutamines per strand, a length suggested also by two-dimensional infrared spectroscopy of K₂Q₂₄K₂W peptide (18) and supported by the minimal polyQ length needed to form a monomeric nucleus (31). A hairpin with two strands of ∼10 glutamines is energetically stable enough to nucleate aggregation. Every next strand within the polyQ monomer stabilizes energetically the fibril relative to the monomer (35). A β-sheet with three β-strands will have a length of at least 36 glutamines, mirroring the pathological polyQ threshold for HD.

The single zipper layer with four strands and N termini of two adjacent zippers antiparallel along the y axis (Fig. 5D, Table 1) is also revealed as a reasonably good fit, and we cannot exclude it as a core structure of the polyQ fibrils. The length of the β-strand in the zipper is the same as in the β-sheet, 10 glutamines, thus fulfilling the requirements for a minimal length to form a stable monomeric nucleus (31). This structure is consistent with the structure deduced from NMR measurements (14). It should be noted, however, that the NMR measurements were performed with polyQ peptides whose solubility was increased by flanking them with residues of opposite charges (14). Thus, an antiparallel alignment of monomers might be additionally favored by stabilizing interactions of the alternating charges at the two opposite ends.

Initially, we also considered other structures, e.g. α-helix (30), β-pseudohelix (15), and water-filled β-tube (9), which, however, due to the limited density of labeling positions, did not fit to the experimentally obtained donor fluorescent decays. An α-helical confirmation of a polyQ monomer is in principle stable enough to nucleate aggregation (36), but kinetically unstable as dimer to support oligomerization (37). Similarly, β-tube and β-helix are too short-lived as dimers to initiate aggregation (37).

In sum, although the single zipper layer with four strands fits reasonably our experimental data, the observed acceleration of polyQ aggregation through structures promoting β-turn (19) and two-dimensional infrared spectroscopy of K₂Q₂₄K₂W (18) rather support the five-layered β-sheet with four-stranded monomer. Unlike the β-sheet, the zipper structure is kinetically unstable to serve as a monomeric nucleus to initiate polyQ fibrillization (36). It is conceivable to assume cross-seeding between the β-sheet and zipper due to their significant structural similarity, whereas the zipper structure seems less likely to be the nucleation-initiating template for polyQ aggregation.