Ions increase strength of hydrogen bond in water

Abstract

Knowledge of water-water potential is important for an accurate description of water. Potential between two molecules depends upon the distance, relative orientation of each molecule and local environment. In simulation, water-water hydrogen bonds are handled by point-charge water potentials and by polarizable models. These models produce good results for bulk water being parameterized for such environment. Water around surfaces and in channels, however is different from bulk water. Using quantum-mechanical methods, hydrogen bond strength was calculated in the vicinity of different monoions. A simple empirical relationship was discovered between the maximum hydrogen bond and the electric field produced by ion.

I. INTRODUCTION

Water is one of the most important and one of the most abundant compounds on Earth. It played a key role in the development of early life and sustaining all known life forms today. It is also one of the most important compounds in the technological processes and industry. Water has some properties that distinguish it from simpler liquids.[1–5] Some of the most important anomalies of pure water are the following: maximum density at 4 °C in the liquid phase, negative coefficient of thermal expansion below that temperature, high surface tension and viscosity, a minimum in the isothermal compressibility, and a large heat capacity. Used as a solvent, water also has many unusual properties: for nonpolar solutes, a large entropy opposes solvation at room temperature, and a large heat capacity of transfer of apolar solvent into water. Water anomalies are related to the ability of water molecules to form tetrahedrally coordinated hydrogen bonds. To understand the behavior and properties of water and aqueous solutions is therefore crucial to understand hydrogen bonding and its molecular background. A crucial step toward understanding water is therefore a knowledge of water-water potential.

One can use quantum-mechanical theories to calculate exact properties of water, but the available computers can not handle systems consisting of more than a few molecules. As a consequence, there has been a persistent need to develop various simplified water models that seek a compromise between the accuracy and computational cost. If one wants to run molecular dynamics or Monte Carlo simulations with such models, an intermolecular potential is required as input. Usually simplified point-charge water models like SPC[6], TIP3P[7], TIP4P[8], TIP4P-Ew[9], TIP5P[10] are used. These models have point charges on or near the oxygen and hydrogens, and van der Waals terms. They are parameterized in a such way as to achieve the best agreement of an arbitrarily chosen bulk property with the experimental data. These parameters do not depend on local environment, meaning that they have the same values even if water local environment is far from bulk. There are also some polarizable models like PSPC[11], but are more complex and time-consuming to use in simulations. In recent work by Znamenskiy and Green [18] and our work[19], it was shown that the strength of hydrogen bond between two water molecules depends on the number of water molecules bonded to both water molecules and those on the second coordination shell. The local environment effect on HB strength is not negligible. Similar findings were also reported in other recent theoretical developments, [12–14] which recognize the extended nature of the hydrogen bond and explicitly include three-body interactions. These three-body effects are the same as cooperative effects of hydrogen bonding in water clusters [15]. When two water molecules form a hydrogen bond, the redistribution of charge happens on both of them. The bond formation changes the feasibility of further hydrogen bonding in comparison to an individual water molecule. The water molecule that donates the hydrogen atom in HB has increased electron density on oxygen and this encourages hydrogen bond acceptance. The water molecule that accepts the hydrogen has reduced electron density on hydrogen atoms, which is beneficial for further donating of hydrogen atoms[16]. These electron density changes are the reason for the so-called cooperativity or anticooperativity in hydrogen bond formation in water networks. Further details and references about cooperativity can be found in a review paper by de Olivera[17].

The goal of this contribution is to show the extensive nature of the hydrogen bond, spreading its influence beyond the hydrogen-bonded pair due to long-range, charge-density shifts accompanying formation of the bond. This was done with calculations of energies of clusters consisting of water molecule pair and different monovalent cations and anions, using post Hartee-Fock calculations.

II. METHODS AND DISCUSSION

Calculations were performed using the Gaussian 09[20] program suite, employing MP2(full) method[21] with def2-QZVP basis sets[22, 23]. Full geometry optimization of the water molecule with MP2(full) method for this basis set yielded the OH bond length 0.9562Å and the HOH angle 104.42° which is very close to the experimental data (OH bond length 0.9572 Å, HOH angle 104.52°)[24] for an isolated water molecule in a vacuum. Water-water potential for two molecules in a vacuum was also calculated with this method and basis set. Electronic energies are reported as the difference between the energy of dimer and the energy of two isolated water molecules at the infinite distance. Calculated maximum interaction is -5.22 kcal mol⁻¹ and the oxygen-oxygen distance 2.8935Å when geometry optimization was done for all distances and angles, and -5.21 kcal mol⁻¹ and 2.8957Å when geometry of water molecule was kept fixed. This confirmed our assumption that we can get good results for the strength of hydrogen bond when internal degrees of freedom of water molecules are kept fixed. Both energies compare favorably with the experimentally measured value, giving an estimate of the electronic interaction energy of -5.4 ± 0.7 kcal mol⁻¹[25, 26] and both distances with the experimental oxygen-oxygen distance. The experimental study by Odutola and Dyke[27] yielded an equilibrium oxygen-oxygen distance of 2.946 Å. Various basis sets have been used in initial calculations and def2-QZVP was ultimately chosen as the best compromise between the computational complexity and the accuracy of the results for the set of monoions. All calculations were carried out with and without basis set superposition error (BSSE), but there was only small difference in results (less than 5%). As a first step, we calculated the bonding energies and distances for ion and single water molecule. In Tables 1 and 2, we presented the equilibrium ion oxygen distance and the bonding energy of systems for different cations and anions and one water molecule. In the vicinity of a cation, water dipole is parallel to electric field of the ion, while in case of an anion, one hydrogen atom points towards the ion. Then we attached the ion to one of the water molecules in a water dimer, either on the water donating hydrogen in hydrogen bond or on the water accepting hydrogen, and calculated the energy of the system while varying oxygen-oxygen distance. This system consists of two waters (particle 1 and 2) and ion (particle 3). In Figure 1 minimum energy geometry of the water dimer and ion is shown. The total energy E of the system depends on all three particles. In physics, it is always possible to split potential of many bodies into the sum over interactions that involve not just two, but clusters of three or more nearby atoms. In our case the total energy of three body system can be split into a three-body term, E₃(1, 2, 3), three two body terms, E₂(i, j), and electronic energy of single particle, E₁(i), as

$$E=E_3(1,2,3)+E_2(1,2)+E_2(1,3)+E_2(2,3)+E_1\left(1\right)+E_1\left(2\right)+E_1\left(3\right),$$ (1)

with 1 and 2 standing for the water molecules and 3 for the ion. We have approximated the strength of the hydrogen bond in the proximity of an ion as sum of three-body energy term and two-body term between the water molecules

$$E_{HB}=E_3(1,2,3)+E_2(1,2).$$ (2)

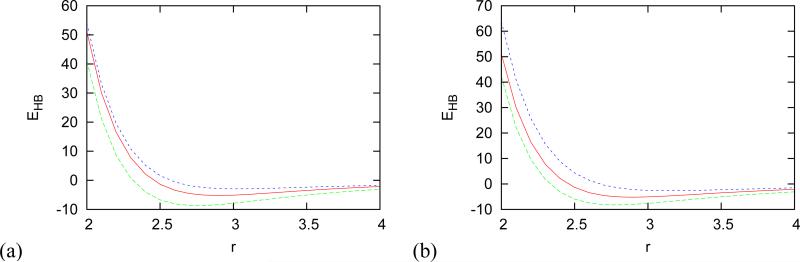
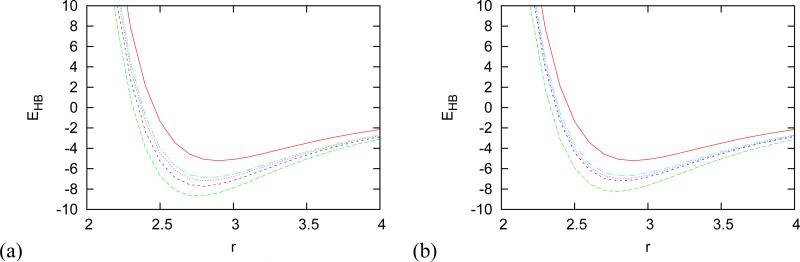
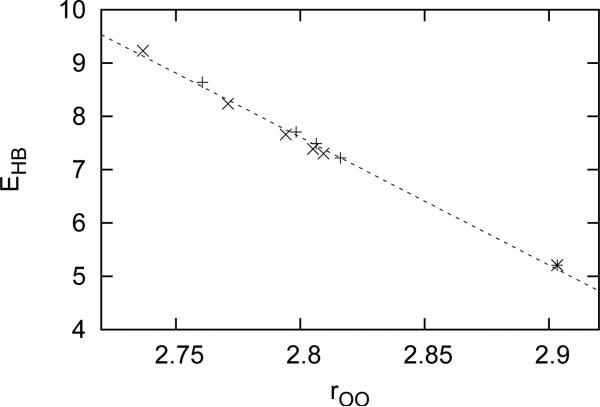
In Figure 2, we plotted the distance dependence of the hydrogen bond strength between two water molecules in the presence of lithium and fluoride ions attached to donor and acceptor water, respectively and also in case of the absence of ions. When a cation is attached to the water donating hydrogen, this cation attracts electrons from water molecule, making hydrogen atom more positive and leading to increase of the strength of HB. When cation is attached to the water acceptor, this cation attracts the electrons from water, making the oxygen atom less negative and leading to a decrease of the strength of HB. With an increase of the strength, the minimum shifts to smaller distances and vice-versa. For anions we have the opposite effect. When an anion is attached to the water donating hydrogen in dimer, this anion causes an increase of partial charges on the hydrogen, which leads to a weaker hydrogen bond. When it is attached to the water acceptor, the negative charge of oxygen becomes more negative, which leads to a stronger hydrogen bond. Figure 3 shows a distance dependence of HB for geometries where HB increases in comparison with an isolated dimer. Figures are plotted for series of cations and anions. Smaller ions have a bigger impact on the strength of HB because strength of electric field of the ion is bigger on position of water dimer. In the presence of lithium and fluoride ions, the HB is the strongest and shifted to smallest distance for all ions. This effect decreases with an increase of radius of ion. Correlation between the maximum HB strength and distance between waters, when this happens, is shown in Figure 4. This relation is approximately linear and can be described as

$$-E_{HB}=A\cdot r_{OO}+B$$ (3)

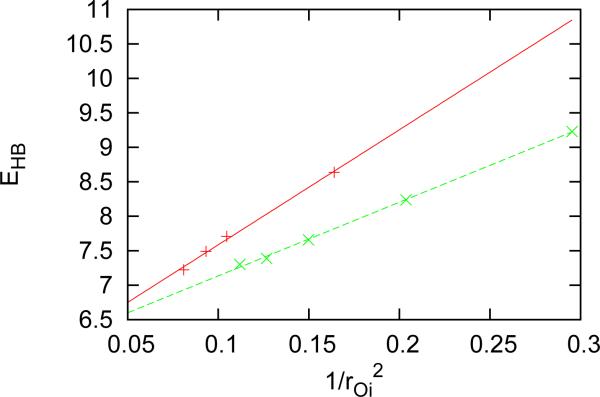
with the parameters A = −24.03 kcal·mol⁻¹Å⁻¹ and B = 74.90 kcal·mol⁻¹, which is in agreement with our previous calculations [19] for clusters of water molecules. This correlation allows us to focus our further research of local environment effects on the HB strength only since by knowing the strength we know also distance. From Figure 3 we saw that the strength of HB depends on type of ion and the type of ion we associated with strength of electric field produced by this ion on position of oxygen atom of water to which ion was attached. Strength of the electric field is proportional to 1/r²_Oi where r_Oi is the distance between ion and oxygen atom of water to which ion is attached. Figures 5 shows this correlation, which can be described with the following relation

$$-E_{HB}=\frac{C}{r_{Oi}^2}+D$$ (4)

with the parameters for cations C_c = 10.69 kcal·mol⁻¹Å², D_c = 6.06 kcal·mol⁻¹ and for anions C_a = 16.70 kcal·mol⁻¹Å², D_a = 5.91 kcal·mol⁻¹. The asymmetry for cations and anions arises because of different bonding of water to single ion, as seen in Figure 1. Furthermore, we also checked the relationship between the transfer of charge from ion to closest water molecule,Δe, and the strength of HB. This relationship is almost linear. We approximated it as

$$-E_{HB}=A_e\cdot \Delta e+B_e$$ (5)

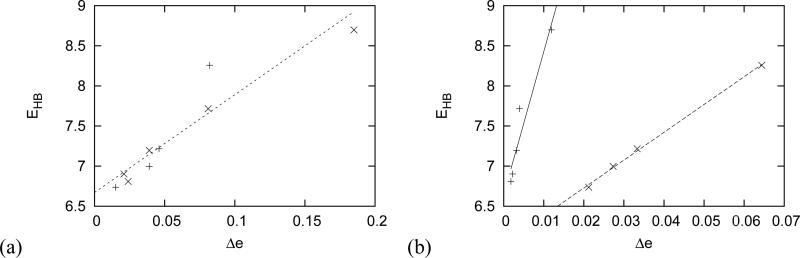
with the parameters A_e = 12.18 kcal·mol⁻¹ and B_e = 6.67 kcal·mol⁻¹. Charges were calculated by Mulliken population analysis. This is plotted on Figure 6a while on figure 6b we plotted the same results, but obtained by Natural Bond Orbital analysis (NBO)[28]. Here we have the same linear relationship, but different function for cations and anions. For anions we have parameters A_e = 34.66 kcal·mol⁻¹ and B_e = 6.03 kcal·mol⁻¹ and for cations A_e = 178.7 kcal·mol⁻¹ and B_e = 6.64 kcal·mol⁻¹.

Table 1.

Oxygen-cation equilibrium distance in Å, and bonding energy in kcal mol^–1 for different cations to one water molecule.

Cation	rcO	Ecw
Li+	1.840	−34.61
Na+	2.216	−24.81
K+	2.583	−18.70
Rb+	2.809	−14.69
Cs+	2.989	−14.04

Table 2.

Oxygen-anion equilibrium distance in Å, hydrogen-oxygen-anion angle and bonding energy in kcal mol^–1 for different anions to one water molecule.

Anion	raO	α HOa	Eaw
F–	2.469	3.06	−27.44
Cl–	3.090	8.25	−15.47
Br–	3.274	10.15	−13.79
I–	3.514	12,56	−11.51

Figure 1.

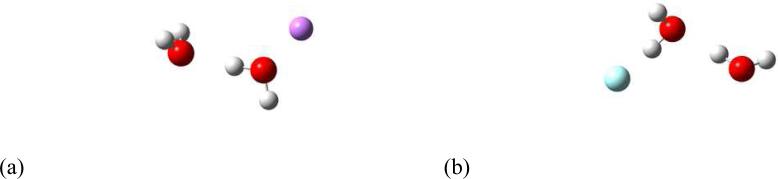
Geometry of water dimer and (a) a lithium ion, (b) a fluoride when strength of hydrogen bond is increased.

Figure 2.

Distance dependence of strength of hydrogen bond for (a) lithium and (b) fluoride ion. Distance is in Å, energy in kcal mol⁻¹, red solid line is for two waters without ion, green long dashed line for ion attached to water donating hydrogen in HB and blue dashed for ion attached to water accepting hydrogen.

Figure 3.

(a) Distance dependence of strength of hydrogen bond for different cations when cation is attached to water donating hydrogen in HB. (no ion - red solid line, Li⁺ - green long dashed line, Na⁺ - blue dashed line, K⁺ - purple dotted line, Rb⁺ - lite blue long dashed dotted line, Cs⁺ - yellow dashed dotted line ) (b) Distance dependence of strength of hydrogen bond for different anions when anion is attached to water accepting hydrogen in HB. (no ion - red solid line, F⁻ - green long dashed line, Cl⁻ - blue dashed line, Br⁻ - purple dotted line, I⁺ - lite blue long dashed dotted line) Distance is in Å, energy in kcal mol⁻¹.

Figure 4.

Correlation between HB strength and distance. Plus signs are cations, exes are anions.

Figure 5.

Correlation between HB strength and electric field produced by ion. Red curve and symbols present anions and green cations.

Figure 6.

Correlation between HB strength and transfer of charge from ion to closest water molecule (a) for Mulliken population analysis and (b) for Natural Bond Orbital analysis. Plus signs are cations, exes are anions.

III. CONCLUSION

We have calculated the dependence of HB strength in water on the presence of different monoions in the local environment by performing quantum chemical calculation. Calculations have shown that the introduction of ions to the local environment increases or decreases the HB strength depending on type of ion and to which water molecule an ion is bonded. In other words, if a water molecule is donor or acceptor of hydrogen in HB, the strength changes. When an increase in the strength of HB is observed, this increase linearly depends on the strength of the electric field produced by an ion and on the transfer of charge. This result provides new insight into understanding the nature of hydrogen bonding. Local environment appears to play far greater role in the HB strength and length than previously thought. Simple water models take into account only pairwise potential interactions between water molecules. Our calculations confirmed that this is not enough. Using only pairwise interactions for water close to surfaces and in channels does not suffice since the presence of charges in additional molecules of surrounding walls considerably changes the potential between two molecules. One way to address this is to use polarisable models of water where interactions are not pairwise. Another option is to construct water models that use pairwise and three-particle interactions [29].

• Hydrogen bond strength was calculated in the vicinity of monoions.

• Introduction of ions to local environment increases or decreases the HB strength.

• The increase linearly depends on the strength of the electric field of an ion.

• The increase linearly depends on the transfer of charge.

• Water around surfaces and in channels is different from bulk water.