A NEW METHOD OF PEAK DETECTION FOR ANALYSIS OF COMPREHENSIVE TWO-DIMENSIONAL GAS CHROMATOGRAPHY MASS SPECTROMETRY DATA

Abstract

We develop a novel peak detection algorithm for the analysis of comprehensive two-dimensional gas chromatography time-of-flight mass spectrometry (GC×GC-TOF MS) data using normal-exponential-Bernoulli (NEB) and mixture probability models. The algorithm first performs baseline correction and denoising simultaneously using the NEB model, which also defines peak regions. Peaks are then picked using a mixture of probability distribution to deal with the co-eluting peaks. Peak merging is further carried out based on the mass spectral similarities among the peaks within the same peak group. The algorithm is evaluated using experimental data to study the effect of different cut-offs of the conditional Bayes factors and the effect of different mixture models including Poisson, truncated Gaussian, Gaussian, Gamma, and exponentially modified Gaussian (EMG) distributions, and the optimal version is introduced using a trial-and-error approach. We then compare the new algorithm with two existing algorithms in terms of compound identification. Data analysis shows that the developed algorithm can detect the peaks with lower false discovery rates than the existing algorithms, and a less complicated peak picking model is a promising alternative to the more complicated and widely used EMG mixture models.

1. Introduction

Multiple analytical approaches such as liquid chromatography mass spectrometry (LC-MS), gas chromatography mass spectrometry (GC-MS), and nuclear magnetic resonance spectroscopy (NMR) have been employed for the comprehensive characterization of metabolites in biological systems. One such powerful approach is comprehensive two-dimensional gas chromatography time-of-flight mass spectrometry (GC×GC-TOF MS). Unlike other existing analytical platforms, GC×GC-TOF MS provides much increased separation capacity, chemical selectivity and sensitivity for the analysis of metabolites present in complex samples. The information-rich output content of GC×GC-TOF MS data has huge potential in metabolite profiling, identification, quantification, and metabolic network analysis (Castillo et al., 2011; Jeong et al., 2011; Kim et al., 2011; Pierce et al., 2005; Sinha et al., 2004).

Metabolites analyzed on a GC×GC-TOF MS system are first separated on two-dimensional GC columns and then subjected to a mass spectrometer, which is usually equipped with an electron ionization (EI) ion source. The EI process fragments the metabolite’s molecular ions and results in fragment ion mass spectrum. For metabolite identification and quantification using the EI mass spectra, the first step is to reduce the instrument data, i.e., a collection of EI mass spectra, to chromatographic peaks. To help readers understand the GC×GC-TOF MS data, a brief introduction is given in the Supplementary Information.

Although numerous algorithms have been developed for peak detection in one dimensional GC-MS data (Dixon et al., 2006; Nicolè et al., 2012; O’Callaghan et al., 2012; Yang, He, and Yu, 2009), there are only four algorithms available for the two-dimensional GC-MS (Peters et al., 2007; Reichenbach et al., 2005; Vivó-Truyols, 2012) including commercial software ChromaTOF from LECO company. However, none of these software packages is publicly available yet, except ChromaTOF that is commercially embedded in the GC×GC-TOF MS instrument. It is therefore highly desirable to develop publicly available peak detection methods for the analysis of GC×GC-TOF MS data. On the other hand, the existing peak detection algorithms for the analysis of GC×GC-TOF MS data perform baseline correction and denoising separately, which may greatly increase the risk of introducing errors from each independent stage. In fact, Wang et al. (2008) introduced a reversible jump Markov chain Monte Carlo (RJ-MCMC)-based peak detection algorithm to perform simultaneous baseline, denoising and peak identification for analysis of one-dimensional surface enhanced laser desorption/ionization (SELDI) MS data and demonstrated that the simultaneous process reduces false discovery rate. However, in practice, the use of applications of RJ-MCMC is limited due to that prior distributions should be appropriately assigned in order to design an effective RJ-MCMC algorithm and make posterior distributions of parameters computationally tractable and that constructing an MCMC chain is in general computationally extensive. Yang et al. (2009) compared the performance of peak detection among several peak detection algorithms for one-dimensional matrix-assisted laser desorption/ionization (MALDI) MS data and showed that the continuous wavelet-based (CWT) algorithm, which has simultaneous baseline and denoising, provides the best performance, but it is still a major challenge to compute accurate peak abundance (area), which is very important in compound quantification, due to its model-free approach. Furthermore, the existing algorithms require manually assigned signal-to-noise ratio (SNR) threshold and/or denoising parameters that are usually not optimized in the existing peak detection algorithms, resulting in a high rate of false-positive and/or false-negative peaks.

To avoid the aforementioned difficulties in analysis of GC×GC-TOF MS data, we propose a novel peak detection algorithm using a normal-exponential-Bernoulli (NEB) model and mixture probability models, and the developed R package msPeak is publicly-available at http://mrr.sourceforge.net. The developed algorithm is composed of the following components: (i) the proposed NEB model performs simultaneous baseline correction and denoising, followed by finding the potential peak regions using a conditional Bayes factor-based statistical test, (ii) the peak picking and area calculations are carried out by fitting experimental data with a mixture of probability model, and (iii) the detected peaks originated from the same compound are further merged based on mass spectral similarity. The advantages of the proposed method are that the proposed NEB-based preprocessing requires no manually assigned SNR threshold and denoising parameters from users, which makes it easy to use; and, instead of searching for the potential peaks using the entire data, the proposed algorithm reduces the entire data to peak regions using a conditional Bayes factor of the test, eliminating the possible computational burden as well as improving the quality of peak abundance (area). The developed algorithm is further compared with two existing algorithms in terms of compound identification.

Besides, we investigated the performance of several probability mixture models for peak picking based on peak regions identified by the NEB model. It has been known that the model-based approach measures more accurately peak abundance (area) and the exponentially modified Gaussian (EMG) probability model performs well for fitting asymmetric chromatographic peaks and the detection of peak position (Di Marco and Bombi, 2011; Vivó-Truyols, 2012; Wei et al., 2012). However, to our knowledge, there is no study to evaluate EMG model by comparing with other possible probability models in analysis of GC×GC-TOF MS data. To address this, we employed five probability mixture models: Poisson mixture models (PMM), truncated Gaussian mixture models (tGMM), Gaussian mixture models (GMM), Gamma mixture models (GaMM), and exponentially modified Gaussian mixture models (EGMM). Here PMM, GMM, and EGMM were chosen based on Di Marco and Bombi (2011)’s work, and we proposed two new models, tGMM and GaMM, as alternatives to GMM and EGMM, respectively.

We hope our research can provide some insight on the following computational/statistical challenges of the current peak detection approaches: (i) baseline correction and denoising are performed separately so that there is no way to communicate the information with each step, (ii) user-defined input values are needed, (iii) entire data are used for peak detection (compared to our proposed approach that finds peak regions first and then detect peaks), and (iv) there is no comparison analysis for the performance of different chromatographic peak models.

The rest of the paper is organized as follows. Section 2 presents the proposed peak detection algorithm and introduces a trial-and-error optimization of the developed algorithm. The real GC×GC-TOF MS data is described in Section 3. In section 4, we apply the developed algorithm to real experimental GC×GC-TOF MS data, followed by the comparison with two existing algorithms in Section 5. In Section 6, we discuss the results and then conclude our work in Section 7.

2. Algorithms

The proposed peak detection algorithm consists of three components with the following four steps: finding potential peak regions, simultaneous denoising and baseline correction, peak picking and area calculation, and peak merging (Supplementary Information Figure S1). The first two steps are performed by hierarchical statistical models at a time, while the peak picking and area calculation are carried out by model-based approaches in conjunction with first derivative test. The peak merging then uses mass spectral similarities to recognize peaks originated from the same metabolite. The selection of the cut-off value of the conditional Bayes factor and the probability model is further optimized by a trial-and-error optimization. On the other hand, when multiple samples are analyzed, each sample will generate a peak list after peak detection. A cross sample peak list alignment is needed to recognize chromatographic peaks generated by the same compound in different samples. Current existing peak-based methods generally perform peak alignment using the mass spectral similarity and peak position (location) distance (e.g., Kim et al., 2011). This peak alignment process will generate a matched peak table for downstream data analysis, such as quantification and network analysis. In this regard, the peak detection process plays an important role in generating the peak list. It should be noted that, due to either systematic (technical) or biological variations, some peaks (molecules) may not be detected in all samples, resulting in an incomplete peak table. There are several remedies to deal with the issue, such as ignoring missing data, filling in zero, or imputing/estimating missing data (e.g., Hrydziuszko and Viant, 2012; Liew, Law, and Yan, 2011).

2.1. Finding peak regions

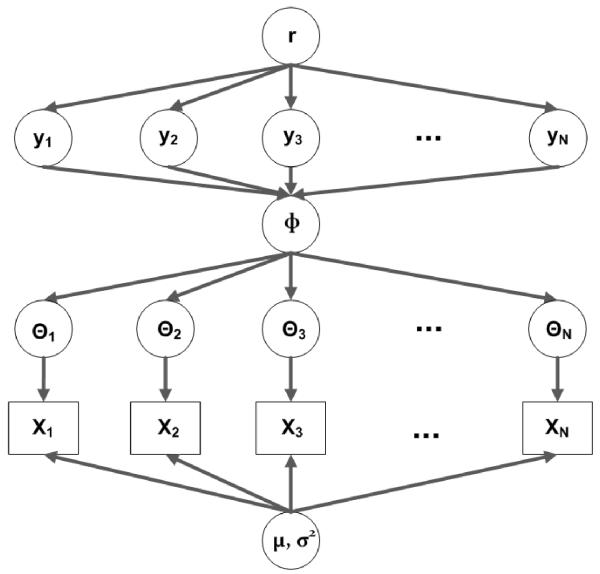
Newton et al. (2001) proposed a hierarchical approach to the microarray data analysis using gamma-gamma-Bernoulli model. Their purpose was to detect the genes that are differentially expressed. In this study, we adopted their idea to simultaneously perform baseline correction and denoising, by replacing the gamma-gamma-Bernoulli model with the normal-exponential-Bernoulli (NEB) model. The proposed hierarchical NEB model has three layers. In the first layer, the observed data, X_i, are modeled through the normal distribution with mean Θ_i + μ and variance σ² for each ith total ion chromatogram (TIC), where i = 1, ⋯, N and N is the number of TICs. Note that a TIC is a chromatogram created by summing up intensities of all mass spectral peaks collected during a given scan (or a given instrumental time). In other words, we assume that the noise follows the normal distribution with mean zero and variance σ². For simplicity, the homogeneous variance is assumed in this model. Here Θ_i is the true signal of the observed signal X_i and μ is either a baseline or a background. The true signal, Θ_i, is further modeled by the exponential distribution with mean φ in the second layer. In case that there is only noise, meaning that no signal is present, the observed signal, X_i, is modeled only with the background and noise signal. Consequently, X_i follows the normal distribution with mean μ and variance σ².

In this approach, we pay attention to whether the observed TIC at a given position is significantly different from background signal. To do this, one more layer is introduced in the model using a Bernoulli distribution, resulting in the NEB model. The true TICs of some proportion r are present (i.e., Θ_i ≠ 0), while others remain at zero (Θ_i = 0). For positions where the true TIC is present, we use the following model:

$$X_i\sim ND({ϴ}_i+\mu ,{\sigma }^2)\text{and}{ϴ}_i\sim Exp\left(\varphi \right),$$ (2.1)

where N D stands for a normal distribution, X_i is an observed TIC at the ith position, Θ_i is the true TIC of X_i of the exponential distribution with φ, and μ is the mean background or baseline with variance σ². In case that no TIC is present, the background signal follows:

$$X_i\sim ND(\mu ,{\sigma }^2).$$ (2.2)

Therefore, the marginal density of X_i when _i ≠ 0 is driven by

$$p_1\left(x_i\right)=\frac{1}{\varphi }\exp \left(\frac{{\sigma }^2}{2{\varphi }^2}-\frac{x_i-\mu }{\varphi }\right)\Phi \left(\frac{x_i-\mu -{\sigma }^2∕\varphi }{\sigma }\right),$$ (2.3)

where Φ(·) is the cumulative distribution function (cdf) of the standard normal distribution. When Θ_i = 0, the marginal density of x_i becomes the probability density function (pdf) of a normal distribution with mean μ and variance σ². The detail derivation of Equation (2.3) can be found in the Supplementary Information. The loglikelihood l(μ, σ², φ, r) is

$$\sum _i\left\{y_i\log \right({\mathrm{p}}_1\left(x_i\right))+(1-y_i\left)\log \right(p_0\left(x_i\right))+y_i\log (r)+(1-y_i\left)\log \right(1-r\left)\right\}$$ (2.4)

where y_i is the value of the binary indicator variable, Y_i, at the ith TIC with 0 unless there is a true significant signal and r is the proportion of the true TICs. As a result, there are four parameters (μ, σ², φ, r) along with the indicator variable Y_i(i = 1, ⋯, N) to estimate. The graphical representation of the proposed NEB model is depicted in Figure 1.

Fig 1.

The graphical representation of a normal-exponential-Bernoulli (NEB) model.

Parameter estimation

The EM algorithm (Dempster, Laird, and Rubin, 1977) is employed to estimate the parameters of Equation (2.4) by considering the indicator variable Y_i(i = 1, ⋯, N) as the latent (or missing) variable. In the E-step, the latent variable Y_i(i = 1, ⋯, N) is estimated, after fixing the parameters (μ, σ², φ, r) at the current estimates, by

$${\widehat{y}}_i=P(y_i=1\mid x_i,\widehat{\mu },{\widehat{\sigma }}^2,\widehat{\varphi },\widehat{r})=\frac{\widehat{r}{p}_1\left(x_i\right)}{\widehat{r}{p}_1\left(x_i\right)+(1-\widehat{r})p_0\left(x_i\right)}.$$ (2.5)

To simplify the M-step, the mixture structure has been separated so that the update estimate of r is the arithmetic mean of ${\widehat{y}}_i$’s and the remaining parameters (μ, σ², φ) are optimized by a numerical approach such as the R package nlminb. It should be noted that our optimization does not guarantee a global optimum since the R package nlminb used is a local optimization. In particular, a Beta(2, 2) is placed as a prior over r to stabilize the computation as well as to enable a nice interpretation of the output, according to Newton et al. (2001), resulting in the following r̂:

$$\widehat{r}=\frac{2+{\Sigma }_i{\widehat{y}}_i}{2\cdot 2+N},$$ (2.6)

where N is the total number of TIC. After fixing $\widehat{r}$, the remaining parameters are estimated by maximizing the loglikelihood as follows:

$$({\widehat{\mu }}^2,{\widehat{\sigma }}^2,\widehat{\varphi })=\arg \underset{\mu ,{\sigma }^2,\varphi }{\max }l(\mu ,{\sigma }^2,\varphi ,\widehat{r}).$$ (2.7)

Finding true signals

The true signals are found by performing the significant test based on the posterior odds. The posterior odds of signal at the ith TIC are expressed by

$$\frac{P(y_i=1\mid x_1,\cdots ,x_N)}{P(y_i=0\mid x_1,\cdots ,x_N)}.$$ (2.8)

The posterior probability of y_i given the entire TIC is

$$\begin{array}{cc}\hfill P(y_i\mid x_1,\cdots ,x_N)=& {\int }_0^{1}p(y_i,r\mid x_1,\cdots ,x_N)dr\hfill \\ \hfill & ={\int }_0^{1}P(y_i\mid r,x_1,\cdots ,x_N)p(r\mid x_1,\cdots ,x_N)dr\hfill \\ \hfill & ={\int }_0^{1}P(y_i\mid r,x_i)p(r\mid x_1,\cdots ,x_N)dr\hfill \end{array}$$ (2.9)

by conditional independence of the data at different TICs given the parameter r. Using the approach in Newton et al. (2001), the posterior odds can be approximated by

$$\frac{p_1\left(x_i\right)}{p_0\left(x_i\right)}\frac{\widehat{r}}{1-\widehat{r}},$$ (2.10)

where w can be called conditional Bayes factors since the prior odds equal unity, P(y_i = 1|x₁, ⋯, x_N) ≈ p₁(x_i)r̂ and P(y_i = 0|x₁, ⋯, x_N) ≈ p₀(x_i)(1-r̂) by approximating Equation (2.9) at the model r = r̂. According to Jeffreys (1961)’ scales, the three values of 1, 10, and 100 are used to interpret the posterior odds, meaning that the TICs are selected using three cut-off values. That is, if the posterior odds of a TIC are less than a selected cut-off value, then this TIC is considered as a noise by fixing it at zero (i.e., Θ_i = 0). Otherwise, the TIC will be preserved for future analysis (i.e., Θ_i ≠ 0).

2.2. Denoising and baseline correction

Once the significant TICs (true signals) are detected by the posterior odds, the baseline correction and denoising are performed simultaneously based on the estimated parameters. That is, under the assumption that the TIC is true signal (Θ_i ≠ 0), the convoluted TIC, x̂_i, is predicted by the expected true TIC (signal) given an observed TIC, i.e., E(Θ_i|x_i). By doing the calculation described in the Supplementary Information, we can obtain the convoluted TIC, x̂_i, as follows:

$${\widehat{x}}_i=x_i-\left(\widehat{\mu }+\frac{{\widehat{\sigma }}^2}{\widehat{\varphi }}\right)+\widehat{\sigma }\frac{\phi \left(\frac{x_i-(\widehat{\mu }+{\widehat{\sigma }}^2∕\widehat{\varphi })}{\widehat{\sigma }}\right)}{\Phi \left(\frac{x_i-(\widehat{\mu }+{\widehat{\sigma }}^2∕\widehat{\varphi })}{\widehat{\sigma }}\right)},$$ (2.11)

where φ and Φ are the probability density and cumulative distribution functions of the standard normal distribution N D(0, 1), respectively.

2.3. Peak detection and area calculation

After denoising and baseline correction, the vector of predicted TICs, ${\left\{{\widehat{x}}_i\right\}}_{i=1,\cdots ,N}$, are converted into the N₁ by N₂ matrix D(= [d_kl]_k=1,⋯,N₁;l=1,⋯, N₂), where N = N₁ · N₂. Here the sizes of the row and column of the matrix D are the same as the intervals of the first and the second dimension retention times, respectively. In order to detect peaks for each significant peak region, we employ five different model-based approaches along with the first derivative test (FDT): Poisson mixture models (PMM), truncated Gaussian mixture models (tGMM), Gaussian mixture models (GMM), Gamma mixture models (GaMM), and exponentially modified Gaussian mixture models (EGMM).

The peak area is calculated based on the highest probability density (HPD) regions of 95% for model-based approaches. We assume that D_k is the kth row vector of the matrix D, where the size of D_k is N₂ and 1 ≤ k ≤ N₁, and D_k = {d_kl}_l=1,⋯,N₂. In other words, D_k is a vector of intensities at each second dimension retention time given the kth first dimension retention time. Then D_k is partitioned into several nonzero peak regions, i.e., $D_k≔Z_k=\{Z_k^1,Z_k^2,\cdots ,Z_k^{M_k}\}$, where 1 ≤ k ≤ N; $Z_k^m={\left\{z_{kl}\right\}}_{l=1,\cdots ,N_2^{m,k}}$; 1 ≤ m ≤ M_{k_}; $N_2\ge {\Sigma }_{m=1}^{M_k}{N}_2^{m,k}$. It is noteworthy that $Z_k^m$ is a nonzero peak region and its intensities z_kl’s are always nonzero.

First derivative test (FDT)

FDT is used to infer the maximum number of components (peaks) of the mixture probability models. The first derivative is calculated over the converted nonzero vector $Z_k^m$ with respect to the second dimension retention times to find a peak, for the given kth first dimension retention time and the mth nonzero peak region where 1 ≤ k ≤ N₁ and 1 ≤ m ≤ M_k. By doing so, the local maxima are found with respect to the second dimension retention time. That is, for each converted vector $Z_k^m$, we examine z_kl whether it is a local maximum with respect to the second dimension retention time as follows:

$$I_{kl}=\{\begin{array}{cc}1\hfill & \text{if}{z}_{k(l-1)}-z_{kl}<0\text{and}{z}_{kl}-z_{k(l+1)}>0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (2.12)

where I_kl is the indicator variable for peaks detected using the second dimension retention time; 1 indicates a local maximum. In fact, we observed that the first derivative test with respect to the first dimension retention time has little information in most cases, due to the relatively large value of modulation period compared to the chromatographic peak width in the first dimension GC. For this reason, we used only the second dimension retention time for peak picking. It is noteworthy to mention again that we use the FDT only for guessing the maximum number of the possible peaks and for an initial value of the optimization of the model-based approach.

Model-based approach

The five different probability models including Poisson, truncated Gaussian, Gaussian, Gamma, and exponentially modified Gaussian distributions are employed along with mixture models. For each converted nonzero vector $Z_k^m={\left\{z_{kl}\right\}}_{l=1,\cdots ,N_2^{m,k}}$, a mixture of the selected probability models are fitted to the observed, convoluted intensities. Suppose f_s(·|ξ_s) is a pdf with a parameter of ξ_s of the sth component, where 1 ≤ s ≤ S, ξ_s is a scalar or a vector, and S is the number of mixture components. Then the converted nonzero intensity z_kl at the kth first dimension retention time is modeled as follows:

$$z_{kl}\sim ND\left\{\sum _{s=1}^S{w}_s\cdot f_s(t_l\mid {\xi }_s),{\tau }^2\right\},$$ (2.13)

where t_l is the second dimension retention time at the lth position, w_s is the nonnegative weight factor of the sth component, ${\Sigma }_{s=1}^S{w}_s=1$, and N D stands for a normal distribution with variance τ². The parameters (ζ, S) are estimated by minimizing −2 times loglikelihood function:

$$(\widehat{\zeta },\widehat{S},{\widehat{\tau }}^2)=\arg \underset{\zeta ,S,{\tau }^2}{\min }\left[N_2^{m,k}\log \left(2\pi {\tau }^2\right)+\frac{1}{{\tau }^2}\sum _{l=1}^{N_2^{m,k}}{\{z_{kl}-\sum _{s=1}^S{w}_s\cdot f_s(t_l\mid {\xi }_s\left)\right\}}^2\right],$$ (2.14)

where $\widehat{\zeta }={({\widehat{w}}_s,{\widehat{\xi }}_s)}_{s=1}^{\widehat{S}}$, and ${\widehat{w}}_s$ and ${\widehat{\xi }}_s$ are the estimated parameters of the sth component. The pdf and its parameters for Poisson, truncated Gaussian, Gaussian, Gamma, and exponentially modified Gaussian can be found in the Supplementary Information.

Then 95% highest probability density (HPD) intervals are calculated with the estimated ${\widehat{w}}_s$ and ${\widehat{\xi }}_s$ for each kth peak, $1\le s\le \widehat{S}$, and the length of its 95% HPD interval is assigned as the peak area. As mentioned before, we consider the number of peaks detected by FDT as the maximum number of peaks that can be detected. Therefore, the number of mixture components estimated by each model-based approach ($\widehat{s}$) always becomes less than or equal to the number of peaks detected by FDT. Furthermore, the intensities are divided by the total sum of nonzero intensities in a given peak region for the purpose of normalization since each model is a probability distribution.

2.4. Peak grouping and merging

It is likely that multiple peaks detected can be from the same compound due to systemic variations. To correct these multiple peaks, we use the mass spectrum (MS) information by calculating the MS similarity among the peaks. Since it might be computationally expensive if all the pairwise MS similarities are calculated, we first group the peaks according to their nonzero peak regions and then merge the peaks having the higher MS similarity using a user-defined cut-off value, only if these peaks are present in the adjacent nonzero peak region(s). For instance, assuming that two peaks z_kl and z_mn belong to the nonzero peak regions $Z_k^i$ and $Z_m^j$, respectively, z_kl and z_mn are considered as members of the same group if these two peak regions are adjacent to each other. Otherwise, they are assigned to different groups. The MS similarities among all peaks within the same group are calculated, and the peak with the highest TIC is selected as the representative peak in case that multiple peaks have the MS similarities greater than the user defined cut-off value (e.g., 0.95) by replacing the peak area with the sum of peak areas of all merged peaks.

2.5. Optimal selection of the cut-off value and the probability model

As can be observed in Section 3, the optimal probability mixture model can be different according to the detected peak regions, so does the cut-off value of the conditional Bayes factor. For this reason, we further consider a trial-and-error optimization of the developed algorithm in order to select the optimal cut-off value of the conditional Bayes factor and the optimal probability mixture model. To do this, three objective functions are considered, which are mean squared error (MSE), Akaike information criterion (AIC), and Bayesian information criterion (BIC) that were used in Section 3. That is, given a selected objective function, we first look for the optimal probability mixture model for each detected peak region and then find the optimal cut-off value of the conditional Bayes factor by the minimum of the sums of all the objective functions for each cut-off value. In detail, the optimal cut-off value $\tilde{\nu }$ is selected by the following trial-and-error optimization:

$$\tilde{\nu }=\arg \underset{\nu }{\min }\left\{\sum _{k=1}^{N_1}\sum _{m=1}^{M_k}\tilde{J}(Z_k^m,{\tilde{\beta }}_m\mid \nu )\right\}\text{with}\tilde{J}(Z_k^m{\widehat{\beta }}_m\mid \nu )=\underset{{\beta }_m}{\min }J(Z_k^m\mid {\beta }_m,\nu ),$$ (2.15)

where ν ∈ {1, 10, 100} is a cut-off value; β_m ∈ {PMM, tGMM, GMM, GaMM, EGMM} is a probability model; and ${\beta }_m={\arg \min }_{{\beta }_m}J(Z_k^m\mid {\beta }_m,\nu )$. In particular, the function $J(Z_k^m\mid {\beta }_m,\nu )$ is varied with respect to the choice of the objective function:

$$J(Z_k^m\mid {\beta }_m,\nu )=\{\begin{array}{cc}\frac{1}{N_2^{m,k}}\cdot SS\hfill & \text{for}\mathrm{MSE};\hfill \\ N_2^{m,k}\log \left(2\pi {\widehat{\tau }}_{{\beta }_m}^2\right)+\frac{1}{{\widehat{\tau }}_{{\beta }_m}^2}\cdot SS+2\cdot \mid {\widehat{\zeta }}^{{\beta }_m}\mid \hfill & \text{for}\mathrm{AIC};\hfill \\ N_2^{m,k}\log \left(2\pi {\widehat{\tau }}_{{\beta }_m}^2\right)+\frac{1}{{\widehat{\tau }}_{{\beta }_m}^2}\cdot SS+N_2^{m,k}\cdot \mid {\widehat{\zeta }}^{{\beta }_m}\mid \hfill & \text{for}\mathrm{BIC};\hfill \end{array}\phantom{\}}$$ (2.16)

where $SS={\Sigma }_{l=1}^{N_2^{m,k}}{\{z_{kl}-{\Sigma }_{s=1}^S{w}_s\cdot f_s^{{\beta }_m}(t_l\mid {\widehat{\xi }}_s^{{\beta }_m}\left)\right\}}^2$; $({\widehat{\tau }}_{{\beta }_m}^2,{\widehat{\zeta }}^{{\beta }_m})$ are the parameter estimates of a given probability model $f_s^{{\beta }_m}$; and $\mid {\widehat{\zeta }}^{{\beta }_m}\mid$ is the number of the parameters of a given probability model. For the case that a certain probability model is preferred, we can just optimize the cut-off value of the conditional Bayes factor by fixing ${\widehat{\beta }}_m$ at a user-defined model. In addition, we can also just optimize the probability model by fixing $\tilde{\nu }$ at a certain cut-off value. Note that the last two approaches are computationally less expensive.

3. GC×GC-MS data and software

To evaluate the performance of the developed peak finding algorithm, an experimental data set generated from a comprehensive two-dimensional gas chromatography time-of-flight mass spectrometry (GC×GC-TOF MS) was used. The sample analyzed on GC×GC-TOF MS is a mixture of 76 compound standards (8270 MegaMix, Restek Corp., Bellefonte, PA) and C₇-C₄₀ n-alkanes (Sigma-Aldrich Corp., St. Louis, MO). The concentration of each compound in the mixture is 2.5 μg/mL. The mixture was analyzed on a LECO Pegasus 4D GC×GC-TOF MS instrument (LECO Corporation, St. Joseph, MI, USA) equipped with a cryogenic modulator. All the statistical analyses were performed using statistical software R 2.13.1 (R Development Core Team, 2012), and the developed R package msPeak is available at http://mrr.sourceforge.net.

4. Applications

We applied the developed algorithm to the two sets of the experimental GC×GC-TOF MS data described in the previous section. The first data set is a small region selected from the experimental data while the second data set is the entire experimental data. The developed algorithm was further compared with the two existing algorithms, continuous wavelet-based (CWT) algorithm and ChromaTOF, in terms of compound identification in Section 5.

4.1. Analysis of selected data

For illustration purpose, we selected a small region from the entire experimental data as shown in Supplementary Information Figure S2(b). Upon this selected data, we performed the process of peak finding according to the algorithm described in Section 2.

Figure S2(c) displays the results of the NEB model-based significant test as well as denoising and baseline correction for the selected data. As described in Section 2, the significant test is rendered by a conditional Bayes factor of the test in Equation (2.10) with the three different odds (cut-off) values such as 1, 10, and 100. Of these, the largest cut-off value is the strictest condition in that there are fewer significant TICs. In other words, there are more TICs of zero in case of the odds of 100. In this figure, the black open circles represent the original TIC, and the red cross ‘×’, green plus ‘+’, and blue open circles indicate the convoluted TICs of the odds of 1, 10, and 100, respectively. Figure S2(d) is the magnified plot of the green box in Figure S2(c). Clearly, we can see that the odds of 1 (red cross ‘×’) has the most nonzero convoluted TICs as depicted in Figure S2(d). The detected peak regions are plotted in Figure S3 of Supplementary Information. In Figure S3, the total number of nonzero peak regions detected is 36, 28, and 27 when the cut-off value of odds is 1, 10, and 100, respectively. As expected, the odds of 1 have the most nonzero peak regions.

Once the nonzero peak regions were detected, we searched for the significant peaks at each nonzero peak region using five probability mixture models, PMM, tGMM, GMM, GaMM, and EGMM. As mentioned before, the number of peaks detected by FDT is considered as the maximum number of peaks to be fitted by each of five probability mixture models. Each of PMM, tGMM, GMM, GaMM, and EGMM has (S · 1+1), (S · 2+1), (S · 2+1), (S · 2+1), and (S · 3+1) parameters to estimate, where S is the number of mixture components. Note that the truncated Gaussian distribution has four parameters including the lower and the upper bounds, but, in this study, these bounds are fixed with the starting and ending indices of a given nonzero peak region. Only when the number of data points for a given nonzero peak region is more than or equal to the required number of parameters for a selected probability model, the normalized intensities are fitted using the probability model.

To evaluate the performance of each probability model for fitting the normalized intensities, we consider four measures: mean squared error (MSE), −2 times loglikelihood (LL), Akaike information criterion (AIC), and Bayesian information criterion (BIC). A probability model is considered as performing better if its MSE, LL, AIC, or BIC is lower. It is noteworthy that LL is given only as a reference and will not be directly used for comparison since each model is not nested. The results of fitting the normalized intensities using the proposed five probability mixture models are reported in Table 1.

Table 1. Results of fitting the normalized intensities using five probability models.

Odds	Measure	PMM	tGMM	GMM	GaMM	EGMM
1	MSE1	41.34	30.35	28.29	33.85	15.63
		(15.03)	(19.65)	(15.21)	(15.92)	(9.64)
	LL	−285.42	−324.10	−322.91	−320.51	−371.78
		(41.38)	(41.27)	(41.66)	(41.24)	(46.43)
	AIC	−277.42	−313.76	−312.57	−308.51	−358.92
		(40.89)	(40.81)	(41.21)	(40.43)	(46.01)
	BIC	−116.04	−112.24	−111.05	−61.99	−110.92
		(18.08)	(17.01)	(17.42)	(18.07)	(20.20)
10	MSE	38.34	2.72	6.41	7.39	5.54
		(10.52)	(0.64)	(1.95)	(2.52)	(2.00)
	LL	−255.80	−310.07	−305.90	−301.83	−336.24
		(39.72)	(39.88)	(40.63)	(39.57)	(44.09)
	AIC	−248.98	−300.51	−296.34	−292.05	−324.98
		(39.28)	(39.36)	(40.11)	(38.91)	(43.67)
	BIC	−119.43	−119.40	−115.23	−101.50	−121.72
		(18.77)	(15.84)	(16.56)	(17.26)	(17.19)
100	MSE	53.75	11.94	19.25	21.05	18.03
		(13.52)	(7.73)	(9.70)	(10.54)	(9.77)
	LL	−223.97	−279.79	−277.68	−272.47	−313.56
		(36.80)	(39.20)	(39.85)	(37.51)	(44.15)
	AIC	−218.05	−271.12	−269.01	−263.58	−302.60
		(36.46)	(38.63)	(39.30)	(36.92)	(43.48)
	BIC	−113.46	−113.01	−112.45	−101.47	−107.04
		(18.06)	(16.28)	(15.65)	(14.15)	(15.20)

The values in parentheses are empirical standard errors.

In case of odds of 1, the MSE, LL, and AIC of EGMM are the lowest and these of PMM are the largest. However, the lowest BIC happens with PMM that has the smallest number of parameters to estimate. On the other hand, when the cut-off value of odds is 10, the MSEs are dramatically reduced up to five times lower than these of odds 1. In this case, tGMM has the lowest MSE, and the largest MSE still occurs when PMM is employed. However, EGMM has the lowest LL, AIC, and BIC. Interestingly, the overall MSE becomes worse than that of odds 1, when the cut-off value increases to 100. Nevertheless, its trend is similar to that of odds 10. Overall, in terms of MSE, a better fitting is achieved when 10 is considered as the cut-off value of odds and when the truncated Gaussian mixture model is used.

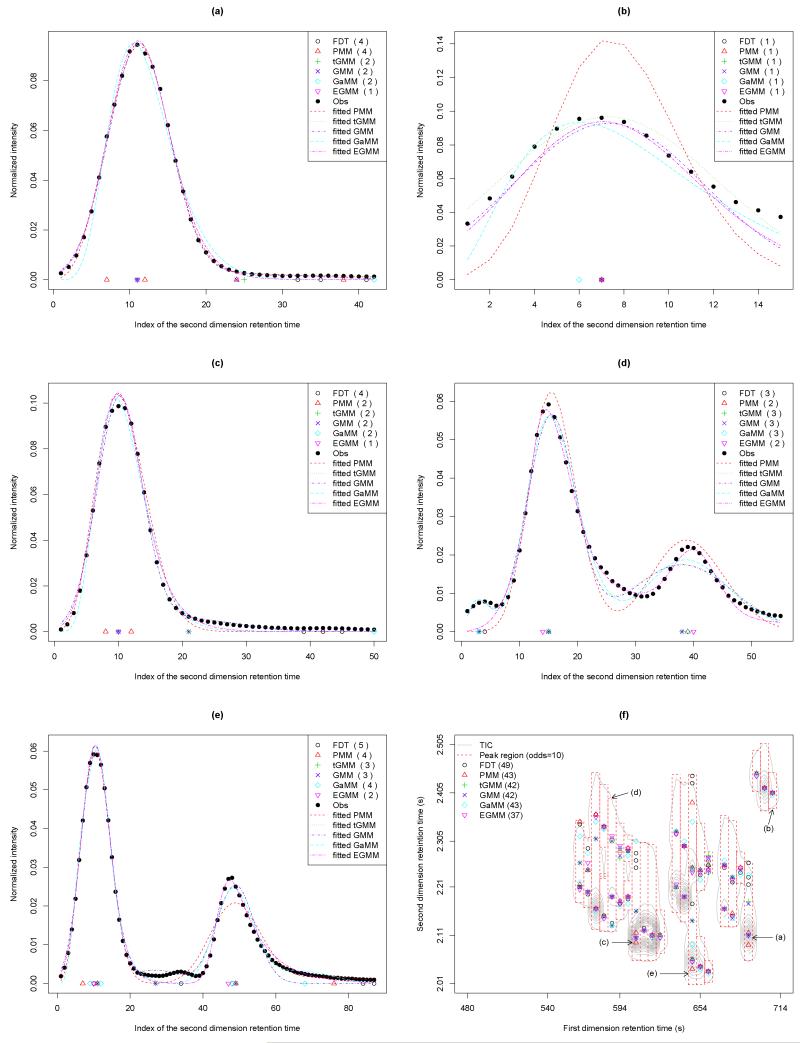
Figure 2 shows the cases when each probability model performs best among other mixture models in terms of MSE, when the cut-off value is 10. That is, Figures 2(a)-2(e) display the fitted curves when PMM, tGMM, GMM, GaMM, and EGMM fit the normalized intensities with the lowest MSE, respectively. In Figure 2(a), PMM has the largest number of peaks detected, which is four as FDT does, while PMM has the lowest MSE (MSE (×10⁵) = 0.06 (PMM), 0.09 (tGMM), 0.10 (GMM), 1.19 (GaMM), 0.21 (EGMM)). Although there is only one peak in this figure, but only EGMM detected one peak. tGMM and GMM have the peaks in the very similar position as expected. GaMM has two peaks detected with one peak positioned at the upper bound of the second dimension retention time. This peak region corresponds to the peak region (a) in Figure 2(f). tGMM has the lowest MSE in Figure 2(b) (MSE (×10⁵) = 83.01 (PMM), 3.20 (tGMM), 6.08 (GMM), 7.40 (GaMM), 5.56 (EGMM)). In this case, all the detected peaks are located at the same position except for GaMM, which is shifted to the left. PMM has much larger MSE, indicating the worst fitted curve to the data points. Figure 2(c) has the similar peak shape to that of Figure 2(a), while GMM is the best fitted model and is marginally better than tGMM at the third decimal point in this case (MSE (×10⁵) = 0.88 (PMM), 0.36 (tGMM), 0.36 (GMM), 0.69 (GaMM), 0.54 (EGMM)). Likewise, all the probability models detected two or more peaks except for EGMM, even though there is only one chromatographic peak. Its index of peak region is (c) as shown in Figure 2(f). Three chromatographic peaks are observed in Figure 2(d). PMM and EGMM detect no peak in the beginning of the curve while the other models correctly detect this peak. GaMM has the lowest MSE (MSE (×10⁵) = 1.90 (PMM), 0.75 (tGMM), 0.76 (GMM), 0.46 (GaMM), 0.62 (EGMM)). The case that EGMM has the lowest MSE is depicted in Figure 2(e) (MSE (×10⁵) = 0.49 (PMM), 0.36 (tGMM), 0.35 (GMM), 0.24 (GaMM), 0.15 (EGMM)). Only tGMM and GMM resolve the peak in the middle of the curve although their peak positions are shifted to the left. Overall, EGMM fits the normalized intensities well with the smaller MSE, but tGMM and GMM have a better capability of detecting the peaks that have a relatively smaller peak height.

Fig 2.

The fitted peak regions and the detected peaks when the cut-off value of odds is 10. The detected peak positions are indicated by black circle (FDT), red triangle (PMM), green ‘+’ (tGMM), blue ‘×’ (GMM), sky-blue rhombus (GaMM), and purple inverted-triangle (EGMM). ‘Obs’ means the observed intensities. The detected nonzero peak regions and peaks before peak merging are in (f). The indices (a)-(e) in (f) indicate the peak region corresponding to each of the fitted plots (a)-(e).

The detected peaks are indicated in the selected GC×GC-TOF MS data as shown in Supplementary Information Figure S4. In this figure, the dotted red box represents the nonzero peak region detected from the proposed NEB model, and the grey contour is plotted based on the original TIC. When the cut-off value of odds is 1, the total number of peaks detected by PMM, tGMM, GMM, GaMM, and EGMM is 61, 53, 53, 60, and 47, respectively, as shown in Figure S4(a). Of these probability models, PMM has the largest number of detected peaks and EGMM has the smallest number of peaks detected. In case of odds 10 and 100, PMM and GaMM have the largest numbers of peaks detected out of five probability mixture models, which are 43 and 40 for odds of 10 and 100, respectively. EGMM still has the smallest number of detected peaks of 37 as can be seen in Figures S4(c) and S4(e). For illustration purpose, the detected peaks when the cut-off is 10 are depicted in Figure 2(f). Comparing Figure S4(a) with Figures S4(c) and S4(e), it can be seen that the peak regions of small sizes have vanished in Figures S4(c) and S4(e) when the odds increase. The detected peaks after peak merging are shown in Figures S4(b), S4(d), and S4(f). The peak merging dramatically reduced the number of detected peaks up to the one-third of the number of peaks before peak merging.

Furthermore, three interesting points can be observed. One is that the cut-off value has little effect on the overall performance of peak detection, although the odds of 10 give us the best average performance. The second is that the peaks detected by each probability model become similar to each other after peak merging. The last is that the detected peaks by EGMM are very similar to these by PMM, after peak merging, although PMM has the worst MSE as can be seen in Table 1. That is, the peak merging makes all probability models comparable to each other in terms of the position of peaks detected.

4.2. Analysis of entire data

We here applied the proposed peak detection algorithm to the entire data. Before using the entire data, we removed the uninteresting areas that were produced due to experimental noise. This can be seen in Supplementary Information Figures S5(a) and S5(b). Then, we found the nonzero TICs by the proposed NEB model as depicted in Supplementary Information Figure S5(c). Similarly to the selected data in the previous section, we selected the nonzero peak regions and then detected the peaks using the proposed methods with the three cut-off values, 1, 10, and 100, of odds. In case of the cut-off value of odds 10 (1 and 100, respectively), the numbers of detected peaks are 230 (263 and 215), 223 (249 and 211), 225 (254 and 211), 229 (265 and 213), and 215 (230 and 201), for PMM, tGMM, GMM, GaMM, and EGMM, respectively, before peak merging, while the numbers of detected peak after peak merging are 97 (104 and 96), 99 (107 and 97), 99 (105 and 96), 99 (106 and 96), and 96 (103 and 92), respectively. As before, the peak merging reduces the variation in the number of detected peaks among different methods.

We further evaluated the performance of peak finding by compound identification using Person’s correlation. To standardize the comparison, we focused on the identification of the 76 compound standards from the peak list generated by each method. Since we knew that 76 compound standards should be present in the sample, we examined the quality of detected peaks by each mixture model through counting the number of 76 compound standards that were identified out of the detected peaks. Table 2 shows the results of the comparison.

Table 2. Results of compound identification of peaks detected before/after peak merging.

		Before peak merging			After peak merging
Odds	Model	Standard1	Unique2	Peak3	Standard	Unique	Peak
1	PMM	32	72	263	32	64	104
	tGMM	32	72	249	32	64	107
	GMM	32	72	254	31	63	105
	GaMM	32	73	265	31	64	106
	EGMM	32	69	230	32	63	103
10	PMM	32	68	230	31	61	97
	tGMM	32	70	223	31	62	99
	GMM	32	70	225	31	61	99
	GaMM	32	71	229	31	63	99
	EGMM	32	67	215	32	61	96
100	PMM	31	66	215	30	60	96
	tGMM	31	67	211	31	60	97
	GMM	31	65	211	30	58	96
	GaMM	31	68	213	30	60	96
	EGMM	31	64	201	30	58	92
10	OPT-MSE4	32	69	230	31	61	97
1	OPT-AIC	32	71	255	32	64	104
1	OPT-BIC	32	70	240	32	64	104

¹the number of 76 compound standards present in the list of ‘Unique’ peaks;

²the number of unique compound names in the list of peaks detected by each method;

³the number of peaks detected by each method;

⁴the trial-and-error optimization.

As expected, the odds of one have the most peaks detected for every model. After peak merging, the total number of detected peaks decreased up to more than 50%, while the number of unique compounds identified and the number of 76 compound standards identified have little variation. Interestingly, the difference among models disappears when we consider the total number of 76 compound standards identified, which ranges from 30 to 32 across all the models.

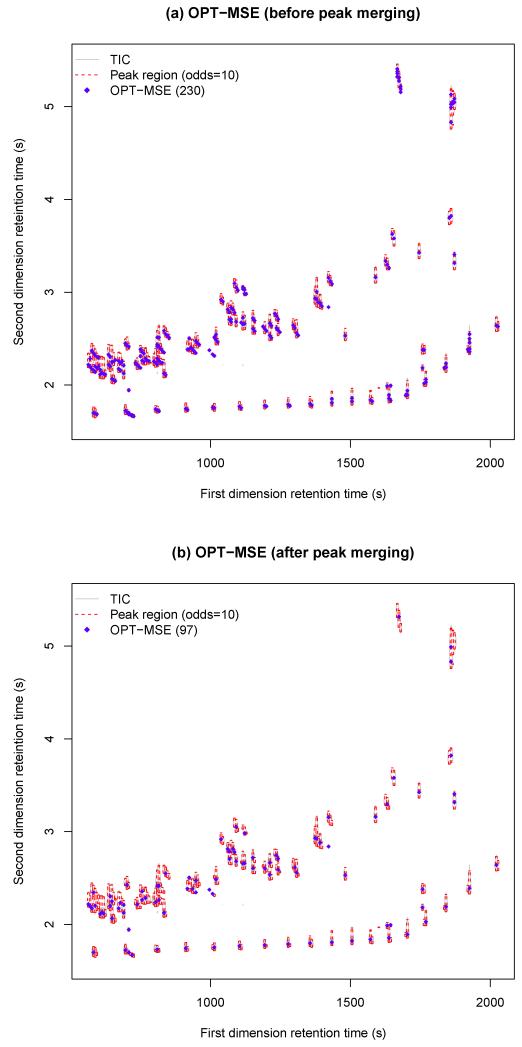
The trial-and-error optimization was also applied to the entire data using Equation (2.15). The last three rows of Table 2 show the results of the optimization with the three different objective functions, MSE, AIC, and BIC. The optimal cut-off values of odds with MSE, AIC, and BIC are 10, 1, and 1, respectively, which is consistent with the results of the selected data (Table 1). Since the optimization with either AIC or BIC selects the cut-off value of one, they detects more peaks than that with MSE. The results are shown in Figure 3 when the objective function is MSE. Overall, the optimization with MSE performs best in the sense that it finds the smallest number of peaks but the same number of 76 compound standards. The peak detection results of the trial-and-error optimization using another replicated data set can be found in the Supplementary Information Figures S7 and S8.

Fig 3.

The detected nonzero peak regions and peaks by the trial-and-error optimization with MSE before (a)/after (b) peak merging.

5. Comparison with existing algorithms

We further evaluated the developed algorithm by comparing with existing algorithms in terms of compound identification. To do this, we employed the two algorithms, continuous wavelet-based (CWT) algorithm and ChromaTOF. As mentioned earlier, there is no publicly available software for GC×GC-TOF MS data and most existing algorithms used one-dimensional approach for denoising and baseline correction, so we employed CWT, which was the best-performing method based on Yang et al. (2009)’s work. Note that ChromaTOF is the only commercial software embedded in GC×GC-TOF MS instrument. To avoid bias in peak merging, we used the peak list generated by each method before peak merging. We examined the performance of CWT with the three different signal-to-noise (SNR) ratios, 1, 2, and 3, using the R/Bioconductor package MassSpec Wavelet. As for ChromaTOF, we used the SNR threshold of 100. It should be noted that the unit of the SNR threshold of ChromaTOF is different from that of CWT, so the SNR thresholds cannot be compared directly with each other. For example, the CWT detected no peak with SNR of 100.

Table 3 shows the results of compound identification of the entire data using CWT and ChromaTOF before peak merging. For ease of comparison, we added the results for the MSE-based trial-and-error optimization of Table 2, which performs best in Section 4.2, into the table and measured the ratios (%) of the number of Standard compounds to the number of Unique compounds (SUR), the number of Standard compounds to the number of detected peaks (SPR), and the number of Unique compounds to the number of detected peaks (UPR).

Table 3. Results of compound identification of peaks detected by the developed, algorithm, CWT, and ChromaTOF before peak merging.

Before peak merging
Method (Cut-off)	Standard	Unique	Peak	SUR1 (%)	SPR2 (%)	UPR3(%)
OPT-MSE (10)	32	69	230	46.38	13.91	30.00
CWT (1)	25	61	1242	40.98	2.01	4.91
CWT (2)	22	50	880	44.00	2.50	5.68
CWT (3)	26	43	618	37.21	2.59	6.96
ChromaTOF (100)	34	178	391	19.1	8.7	45.52

¹Standard/Unique;

²Standard/Peak;

³Unique/Peak.

CWT detects the largest number of peaks before compound identification, but it detects the smallest number of unique compounds as well as the smallest number of the 76 compound standards (the true positive compounds) identified by compound identification, resulting in the highest false discovery rate. The commercial software ChromaTOF detects the largest number of unique compounds and the largest number of 76 compound standards. On the other hand, although the developed algorithm finds the smallest number of peaks, the identified number of 76 compound standards is comparable to that of ChromaTOF. Furthermore, the highest SUR and the highest SPR are achieved by the developed algorithm, while the highest UPR is carried out by ChromaTOF. It suggests that the developed algorithm greatly reduces false discovery rate in terms of SPR. In addition, the number of detected peaks of CWT is very sensitive to the choice of SNR threshold, while the developed algorithm has little effect of the cut-off value of odds on peak detection as can be seen in Table 2. Overall, the comparison analysis shows that ChromaTOF has much worse specificity than our algorithm although it has better sensitivity. Moreover, CWT has the similar specificity to the developed algorithm, but the developed algorithm has better sensitivity,

6. Discussion

To analyze GC×GC-TOF MS data, we developed a new peak detection algorithm. Unlike the existing peak detection algorithms, the proposed algorithm performs baseline correction and denoising simultaneously using the NEB model without any input, such as manually assigned SNR threshold and denoising parameters, from users. In particular, the proposed NEB model has the ability to remove the background noise (the series of black dots in the middle of the plot) from the raw signal as shown in Supplementary Information Figure S5(d). Another advantage is that it can reduce the entire data into a set of peak regions using a statistical test of conditional Bayes factors. This is an important aspect on peak detection because the information-rich output of MS data is usually enormous and so the processing time is one of key bottlenecks in data analysis.

In this work, we marginalized the MS information and then detected the peaks using the marginalized chromatogram data (i.e., TIC). In our proposed peak detection, the marginalization of the MS data is used only for the peak detection. As for the metabolite identification, we used the non-marginalized mass spectrum for each metabolite. In the ideal case, each peak of chromatogram (marginalized MS data, i.e., TIC) should represent a unique metabolite (compound or peak) in GC×GC-TOF MS data. However, there are still co-eluting metabolites from GC×GC-TOF MS due to limited separation power. For this reason, to resolve the co-eluting metabolites, ChromaTOF uses the non-marginalized MS data (i.e., Single Ion Chromatogram: XIC). A key objective of using XICs of ChromaTOF is to resolve the co-eluting metabolites, so, if there is no co-eluting peak, we think TIC should be sufficient to detect the peaks. Furthermore, there is much less amount of metabolites co-eluting from GC×GC than GC does owing to the increased separation power. For these reasons, we tried to resolve the co-eluting metabolites based on TIC along with a mixture model in the proposed approach. By doing so, although there is a certain degree of information loss due to marginalization, we could also see several benefits from this marginalization: (i) it reduced the size of data, (ii) consequently, it spent the less computational expense, and (iii) it made the data much smoother (Morris et al., 2005). Furthermore, in comparison analysis, our approach is comparable with ChromaTOF, which uses no marginalization of the MS data. It should be noted that neither the commercial software ChromaTOF nor our developed method completely detected all of the known compounds. There could be many reasons for this, including low concentration, low ionization frequency, inaccuracy of the peak detection algorithms, etc.

It is a challenge to estimate the unknown number of components for a mixture model, especially, under the presence of many local optima. To circumvent this potential issue, the developed algorithm uses the number of peaks detected by FDT as the upper bound of the number of components. Although this saves the computation time as well as removes the potential difficulty, it can be a potential drawback of the proposed algorithm when the true number of components is larger than the number of peaks detected by FDT. However, since the FDT used in this study was very sensitive to noise, we observed, with limited testing data, that FDT overestimates the number of peaks in most cases (e.g., Figure 2).

The most dominated parametric model to describe the shape of chromatographic peaks in GC-MS and LC-MS data is an exponentially modified Gaussian (EMG) function (Di Marco and Bombi, 2001). In this work, four mixture models were compared with the EMG model as can be seen in Tables 1 and 2. EMG model shows the least MSE and the least number of detected peaks. However, there is no performance difference between the mixture models in terms of metabolite identification and detected peaks, implying that the less complicated model has an advantage on the computation.

As mentioned, Table 2 shows no preference among different mixture models on compound identification, although there is a clear difference in fitting the intensities (Table 1). For this reason, we analyzed the MS similarity within a peak region displayed in Figure 2(e). The results of MS similarity analysis are depicted in Supplementary Information Figure S6. In this analysis, we calculated the pairwise MS similarities among the data points, and then displayed the pairwise MS similarities for each data point in Figure S6(a). For example, a dotted line represents the MS similarities between the ith point and all other jth points, j ≠ i, given the ith data point. Therefore, the ith data point must have the MS similarity of one at the ith point in the plot since it is the MS self-similarity. In this figure, we can cluster the MS similarity lines into three groups which are the same as the number of apparent local maxima. Furthermore, although a data point is located far from its local maximum, its MS similarity is more than 0.8, demonstrating that the peak region plays a more important role in compound identification than the peak position. A similar trend can be seen in the heatmap depicted in Figure S6(b). This can not only explain why we observe no difference among the different models in compound identification, but also give an insight that MS similarity-based peak detection is a promising approach.

Since the proposed model-based algorithms require a fitting of the peak shape, the peak finding procedure would run long time. To evaluate the running time, we compared the computation time between CWT with the cut-off of 1 and the proposed algorithm with/without optimization with odds of 10, on a desktop with Intel Core 2 Duo CPU 3.00 GHz. The running time of CWT was 0.24 minutes, while the proposed algorithms with PMM and optimization took 6.86 minutes and 14.10 minutes, respectively. The full optimization version of the proposed algorithm further took 33.37 minutes. Although the proposed algorithms relatively take more running time than CWT, it still finds peaks in a reasonable time frame. The running time of the full optimization approach may be a bottleneck compared to CWT, however. One solution to speed up the computation time is to rely on parallel computation. In general, the parallel computation is more e cient when a lot of independent calculations are required, and the peak shape fitting of the proposed method can be performed independently using parallel computation for each of the peak region.

Even though there is not much of a difference between the developed algorithm and the only commercial software available for GC×GC-TOF MS in terms of the number of 76 compound standards identified, the total number of peaks detected by the proposed algorithm is about 100 peaks less than that of ChromaTOF (e.g., 230 vs. 391 in Table 3). This is because ChromaTOF uses XIC, while the developed algorithm uses total ion chromatogram (TIC). The XIC-based approach requires more computation since it independently deals with each XIC of m/z values, while the TIC-based approach needs a one-time computation. The use of XIC on the developed algorithm is left as future work.

7. Conclusions

We developed a novel, publicly-available algorithm to identify chromatogram peaks using GC×GC-TOF MS data, which includes three components: simultaneous baseline correction and denoising by the NEB model, peak picking with various choices of mixture models, and peak merging. The proposed algorithm requires no SNR threshold and denoising parameters from users to perform baseline correction and denoising. The data analysis demonstrated that the NEB model-based method can detect the peak regions in the two dimensional chromatogram that have chromatographic peaks, with a simultaneous baseline removal and denoising process. Furthermore, the comparison analysis with limited data shows that the developed algorithm can greatly reduce false discovery rate in terms of compound identification. Among the model-based approaches for peak picking, PMM and GMM detect more peaks, while tGMM and EGMM have smaller MSE. However, there is no apparent preference among the five model-based approaches in terms of compound identification, and the peak shape is data-dependent. For this reason, we further introduced a trial-and-error optimization into the proposed algorithm to select a proper peak shape model according to a different peak region. Among the four measures (MSE, LL, AIC, and BIC), MSE will be considered to find an optimal peak shape model in terms of the compound identification.