3D Viscoelastic Traction Force Microscopy

Abstract

Native cell-material interactions occur on materials differing in their structural composition, chemistry, and physical compliance. While the last two decades have shown the importance of traction forces during cell-material interactions, they have been almost exclusively presented on purely elastic in-vitro materials. Yet, most bodily tissue materials exhibit some level of viscoelasticity, which could play an important role in how cells sense and transduce tractions. To expand the realm of cell traction measurements and to encompass all materials from elastic to viscoelastic, this paper presents a general, and comprehensive approach for quantifying 3D cell tractions in viscoelastic materials.

This methodology includes the experimental characterization of the time-dependent material properties for any viscoelastic material with the subsequent mathematical implementation of the determined material model into a 3D traction force microscopy (3D TFM) framework. Utilizing this new 3D viscoelastic TFM (3D VTFM) approach, we quantify the influence of viscosity on the overall material traction calculations and quantify the error associated with omitting time-dependent material effects, as is the case for all other TFM formulations. We anticipate that the 3D VTFM technique will open up new avenues of cell-material investigations on even more physiologically relevant time-dependent materials including collagen and fibrin gels.

1 Introduction

Over the past two decades Traction Force Microscopy (TFM) has emerged as a powerful, quantitative approach for characterizing the physical interactions between cells and their surroundings^1–4. TFM has provided a deeper understanding on the role of physical forces during cellular homeostasis, disease progression, and many other cellular processes. For example in 2005, Paszek et al. showed, using TFM that tensional homeostasis, i.e., the regulation of intracellular tension, plays a significant role in determining the ultimate outcome in cancer cell malignancy⁵.

With the availability of improved spatial imaging techniques, TFM has evolved to deliver two-dimensional and three-dimensional (3D) descriptions of cell-surface traction measurements of single cells and cell sheets^6–11. It has been shown that most of the tissues in the body are characterized as time-dependent viscoelastic materials^12–14. Yet, until recently, almost every TFM approach featured a linear elastic continuum mechanics framework^15–17. Through a recent significant advancement in our displacement detection scheme we showed that cells on soft gels are capable of generating large material deformations exceeding the traditional linear formulation limits¹⁸. We addressed these observations by presenting a new, reformulated hyperelastic 3D TFM approach, capable of accurately capturing finite elastic material deformations¹⁸.

Still, there is currently no documented approach of incorporating material viscosity into a TFM framework. Such a formulation may be of significant importance given that the literature has shown that most tissues, including more sophisticated in-vitro culture systems, possess some level of viscosity as part of their microstructure^19–22. Since cells possess the ability to sense and probe their microenvironment dynamically, incorporating viscoelastic material properties into a TFM framework is important to provide the most accurate measurements of cell-material interactions^23–26.

In this paper, we address this challenge by presenting an integrated material characterization and 3D TFM approach to perform cell traction force measurements on materials with time-dependent physical properties. This technique, named 3D Viscoelastic Traction Force Microscopy (3D VTFM) is general enough to allow the incorporation of any linear or non-linear elastic and viscous material properties. Specifically, we present a combined experimental and numerical approach on determining the viscoelastic material properties of soft agarose substrates, and their subsequent use in determining cell-induced material tractions. To examine differences in the spatial distribution and magnitude of the time-dependent surface traction fields due to the viscosity of the substrate material, we construct an analytical test case. Finally, we present actual experimental cell surface traction data using our 3D VTFM technique of breast cancer cells deforming collagen-functionalized agarose substrates.

2 Materials and Methods

Glass Coverslips and Microscope Slides Surface Modification

Circular glass coverslips (25 mm, diameter, Fisher Scientific, Waltham, MA) were chemically modified to allow covalent attachment of polyacrylamide substrates using previously developed protocols^{1, 6, 7}. Briefly, glass coverslips and slides were rinsed with ethanol and placed in a petri dish containing a solution of 0.5% (v/v) 3-aminopropyltrimethoxysilane (Sigma-Aldrich, St. Louis, MO) in ethanol for 5 minutes. Next, coverslips were washed with ethanol and submersed in a solution of 0.5% glutaraldehyde (Polysciences, Inc., Warrington, PA) in deionized (DI) water for 30 minutes. Activated coverslips were washed with DI water and left to dry.

To allow easier gel detachment, rectangular glass microscope slides (75×25 mm) were chemically modified to create hydrophobic surface. Briefly, glass coverslips were placed in a petri dish containing 97% (v/v) hexane (Fisher Scientific, Waltham, MA), 2.5% (v/v) (tridecafluoro-1,1,2,2-tetrahydrooctyl)-triethoxysilane (SIT) (Gelest, Morrisville, PA), and 0.5% (v/v) acetic acid (Sigma-Aldrich, St. Louis, MO) for approximately 1 minute. Coverslips were then removed and left to dry.

Preparation of Polyacrylamide-covered Coverslips

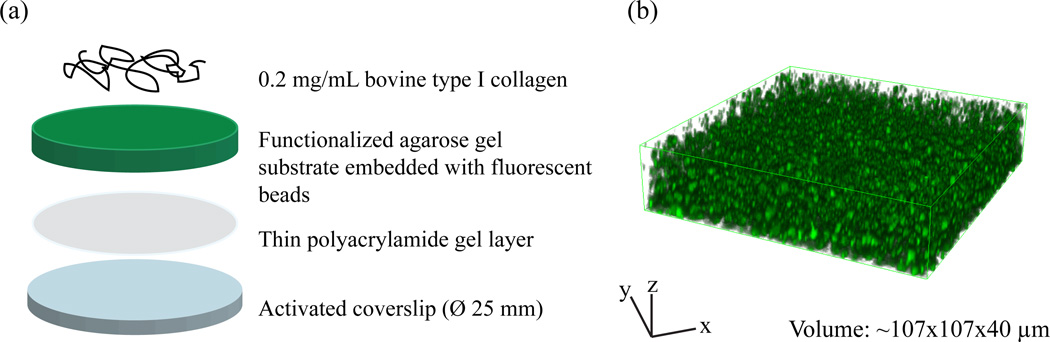
Polyacrylamide (PA) gels were prepared from acrylamide (40% w/v,Bio-Rad Laboratories, Hercules, CA) and N,N-methylene-bis-acrylamide (BIS, 2% w/v, Bio-Rad Laboratories, Hercules, CA) stock solutions as described previously^{1, 6, 7}. The concentrations of acrylamide and BIS were chosen to be 8%/0.1%. Crosslinking was initiated through the addition of ammonium persulfate (Sigma-Aldrich, St. Louis, MO) and N,N,N,N-tetramethylethylenediamine (Life Technologies, Grand Island, NY). The PA solution was vortexed for about 30 seconds, and 12 μL of the PA solution were pipetted on the surface of an activated coverslip and sandwiched with a hydrophobic glass slide. PA gel thickness was measured to be ~ 5 μm. PA gel substrates were then submerged in distilled water and allowed to polymerize and hydrate for approximately an hour. Once the coverslip was removed, PA gel substrates were left uncovered at room temperature to dry out. Exploiting the strong cohesion between agarose and PA, the thin PA layer was used to firmly attach each agarose substrate to the underlying glass coverslip (Fig. 1(a)).

Fig. 1.

Schematic of (a) the agarose substrate preparation and (b) a representative volumetric image of the agarose substrate embedded with green fluorescent microspheres recorded by laser scanning confocal microscopy. (Online version in colour)

Preparation of Agarose Substrates

For agarose substrate preparation, 0.5%(w/v) agarose powder (Benchmark Scientific, Edison, NJ) was dissolved in 1× PBS (Invitrogen, Carlsbad, CA). Each agarose solution was heated in an oven to approximately 90°C for complete dissolution. It should be noted, that the vial with the solution was loosely covered, yet boiling was avoided at all times. While heating, the solution was stirred occasionally, until the agarose powder had completely dissolved. Next, the agarose solution was combined with 10% (v/v) of 0.5 μm yellow-green fluorescent microspheres (Invitrogen, Carlsbad, CA). All agarose samples were thoroughly vortexed, and 35 μL of the final agarose solution were sandwiched between a dried PA gel-covered coverslip and a plain glass slide (75×25 mm). Upon complete gelation of the agarose solution, the assembly was immediately immersed in distilled water for approximately one hour. Finally, agarose coverslips were carefully peeled off the plain glass cover slide (Fig. 1(a)). The final thickness of agarose gel layer after swelling was measured to be ~ 40 μm.

Collagen-Functionalization of Agarose Substrates

To promote cell attachment, agarose substrates were functionalized with type I collagen using the bifunctional crosslinker, sulfo-SANPAH (Thermo Fisher Scientific, Waltham, MA)^{2, 6, 7}. Figure 1 presents a complete overview of the functionalized agarose substrate preparation setup. Excess water was removed prior to deposition of 100 μL of sulfo-SANPAH (1mg/mL) onto the surface of each film, followed by a 15 minute exposure to UV light. The darkened sulfo-SANPAH solution was aspirated and the procedure was repeated. The samples were thoroughly washed with DI water, and covered with a solution of 0.2 mg/mL bovine type I collagen (BD Bioscience, Franklin Lakes, New Jersey) and left undisturbed at 4 °C overnight. Following overnight incubation, the substrates were rinsed three times with 1× PBS and sterilized with UV irradiation before depositing cells.

Cell Culture and Seeding

MDA-MB-231 metastatic breast adenocarcinoma cells were chosen as a representative contractile cell phenotype. Cells were cultured in medium containing 10% fetal bovine serum and 1% penicillin-streptomycin in Dulbecco’s Modified Eagle Medium (DMEM, Invitrogen, Carlsbad, CA). Cells were maintained in the incubator at 37 °C and 5% CO₂. Seeding density was 30 cells/mm². Once seeded, cells were allowed to spread for approximately 5 hours in the incubator prior to imaging.

Live Cell Imaging

Three-dimensional image stacks were acquired using a Nikon A-1 confocal system mounted on a TI Eclipse inverted optical microscope controlled by NI-Elements Nikon Software. A 40× plan fluor air objective mounted on a piezo objective positioner was used for all the experiments, which allowed imaging at speeds up to 30 frames per second. Green 0.5 μm fluorescent microspheres were embedded into the substrate and excited with an Argon (488 nm) laser. 512 × 512 × Z voxels (102μm × 102 μm × Z) confocal volume stacks were recorded every 100 seconds with Z ~ 128 voxels (38 μm), illustrated in Fig. 1(b). To ensure physiological imaging conditions within the imaging chamber, temperature and pH were strictly maintained at 37 °C and ~ 7.4 during time lapse recording as previously described^{6, 7}. The outline of the cell was estimated from phase contrast microscopy images.

Calculation of Cell-generated Displacements

Cell-generated full-field displacements were determined following a similar methodology described in Tojanova et al.¹⁸. First, three-dimensional time-lapse volumetric images of fluorescent beads embedded in agarose substrates were recorded using laser scanning confocal microscopy (LSCM). Then, the motion of embedded fluorescent beads was tracked in all three dimensions using a new fast iterative digital volume correlation (FIDVC) algorithm²⁷. This cross correlation-based algorithm has the capability to capture large material deformations by utilizing a built-in iterative deformation method (IDM). By utilizing the IDM, our FIDVC technique is capable of reducing its volumetric subset size to 32 voxels, or lower depending on the signal content within each subset, without introducing significant correlation error²⁷. The final results feature significantly higher spatial resolution, signal-to-noise, and faster computation times than our previous DVC method²⁸.

Nanoindentation Measurements

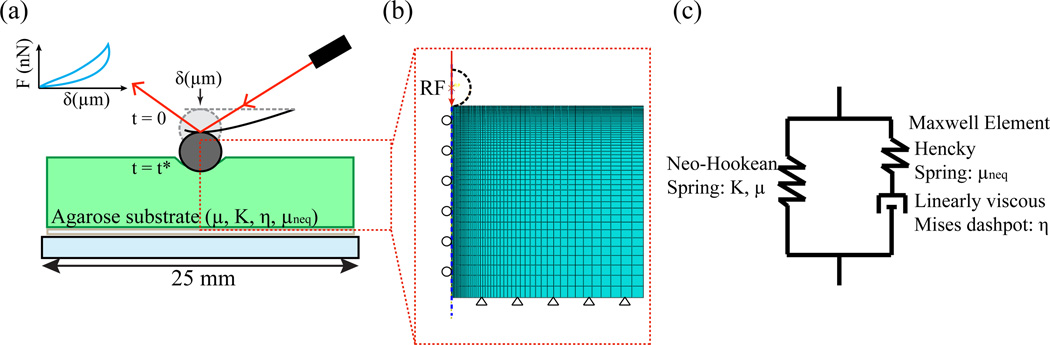
Force-indentation measurements of agarose gels were collected using an Asylum MFP-3D-BIO atomic force microscope (AFM) (Asylum Research, Santa Barbara, CA) following a similar procedure as previously described^{29, 30}. The indenter geometry consisted of individual borosilicate glass spheres (5 μm diameter) attached to the tip of AFM cantilevers (Novascan Technologies, Inc., Ames, IA). Figure 2(a) provides a schematic overview of the indentation experiments. The cantilever spring constant was determined to be 0.02 N/m using the power spectral density of the inherent thermal noise fluctuations of the cantilever³¹.

Fig. 2.

Schematic of (a) the experimental setup of AFM indentation of the agarose substrate with a spherical cantilever tip radius of 2.5 μm. (b) Modeling setup mimicking the indentation experiment. The reference point (RF) to control the indentation is set at the center of the sphere. (c) Schematic of the finite-deformation viscoelastic agarose constitutive model. (Online version in colour)

To probe the viscoelastic material properties of our agarose substrates, loading-unloading indentation experiments were performed at three different cantilever approach velocities: 0.1 μm/sec, 1 μm/sec, and 10 μm/sec. Additionally, 30 second force relaxation tests were performed using an initial loading velocity of 10 μm/sec and an indentation depth of 450 nm.

Data were sampled at 5 kHz for loading-unloading measurements and at 200 Hz for 30 s for viscoelastic relaxation measurements. A 2–3 nN force trigger, resulting in 400–600 nm indentation depths, was used to prescribe the point at which the cantilever approach was stopped and either retracted for loading-unloading tests, or held constant for relaxation tests. To determine the initial point of contact, we used a contact point extrapolation method³². In brief, the upper 50% of force and indentation data were fit with a linearized version of the Hertz model, and the contact point was extrapolated by back calculation with the slope and intercept. All data past the contact point were used in our least-squares analysis with our finite element simulation results. To account for any day-today variability among the agarose substrates, all AFM indentation tests were performed on the same batch of agarose, and on the same day as the cell experiments. All experiments were carried out at room temperature in a fluid environment. The AFM was allowed to equilibrate before each measurement period to minimize deflection laser and/or piezo drift.

Finite Element Simulation

Simulations of the nanoindentation process were conducted using the commercial finite element software, ABAQUS 6.12 (Dassault Systemes Simulia Corporation, Providence, RI). The geometry of the agarose substrate was discretized by using 2D axisymmetric elements (CAX4H). The indenting spherical tip was modeled as analytical rigid solid with a radius of R = 2.5 μm. The agarose substrate boundary conditions were set to mimic those of the indentation experiments with frictionless interactions between the indenter tip and sample surface (Fig. 2(b)). The indentation simulation was executed using the same displacement control loading condition as in the AFM experiments with the same loading rates. The material behavior of agarose used for fitting the experimental force-indentation curves is a Neo-Hookean rubber elasticity model with a finite-deformation Maxwell element in parallel, shown schematically in Fig. 2(c) and detailed mathematically in the appendix. Our process of material parameter determination is described in the following section.

3 Agarose Material Characterization

The objective of this investigation is to present the reader with a complete approach of determining the viscoelastic material properties of a given substrate material, and provide a straightforward approach of implementing the determined material model into a 3D TFM framework for cell traction measurements. To illustrate this process in detail, we chose an agarose gel as a model viscoelastic substrate material^{33, 34}. Typical material characterization techniques for determining the material properties of soft hydrogels and tissue-mimicking materials have involved uniaxial compression, tension, AFM indentation and shear rheometry experiments. AFM indentation characterizations are attractive for determining TFM-substrate properties, since they have the ability to measure the local mechanical properties directly at the surface where the cell is applying its tractions.

While elastic material AFM-based characterization approaches are relatively straightforward, the analysis of time-dependent material properties usually requires additional experimental measurements, such as creep or stress (force) relaxation tests³⁰. If a large strain constitutive relation is sought, numerical simulation of the experimental procedure, followed by least-square fitting of the numerical to the experimental data provides a robust overall material characterization approach.

Figure 2(a) presents a schematic of the AFM indentation experiments that were utilized to collect force-indentation curves of agarose substrates at different loading rates, as well as force relaxation tests (see technical details in Materials and Methods). Next, we constructed a simple, axisymmetric FEM model (Fig. 2 (b)) mimicking the experimental indentation process using the non-linear viscoelastic material model shown schematically in Fig. 2(c). For a full mathematical description of the model, the reader is referred to the appendix. Briefly, the constitutive model consists of two contributions, represented as branches in Fig. 2 (c). The equilibrium, or time-independent, response is modeled through a Neo-Hookean spring (represented schematically as the left branch in Fig. 2(c)) with its free energy given mathematically by Eq. (1). The material parameters associated with the equilibrium response are the equilibrium ground-state shear modulus μ and bulk modulus K. The right branch of Fig. 2(c) represents the non-equilibrium, or time-dependent, contribution and is modeled through a finite-deformation Maxwell element. We note that the Maxwell element only affects the deviatoric, or shear, response, leaving the volumetric response time-independent. The Maxwell element includes a Hencky spring with free energy given by Eq. (17) – referred to in this way due to the use of the Hencky, or logarithmic, strain in Eq. (17) – in series with a Mises dashpot whose flow rule is given by equations Eq. (20) and Eq. (21). The non-equilibrium materials parameters are the non-equilibrium shear modulus μ_neq and viscosity η. Here, the use of the word non-equilibrium is for purely descriptive purposes to denote all material properties associated with the time-dependent Maxwell element.

The emphasis behind the model was to use a minimal set of fitting parameters to appropriately describe the viscoelastic behavior of agarose under finite deformations. The characteristic size of our indentation process – as well as the deformation processes induced by cells – is comparable or smaller than the average pore size of typical agarose gels^{35, 36}. Therefore, it is reasonable to assume that solvent diffusion relative to the gel network equilibrates quickly compared to deformation time-scales, so that the diffusion process is always in equilibrium. To inform our choice of bulk modulus, we utilize the observations of Zhao et al.³⁷ and set the equilibrium Poisson’s ratio in the linear (small) deformation regime to be 0.3. That is to say, using the familiar relations between elastic constants in linear elasticity, we have that the bulk modulus is given by K = 2μ (1 + ν)/(3 − 6ν) with μ the equilibrium shear modulus and ν taken to be 0.3. Once the bulk modulus K has been fixed in this manner, the remaining three material parameters, μ, μ_neq, and η were determined by iteratively adjusting the numerical FEM simulation to fit the experimental force relaxation data in a least-squares sense. The resulting best-fit material parameters describing the finite viscoelastic behavior of agarose are presented in Table 1.

Table 1.

Table of the viscoelastic material constants for agarose substrate

μ	Shear modulus of hyperelastic spring	1600 Pa
K	Bulk modulus of hyperlastic spring	3700 Pa
μneq	non-equilibrium shear modulus	700 Pa
η	Maxwell element viscosity	800 Pa·s

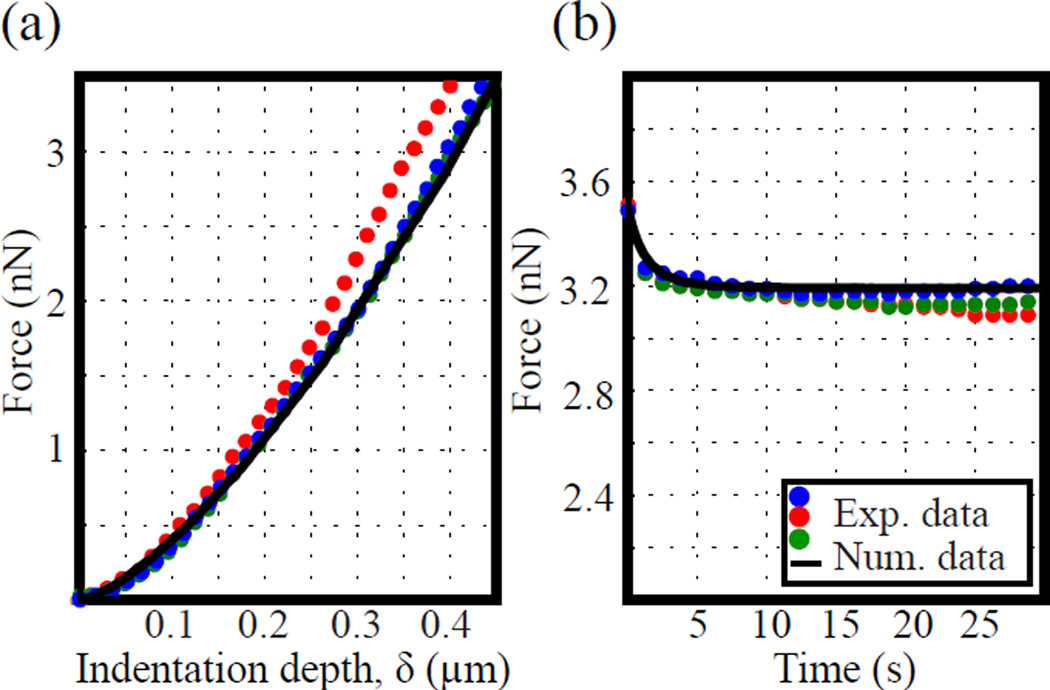
Figure 3 (a) and (b) present the experimental and best-fit numerical indentation results for a typical force-relaxation experiment. The agarose sample is first indented to a depth of approximately 450 nm using a constant loading rate of 10 μm/sec (Fig. 3(a)). Then, while maintaining the current indentation depth, the force is allowed to relax over a total period of 30 seconds (Fig. 3 (b)). Comparison between the experimental and numerical force-indentation curves shows good agreement. Given the relatively simple nature of the viscoelastic material model presented in Fig. 3(b) (see simple shear example in Supplemental Figures 1–2), some differences especially at larger indentation depths (Fig. 3(a)) can be expected.

Fig. 3.

Representative experimental indentation results for agarose substrates (dots) and corresponding numerical results (solid line) as computed from fitted material constants. (a) Force (nN) vs. indentation depth, δ (μm) at a loading rate of 10 μm/sec. (b) A representative force relaxation plot for agarose substrates. (Online version in colour)

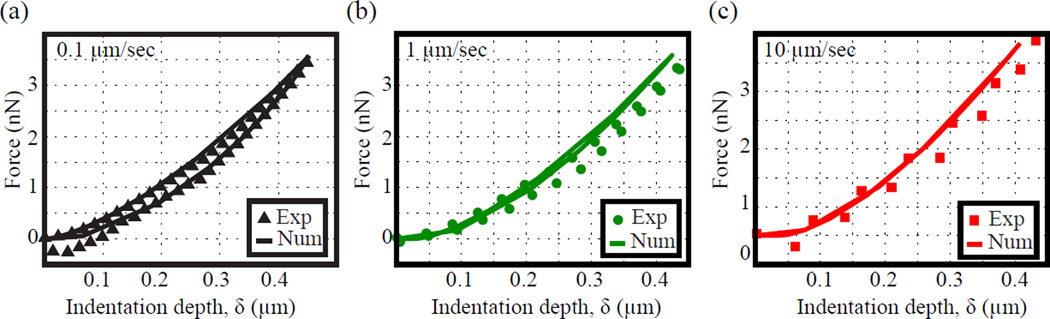
Figure 4 compares the experimental indentation loading-unloading force curves to the numerical indentation results based on the same material parameter set (given in Table 1) used to describe the force relaxation curves in Fig. 3. As Fig. 4 shows, the FEM simulations are in good agreement with the experimental results for all three different loading rates. Indenting the agarose gel at different loading rates allows for the examination of the time-dependent, viscous material behavior, which the model seems to capture adequately. When comparing Figs. 4(a) – (c), only the loading rate of 0.1 μm/sec leads to significant loading-unloading hysteresis, which is indicative of viscoelastic relaxation during the indentation cycle. This is expected as the intrinsic material relaxation time, τ, is on the same order of magnitude as the time duration for the loading-unloading cycle for the 0.1 μm/sec loading rate. The indentation force curves shown in Fig. 4 are representative of 5 indentation measurements at each loading rate.

Fig. 4.

Representative loading-unloading indentation results for loading rates of (a) 0.1 μm/sec, (b) 1 μm/sec, and (c) 10 μm/sec. Dotted curve denotes experimental results, continuous solid lines are best fits based on the fitted agarose material constants. (Online version in colour)

4 3D Viscoelastic Traction Force Microscopy (3D VTFM)

Cell-generated full-field displacements and tractions can be determined in a variety of different ways, with two of the most common approaches being image correlation-based measurements and single particle tracking algorithms. We previously presented a large-deformation 3D image correlation-based approach for determining cellular displacement fields with high resolution^{18, 27}. Regardless of the chosen displacement detection scheme, once the 3D displacement field is obtained, its spatial derivative, i.e. the deformation gradient, is used within the framework of the previously described viscoelastic material model (Fig. 2 (c)) to determine the cell surface tractions. Given that most tissue materials and more complex hydrogels exhibit some time-dependent and viscous behavior^19–21, and the observation that cells can generate finite deformations¹⁸, accurate cell traction analysis requires the utilization of a finite-deformation viscoelastic material model. Although our example is specific to agarose, we purposefully set up the methodology such that the same steps can be utilized to incorporate other, experiment-specific, viscoelastic material models into the same overall 3D VTFM framework.

Finite deformations are described by a displacement function, y = x + u(x, t), which represents a one-to-one mapping of points x in the reference configuration to points y in the deformed configuration at each time t.^* The deformation gradient is then the gradient of the displacement function with respect to x, that is F = ∇y = I + ∇u(x), with the volume ratio given by the Jacobian of F, J = det F > 0. Experimentally, the deformation gradient tensor, F, can be directly calculated from the full-field displacements using various discrete differentiation kernels. Farid et al., and Bar-Kochba et al. provide a description of several robust differentiation kernels^{27, 38}.

To specify the mechanical response of the equilibrium branch of the material model in Fig. 2(c), we assume that the spring is described by a Neo-Hookean free energy of the form

$${\psi }^{\text{eq}}(\mathbf{F})=\frac{\mu }{2}(\frac{(\text{tr}\mathbf{B})}{J^{2/3}}-3)+\frac{1}{2}K{(J-1)}^2,$$ (1)

where μ and K are the ground-state, equilibrium shear and bulk moduli, respectively, and B = FF^⊤ is the left Cauchy-Green tensor. The first term represents the free energy due to distortional (constant volume) deformations, and the second term represents purely volumetric deformations. The associated Cauchy stress is then

$${\mathbf{\sigma }}^{\text{eq}}=J^{-1}\frac{\partial {\psi }^{\text{eq}}(\mathbf{F})}{\partial \mathbf{F}}{\mathbf{F}}^{\top }=\frac{\mu }{J^{5/3}}(\mathbf{B}-\frac{1}{3}(\text{tr}\mathbf{B}))\mathbf{I})+K(J-1)I.$$ (2)

The time-dependent, viscous material response is described by the Maxwell element (Fig. 2 (c), right branch). For this branch, the deformation gradient, F, is decomposed into its elastic and viscous parts: F = F^eF^v, where F^e is the elastic deformation gradient, representing the deformation of the spring, and F^v is the viscous deformation gradient, representing the deformation of the dashpot. To specify the mechanical response of the non-equilibrium branch, we take the spring to be described by a Hencky spring with shear modulus μ_neq and the dashpot to be in a linearly viscousMises form with viscosity η. The details of the constitutive equations describing this branch are given in the Appendix. Here, we give the recipe for handling the Maxwell element in time-discrete form.

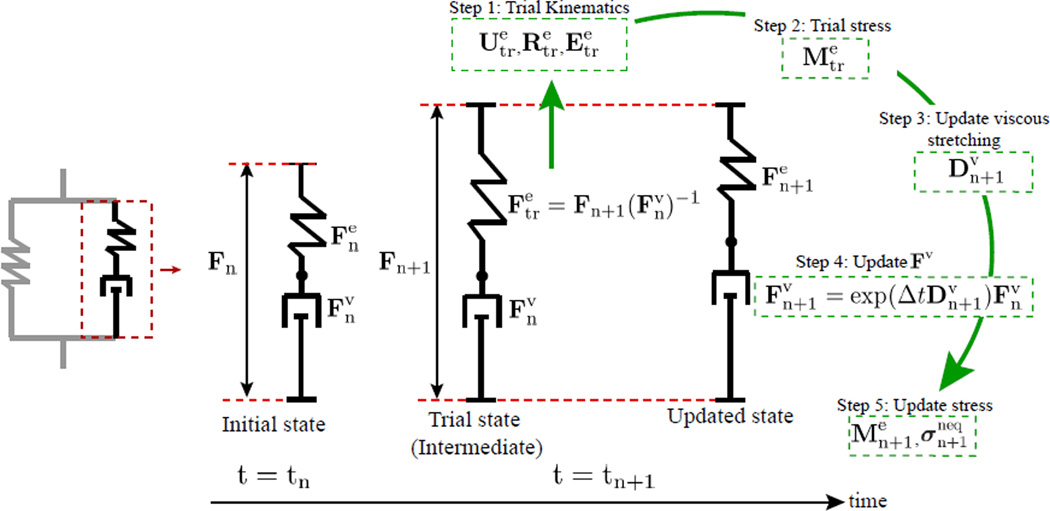
The approach is summarized in Fig. 5. At a given time t = t_n, the deformation gradient F_n and viscous deformation gradient ${\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}}$ (and hence the non-equilibrium elastic deformation gradient ${\mathbf{F}}_{\mathrm{n}}^{\mathrm{e}}$) are known. (Note that if t_n corresponds to the initial time, ${\mathbf{F}}_{\mathrm{n}}={\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}}=\mathbf{I}$.) Then at time t = t_n+1 = t_n + Δt, the deformation gradient F_n+1 is given. In an experiment, this is simply the deformation gradient measured at the subsequent time point. To proceed forward in time, we need to calculate the Cauchy stress due to the Maxwell element, ${\mathbf{\sigma }}_{\mathrm{n}+1}^{\text{neq}}$, and viscous deformation gradient, ${\mathbf{F}}_{\mathrm{n}+1}^{\mathrm{v}}$, at time t_n+1. The steps are given below:

1. First, we consider a trial state, in which viscous flow is frozen, see Fig. 5, and calculate a trial non-equilibrium elastic deformation gradient, ${\mathbf{F}}_{\text{tr}}^{\mathrm{e}}$, based on the old value of the viscous deformation gradient ${\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}}$:

   $${\mathbf{F}}_{\text{tr}}^{\mathrm{e}}={\mathbf{F}}_{\mathrm{n}+1}{({\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}})}^{-1}.$$ (3)
   In this intermediate state, all deformation between times t_n and t_n+1 is assumed to be accommodated by the Hencky spring. We then perform the polar decomposition of ${\mathbf{F}}_{\text{tr}}^{\mathrm{e}}$ and calculate the trial strain:

   $${\mathbf{F}}_{\text{tr}}^{\mathrm{e}}={\mathbf{R}}_{\text{tr}}^{\mathrm{e}}{\mathbf{U}}_{\text{tr}}^{\mathrm{e}},{\mathbf{E}}_{\text{tr}}^{\mathrm{e}}=\text{ln}{\mathbf{U}}_{\text{tr}}^{\mathrm{e}},$$ (4)

   where ${\mathbf{R}}_{\text{tr}}^{\mathrm{e}}$ is the trial rotation, ${\mathbf{U}}_{\text{tr}}^{\mathrm{e}}$ the trial right stretch tensor, and ${\mathbf{E}}_{\text{tr}}^{\mathrm{e}}$ the trial Hencky (logarithmic) strain.
2. Next we use the trial strain to calculate a trial stress

   $${\mathbf{M}}_{\text{tr}}^{\mathrm{e}}=2{\mu }_{\text{neq}}\text{dev}\left({\mathbf{E}}_{\text{tr}}^{\mathrm{e}}\right),$$ (5)

   where μ_neq is the non-equilibrium shear modulus. This particular stress measure is work conjugate to the Hencky strain and is referred to as the Mandel stress, and the specific stress-strain relation reflected in Eq. (5) arises due to a free energy function ψ^neq associated with the non-equilibrium spring (see the Appendix for details). Note that we only consider the contribution to the stress due to the deviatoric, or shear, strain. In this manner, the nonequilibrium Maxwell element only adds viscoelasticity to the shear deformation and leaves the volumetric response of Eq. (2) unaffected.
3. Next, we calculate the viscous stretching – that is, the strain rate in the dashpot – at time t_n+1:

   $${\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}=\frac{{\mathbf{M}}_{\text{tr}}^{\mathrm{e}}}{2(\eta +\mathrm{\Delta }t{\mu }_{\text{neq}})},$$ (6)

   where η is the constant viscosity of the dashpot. See the Appendix for the derivation of this important step.
4. Calculation of ${\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}$ allows for the update of F^v by means of the exponential map:

   $${\mathbf{F}}_{\mathrm{n}+1}^{\mathrm{v}}=\text{exp}(\mathrm{\Delta }t{\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}){\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}}.$$ (7)

   This brings us to the corrected, updated state in Fig. 5.

5. Finally, we may update the Cauchy stress due to the Maxwell element σ^neq:

   $${\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{e}}=2\eta {\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}},{\mathbf{\sigma }}_{\mathrm{n}+1}^{\text{neq}}={(\text{det}{\mathbf{F}}_{\text{tr}}^{\mathrm{e}})}^{-1}{\mathbf{R}}_{\text{tr}}^{\mathrm{e}}{\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{e}}{\mathbf{R}}_{\text{tr}}^{\mathrm{e}\top },$$ (8)

   where ${\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{v}}$ is the Mandel stress at time t_n+1.

Fig. 5.

Schematic of the time-discrete algorithm for the non-equilibrium, Maxwell branch of the constitutive model.

The total Cauchy stress due to both the equilibrium and non-equilibrium branches (Fig. 2(c), left and right branch) may then be calculated by

$${\mathbf{\sigma }}_{\mathrm{n}+1}={\mathbf{\sigma }}_{\mathrm{n}+1}^{\text{eq}}+{\mathbf{\sigma }}_{\mathrm{n}+1}^{\text{neq}},$$ (9)

where ${\mathbf{\sigma }}_{\mathrm{n}+1}^{\text{eq}}$ is calculated by Eq. 2 using F_n+1. One may then repeat these steps, marching forward in time, to calculate the stress history corresponding to a measured deformation history^{39, 40}. We encourage readers who are interested in the details of the model as well as the derivation of the time-discrete version to refer to the Appendix.

Once the Cauchy stress is calculated, the cell surface tractions can be found using the well-known Cauchy relation

$$\mathbf{t}=\mathbf{\sigma }\mathbf{n},$$ (10)

where n is the surface normal, and we have dropped the (n+1) subscript for simplicity of notation. The surface normal vectors can be determined directly from the laser scanning confocal images. Toyjanova et al. previously described such a method in-detail¹⁸. The magnitude of the three-dimensional traction vector is then calculated as

$$\left|\mathbf{t}\right|\sqrt{t_x^2+t_y^2+t_z^2},$$ (11)

where t_x and t_y are the in-plane traction force components under the cell and t_z corresponded to the out-of-plane component. The total cell force, a common metric used in cell TFM studies, is calculated by integrating the magnitude of the substrate surface tractions over the total cell area S, i.e.,

$$\mathbf{F}={\int }_{\mathbf{s}}\left|\mathbf{t}\right|\mathbf{d}\mathbf{S}.$$ (12)

Another metric that can be calculated from measured tractions – the root mean-squared tractions, t_RMS is defined as

$$t_{RMS}\sqrt{\frac{1}{N}\sum _{i=1}^N{\mathbf{t}}_i^2,}$$ (13)

where t_i is the traction vector located at every ith point along the surface of the cell boundary, enclosing total of N points. Further details on how to calculate cell forces from 3D traction data can be found elsewhere¹⁸.

5 Analytical and Experimental 3D VTFM Examples - Influence of Material Viscosity on Surface Tractions

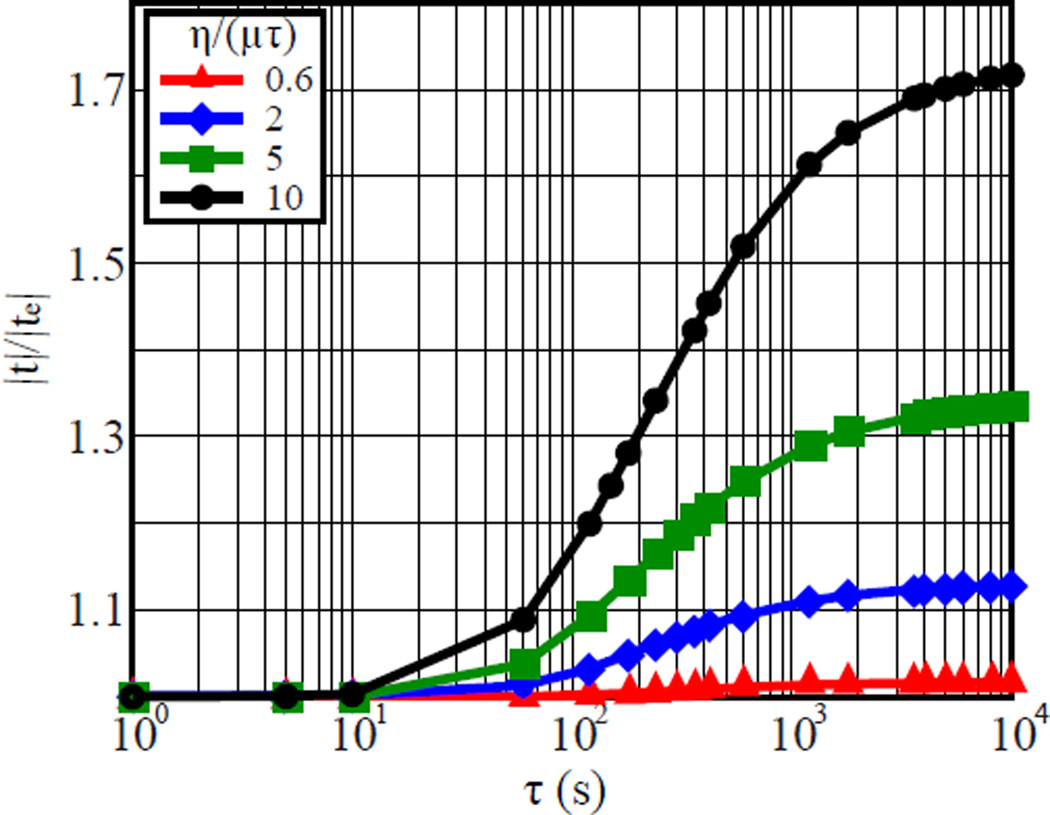
Given the slightly higher complexity of a viscoelastic over a purely elastic 3D TFM formulation, our intent is to provide the reader with a quantitative metric to determine the penalty associated with ignoring the viscous effects for a given substrate material. Figure 6 plots the ratio between the total traction magnitude that includes the time-dependent contribution, |t|, and the purely elastic traction magnitude, |t_e|, in the absence of the viscous dashpot in Fig. 2(c) as a function of the viscoelastic material properties of the substrate. Depending on the intrinsic relaxation time, τ = η/μ_neq, and the viscosity, η, of the material at hand, the error associated with neglecting the viscoelastic nature of the substrate can be significant. Since any 3D and 2D TFM framework requires careful material characterization of its substrate material, Fig. 6 can be utilized to determine whether a viscoelastic 3D TFM framework is necessary or whether a simpler, purely elastic formulation will suffice to estimate the cell-generated surface tractions.

Fig. 6.

Plot of the ratio of the total traction magnitude to the purely elastic traction contribution vs. relaxation time, τ = η/μ_neq. The calculations are shown for (η)/(μτ) of 0.6 (triangle), 2 (diamond), 5 (square) and 10 (circle). (Online version in colour)

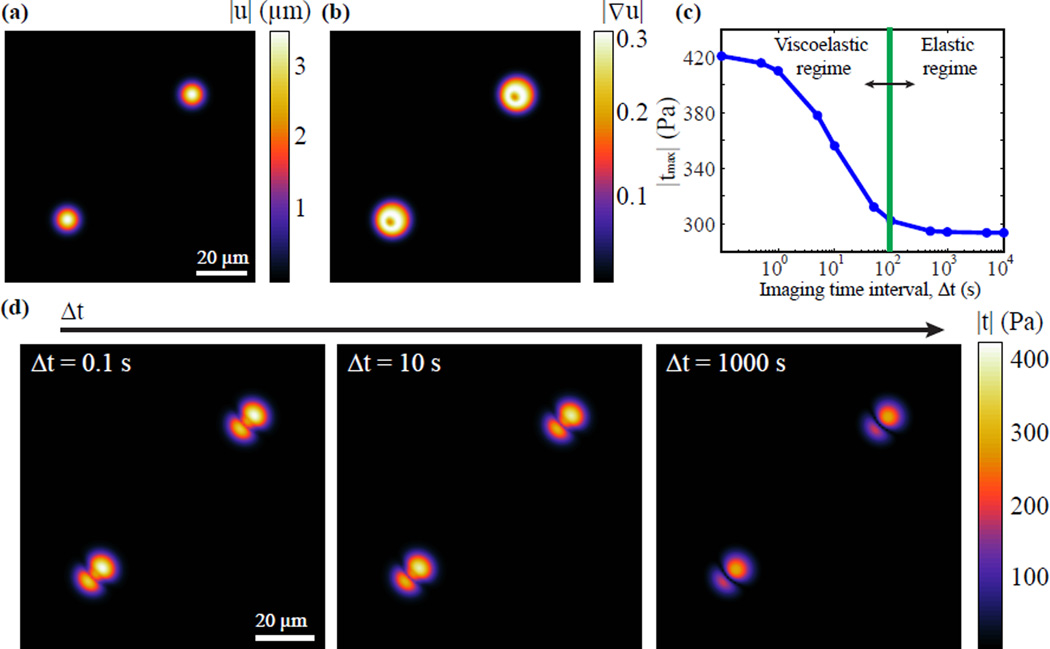
Analytically Simulated Viscoelastic Cell Deformation Fields

While Fig. 6 provides a quantitative estimate on the penalty associate with neglecting the viscous stresses in a material as a function of the characteristic relaxation time, τ, it is important to understand the relationship between τ and the actual imaging intervals utilized during live cell imaging. If τ is much less than the minimal time-lapse imaging interval, i.e., τ << Δt, then only the elastic contributions of the material behavior can be estimated. This concept is illustrated in Fig. 7 using an analytically generated Gaussian displacement dipole on a viscoelastic material obeying the constitutive model shown in Fig. 2(c). The material constants were chosen such that it matches the properties of embryonic liver and heart tissues¹⁹. The characteristic relaxation time, τ, is set to 10 seconds. The analytical displacement dipole is applied along the free surface of the x₁ − x₂ plane in the form of

$$\mathbf{u}(\mathbf{x})=A\text{exp}(-\frac{{(x_1-b_1)}^2+{(x_2-b_2)}^2+{(x_3-b_3)}^2}{2{\sigma }^2})$$ (14)

Fig. 7.

Analytical traction example of (a) prescribed Gaussian displacement dipole and its (b) associated displacement gradient magnitude. (c) Plot of the magnitude of the maximum total surface tractions, |t_max| (Pa), vs. imaging time interval, Δt (seconds). (d) Contour maps of the calculated surface tractions at imaging time intervals of Δt = 0.1 seconds, Δt = 10 seconds, and Δt = 1000 seconds. (Online version in colour)

Fig. 7 (a)–(b) depict the magnitude of the applied Gaussian displacement dipole and its associated displacement gradient. Using the displacement data, the viscoelastic cell surface tractions are calculated and are plotted in Fig. 7 (d) for different time-lapse imaging intervals. Figure 7 (d) presents a panel series of the magnitude of the 3D surface traction vector for the analytical displacement dipole shown in Fig. 7(a) for different imaging intervals, Δt. Given a material relaxation time, τ of 10 seconds, Fig. 7(c) quantitatively describes the effect different time-lapse imaging intervals have on accurately estimating the applied traction magnitude. For fast acquisition times, i.e., Δt ≤ 1 second, most of the viscoelastic traction magnitudes are sufficiently captured. If the imaging interval is increased to ~ 10 seconds, the peak tractions will be underestimated by approximately 17%, and with imaging times on the order of 100 seconds most of the viscoelastic material response has reached the equilibrium state, resulting in an traction estimation error of ~30%. The shape of the curve and the absolute numbers will vary depending on the particular viscoelastic material model employed, but can be generated via means of Eqs. 1 – 12.

While Fig. 7 shows that the particular time-lapse imaging interval, Δt, can have a profound effect on accurately representing the spatial distribution and magnitude of the traction pattern in a viscoelastic medium, practical considerations, such as low signal to imaging noise, phototoxicity, and photo-bleaching might limit the range of available imaging intervals. Thus, once the material of interest has been characterized and evaluated, the error associated with practical imaging intervals can be evaluated by generating the type of plot shown in Fig. 7(c). This should allow the user to directly evaluate whether a viscoelastic TFM framework is necessary for the desired TFM measurements or whether a simpler, purely elastic formulation suffices. Furthermore, for small linear elastic deformations, the reader has several TFM choices with recent developments provided by del Alamo in 3D⁴¹, and the well-established Fourier Transform Traction Cytometry by Butler et al. in 2D¹⁵ as means for accurate estimation of cellular traction fields.

Experimentally Observed Viscoelastic Cell Deformation Fields

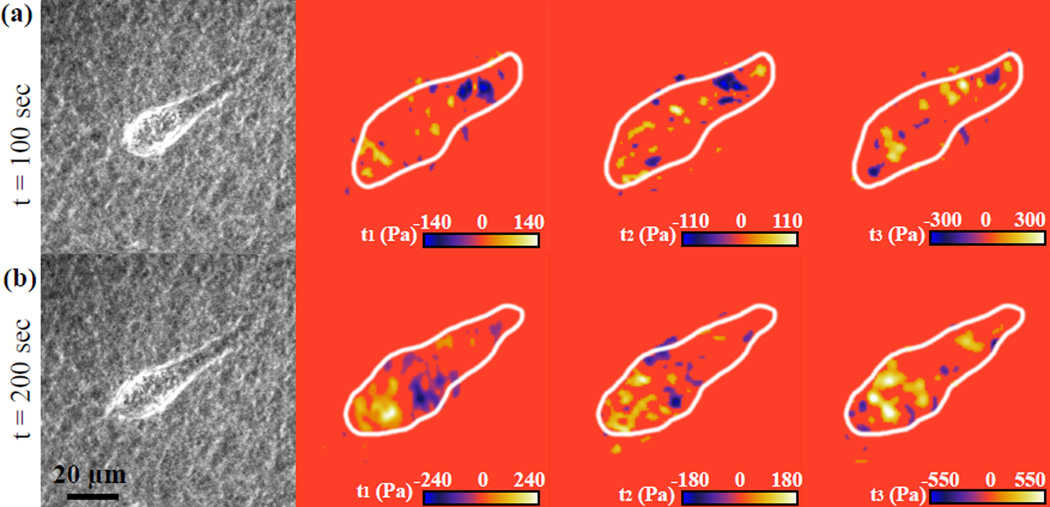
To illustrate the resolution and applicability of the 3D VTFM technique to capture actual cell-induced traction data, Fig. 8 shows snapshots of a MDA-MB-231 cell deforming an agarose substrate at two different time points. The left panel shows phase contrast images of the cell on top of the agarose substrate, followed by the in-plane and out-of-plane tractions. The traction resolution sensitivity was 50 Pa for in-plane and 80 Pa for out-of-plane tractions. The observed traction patterns in Fig. 8 are similar in shape and magnitude to previously observed traction patterns for mesenchymal cells^{6, 15, 42–44}. As can be seen from Fig. 8, the utilization of the 3D VTFM methodology produces high-resolution traction maps with similar resolution and sensitivity capabilities to our previously published 3D large deformation elastic TFM approach¹⁸.

Fig. 8.

Experimental example of a migrating MDA-MB-231 cells on the surface of an agarose substrate. The phase contrast image (left panel) presents the outline of the cell, followed by contour plots of surface tractions, t₁, t₂, and t₃ in kPa. (Online version in colour)

It should be noted that the characteristic relaxation time for the agarose gels used in this study was ~ 1:1 seconds, and that time-lapse images were acquired every 100 seconds. Any shorter time-lapse intervals yielded negligible material deformations indistinguishable from noise.

6 Conclusion

This paper presents a 3D Viscoelastic Traction Force Microscopy (3D VTFM) technique that allows the computation of cell-generated material tractions on viscoelastic materials. Using a combined experimental and numerical AFM indentation approach, our study details how to determine the material properties of the viscoelastic substrate material of interest, which in our simple example is an agarose gel. We would like to note, that the extraction of the viscoelastic material properties of the substrate material at hand can also be achieved by various other mechanical testing approaches besides indentation, including stress relaxation, creep and frequency-dependent tests in rheometer or tension/compression setups. As long as the material stress-strain state is recorded as a function of time, the viscoelastic material properties of the particular substrate material can be determined. Next, utilizing the obtained material properties we provide a general, finite deformation framework for integrating the viscoelasticity of the substrate material into a 3D TFM methodology. The same general framework we described can be simply modified by the reader to allow the incorporation of his/her own substrate specific viscoelastic material properties into our 3D VTFM code structure to perform 3D traction measurements. Finally, we provide the reader with a quantitative estimate on the penalty associated with neglecting the viscous effects for the given viscoelastic material, and what the minimum TFM time-lapse interval is required to adequately capture the viscous contribution of the material response. We conclude by showing traction contour plots of breast cancer cells migrating on collagen-functionalized agarose substrates. The 3D VTFM code package can be downloaded from our website (http://franck.engin.brown.edu).

In conclusion, this study provides a new 3D TFM technique that is capable of incorporating time-dependent material characteristics for studies that involve more realistic tissue-mimicking substrate materials. While the last two decades have provided a wealth of cell-material interactions on elastic substrates, we anticipate that the 3D VTFM technique will open up new avenues of cell-material investigations on even more physiologically relevant time-dependent materials including native tissue derivatives such as collagen and fibrin gels.

Appendix: Viscoelastic Model Details

In this appendix, we give a detailed account of the finite-deformation viscoelastic model used to describe experimental data, as well as a derivation of the time-discrete version summarized in Section 4. Mathematically, the viscoelastic model involves the following definitions: u(x, t), displacement; y = x + u(x, t), motion; F = ∇y, J = det F > 0, deformation gradient; B = FF^⊤, left Cauchy-Green tensor. We take the free energy due to the equilibrium branch to be given in Neo-Hookean form

$${\psi }^{\text{eq}}(\mathbf{F})=\frac{1}{2}\mu (\frac{(\text{tr}\mathbf{B})}{J^{2/3}}-3)+\frac{1}{2}K{(J-1)}^2,$$ (15)

where μ and K are ground-state, equilibrium shear and bulk moduli, respectively. The first term represents free energy due to distortional (constant volume) deformation, and the second term arises due to purely volumetric deformation. The associated Cauchy stress is then

$${\sigma }^{\text{eq}}=J^{-1}\frac{\partial {\psi }^{\text{eq}}(\mathbf{F})}{\partial \mathbf{F}}{\mathbf{F}}^{\top }=\mu J^{-5/3}\text{dev}(\mathbf{B})+K(J-1)\mathbf{I}.$$ (16)

The Maxwell element in parallel with the Neo-Hookean spring then allows for modeling non-equilibrium time-dependent behavior. To describe deformation in this element, the deformation gradient, F, is multiplicatively decomposed into elastic and viscous parts: F = F^eF^v; with F^v, J^v = det F^v = 1, denoting the (constant-volume) viscous distortion and F^e, J^e = det F^e > 0, denoting the non-equilibrium elastic distortion. The free energy due to the non-equilibrium spring is based on the elastic Hencky (logarithmic) strain, utilizing the following definitions: F^e = R^eU^e, polar decomposition of F^e; ${\mathbf{U}}^{\mathrm{e}}={\sum }_{\alpha =1}^3{\lambda }_{\alpha }^{\mathrm{e}}{\mathbf{r}}_{\alpha }^{\mathrm{e}}\otimes {\mathbf{r}}_{\alpha }^{\mathrm{e}}$, spectral decomposition of U^e; and ${\mathbf{E}}^{\mathrm{e}}={\sum }_{\alpha =1}^3(\text{ln}{\lambda }_{\alpha }^{\mathrm{e}}){\mathbf{r}}_{\alpha }^{\mathrm{e}}\otimes {\mathrm{r}}_{\alpha }^{\mathrm{e}}$, the elastic Hencky (logarithmic) strain. We take the free energy due to the non-equilibrium spring as

$${\psi }^{\text{neq}}({\mathbf{E}}^{\mathrm{e}}){\mu }_{\text{neq}}|\text{dev}({\mathbf{E}}^{\mathrm{e}}){|}^2,$$ (17)

where μ_neq is the non-equilibrium shear modulus. The stress conjugate to the elastic strain, E^e, is referred to the Mandel stress:

$${\mathbf{M}}^{\mathrm{e}}=\frac{\partial {\psi }^{\text{neq}}({\mathbf{E}}^{\mathrm{e}})}{\partial {\mathbf{E}}^{\mathrm{e}}}=2{\mu }^{\text{neq}}\text{dev}({\mathbf{E}}^{\mathrm{e}}),$$ (18)

and the contribution to the Cauchy stress due to the Maxwell element is then given through

$${\mathbf{\sigma }}^{\text{neq}}=J^{\mathrm{e}-1}{\mathbf{R}}^{\mathrm{e}}{\mathbf{M}}^{\mathrm{e}}{\mathbf{R}}^{\mathrm{e}\top }.$$ (19)

Finally, the evolution of F^v is given by

$${\dot{\mathbf{F}}}^{\mathrm{v}}={\mathbf{D}}^{\mathrm{v}}{\mathbf{F}}^{\mathrm{v}},{\mathbf{F}}^{\mathrm{v}}(\mathbf{x},t=0)=\mathbf{I},$$ (20)

with the viscous stretching, D^v, given by

$${\mathbf{D}}^{\mathrm{v}}=\frac{1}{2\eta }{\mathbf{M}}^{\mathrm{e}},$$ (21)

where η is the Maxwell element viscosity. (We refer to the dashpot as a Mises dashpot since this choice of constitutive equation asserts that the viscous stretching and Mandel stress tensors are codirectional, a hallmark of Mises plasticity.) Note that since ψ^neq is taken to not depend upon J^e, the contribution of the Maxwell element to the stress is purely deviatoric. In this way, we have only added viscoelasticity to the shear deformation and left the volumetric response of Eq. (16) unaffected. The four material parameters appearing in the model are the equilibrium shear modulus μ, the non-equilibrium shear modulus μ_neq, the Maxwell element viscosity η, and the bulk modulus K. The three parameters {μ, μ_neq, η} are selected to best fit the experimental behavior, while the K bulk modulus is chosen so that the equilibrium Poisson’s ratio in the linear (small) deformation regime, i.e., ν = (3K − 2μ)/(6K + 2μ), is 0.3, following³⁷.

Since experimental measurements are made at discrete time-points, we next derive the time-discrete version of the model used both to analyze the experimental data as well as the one implemented in the Abaqus UMAT used in the simulations. At a time t_n, the deformation gradient, F_n, and the viscous deformation gradient, ${\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}}$, are known. Then, given the deformation gradient, F_n+1, at a time t_n+1 = t_n + Δt, we are to determine the Cauchy stress, σ_n+1, and viscous deformation gradient, ${\mathbf{F}}_{\mathrm{n}+1}^{\mathrm{v}}$, at time t_n+1. In the experiments, Δt is the time increment between the two successive images. The evolution equation for F^v is implicitly integrated by means of an exponential map^{45, 46}:

$${\mathbf{F}}_{\mathrm{n}+1}^{\mathrm{v}}=\text{exp}(\mathrm{\Delta }\mathrm{t}{\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}){\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}}\text{with}{\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}=\frac{1}{2\eta }{\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{e}}.$$ (22)

Using (22)₁, we have that the elastic deformation gradient at the end of the step is

$${\mathbf{F}}_{\mathrm{n}+1}^{\mathrm{e}}={\mathbf{F}}_{\mathrm{n}+1}{\mathbf{F}}_{\mathrm{n}+1}^{\mathrm{v}-1}=\underset{={\mathbf{F}}_{\text{tr}}^{\mathrm{e}}}{\underbrace{{\mathbf{F}}_{\mathrm{n}+1}{\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}-1}}}\text{exp}(-\mathrm{\Delta }t{\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}})={\mathbf{F}}_{\text{tr}}^{\mathrm{e}}\text{exp}(-\mathrm{\Delta }t{\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}),$$ (23)

where ${\mathbf{F}}_{\text{tr}}^{\mathrm{e}}$ is the trial value of the elastic deformation gradient. A trial quantity represents the value of that quantity evaluated when viscous flow is frozen. With (i) the polar decompositions ${\mathbf{F}}_{\mathrm{n}+1}^{\mathrm{e}}={\mathbf{R}}_{\mathrm{n}+1}^{\mathrm{e}}{\mathbf{U}}_{\mathrm{n}+1}^{\mathrm{e}}\text{and}{\mathbf{F}}_{\text{tr}}^{\mathrm{e}}={\mathbf{R}}_{\text{tr}}^{\mathrm{e}}{\mathbf{U}}_{\text{tr}}^{\mathrm{e}}$ (ii) the knowledge that ${\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}},{\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{e}},\text{and}{\mathbf{U}}_{\mathrm{n}+1}^{\mathrm{e}}$ share principal directions and therefore commute; and (iii) the uniqueness of the polar decomposition; we have that

$${\mathbf{R}}_{\mathrm{n}+1}^{\mathrm{e}}={\mathbf{R}}_{\text{tr}}^{\mathrm{e}}\text{and}{\mathbf{U}}_{\mathrm{n}+1}^{\mathrm{e}}={\mathbf{U}}_{\text{tr}}^{\mathrm{e}}\exp (-\mathrm{\Delta }t{\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}})$$ (24)

Taking the logarithm of (24)₂, we have

$${\mathbf{E}}_{\mathrm{n}+1}={\mathbf{E}}_{\text{tr}}-\mathrm{\Delta }t{\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}\text{with}{\mathbf{E}}_{\text{tr}}=\text{ln}{\mathbf{U}}_{\text{tr}}.$$ (25)

Multiplying the deviatoric part of Eq. (25) by 2μ_neq, by the stress relation Eq. (18), we have

$${\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{e}}={\mathbf{M}}_{\text{tr}}^{\mathrm{e}}-2{\mu }_{\text{neq}}\mathrm{\Delta }t{\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}\text{with}{\mathbf{M}}_{\text{tr}}=2{\mu }_{\text{neq}}\text{dev}({\mathbf{E}}_{\text{tr}}),$$ (26)

which upon combining with (22)₂ yields

$${\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}=\frac{{\mathbf{M}}_{\text{tr}}^{\mathrm{e}}}{2(\eta +\mathrm{\Delta }t{\mu }_{\text{neq}})}.$$ (27)

Finally, the viscous deformation gradient is updated by (22)₁, and the Mandel and Cauchy stresses due to the Maxwell element are updated by

$${\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{e}}=2\eta {\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}},{\mathbf{\sigma }}^{\text{neq}}={(\text{det}{\mathbf{F}}_{\text{tr}}^{\mathrm{e}})}^{-1}{\mathbf{R}}_{\text{tr}}^{\mathrm{e}}{\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{e}}{\mathbf{R}}_{\text{tr}}^{\mathrm{e}\top },$$ (28)

The sequence of time-integration steps for the Maxwell element, with reference to the steps shown in Fig. 5, is outlined below.

1. Compute the trial elastic deformation gradient, ${\mathbf{F}}_{\text{tr}}^{\mathrm{e}}$, and its associated kinematic quantities using the viscous deformation gradient from the previous time increment:

   $${\mathbf{F}}_{\text{tr}}^{\mathrm{e}}={\mathbf{F}}_{\mathrm{n}+1}{\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}-1},{\mathbf{F}}_{\text{tr}}^{\mathrm{e}}={\mathbf{R}}_{\text{tr}}^{\mathrm{e}}{\mathbf{U}}_{\text{tr}}^{\mathrm{e}},{\mathbf{E}}_{\text{tr}}^{\mathrm{e}}=\text{ln}{\mathbf{U}}_{\text{tr}}^{\mathrm{e}},$$ (29)
2. Compute the trial Mandel stress:

   $${\mathbf{M}}_{\text{tr}}^{\mathrm{e}}=2{\mu }_{\text{neq}}\text{dev}\left({\mathbf{E}}_{\text{tr}}^{\mathrm{e}}\right),$$ (30)
3. Calculate the viscous stretching

   $${\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}=\frac{{\mathbf{M}}_{\text{tr}}^{\mathrm{e}}}{2(\eta +\mathrm{\Delta }t{\mu }_{\text{neq}})},$$ (31)
4. Update the viscous deformation gradient:

   $${\mathbf{F}}_{\mathrm{n}+1}^{\mathrm{v}}=\text{exp}(\mathrm{\Delta }t{\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}}){\mathbf{F}}_{\mathrm{n}}^{\mathrm{v}}.$$ (32)
5. Update the Mandel stress and Cauchy stress due to the Maxwell element:

   $${\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{e}}=2\eta {\mathbf{D}}_{\mathrm{n}+1}^{\mathrm{v}},{\mathbf{\sigma }}_{\mathrm{n}+1}^{\text{neq}}={(\text{det}{\mathbf{F}}_{\text{tr}}^{\mathrm{e}})}^{-1}{\mathbf{R}}_{\text{tr}}^{\mathrm{e}}{\mathbf{M}}_{\mathrm{n}+1}^{\mathrm{e}}{\mathbf{R}}_{\text{tr}}^{\mathrm{e}\top },$$ (33)

This completes the calculation of the contribution to the Cauchy stress due to the Maxwell element. The contribution due to the equilibrium Neo-Hookean spring is simply computed from the deformation gradient at the end of the step F_n+1:

$${\mathbf{B}}_{\mathrm{n}+1}={\mathbf{F}}_{\mathrm{n}+1}{\mathbf{F}}_{\mathrm{n}+1}^{\top },{\mathbf{\sigma }}_{\mathrm{n}+1}^{\text{eq}}=\mu {(\det {\mathbf{F}}_{n+1})}^{-5/3}\text{dev}({\mathbf{B}}_{\mathrm{n}+1})+K[(\det {\mathbf{F}}_{\mathrm{n}+1})-1]\mathbf{I}.$$ (34)

allowing for the calculation of the total Cauchy stress:

$${\mathbf{\sigma }}_{\mathrm{n}+1}={\mathbf{\sigma }}_{\mathrm{n}+1}^{\text{eq}}+{\mathbf{\sigma }}_{\mathrm{n}+1}^{\text{neq}},$$ (35)