Differential triggering of spontaneous glutamate release by P/Q-, N-, and R-type Ca²⁺ channels

Abstract

The role of voltage-gated Ca²⁺ channels (VGCCs) in spontaneous miniature neurotransmitter release is incompletely understood. Here we show that stochastic opening of P/Q-, N-, and R-type VGCCs accounts for ~50% of all spontaneous glutamate release at rat cultured hippocampal synapses, and that R-type channels play a far greater role in spontaneous than in action potential-evoked exocytosis. VGCC-dependent ‘minis’ show similar sensitivity to presynaptic Ca²⁺ chelation as evoked release, arguing for direct triggering of spontaneous release by transient spatially localized Ca²⁺ domains. Experimentally constrained three-dimensional diffusion modeling of Ca²⁺ influx-exocytosis coupling is consistent with clustered distribution of VGCCs in the active zone of small hippocampal synapses, and shows that spontaneous VGCCs openings can account for the experimentally observed VGCC-dependent minis, although single channel openings trigger release with low probability. Uncorrelated stochastic VGCC opening is thus a major trigger for spontaneous glutamate release, with differential roles for distinct channel subtypes.

Introduction

Action potential-independent spontaneous miniature neurotransmitter release has important physiological functions including regulation of dendritic protein expression and maintenance of spines in glutamatergic synapses^{1, 2}. Although ‘minis’ occur without extracellular Ca²⁺ the majority of spontaneous release under physiological conditions is Ca²⁺-dependent (e.g. refs.^{3, 4}). Unlike action potential-evoked release, which is triggered by transient activation of presynaptic voltage-gated Ca²⁺ channels (VGCCs) and formation of local Ca²⁺-nano/microdomains in the immediate vicinity of release-ready synaptic vesicles⁵, Ca²⁺ regulation of miniature release remains incompletely understood. It has recently been shown that stochastic opening of presynaptic VGCCs at resting membrane potential (V_rest) is a major trigger of spontaneous release at GABAergic synapses with either tight (‘Ca²⁺-nanodomain’)⁶ or loose (‘Ca²⁺-microdomain’)⁷ coupling between VGCCs and vesicular Ca²⁺-release sensors. These findings are consistent with the low affinity Ca²⁺ sensor synaptotagmin-1 being the major Ca²⁺ sensor not only for evoked but also for spontaneous release⁴. In contrast, VGCCs have been reported not to be involved in triggering spontaneous glutamate release, because the broad non-specific inorganic VGCC blocker Cd²⁺ (50–100 μM) failed to consistently reduce the frequency of miniature excitatory postsynaptic currents (mEPSCs) (e.g. refs. ^{8, 9}). This difference between spontaneous GABA and glutamate release is paradoxical, because the mechanisms of evoked release are broadly similar between inhibitory and excitatory central synapses^{4, 5}. Evoked release of glutamate at central synapses is triggered by mixed populations of P/Q-type, N-type, and R-type VGCCs^10-15. How these different VGCCs contribute to spontaneous release, and whether they do so through similar spatiotemporal domains as in evoked release, remains incompletely understood.

Here we use electrophysiological, optical, pharmacological and modeling approaches to understand the roles of different VGCC subtypes in spontaneous glutamate release at small hippocampal synapses. We show that stochastic uncorrelated activation of individual VGCCs at V_rest is a major source of spontaneous glutamate release. We further show that, consistent with a lower voltage activation threshold, R-type VGCCs are much more efficient in triggering spontaneous release than P/Q- and N-type channels. Finally, by comparing the effects of fast (BAPTA) and slow (EGTA) Ca²⁺ buffers on spontaneous and evoked release, complemented by experimentally constrained modeling of Ca²⁺ dynamics and activation of vesicular release sensors, we demonstrate that VGCC-dependent minis can be accounted for by fast, transient, 25–70 nm Ca²⁺-nano/microdomains around single VGCCs that open spontaneously at V_rest.

Results

Blockade of VGCCs inhibits spontaneous glutamate release

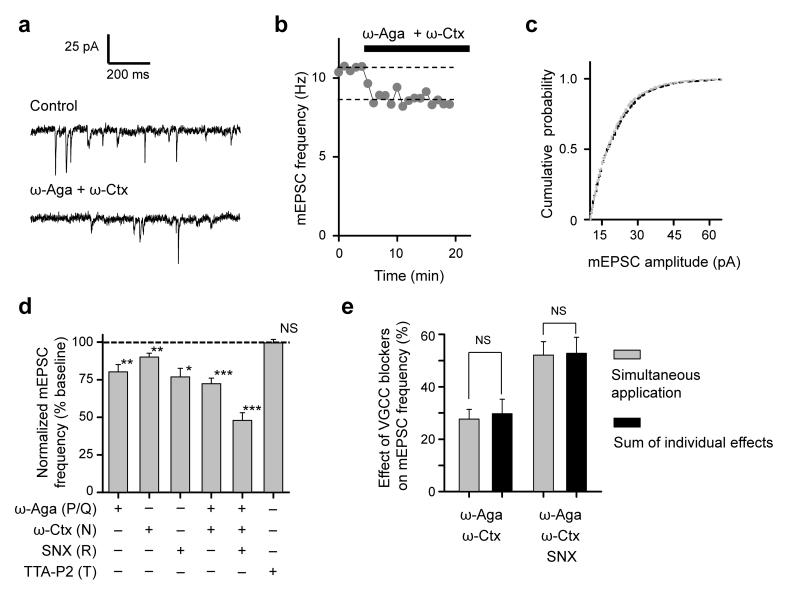
To determine the contribution of different presynaptic VGCCs to spontaneous miniature release at small excitatory synapses we tested the effects of specific VGCC blockers on mEPSC frequency in cultured hippocampal neurons. Acute blockade of P/Q-type (with 0.25 μM ω-Agatoxin-IVA, ω-Aga), N-type (with 5 μM ω-Conotoxin-GVIA, ω-Ctx), or R-type channels (with 0.5 μM SNX-482, SNX), each significantly decreased the frequency of mEPSCs. In contrast, blockade of T-type channels (with 1.0 μM TTA-P2) had no significant effect (Fig. 1a–d, and Supplementary Table 1). We also observed no evidence for non-linear summation of the effects of individual blockers (Fig. 1e).

Figure 1.

Differential triggering of spontaneous excitatory neurotransmission by P/Q-, N- , and R-type Ca²⁺ channels. (a–c) Representative experiment illustrating the effect of P/Q- and N-type VGCC blockade with ω-Aga and ω-Ctx on excitatory miniature release. (a) mEPSCs before (Control) and 10 min after application of both toxins, (b) time-course of mEPSC frequency, and (c) cumulative distributions of mEPSC amplitudes before (black) and after (gray) application of toxins, showing no effect of ω-Aga and ω-Ctx. (d) Summary graphs showing effects of the selective P/Q-, N-, R-, and T-type channel blockers on mEPSC frequency (mean ± s.e.m, ω-Aga, N = 14; ω-Ctx, N = 12; SNX N = 5; ω-Aga and ω-Ctx, N = 25; ω-Aga, ω-Ctx and SNX, N = 17; TTA-P2, N = 12 cells). See also Supplementary Table 1. (e) Linear summation of ω-Aga, ω-Ctx and SNX effects on mEPSC frequency (mean ± s.e.m). Sums of individual effects of the VGCC blockers (black bars) were calculated using data from (d). *** P < 0.001, ** P < 0.01, * P < 0.05, NS P > 0.75; single group mean (d) and unpaired comparison (e) t-tests.

A quantitative comparison of the different blockers revealed that simultaneous application of ω-Aga and ω-Ctx decreased mEPSC frequency by 27.7 ± 3.7%, implying that approximately one quarter of spontaneous glutamate release depends on P/Q- and N-type VGCCs, which underlie the majority of evoked Ca²⁺ influx and vesicular release^{10, 12, 14}. Surprisingly, SNX reduced mEPSC frequency by a similar extent (23.1 ± 5.7%) as the combined application of ω-Aga and ω-Ctx, despite a much smaller contribution of R-type channels to evoked Ca²⁺ influx and exocytosis^{10, 12, 14} (and see below). A disproportionate role for SNX-sensitive VGCCs in spontaneous release is however consistent with the hypothesis that VGCC-mediated glutamatergic minis are triggered by stochastic VGCC opening: R-type channels have been shown to activate at more negative potentials, with slower gating kinetics, than P/Q- or N-type channels^{12, 16}. This implies that, at physiological V_rest (between −80 mV and −60 mV) R-type channels should open more often and for a longer time than P/Q- and N-type channels, and therefore should be more efficient in triggering miniature release. Furthermore, in agreement with the hypothesis that spontaneous VGCC openings can trigger exocytosis, increasing the opening probability of VGCCs by depolarizing the presynaptic membrane with raised extracellular [K⁺]_ext (20 mM) increased the frequency of VGCC-dependent minis (Supplementary Fig. 1).

Roles of different VGCCs in presynaptic Ca²⁺ dynamics

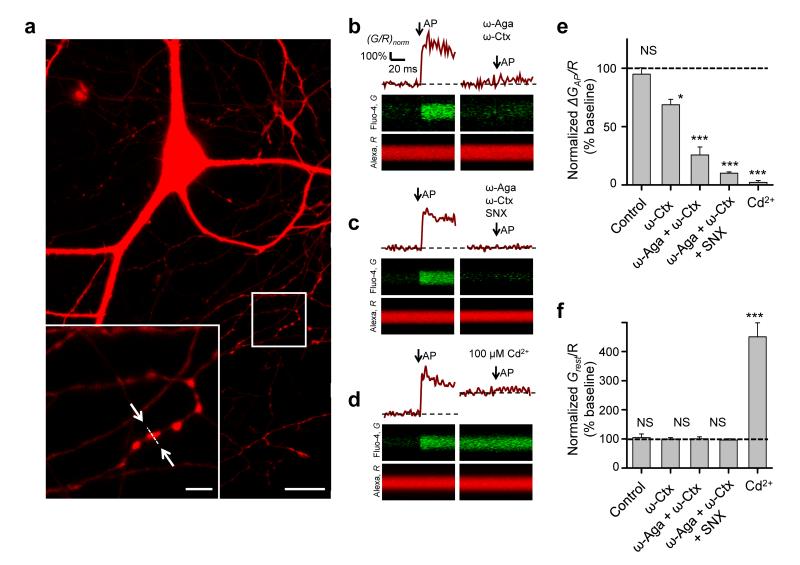
We next compared the relative contributions of different VGCCs to presynaptic Ca²⁺ dynamics and to spontaneous miniature release by examining the effects of VGCC blockers on presynaptic [Ca²⁺] at rest and following action potentials using fast fluorescence imaging of the Ca²⁺ indicator Fluo-4 (Fig. 2a–d, Online Methods). Consistent with previous reports^{10, 12, 15} ω-Aga and ω-Ctx profoundly reduced the evoked Ca²⁺ fluorescence transient, normalized by the fluorescence of a morphological indicator AP ΔG_AP/R (by 74.3 ± 6.4%, Fig. 2b,e), confirming that P/Q-type and N-type VGCCs are the major source of spike-evoked Ca²⁺ entry. Simultaneous application of ω-Aga, ω-Ctx, and SNX almost completely abolished the evoked Ca²⁺ transient (by 90.0 ± 6.4%, Fig. 2c,e) arguing that the ω-Aga- and ω-Ctx-resistant Ca²⁺ influx is mainly mediated by R-type VGCCs. The inorganic non-specific VGCC blocker Cd²⁺ (100 μM) completely abolished the residual evoked Ca²⁺ fluorescence transient (Fig. 2d,e), implying that it was mediated by toxin-insensitive VGCCs.

Figure 2.

Relative contributions of P/Q-, N-, and R-type VGCCs to presynaptic Ca²⁺ dynamics assessed with fast Ca²⁺ fluorescence imaging. (a) Fluorescence image of a typical cultured hippocampal neuron loaded with AlexaFluor 568 and Fluo-4 (Alexa channel is shown). Bottom left: magnified image of axonal fragment containing several presynaptic boutons; arrows indicate position of the line-scan used to measure Ca²⁺ transients illustrated in (b). Scale bars 20 μm and 4 μm. (b–d) Line-scan fluorescence responses to a single action potential (average of 5 sweeps) in typical boutons from representative experiments before (left) and after (right) application of different VGCC blockers as indicated. (e, f) Summary graphs illustrating differential effects of organic VGCC blockers and Cd²⁺ on action potential-evoked (e) and resting (f) presynaptic Ca²⁺ fluorescence (mean ± s.e.m, N = 9 (Control), N = 7 (ω-Ctx), N = 18 (ω-Aga + ω-Ctx), N = 40 (ω-Aga + ω-Ctx + SNX) and N = 13 (Cd²⁺) boutons from 4–6 independent experiments for each condition. Stability of Ca²⁺ responses in control experiments was tested after the same duration as for VGCC blockers. * P < 0.05, *** P < 0.001, NS P > 0.3, Wilcoxon signed rank test for single group median.

Unexpectedly, the organic VGCC blockers and Cd²⁺ had very different effects on the resting Fluo-4 fluorescence (G_rest/R). While ω-Aga, ω-Ctx and SNX did not change G_rest/R, Cd²⁺ caused a several-fold increase of G_rest/R (Fig. 2b–d,f). This could be due to a Cd²⁺-induced elevation of intracellular Ca²⁺ levels, or to a gradual accumulation of presynaptic Cd²⁺ binding to the Ca²⁺ indicator^{17, 18}. In either case, the increase in Ca²⁺ indicator fluorescence suggests that Cd²⁺ may substantially alter resting presynaptic concentrations of divalent cations, which could affect miniature release through a mechanism separate from the direct blockade of VGCCs. We therefore only used organic VGCC blockers (ω-Aga, ω-Ctx and SNX) in the rest of the study.

Distinct effects of BAPTA and EGTA on VGCC-mediated minis

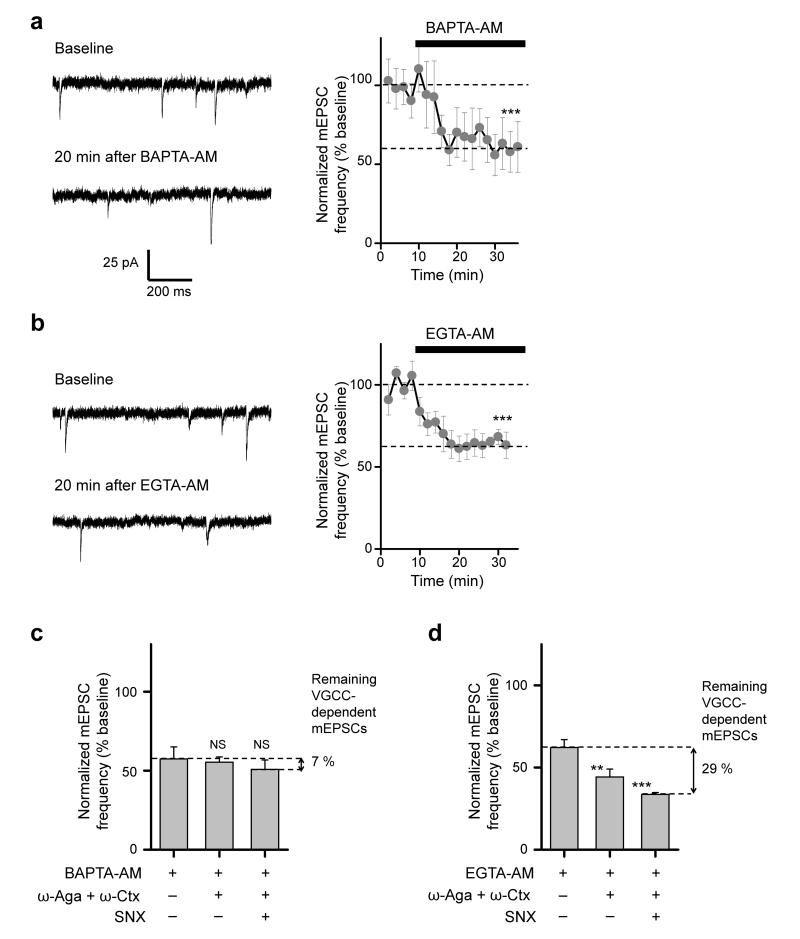
How do presynaptic VGCCs trigger spontaneous glutamate release? One possibility is that VGCC-dependent minis are directly triggered by the formation of fast transient Ca²⁺-nano/microdomains around individual spontaneously opening channels, akin to those that underlie evoked exocytosis. Alternatively, stochastic opening of VGCCs may control the presynaptic resting [Ca²⁺]_rest and thus affect the rate of miniature release on a slower timescale¹⁹. Ca²⁺ imaging however failed to detect a significant change in [Ca²⁺]_rest upon blockade of VGCCs with the specific organic blockers (Fig. 2f). This argues against the hypothesis that stochastic opening of VGCCs facilitates spontaneous release simply by increasing [Ca²⁺]_rest, and suggests instead that VGCC-dependent glutamatergic minis are directly triggered by the formation of transient Ca²⁺-nano/microdomains. If so, VGCC-dependent minis should be inhibited by intracellular Ca²⁺ chelation, because rapid Ca²⁺ transients are much more sensitive to exogenous Ca²⁺ buffers⁵ than [Ca²⁺]_rest (which is determined by the balance of passive membrane Ca²⁺ fluxes and active pumping mechanisms²⁰). To test this prediction we measured the effects of intracellular loading of either fast or slow membrane-permeable Ca²⁺ buffers (BAPTA-AM or EGTA-AM, respectively).

Both chelators applied at 20 μM significantly decreased the mEPSC frequency within 10–20 min: at steady state, BAPTA-AM by 42.6 ± 7.7% (Fig. 3a), and EGTA-AM by 37.8 ± 4.7% (Fig. 3b). At first sight the similar effects of BAPTA-AM and EGTA-AM argue that spontaneous glutamate release is triggered by relatively slow changes in intracellular [Ca²⁺]. However, the overall mini rate includes both VGCC-dependent minis and a residual population that persists in the presence of VGCC blockers (Fig. 1d). Moreover, the absolute concentrations of intracellular BAPTA and EGTA cannot be determined precisely in experiments where the AM esters are applied extracellularly²¹, so in principle BAPTA and EGTA may reach different steady-state concentrations in presynaptic terminals. Therefore, to compare the sensitivity of VGCC-dependent minis to BAPTA and EGTA, we measured the effects of ω-Aga, ω-Ctx and SNX on the mEPSC frequency in cultures pre-equilibrated with EGTA-AM or BAPTA-AM (Fig. 3c,d). Both Ca²⁺ chelators significantly reduced the effect of the combined VGCC blockers. However, while BAPTA-AM almost completely occluded the effect of the toxins (~7% inhibition, Fig. 3c, versus 52.1% in control conditions, Fig. 1d), EGTA-AM only reduced their effect by approximately half (28.6% inhibition, Fig. 3d, versus 52.1% in control conditions, Fig. 1d).

Figure 3.

Differential effects of slow (EGTA) and fast (BAPTA) exogenous Ca²⁺ buffers on VGCC-dependent minis. (a, b) Time-course of mEPSC frequency changes during incubation in BAPTA-AM (a) and EGTA-AM (b). Left, mEPSC traces from representative experiments before and after addition of the Ca²⁺ chelators. Right, average responses in N = 7 cells for BAPTA-AM and N = 9 cells for EGTA-AM. (c, d) Differential effects of VGCC blockers on mEPSC frequency in BAPTA-AM (c) and in EGTA-AM (d) pre-treated cultures (both in (c) and (d) N = 7 cells for ω-Aga and ω-Ctx, and N = 6 cells for ω-Aga, ω-Ctx, and SNX). To determine the remaining fraction of mEPSCs sensitive to VGCC blockade after BAPTA-AM and EGTA-AM treatment (shown on the right), the initial mEPSC frequencies in this set of experiments were normalized to the effects of BAPTA-AM or EGTA-AM determined in (a) and (b). In contrast to EGTA-AM, pretreatment with BAPTA-AM almost completely occluded the effect of toxins on miniature release. All data are mean ± s.e.m, *** P < 0.001 and ** P < 0.01, NS P > 0.3, single group mean t-test.

Distinct effects of BAPTA and EGTA on evoked exocytosis

The differential sensitivity of VGCC-dependent mEPSCs to BAPTA and EGTA observed here is similar to the effects of these buffers on evoked glutamate release at small central synapses in acute brain preparations^{5, 22}. Indeed, in contrast to synapses with tight 10–20 nm Ca²⁺-nanodomain coupling, where EGTA fails to inhibit evoked release²³, evoked release in small glutamatergic neocortical synapses is inhibited by intracellular EGTA in the millimolar range^{5, 22}, and therefore is thought to be triggered by larger Ca²⁺-microdomains. Thus our data imply that VGCC-dependent glutamatergic minis in small hippocampal synapses are also mediated by the formation of transient Ca²⁺-microdomains in the vicinity of spontaneously opening VGCCs.

To test this model more directly we compared the effects of EGTA-AM and BAPTA-AM on VGCC-dependent mEPSCs to their effects on evoked release measured in the same preparation. Because whole-cell patch-clamp recordings would inevitably perturb cytoplasmic integrity in the presynaptic axon, and likely interfere with BAPTA-AM and EGTA-AM equilibration, we used an alternative approach based on imaging of evoked vesicular exocytosis in intact synapses with FM dyes^24-26. We first labeled recycling vesicles with the fluorescent styryl dye SynaptoRedC1 (SRC1), and then measured the specific action potential-evoked SRC1 de-staining rate (k_AP) during low frequency (0.5 Hz) stimulation, in control conditions or in the presence of BAPTA-AM or EGTA-AM (Fig. 4a–d and Online Methods). We have previously shown that k_AP is proportional to the average release probability of individual release-ready vesicles²⁵. The decrease of k_AP in BAPTA- or EGTA-loaded boutons should thus report the specific reduction of evoked vesicular release by fast or slow Ca²⁺ chelation.

Figure 4.

FM dye imaging of action potential-evoked exocytosis reveals similar sensitivity of evoked and VGCC-dependent miniature release to presynaptic Ca²⁺ chelation. (a) Experimental paradigm (see also Online Methods). (b) Example of fluorescence loss in individual synaptic boutons during the time course of a typical control experiment. Arrows: individual boutons examined in (c). Scale bar 5 μm. (c) FM dye de-staining profiles in boutons 1 and 2; exponential fits of de-staining rates at rest (k_rest) and during 0.5 Hz action potential stimulation (k_stim) are shown by red dashed lines. The effective specific action potential-evoked FM dye (SRC1) de-staining rate in each bouton was calculated as k_AP = k_stim – k_rest. (d) Effect of BAPTA-AM and EGTA-AM on SRC1 de-staining kinetics. Average de-staining profiles from three representative experiments: Control (black), BAPTA-AM (gray) and EGTA-AM (white) symbols. Each profile is an average of 100–200 boutons. (e) Comparison of BAPTA-AM and EGTA-AM relative effects on the rate of action potential-evoked vesicular exocytosis k_AP (left 2 bars, BAPTA-AM N = 6 experiments, EGTA-AM N = 5 experiments) and on the frequency of VGCC-dependent minis (right 2 bars). The latter was calculated from electrophysiological mEPSC recordings in Figs. 1 and 3 as detailed in Online Methods. Data are mean ± s.e.m, * P < 0.05, *** P < 0.001 unpaired t-tests.

Both BAPTA-AM and EGTA-AM loading significantly decreased k_AP in comparison to interleaved control cultures (Fig. 4d). BAPTA-AM almost completely blocked evoked exocytosis (by ~87%), while EGTA-AM inhibited it only by 33% (Fig. 4e, left pair of bars). A similar effect of EGTA-AM on evoked glutamate release in cultured hippocampal neurons has previously been reported by imaging vesicular release with vGLut-pHluorin²⁷. Thus we conclude that, similar to small glutamatergic synapses in the brain, evoked release at synapses in hippocampal cultures is mediated by Ca²⁺-microdomains that are quenched by BAPTA and reduced by EGTA. Notably, the observed BAPTA-AM and EGTA-AM induced reductions in evoked release were quantitatively similar to the calculated specific effects of these chelators on VGCC-dependent mEPSCs (Fig. 4e, right pair of bars and Online Methods).

The conclusion that VGCC-dependent glutamatergic minis are triggered by transient Ca²⁺-microdomains is however difficult to reconcile with previous modeling studies that suggest that evoked release in synapses with loose Ca²⁺-microdomain coupling is likely to be controlled by several tens of VGCCs ^{5, 28} (although see ref.²⁹). Indeed, the steep power relationship between vesicular release probability and presynaptic Ca²⁺ influx^{14, 22, 25, 28-31} implies that the release rate should be very low following stochastic opening of individual VGCCs. To address this paradox we assessed the properties of VGCC-dependent evoked and spontaneous glutamate release in small hippocampal boutons using quantitative modeling of presynaptic Ca²⁺ dynamics and activation of vesicular fusion.

Numbers of different VGCCs in an average synaptic bouton

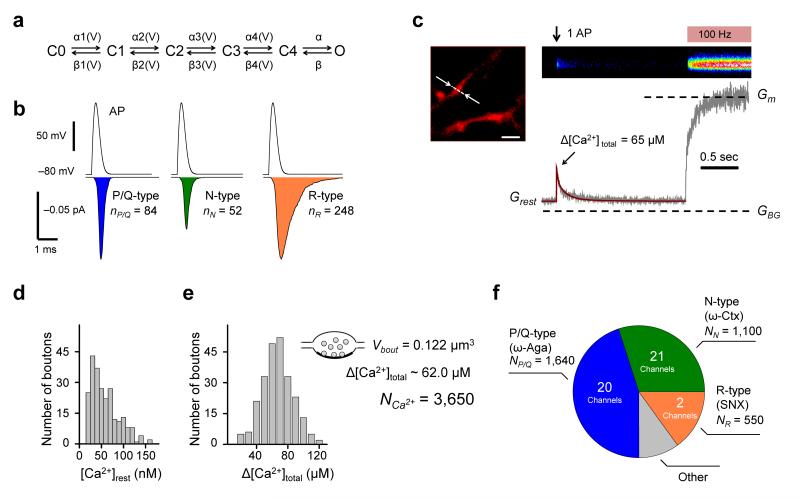
To constrain the model parameters we first estimated the numbers of P/Q-, N-, and R-type VGCCs in an average presynaptic bouton. We simulated the stochastic behavior of different VGCC subtypes during action potentials using a six-state gating kinetic model describing VGCCs in hippocampal mossy fiber boutons¹² (Fig. 5a, Supplementary Fig. 2 and Online Methods). By integrating the average Ca²⁺ current traces (including failures) (Fig. 5b) we estimated the number of Ca²⁺ ions entering the bouton during an action potential through single P/Q-type (n_P/Q = 84), N-type (n_N = 52), or R-type (n_R = 248) channels.

Figure 5.

Estimation of the numbers of P/Q-, N-, and R-type VGCCs in an average presynaptic bouton. (a) Gating model for presynaptic VGCCs. (b) Average (500 simulations) action potential-evoked current traces (including failures) through P/Q-, N-, and R-type channels. Action potential waveform is shown above. Integration of the current traces (colored areas) yields estimates for the average number of Ca²⁺ ions entering the bouton following an action potential through single VGCCs of each subtype. (c) Representative Ca²⁺ imaging experiment. Top left, an axonal fragment loaded with Fluo-4 and AlexaFluor 568 (Alexa channel is shown), arrows indicate line-scan position, scale bar 2 μm. Top right, average of 5 line-scan Fluo-4 responses to a single spike followed by a saturating 100 Hz spike-train (brightness is color-coded). Bottom right, corresponding fluorescence time-course. Dashed lines, background (G_BG) and maximal (G_m) Fluo-4 fluorescence. Brown curve, non-stationary single compartment model fit corresponding to Δ[Ca²⁺]_total = 65 μM. (d, e) Distribution of [Ca²⁺]_rest (d) and Δ[Ca²⁺]_total (e) in 242 boutons from 12 axons. Insert in (e), the number of Ca²⁺ ions (N_Ca2+ ~3,650) entering a bouton of volume V_bout ~0.122 μm³ during action potential corresponding to the average Δ[Ca²⁺]_total = 62.0 μM (see text for details). (f) Pie-chart illustrating the complement of presynaptic VGCCs in an average presynaptic bouton. The colored areas correspond to the fractions of spike-evoked Ca²⁺ influx mediated by ω-Aga-sensitive P/Q-type VGCCs (blue, 45%), ω-Ctx-sensitive N-type channels (green, 30%) and SNX-sensitive R-type channels (brown, 15%) as determined in Fig. 2e, together with the corresponding numbers of VGCCs.

We next imaged Fluo-4 Ca²⁺ fluorescence transients triggered by single spikes in individual boutons, followed by 100 Hz spike-trains to define the saturated fluorescence level (Fig. 5c and Online Methods). We have previously shown that fast presynaptic Ca²⁺ dynamics are well approximated by a non-stationary single compartment model²⁵. Using direct fitting of individual Ca²⁺ traces (Fig. 5c and Online Methods) we obtained an estimate of [Ca²⁺]_rest = 53.9 ± 2.2 nM and of the total action potential-evoked Ca²⁺ concentration change Δ[Ca²⁺]_total = 62.0 ± 1.3 μM (Fig. 5d,e). The latter value allowed us to estimate the average number of Ca²⁺ ions entering the bouton during an action potential as Ca²⁺ ions entering the bouton during an action potential as N_Ca²⁺ = Δ[Ca²⁺]_total · λ_free · V_bout · N_A ~3.650 (where V_bout ~0.122 μm³ is the average bouton volume in cultures^32,33, λ_free is the fraction of intra-terminal volume free of synaptic vesicles, mitochondria, other presynaptic organelles, and cytomatrix^{32, 34, 35}, and N_A is Avogadro’s number). By multiplying N_Ca²⁺ by the proportions of spike-evoked Ca²⁺ influx mediated by each channel subtype (P/Q ~0.45, N ~0.3, and R ~0.15, Fig. 2e) we estimated the average number of Ca²⁺ ions entering the bouton through P/Q-, N-, and R-type channels (N_P/Q ~1,640, N_N ~1,100, and N_R ~550). Finally by dividing these values by the number of Ca²⁺ ions entering through individual VGCCs (Fig. 5b) we estimated that an average presynaptic bouton contains ~20 P/Q-type, ~21 N-type, and ~2 R-type VGCCs (Fig. 5f).

Modeling of action potential-evoked glutamate release

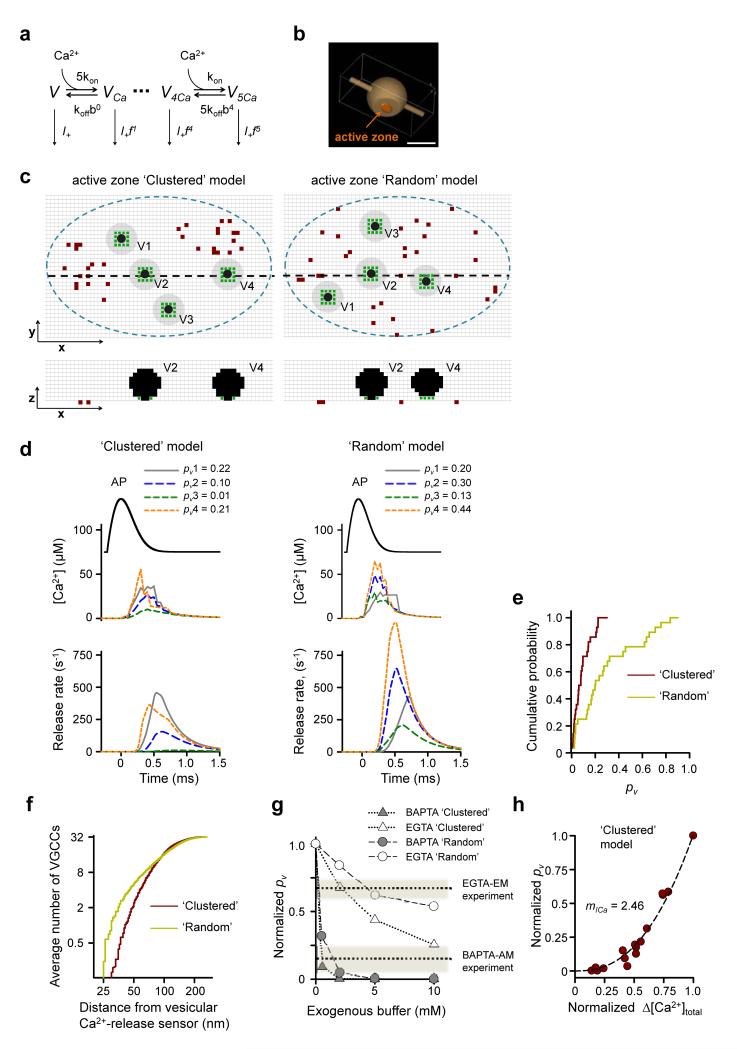
To model VGCC-glutamate release coupling in small hippocampal synapses we used an allosteric model of Ca²⁺ activation of vesicle fusion developed in the calyx of Held¹⁹ (Fig. 6a). Guided by available ultrastructural data^{15, 32} we considered a typical active zone as an elliptical disk (with area S_AZ = 0.04 μm²) located within the truncated surface of a sphere corresponding to a synaptic bouton of radius R_bout = 0.35 μm (Fig. 6b). Each active zone contained 4 docked release-ready vesicles. Accumulating experimental data demonstrate that presynaptic VGCCs in central synapses are almost exclusively located in the active zone^{11, 15, 23, 33}. Because small hippocampal boutons contain on average 1.3 active zones^{15, 32} we adjusted the numbers of VGCCs in a whole bouton by this factor and considered that a typical active zone contains: ~15 P/Q-type (equivalent to ~375 μm⁻²), ~16 N-type (~400 μm⁻²), and ~1.5 R-type VGCCs (~37.5 μm⁻²). This result is consistent with an estimate of the P/Q-type channel density in the active zones of small CA3 synapses obtained with immunogold electron microscopy (~396 μm⁻² or ~16 P/Q-type channels)¹⁵. The exact distribution of different VGCCs subtypes within the active zone however remains largely unknown. Most P/Q-type VGCCs are not distributed uniformly in the active zones of small CA3 glutamatergic synapses, but instead occur in oval clusters with characteristic dimensions of 50–100 nm¹⁵. In some active zones however the spatial distribution of P/Q-type VGCCs could not be distinguished from a random distribution. Therefore we initially considered both limiting cases in parallel: ‘Clustered’ and ‘Random’ VGCC distributions in the active zone (Fig. 6c). To account for the EGTA sensitivity of VGCC-dependent release (Fig. 4e) we also assumed that the minimal distance between VGCCs and vesicular release sensors was 25 nm (ref. ⁵).

Figure 6.

Modeling action potential-evoked release in small hippocampal synapses. (a) Allosteric model of Ca²⁺ activation of vesicle fusion¹⁹. (b) Presynaptic bouton geometry used in VCell simulations. Scale bar 0.5 μm. (c) Representative distributions of VGCCs and vesicles in the active zone for Clustered (left) and Random (right) models. Top, XY cross-sections 2.5 nm above the active zone; bottom, XZ cross-sections corresponding to black dashed lines in the XY plane. Blue dashed lines, active zone borders; brown dots, VGCCs; black dots, space occupied by vesicles; gray circles, vesicle projections on the XY plane; green dots, locations of Ca²⁺-release sensors, grid 5 nm. (d) Simulation results corresponding to geometries in (c). Top, action potential waveform; middle, average [Ca²⁺] transients at Ca²⁺-release sensors; bottom, corresponding release rates; legends, resulting fusion probabilities p_v. (e) Cumulative probability plots of p_v for Clustered and Random models. (n = 28 vesicles from 7 simulated synapses for each model). (f) Cumulative probability plots showing the average number of VGCCs located within a given distance from the vesicular Ca²⁺-release sensors (n = 240 vesicles from 60 simulated synapses). (g) Model predictions for inhibition of evoked release by BAPTA and EGTA. Dotted lines show the experimental effects of BAPTA-AM and EGTA-AM as determined in Fig. 4e. (h) Dependency of p_v on Δ[Ca²⁺]_total simulated by progressive deletion of active VGCCs. Data are from 5 simulated synapses, each point represents average p_v for 4 release-ready vesicles. Data on both axes are normalized to the corresponding maximal values at basal conditions. Dotted lines, fitted power function, with the slope corresponding to Ca²⁺ current cooperativity m_ICa = 2.46.

The results of two typical simulations for the Clustered and Random models are illustrated in Fig. 6c,d. Each run consisted of the following steps (see Online Methods for details): (1) generate the spatial distribution of docked synaptic vesicles and VGCCs within the active zone (Fig. 6c); (2) simulate the action potential-evoked Ca²⁺ influx and three-dimensional buffered diffusion using the Virtual Cell (VCell) environment, and estimate [Ca²⁺] transients at vesicular release sensors (Fig. 6d middle traces); and (3) calculate vesicular release rates (Fig. 6d bottom traces) and corresponding vesicle fusion probabilities p_v (Fig. 6d top) using the allosteric model of the Ca²⁺ activation of vesicle fusion¹⁹ (Fig. 6a).

For each model we simulated exocytosis in seven active zones with different VGCC-vesicle distributions and different realizations of stochastic VGCC behavior during an action potential (i.e. in total 28 vesicles for each model). Although the overall VGCC density in the active zone and the total evoked Ca²⁺ influx were the same in the Clustered and Random models, the average peak [Ca²⁺]_peak at the vesicular release sensors and the corresponding vesicular fusion probability p_v were substantially lower in the Clustered model ([Ca²⁺]_peak = 27.7 μM, coefficient of variation CV = 0.648; p_v = 0.09, CV = 0.82) than in the Random model ([Ca²⁺]_peak = 49.4 μM, CV = 0.61; p_v = 0.29, CV = 0.88) (Fig. 6d,e). This difference was a direct consequence of a lower number of VGCCs located in the immediate vicinity of docked vesicles (Fig. 6f) in the Clustered than in the Random model. In agreement with this, evoked release in the Clustered model was more sensitive to Ca²⁺ chelation than in the Random model, and as expected for synapses with loose VGCC-release coupling, both models revealed differential effects of BAPTA and EGTA on evoked vesicle fusion (Fig. 6g). Notably, whilst the average p_v predicted by the Clustered model (0.09) is within the range of experimentally determined average p_v values at hippocampal synapses (0.05–0.1)^{24, 25, 30}, the average p_v predicted by the Random model (0.29) is several-fold higher. Thus our modeling results are consistent with the hypothesis that the majority of presynaptic VGCCs within the active zone are indeed clustered¹⁵.

How many VGCCs from each cluster contribute to the release of a single vesicle during an action potential? In other words, what is VGCC cooperativity (m_Ch) of triggering glutamate release at small hippocampal synapses? The six-state VGCC gating model¹² provides estimates for the opening probabilities of P/Q-type (P_{open_P/Q} = 0.5), N-type (P_{open_N} = 0.4), and R-type VGCCs (P_{open_R} = 0.32) during an action potential (Supplementary Fig. 2). Thus on average ~14 VGCCs are open in the whole active zone during an action potential, which yields an upper bound for m_Ch. To estimate the lower bound of m_Ch we simulated the dependency of p_v on the magnitude of total calcium influx Δ[Ca²⁺]_total as the number of open channels during an action potential decreased (without changing the currents through the channels that remained open) (Fig. 6h). This model corresponded to experiments where evoked Ca²⁺ influx was progressively reduced with slowly dissociating VGCC blockers^{29, 36}. By fitting the obtained dependency with a power function we thus obtained a slope value for Ca²⁺ current cooperativity m_ICa = 2.5, which is close to the lower bound of VGCC cooperativity m_Ch³⁷.

Furthermore our modeling showed that the apparent m_Ch differed among vesicles in the active zone. For vesicles with high p_v which were located close to VGCC clusters (e.g. vesicles V1 and V4 in Fig. 6c Clustered model and Supplementary Fig. 3) release was almost completely controlled by the VGCCs from the nearest cluster and [Ca²⁺] transients around such vesicles were largely determined by the 2–3 closest VGCCs. This effect was most prominent at the end of the action potential repolarization phase when the channel open probability was low but the current through individual VGCCs was high because of the increased Ca²⁺ driving force. In contrast, in the other limiting case, for vesicles with low p_v that were located further away from VGCC clusters (e.g. vesicle V3 in Fig. 6c Clustered model and Supplementary Fig. 3) release was jointly controlled by all the VGCCs that opened during the action potential.

Modeling of VGCC-dependent miniature glutamate release

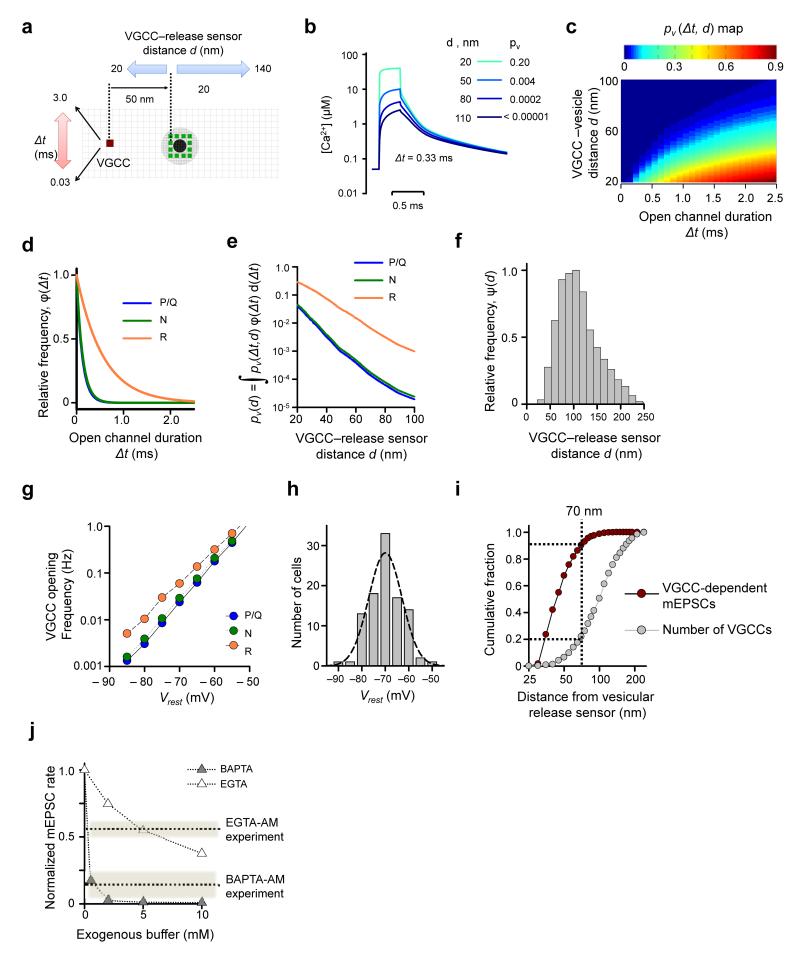
To model VGCC-dependent miniature release we simulated [Ca²⁺] transients at vesicular release sensors produced by spontaneous openings of a single VGCC for different VGCC open-channel durations (Δt) and at different VGCC-vesicle distances (d) (Fig. 7a,b). Here we assumed a constant single channel current of 0.34 pA, corresponding to V_rest = −70 mV (Online Methods and ref. ³⁸). Using the same allosteric model (Fig. 6a) and the simulated [Ca²⁺] transients corresponding to different (Δt,d) pairs we then calculated a p_v (Δt,d) map, which showed that stochastic opening of a single VGCC can indeed trigger vesicular fusion, with a steep dependence on both the VGCC-distance and the open-channel duration (Fig. 7c).

Figure 7.

Modeling VGCC-dependent glutamate miniature release. (a) Schematics illustrating VCell simulations. As in Fig. 6c the black dot indicate space taken up by the vesicle in the XY plane 2.5 nm above the active zone; gray circle, vesicle projection on the active zone plane; green dots, assumed positions of Ca²⁺-release sensors, grid 5 nm. (b) Examples of average [Ca²⁺] transients at release sensors produced by single VGCC openings (for 0.33 ms) for 4 different VGCC-release sensor distances. Insert, corresponding vesicle fusion probabilities. (c) Color-coded map showing dependency of vesicle fusion probability p_v(Δt,d) on VGCC-vesicle distance d and VGCC open-channel duration Δt. (d) Frequency histograms φ(Δt) for the durations of spontaneous P/Q-, N-, and R-type channel opening at V_rest obtained using the VGCC gating model¹² (Fig. 5a). (e) Dependencies of vesicle fusion probability p_v(d) on VGCC-vesicle distance for different VGCC subtypes. (f) Frequency histogram ψ(d) for the relative VGCC-vesicle distances in the Clustered model (n = 60 simulated active zones). (g) Dependency of spontaneous P/Q-, N-, and R-type channel opening on V_rest, calculated using the six-state VGCC gating model¹² (Fig. 5a). (h) Distribution of V_rest in cultured hippocampal neurons (mean 71.9 ± 0.7 mV, n = 98 neurons). (i) Cumulative fractions of VGCC-mediated mEPSCs and VGCC numbers plotted as functions of the distance from the vesicular release sensor. ~90% of all VGCC-dependent minis are mediated by only ~20% of all VGCCs present in the active zone located within 70 nm of docked vesicles. (j) Model predictions for the effects of BAPTA and EGTA on VGCC-dependent mEPSC frequency. Dotted lines, experimental effects of BAPTA-AM and EGTA-AM as estimated in Fig. 4e.

We next determined the relative efficiency of different VGCCs in triggering spontaneous miniature release. For each channel subtype we multiplied the p_v(Δt,d) map by the probability density function for open-channel duration φ(Δt) (Fig. 7d). By integrating the products over the entire range of possible open-channel durations we thus obtained p_v(d)=∫p_v(Δt,d)·φ(Δt)·d(Δt) dependencies of the vesicular fusion probability on VGCC-release sensor distance for P/Q-, N-, and R-type VGCCs (Fig. 7e). Consistent with a longer duration of spontaneous channel openings, R-type VGCCs were ~30 fold more efficient in triggering vesicular fusion than P/Q- and N-type channels (e.g. at d = 50 nm, for R-type VGCCs p_v(d) ~0.03, whilst for P/Q- and N-type VGCCs p_v(d) ~0.001, Fig. 7e). Finally, by multiplying p_v(d) by the probability density function ψ(d) for the distribution of VGCC-release sensor distances in the Clustered model (Fig. 7f) and by integrating the product p_v(d)·ψ(d) for each channel subtype over the entire range of distances, we estimated the average probabilities 〈p_v〉 of vesicle fusion in response to single P/Q-, N-, and R-type VGCC openings (Table 1, 〈p_v〉 ~0.0006 for P/Q- and N-type channels, and 〈p_v〉 ~0.009 for R-type channels).

Table 1. Triggering of miniature glutamate release by spontaneous opening of P/Q-, N-, and R-type VGCCs. Model results.

	〈pv〉 Average vesicle fusion probability in response to a single VGCC opening	ν Average single channel opening frequency (Hz)	NCh_type Number of VGCCs in an average active zone	$f_{\mathit{VGCC}}^{\mathit{Ch\_type}}=\langle p_v\rangle \cdot v\cdot N_{\mathit{Ch\_type}}\cdot \mathit{RRP}$ VGCC-dependent mEPSC rate at a single synapse* (Hz)
P/Q-type	0.0006	0.067	15	0.0029
N-type	0.0006	0.069	16	0.0035
R-type	0.0089	0.115	1.5	0.0080
Total			32.5	0.0144

^*By taking into account that on average there are 4 release ready vesicles per active zone, and that there are ~ 1.3 active zones per synaptic bouton we considered the readily releasable pool size RRP = 5.2 vesicles.

To estimate VGCC-mediated miniature release rates in a typical bouton we modeled the stochastic opening of single P/Q-, N-, and R-type VGCCs at different V_rest (Fig. 7g, Supplementary Fig. 4 and Online Methods) and calculated the average frequencies of spontaneous channel opening (ν, Table 1) for each channel subtype corresponding to the experimentally determined distribution of V_rest in hippocampal neurons in culture (Fig. 7h). This allowed us to estimate the frequencies of VGCC-dependent minis mediated by each channel subtype in a typical synapse as: $f_{\mathit{VGCC}}^{\mathit{Ch\_type}}=\langle p_v\rangle \cdot v\cdot N_{\mathit{Ch\_type}}\cdot \mathrm{RRP}$, where N_{Ch_type} stands for the average number of each VGCC subtype in the active zone, and RRP is the average size of the readily releasable pool of vesicles (Table 1).

Consistent with our experimental data (Fig. 1d) the modeling results confirmed that R-type VGCCs have a privileged role in triggering spontaneous glutamate release (~50% of VGCC-dependent minis). The frequency of all VGCC-dependent mEPSCs in an average synapse predicted by the model was f_VGCC ~0.014 Hz (or ~0.85 vesicles per minute). Taking into account that this subset of minis accounts for ~50% of all mEPSCs (Fig. 1d), the model predicts the overall mEPSC rate at a single synapse f_total ~0.028 Hz (or 1.7 vesicles per minute). This value is consistent with experimentally determined spontaneous vesicular release rates at individual synaptic boutons (0.7–2 vesicles per minute) ^39-41. Furthermore, the average mEPSC frequency across all cells recorded in standard conditions was 5.3 ± 0.5 Hz (n = 110 recordings). Dividing this value by the model-predicted mEPSC rate in a single bouton yields a plausible estimate (~190) for the number of synapses whose activity can be readily monitored by somatic patch clamp in a typical neuron in culture. Thus the modeling results demonstrate that uncorrelated spontaneous opening of VGCCs at V_rest can fully account for the experimentally observed VGCC-dependent mEPSC rates.

What fraction of VGCCs contributes to spontaneous miniature release? To answer this we simulated VGCC-vesicle distributions according to the Clustered model (n = 60 synapses) and then calculated VGCC-dependent mEPSC rates during progressive removal of VGCCs that were more distant from the docked synaptic vesicles in the active zone. Direct comparison of the obtained cumulative fractions of VGCC-mediated minis and of VGCC number (plotted as functions of VGCC-vesicle distance, Fig. 7i) revealed that 90% of all VGCC-dependent mEPSCs were triggered by only 20% of all VGCCs that are located within 70 nm from the docked vesicles.

Similar to evoked release, model simulations revealed differential effects of BAPTA and EGTA on VGCC-dependent miniature release (Fig. 7j). Comparing the modeling results with the experimentally determined effects of BAPTA-AM and EGTA-AM (see also Fig. 6g) allowed us to make an estimate of the unknown concentrations of BAPTA (~0.5 mM) and EGTA (~5 mM) after AM-ester loading, implying that EGTA-AM in our experimental conditions was taken up by cultured hippocampal neurons ~10 fold more efficiently than BAPTA-AM. This provides a plausible explanation for the paradoxical finding that VGCC-dependent mEPSCs were much more sensitive to BAPTA-AM than EGTA-AM loading, whilst the overall mEPSC frequency was reduced to the same extent by both chelators (Fig. 3). Indeed, it is likely that at least some of the ~50% of mEPSCs that remain in the presence of VGCC blockers depend on slow global intracellular [Ca²⁺] changes as might occur from intracellular stores^{42, 43}. Then according to this model 0.5 mM BAPTA should be much less efficient than 5 mM EGTA in inhibiting such minis, as demonstrated by modeling of vesicular release (using the same allosteric model) triggered by small (~1 μM) and slow (~2 s) elevation of presynaptic [Ca²⁺] from [Ca²⁺]_rest = 50 nM (Supplementary Fig. 5).

Discussion

We have shown that presynaptic P/Q-, N-, and R-type VGCCs directly trigger approximately half of spontaneous miniature glutamate release events at small hippocampal synapses. The finding that the relative sensitivity of VGCC-dependent mEPSCs to EGTA and BAPTA was similar to that of action potential-evoked neurotransmitter release argues that both forms of exocytosis are triggered by similar Ca²⁺-nano/microdomains resulting from VGCC opening, which in turn are sensed by the same low-affinity Ca²⁺ sensor synaptotagmin-1 (ref. ⁴). The results of experimentally constrained modeling of Ca²⁺ influx-exocytosis coupling are consistent with this hypothesis, and show that spontaneous VGCCs openings can fully account for the experimentally observed VGCC-dependent minis, although single channel openings trigger release with low probability. Taken together, our results argue that stochastic VGCC opening can engage the same signaling cascade that underlies fast evoked neurotransmitter release, and thus challenge the view that action potential-evoked and action potential-independent release of glutamate are mediated by non-overlapping sources of Ca²⁺.

We have also identified an unexpectedly large role for R-type VGCCs in miniature release. This finding suggests a potential mechanism for differential regulation of evoked and spontaneous exocytosis at the level of individual presynaptic boutons. Indeed, the complement of presynaptic VGCCs varies substantially among small glutamatergic boutons both in cultures and the brain^{10, 13-15}. Synapses with higher proportions of R-type channels are therefore expected to have significantly higher rates of spontaneous miniature release relative to evoked release.

It has been proposed that spontaneous release of GABA is triggered by synchronized activation of multiple VGCCs of different types⁶. Indeed, similar to evoked release, which is normally triggered by several VGCCs, ω-Aga and ω-Ctx caused non-additive supralinear reductions of GABAergic minis in cultured neocortical neurons⁶. In contrast, we did not observe such non-additive effects of VGCC blockers: simultaneous application of specific VGCC blockers reduced mEPSCs frequency to the same extent as the sum of the effects of the individual blockers (Fig. 1e). Furthermore, assuming independent operation of individual VGCCs, our modeling predicts that the baseline probability of coincident opening of more than one channel in the active zone is low (Supplementary Fig. 4). Thus our results argue that VGCC-dependent glutamatergic minis are triggered by uncorrelated opening of individual VGCCs.

At a first sight this finding contradicts to the prevailing view that several VGCCs are required to trigger exocytosis at synapses with loose Ca²⁺-microdomain VGCC-Ca²⁺ sensor coupling, where neurotransmitter release is sensitive to the slow Ca²⁺ buffer EGTA in the millimolar concentration range^{5, 22, 28}. The detailed modeling of presynaptic Ca²⁺ dynamics and vesicular release performed here provides a plausible explanation for the apparent inconsistency. In line with previous modeling of the calyx of Held²⁸ our model revealed a large heterogeneity of vesicular fusion probabilities within the same active zone. This was mainly a consequence of variable distances between docked vesicles and VGCC clusters. Furthermore, our simulations showed that the number of VGCCs that control vesicular fusion (i.e. VGCC cooperativity, m_Ch ³⁷) varies several-fold depending on the position of an individual docked vesicle in the active zone. Release of ‘distal’ vesicles with low p_v (located >100 nm away from VGCC clusters) was controlled by overlapping Ca²⁺ domains from all VGCCs in the active zone that open during an action potential (~14). In contrast, in the other limiting case, release of ‘proximal’ vesicles with high p_v (located within ~30–40 nm of the nearest cluster) was mainly controlled by the 2–3 closest VGCCs. In a full agreement with this, our model demonstrated that 90% of all VGCC-dependent mEPSCs could be accounted for by stochastic opening of single VGCCs located within 25–70 nm of the docked vesicles.

It should be noted that although our results are consistent with non-uniform (Clustered) VGCC distribution in the active zone, the real distributions of different VGCCs subtypes and docked synaptic vesicles in active zones of central synapses remain largely unknown. Evidence exists for a direct interaction between presynaptic VGCCs and the release machinery^{44, 45}, implying that some channels are likely to be directly tethered to the vesicular release sites. This subpopulation of VGCCs should therefore have a disproportionately important role in triggering both evoked and spontaneous release.

Previous studies have reported that blockade of VGCCs with the non-selective inorganic channel blocker Cd²⁺ either failed to reduce the rate of spontaneous glutamate release (e.g. at cortical⁸ and hippocampal⁹ synapses), or even increased the mEPSC frequency (e.g. in the spinal cord⁴⁶). This apparent contradiction with the present evidence that VGCCs contribute to triggering miniature release can be explained by other presynaptic actions of Cd²⁺ than simple blockade of VGCCs. Indeed, there is accumulating evidence that Cd²⁺ applied extracellularly disrupts intracellular divalent cation homeostasis and leads to an elevation of intracellular Ca²⁺ and/or Cd²⁺ levels (e.g. refs. ^{17, 18} and Fig. 2f). An alternative possible explanation for previous evidence that Cd²⁺ fails to inhibit minis is that V_rest (the parameter that sets the rate of spontaneous VGCC opening) differed among studies. In our experimental conditions the average V_rest was approximately −72 mV (ranging from −55 to −80 mV), similar to previous estimates of V_rest in excitatory hippocampal neurons in acute brain preparations^47-49. This argues that estimates of VGCC-dependent miniature release rates in cultured hippocampal neurons can be extrapolated to small excitatory synapses in the brain.

Does VGCC-mediated miniature release have a physiological significance, or is it simply a consequence of the inevitable spontaneous openings of VGCCs that are arranged within the active zone to optimize evoked release? Because the opening probability of VGCCs depends steeply on the membrane potential, spontaneous exocytosis is likely to be modulated by subthreshold axonal voltage fluctuations, including those propagating passively from the cell body⁵⁰. Thus, VGCC-dependent minis potentially provide a mechanism for synaptic homeostasis^{1, 2} to be regulated by activity in the parent axon. This complements other forms of modulation of spontaneous exocytosis by neurotransmitters that act via presynaptic receptors and activate signaling cascades linked to intracellular Ca²⁺ stores (e.g. refs. ^{42, 43}). It is tempting to speculate that the co-existence of VGCC-dependent and VGCC-independent minis provides for two forms of homeostasis, one reflecting the degree of depolarization of the presynaptic neuron, and the other reflecting the synaptic microenvironment, allowing complementary processes to control the excitability and development of neuronal networks.

Online Methods

Cell cultures and solutions

Animal care and use protocols were approved by the UK Home Office. Hippocampal neurons were isolated from P0–P1 Sprague Dawley rat pups and cultured in Neurobasal A / B27-based medium on a rat astrocyte feeder layer. All experiments were conducted in a custom-made open field-stimulation chamber (0.35 ml) at ambient temperature (23°C–25°C) 14–19 days after plating. The standard extracellular solution contained (in mM) 125 NaCl, 2.5 KCl, 2 MgCl₂, 2 CaCl₂, 30 glucose, 25 HEPES (pH 7.4). Drugs were directly added to the recirculating perfusion system (total volume 10 ml) to achieve the following final concentrations: 0.25 μM ω-Aga (Bachem, Germany), 5 μM ω-Ctx, 0.5 μM SNX 482 (Abcam, UK), 1.0 μM TTA-P2⁵¹ (Merck, USA), 100 μM CdCl₂ (Sigma), 20 μM EGTA-AM and 20 μM BAPTA-AM (Invitrogen, USA). The time required for complete equilibration of the added drugs throughout the perfusion system (~3–4 min) was determined using the soluble fluorescence tracer Alexa Fluor 568 (Alexa 568, Invitrogen, USA).

Electrophysiology

Somatic whole-cell voltage-clamp recordings of spontaneous mEPSCs were performed in extracellular solution supplemented with 1 μM tetrodotoxin, 50 μM AP5, 50 μM picrotoxin and 5 μM CGP52432, using 3-6 MΩ pipettes filled either with a K gluconate based intracellular solution containing (in mM): 130 K gluconate, 10 KCl, 1 EGTA, 4 Mg-ATP; 0.5 Na₂GTP, 10 phosphocreatine, 10 HEPES (pH 7.36), or with a CsCl based solution containing (in mM): 120 CsCl, 8 NaCl, 2 EGTA, 2 Mg-ATP, 0.3 Na-GTP, 5 QX314-Br, 10 phosphocreatine, 10 HEPES (pH 7.36). In some experiments 10 μM cyclothiazide was added to the extracellular solution to facilitate detection of mEPSCs. Recordings were obtained using a MultiClamp 700B amplifier (Molecular Devices, USA), filtered at 4 kHz, digitized at 10 kHz. Data acquisition and off-line analysis were performed using either Strathclyde Electrophysiology Windows Electrophysiology Disk Recorder (WinEDR v3.0.1, Dr. John Dempster, University of Strathclyde, Glasgow, UK) or LabView 8.0 (National Instruments, Austin, TX, USA). For mEPSC recordings neurons were held at −70 mV and the series resistance was monitored throughout the experiment using a −5 mV step command. All mEPSC recordings were performed between 10 min and 45 min after establishing the whole-cell configuration to allow for stable recording conditions. Cells showing a > 25% change in series resistance, or an unstable holding current, were rejected. The acute effects of organic VGCC blockers were determined by comparing mEPSC frequencies averaged over 5–10 min of continuous recording, immediately before and 10 min after toxin application. Individual mEPSCs were detected using a peak detection algorithm of MiniAnalysis 6.0 software (Synaptosoft Inc., Decatur, GA, USA), which measured the peak amplitude, and rise and decay times. Automated search parameters were selected based on the typical mEPSC kinetics. Amplitude threshold values were set at three times the root mean square of the baseline noise amplitude. All undetected events and false positives were corrected by visual inspection. V_rest was measured in the whole-cell current clamp mode (immediately after of breaking in, <1 min) with either K gluconate-based intracellular solution (used to record mEPSCs) or KMeSO₃-based intracellular solution (used for Fluo-4 and Alexa 568 loading in imaging experiments, see below) and corrected for the liquid junction potentials (−15.5 mV for K gluconate and −10.2 mV for KMeSO₃) calculated using Clampex software (Molecular Devices).

Estimation of the specific effects of BAPTA-AM and EGTA-AM on VGCC-dependent component of mEPSCs

The specific effects of BAPTA-AM and EGTA-AM treatment on VGCC-dependent minis (Fig. 4e) were estimated as follows. Let us denote: f_total, average overall mEPSCs frequency in control conditions; f_VGCC, average frequency of VGCC-dependent mEPSCs in control conditions; $f_{\text{total}}^{\mathit{BAPTA}-\mathit{AM}}$ and $f_{\text{total}}^{\mathit{EGTA}-\mathit{AM}}$, average mEPSCs frequencies after BAPTA-AM or EGTA-AM pre-incubation; $f_{\mathit{VGCC}}^{\mathit{BAPTA}-\mathit{AM}}$ and $f_{\mathit{VGCC}}^{\mathit{EGTA}-\mathit{AM}}$, average frequencies of VGCC-dependent mEPSCs after EGTA-AM or BAPTA-AM pre-incubation.

Then the proportions of VGCC-dependent mEPSCs remaining after BAPTA-AM or EGTAAM loading were calculated as $f_{\mathit{VGCC}}^{\mathit{BAPTA}-\mathit{AM}}∕f_{\mathit{VGCC}}=(f_{\mathit{VGCC}}^{\mathit{BAPTA}-\mathit{AM}}∕f_{\text{total}}^{\mathit{BAPTA}-\mathit{AM}})\cdot (f_{\text{total}}^{\mathit{BAPTA}-\mathit{AM}}∕f_{\text{total}})\cdot (f_{\text{total}}∕f_{\mathit{VGCC}})$ and $f_{\mathit{VGCC}}^{\mathit{EGTA}-\mathit{AM}}∕f_{\mathit{VGCC}}=(f_{\mathit{VGCC}}^{\mathit{EGTA}-\mathit{AM}}∕f_{\text{total}}^{\mathit{EGTA}-\mathit{AM}})\cdot (f_{\text{total}}^{\mathit{EGTA}-\mathit{AM}}∕f_{\text{total}})\cdot (f_{\text{total}}∕f_{\mathit{VGCC}})$, using the experimentally determined values for the ratios $(f_{\mathit{VGCC}}^{\mathit{BAPTA}-\mathit{AM}}∕f_{\text{total}}^{\mathit{BAPTA}-\mathit{AM}})$, $(f_{\mathit{VGCC}}^{\mathit{EGTA}-\mathit{AM}}∕f_{\text{total}}^{\mathit{EGTA}-\mathit{AM}}),(f_{\text{total}}^{\mathit{BAPTA}-\mathit{AM}}∕f_{\text{total}}),(f_{\text{total}}∕f_{\mathit{VGCC}})$ outlined in Supplementary Table 1. The error bars (s.e.m.) were calculated using the standard formula for error propagation: $y\equiv y(x_1,x_2,\dots ,x_n),\Delta y=\sqrt{{\sum }_{i=1}^n{\left(\frac{\partial y}{\partial x_i}\right)}^2{\left(\Delta x_i\right)}^2}$.

Imaging of presynaptic Ca²⁺ dynamics

Fluorescence imaging experiments were performed on an inverted LSM 510 confocal microscope (Zeiss) using a 63x (1.4 NA) oil immersion objective as previously described²⁵. The high affinity calcium indicator Fluo-4 (Invitrogen, USA) was excited using the 488 nm line of an argon laser and its emission was recorded using a band-pass 505–550 nm filter. AlexaFluor 568 (Invitrogen, USA) was excited by a 543 nm He-Ne laser and its emission was recorded using a band-pass 560–615 nm filter.

To image presynaptic Ca²⁺ dynamics a neuron was loaded, via a whole-cell pipette, with 200 μM Fluo-4 and 200 μM AlexaFluor 568 in a solution containing (mM): 135 KMeSO₃, 10 HEPES, 10 Na-phosphocreatine, 4 MgCl₂, 4 Na₂ATP, 0.4 Na₂GTP. Five minutes after breaking in, the patch pipette was slowly withdrawn to minimize cytosol dialysis. Experiments were terminated if V_rest was above −55 mV, or if the gigaseal was lost during pipette withdrawal. The fluorophores were allowed to equilibrate throughout the neuron for at least 30 min after retracting the patch pipette, before Ca²⁺ fluorescence recordings were started. Action potentials were evoked by field stimulation via platinum bath electrodes separated by 1 cm (12.5–15 V, 1 ms pulses). To avoid recurrent activity, synaptic transmission was blocked in all imaging experiments by supplementing the extracellular solution with 25 μM NBQX, 50 μM AP5 and 50 μM picrotoxin.

Axons were identified using Alexa fluorescence by their thin shaft, tortuous trajectory, and occurrence of varicosities with diameter ~1 μm (Fig. 2a). Fluorescence transients in identified boutons were recorded in fast line-scan mode (~500 Hz, 5 trials averaged for analysis). The background fluorescence values in Fluo-4 (G_BG) and Alexa (R_BG) channels were determined in the image areas adjacent to the loaded axon and subtracted from the recorded fluorescence transients. At the beginning of each experiment the [Ca²⁺]_rest in individual boutons was estimated using the formula (1): [Ca²⁺]_rest = K_d · (G_rest/G_m – 1/γ)/(1 – G_rest/G_m) (ref. ⁵²), where K_d = 350 nM and γ = 100 are the Ca²⁺ dissociation constant and dynamic range of Fluo-4 respectively⁵², and G_m is the maximal fluorescence of Fluo-4 determined during a saturating 100 Hz action potential train, as previously described^{25, 52}. Experiments where the initial [Ca²⁺]_rest was higher than 100 nM were rejected. To minimize optical artifacts during application of VGCC blockers the Fluo-4 fluorescence was normalized to the average AlexaFluor 568 fluorescence determined in each sweep (G/R ratio). The effect of VGCC blockers was measured 10–20 min after application. Stability of the baseline (G_rest/R) and action potential-evoked Ca²⁺ responses (ΔG_AP/R) during this time course were confirmed in control experiments (Fig. 2e,f). The sensitivity of the method to estimate the changes in [Ca²⁺]_rest was principally limited by variability in basal Fluo-4 fluorescence during the time course of the experiment (Fig. 2f, G_rest/R, coefficient of variation in control conditions CV ~30%). Formula (1) then yields an upper limit for the error in the [Ca²⁺]_rest estimate ~20–40 nM.

FM dye imaging

FM dye imaging of vesicular release rates was performed as previously described²⁵. Because hippocampal cultures are dominated by glutamatergic neurons (~94%)⁵³ the FM-dye approach mainly reports vesicular release in glutamatergic synapses. The experimental paradigm is illustrated in Fig. 4a. Recycling vesicles were first labeled with 200 μM SRC1 by saturating high-frequency field stimulation (4 trains of 120 action potentials at 30 Hz delivered at 20 sec intervals) followed by dye washout for 15 min. SRC1 de-staining kinetics at rest and during low frequency stimulation (450 action potentials at 0.5 Hz) were imaged in a ~150 μm × 150 μm region of interest (ROI, 1024 × 1024 pixels) containing several hundred boutons. The background SRC1 fluorescence was determined by applying 3 rounds of high frequency stimulation used for loading. Images were analyzed using ImageJ (National Institutes of Health, Bethesda). Following the X-Y alignment of consecutive recorded SRC1 images, active boutons were identified by subtracting the five-frame background average from the five-frame average immediately after completion of SRC1 washout. SRC1 de-staining rates were measured in circular ROIs of 1.6 μm diameter centered at the fluorescence maxima of individual boutons. Boutons with overlapping ROIs were excluded from the analysis. The de-staining rates at rest (k_rest) and during 0.5 Hz stimulations (k_stim) were calculated by fitting monoexponential functions to the fluorescence time course in each selected ROI, after subtracting the background value. Boutons with low signal to noise ratio (goodness of the fit χ² > 0.025) were excluded from the analysis. To correct for spontaneous SRC1 vesicular release and for the non-specific loss of SRC1 fluorescence, the effective specific action potential-evoked release rate in each bouton was calculated as k_AP = k_stim – k_rest.

Modeling of VGCC gating

The stochastic behavior of VGCCs at rest and during action potentials was modeled in the NEURON simulation environment⁵⁴ using the six-state channel gating kinetics previously used to describe P/Q-, N-, and R-type VGCCs in hippocampal mossy fiber boutons at room temperature¹².

The model consisted of five closed and one open states:

$$C0\underset{{\beta }_1\left(V\right)}{\overset{{\alpha }_1\left(V\right)}{\rightleftarrows }}C1\underset{{\beta }_2\left(V\right)}{\overset{{\alpha }_2\left(V\right)}{\rightleftarrows }}C2\underset{{\beta }_3\left(V\right)}{\overset{{\alpha }_3\left(V\right)}{\rightleftarrows }}C3\underset{{\beta }_4\left(V\right)}{\overset{{\alpha }_4\left(V\right)}{\rightleftarrows }}C4\underset{\beta }{\overset{\alpha }{\rightleftarrows }}O$$

Voltage-dependent forward and backward rates were calculated as follows: α_i(V) = α_i,0exp(V/k_i), β_i(V) = β_i,0exp(V/k_i). The values for forward and backward rates at 0 mV, α_i,0 and β_i,0, and for the slope factors k_i were taken for each channel type from Table 2 in ref.¹². We assumed the same action potential waveform as in the previous modeling study in the Calyx of Held²⁸ but with action potential half-width of ~0.37 ms. This estimate (for recording temperature 23–25°C) was obtained by using the action potential half-width of ~0.2–0.25 ms recorded in the axons of CA3 pyramidal cells in slice hippocampal cultures at 32°C⁵⁵, and the Q₁₀ temperature coefficient for action potential duration ~1.8 (estimated from data in ref.⁵⁶). Ca²⁺ currents were calculated as i_Ca²⁺(V) = g(V – E_Ca²⁺), where E_Ca²⁺ = 55 mV is the reversal potential for Ca²⁺ and g = 2.7 pS is VGCC conductance at 2 mM extracellular [Ca²⁺]_ext ³⁸ (we assumed the same conductance for all three VGCC subtypes¹¹).

Non-stationary single compartment model of presynaptic Ca²⁺ dynamics

The total magnitude of action potential-evoked presynaptic Ca²⁺ influx was estimated using a non-stationary single compartment model, which was previously developed for quantification of fast action potential-evoked Ca²⁺ fluorescence transients(e.g. refs. ^{25, 57}). The model assumes spatial homogeneity of Ca²⁺ concentration in the nerve terminal, and the presynaptic Ca²⁺ dynamics governed by the Ca²⁺ entry and removal rates and binding-unbinding reactions with the endogenous and exogenous buffers as well as the fluorescent Ca²⁺ indicator. These considerations are reflected in the system of equations below, where the square brackets denote concentrations, and the superscript indices of the reaction rate constants denote endogenous Ca²⁺ buffers B_i or the indicator I.

$$\begin{array}{cc}\hfill & \frac{d\left[{\mathit{Ca}}^{2+}\right]}{\mathit{dt}}=j_{\mathit{Ca}}+k_{\mathit{off}}^I\left[\mathit{CaI}\right]-k_{\text{on}}^I\left[{\mathit{Ca}}^{2+}\right]\left[I\right]+\sum _i\left(k_{\text{off}}^{B_i}\right[{\mathit{CaB}}_i]-k_{\text{on}}^{B_i}[{\mathit{Ca}}^{2+}\left]\right[B_i\left]\right)-P_{\text{rem}}\hfill \\ \hfill & \frac{d\left[I\right]}{\mathit{dt}}=k_{\mathit{off}}^I\left[\mathit{CaI}\right]-k_{\text{on}}^I\left[{\mathit{Ca}}^{2+}\right]\left[I\right]\hfill \\ \hfill & \frac{d\left[B_i\right]}{\mathit{dt}}=k_{\mathit{off}}^{B_i}\left[{\mathit{CaB}}_i\right]-k_{\text{on}}^{B_i}\left[{\mathit{Ca}}^{2+}\right]\left[B_i\right]\hfill \end{array}$$

The action potential-dependent Ca²⁺ influx time course j_Ca was approximated by the Gaussian function $j_{\mathit{Ca}}=\frac{\Delta {\left[{\mathit{Ca}}^{2+}\right]}_{\text{total}}}{\sigma \sqrt{2\pi }}\exp \left(-\frac{{(t-t_{\mathit{AP}})}^2}{2{\sigma }^2}\right)$ where t_AP denotes the time of peak of action potential-evoked Ca²⁺ current, and Δ[Ca²⁺]_total denotes the total time integral of the volume averaged presynaptic Ca²⁺ entry. We assumed σ ~0.4 ms (Fig. 5b). The mass conservation rules for this system are: [I]_total = [I]+[CaI], [B_i]_total = [B_i]+[CaB_i], $\Delta {\left[{\mathit{Ca}}^{2+}\right]}_{\text{total}}=\Delta \left[{\mathit{Ca}}^{2+}\right]+\Delta \left[\mathit{CaI}\right]+{\sum }_i\Delta \left[{\mathit{CaB}}_i\right]$ Ca²⁺ removal was approximated by a first-order reaction P_rem = k_rem ([Ca²⁺]–[Ca²⁺]_rest)⁵⁷.

We assumed that a typical small hippocampal excitatory presynaptic bouton contains two types of mobile endogenous buffers (ATP^{5, 28, 58} and calbindin-D_28K ^{5, 59}) and a single immobile endogenous buffer (calmodulin⁵⁸, which is immobilized at rest due to its binging to neuromodulin⁶⁰). The complete set of model parameters and Ca²⁺ binding reactions is specified in Supplementary Table 2. To estimate Δ[Ca²⁺]_total in individual synaptic boutons the above model was numerically solved using the adaptive step-size Runge-Kutta algorithm, and the Fluo-4 fluorescence profile normalized to maximal fluorescence of the saturated indicator was calculated as $\frac{G\left(t\right)}{G_m}=\frac{\left[\mathit{CaI}\right]\left(t\right)\cdot \gamma +\left[I\right]\left(t\right)}{{\left[I\right]}_{\text{total}}\cdot \gamma }$, where γ ~100 is the dynamic range of Fluo-4. As was previously shown the model operated with only two adjustable (free) parameters Δ[Ca²⁺]_total and k_rem which have virtually independent effects on Ca²⁺ fluorescence signal⁵⁷. Thus both of these parameters were constrained by a straightforward fitting procedure that would match the calculated and experimental fluorescence profiles. The model predicts that the fast high affinity buffer calbindin-D_28K has only limited effects on the peak amplitude of action potential-evoked Ca²⁺ fluorescence (10%–20% reduction for 100–200 uM of total calbindin binding sites)²⁵, and that the low affinity buffers ATP and calmodulin have even smaller effects on the amplitude of Ca²⁺ fluorescence transients. Thus the error in determining of Δ[Ca²⁺]_total due to possible variations in concentration of endogenous Ca²⁺ buffers was limited to 20%.

Modeling of action potential-evoked and spontaneous glutamate release

Modeling of Ca²⁺ influx and buffered diffusion was performed in the VCell simulation environment (http://vcell.org) using the fully implicit finite volume regular grid solver and a 5 nm mesh. In line with electron microscopy data^{15, 32, 34} the synaptic bouton was considered as a truncated sphere of radius R_bout = 0.35 μm (described by the equation [x² + y² + z² < 0.35²]·[z < 0.25], all distances are in μm). Readily releasable vesicles and VGCCs were placed within an ellipse shaped active zone of area S_AZ = 0.04 μm² (described by the equation [(x/0.146)² + (y/0.089)² <1]) situated in the centre of the truncated plane z = 0.25 according to either the Clustered or Random distribution models (as described below). Readily releasable vesicles docked at the active zone were described by the equations (x – x_v)² + (y – y_v)² + (z – 0.228)² < R_v², where x_v and y_v denote x and y coordinates of the vesicle centre and R_v = 0.02 μm is the outer vesicle radius. Ca²⁺ vesicular release sensors were assumed to be evenly distributed around the vesicle periphery within a 5 nm thick z-slice directly above the active zone (i.e. 12 voxels for each vesicle highlighted in green in Fig. 6c). The concentrations and properties of endogenous and exogenous Ca²⁺ buffers used in VCell simulations are specified in Supplementary Table 2. Ca²⁺ removal was approximated by a first-order reaction at the bouton surface (excluding the active zone): $j_{\mathrm{rem}}=-k_{\mathrm{rem}}\cdot \frac{V_{\text{bout}}}{S_{\text{bout}}}\cdot \left(\right[{\mathit{Ca}}^{2+}]-{\left[{\mathit{Ca}}^{2+}\right]}_{\text{rest}})$, where k_rem ~3600 s⁻¹ was estimated by fitting experimental data with non-stationary single compartment model (described above), and the ratio of bouton volume to its surface area was $\frac{V_{\text{bout}}}{S_{\text{bout}}}$ = 0.104 μm. After performing several test simulations we restricted the computations to a dome described by the equation [x² + y² + (z – 0.35)² < 0.35²]·[z < 0.25] . This modification did not significantly affect Ca²⁺ dynamics calculated near the docked vesicles (less than 1% difference with the original model), but substantially increased the computation speed.

The spatial distributions of VGCCs and vesicles within the active zone used in VCell simulations were obtained from Monte Carlo simulations performed in MathCad 15.0 (Parametric Technology Corporation, USA). In the Clustered model we first randomly simulated positions of 2 ellipse shaped VGCC clusters (each 100 nm long and 50 nm wide) and then randomly distributed 32–33 VGCCs within these two clusters (i.e. VGCC density 4000 μm⁻² within the clusters and 800 μm⁻² in the whole active zone). We next randomly simulated position of 4 release-ready vesicles (vesicle centers were separated by a minimal distance of 45 nm to prevent them from overlapping). To account for the EGTA-sensitivity of action potential-evoked release the minimal distance between VGCC clusters and docked synaptic vesicles was set to 25 nm. For the Random model we fist simulated positions of 4 docked vesicles and then randomly distributed 32–33 VGCCs the whole active zone. Again, the minimal distance between VGCCs and docked synaptic vesicles was set to 25 nm. The subtype of each VGCC was randomly simulated according to the relative occurrence frequency: 20/43 (P/Q-type), 21/43 (N-type), and 2/43 (R-type) (Fig. 5f). Thus on average there were 15 P/Q-type, 16 N-type, and 1.5 R-type VGCCs in the active zone. Action potential-evoked Ca²⁺ currents through each of the VGCCs were simulated in NEURON simulation environment as described above.

Vesicular release rates were calculated using a previously published six-state allosteric model of Ca²⁺ activation of vesicle fusion in the calyx of Held (Fig. 6a)¹⁹. All the model parameters were as in the original calyx of Held model: k_on = 1 × 10⁸ M⁻¹ s⁻¹, k_off = 4,000 s⁻¹, b = 0.5, f = 31.3, and I₊ = 2 × 10⁻⁴ s⁻¹. At the beginning of each simulation we assumed that the relative occupancy of different model states corresponded to [Ca²⁺]_rest = 50 nM.

The model was solved using a variable-order stiff multistep method based on the numerical differentiation formulas (function ode15s in MATLAB, MathWorks USA) for action potential-evoked Ca²⁺ concentration profiles obtained in VCell simulations at each of the 12 voxels surrounding the vesicle (assumed positions for Ca²⁺ release sensors, green pixels Fig. 6c). The average occupancies for the different model states 〈V_i(t)〉 were calculated by averaging the obtained 12 solutions. Finally the time dependency of vesicular release probability was calculated as $p_v\left(t\right)=1-{\sum }_i\langle V_i\left(t\right)\rangle$ and the release rate as R_rel = dp_v(t)/dt. The three dimensional p_v(Δt,d) maps (Fig. 7c) were obtained by piecewise cubic Hermite polynomial interpolation (pchip function in MATLAB) of the p_v(Δt,d) array calculated on the grid corresponding to VGCC open times (ms) 0.03, 0.1, 0.33, 1.0, 2.0, and 3.0 and to VGCC-vesicle distances (nm) 20, 30, 40, 50, 60, 70, 80, 90, 100, 120, and 140.

Statistical analysis

All data are presented as mean ± s.e.m. The distribution of data in each set of experiments was first tested for normality using a Kolmogorov-Smirnov test. The similarity of variances between each group of data was tested using the F-test. For normally distributed data Student’s t-tests for single group mean, unpaired and paired comparisons were used as indicated. For the data that failed the normality test Wilcoxon singed rank tests for single group median, unpaired and paired comparisons were used. No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in previous publications in the field^{6-8, 25}. For normally distributed data, standard post hoc power calculations for t-test were performed using the experimentally determined standard deviations, to verify that the sample sizes were sufficient for detecting with 90% power 5–15% changes in the mean values at P < 0.05. Data collection and analysis were not performed blind to the conditions of the experiments. The effects of different VGCC blockers were tested in randomly interleaved experiments. All statistical tests were performed using SigmaPlot 11 (Systat Software, Inc.).