From histology to micro-CT: Measuring and modeling resorption cavities and their relation to bone competence

Abstract

The process of bone remodelling plays an essential role in the emergence and maintenance of bone geometry and its internal structure. Osteoclasts are one of the three main bone cell types that play a crucial role in the bone remodelling cycle. At the microstructural level, osteoclasts create bone deficits by eroding resorption cavities. Understanding how these cavities impair the mechanical quality of the bone is not only relevant in quantifying the impact of resorption cavities in healthy bone and normal aging, but maybe even more so in quantifying their role in metabolic bone diseases. Metabolic bone diseases and their treatment are both known to affect the bone remodelling cycle; hence, the bone mechanical competence can and will be affected. However, the current knowledge of the precise dimensions of these cavities and their effect on bone competence is rather limited. This is not surprising considering the difficulties in deriving three-dimensional (3D) properties from two-dimensional (2D) histological sections. The measurement difficulties are reflected in the evaluation of how resorption cavities affect bone competence. Although detailed 3D models are generally being used to quantify the mechanical impact of the cavities, the representation of the cavities themselves has basically been limited to simplified shapes and averaged cavity properties. Qualitatively, these models indicate that cavity size and location are important, and that the effect of cavities is larger than can be expected from simple bone loss. In summary, the dimensions of osteoclast resorption cavities were until recently estimated from 2D measures; hence, a careful interpretation of resorption cavity dimensions is necessary. More effort needs to go into correctly quantifying resorption cavities using modern 3D imaging techniques like micro-computed tomography (micro-CT) and synchrotron radiation CT. Osteoclast resorption cavities affect bone competence. The structure-function relationships have been analysed using computational models that, on one hand, provide rather detailed information on trabecular bone structure, but on the other incorporate rather crude assumptions on cavity dimensions. The use of high-resolution representations and parametric descriptions could be potential routes to improve the quantitative fidelity of these models.

Core tip: Osteoclasts create bone deficits by eroding resorption cavities. Understanding how these cavities impair the mechanical quality of the bone is relevant in both in healthy bone and in metabolic bone diseases. However, the current knowledge of their dimensions and effect on bone competence remains limited. Until recently cavity dimensions were estimated from two-dimensional measures (histology), hence, careful interpretation was necessary. With new imaging techniques quantifying resorption cavities in three-dimensional becomes feasible. Computational models have shown that resorption cavities affect bone competence. The use of high-resolution representations and parametric descriptions could improve the quantitative fidelity of these models.

INTRODUCTION

The process of bone remodelling plays an essential role in emergence and maintenance of bone geometry and its internal structure. This system has been extensively investigated from different angles, including its biology, chemistry and (bio) mechanical consequences. From a structural and mechanical point of view the most essential part of the process is the resorption and formation of bone performed by the basic multicellular units (BMU). This group of cells is responsible for bone loss and bone gain and determines the mechanical properties of the bone both in structure and material properties. In case of metabolic bone diseases, the functioning of these cells is altered. Structurally, and consequently mechanically, resorption cavities formed during resorption, determine the bone deficit. These cavities are an essential element in modelling and predicting the effect of bone disease and treatment. Despite this fact, the effort going into specifically quantifying these cavities and their effect on bone strength is relatively limited. Besides that, measuring methods are numerous and their results require careful interpretation when used for modelling purposes. This review aims at bundling the knowledge on these cavities and their biomechanical role. More specifically, its goal is: (1) to provide an overview of methods that can quantify the geometric properties of resorption; and (2) to apply this information to critically review biomechanical models that incorporate these geometric properties. Our premise is a mechanical point of view; hence, for the purpose of this review we will focus on direct impact of the presence of cavities on bone competence rather than investigating the dynamic parameters of the remodelling process. Our focus lies on bone remodelling in trabecular bone. Since trabecular bone has a much higher specific bone surface than cortical bone, it is more vulnerable to these surface-based processes[1,2].

RESEARCH

PubMed was searched in the first half of 2012 to identify relevant literature. The search terms used were “resorption cavities”, “Howship’s lacunae”, “resorption”, “erosion”, “remodelling” separately and in combination with “bone”, “trabecular bone” or “cancellous bone”. For the modelling section combinations with “remodelling”, “model” and “finite elements“ were also used. Subsequently numerous cross-references were followed through. This review does not claim to cover all publications related to the subject. Specifically in section 5 (Characteristics of resorption cavities) only a selection of publications was included, given the vast amount of studies analysing transiliac bone biopsies.

RESORPTION CAVITIES AND THE BONE REMODELLING CYCLE

Frost first introduced the concept of the BMU[3]. These units are a group of cells which, in a coordinated way, control the bone remodelling process. A team of osteoclasts perform the bone resorption. These irregularly shaped cells remove old bone and form the resorption cavities or Howship’s lacunae, which are later refilled by the osteoblasts. The osteoblasts perform the bone formation by excreting the building blocks of the bone matrix (unmineralised bone or osteoid) and have a role in the mineralisation of this soft bone[4,5]. Some osteoblasts get entombed in the bone matrix and differentiate to osteocytes. The cytoplasmic processes of these osteocytes extend trough a network of canaliculi. It is assumed that this network monitors the local strain environment and thus has a role in the signalling process of bone remodelling[2,5,6]. Other osteoblasts die or become bone lining cells. These cells digest unmineralised osteoid and might be involved in the localization and initiation of remodelling[5]. The result of BMU action, the packet of new bone, is called a bone structural unit (BSU)[7]. Bone structural units are the Haversian systems or osteons in cortical bone, and semi lunar structures separated by cement lines in trabecular bone[8]. The BMU exists and moves in three dimensions, excavating and refilling a tunnel through cortical bone or a trench across the surface of cancellous bone[9].

After resorption, an intermediary phase, called “reversal phase” as introduced by Baron[10], exists in which mononuclear cells occupy the lacunae and no resorption takes place[11]. It is in this phase that the cement line is formed.

Formation and resorption are coupled, both in space and in time. It has been observed that osteoclasts occupy the more superior parts of resorption lacunae, while mononuclear cells and preosteoblast-like cells are situated in the deeper parts. This supports the hypothesis that these cell types precede each other in the remodelling process[11]. It is likely that formation is preceded by resorption and they may even occur simultaneously in the same remodelling unit[4,6,12-15], yet interruptions in the process, both in formation and resorption, have been hypothesized[14]. It has been suggested that mononuclear cells are also active in the resorption process, by digesting the organic matrix constituents[11].

QUANTIFICATION OF RESORPTION CAVITIES

Almost all knowledge concerning resorption cavities is derived from transilliac bone biopsies. The main focus in this review is therefore on the measurement and interpretation of resorption cavity properties obtained from biopsies following the nomenclature conventions proposed by Parfitt et al[16]. Biomarker data is increasingly used to analyse bone remodelling. However despite the problems cited below, the transilliac bone biopsies remain the golden standard for measuring bone turnover[17].

Transillac bone biopsies

The three-dimensional (3D) characteristics of resorption cavities are generally extrapolated from two-dimensional (2D) features measured on histological sections using stereological formulas. However this extrapolation is not without flaws since it assumes unbiased and random sampling and isotropy, which are not fulfilled in bone[18]. 2D widths are transformed to 3D thicknesses by using the parallel plate model[19] and the distribution is corrected for missing measurements[20]. There are also intraobserver, interobserver, intermethod and sample variations that have to be taken into account[11,13,18,21].

During histomorphometric analysis different staining methods can be used which highlight certain features. Toluidine blue is used to identify cavities under polarized light by looking at the presence of cut off collagen fibers (disruption of the lamellar system) at the edge of the cavity[13,18,22]. The polarized light allows visualisation of the orientation of collagen lamellae along the mineralized bone surface. The identification of scalloped surfaces can however be subjective[23]. Tartrate-resistand acid phospahtase can be used to mark active osteoclasts and thus “active” cavities[24]. Von Kossa/van Gieson staining allows to discriminate osteoid from mineralized bone[18].

Besides the general problems with histomorphometry, cavity related measurements are also influenced by choosing which cavities to include. Measurement of cavities always presents a snap shot, where not only active sites are visible but also aborted sites, where resorption “prematurely” stopped, interrupted sites, where resorption is temporarily halted, and reversals sites[25]. Distinguishing between these sites is not straightforward and assuming cavities are first completely eroded before osteoblasts start refilling is also an oversimplification[25]. Some authors[11] perform the technically difficult task of identifying specific cell types (osteoclasts, mononuclear cells, pre-osteoblast-like cells) in the cavities to distinguish between different stages in resorption and thus identify “completed” cavities with the largest depth obtained in the cycle[22,18]. But the presence of these cells might be heterogeneous and might be dependent on the specific histological section[13]. Therefore, most cavities might not represent effective “active” resorption and cautious interpretation of resorption related parameters is necessary. Moreover, small erosions may be difficult to distinguish from minor surface irregularities and whether these erosions are seen depends on the magnification[25]. Specifically, cavities with depth below 3 µm are often omitted[14,26]. When all cavities are included, the resulting average size is smaller than the size of the completed ones, but including all cavities leads to valuable information concerning the distribution of cavities and the eroded surface at a certain time point. It has to be realized that the deep cavities that cause perforation cannot be identified or included in the measurements[13,18,23,27]. When investigating treatment effects it is useful to label surfaces using calcein in order to be sure that they were actively forming during the period of treatment[28].

The administration of two time-spaced doses of tetracycline prior to bone biopsy enables assessment of dynamic indices of bone formation[18]. However, resorption can’t be assessed dynamically (with the exception of biological markers), since removed bone is invisible; hence only indirect measurements are available. As a consequence it is not possible to tell from these static measures how much resorption is actually going on[4,13].

Quantification of erosion depth in transilliac bone biopsies

The depth of a cavity is generally indicated by erosion depth (E.De). Indirect measurements are more common, in which the depth is calculated from other parameters or assumed to be similar to formation parameters. Wall thickness (W.Th) is the most widely used (Figure 1). It is the distance between cement lines of “resting” cancellous surfaces without osteoid or lacunae, reflecting the amount of bone created during a remodelling event[4,5,11,13]. Eriksen[11] did not find a significant difference between the distribution of completed wall thickness and pre-osteoblast-like cell, or deepest, resorption depths in healthy subjects. Another measure is osteoid thickness[13]. A third measure is mean interstitial bone thickness, calculated from measurement of W.Th on both sides of a trabecula and the mean trabecular plate thickness, but this is not as reliable[13,29]. However, when the bone balance, calculated as the difference between W.Th and E.De[8], is not zero, these parameters do not correctly represent the resorption depth.

Figure 1.

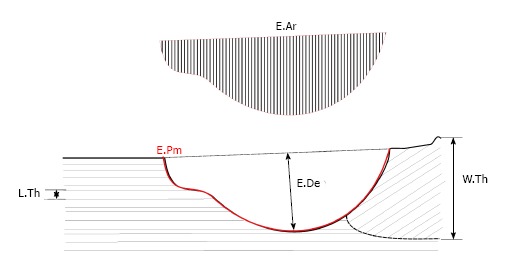
Schematic representation of different resorption cavity related measurements on 2D histological sections: Eroded area, erosion perimeter, wall thickness and lamellar thickness. E.Ar: Eroded area; E.Pm: Erosion perimeter; W.Th: Wall thickness; L.Th: Lamellar thickness.

Two direct methods have been developed to quantify the depth of a cavity (E.De) (Figure 1). Eriksen et al[11] introduced the method of lamellar counting. The average lamellar width is measured and the number of lamellae cut at the cavity edges is counted (Figure 1). The method relies heavily on accurate identification of cells to classify cavities: when this identification is not possible, cavities are excluded (about 24%)[13]. A disadvantage of this method is that it is impossible to count the lamellae correctly when different BSU with different orientations overlap. Besides that, the lamellar thickness inside an osteon can vary and not all lamellae are parallel to the surface which is an assumption in this method[30].

In the other direct method, the pre-resorption surface is reconstructed and used to measure cavity dimensions[31]. This method is generally computerized and applies an interactive curve fitting method to the cavity edge. All identifiable cavities are included regardless of their stage of completion[27]. Large differences between the results of both methods have been observed[13,32]. They are partly explained by the number of cavities included and the choice of maximum or mean depth: Eriksen method measures are systematically larger because the cavities are “completed” (with pre-osteoblast like cells), unidentified cavities were omitted and a constant lamellar width is assumed[27,32]. Cohen-Solal et al[32] used the Garrahan method on completed cavities only (covered with osteoid), but still found values significantly lower than Eriksen. Roux et al[30] developed a method similar to Garrahan’s, and performed a direct comparison with the lamellar counting method. A rather high correlation was found (R² = 0.76, P = 0.0001) but with significantly lower values for the computerized method. Due to line reconstruction problems, cavities at the end of a trabecula could not be measured, while a higher number of lacunae were omitted during lamellar counting due to poor visibility of eroded lamellae. Again, the lacunae included seemed to determine the E.De outcome.

The measurement difficulties including the large variability and lack of consensus on the measurement technique have led to the publication of a recommendation not to directly evaluate resorption cavity depth in transiliac biopsies[33]. However, E.De has a large mechanical impact (see below) and thus remains an important parameter in the assessment of the impact of resorption cavities on bone competence.

Quantification of erosion surface and volume in transilliac bone biopsies

The shape of a cavity can very; hence cavity width and area can differ even for constant E.De[28]. Consequently, taking parameters into account that go beyond erosion depth can be important when investigating the effect of disease and treatment on bone resorption. On histological sections, the total eroded perimeter (E.Pm) is the basic measure for the extend of cavities (Figure 1). The widely used erosion surface (ES/BS) is calculated using this E.Pm. Just like all cavity measurement on biopsies, ES/BS is a snapshot of resorption and not a dynamic parameter[33]. ES/BS is also a relative measure: adding a resorption cavity to the surface not only increases the eroded surface (ES) but also increases the total bone surface (BS) in the histological section, since the crenate surface of a cavity is larger than undamaged surface before resorption (Figure 1). Similar to E.De, some authors[11] further specify this surface depending on the cells and activity present in the lacunae. Osteoclast surface, Oc.S/BS, is often interpreted as “active” erosion surface in contrast to reversal surface. The relative amount of both types is case-dependent and interpretation of ES/BS can therefore be misleading, i.e., an increased ES/BS can be caused by an increased reversal phase and not necessarily by increased osteoclast activity[33]. Other formation parameters like osteoid surface (OS/BS) and osteoblast surface (Ob.S/BS) might be good indicators for related resorption parameters in healthy subjects with a stable bone balance. In general OS/BS seems to be larger than ES/BS. Several possible explanations exist: formation is slower, formation is initiated before the completion of resorption and/or the presence of arrested resorption cavities[34].

The erosion volume or remodelling space, calculated from eroded area (Figure 1), is rarely determined on biopsies although it is highly correlated to bone resorption rate as indicated by urinary excretion of total deoxypyridioline[30]. Some authors measure the E.Pm for each individual cavity (cavity length or eroded length) as an indication for shape changes of individual cavities[31,35].

Quantification of number of cavities in transilliac bone biopsies

The number of cavities per bone surface (Nc/BS) is rarely measured, although it is a simple measure. Activation frequency (Ac.f) is more widely used. In theory, Ac.f is the number of new remodelling units activated anywhere on the surface in a given time and thus a good measure for the number of cavities present at a certain time. In practice the Ac.f is calculated as the inverse of the total period (remodelling period + quiescent period). This doesn’t correspond exactly with the conceptual definition[13] and doesn’t take into account the 3D organisation of a BMU and the distance it travels[9]. Being a highly derived variable the issues in calculation, assumptions and interpretation are numerous[33] and interpretation is often complicated. Ac.f is thus especially interesting in a qualitative sense as to compare whether, in a certain situation, new cavities are introduced. Since cavities exist in different stages of resorption and cavities with interrupted resorption exist, the quantitative values cannot be readily used to assess the total numbers of cavities present at a certain time point.

New imaging techniques

The use of 2D histomorphometry has limitations. Neither can it discriminate an increase in the number of remodelling events from an increase in the size of each individual event[9] nor can the full volumetric extend of a cavity be measured[36]. The development of 3D methods to asses BMU’s are essential to advance our ability to study how alterations in its morphology occur with disease and treatment[28]. Scanning Electron Microscope (SEM) images give a good indication of the 3D nature of resorption cavities as can be seen in Figure 2A and B[37]. But currently, no clinical imaging devices are able to detect resorption cavities because of their small size compared to image resolution. It has been shown that high-resolution images (at least 1.4 µm or better) are required to consistently identify and measure individual resorption cavities[38].

Figure 2.

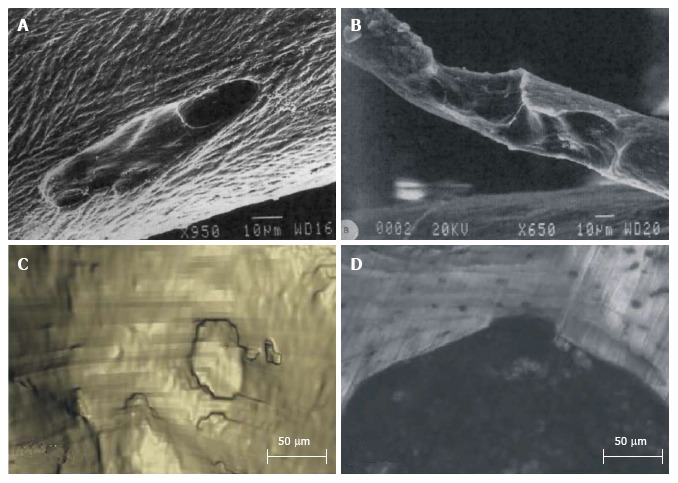
Three-dimensional visualizations of resorption cavities. Using scanning electron microscope (A, B) reprinted from ^[37] and serial milling (C: Three-dimensional reconstruction; D: Corresponding cross section image) reprinted from ^[38].

Recent developments in imaging techniques show great potential to quantify cavities in 3D and detect them automatically. Specifically, individual resorption cavities were measured in 3D on animal vertebrae using serial milling[38] (Figure 2C and D). This technique was able to reveal that cavity size and location are related to the local trabecular microarchitecture. Goff et al[39] found that, on the human vertebral trabecular bone samples they investigated, half of the cavities were located on the intersections of trabeculae and most others were on plate like-trabeculae oriented in the main loading direction (cranial-caudal). Next to that confocal laser microscopy and vertical scanning profilometry have recently been used to measure bone resorbing activity, extending in vitro measurements from ES/BS under microscope to full 3D measurements of volume and depth[40,41].

Synchrotron-radiation based computer tomography (SR-CT) and high-resolution micro computer tomography (µCT) are technically able to obtain the necessary detail, but might not be able to capture enough cavities per specimen to characterize a population. The most promising development probably lies in high-resolution in-vivo µCT. Schulte et al[42] recently presented a new time-lapsed imaging method which allows quantification of dynamic resorption parameters at a resolution of 10.5 µm. They were able to effectively measure 3D ES and BS by comparing subsequent 3D reconstructions of the same bone separated by 4 wk. The non-invasive nature of this technology allows longer periods of investigation and might enable researchers to reveal time-dependent evolutions in resorption; yet improvements in image resolution are needed to be able to dynamically track individual resorption cavities.

CHARACTERISTICS OF RESORPTION CAVITIES

The following section will provide a limited overview of measured cavity properties in health and specific disease. It does not cover the full range of studies analysing transiliac bone biopsies, but aims at providing a general indication of resorption cavity properties found in literature and showing the wide range of values that have been reported. This is relevant in relation to biomechanical modelling since, as discussed in section 6, several biomechanical models neither incorporate the most relevant nor most accurate properties. Based on measurement issues described before, we will focus on E.De and W.Th as measures for cavity depth. For the extend of cavities we will provide data on ES.BS and when available on EV/BV. All reported data in this section are related to transiliac bone biopsies, except when indicated differently.

Healthy bone

Cavities are often elongated, have varying depths and can lie close together. Sizes varied from 50 µm × 20 µm to 1000 µm × 1000 µm, most were 200 µm × 500 µm in size[37]. In a single cavity about 0.05 mm³ of bone tissue is removed[5]. The frequency distribution of cavity sizes in a trabecular bone sample is skewed: there are few very deep cavities and a large amount of shallow ones[13]. This is the case for all measurement methods, although, as explained above, the method and choice of included cavities does make a difference[8,11,14,43].

It seems reasonable to accept that there is no difference in the biology of the bone remodelling process at different skeletal sites. Hence, if there would be a link between microdamage and resorption activity, this would impact local erosion measurements, since some bones are more heavily and frequently strained leading to more microdamage[2]. Since the local loading environment is site-dependent and leading to differences in local trabecular microstructure, it is expected that different erosion patterns occur as well. Indeed, bone structure and turnover appeared different between the distal radius and the iliac crest. Specifically, W.Th, ES/BS and Ac.f were significantly lower in the distal radius[44]. Given the fact that most cavity-related studies are based on bone biopsies from the iliac crest, these results should be critically reviewed before extrapolating the results to other skeletal sites.

There is little information regarding the location of the cavities on the trabecular surface itself. Analysis of trabecular thinning and connectedness of trabecular bone revealed that the site of activation of new BMU’s may be preferentially located were trabeculae are either thinner or thicker, such as trabecular intersections[27,45,46]. This would be consistent with the microdamage-theory since these locations are highly strained. Most remodelling is likely targeted at replacing fatigue-microdamaged bone or at removing hyper mineralized bone[9].

Age-related changes in resorption cavity properties have been observed (Table 1). For children, growth to peak bone mass is realised by high formation, with Ac.f and W.Th decreasing with age, while bone resorption parameters (ES/BS) don’t vary significantly[23]. In adults, there is continued reduction in bone formation taking place with age as shown by a reduced W.Th[8,29,47,48], while resorption continues with an unchanged or even increased amount of resorbed surface[24,27,43,49]. No or only a small decrease in E.De has been reported[22,24,27]. A small decrease in (average) E.De would be a logical consequence of reduced W.Th because more shallow cavities, which were incompletely refilled, remain on the bone surface. But it also possible that resorption has increased and has caused deep perforation cavities, which are not measured: their absence in the cavity depth distribution would also shift the average depth to lower values.

Table 1.

Normal values for specific eroded surface, erosion depthand wall thickness as reported in literature for healthy patients

Sex	Parameter	Change with age	Mean age	Values
F	ES/BS (%)	↓2↑	10-30	2.15 (0.36)[43] 3.23 (2.6-4.02)[22]
			30-60	3.43 (2.68-4.4)[22] 1.85 (0.82-4.21)[27] 1.78“[43]
			60-90 (post-meno)	4.59 (3.72-5.66)[22] 4.2 (1.7)[24] 7.11 (2.9-16.9)[56] 4.0 (2.0)[57] 1.66 (0.66)[43]
			All ages	6.2 (2.9)[21]
	E.De (μm)	2↓	10-30	56.8 (50.2-63.4)[22]
			30-60	63.4 (57.5-69.3)[22] 33.7 (24.4-46.6)[27]
			60-90 (post-meno)	50.8 (46.9-54.7)[22] 27.21 (2.27)[24] 49.11 (38.3-61.7)[56] 49.4 (12.1)[32]
	W.Th (μm)	↓	10-30	62.0 (8)[29]
			30-60	49.0 (9.1)[48] 37.2 (3.8)[51] 38.1 (28.6-68.8)[53] 56.2 (7.1)[50] 50.4 (7.4)[29]
			60-90 (post-meno)	48.81 [37.8-62.2][56] 33.9 (4.7)[51] 32.2 (23.2-39.3)[53] 39.5 (2.0)[32] 32.1 (4.13)[57] 44.3 (4.9)[50] 40.2 (4.6)[29]
			All ages	31-43.9[13] 49.0 (2.5)[21]
M and F	ES/BS(%)	↓2	10-30	16.3 (11.6-18.1)[102] 16.6 (5.6)[23]
			30-60	4.03 (1.42)[11]
			All ages	1.35 (0.39)[31] 1.94 (0.76-4.93)[103]
	E.De (μm)	2↓	30-60	62.6[11]
			All ages	28.9 (23.4-39.3)[31] 34.2 (22.8-51.3)[103]
	W.Th (μm)	↓	10-30	44.2 (5.7)[102] 41.4 (5.7)[23]
			30-60	61.9 (6.8)[11]
			60-90	59.4[13]
			All ages	51.6 (35.8-74.4)[103]
M	ES/BS(%)	↓2↑	10-30	3.32 (2.34-4.7)[22] 6.3 (0.6)[49] 2.84 (1.27)[43]
			30-60	3.55 (2.55-4.95)[22] 3.7 (0.9)[24] 1.81 (0.72-4.56)[27] 6.62[51] 1.722[43]
			60-90	3.99 (3.11-5.13)[22] 3.7 (0.6)[24] 6.4+[49] 1.91 (0.42)[43]
	E.De (μm)	2↓	10-30	66.1 (57.1-75.1)[22]
			30-60	64.1 (48.0-60.2)[22] 33.0 (3.16)[24] 35.6 (23.2-54.7)[27]
			60-90	46.3 (44.3-48.3)[22] 28.94 (1.78)[24]
	W.Th (μm)	↓	10-30	62.0 (8.1)[29] 32.8 (2.6)[49]
			30-60	50.2 (8.7)[48] 53 (8.6)[50] 49.2 (4.6)[29] 35.02[49]
			60-90	48.5 (8.6)[50] 43.8 (2.8)[29] 32.82[49]
			All ages	40.6[13]

¹Median;

²Indicates recalculation to age groups. Data ordered by sex [Female (F), Female and male (FM), Male (M)] and age groups (10-30 year, 30-60 year, 60-90 year or all ages mixed). Values presented as mean ± SD, mean [95% confidence interval (CI)], mean [10^th-90^th percentile], mean [Q 1^st -3^rd quartile], Also indicated is whether the parameters increase (↑), decrease (↓) with age or stay constant (b). ES/BS: Eroded surface; E.De: Erosion depth; W.Th: Wall thickness.

Neither sex nor ethnic differences seem to exist when it comes to resorption parameters like E.De, W.Th and ES/BS, at least before menopause[14,24,27,43,48,50,51]. But with menopause, there are significant differences between the sexes. In menopause, the age-related reduction in W.Th is accelerated and more BMU’s are born (increased Ac.f), while resorption itself is hardly affected. As a consequence bone turnover is accelerated and females are subjected to an accelerated trabecular bone loss[5,6,15,51-53]. Three to five years after menopause, the W.Th seems to recover to the premenopausal values and a more or less steady state emerges, in which the remodelling rate is still higher than premenopausal due to a higher Ac.f, but lower than during menopause[6,53]. In men, this “temporarily”acceleration does not happen and the “normal” decrease in W.Th with age accompanied by with unchanged resorption, continues[51,54,55].

Effect of osteoporosis

Metabolic bone diseases alter the bone remodelling cycle and can thus change the resorption cavity properties (Table 2). As we demonstrate below for osteoporosis, the limitations of the measurement methods hinder clear interpretation of the results.

Table 2.

Change of eroded surface, erosion depth and wall thickness in common bone diseases (postmenopausal osteoporosis, male idiopathic osteoporosis, glucocorticoid induced osteoporosis) as reported in literature

Disease	Parameter	Change	Values1 1Significantly lower than control 2Significantly higher than control
PmOP	W.Th (μm)	↓	40.74a (31.6-54.3)1[56] 36.2 (6.4)1[21] 28.3 (20.1-34.8)1[53] 35.3 (2.0)1[32] 28.0 (4.44)1[57] 29.3 (1.4)[73] 31.2 (0.4)-32.1 (0.5)[64] 41.8 (4.25)-49.0 (8.93)[67]
	ES/BS (%)	b↓	5.3a (1.7-18.1)[56] 6.0 (3.0)[21] 4.8 (2.7)[57] 1.67 (0.48)[73] 4.9 (2.9)[71] 1.89 (0.12)-3.41 (0.5)[64] 4.49 (1.6) - 6.55 (1.62)[65] 2.18 (1.24)[61] 2.42 (Q 1.31-2.93)[72] 4.7 (Q 3.3-5.7)-5.2 (Q 3.2-6.9)[67]
	E.De (μm)	b	55a (37.3-82)[56] 48.5 (43.8-53.2)[8] 50.0 (13.4)[32] 22 (5)[71] 13.5 (0.43)-15.8 (0.91)[64]
	EV/BV (%)		0.46 (0.04)-1.21 (0.29)[64]
MIOP	ES/BS (%)	↑	9.7 (1.7)[55] 7.5 (1.3-17.7)[58]
	E.De (μm)	b	44.7 (9.3)[58]
	W.Th (μm)	b↓	35.3 (7.5)1[58]
GC induced OP	EV/BV (%)		0.44 (0.1)[60]
	ES/BS (%)	b↑	2.3 (0.4)[60] 4.06 (2.45)[61]
	E.De (μm)	↑	15.0 (1.3)[60]
	W.Th (μm)	↓	30.6 (0.8)[60]

Significant difference vs control indicated (¹Significantly lower than control;

²Significantly higher than control);

^aMedian; Values presented as mean ± SD, mean (95%CI), mean [10^th-90^th percentile], mean [Q 1^st-3^rd quartile];

^bAlso indicated in table is whether the parameters increase (↑), decrease (↓) due to the disease or stay constant. When more then one value is reported for the same reference, it concerns measurements at different time points. ES/BS: Eroded surface; E.De: Erosion depth; W.Th: Wall thickness; PmOP: Postmenopausal osteoporosis.

As indicated earlier, the menopause causes, even in normal subjects, an increase in Ac.f and a negative bone balance. In post-menopausal osteoporosis (PmOP) these effects on Ac.f and W.Th are even stronger, with extreme loss in bone mass as a consequence[17,32,56,57]. Again, given the likely increased presence of underfilled cavities associated with a reduced W.Th, one would expect a reduced average E.De, but an increased ES/BS. In contrast to normal post-menopausal women, a small but not significant increase in resorption depth has been observed[15,17,32,56,57]. Furthermore, ES/BS is reduced or unchanged[56,57]. Given this difference from normal age-related changes, we hypothesize that individual cavity depth might actually have increased in PmOP, but that this increase is not detected with the averaged values for E.De reported in literature. The presence of underfilled cavities and absence of perforating cavities in the measurement, shift this average to lower values, masking the real increase. The increased cavity depth might cause more perforations on already thinner trabeculae and, again, because these perforating cavities are not included in the ES/BS measurement, the real ES is underestimated. Idiopathic (primary) male osteoporosis leads to similar effects but while some studies find similar results as for PmOP[54,58], others found unchanged W.Th and increased resorption parameters (ES/BS)[47].

Prolonged corticoid treatment leads to secondary OP. The main effect is osteoblastic dysfunction, with significantly reduced W.Th as a consequence. Next to that, the lifespan of osteoclasts seems to be increased and changes in cavity surface shape have been observed[59]. The change in cavity surface shape might have a different mechanical impact, especially in combination with an increased E.De and ES/BS, as indicated in most studies[5,60-63].

Effect of anti-osteoporotic medication

Treatment for OP interferes with the bone remodelling cycle, hence, may affect osteoclast resorption cavities. This section presents an overview of the effect of some of the major anti-osteoporotic medication for which resorption cavity properties were reported and compared to untreated PmOP patients (Table 3).

Table 3.

Change of eroded surface, erosion depth and wall thickness with treatment for postmenopausal osteoporosis as reported in literature

Treatment for PmOP	Parameter	Change	Values1 1Significantly lower then no treatment 2Significantly higher then no treatment
Bisphosphonates (oral/IV ibandronate, alendronate, risendronate)	EV/BV (%)	b	0.40 (0.1)-0.50 (0.1)[60]
	ES/BS (%)	b	2.2 (0.4)-2.6 (0.5)[60]
			5.3 (2.75)[67]
			1.29 (90%CI: 1.04-1.95)-1.62 (90%CI: 1.32-1.88)[66]
	E.De (μm)	b	13.4 (1.0)-16.2 (1.0)[60]
			45.6 (9.45)[67]
	W.Th (μm)	b	30.0 (1.0)-31.4 (1.0)[60]
			41.6 (4.86)[67]
Strontium ranelate	ES/BS (%)	b	2.92 (1.48-3.89)[52]
Strontium ranelate 6 m	ES/BS (%)	↓	1.21 (0.21)1[74]
hPTH (1-34)	ES/BS (%)	↑	0.78 (0.11)[74]
(teriparatide)			10.1 (4.9)2-11.8 (7.1)2[71]
			3.51 (Q 2.67-5.64)-4.0 (Q 2.8-6.0)[72]
	W.Th (μm)	b	22 (5)-28 (7)[71]
PTH (1-84)	ES/BS (%)	↑b	1.75 (0.35)[73]
	W.Th (μm)	b	33.1 (1.4)[73]

Significant difference vs control (no treatment) indicated (¹Significantly lower than control;

²Significantly higher than control). Values as mean ± SD, mean (95%CI), mean [10^th-90^th percentile], mean[Q 1^st-3^rd quartile];

^bAlso indicated in table is whether the parameters increase (↑), decrease (↓) due to the treatment or stay constant. When more than one value is reported for the same reference, it concerns measurements at different time points or different doses. ES/BS: Eroded surface; E.De: Erosion depth; W.Th: Wall thickness; PmOP: Postmenopausal osteoporosis.

Bisphosphonates (BP) reduce bone resorption by reducing the Ac.f: the number of new BMU’s that initiate and thus the remodelling space decreases[28,52,60,64-66]. The W.Th is reduced as well but no evidence of changes in ES/BS was found[52,60,64,66,67]. It is debated whether osteoclasts are only prevented from starting new BMU’s or that the amount of bone resorbed by a BMU is reduced as well; also the number and size of the resorption cavities might be reduced[28,68,69]. The impact on resorption cavity properties would be similar: either only underfilled and thus shallow cavities remain or only new shallow cavities are resorbed. Indeed, superficial cavities have been observed next to giant hypernucleated osteoclasts[70]. BPs thus prevent a significant increase in erosion depth and prevent further progression of the resorption pits[67].

The trends observed for resorption parameters in other treatments are less clear and few studies found conflicting results. In contrast to BPs, both parathyroid hormone (PTH 1-84) and the cyclic hPTH(1-34) (Teriparatide), caused an increase in ES/BS, next to an increased Ac.f and W.Th, although it was not always significant[71-73]. A larger surface is thus occupied by cavities, but the increased W.Th may keep them superficial. For patients treated with strontium Ranelate, a dual action bone agent, some studies found no significant differences in Ac.f or ES/BS while others found a significantly reduced ES/BS[52,74].

In a recent three-dimensional dynamic bone histomorphometric study, Matheny et al[75] showed reductions in resorption cavity size (depth, width and volume) with antiresorptive agents (Raloxifene and Risondrenate) while the ES/BS was unchanged.

BIOMECHANICAL CONSEQUENCES OF RESORPTION CAVITIES

Resorption by osteoclasts, as part of the bone remodelling cycle, causes cavities on the bone surface, since the cells reach their location through the bone marrow. During resorption and the following reversal phase, these cavities form structural defects, that weaken the bone[6]. With a normal bone balance, this mechanical effect is quasi-constant, since an equal amount of cavities is refilled simultaneously. If this balance is disrupted, the changes cause a structural and thus mechanical effect[4,12].

Three main possible mechanisms have been identified by which bone turnover in general can influence bone biomechanics[36]. These mechanisms are related to bone mass, yet they have effects that go beyond their direct impact on the bone volume and thus go beyond “standard”density-strength power relationships[76,77]. First, there is the effect of modifications in tissue degree of mineralisation, which is not directly related to resorption. Second, the fenestration or disconnection of individual trabeculae that modify the trabecular architecture is a direct result of resorption[76,78-80]. And third, the resorption cavities also act as stress risers. Experimental evaluation of these effects is difficult, forcing researchers to rely on modelling. In the next paragraph we focus on different modelling approaches and their findings.

Modelling resorption cavities in finite element analyses

Numerous authors have tried to model the bone remodelling sequence, but few have directly incorporated the 3D microstructural properties of resorption. There have mainly been attempts using analytical models to predict local changes of bone properties like the bone density, based on BMU properties like birth-rate, formation, resorption and mineralisation rates[81,82]. These models don’t incorporate the real resorption cavity properties and are thus not further described in this review.

Simplified structural models can give insight in some of the basic mechanism of the effect of cavities on bone mechanical properties. Mechanical analyses of the effect of a cavity on a straight beam shows that the number and size of remodelling cavities may influence the mechanical behaviour of a trabecula independent of bone volume or total amount of bone turnover[36].

Using a mechano-regulation algorithm to model and refill cavities of different depths on a 2D and 3D simplified finite element model of a bone trabeculum, it was shown that beyond a certain cavity depth the remodelling was not able to refill the cavity and a notching effect caused perforation[83,84].

An extension of simple beam models is 2D and 3D lattice structures. Langton proposed a 2D stochastical model of resorption on a lattice structure where resorption was guided by a probability that a surface pixel is activated and a probability for the duration of resorption[85]. Small bone volume losses caused high stiffness losses which are related to 2D nature of that model. Lattice 3D models are more robust, A model presented by Tayyar et al[86] used planar structural units to test the effect of increased activation frequency during menopause on bone volume. He used rectangular shaped cavities with a maximum depth of 50 µm and 2% of the cavity volume was not refilled during formation[86]. The volume loss was larger in case of menopause, with almost 40% of the bone loss caused by perforation (disconnection from the network).

Lattice models are unable to capture the complex and heterogeneous nature of trabecular bone. In a trabecular network, the mechanical effect of perforations or ruptures depends on the cavity location and specific trabecular properties. µCT-scans have enabled researchers to take the intricate trabecular structure into account when modelling resorption effects.

The stress-concentrating effect of resorption cavities on real isolated trabeculae was first investigated by McNamara et al[87]. Cavities were identified on µCT-scans and the authors found from finite element analysis that micro-damage was inevitable around these lacunae, which might lead to more resorption than ‘initially’ intended to restore damaged bone[87].

Different cavity-based erosion and formation algorithms have been applied to complete trabecular samples as well, and FE analyses were performed to investigate the mechanical impact[88-93]. These algorithms have been applied iteratively to simulate the effect of a sequence of remodelling cycles, with both formation and resorption, sometimes spanning several decades in the virtual life of the sample. The algorithms used had different grounds. One approach was to remove voxels on the entire bone surface based on a gaussian filter constrained to a certain cavity volume[90,94], which not necessarily erodes individual cavities. Using this method they showed that a negative bone balance and increased activation frequency can cause extreme bone loss[90]. Others considered the local mechanical environment of voxels and removed them based on the nonuniformity of local stress on the surface or a strain signal[91,93]. Both models caused an evolution towards a typical anisotropic bone structure after several cycles, with a higher stiffness in the loading direction.

The approach of Van der Linden et al[92] was the first to specifically take the cavity shape into account. They developed a computer simulation of bone remodelling on a 3D-µCT-based structure where voxels of bone matrix were removed as hemispherical cavities located at random locations on the bone surface. In a sequence of bone remodelling cycles, a formation deficit was modelled hence the cavities were not refilled completely. The model was used to simulate several bone loss scenarios[95] as well as the effect of treatment with anti-resorptive agents by gradually changing cavity properties[96]. They clearly showed the complex relationship between bone loss and stiffness loss and that bone loss alone cannot explain the mechanical changes. While Van der Linden et al based their amount of remodelling on the remodelling volume, Liu et al[89] added hemispherical cavities at random locations according to the activation frequency. They observed a shift to less plate-like trabeculae and more, but thinner, rod-like trabeculae after the simulated menopause.

Hernandez et al[88] used a similar 3D model to test the effect of resorption cavities on the trabecular bone strength. They digitally added cavities at regions of high strain or at random locations. For the first time, the cavities were modelled with an ellipsoidal shape. Adding resorption cavities caused a significant reduction in stiffness and yield strength, with even higher reduction for cavities at regions of high strain. The total removed bone volume was however the same, showing that cavities may influence bone mechanics independent of their effect on bone volume. The same research group continued to model the biomechanical effect of (uniform size) resorption cavities on voxel-based models and have shown a larger impact of cavities located in highly strained areas on the trabecular bone structure[97].

Using a new approach that overcomes some of the modelling limitations described above and below, we recently simulated the effect of resorption cavities on the stiffness of a wide variety of trabecular bone structures using a parametric beam-shell finite element model[98]. The reduction in bone stiffness due to cavities was significantly larger than for homogeneous erosion of the same bone volume and depended on the nature of the bone structure (rod-like vs plate-like trabeculae). A more specific study using the same modelling technique showed that glucocorticoid changes in the geometry of osteoclast resorption cavities affect trabecular bone stiffness[99].

Slyfield et al[100] were recently able to take the ultimate step in the 3D analysis of the mechanical effect of resorption cavities. They were able to demonstrate the role of resorption cavity size and location on mechanical failure (damage) of bone using 3D imaging of the failure process.

Modelling limitations

As described above, the different modelling approaches have revealed interesting effects of resorption on bone mechanical properties. There are however several disadvantages in the methods and potential flaws in the presented studies.

First, simplified (lattice) models are unable to capture the complex and heterogeneous nature of trabecular bone and are therefore less suited to model the combined mechanical effect of all the interacting structural properties.

Second, detailed µCT-based models of trabecular bone have been used, but so far applied only to a limited number of trabecular bone samples. Given the enormous heterogeneity of trabecular bone structures, related to the anatomical site, the influence of the initial structure should be taken into account. It is as yet unclear whether resorption cavities have a similar impact on plate-like samples then on rod-like bone samples.

Third, state-of-the-art µCT-based models add en remove bone by adding or removing voxels. Cavity shapes and sizes are thus limited to the voxel resolution. As our review of resorption cavity properties shows, a large variation in sizes exists and changes often occur on a sub-voxel-resolution level. High resolution imaginghas shown that resorption cavities have very irregular shapes of which the mechanical impact can possibly not be modelled correctly on a voxel-basis[37]. Potential solutions to this problem lie in the use of tetrahedral-based FE models, where surface nodes can be moved inwards to model cavities or by using parameter-based models of trabecular bone, like beam-shell finite element models[101].

Fourth, state-of-the-art µCT-based models assume, partly due to their voxel-based nature, cavities of a fixed size. However, cavity shapes and sizes are far from constant. In vivo, they exist in a skewed distribution of surface area and cavity depth. Moreover, at a certain snapshot in time, not all cavities are in the same remodelling stage: some may have just started while others are already being refilled. Furthermore all simulation studies have shown that the highest mechanical impact occurs when trabeculae are perforated or ruptures, especially when occurring in highly strained locations. The presence of just a few deep perforating cavities can thus change the mechanics decisively, while an averaged cavity depth might not cause perforation. It is thus advisable to use a realistic spread of resorption cavity properties when modelling their mechanical impact.

Fifth, the choice of modelling parameters remains problematic. As we explained above, different measuring methods exist and all have specific disadvantages, requiring careful interpretation of the values before using them as a model basis. Resorption cavity depths used in simulation studies seem to be large compared to literature values, again due to the voxel-based nature of the models. Using dynamic parameters like the total remodelling space or Ac.f as a basis for a static study, might lead to an overestimation of the impact of resorption cavities[88,89]. There is no single timepoint where the entire remodelling space has been removed by osteoclasts. Given the fact that ES/BS is commonly measured and there is less discussion concerning the measurement technique, it is likely the best parameter to quantify the extend of erosion.

CONCLUSION

Osteocyte resorption cavities affect bone competence. Hence, a proper quantification of the cavity dimensions will be beneficial in estimating the effect of metabolic bone diseases on bone mechanical quality. Until recently, the dimensions of osteoclast resorption cavities have been estimated from 2D measures. Their role in affecting bone quality has been analyzed using computational models that, on one hand, provide rather detailed information on trabecular bone structure, but on the other incorporate rather crude assumptions on cavity dimensions. Considering the 3D nature of the cavities this approach has clear limitations, requiring a careful interpretation. The introduction of 3D imaging techniques like µCT and SR-CT has opened the door to quantifying these dimensions in an unbiased manner in 3D space. These data can be included in high-resolution computational models and in parametric descriptions of bone, thereby improving our understanding of their effect on bone competence. Further exploration of this area of research will disclose relevant information on the mechanical consequences of metabolic bone diseases and can aide in the development of (bio)mechanically relevant pharmacological and physical treatments.