Towards Elimination of the Dark-Rim Artifact in First-Pass Myocardial Perfusion MRI: Removing Gibbs Ringing Effects Using Optimized Radial Imaging

Abstract

Purpose

Subendocardial dark-rim artifacts (DRAs) remain a major concern in first-pass perfusion (FPP) myocardial MRI and may lower the diagnostic accuracy for detection of ischemia. A major source of the DRA is known to be the “Gibbs ringing” effect. We propose an optimized radial acquisition strategy aimed at eliminating ringing-induced DRAs in FPP.

Theory and Methods

By studying the underlying point spread function (PSF), we show that optimized radial sampling with a simple reconstruction method can eliminate the oscillations in the PSF that cause ringing artifacts. We conduct realistic MRI phantom experiments and in-vivo studies (n=12 healthy humans) to study the artifact behavior of the proposed acquisition scheme in comparison to a conventional Cartesian protocol.

Results

Simulations and phantom experiments verify the theoretical expectations. Our in-vivo studies show that optimized radial imaging is capable of significantly reducing DRAs in the early myocardial enhancement phase (during which the ringing effect is most prominent and may obscure perfusion defects) while providing equivalent resolution and similar image quality as conventional Cartesian imaging.

Conclusion

The developed technical framework and results demonstrate that, compared to conventional Cartesian techniques, optimized radial imaging with the proposed optimizations significantly reduces the prevalence and spatial extent of DRAs in FPP imaging.

Introduction

A decrease in myocardial perfusion represents an early marker reflecting the functional effects associated with abnormalities in the coronary arteries (1). In fact, direct visualization of perfusion deficits is the preferred diagnostic test in patients with suspected myocardial ischemia or coronary artery disease. With recent hardware and software improvements, MR myocardial first-pass perfusion (FPP) imaging (2) is emerging as an attractive alternative to the widely available nuclear imaging modalities (3-7). Despite significant technical advances during the past decade, a persistent problem in myocardial FPP imaging — and perhaps the most frustrating one — is the well-known subendocardial dark-rim artifact (5-10).

The dark rim artifacts (DRAs) remain as a major drawback for accuracy and wide-spread adoption of FPP imaging (6,7,11) since they impede diagnosis of hypoperfusion in the subendocardium which is the most and typically the earliest affected myocardial layer in ischemic disease (12). Specifically, when FPP is used to diagnose patients with mild or moderate level of hypoperfusion DRAs may be interpreted as perfusion defects and therefore may reduce the diagnostic specificity. Alternatively, they may reduce the sensitivity if the reader dismisses true deficits as artifact. Another example highlighting the need for eliminating DRAs involves diagnosis of patients with coronary microvascular dysfunction (13,14) since their perfusion deficits tend to be mild and subendocardial (15,16). Therefore, establishing an acquisition scheme that is robust to DRAs can significantly increase the diagnostic performance of FPP imaging and its clinical utility for a variety of patient cohorts.

For qualitative (visual) assessment of FPP, the current approaches for distinguishing artifacts from true deficits (e.g., examining the spatial/temporal characteristics of the artifact or stress-rest comparisons) are subjective and, although potentially helpful (6,17,18), do not provide a systematic solution and are limited due to inherent variability of DRAs (10,19). Furthermore, even if an experienced reader can “read through” DRAs, it could be the case that some subendocardial deficits “fill in” early while the DRA is still present, i.e., during the early myocardial enhancement phase (7). This will inevitably result in missed or misread perfusion defects. Moreover, in quantitative perfusion assessment the DRA problem is even worse and may result in significant errors (11).

DRAs have been linked to multiple factors: Gibbs ringing or truncation artifact (9), cardiac motion (20), susceptibility effects from contrast dynamics (21-23), and signal variation during acquisition (6). Recently, there have been several attempts at minimizing DRAs, mainly by improving the spatial resolution using temporally accelerated reconstruction, e.g., using model-based (so called “k-t”) (24-27) or compressed sensing techniques (28-30). The attempts at decreasing DRAs based on increased spatial resolution is motivated by minimizing the “Gibbs ringing” effect that is thought to be a central source of DRA (7,9). Gibbs ringing is a fundamental property of practical Fourier imaging systems since the underlying spectrum (k-space data) has infinite support but is approximated by a finite number of samples (31,32). The ringing phenomenon refers to oscillations in the reconstructed image intensity that include signal dips (undershoot) at sharp image edges (e.g., the LV cavity-endocardium boundary), which may manifest as the DRA (9). In this work, we focus on the contribution of Gibbs ringing to the DRA and propose a radial imaging strategy that effectively eliminates ringing-induced artifacts. The underlying theory is inspired by results from classical computed tomography (CT) and tomographic reconstruction literature (33), which show that projection imaging with a high resolution exhibits minimal Gibbs-like ringing artifacts (34).

Our first objective is to design and optimize a radial sampling scheme that, combined with a simple reconstruction scheme, is virtually free of ringing-induced artifacts. Based on theoretical derivations combined with numerical and imaging verifications, we show that optimized radial imaging with wide k-space coverage can effectively remove Gibbs ringing effects. The second objective of this work is to evaluate whether radial imaging using our proposed optimized scheme will significantly reduce the prevalence and spatial extent of DRAs in FPP imaging compared to the conventional Cartesian technique, while providing equivalent resolution and similar image quality.

Theory

Preliminaries

We use the following terminology and notations in connection with Cartesian and radial sampling schemes. We denote the number of readouts N_RO by and the number of samples per readout by N_S. The field of view (FOV) along the “readout direction” (x or r for Cartesian and radial sampling, respectively) is assumed to be the interval [-L,L] for a fixed L>0. Therefore, the readout resolution (for either scheme) is proportional to N_S. In Cartesian and radial k-space, the readout dimension is denoted by k_x and k_x, respectively, and the sampling interval along readout Δk is assumed to satisfy the conventional 2-fold oversampling (relative to the Nyquist criterion) used in modern MR scanners, namely, Δk<1/4L. In case of Cartesian sampling, we refer to “readouts” to denote the phase encode (PE) lines, “readout resolution” to represent the resolution along the frequency encode (FE) direction, and “samples per readout” to be the number of FE samples. In general, the spatial resolution along a certain dimension is proportional to the maximum sampled frequency along the corresponding k-space dimension, denoted here by adding a max superscript to the k-space dimension. Specifically, $k_y^{\max }={\mathrm{N}}_{\mathrm{RO}}\Delta k∕2$ determines the PE resolution; and, the readout resolution for Cartesian and radial sampling are determined by $k_x^{\max }={\mathrm{N}}_{\mathrm{S}}\Delta k∕2$ and $k_r^{\max }={\mathrm{N}}_{\mathrm{S}}\Delta k∕2$ respectively. Finally, we assume uniform sampling between the readouts, i.e., uniform PE spacing (1/FOV_y) for the Cartesian scheme and uniform angular sampling for the radial scheme.

PSF Analysis: Sufficiently Sampled (Ideal) Scenario

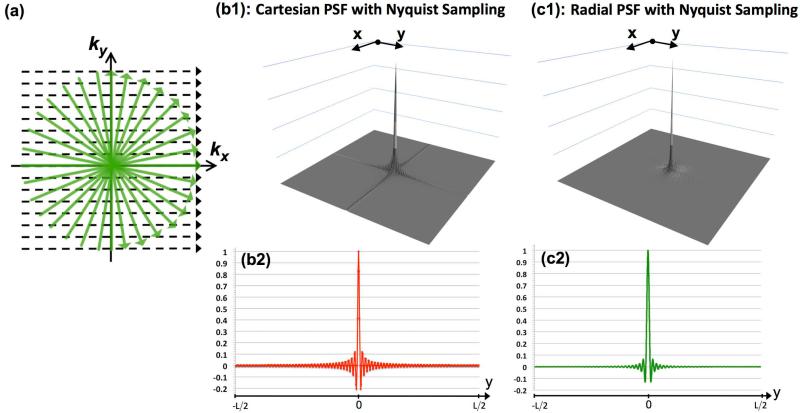
We study the difference in general properties of Cartesian and radial k-space sampling schemes, focusing on the components that contribute to ringing artifacts in the acquired images. A classical method for describing the effect of different sampling patters in imaging is to characterize the corresponding PSF (35). Given the PSF corresponding to a k-space sampling pattern, the reconstructed image is the result of 2D convolution of the PSF with the magnetization density (i.e., the ground-truth image). Fig. 1(a) depicts an example of isotropic-resolution Cartesian and radial sampling patterns with the same resolution ($k_x^{\max }=k_y^{\max }=k_r^{\max }$).

Figure 1.

PSF analysis for the sufficiently sampled scenario: (a) Schematic for sufficiently sampled Cartesian and radial sampling patterns with the same readout resolution; Panels (b1) and (c1) show the absolute value of the PSFs for Nyquist-sampled Cartesian and radial acquisitions, respectively (with N_S=256 samples per readout and a fixed FOV of [-L,L]); Panels (b2) and (c2) are 1D cuts of the respective PSFs along the y axis (same as the cut along x axis).

To study the Cartesian acquisition scheme, we calculate the PSF for a Nyquist-sampled Cartesian pattern with N_RO readouts (PEs) and N_S samples per readout (FEs). Without loss of generality, we proceed by assuming N_RO = 256 and N_S = 192. The FOV along y is assumed to be 25% smaller yielding a rectangular FOV, which is typically used in Cartesian imaging. The PSF is numerically approximated by 20-fold zero-padding of an all-unity k-space matrix of size 256x192 (equivalent to the underlying image being a 2D Dirac delta function) and computing the 2D inverse discrete Fourier transform. The resulting real-valued image is then scaled (peak value normalized to 1) to yield the PSF in (x,y) domain. Figure 1(b1) shows the absolute value of the computed 2D PSF for the described Cartesian scheme (2-fold zoom). The analytical PSF expression for 2D Cartesian sampling is the well-known 2D periodic “sinc” function (36), also called the Dirichlet kernel (31):

$${\mathrm{PSF}}_{\mathrm{C}}(x,y)=\Delta k^2\frac{\sin \left(2\pi x{k}_x^{\max }\right)}{\sin \left(\pi x\Delta k\right)}\frac{\sin \left(2\pi y{k}_y^{\max }\right)}{\sin \left(\pi y\Delta k\right)}$$ [1]

Panel (b2) shows a 1D cut of the PSF along the y, which coincides with the x-axis cut (consistent with Eq. [1]). If convolved with a 2D image with sharp edges (e.g., bloodpool-myocardium border in FPP images), these oscillations will result in image artifacts, referred to as Gibbs ringing artifacts. In effect, signal values around the image edge are modulated by the positive/negative side-lobes of the PSF, resulting in reconstructed intensities above/below the ground truth.

Next, we compute the PSF for a radial acquisition scheme with the same readout resolution (N_S = 256) and N_RO = 402 readouts (projections), which matches the requirement for zero angular aliasing according to the Nyquist criterion (33). The radial PSF is computed as follows: (i) sampling a uniform (all unity) k-space along the described radial trajectory; (ii) regridding the sampled data using a conventional Kaiser-Bessel gridding kernel (width 4) and density compensation function (DCF); (iii) scaling the resulting real-valued image (peak normalized to 1). This conventional DCF is ramp-shaped and equal to ∥_kr∥ (except for the origin), which hereafter is referred to as the “ramp DCF” (37). The corresponding PSF (absolute value) is shown in Fig. 1(c1). The analytical formula describing the behavior of this circularly symmetric PSF in (r,Θ) polar coordinates can be written as:

$${\mathrm{PSF}}_{\mathrm{R}}\left(r\right)\approx \frac{\pi {\left(\Delta k\right)}^2}{4}+{\left(2k_r^{\max }\right)}^2\mathrm{jinc}\left(2k_r^{\max }r\right)$$ [2]

where in jinc(r)= J₁(πr)/2r which J₁(r) is the first-order Bessel function (38). This radially symmetric function has been described before in the MR literature by Lauzon and Rutt (39) using classical results from radio astronomy (40). The “jinc” function in Eq. [2] is the analog of sinc (Eq. [1]) in 2D polar coordinates and equal to the spectrum (Hankel transform) of a unit-height disk (38,40). Note that the PSF depicted in Panel (c1) does not exactly conform to Eq. [2] because of the effects of higher order terms in the PSF located at multiples of 1/Δk in addition to underlying numerical errors. However, these effects are negligible for the described sampling scheme and Fig. 1(c1) closely follows ∥PSF_R(r)∥ because the effect of higher order terms is negligible for a small enough readout sampling interval Δk satisfying Δk<1/4L. [Specifically, this condition ensures that the “polar ring” components of the radial PSF can be ignored in the imaged FOV (39).] Figure 1(c2) shows a 1D cut of the real-valued PSF along y. Similarly to Cartesian imaging, the PSF consists of a narrow main lobe and oscillating side lobes, which may also result in ringing artifacts when convolved with the underlying image; this effect is sometimes referred to as “radial ringing” in MRI literature (39) or the “Airy pattern” in Fourier optics (38).

For both Cartesian and radial schemes, the frequency (spatial density) of PSF oscillations is proportional to the resolution (Panels b2 and c2). Consequently, any potential ringing-induced DRAs become more compact and therefore visually less significant (9,10). However, a key difference between Cartesian and radial schemes is that the oscillation frequency for radial PSF in both x and y directions only depends on the readout resolution, i.e., $k_r^{\max }$, which is proportional to N_S. In contrast, the frequency of oscillations along y for the Cartesian PSF is a function of the PE resolution, i.e., $k_y^{\max }$, which is proportional to N_RO. Therefore, increasing the oscillation frequency of the underlying PSF for radial imaging comes with almost no acquisition time penalty (since it only requires increasing N_S for a fixed FOV), whereas accomplishing the same for Cartesian imaging may incur significant acquisition time penalty (since it requires increasing N_RO, i.e., more readouts). In addition to the oscillation frequencies, there are other differences between the characteristics of the PSFs shown in Fig. 1 (Eqs. [1]-[2]), which include the peak amplitude and decay-rate of the side-lobes, both of which are more desirable for the radial PSF (38,41). However, these differences correspond to 1D cuts of the PSFs and their effects on the reconstructed image are difficult to analyze analytically. Consequently, we will use numerical simulations to study such differences (in Methods).

PSF Analysis: Limited Readouts (Practical) Scenario

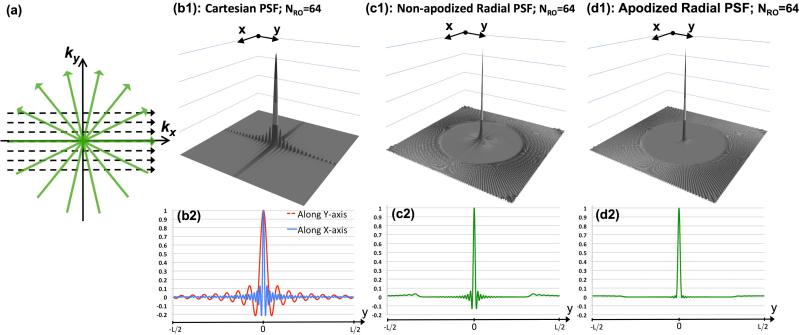
Figure 2 describes the PSF properties of Cartesian and radial acquisitions for a practical scenario wherein only a limited number of readouts is acquired while the readout resolution is the same as before (N_S = 256 samples). The schematic for this “limited readouts” scenario is depicted in Fig. 2(a). In contrast, to the previous section (“sufficiently sampled” scenario in Fig. 1), here we assume that the same number of readouts N_RO is acquired for both Cartesian and radial sampling schemes. Without loss of generality, in the following we assume N_RO = 64. For Cartesian imaging, given the rectangular FOV (25% reduced FOV along PE), this sampling scheme implies a 3-to-1 resolution difference between x and y dimensions ($\times k_y^{\max }=k_x^{\max }∕3$). The corresponding PSF and 1D cuts are shown in Figs. 2(b1) and 2(b2), respectively. The Cartesian PSF oscillations along y have a 3-times lower frequency compared to the one in Fig. 1(b2) with similar peak side-lobe amplitudes. The wider main-lobe along y implies lower spatial resolution; more importantly, the wider side-lobes yield a wider (more spatially prominent) ringing artifact.

Figure 2.

PSF analysis for the limited readouts scenario: (a) Schematic for the limited-readout sampling scenario for Cartesian and radial acquisition with equal number of readouts and readout resolution; Panels (b)-(d) show PSFs with N_RO=64 readouts and N_S=256 samples per readout (fixed readout FOV [-L,L]); (b1,b2) absolute value of the Cartesian PSF and its 1D cuts along x and y; the FOV along PE is [-0.75L,0.75L]; Panels (c1,c2) and (d1,d2) show the radial PSF and its 1D cut corresponding to non-apodized reconstruction and apodized reconstruction (apodizer as in Eq. [3] using Ω = 1.17), respectively. In contrast to radial sampling, insufficient k-space coverage along k_y (PE) in Cartesian sampling results in low frequency oscillations along y (3 times wider side lobes than x), as shown in (b1,b2).

In the following, we refer to conventional regridding reconstruction of radial acquisition using the ramp DCF as “non-apodized” reconstruction. The computed non-apodized radial PSF and its 1D cut are shown in Figs. 2(c1)-(c2) and correspond to non-apodized regridding reconstruction of N_RO = 64 projections. Figure 2(c1) matches the previous description in the literature (42,43): the PSF for angularly undersampled radial acquisition consists of a superposition of the principal jinc component and its associated side-lobes (Panels (c1)-(c2) in Fig. 1) plus the “streaking” components that start outside of a certain radius. This radius for the described sampling scheme is approximately i.e., 0.3 L, 15% of the FOV; also, the peak amplitude of the streaking components is located 0.35 L at and has a value of 3.4%. In comparison, the peak negative and positive side-lobe amplitudes (jinc component) of this PSF are -13.2% and 6.4%, respectively, which is the same as the sufficiently-sampled radial PSF in Fig. 1. The key observation in comparing the limited-readout radial scheme in Figs. 2(c1)-(c2) to the sufficiently-sampled one in Figs. 1(c1)-(c2) is that both PSFs show almost identical oscillatory (jinc) components.

Comparing the radial and Cartesian sampling schemes in Fig. 2, it is worth emphasizing that the total acquisition time is the same between the two (note that N_RO = 64 is fixed and $k_x^{\max }=k_r^{\max }$). However, the radial trajectory samples the high-frequency k-space regions in all directions, yet the Cartesian trajectory misses some of the high frequency regions specifically along the PE direction, which results in low-frequency oscillations in the PSF along y. Hence, the expected ringing artifact for radial sampling (with non-apodized reconstruction) is expected to be less significant (smaller width) compared to Cartesian sampling (along PE) (44).

PSF Analysis: Radial Imaging with Optimized Apodization

The PSF for radial imaging also depends on the reconstruction method used, i.e., the PSF corresponding to non-apodized reconstruction (discussed above) is different from the one corresponding to filtered back-projection or regridding reconstruction incorporating apodization (41,45). Here, we consider the radial PSF corresponding to regridding reconstruction using an apodized k-space weighting instead of the non-apodized ramp-shaped DCF. We use a Gaussian kernel as the “apodizer” (apodizing function) with the following form:

$$A\left(k_r\right)=e^{-\pi {\left(\frac{k_r∕k_r^{\max }}{\Omega }\right)}^2}$$ [3]

for some pre-defined parameter Ω. In the apodized reconstruction, the radial readouts are first multiplied by A(k_r), which reduces the weighting of high frequency k-space samples, before conventional density compensation (i.e., weighting by the ramp-shaped DCF) and regridding. The typical motivation for using an apodized reconstruction in projection imaging is to achieve high-frequency noise suppression to improve signal to noise ratio (SNR), which comes at the expense of reduced effective resolution (35,37). The equivalent image-domain operation for the described Gaussian apodization is smoothing by a 2D circularly symmetric Gaussian kernel. It can be shown that the effective full width at the half maximum (35) of the underlying PSF will increase with decreasing Ω, thereby reducing the effective isotropic resolution. Note that since $k_r^{\max }$ is the same for the apodized scheme, the PSF oscillation frequency will stay the same but the amplitude of oscillations can be significantly suppressed (32) — and even effectively eliminated for a small enough Ω

To apply the apodizer and study its effect of the radial PSF, we first need to choose an optimal parameter Ω for the Gaussian kernel in Eq. [3]. Our optimization criterion is to minimize the resolution penalty (reduction factor), i.e., to find the maximal Ω* such that the peak negative side-lob of the resulting PSF will be lower than 1%, i.e., an apodizer that essentially eliminates all ringing components (side-lobes) from the PSF. The Gaussian apodizer in Eq. [3] can be shown to be near optimal in the sense of providing maximum suppression in the amplitude of the largest side-lobe for a given resolution penalty. The proof is beyond the scope of this work but a related work has been described recently for Fourier spectrometry (46). The result of the numerical search algorithm for the described radial sampling pattern was Ω* = 1.17. To quantify the effect of the corresponding apodization on the reconstructed resolution, we compared the FWHM of the main-lobe of the resulting PSF to that of the nonapodized PSF in Fig. 2(c1). The ratio of FWHMs (apodized over non-apodized) is 1.28, implying a 1.28-fold reduction in effective resolution along x and y.

Figures 2(d1)-(d2) show the radial PSF corresponding to the same sampling scheme as in Figs. 2(c1)-(c2) but using the optimized apodized reconstruction instead of the non-apodized reconstruction. As seen in the 1D cut shown in Panel (d2), we have eliminated almost all ringing components (peak negative amplitude is -0.95%, which is 14 times smaller than (c2)) and significantly reduced the streaking components (peak streak amplitude is 1.3%, about 2.6 times smaller than (c2)). Therefore, besides improving SNR, the apodized reconstruction also reduces streaking and effectively eliminates oscillations in PSF (source of ringing artifacts) at the cost of reduced resolution. An acquisition scheme that samples the data at this reduced resolution and does not use apodization is more SNR-efficient (compared to the apodized scheme) but will not achieve the desired reduction of the ringing components. In practice and as will be described in Methods and Results, given a desired spatial resolution for the reconstruction, this trade-off (resolution vs. ringing) can be flexibly adjusted using the described Gaussian apodizer.

Methods

Numerical Simulation

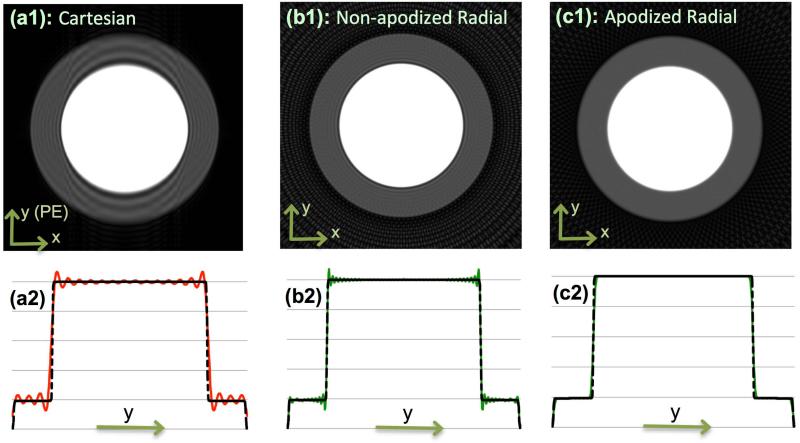
The PSF properties described in Theory were verified by simulating k-space sampling and reconstruction for a noise-free numerical phantom consisting of two overlapping inner/outer disks (as shown in top row of Fig. 3) with the following specifications: ratio of inner to outer disk radius = R_in/R_out = 2/3 and signal intensity ratio between the two disks was 6 to 1, which represents a maximal (“worst case”) contrast ratio along the subendocardial border for FPP. We used the same Cartesian and radial sampling patterns as in Fig. 2. To compute the k-space data samples accurately for a given sampling pattern, we applied the following analytical expression for D(k_r) the circularly symmetric 2D Fourier representation of the described phantom (36,38):

$$\mathrm{D}\left(k_r\right)=10\pi \cdot R_{\mathrm{in}}^2\frac{{\mathrm{J}}_1\left(k_r{R}_{\mathrm{in}}\right)}{k_r{R}_{\mathrm{in}}}+2\pi \cdot R_{\mathrm{out}}^2\frac{{\mathrm{J}}_1\left(k_r{R}_{\mathrm{out}}\right)}{k_r{R}_{\mathrm{out}}}$$ [4]

Figure 3.

Numerical phantom results: (a1) Cartesian reconstruction of analytical disk phantom with same acquisition scheme as in Fig. 2 (3-times lower resolution along y); (b1) Non-apodized radial reconstruction (same number of readouts and readout resolution); (c1) Apodized radial reconstruction with the same k-space data as in (b1) (same apodizer as Fig. 2(d)). All images use zero-filled interpolation to 512x512 image matrix. Panels (a2), (b2), and (c2) are 1D cuts of the images in the top panel along the center of the image parallel to the y axis that are overlaid on the ground truth (dotted line). The Cartesian image in (a1) exhibits significant ringing artifacts (Gibbs) along y (PE) whereas apodized radial reconstruction in (c1) eliminates all ringing-induces artifacts and has reduced streaking compared to (b1). Specifically, the energy (2-norm) of the streak region outside of the disks as a percentage of the energy of the disk phantom is 40% lower in (c1) compared to (b1) (11.5% vs. 19%). Overall, the results verify the PSF effects described in Figs. 1-2, and demonstrate that radial sampling with wide k-space coverage and apodized reconstruction can effectively eliminate the DRAs caused by Gibbs-like ringing effects.

Phantom Experiment

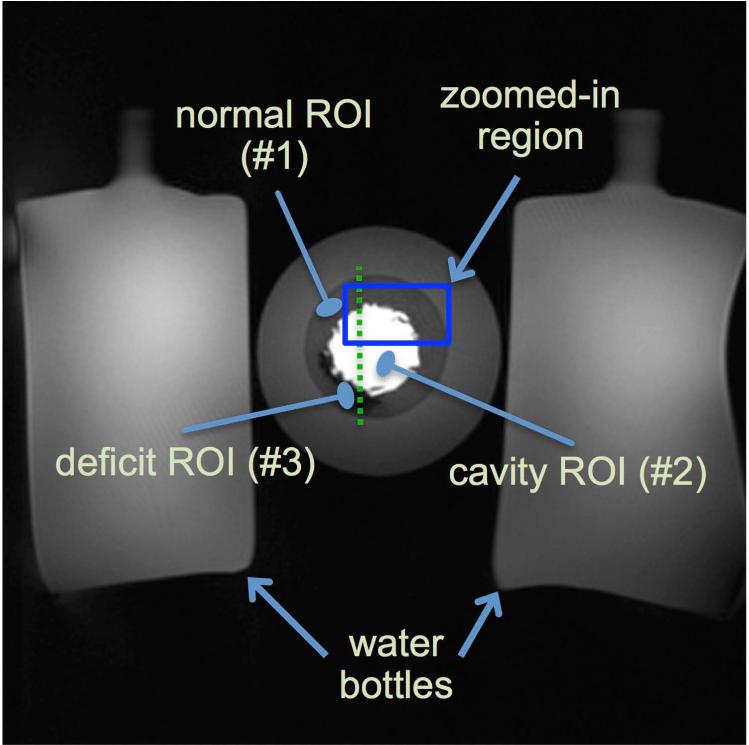
To verify the theoretical assertions, an MR phantom intended to simulate a geometrically-realistic FPP scenario with worst-case signal intensity variations (similarly to the numerical phantom above) was designed. The phantom was composed of multiple regions of interest (ROIs) made of gelatin and saline doped with various concentrations of a Gadolinium-based contrast agent (gadoversetamide), and surrounded by 2 bottles. Figure 4 shows the result of a fully sampled scan of the phantom, which was used as the “ground truth” image. The phantom was intended to resemble the left ventricle (ROIs: “LV cavity” region, “normal” region, “deficit” region) during the wash-in phase of contrast agent, and the bottles were to represent the surrounding tissue (see caption for details including T1 values).

Figure 4.

Description of imaged MR gelatin-Gadolinium phantom with realistic signal intensity ratios, used to demonstrate robustness of projection imaging to Gibbs ringing. This “ground truth” image is acquired at 1.0x1.0 mm² resolution using a SR-prepared FLASH radial pulse sequence with 384 readouts (projections). The ratio of the signal intensity in the cavity (ROI #2) to the normal region (ROI #1) is approximately 6 to 1 (range: 5.5-6.1). The cavity and normal regions were composed of a mixture of gelatin, saline, and contrast whereas the deficit region (ROI #3) contained almost no contrast agent. The T1 values ROIs #1, #2, and #3, are approximately 750 ms, 60 ms, and 1200 ms, respectively (estimated based on pixel-by-pixel T1 fitting using Cartesian data acquired separately with 6 different TIs). The highlighted box is the zoomed-in region shown in Fig. 5. The dotted line shows the location of the cut for the 1D profiles shown in Fig 5.

MR data was acquired on a 3T clinical scanner (Magnetom Verio, Siemens Healthcare, Erlangen, Germany) with a standard cardiac-torso receiver array. The scan parameters used to image the phantom in Fig. 4, i.e., our ground-truth scan, were as follows: radial FLASH with saturation recovery (SR) preparation, 1.0x1.0 mm² resolution, slice thickness: 6mm, FOV: 384x384 mm², 384 projections with 384 samples per readout, number of channels = 15, received bandwidth (rBW) = 650 Hz/pixel; flip angle = 12°; TR/TE = 3.0/1.8 ms; TI = 90 ms. The ratio of the signal intensity in the cavity (ROI #2) to the normal region (ROI #1) was approximately 6 to 1 (range along the edge: 5.5-6.1). This signal intensity ratio is higher than the typical 5-to-1 or 3-to-1 ratio encountered in-vivo. However, as stated above, the goal was to test the robustness of radial imaging (with wide k-space coverage) to ringing artifacts and as such, the 6-to-1 ratio represented a general “worst-case scenario.”

We conducted Cartesian and radial phantom scans using Cartesian/radial SR-prepared FLASH pulse sequences. Both datasets were acquired using N_RO = 77 readouts with N_S = 256 samples per readout, and similar sequence parameters as the ground-truth scan above. Consequently, the acquired readout resolution for both datasets was 1.5 mm. The Cartesian dataset used a rectangular FOV of size 384x230 mm² (PE resolution: 3.0 mm). Two reconstructions were performed from the radial dataset using: (i) non-apodized (k-space data only weighted by ramp DCF before regridding); and (ii) Gaussian-apodized (data also weighted by the optimized Gaussian kernel before DCF weighting and regridding). All radial/Cartesian reconstructions used sum-of-squares coil combination followed by standard zero-filled interpolation to a 512x512 image matrix (to minimize variability to sub-pixel shifts (10)).

In-vivo Studies

Following informed consent, healthy human volunteers (n=12; 7 women; average age: 24 years) with no history of heart disease or diabetes were imaged on the same 3T scanner according to a study protocols approved by the Institutional Review Board at Cedars-Sinai Medical Center. Two FPP scans, both using SR-prepared FLASH acquisition, were performed at rest (breathhold scans during 50 heartbeats; mean scan time: 42 s) using an optimized radial pulse sequence followed by the product FPP Cartesian sequence (details below), with a 10-12 minute time gap in between the two scans to allow for contrast wash out. The contrast injection dose (gadoversetamide) for each perfusion scan was 0.04 mmol/kg. All scans were “single shot,” i.e., there was no data-sharing between heartbeats, and the number of readouts were matched between the radial and Cartesian scans within ±3 readouts (range: 48-56). The readout resolution for the Cartesian scans was matched to that of the radial scan (range: 1.8-1.9mm; average = 1.8 mm; reconstructed resolution for radial images is different as described below) and the PE resolution was 2.7-2.9 mm (average = 2.8 mm). The parameters for the Cartesian scan (product sequence) were as follows: FOV read = 270-350 mm; flip angle = 12°, 15 receiver channels, rBW ≈ 680 Hz/pixel, TR = 2.5-2.6 ms, TE = 1.3-1.4 ms, TI = 100 ms with linear PE ordering; 3 contiguous slices per heartbeat (8 mm thickness, centered at mid ventricle) each acquired following a composite (product) SR preparation pulse train (6); TGRAPPA rate 2; online image reconstruction on the scanner. The radial FPP scans used a customized pulse sequence with similar parameters except the following: a fixed FOV of 285 mm (2-fold readout oversampling with 320 samples/spoke) and a BIR-4 adiabatic 90° pulse for SR preparation prior to acquisition of each slice. Due to the SAR limitations of the employed BIR-4 pulse at 3T, we anticipated that we will be limited to acquisition of 2 slices per R-R interval for some of the subjects and therefore scanned one slice position (mid ventricular) 2-3 times per heartbeat in all radial scans. The motivation for using a BIR-4 SR pulse was to minimize B₁ inhomogeneities (6,47); nevertheless, the composite SR pulse train (product sequence used in Cartesian scans) has been shown to perform almost as well in the LV region for Cartesian imaging at 3T (48).

The radial pulse sequence included gradient-delay correction (prospectively optimized for the scanner (49)), and acquisition of the radial spokes was 8-fold interleaved to minimize “smearing” artifacts caused by T1 relaxation after the SR pulse (29,50). The interleaving pattern was implemented by first partitioning the total number of spokes (48 or 56) into 8 uniformly-spaced subsets labeled from G₁ to G₈. The acquisition order for these disjoint groups (each containing 7-8 spokes) was as follows: {G₁, G₅, G₃, G₇, G₂, G₆, G₄, G₈}. To further reduce the effects of T1 relaxation and similarly to the KWIC scheme (51), the central k-space data used in the reconstruction was limited to the spokes in the middle of the acquisition window, i.e., {G₇, G₂}. Specifically, 15 central k-space samples (the DC sample and 7 samples on each of its two sides) for spokes in {G₃, G₆} and 27 central k-space samples for {G₁, G₅, G₆, G₄, G₈} were excluded in the reconstruction (the DCF was adjusted accordingly). In addition, the radial readout direction (polarity) was alternated within each shot to reduce potential off-resonance effects (52). Coil sensitivity profiles were computed by applying an eigenvector-based estimation method (53).

Image Reconstruction and Analysis

Image reconstruction for radial acquisitions was done on a frame by frame basis (no temporal acceleration) using non-Cartesian SENSE and performed offline on a workstation (Pentium Dual-Xeon 3.3 GHz) in MATLAB (Mathworks, Natick, MA) employing 12 computing cores (reconstruction time: ≈75 s/slice). The reconstruction algorithm was according to a conjugate-gradient scheme with no explicit regularization (54) and employing the Gaussian apodizer (Eq. [3]). The kernel parameter Ω for the apodizer was chosen on the basis of the desired in-plane reconstructed resolution, which was set to be 2.15 mm x 2.15 mm. Given that the acquisition resolution was 1.8 mm (isotropic in-plane), we determined that the apodization should correspond to a 1.2-fold reduction in resolution along each dimension (1.2-fold increase in FWHM of the PSF). We then used the computational framework described in Theory (Fig. 2) and selected g=W = 1.24 to yield the desired apodizer. Compared to the apodized radial PSF discussed in Theory, the peak negative PSF side-lobe amplitude for this setup is -1.6% and therefore is expected to have negligible ringing components, similarly to Figs. 2(d1)-(d2).

One representative mid-ventricular image from each radial/Cartesian FPP image series (total of 24) was selected from the “early myocardial enhancement” phase (defined as 8 R-R cycles after initial LV cavity enhancement). All representative images were visually scored for artifact by two expert readers blinded to the study protocol using a consensus 0-4 scoring scheme (0: no artifact; 1: negligible; 2: mild; 3: moderate; and 4: severe artifact). For the radial images, the reconstructed frame (among 2-3 frames per R-R cycle) that best matched the Cartesian mid-ventricular image in terms of cardiac phase was chosen for the blind read (to “equalize” the motion effects in the visual comparison as much as possible). The following procedure was followed for quantitative scoring of the artifact. Radial reconstructions were converted to DICOM images (using the scanner-produced tags) and imported in an expert viewer (Osirix by Pixmeo, Geneva). For quantitative evaluation, we estimated the spatial width of the DRA in each representative image as a surrogate measure for its severity (24). In particular, spatial width of the DRAs were computed from the interpolated DICOMs as a measure of the maximal length (largest transmural extent) of the signal dips along all polar directions (along rays starting from the cavity center and extending towards the endocardium). All statistical tests comparing radial and Cartesian results used the Mann-Whitney U-test (equivalent to Wilcoxon rank-sum test) computed in MATLAB (55).

Results

Numerical Simulation

Figure 3 presents the simulation results for the disk-shaped numerical phantom. The top-row panels (a1), (b1), and (c1) show the reconstructed images corresponding to the PSFs in Figs. 2(b1), 2(c1), and 2(d1), respectively. The lower panels (a2), (b2), and (c2) show a 1D cut along y, which is overlaid on top of the ground truth (dotted line). As seen from the figure, the non-apodized radial reconstruction yields negligible (very thin) ringing and the Gaussian-apodized reconstruction completely eliminates any ringing artifact, although at the cost of lower resolution. Specifically, the width of the DRA caused by Gibbs ringing in Fig. 3(a1) is approximately 17% of the width of the outer disc. In contrast, this measure is 5% for the nonapodized radial reconstruction in Fig. 3(b1), and is zero for the apodized reconstruction (with Ω = 1.17) in Fig. 3(c1). Moreover, the apodized reconstruction has less streaking (see caption). In summary, the simulation results verify the PSF effects described in Theory (Figs. 1-2).

Phantom Experiment

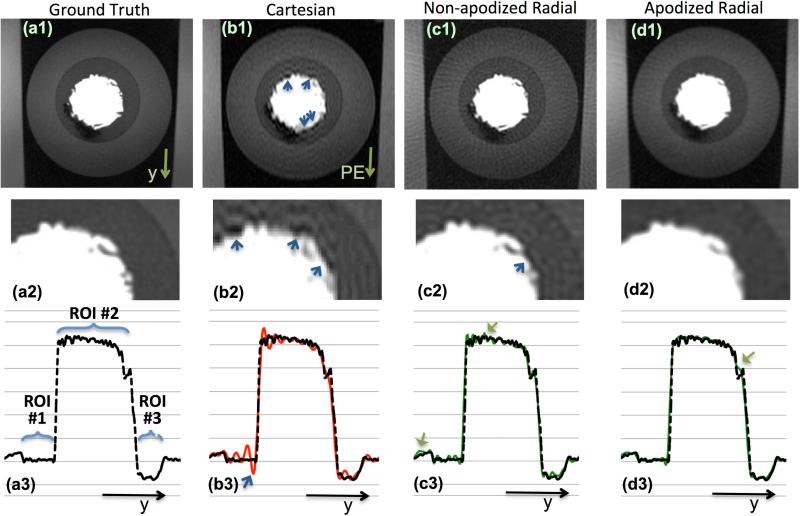
The reconstructions results for the MR phantom are shown in Fig. 5. The first column, which includes (a1)-(a3), show the ground-truth image (from Fig. 4) with 1.0 mm x 1.0 mm resolution. All other panels correspond to reconstructions of N_RO = 77 readouts with N_S = 256 samples per readout. Panels in the top row, (a1)-(d1), show cropped reconstruction results for each acquisition/reconstruction method. Zoomed-in versions of the images (highlighted box in Fig. 4) are shown in the middle row, (a2)-(d2). Panels (a3)-(d3) in the bottom row are 1D cuts of the top-row images (see caption). The 2^nd column of Fig. 5, Panels (b1)-(b3), show the Cartesian reconstruction with 1.5 x 3.0 = 4.5 mm² resolution; arrows in (b2) and (b3) point to DRAs. Panels (c1)-(c3) in the 3^rd column show the non-apodized radial reconstruction with 1.5 x 1.5 = 2.25 mm² resolution. The arrow in (c2) points to negligible (very thin) DRA, and those in (c3) show mild streaking artifacts. Lastly, Panels (d1)-(d3) in the 4^th column show the apodized radial reconstruction (apodizer as in Eq. [3] Ω = 1.17 using) with 1.92 x 1.92 = 3.7 mm² resolution. This is somewhat better than the overall Cartesian resolution (4.5 mm²). More importantly, (d1) exhibits no discernable DRAs and has negligible streaking. The arrow in (d3) points to a small feature, which is somewhat over-smoothened compared to the ground truth in (a1)-(a3) because of the lower resolution. Note that a similar resolution limitation is seen in the Cartesian image (b3) for reconstruction of the same feature. To quantitatively evaluate the image quality differences in Fig. 5, we computed the relative contrast difference between the normal ROI (#1 in Fig. 4) and deficit ROI (#3 in Fig. 4) as a percentage of the normal ROI. This relative contrast for the ground-truth image (a1), Cartesian image (b1), non-apodized radial image (c1), and apodized radial image (d1) are 79.3%, 68.1%, 70.3%, and 74.5%, respectively.

Figure 5.

Reconstructions results for the MR phantom in Fig. 4. The top row (a1-d1) shows zoomed-in reconstruction result; the middle row (a2-d2) shows images in the top row further zoomed-in to the box in Fig. 4; and the bottom row (a3-d3) are 1D cuts along the cut line in Fig. 4, with (a3) overlaid on (b3)-(d3) for comparison (ROIs in (a3) are defined in Fig. 4). Panels (a1)-(a3) show the “ground truth” image with 1.0 mm x 1.0 mm resolution. All other panels correspond to reconstructions with 77 readouts (256 samples each). Panels (b1)-(b3) shows the Cartesian reconstruction with 1.5x3.0=4.5 mm² resolution (FOV size = 384x230 mm²); arrows in (b2) and (b3) point to DRAs. Panels (c1)-(c3) show the non-apodized radial reconstruction with 1.5x1.5=2.25 mm² resolution; arrow in (c2) points to negligible DRA, and those in (c3) show mild streaking. Panels (d1)-(d3) show the apodized radial reconstruction (same apodizer as Fig. 2(d) and Fig. 3(c)) with 1.92x1.92=3.7 mm² resolution (no DRAs, negligible streaking); arrow in (d3) points to over-smoothening of a small feature, which is a consequence of the lower resolution compared to the ground truth in (a3).

In-vivo Studies

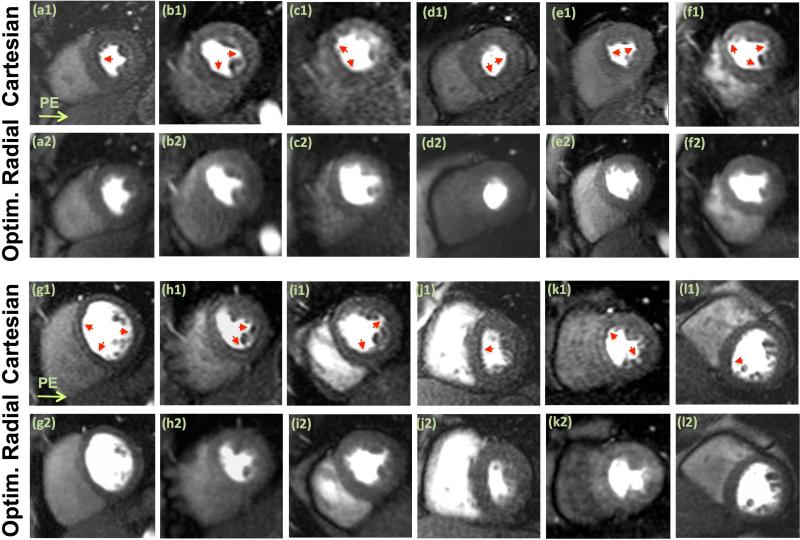
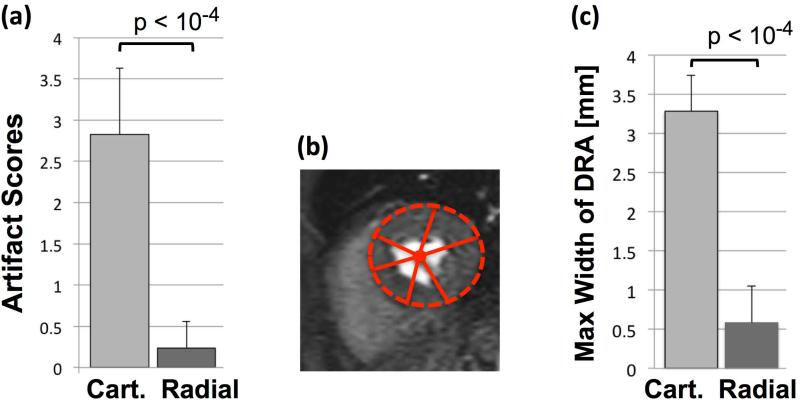
Representative images from all volunteer studies (n=12) are shown in Fig. 6. The image quality in terms of the measured myocardial SNR for the radial and Cartesian images is similar (Cartesian: 10.4±2.5 vs. radial: 11.7±2.2, P=0.40; see caption for details); however, unlike the Cartesian images, the reconstructed radial images (optimized scheme) are free of noticeable DRAs. Figures 6(a1)-(a2) and 6(e1)-(e2) correspond to large heavyset subjects (>110 kg): 6(e2) shows mild streaking (the only radial FPP image with noticeable streaking in the heart region among the 12 studies) but 6(a2) does not. An example movie of the FPP image series for the volunteer study in (a1)-(a2) is provided as online Supplementary Material. Figure 7(a) shows mean artifact scores assigned by the expert readers, clearly showing superiority of the optimized radial imaging method in reducing the DRA (P<0.0001). Fig. 7(b) depicts the quantification scheme for estimating the DRA width and Fig. 7(c) summarizes the measurements, indicating that the DRA width is significantly reduced for optimized radial imaging (P<0.0001). In summary, the in-vivo results show a very significant reduction of the DRA using the optimized radial imaging scheme, both in terms of qualitative scores and quantitative assessment.

Figure 6.

Representative first-pass myocardial perfusion images (mid-ventricular slice) from each of the 12 healthy volunteer studies; all images correspond to a similarly selected early myocardial enhancement phase (defined as 8 R-R cycles after initial LV cavity enhancement). The first row in each panel, (a1)-(f1) in the top panel and (g1-l1) in the bottom panel, show Cartesian images (phase-encode direction from left to right). The second row in each panel, (a2)-(f2) in the top panel and (g2-l2) in the bottom panel, show the corresponding images for the optimized radial imaging scheme. For the radial images, the reconstructed frame (among 2-3 mid-ventricular frames in one R-R cycle) that best matched the mid-ventricular Cartesian image in terms of cardiac phase is shown. Arrows point to the observed dark-rim artifacts. No noticeable dark-rim artifact is seen in the radial images (although Panel (e2) shows mild streaking in the septum). Examples of qualitative artifact scores are as follows: for (a1)-(a2), Cartesian = 3.5, Radial = 0; and for (i1)-(i2): Cartesian = 3; Radial = 1. The signal-to-noise ratio (SNR) in the myocardium (mean intensity divided by standard deviation in a homogeneous region at peak enhancement) is similar between Cartesian and radial images (Cartesian: 10.4±2.5 vs. radial: 11.7±2.2, P=0.40).

Figure 7.

(a): Summary of artifact scores for the representative first-pass perfusion images (Fig. 6) assigned by two expert readers (consensus 0-4 scale scoring; 0: no artifact, 1: negligible, 2: mild, 3: moderate, 4: severe artifact); the results clearly show the superiority of optimized radial imaging in reducing the DRA (Cartesian: 2.83±0.8 vs. optimized radial: 0.24±0.32, P<0.0001). (b): Quantification scheme for measuring the maximum width (largest transmural extent) of the dark-rim artifact along angular directions (as explained in Methods). (c) Summary of the DRA width measurements as shown in (b), indicating that the maximal width of DRA is significantly reduced with optimized radial imaging (Cartesian: 3.28±0.46 vs. optimized radial: 0.58±0.47, P<0.0001). Note that quantitative DRA measurements become less accurate for sub-pixel widths.

Discussion

In this work, we proposed a radial sampling strategy that, based on optimization of the associated point-spread function, eliminates ringing-induced artifacts and hence may enable reconstructing first-pass myocardial perfusion images free of the dark-rim artifact. For imaging experiments, we developed and applied an optimized FPP imaging technique based on the proposed radial sampling scheme with wide k-space coverage, and a rather simple frame-by-frame reconstruction method (i.e., each frame reconstructed independent of others and without temporal acceleration) using numerically optimized apodization. We demonstrated the capability of the proposed method through a systematic theoretical description combined with numerical simulations, as well as phantom and in-vivo experiments:

• – First, our study highlighted the fact that, unlike conventional Cartesian sampling, radial sampling has the following property: the frequency of PSF oscillations along both spatial dimensions becomes narrower using a wider k-space readout (i.e., a higher readout resolution or $k_r^{max}$, which is equivalent to more samples per readout for a fixed FOV) which implies narrower (less significant) ringing artifacts for the reconstruction.

• – Second, we noted that widening the k-space readout yields negligible temporal resolution penalty (although it results in an expected SNR cost).

• – Third, we showed that, with a simple scheme for optimized apodized reconstruction, one can trade-off in-plane resolution to simultaneously eliminate the PSF oscillations — hence the associated ringing artifacts — and improve the image quality (thanks to reduced streaking and higher SNR).

• – Fourth and most importantly, using the proposed radial acquisition scheme with typical FPP sequence parameters, the level of apodization needed for achieving the desired PSF behavior (i.e., highly suppressed ringing/oscillatory components) is quite mild and, therefore, implies a benign loss in reconstructed resolution. We specifically chose the apodization parameter (Gaussian kernel in Eq. [3]) such that the effective in-plane resolution of radial images matches or slightly outperforms the typical resolution in conventional Cartesian imaging. For the presented in-vivo results (Fig. 6), the radial dataset was acquired at 1.8x1.8 mm² resolution and all acquired samples were used in the reconstruction but, by applying the apodizer (Eq. [3]), we reconstructed the images at a lower resolution, namely, 2.15x2.15 mm², with almost no ringing-induced dark-rim artifacts. The optimized apodization effectively eliminated the oscillatory side-lobes in the PSF, thereby eliminating nearly all of the ringing effects. Specifically, the peak PSF side-lobe amplitude was suppressed form −13.2% for nonapodized PSF to −1.6%, i.e., an 8.3-fold reduction.

Results from in-vivo studies clearly showed that the optimized radial imaging scheme can yield significant reductions in DRAs during the early myocardial enhancement phase of a FPP image series, where clinical interpretation of the DRA is most difficult. The quantitative artifact measurements (Fig. 7) show that the DRA width is on average slightly larger that 1 pixel along PE for Cartesian images. This is consistent with previous reports asserting that the DRA width for Cartesian imaging is typically 1-2 times the pixel width along PE (10,56-58). In contrast, the DRA width measurements for radial images indicate that, on average, the estimated width of the signal loss was smaller than a third of a pixel width, which is negligible. The average in-plane resolution for Cartesian images was approximately 1.8x2.8 ≈ 5.0 mm² and for radial images was 2.15x2.15 ≈ 4.6 mm², which is slightly better than the parallel-imaging-accelerated Cartesian scheme. It is clear that either method will not be capable of accurately resolving myocardial features that are smaller than ≈5 mm² in area (roughly 2 mm along x and y for radial images). Nevertheless, the 2.15x2.15 mm² resolution achieved by the radial FPP method is considered relatively high among conventional FPP schemes that do not use advanced reconstruction methods and/or temporal acceleration; e.g., in the recent work by Motwani et al. (27), spatial resolution of the conventional SENSE-accelerated Cartesian method is 2.5x2.5 mm². For all in-vivo studies, we deliberately performed the radial scans as the first perfusion scan (before Cartesian), which may have disadvantaged the radial FPP scans in term of the effect of residual contrast in potentially reducing DRAs for subsequent FPP scans.

In addition to ringing effects, there may be other potential contributing factors to the DRA as listed in Introduction. Further, it is difficult to decouple the contribution of each factor, e.g., motion versus ringing (19,59). Nevertheless, the left-to-right pattern of the observed DRAs in Cartesian images matches the PE direction (Fig. 6) and is consistent with described PSF ringing effects (Figs. 2(b1), 3(a1), and 5(b1)). Furthermore, the relatively low heart rates (rest scan), relatively small acquisition window (≈135 ms) and contrast dose (0.04 mmol/kg), all combined with short echo times (1.3-1.4 ms), alternating-readout-direction acquisition and local cardiac shimming should minimize the motion and susceptibility effects. All of these observations—in conjunction with our results and derivations—suggest that the main driver for reducing DRAs in our in-vivo studies is elimination of the PSF ringing effects, achieved by utilizing the optimized radial scheme. It is worth mentioning that a similar apodization scheme (tapered weighting of k-space data) can also be applied to the other non-Cartesian (60) or even Cartesian (9) datasets to reduce the ringing effects; however, for Cartesian datasets, the apodization will reduce the already-low PE resolution to unacceptable levels.

Relation to Previous Work

Recent studies using high-resolution Cartesian imaging with temporally accelerated k-t schemes (24-27) have shown success in reducing DRAs by decreasing the spatial width of Gibbs ringing effects as compared to conventional Cartesian schemes. These results imply that Gibbs ringing is most likely a significant, if not the dominant, contributing factor to the DRA. However, achieving such resolutions (1.3-1.8 mm isotropic in-plane) with Cartesian imaging inevitably requires a high level of temporal acceleration which has its own issues: the possibility of reduced temporal fidelity or loss of robustness due to modeling (“training data”) assumptions (56,61) especially with regards to breathing motion, and a need for specialized computational platforms. Furthermore, taking this approach, there is always the possibility that the images would still exhibit ringing-induced DRA with a 1-2 pixel width (e.g., the mean DRA width for rest imaging is reported to be 1.3-2.7 mm in (56)). In contrast, our approach is based on sampling design and optimization of the PSF without a need for additional acceleration beyond conventional parallel imaging. Indeed, the imaging experiments in this work were performed using frame-by-frame reconstruction, i.e., without temporal acceleration. Moreover, we refrained from using highly accelerated (e.g., compressed sensing or nonlinearly regularized) reconstruction to achieve a fair comparison with the conventional Cartesian imaging scheme. However, incorporation of an edge-preserving regularized reconstruction scheme, such as 2D total variation regularization combined with radial SENSE, may improve the image quality.

Limitations

Our studies were limited to rest perfusion scans (maximum imaged heart rate: 78 beats per minute). Previous works have suggested that stress imaging is more prone to DRAs, which has been attributed to higher degree of Gibbs ringing (7,10) and increased cardiac motion (19,59). Results of our phantom study suggest that, even for sharp signal-intensity discontinuities (6 to 1 ratio in Fig. 5), the optimized radial imaging method effectively eliminated ringing-induced DRAs. Therefore, similar results, i.e., significantly reduced DRAs compared to Cartesian imaging, are expected for stress imaging. Lastly, although our results show that the proposed optimized radial imaging scheme is effective in reducing DRAs, the diagnostic accuracy of this approach in terms of detecting subendocardial ischemia remains to be tested in future work.

Conclusions

Based on a series of systematic investigations, from theoretical and phantom experiments to in-vivo studies, we demonstrated that optimized radial first-pass perfusion imaging with wide k-space coverage and a simple reconstruction method can effectively eliminate ringing-induced dark-rim artifacts, while providing equivalent resolution and similar image quality as conventional Cartesian imaging. The potential clinical benefits of the proposed approach remain to be evaluated in patients with known or suspected coronary artery disease.