Encoding and decoding in parietal cortex during sensorimotor decision-making

Abstract

The lateral intraparietal area (LIP) of macaques has been asserted to play a fundamental role in sensorimotor decision-making. Here we dissect the neural code in LIP at the level of individual trial spike trains using a statistical approach based on generalized linear models. We show that LIP responses reflect a combination of temporally-overlapping task and decision-related signals. Our model accounts for the detailed statistics of LIP spike trains, and accurately predicts spike trains from task events on single trials. Moreover, we derive an optimal decoder for heterogeneous, multiplexed LIP responses that could be implemented in biologically plausible circuits. In contrast to interpretations of LIP as providing an instantaneous code for decision variables, we show that optimal decoding requires integrating LIP spikes over two timescales. These analyses provide a detailed understanding of the neural code in LIP, and a framework for studying the coding of multiplexed signals in higher brain areas.

Introduction

Perceptual decision-making is an important and experimentally-tractable cognitive ability that involves the timely integration of sensory, cognitive, and motor information. Recent work has hypothesized that the lateral intraparietal area (LIP) plays a key role in simple forms of perceptual decision-making. Much of this literature has focused on either normative models, which aim to derive the optimal decision-making strategy for a given task from first principles^1–8, or mechanistic models, which aim to qualitatively reproduce the dynamics governing neural activity in decision-making circuits^9–15. Although these lines of work have generated many intriguing hypotheses and experiments, both of these approaches start with strong assumptions about the function of LIP and a limited view of its functional heterogeneity.

Here we describe a data-driven, statistical approach for investigating the encoding and decoding of information in LIP spike trains during a sensorimotor decision-making task. We begin by formulating a generalized linear encoding model characterizing LIP spike responses as a function of the external variables of interest on the scale of individual trials. Encoding models have been used to describe and quantify information transfer in early sensory areas^16–19 as well as motor cortices^20–22 and rodent hippocampus^23,24, but have so far had limited application to decision-making areas^25–27.

A statistical model based approach differs from other methodologies in that it does not seek a particular mechanistic or normative theory of LIP function. Rather, it aims to develop a rich, descriptive model of the statistical features of LIP spike responses and their dependencies on task and behavioral variables. The primary challenge here is that, in contrast to primary sensory or motor areas, an area like LIP may reflect a panoply of signals, some of which are tightly coupled with known sensory and motor events, and some of which may be the product of more elusive cognitive operations^28–30. Here we show that the sort of generalized linear model (GLM) previously applied to spike representations in the early visual system can be extended to model LIP activity recorded during a decision-making task, in which many of the key elements of the task were variable, either temporally or in their value, and hence dissociable. The model reveals that LIP responses are best described as an interacting set of temporally-overlapping response components, implying that some of the spikes emitted during decision formation are potentially related to a number of factors, some of which are irrelevant to the accumulation of evidence. The model also provides a framework for understanding statistically optimal readout of various kinds of information from single-trial spike trains. Our analyses show that the superposition of sensory, decision, and motor variables encoded in LIP can be demultiplexed to read out decisions using a simple linear mechanism that spans multiple timescales. This encoding-decoding approach thus both identifies and then resolves a puzzle: LIP spike rates do not purely encode the accumulation of evidence during the formation of decisions, but LIP (or another area with similar responses) could feasibly be decoded to extract more choice-related information than conventional spike-counting analyses have suggested.

Generally, the analyses of LIP based on the GLM provide a detailed account of the time-varying information carried by LIP spikes, and operates at the level of single trials, providing a testing ground for interpreting the functional meaning of LIP spikes on the timescale of individual stimulus events and decisions. This approach provides a platform for quantitatively characterizing the information carried by LIP, for comparing LIP responses across experiments, and for assessing the adequacy of various theories of LIP function. After explaining the statistical model in the context of the moving dots task, we discuss the implications of this framework for a broader range of ongoing debates and future work surrounding LIP’s functional role in sensorimotor behaviors.

Results

We analyzed the spiking activity of 80 LIP neurons recorded from two monkeys while they performed a moving-dot direction-discrimination task³¹. In this well-known task³², monkeys view a random dot kinetogram and make decisions about the net direction of dot motion. They communicate their choice by making a saccadic eye-movement to one of two choice targets on the screen. From trial to trial, the fraction of dots moving coherently in the correct direction is varied, spanning a range of difficulties from easy (high coherence) to hard (low coherence). Fig. 1a illustrates the decision-making task and the variable timings of the four principal task elements: fixation point, choice targets, moving dots, and saccade. We varied the timings (and/or values) of the first three elements independently, and the saccade exhibited intrinsic timing variability as a part of the animal’s behavior (see Methods).

Figure 1. Decision-making task and classical analysis of LIP responses.

(a) The task requires an observer to fixate, judge the direction of a moving (dots) stimulus, and report a decision by moving the eyes to one of two targets. Temporal variability in the task design variables (indicated by gray arrows) allows for statistical dissociation of the effects of different extrinsic variables on neural responses. (b) Standard analysis of spike responses from an LIP neuron: Spike trains are conditioned on the stimulus coherence, the fraction of dots moving towards (’+’) or away from (’−’) the neuron’s response field, and aligned to the stimulus onset (left) or saccade time (right). Although the spike trains exhibit substantial variability (top), their average time-courses (below) exhibit coherence-dependent ramping. The gray area indicates the short portions of trials often considered in prior work³³.

Classical analyses of coding in LIP rely on the peri-stimulus time histogram (PSTH) aligned to events such as the onset of the moving dots or the occurrence of the saccade (Fig. 1b). Other approaches might regress binned spike rates against levels of various experimental variables, and are sometimes applied at the level of single trials or single neurons^7,33–35. Our model works at the resolution of individual spikes, neurons, and trials—quantifying the dependencies of the neural response on multiple task variables by regressing single trial spike trains against the timing and value of each variable represented on each trial—while also capturing the (autoregressive) influence of a spike history on subsequent spikes, and a nonlinearity associated with spike generation from these inputs. It is therefore possible to dissociate firing rate components associated with each element given the decorrelated design of the task components (e.g., trial-to-trial variability in the relative timings of events, and independent variation of intensities such as motion coherence relative to other factors), while also capturing the neuron’s own temporal response properties (e.g., refractoriness, burstiness, longer time scale autocorrelations).

Encoding: a description of the neural code in area LIP

An encoding model aims to describe p(r|x), the probability of a spike train response r given a set of external variables x on a single trial. Our model defines this probability in terms of a time-varying spike rate λ_t, given by

$${\lambda }_t=\text{exp}(\sum _i({\mathit{k}}_i*x_i)(t)+(\mathit{h}*{\mathit{r}}^{\mathit{\text{hist}}})(t)),\mathit{\text{conditional spike rate}}$$ (1)

where (k_i * x_i)(t) denotes linear convolution of x_i(t), the timecourse for the i’th external event (e.g., it’s zero everywhere except the time at which the saccade targets appear), with the linear filter or kernel k_i, which captures the time-varying relationship between this event and the neuron’s probability of spiking. The second term (h * r^hist)(t) denotes the linear convolution of the neuron’s spike history r^hist with the post-spike filter h. This filter allows the model to capture non-Poisson spike-history effects such as refractoriness, bursting, and spike rate adaptation. We illustrate these components in a model diagram shown in Fig. 2a.

Figure 2. Encoding model, fitted components, and rate predictions.

(a) The model specifies the probabilistic relationship p(r|x) between external variables x and a set of neural spike trains r. The parameters consist of linear weights specifying the neuron’s dependence on the external variables and spike history. (b) Illustration of fitted model components for an example LIP neuron. Because the nonlinearity is exponential, we can plot the exponentiated output of each filter as a gain signal reflecting the influence of each task element on the time-varying spike rate. These signals are combined multiplicatively to obtain the instantaneous spike rate, which drives spiking via a conditionally Poisson process with feedback (8 out of 12 total kernels shown; see Methods, Supplementary Figs. 1 and 2 for more detail). (c) Peri-stimulus time histograms (PSTHs) predicted by the model (above) and computed from real data (below). Each trace reflects a different coherence level and saccade direction.

Under this model, the probability of a spike train for a single trial is given by a Poisson likelihood:

$$p(\mathit{r}|\mathit{x},\theta )=\prod _{t=0}^{T}p(r_t|\mathit{x},\theta )\propto \prod _{t=0}^T{(\Delta {\lambda }_t)}^{r_t}{e}^{-\Delta {\lambda }_t},\mathit{\text{encoding distribution}}$$ (2)

where Δ is the time bin size, T is the number of time bins in the trial, r_t is the spike count at time t, and θ = {{k_i}, h} are the model parameters.

Fig. 2 illustrates the model fit to data from a typical LIP neuron. To provide intuition for the model’s basic capabilities, we plot the three kernels related to the three primary task elements that occur on each trial: (1) the appearance of the choice targets; (2) the moving dots stimulus; and (3) the saccade made by the monkey to indicate a decision (either into or out of the response field of the neuron under study, which we refer to as IN and OUT). At right, we plot the predicted time-varying change in spike rate due to each task element, for each of five possible motion coherences and two possible saccade directions (Fig. 2b). For each component, we show the linear convolution of the kernel with the timecourse of the corresponding task element, and passed through an exponential nonlinearity. The resulting traces show the multiplicative effect of each task element on the neuron’s probability of spiking. The product of three such components, forms the predicted spike rate for a single trial (Eq. 1). These predictions closely match the neuron’s actual PSTH (Fig. 2c).

Randomness and variability in the timings of experimental events are essential factors for dissociating the different components of the response. For example, if the interval between the onset of the choice targets and the saccade were constant, we could not differentiate spikes time-locked to the targets from those time-locked to the saccade. Similarly, stimulus kernels for each motion coherence can be dissociated thanks to randomized coherences and duration, despite having onset locked to the appearance of targets. The large number of task elements makes for a large number of model parameters; we therefore fit kernels in smooth temporal basis and applied Bayesian regularization methods to prevent over-fitting (see Methods). We verified the fits via PSTH prediction (Fig. 3b), single trial prediction on the test set (Fig. 5a), time-varying spike count variance (Supplementary Fig. 4), and inter-spike interval statistics (Supplementary Fig. 5).

Figure 3. Encoding model captures responses across a heterogeneous population.

(a) Fitted model components for five additional neurons (columns 1–5), showing the relative contributions of targets, moving dots, and saccades to the predicted spike rate of each neuron (rows 1–3) and predicted and observed PSTH (rows 4–5) as in Fig. 2. The population exhibits substantial heterogeneity across neurons: e.g., the fourth neuron’s PSTH peaks early and then declines, regardless of choice (column 4, bottom row), yet the model still extracts a classical “ramping” choice-related component (3rd row). More unusually, the fifth neuron’s choice-dependent component (5th column, row 3) exhibits a time-dependent reversal, meaning that early in the trial, the neuron fires more spikes before saccades to the anti-preferred (OUT) target. (b) Goodness-of-fit across the population. Each point corresponds to the percent of variance accounted for in the PSTH of each neuron.

Figure 5. Spike history effects captured by the post-spike filter.

(a) Spike train prediction accuracy, quantified by the log-likelihood per spike under the model fit with and without spike history (cross-validation data). Positive values indicate how much better each model is compared to a baseline model (homogeneous Poisson). The model with post-spike filters captures an average of 137% more information about single-trial spike trains. (b) Spike train autocorrelations computed on neural data (blue), and on spike trains simulated from the model fit without (green) and with post-spike filter (red). The model with a post-spike filter almost perfectly captures the empirical autocorrelation function (red curve overlaps blue curve). Example cells chosen to illustrate the diversity of history effects. (c) Fitted post-spike filters for the three neurons shown in b. These filters express the multiplicative change in spike probability as a function of time since a spike. These effects accumulate across multiple spikes, allowing the model to capture the complex temporal structure observed in the autocorrelations in b. See Supplementary Fig. 2 for diversity in population.

Previous work has shown that LIP neurons are heterogeneous³⁶, with diverse response characteristics during the moving-dots task³¹. We fit the model to each LIP neuron in the dataset, and found that it captures the responses of both conventional and radically unconventional LIP neurons with high accuracy (Fig. 3a). The fitted model parameters reveal that LIP neurons carry information about a variety of task elements, and that the output of each LIP neuron reflects a roughly multiplicative combination of signals (Supplementary Fig. 6 and Supplementary Fig. 7). Furthermore, individual cells may encode these elements in distinct ways, both in terms of overall magnitude and in more nuanced aspects of the time course. This cell-by-cell analysis suggests that the striking differences in PSTHs may arise from the combination of heterogeneous task-related components that can now be considered in isolation at the level of single neurons.

In addition to capturing the average timecourse of neural activity for different stimulus and choice conditions, the model can predict spiking activity on single trials from the timings and values of task elements (Fig. 4). Despite the diversity of responses across trials and across neurons, the model captures the details of single-trial spike rate modulations very well, on par or better than the model’s account of the full PSTH. Note that these predictions are unique to each neuron, and differ for each trial because the task elements have randomized times.

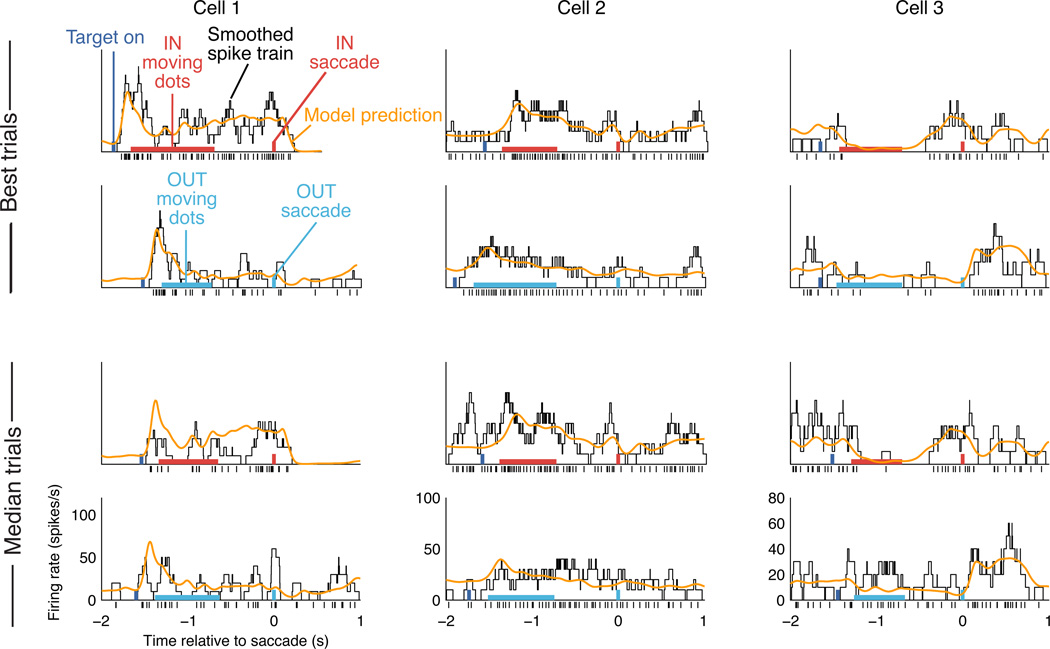
Figure 4. Model-based single trial predictions.

Each column shows 4 example trials from a single neuron. Black ticks at the bottom indicate the observed spike train, and the black trace shows an estimate of spike rate obtained by smoothing the spike train with a 100 ms boxcar. Colored rectangles show the timing and identity of task elements for the trial in question (targets, moving dots, and saccade), and the orange trace shows the model-based spike rate prediction for that trial. The top two rows show example cross-validation trials for which prediction accuracy was highest, while the bottom two rows show example trials with median prediction accuracy. More trials are shown in Supplementary Fig. 3.

Single-trial prediction accuracy improves even further when the model includes a post-spike filter, which captures the effects of spike history on a neuron’s probability of firing (Fig. 5a). The autocorrelation functions of spike trains in LIP vary substantially across neurons (Fig. 5b), and frequently exhibit fine timescale structure that is inconsistent with a Poisson response model (or a Poisson model with refractory period). A model without post-spike filters cannot account for the detailed shape of these autocorrelation functions, yet the full model captures them accurately. The fitted post-spike filters (Fig. 5c) reveal detailed and diverse shapes that are not obvious from the autocorrelation function. One striking observation is that for these neurons, the probability of firing is enhanced for more than 200 ms after a spike (but not much longer; see Supplementary Fig. 8). Note that such a long timescale of self-excitation is a statistical description (as opposed to a proposed recurrent mechanism), and reflects a form of temporal integration above and beyond that explained by the components linked to external task elements. Despite their contribution to spike train prediction, it is reassuring that the inclusion of the post-spike filters in the model exerts only a modest scaling effect on the other temporal kernels (i.e., the median correlation coefficient of the kernels fit with or without the post-spike filter is 96%, and the median scaling effect is 75%).

We can validate the use of an exponential nonlinearity by non-parametrically reconstructing the nonlinear relationship between filter output and firing rate, and we find a close match between the non-parametric estimate and an exponential (Supplementary Fig. 6a). This is consistent with multiplicative interaction among components (but see Supplementary Fig. 6b,c for comparison to rectified linear function), which is critical for the statistically optimal linear decoding mechanism we will describe below.

Together, these parts of the encoding model—linear kernels for task variables, a post-spike filter, and an approximately exponential nonlinearity—work together to capture the statistical relationship between LIP responses and various external and internal variables relevant to a sensorimotor decision-making task, enabling the model to predict spike trains on single trials and capture the fine structure of each cell’s autocorrelation function. These results suggest that, despite LIP’s cognitive function and more distant relation to simple sensory and motor processing, simpler neural signals may make up the bulk of LIP responses and can be captured by a type of statistical model already shown to be successful in sensory and motor circuits. However, the value of the encoding model goes beyond its ability to account for what makes an LIP neuron respond during the dots task, as we demonstrate below with an application for decoding (or de-multiplexing) of decision-related information from single-trial responses.

Decoding: readout of decision-related information from LIP spike trains

Encoding models specify an explicit probability distribution over neural activity given a set of external task variables. They also provide a powerful tool for analyzing the readout of information from spike trains. In this particular application, we can decode decisions from spiking activity in LIP by using the fitted model to evaluate the probability of the spikes on a single trial under both possible choices (i.e., saccades to one target or the other). For each trial, the model provides a prediction in the form of a Poisson spike rate hypothesized to have generated the activity on that trial. Intuitively, decoding amounts to evaluating whether the spikes are more probable under the rate function consistent with a saccade IN or an OUT of an LIP neuron’s response field.2

Fig. 6a shows spike trains and corresponding rate predictions for pairs of randomly-selected IN and OUT trials from three different neurons. By considering the spikes up to each point in time, we can obtain a time-varying estimate of the animal’s eventual decision (shown below each trial’s spike train and rate predictions). Note that these probabilistic estimates diverge from 0.5 (the prior probability of an IN decision) as soon as the rate predictions diverge. For the six trials shown, the decoder achieves near certainty (probability of an IN choice close to one or zero) by the time of saccade, although this does not occur for all trials or in all neurons.

Figure 6. Single-trial prediction and model-based decoding of spike trains.

(a) Single trial responses from three neurons, for one randomly selected IN (top row) and OUT trial (bottom row) spanning a range of coherences. For each trial, the model predicts time-varying spike rate both under IN (red) and OUT (blue) choices. Model-based decoding amounts to assessing whether the observed spikes on a single trial (black ticks) are more likely generated from IN or the OUT spike rate. (Thin black traces show estimated rate by filtering spikes with a 100 ms boxcar, for visualization purposes only). Thick black traces (below) indicate the probability that the monkey will saccade IN given the spikes observed so far in the trial, as computed under the model. When the model predicts a higher rate for the IN choice, every spike evokes a jump in the probability of an IN choice, whereas silence evokes a gradual decrease. (b) Red and blue traces show saccade-related model components for movements IN or OUT of the neuron’s RF. The difference of these components gives linear decoding weights (black), which determine how spikes from each neuron should be integrated in order to optimally predict the saccade direction. (c) Traditional and model-based choice probability (CP), as a function of time interval used to integrate spikes, for zero-coherence trials (cross-validation data). Traditional CP (red) weights all spikes in the decoding window equally, while model-based CP (black) uses the time-dependent weights shown in b. Model-based CP exceeds or matches traditional CP for nearly all time windows, and accurately deciphers the peculiar time-varying decision signal from Cell 3 (shown previously in Fig. 4, column 5) using weights that change sign midway through the trial. (d) Comparison of traditional and model-based choice probability for all neurons in the population, using spikes at least 50 ms prior to saccade on zero-coherence trials. Vertical and horizontal lines show SD bootstrap confidence intervals. For the majority of neurons in the population, model-based decoding supports more accurate readout of the animal’s decisions from LIP spike trains.

Formally, model-based decoding of the animal’s decision relies on the posterior distribution over choice given the spikes, which can be derived from the encoding distribution using Bayes’ rule. If we assume that IN and OUT choices are equally probable a priori, the posterior probability is given by

$$p(x_c=\text{IN}|\mathit{r},\mathit{x̃})=\frac{p(\mathit{r}|x_c=\text{IN},\mathit{x̃})}{p(\mathit{r}|x_c=\text{IN},\mathit{x̃})+p(\mathit{r}|x_c=\text{OUT},\mathit{x̃})},\mathit{\text{decoding distribution}}$$ (3)

where x̃ denotes all other covariates besides the choice direction component x_c. The posterior probability of an OUT choice is simply 1 − p(x_c = IN|r,x̃), as the posterior must sum to 1.

Fortuitously, these posterior probabilities can be computed very simply under our model. For a GLM with Poisson noise and exponential nonlinearity, Bayesian decoding can be achieved with a linear weighting of the spike response. Specifically, the log-likelihood ratio (LLR), which is also the log of the ratio of posterior probabilities, is given by

$$\mathrm{L}\mathrm{L}\mathrm{R}=\text{log}\frac{p(x_c=\text{IN}|\mathit{r},\mathit{x̃})}{p(x_c=\text{OUT}|\mathit{r},\mathit{x̃})}={\mathit{w}}^{\mathbf{T}}\mathit{r}+\mathit{\text{constant}},\mathit{\text{linear decoding}}$$ (4)

where w denotes a set of linear decoding weights over time, and the additive constant does not depend on the response r (see Methods). The LLR leads to a simple decoding rule for predicting the animal’s choice: whenever LLR > 0, an IN saccade is more probable; whenever LLR < 0, an OUT saccade is more probable. The optimal decoding weights are in fact given by w = k_IN − k_OUT, the difference of the fitted saccade kernels for IN and OUT choices (see Fig. 6a).

Bayesian decoding of decisions from LIP spike trains can therefore be implemented with a set of time-varying linear weights. The shape of each neuron’s weight profile tells us how much information that neuron’s spikes carry about the animal’s decision, as a function of time before the movement. The weights determined empirically from data challenge the view that instantaneous spike rate encodes the animal’s accumulated evidence for a decision, as they frequently extend out to 1.5 s before the movement, indicating that spikes from LIP should themselves be integrated over a relatively long window to optimally predict the decision. Note that this linear readout mechanism would not be statistically optimal if the nonlinearity were not exponential, since our model technically sits within the family of log-linear models with “Poisson-like” noise known as probabilistic population codes (PPC)^6,37,38.

This decoding analysis supports a model-based extension of the basic concept of Choice Probability (CP), a metric for quantifying the information that neural responses carry about an animal’s decision³⁸. Conventional CP applies to scalar quantities such as spike count, and assumes that the optimal rule for reading out a pair of neuron and “anti-neuron” responses is to choose the option with larger response (a “max” decoding rule). Model-based CP, on the other hand, can be defined using any model-based decoding rule, and applies to non-scalar representations of neural activity such as a binned spike train. If we assume an anti-neuron for the neuron we are decoding to have exactly the same model weights, except with swapped choice related decoding weights k_IN for k_OUT, and vice versa), then a simple comparison rule for the projection to both neurons suffices for decoding, because the threshold is exactly the same for both neurons. We can therefore decode choices using the model-based projection of a spike train, instead of simple spike count.

The key difference between conventional CP and model-based CP is that the model weights provide the relative importance of different time bins for reading out the choice. Fig. 6b–d shows a comparison of model-based and conventional choice probability for quantifying decoding performance. Model-based CP outperforms conventional CP as the time window grows towards the saccade (Fig. 6c). Moreover, model-based CP increases almost monotonically, while conventional CP fluctuates more around chance levels. Conventional CP is clearly inadequate for decoding LIP neurons like example cell 3, where the polarity of rate associated with IN trials and OUT trials are reversed through time. But even for the more canonical example cell 1, model-based decoding extracts significantly more decision-related information than the conventional approach. Model-based CP is on average 6.2% point higher than conventional CP on average (mean model-based CP, 75.2%; mean traditional CP, 69.9%). Fig. 6d illustrates the advantage of model-based decoding for a population of 80 neurons.

Implementation: low-dimensional readout of LIP population activity

So far we have considered the problem of decoding choices from spikes in LIP using an ideal observer with access to the saccade time and other task variables for the trial in question. This perspective is useful for determining theoretical limits on the accuracy with which downstream neurons could read out choice-related information from LIP, but it does not necessarily appl to neurally plausible readout mechanisms. At first glance, statistically optimal readout seems difficult due to the fact that each neuron has a unique decoding-weight profile, and these weights exhibit significant cell-to-cell heterogeneity.

However, there exists a practical mechanism for population readout that requires no knowledge of the saccade (or decision) timing, is insensitive to other task variables, and flexibly accommodates the heterogeneity of the temporal decoding weight profiles—but which still performs very close to theoretically optimal decoding. First, we can compute the linear projection of the spike trains onto the decoding weights in continuous time via linear filtering: at each time the output of the linear filter is exactly the log-likelihood ratio (Eq. 4) for a “preferred” saccade at the current time. Second, instead of projecting to the time-varying decoding weights associated with each neuron—which are highly diverse Fig. 7a (top row)—we can approximately decompose each decoding weight as a linear combination of a few principal components of the collection of decoding weights (Fig. 7a bottom row), and then sum the results. Indeed, we find that the constellation of decoding weights are well spanned by 2 principal components (explaining 93.3% of the variance). To represent the total log-likelihood of LIP neurons corresponding to the same decision (i.e., with overlapping RFs), the filter outputs corresponding to each RF can simply be summed. Third, we find that the “decoding subspace” spanned by these two principal components can be well approximated by a pair of exponential filters. This simplifies the problem of implementation because, while single neurons may not be able to perform arbitrary time-dependent weightings of spikes on the timescale of a second, a neuron or a population of neurons can naturally implement a leaky integrator. We find that two exponential filters e^−t/τ with τ = 237,410 ms explain 92.1% of the variance of the seemingly diverse decoding weights (dashed lines in Fig. 7a). Finally, we posit the existence of two competing populations, each integrating evidence for one of the choice alternatives (i.e., two opposite RF locations), with balanced contributions from the other response components so that the influence of the other task variables cancels.

Figure 7. Decoding from low dimensional decoding weight space.

(a) Top, decoding weights from all cells. Bottom, corresponding principal components (PC) that span the weights (numbers indicates variance explained). Dashed lines show the 2 PCs approximated with 2 optimized exponential functions (τ = 237,410 ms). For more details, see Supplementary Fig. 9 and Supplementary Table 1. (b) Schematic for decoding LIP neurons. Two populations with opposing RFs have corresponding readout populations. Each neuron projects to a subpopulation that filters their spiking activity with first order dynamics. The population response is averaged within the two pools of neurons that compete with each other to control the saccade. (c) Decoding performance comparisons on zero-coherence trials assuming neuron-antineuron pools. Higher log-likelihood ratio implies easier distinction between the choices given a pair of trials.

Fig. 7b shows a schematic of the proposed decoding circuit: (1) Each subpopulation of LIP neurons associated with the same choice/RF project to two readout populations with appropriate weights, (2) each readout population acts as a simple first-order temporal filter with different time constants, (3) the overall activity of the readout population can be instantaneously summed to represent choice activity, and (4) through a winner-take-all mechanism the choice information is selected, then transmitted to the motor system that controls the saccade.

The proposed scheme yields compelling improvements over traditional decoders (Fig. 7c): Decoding performance using the model-derived weights is substantially better than simply adding the spike counts in a fixed time window (i.e., a boxcar). Moreover, decoding with two leaky integrators performs virtually as well as with the seemingly complex individual decoding weights.

In summary, this decoding scheme lays out one plausible way to read out the choice given the population activity of LIP neurons. It characterizes how decision-related information is represented in the temporal evolution of population spiking activity. The dimensionality reduction implementation shows that this information could be exploited by a biologically-reasonable neural circuit. This exercise suggests that statistically-optimal readout of decisions could be implemented by neural circuits that read out the activity of LIP, even in the face of multiplexed signals and considerable heterogeneity across neurons.

Invariance to target-induced changes in firing

In addition to its neural plausibility, the decoding mechanism we have proposed achieves performance that is invariant to firing rate modulations induced by variables not directly relevant to the task. In particular, we manipulated the visual saccade targets so that on half of the trials they persisted until the end of the trial ("targets-ON" trials), while on the other half they flashed briefly and then disappeared ("targets-FLASH" trials; the animal made a saccade to the remembered, stereotyped target location). Although this manipulation did not affect choice behavior, it produced large changes in spike rate in many neurons³¹. This presents a major challenge to models in the prior literature that regard the firing rate of an LIP neuron as a direct neural correlate of log-likelihood ratio or some other normative quantity⁵. Our descriptive model, however, capture the effects of target removal through a multiplicative interaction with a target-related kernel. (Although saccade endpoints were affected by the targets-FLASH manipulation, the single target-based kernel appears sufficient to account for the changes in LIP response; see also⁴⁰).

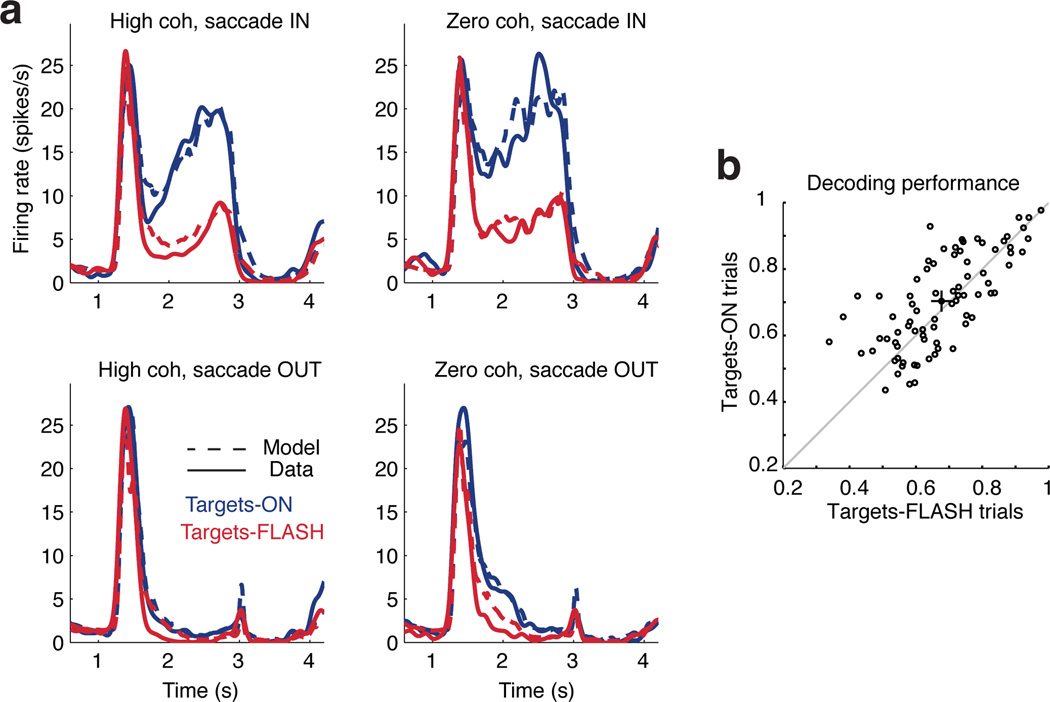
Fig. 8a shows an example neuron that reduces its response drastically when visual targets are extinguished early in the trial (i.e., before the onset of the moving dots). The model captures the difference with a single filter aligned to the time when targets disappear. Furthermore, model-based decoding is unaffected by the inclusion of this component, and there is negligible difference in decoding performance for the two kinds of trials (Fig. 8b). This robustness indicates that the superposition of the target-related kernels and the decision-related (saccade-locked) kernels is appropriate. More generally, it demonstrates that additional decision-irrelevant factors that affect LIP responses in other tasks might similarly be isolated so as to preserve the readout of decisions.

Figure 8. Targets absent manipulation.

(a) On half of the trials, the targets disappeared early (Targets-FLASH condition), which often resulted in large changes in firing rate (blue vs. red curves). The encoding model captures this effect well with a single kernel aligned to target offset. The four sub-panels show high (left), zero (right) coherence conditions for IN (top) and OUT (bottom) eventual saccades. (b) Decoding performance of zero-coherence trials with and without targets (80 neurons). Using the same decoding kernel, the trials can be decoded almost as well. Filled circle indicates the population average with standard errors. Decoding targets-ON trial is 2.6% easier (p-value 0.003; paired t-test), a significant but small effect.

Discussion

We have developed a generalized linear model to describe LIP responses during a complex perceptual decision-making task. This framework yields several new insights into the coding of information in LIP spike trains. First, it reveals that representations in LIP are multiplexed: they can be decomposed into separate components related to the targets, the visual stimulus, and the eventual saccadic decision; the superposition of these components, in turn, provides accurate prediction of spike responses on single trials. Second, LIP neurons exhibit notably long-time-scale self-excitation that is statistically separable from the effects of sensory and motor drive, an effect that can be captured with a spike-history dependent model component. Third, despite substantial population-level heterogeneity in LIP response characteristics, decision-related information is well captured by a two-dimensional linear projection of the spike trains, which leads to an implementation of statistically optimal decoding using a pair of leaky integrators with distinct timescales.

Our model-based approach assumes that the spike rate at any time depends on a combination of multiple task components. By exploiting the randomized structure of the experimental design on a single-trial basis, our analysis shows that LIP activity can be well modeled as reflecting a superposition of contributions from different sources. This result mirrors insights recently reported in rodent⁴¹ and other primate²⁸ decision-making tasks. The dominant normative model in the context of the moving dots task—drift diffusion to bound—takes the coherence-dependent ramping signals seen in averages as a neural correlate of an evolving decision variable. This framework assumes that the instantaneous firing rate in LIP should reflect the eventual choice. Our analysis adds a dimension to this perspective, suggesting a readout rule involving much longer temporal integration of LIP response, on the time scale of seconds. In other words, if LIP is the critical encoder of the accumulation of evidence, an optimal mechanism would still need to decode it using a time-varying weighting function, as opposed to simply thresholding its instantaneous spike rate. Time-varying decoding weights may be more generally applicable in other contexts for which a fixed threshold on LIP responses has also been shown to be untenable⁴².

Multiplexing applies even to the decision formation period, where spikes are influenced by the moving dots stimulus, but also by the placement of the choice targets and the upcoming saccade. Although LIP clearly carries decision-related signals, the mixture of sensory, cognitive, and motor signals that simultaneously affect it argues against the assumption that it is a pure integrator underlying the accumulation of sensory evidence^28–30. Instead, our encoding analysis suggests that LIP should be regarded as the recipient of multiple task-related signals, only some of which are directly related to the formation of decisions. Our decoding analyses show that it is still possible to read out decisions in the face of this multiplexing, with higher accuracy than indicated by conventional choice probability. This perspective raises the possibility that the difficulties in distinguishing between various functional roles of LIP (e.g., attention/salience, decision-making, motor intention) may have arisen because LIP does not have single functional role, but because it simultaneously encodes multiple signals that are at least partially separable downstream. The application of descriptive statistical models in other tasks and task variants may thus provide the means for further integration of visual, attentive, decisional, and motor function in LIP. Further causal manipulations of the circuit are likely necessary for a definitive resolution, but our statistical analyses have shown that the information is multiplexed at encoding and can be demultiplexed by a plausible readout stage. One implication is that if LIP responses are critical for decision-making, future empirical work should shift focus from demonstrating the encoding of various cognitive factors in LIP, to how these complex signals are de-multiplexed by later stages of neural processing.

Although our model provides an illuminating perspective on LIP function, it is not without limitations. It makes very few assertions about the function of LIP, but does require making some assumptions in the structure of the model. However, these assumptions amount to decisions about how to represent external, observable variables within a regression framework, and thus involve far less conceptual baggage, and a tighter reliance on the data, than normative approaches. In this initial report, we attempted to use the simplest approach, modeling brief events as impulses and prolonged events as boxcars. Future work will benefit from more nuanced manipulation and modeling of finer-grained temporal structure on each trial. Additionally, prior applications of generalized linear models have provided insights into the form of dependencies between neurons and the relevance of correlated firing to information carried by a neural population; such analyses motivate follow-up work that involves recording multiple cells simultaneously⁴³. Our findings about neurally plausible implementations of decoding also motivate future investigations into how or where the brain might accomplish readout involving simultaneous recordings in multiple brain areas. Indeed, work in related structures and paradigms has already been to explore how neurally-constrained models of the oculomotor system can be applied^44,45.

Dynamical models provide another kind of approach to understanding the function of area LIP¹³, and such models have been elaborated to include multiple factors that drive LIP, such as the response to visual targets¹¹. A key difference is that such models start with a semi-biological circuit structure that constrains the neural dynamics, and the framework for adding other components is rather flexible. Statistical models of the kind we propose could complement these models by providing a principled technique for assessing which components to incorporate; these models may thus provide a key tool not just for interpreting LIP activity, but for linking normative and mechanistic models of the sorts already proposed in this context^6,13,46,47.

More generally, we note that a variety of both classical and recent controversies regarding LIP’s functional role have relied on attempts to dissociate or isolate various response components. For example, a recent paper reported that LIP responses were modulated by the magnitude of either appealing or aversive outcomes (consistent with a "salience" account) as opposed to being sensitive to value (in the neuroeconomic sense) per se⁴⁸. A follow-up debate then focused on whether the data were generalizable, owing to the lack of strong persistent activity seen during the task^49,50. Our analysis could provide a path towards resolution of this sort of debate, by testing whether persistent activity can be modeled as an independent driver of the LIP response (in which case, its presence or absence is irrelevant to the salience/value issue), or whether it indeed interacts with salience/valuation. The latter outcome would not just demonstrate that persistent activity is necessary to observe value signals in LIP, but would suggest intriguing computations that link these two components.

More consideration will be required to create families of experimental designs amenable to analysis via the generalized linear model. However, we feel that the framework promises both to enrich interpretations within well-studied paradigms and to pave the way for more ambitious and direct tests of hypotheses about higher brain function²⁷.

Online Methods

The data analyzed in this paper were initially described in a previous empirical report³¹. Here, we briefly summarize the experimental methods as most important to the analyses described here.

Preparation, neurophysiology, and tasks

All procedures were performed in accordance with National Institutes of Health guidelines and the Institutional Animal Care and Use Committee at the University of Texas at Austin. Two male rhesus macaque monkeys underwent surgery for implantation of a head-holder and a recording chamber over the posterior parietal cortex. A single electrode was advanced into LIP based on anatomical references, and was further located by signature neural activity observed during an instructed saccade task, which was also used to locate the response field (RF) of a neuron. Only neurons that were spatially selective during an instructed saccade task are included in this paper³¹. After the RF was determined using an instructed saccade task, the neuron’s spiking responses were recorded during the decision task.

The decision task was a standard variable-duration moving-dot direction-discrimination that has been used previously. In order to achieve fixation at a trial’s start, the monkey’s eye position had to register within a window around the central fixation point within 3 seconds of fixation point appearance. The monkey then needed to maintain eye position within that window until the fixation point vanished, which was the “go-signal” for the monkey to make a saccade to a target.

500 ms after the monkey achieved fixation, two saccadic target choices appeared. One choice target was located in the RF of the neuron (the IN choice), whereas the other choice target was diametrically opposite (the OUT choice). Randomly, on half of the trials, the targets disappeared after 100 ms (in figures showing PSTHs or single trials, we show only the “targets-ON” trials). 200 ms after the appearance of the choice targets, a motion stimulus appeared in a circular aperture and the monkey had to decide the net direction of motion and communicate their decision with a saccade to one of the two choice targets.

The algorithm for generating the dot motion display was identical to that used in prior LIP studies by Shadlen and colleagues^31,33. Motion coherence strengths of 0, 3.2, 6.4, 12.8, 25.6 and 51.2% were used. At 0% coherence (no motion on average), the monkey was randomly rewarded with 50% probability. After the motion was displayed for a specified time (500–1000 ms, uniform distribution), the motion stimulus vanished. The monkey continued to maintain fixation for another 500 ms until the fixation point also disappeared, thus signaling that he could now saccade to the correct target location to obtain a reward. The monkey received a liquid reward 200 ms after eye position entered the spatial window around the correct target. The monkey was considered to have made a saccade to a target location if eye position registered within the spatial window around the target location within 100 ms after leaving the fixation point window. Entry into the spatial window around the target also had to occur within 450 ms after the go-signal to be considered a complete trial. About 800–1200 trials were collected per recording session (per neuron).

Plotting neural response

PSTHs were smoothed with a gaussian filter (standard deviation, 75 ms). In Figs. 2 and 3, each conditional PSTH was stitched together by averaging temporally overlapping local PSTHs of length 500–1000 ms that were obtained by aligning at the median event time. The spike trains corresponding to fixed windows around the aligned time are collected and averaged to obtain the local PSTHs. For example, for the dots motion event, we aligned to the onset and offset separately with −25–600 ms and −400–500 ms time windows, respectively. Conditional PSTHs with less than 20 trials are not shown and were excluded from the variance explained analysis.

Trials in Fig. 4 were chosen by sorting the mean square error between the predicted spike rate and the boxcar smoothed spike trains within the 2 second window around saccade time. Only the correct decision trials with high coherence in the cross-validation set were used.

The autocorrelation function R(τ) was normalized by the mean firing rate m to quantify excess spike rate:

$$R(\tau )=\frac{1}{m}(\frac{1}{N(\tau )}\sum _{t}r(t)r(t-\tau ))-m,$$

where t is over all bins, r(t) is the binned spike train, and N(τ) is the number of bins such that both r(t) and r(t − τ) are valid. We have removed the 0-th lag component from the autocorrelation plots in Fig. 5b.

Model parameter representation

The spike trains were discretized into 1 ms bins. Each event was represented as a delta-function over time, and convolved with a filter (or a kernel, see Supplementary Fig. 1). We used smooth temporal basis functions defined by raised cosine bumps separated by π/2 radians (50 ms) to parameterize the filters (see Supplementary Fig. 10). Each event kernel was represented as a linear combination of basis functions that cover a specified range of time: 2 s window after fixation point onset, 1 s window after target onset, 4 s window after target disappearance, and 500 ms window after the dots disappearance. For the saccade response, we had two kernels, one for each direction which was anti-causal for 2504 ms for monkey J, and 2662 ms for monkey P and with total duration of 5.3 s. We grouped the directional coherence levels into 5 groups (to reduce the number of parameters): one for zero-coherences (0%), and two each for high (51.2%, 25.6%, 12.8%), and low (6.4%, 3.2%) in each direction. The dot-motion stimulus was represented as a boxcar of corresponding duration, and the filter duration for each coherence level was 800 ms. The post-spike history filter was parameterized by 20 linear weights; ten 1 ms uniform basis (to represent the fast refractory effects) followed by ten raised cosine basis stretched in a logarithmic scale that spanned 265 ms¹⁷ (see Supplementary Fig. 10). The total number of parameters for each neuron was 402 (or 422 with post-spike history filter) from the 11 (or 12) filters above. To facilitate visual interpretation, a rank-2 parametrization was used for the 5 coherence kernels for Figs. 1 and 2.

Fitting

The encoding model was fit by maximizing the log posterior, where we used a ridge prior to regularize the weights:

$$ℒ(\theta )=\sum _{t=0}^T(r(t)\text{log}({\lambda }_t\Delta )-{\lambda }_t\Delta )-\xi {\Vert \theta \Vert }^2,$$

where θ is a vector representing the weights on the basis functions, and ξ is chosen from a grid to maximize the marginal likelihood. The marginal likelihood p(r|ξ) = ∫ p(r|θ,ξ)p(θ|ξ)dθ was computed using Laplace approximation. For each neuron, we divided the trials randomly into five equally-sized sets to perform 5-fold cross-validation. Maximizing marginal likelihood for selecting the hyperparameter ξ is known as “evidence optimization”, and it does not require cross-validation, hence we only use cross-validation sets for evaluating the resulting fits.

Goodness-of-fit in Fig. 3 was computed on the stitched PSTH smoothed with a 25 ms Gaussian for each stimulus coherence and behavioral choice pair. Conditions with less than 30 trials were discarded from the comparison. Spike prediction accuracy in Fig. 5a were computed by taking the difference between the full model log-likelihood and the log-likelihood of a (single parameter) homogeneous Poisson model normalized by the number of spikes on the cross-validation set¹⁷.

Decoding

We derive the log-likelihood ratio (Eq. 4) decoding rule. Let t_c be the time when the decision is read out.

$$\mathrm{L}\mathrm{L}\mathrm{R}=\text{log}\frac{p(\mathit{r}|\mathit{x̃},x_c=\text{IN})}{p(\mathit{r}|\mathit{x̃},x_c=\text{OUT})}=\text{log}\left[\prod _{t=0}^T\Delta {\lambda }_t{(x_c=\text{IN})}^{r_t}{e}^{-\Delta {\lambda }_t(x_c=\text{IN})}\right]-\text{log}\left[\prod _{t=0}^T\Delta {\lambda }_t{(x_c=\text{OUT})}^{r_t}{e}^{-\Delta {\lambda }_t(x_c=\text{OUT})}\right]=\sum _{t=0}^T{r}_t\text{log}(\Delta {\lambda }_t(x_c=\text{IN}))-\Delta {\lambda }_t(x_c=\text{IN})-r_t\text{log}(\Delta {\lambda }_t(x_c=\text{OUT}))+\Delta {\lambda }_t(x_c=\text{OUT})=\sum _{t=0}^T{r}_t(\sum _{\mathrm{i}\ne \mathrm{c}}({\mathit{k}}_i*x_i)(t)+({\mathit{k}}_c^{\text{IN}}*x_c)(t)+(\mathit{h}*{\mathit{r}}^{\mathit{\text{hist}}})(t)-\sum _{\mathrm{i}\ne \mathrm{c}}({\mathit{k}}_i*x_i)(t)+({\mathit{k}}_c^{\text{IN}}*x_c)(t)+(\mathit{h}*{\mathit{r}}^{\mathit{\text{hist}}})(t))+\mathit{\text{constant}}=\sum _{t=0}^T{r}_t\left(\right({\mathit{k}}_c^{\text{IN}}*x_c)(t)-({\mathit{k}}_c^{\text{OUT}}*x_c)(t))+\mathit{\text{constant}}=\sum _{t=0}^T{r}_t({\mathit{k}}_c^{\text{IN}}(t-t_c)-{\mathit{k}}_c^{\text{OUT}}(t-t_c))+\mathit{\text{constant}}={\mathit{w}}^{\mathbf{T}}\mathit{r}+\mathit{\text{constant}}$$

where the constant terms do not depend on r.

Note that the dot product can be computed continuously at every time point by a simple linear filter since ${\mathit{w}}^{\mathit{T}}\mathit{r}={\sum }_{i=1}^{L}w(i)r(t-L+i)=\mathit{w̃}*\mathit{r}(t)$ where L is the length of the weight vector, w̃ is the time reversed weight, and r(t) is the length L vector of response approaching up to t.

Choice probability (CP) quantifies the dependence between the spike counts of a neuron and a binary decision variable while keeping all sensory information constant. Given a randomly selected IN trial, and an OUT trial, the probability that the higher spike count belongs to the IN trial is CP. A high CP implies that the spike count contains much “information” about the decision. CP in Fig. 6c,d was computed by randomly drawing 1000 pseudorandom (IN, OUT) pairs of trials. We estimated repeated this procedure 40 times to obtain the error bars. For the traditional CP, we used the spikes count in the −1500–50 ms window before the saccade detection (for Fig. 6c, the beginning of the window was fixed at −1500 ms, and x-axis shows the end of the window). For the model-based CP, spike trains on the cross-validation set were projected with the weights obtained from the corresponding training set.