A Comparative Approach to Hand Force Estimation using Artificial Neural Networks

Abstract

In many applications that include direct human involvement such as control of prosthetic arms, athletic training, and studying muscle physiology, hand force is needed for control, modeling and monitoring purposes. The use of inexpensive and easily portable active electromyography (EMG) electrodes and position sensors would be advantageous in these applications compared to the use of force sensors which are often very expensive and require bulky frames. Among non-model-based estimation methods, Multilayer Perceptron Artificial Neural Networks (MLPANN) has widely been used to estimate muscle force or joint torque from different anatomical features in humans or animals. This paper investigates the use of Radial Basis Function (RBF) ANN and MLPANN for force estimation and experimentally compares the performance of the two methodologies for the same human anatomy, ie, hand force estimation, under an ensemble of operational conditions. In this unified study, the EMG signal readings from upper-arm muscles involved in elbow joint movement and elbow angular position and velocity are utilized as inputs to the ANNs. In addition, the use of the elbow angular acceleration signal as an input for the ANNs is also investigated.

Introduction

In applications, such as control of prostheses,1,2 sports medicine3–5 or ergonomic design analysis,6 the measurement of muscle or limb force is required. The use of force sensors for interface in normal operation is often impractical or inconvenient for direct measurement of forces. Additionally, the high cost of commercially available force/torque sensors makes the alternate method of force estimation from a group of muscles using electromyography (EMG) signals, which requires only comparatively inexpensive electrodes, very attractive.7 The estimated force/torque can also be used for research in biomechanics and muscle physiology.8,9

The torque induced at each body joint is generated by muscle actuators driving the motion of that joint. The generated force in muscles is caused by two processes; activation dynamics and muscle contraction dynamics.10 Muscle contraction dynamics include the mechanical properties of muscle tissues and tendons, which are expressed as force-length and force-velocity relations. The activation dynamics include the voluntary and non-voluntary excitation reflex signals and motor unit recruitment level in muscle. It is well-known that regardless of fatigue, the generated torque in each joint is dependent on muscle activation level (MAL) and joint angle when in a stationary position.11,12 When in motion, joint torque is also a function of joint angular velocity.13 Therefore, joint torque (and force) can be predicted using EMG signals, and joint angle and velocity measurements. In this work, it is assumed that the wrist and shoulder angles are fixed. Thus, hand force can be determined directly from elbow torque.

In the past, parametric and non-parametric model-based approaches have been proposed for muscle force or human joint torque estimation using EMG signals. Parametric approaches have used the Hill muscle model,8,9,14 which takes muscle MAL as an input and outputs the generated muscle force based on muscle length and contraction speed.13 Musculoskeletal kinematic models15 and inverse-dynamics models16 have also been employed to derive joint torque. Nonparametric model-based methods use polynomial functions,1,10,17 linear regression,18 Volterra-series,19 Fast Orthogonal Search (FOS),9,20 Parallel Cascade21 or ANNs.22–27 The advantage of non-parametric estimation of the EMG-force relationship is that it does not require any knowledge about muscle and joint dynamics. Moreover, they often have the capability of accounting for nonlinearities in the EMG-force relationship.

Clancy and Hogan17 proposed the use of a third-order polynomial to estimate the generated torque in the elbow joint under isometrica and quasi-isotonicb conditions. An off-line least squares method was employed to identify the polynomial coefficients. Misener and Morin used an exponential force/velocity function in addition to a third-order polynomial model to estimate the elbow torque.10 The prediction was accurate within 10% for elbow flexion and extension under isotonicc conditions. Clancy et al. used a 15th-order linear finite impulse response (FIR) model to map EMG to torque errors within 7.3% of maximum voluntary contraction during isometric contractions.18 Xu et al.19 and Hashemi et al.21 employed second-order Volterra series and parallel cascade methods to find the EMG-Force relation during isometric flexion of the human elbow joint. Mobasser et al.20 used the FOS, a nonlinear identification method, to map EMG to force. They proposed that the FOS-based force observer would select its pre-determined basis functions from a pool of candidate functions consisting of groupings of linear, cross and square root terms and sinusoidal functions. Later, Mountjoy et al. incorporated Hill-based muscle model as the candidate functions for more accurate force prediction and for estimating upper-arm muscle physiological parameters.9

The first use of ANN for EMG-based force estimation was reported by Sepulveda et al. where they proposed an MLPANN to estimate joint moments in human gait.22 The EMG signals from 16 leg muscles were fed to the ANN to estimate joint moments of the hip, knee and ankle. Savelberg et al. employed MLPANN with a back propagation training method for the estimation of a cat leg dynamic tendon force using recorded EMG data and kinematic information (joints angle and velocity).23,25 The ANN could estimate non-trained data with the root mean square error (RMSE) of less than 15%, under dynamic contraction conditions. Luh et al. utilized the EMG signals collected from the biceps and triceps, and elbow joint angle and velocity in an MLPANN to estimate the elbow joint torques under isokineticd contractions.24 In a hybrid approach, Wang et al.27 employed an MLPANN with two hidden layers to predict the MAL from the EMG signal recorded from the agonist and antagonist elbow muscles. The predicted MAL was then input to a Hill muscle model to calculate the generated muscle force. Finally, the estimated muscle force was employed in an elbow joint geometric model to predict the joint torque. Since the actual MAL was not available, an adjusted back-propagation method was used to train the ANN. The use of MLPANN, such as in the above, has been reported for force estimation on various anatomies of humans or animals under single or often dissimilar operational conditions.

Radial Basis Function ANN (RBFANN) has mostly been used for EMG signal classification.28,29 It has also been used along with acceleration and force data collected during walking to replicate EMG signals from major lower limb muscles for gait analysis.30 RBFANN has also been used to identify changes in the truck muscle stiffness during a sudden load.31 To the authors best knowledge, RBFANN has been reported only for predicting muscle forces using evoked electromyogram (EEMG) signals.32,33 In this work,e RBFANN will be employed in addition to the MLPANN architecture on the data collected from a single human anatomical feature, i.e. elbow joint. The performance of the two ANN architectures will be experimentally studied and compared on a 1-DOF exoskeletal robotic testbed under the same set of operational conditions, i.e. isometric, isotonic and light load.

Methods

In this paper two major architectures are utilized: MLPANN and RBFANN. These two ANNs are both known as universal approximators for nonlinear input-output mapping, which are briefly introduced.35,36

Multilayer Perceptron ANN (MLPANN)

MLP network architecture mimics the structure of the neural networks in the human nervous system. It consists of an interconnection of multiple layers of neurons (Fig. 1A) and can have more than one hidden layer. In the MLP architecture (as shown in Fig. 1A), all the outputs in each layer are connected to the inputs of neurons in the next layer. Moreover, each node has a bias input. The sigmoid function f (x) = 1/(1 + e^−x) is often utilized as the activation function, which behaves like a smoothed step function. To train the network for the corresponding weight for each node, the back-propagation method is used. In this method, the error measure for an input vector x is considered to be

$$E=\parallel e\parallel =\parallel y-\widehat{y}\parallel$$ (1)

Figure 1.

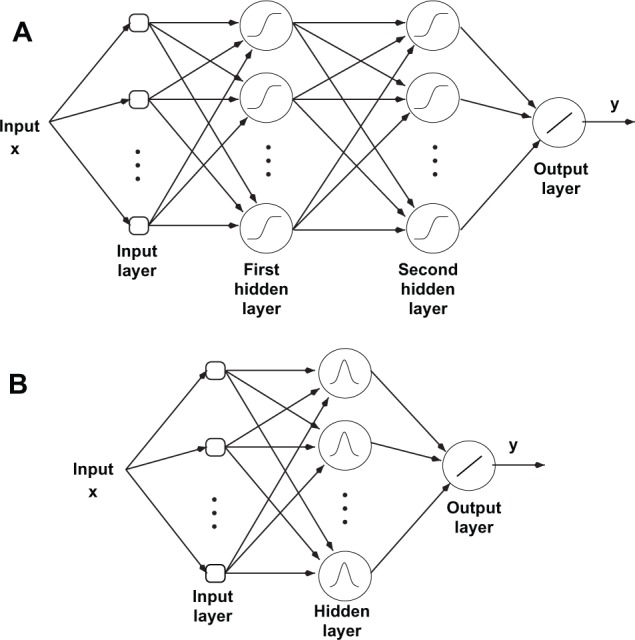
(A) MLPANN architecture; (B) RBFANN architecture.

with y as the desired output, and ŷ as the output of the network, where ||·|| is the vector Euclidean norm and e is the output error. To train the network, the error measure E is minimized by employing an optimization algorithm such as Gradient decent, Conjugate gradient, Quasi-Newton or Levenberg Marquardt (LM).37 The LM method is commonly used in situations involving function approximations with less than a hundred neuron weights where accuracy is paramount.37 The LM training method can be implemented in the MATLAB Neural Network Toolbox using the TRAINLM function. The training algorithm can be written as

$${\mathrm{W}}_{k+1}={\mathrm{W}}_k-{[{\mathrm{G}}_k^{T}Gk+\delta \mathrm{I}]}^{-1}{\mathrm{G}}_k^T{e}_k$$ (2)

$${\mathrm{G}}_k=\frac{\partial e_k}{\partial {\mathrm{W}}_{k-1}}$$ (3)

at the kth time iteration, where W is a vector of all network weights, G is the gradient vector of the network errors and δ is an adjustable scalar. When δ is zero, the algorithm is Newton’s method, whereas for large δ the algorithm becomes a gradient descent algorithm.

Radial Basis Function ANN (RBFANN)

On the other hand, an RBF network is constructed of a summation of a number of exponentially decaying localized nonlinear functions (e.g. Gaussian), approximating the input-output mapping globally (Fig. 1B). An RBF network has a single hidden layer, as opposed to an MLP network that can have more than one hidden layer. The output of an RBFANN with N nodes, as shown in Figure 1B, is expressed by

$$y={\displaystyle \sum _{i=1}^N{w}_{i}f(\parallel {\mathrm{x}}_i-{\mu }_i\parallel )}$$ (4)

where w_i is the weight of the output layer for neuron i. f (·) is an RBF function that decreases (or increases) monotonically as the distance between the input x and centroid point μ_i increases. The parameter vector μ_i = (μ_i1, …, μ_iM) describes the centroid coordinates of the ith node of an RBF network, where M is the dimension of input x.

The Gaussian f_g with constant σ described by

$$f_g(u)=e^{-{(u/\sigma )}^2}$$ (5)

is the most commonly used radially symmetric function. To train for the centroid and output weight for all nodes, that is

$$w_1,\dots ,w_N,{\mu }_1,\dots ,{\mu }_{{\rm N}}$$ (6)

the error measure (1) is minimized by using an optimization method, such as the gradient descent method. The optimization is initiated with a random choice of parameters.

RBF is generally faster in the learning process and insensitive to the order of presentation of training data. As a drawback, the number of neurons in RBF, which is necessary to reach a desired accuracy, may be large.

ANN-based Hand Force Observers

Figure 2 illustrates the schematics of the MLPANN and RBFANN force observers. The inputs to the ANNs are the EMG signals recorded from the upper-arm muscles (biceps brachii, triceps brachii, brachialis, and brachioradialis) and the elbow joint angle and angular velocity. The network output is the estimated hand force. The neural networks are trained off-line using the network input data and measured force collected under different conditions, as will be explained in Section 4 (Fig. 2A). The trained networks will then be used for force estimation for real-time applications. The use of elbow joint angular acceleration as an input to ANN will also be explained in Section 5.

Figure 2.

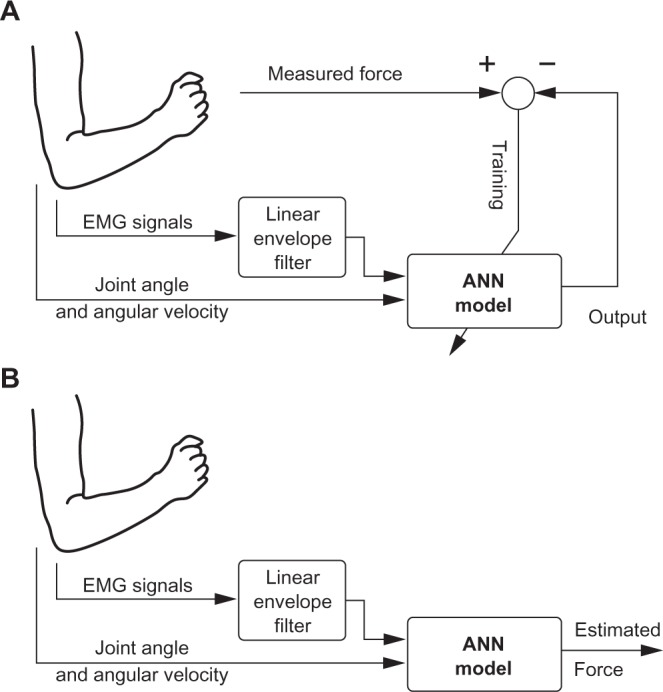
Schematics of the proposed ANN for hand force estimation. (A) Training phase; (B) Operation phase.

One important parameter of choice is the number of nodes in each layer. By increasing this number, training performance improves at the cost of an increase in training time. On the other hand, increasing the number of nodes does not necessarily help the network generalization; hence the network may not truly estimate the hand force. Tests will be conducted in Section 5 to find the number of nodes for both RBFANN and MLPANN resulting in the best achievable generalization for the networks for real-time applications with high accuracy.

Experimental Setup and Procedures

Experimental setup

Figure 3 shows the Queen’s University Arm (QArm1), used for the implementation and comparison of the two MLPANN and RBFANN based force observers. The apparatus is composed of a platform accommodating a Maxon DC motor, a 4:1 cable-driven power transmission system, and an aluminum bar on which the subject’s arm is placed. In this design, the subject’s upper-arm is fixed in position with a brace and the wrist is placed in a second brace attached to a pivoting bar through an ATI Gamma 6-DOF force/torque sensor. The axis of rotation of the bar pivot is aligned with the elbow’s axis of rotation. A high resolution encoder signal provides the motor shaft angle, which is proportional to the elbow angle. The resolution of elbow angle measurement is 1/4000 of a degree. The apparatus can apply up to 6.32 Nm continuous torque to the elbow joint, which is mapped to about 16 N at the wrist. The Quanser WinCon/Venturcom RTX real-time control system is employed for data collection and control of the apparatus at the rate of 1 kHz.

Figure 3.

The 1-DOF experimental setup (QArm1).

To collect EMG signals from upper-arm muscles, active electrodes containing differential amplifiers are employed to cancel the effect of environmental electromagnetic interference. The recorded raw EMG data is passed through a linear-envelope filter.38 The bias of the recorded EMG is detected by applying a moving average filter, and is removed from the original signal. The resulting signal is then rectified and passed through a second moving average filter with a size of 300. This produces 150 ms of delay in the final EMG signal. The filter length and the resulting delay are chosen to match the average delay between the collected EMG signal (or motor nerve excitations) and the force generated by the muscle.13

Experimental procedure

Electrode attachments

EMG signals are collected from the four muscles biceps, tricps, brachialis and brachioradialis. Due to the size of the biceps and triceps muscles multiple electrodes are placed at different locations for more accurate results. The subject’s shoulder and wrist are placed in the arm braces ensuring that the upper-arm is stabilized and the elbow joint axis coincides with the bar rotation axis. The shoulder is stabilized at 90° abduction, 15° horizontal adduction and neutral pronation-supination. Subjects are asked to relax all muscles not directly involved in elbow flexion/extension.

EMG normalization

The level of EMG readings is dependent on skin impedance at the electrodes location, which may vary between experimental sessions. To compensate for this variability, the EMG readings have to be normalized for each recording session and after electrode placement. A widely used EMG normalization method is the Maximum Voluntary Contraction (MVC) method,13 in which the subject is asked to maximally contract the muscle under study. The corresponding EMG reading is used for normalization of EMG readings from that muscle. The MVC method was originally employed by mobasser, et al. for EMG normalization in the but did not produce satisfactory estimation results.20 In fact, using the MVC method raised concerns about whether or not subjects generated the true maximum force.13

As an alternative approach, at the beginning of each experiment, 6 Nm torque is applied by the robotic arm to the elbow joint in the flexion and extension directions, while the subject is asked to keep the elbow angle at 0° flexion.f The average value of the recorded EMG is used for the normalization of the collected EMG data from the biceps and brachioradialis in flexion and from the lateral triceps in extension. This method has shown better results in comparison to the MVC method. In the case of operation outside a laboratory environment where QArm1 or any other manipulandum is not available, the subject can be asked to hold a specific weight for EMG normalization.

Experiments

In each experiment, after normalization, the elbow joint kinematics and muscle EMG data are recorded under the following sequence of conditions:

Light Load

No torque is applied to the elbow joint by the QArm1 and the subject is asked to move her/his arm in a random pattern for 50 seconds. The only load that is sensed by the subject is the light inertia of QArm1.

Isotonic

QArm1 applies a constant torque to the subject’s elbow joint while the subject moves her/his arm in a random pattern. Equivalent wrist force level of 5 N and 10 N are applied at the joint both in flexion and extension directions for a total duration of 50 seconds.

Isometric

The subject performs a number of isometric flexion and extension tasks at the elbow position of 0° and 30° degrees, while QArm1 is held fixed by the subject’s free hand. The level of force applied by the subject is variable and arbitrary.

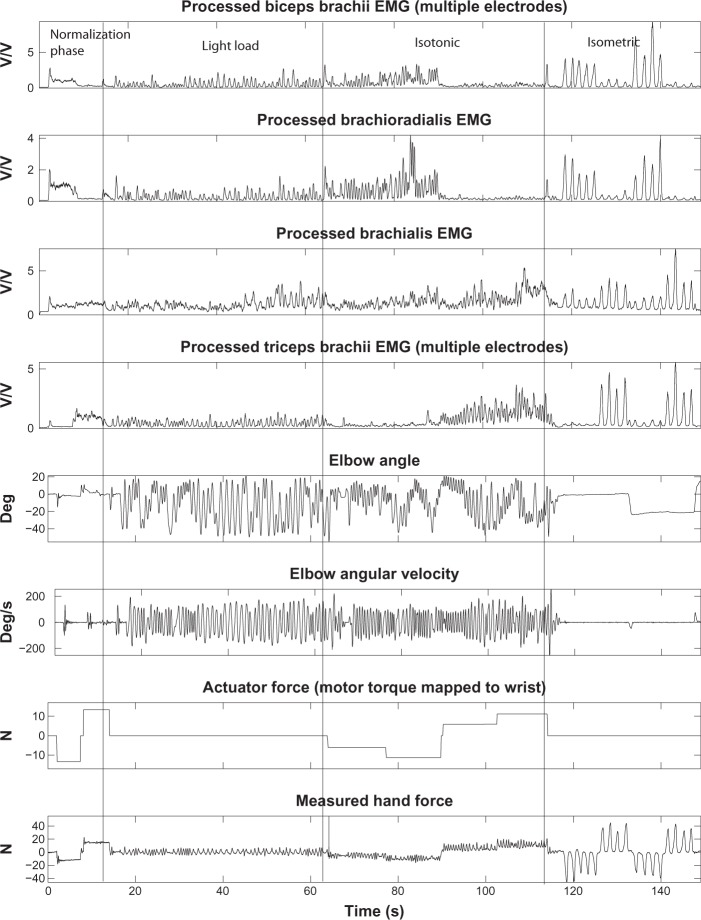
For this research, EMG data were collected from the right arm of two female and six male subjects with an average age of 27 and a standard deviation of 5 years. The subjects had no known neuromuscular deficits in their right shoulder, arm or hand. Informed consent was received from each subject and the experiment protocol was explained to each subject prior to the experiment. For each experiment type, subjects were tested in three sessions each. In each recording session, the above described experiment was conducted four times and four sets of data were recorded. The three sessions were conducted at three different times to study the intra-session effect of variations in human subject physiology and EMG electrode placement. The outlier data that were mainly caused by faults in EMG readings, due to amplifier saturation or electrode detachment from skin, were excluded. Therefore, for each experiment type, up to a maximum of twelve data sets were collected and kept for the analysis of each subject performance. Sample data collected from subject F1 performing experiment type I is shown in Figure 4.

Figure 4.

Sample data set recorded from subject F1 performing experiment type I.

Note: The EMG data are expressed in V/V since they are normalized.

Experimental Results

Network settings

In MLPANN, a hyperbolic tangent sigmoid function and linear function were used as activation functions for hidden layers and output layer nodes, respectively. Before training network, the input and output data in each training set were normalized to [−11] to correspond to a [minimum maximum] range of the data. Moreover, the data from the validation sets were normalized by the [minimum maximum] range of the training set. Since the RBFANN activation function is Gaussian and does not saturate, the inputs of RBFANN were not normalized. To avoid overtraining,24 the collected data were down-sampled by 10 for both the MPLANN and RBFANN.

To avoid networks from being trapped in local minima in training processes, ten networks were trained for 1000 epochs with a very small target training goal (smaller than the lowest estimation error that the networks could meet). The best performing network was chosen and trained for an additional 1000 epochs. The codes were implemented in MATLAB on a 3GHz Pentium 4 CPU.

Evaluation criteria

To validate the trained networks, each network was evaluated against all data sets with the three criteria, Relative Mean Square Error (RMSE), Cross-Correlation (CC) and Average Absolute Error (AAE) as formulated below

$$\begin{array}{l}RMSE=100*\frac{{\sum }_i{(y_i-{\widehat{y}}_i)}^2}{{\sum }_i{y}_i^2}\\ CC=100*\frac{{\sum }_i{y}_i*{\widehat{y}}_i}{\sqrt{{\sum }_i{y}_i^2}\sqrt{{\sum }_i{\widehat{y}}_i^2}}\\ AAE=\frac{{\sum }_i|y_i-{\widehat{y}}_i|}{n}\end{array}$$

where y_i and ŷ_i are the measured and the estimated hand forces, respectively, and n is the number of samples. Cross-correlation is a measure of similarity between y and ŷ of the signals regardless of scaling. The closer the value is to 100, the higher the level of similarity between signals.23 In conditions such as light load in which measured force is very small, RMSE becomes very large, hence AAE serves as a better performance index than RMSE.

Number of nodes

Different number of nodes were examined for both types of networks. Two hidden layers were chosen for MLPANN since it is proven that a network type with two hidden layers can approximate any continuous function.35 The average RMSE for validation results for a different number of nodes in the first and second layers for subject M1 are shown in Figure 5. MLPANN with two hidden layers, 4 nodes in the first layer and 3 nodes in the second layer demonstrated the best generalization and the most consistent performance. For RBFANN, as shown in Figure 6, although the training average RMSE is at its minima for a node number higher than 3, the average RMSE for validation which determines network generalization is a minimum within the range of 30–50 nodes. Therefore, 40 nodes are chosen for the RBFANN network.

Figure 5.

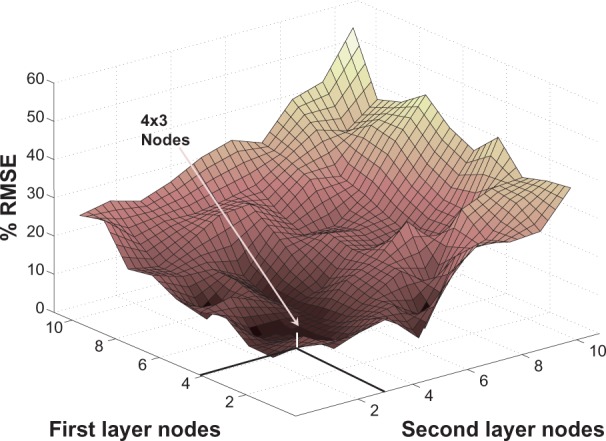
MLPANN architecture. Average RMSE of the validation results for subject M1 for different number of nodes in the first and the second hidden layers.

Figure 6.

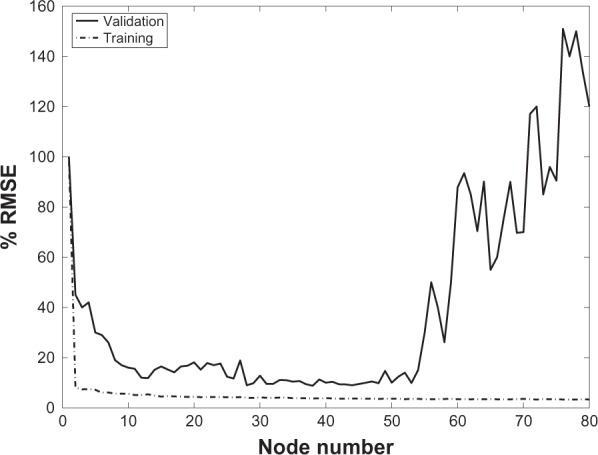
RBFANN architecture. Average RMSE of the training and validation results for subject M1 for different number of nodes.

The training elapsed time for the two network architectures, trained with full-length data collected from experiment type I, is shown in Table 1. The results indicate that training RBFANN is approximately 5–6 times faster than MLPANN. The inclusion of the acceleration signal in ANN inputs increases the training time, with a larger effect on RBFANN. For real-time operations, the online calculations of ANN output takes a fraction of a second since it only requires a forward pass of inputs through the network.

Table 1.

Average training time for MLPANN and RBFANN architectures.

	MLPANN	RBFANN
With acceleration	52.26 sec	12.43 sec
Without acceleration	50.98 sec	8.89 sec

Multiple electrodes vs. single electrode

In this work, multiple electrodes were used on biceps and triceps muscles. Three electrodes were placed on the belly of the triceps brachii long head, lateral head and medial head, and two electrodes on the belly of the bicep brachii short head and long head. The locations follow the SENIAM39 recommendations, which are on the line between the acromion and the fossa cubit at 1/3 from the fossa cubit for the biceps and at 50% on the line between the acromion and the olecranon for the triceps. To combine the measured electrodes data and achieve the best overall EMG, the processed and normalized EMG signals from electrodes corresponding to a specific muscle (e.g. Biceps) were averaged at each instance of time.

The ANNs provided better performance when averaged EMG from multiple electrodes were utilized instead of a single electrode for biceps and triceps muscles. The validation results after training on full-length data for all subjects using single-electrode and multiple electrodes EMG data are displayed in Table 2. It can be observed that the use of multiple-electrodes improved force estimation performance by 10%–70%, verifying the results reported in.40 Therefore, in this paper, multiple-electrode EMG data from the biceps and triceps muscles have been collected and input to ANNs.

Table 2.

Average RMSE (standard deviation) of the validation results over 11 data sets for RBFANN network trained with full-length data for single-electrode and multiple-electrode EMG readings.

	Subj. F1	Subj. F2	Subj. M1	Subj. M2	Subj. M3	Subj. M4	Subj. M5	Subj. M6
Single-electrode	16 (3)	20 (7)	21 (6)	31 (15)	62 (64)	17 (5)	40 (11)	35 (18)
Multiple-electrode	14 (4)	11 (4)	7 (1)	9 (4)	32 (11)	14 (3)	24 (4)	20 (7)

Estimation results

The 12 data sets acquired from each subject across three sessions were used for training 12 networks. Each trained network was validated with the remaining 11 data sets. The network that provided the best validation and generalization performance was recorded. Then the same procedure was conducted for the three segments of data corresponding to the three subtasks, light load, isotonic and isometric. Each subtask resulted in 12 networks out of which one was chosen for the best validation. The training and validation RMSE, RMSE standard deviation, AAE, CC and CC standard deviation results, averaged over all subjects, are presented in Table 3. The detailed training and validation RMSE, RMSE standard deviation, AAE for each subject are also presented in Table 4 in Appendix A.g The right-hand columns represent the result for each subtask based on training with the corresponding subtask of the data for the particular task.

Table 3.

Average RMSE (standard deviation) [AAE] and CC averaged over all subjects using the full-length and subtask data.

	Full-length data set used for training					Only subtask data used for training
	Full-length	Isometric	Isotonic	Light load (LL)	LL + accel.	Isometric	Isotonic	LL	LL + accel.
Verification average for RMSE (standard deviation) [AAE]
RBF	16 (8) [7]	12 (6) [11]	34 (29) [6]	[3]	[3]	14 (9) [12]	17 (6) [4]	[1.2]	[0.9]
MLP	26 (15) [10]	15 (11) [10]	111 (43) [11]	[5]	[5]	12 (8) [9]	13 (7) [4]	[1.1]	[0.9]
Verification average for cross correlation (standard deviation)
RBF	93 (4)	95 (3)	88 (6)	57 (18)	47 (18)	94 (3)	90 (4)	72 (9)	85 (6)
MLP	85 (8)	93 (4)	54 (27)	27 (20)	23 (20)	94 (4)	92 (5)	75 (7)	80 (12)

Note: The results for the best performing architecture are shown in boldface.

Table 4.

Experiment type I results. Average of RMSE (standard deviation) [AAE] for validation using the full-length and subtask data.

	Full-length data used for training					Only subtask data used for training
	Full-length	Isometric	Isotonic	Light load (LL)	LL + accel.	Isometric	Isotonic	LL	LL + accel.
Sub. F1
RBF	14 (4) [4]	11 (4) [6]	17 (8) [3]	[2]	[2]	11 (4) [6]	13 (4) [3]	[1.3]	[0.9]
MLP	32 (6) [6]	12 (3) [9]	65 (81) [7]	[5]	[4]	9 (2) [1]	8 (2) [2]	[1.3]	[1]
Sub. F2
RBF	11 (4) [6]	11 (5) [12]	8 (2) [3]	[1]	[2]	19 (3) [16]	9 (2) [1]	[1.3]	[0.7]
MLP	31 (5) [10]	7 (2) [10]	118 (27) [12]	[7]	[6]	7 (1) [10]	4 (1) [2]	[0.8]	[0.7]
Sub. M1
RBF	7 (1) [7]	5 (2) [11]	22 (11) [6]	[3]	[3]	9 (6) [14]	26 (11) [4]	[1]	[0.6]
MLP	17 (6) [10]	11 (6) [15]	89 (16) [9]	[6]	[3]	9 (7) [14]	28 (15) [5]	[1]	[0.7]
Sub. M2
RBF	9 (4) [6]	5 (2) [8]	27 (19) [6]	[5]	[3]	3 (1) [7]	17 (5) [5]	[1]	[0.8]
MLP	17 (2) [9]	4 (2) [8]	97 (23) [12]	[5]	[3]	5 (2) [8]	13 (10) [4]	[0.8]	[0.9]
Sub. M3
RBF	32 (11) [7]	22 (9) [13]	51 (41) [6]	[5]	[4]	18 (10) [11]	27 (16) [4]	[1.8]	[1.6]
MLP	55 (11) [10]	32 (11) [14]	102 (23) [9]	[7]	[8]	29 (16) [4]	15 (10) [3]	[1.8]	[1.8]
Sub. M4
RBF	14 (3) [7]	11 (3) [11]	20 (8) [4]	[3]	[3]	7 (2) [9]	17 (7) [4]	[1.4]	[1.1]
MLP	23 (5) [8]	9 (3) [10]	98 (3) [10]	[2]	[2]	7 (3) [9]	10 (5) [3]	[1.4]	[1.1]
Sub. M5
RBF	24 (4) [8]	21 (3) [14]	28 (13) [6]	[2]	[1]	33 (17) [17]	15 (5) [4]	[0.7]	[0.4]
MLP	29 (2) [9]	14 (4) [11]	106 (11) [10]	[2]	[7]	9 (2) [9]	9 (7) [3]	[0.6]	[0.5]
Sub. M6
RBF	20 (7) [10]	13 (4) [15]	99 (15) [10]	[4]	[4]	15 (6) [16]	15 (5) [4]	[1.3]	[0.8]
MLP	5 (31) [17]	34 (25) [5]	210 (71) [15]	[8]	[6]	17 (9) [19]	21 (6) [6]	[0.8]	[0.7]
Average of verification results
RBF	16 (8) [7]	12 (6) [11]	34 (29) [6]	[3]	[3]	14 ([12]	17 (6) [4]	[1.2]	[0.9]
MLP	26 (15) [10]	15 (11) [10]	111 (43) [11]	[5]	[5]	12 (8) [9]	13 (7) [4]	[1.1]	[0.9]

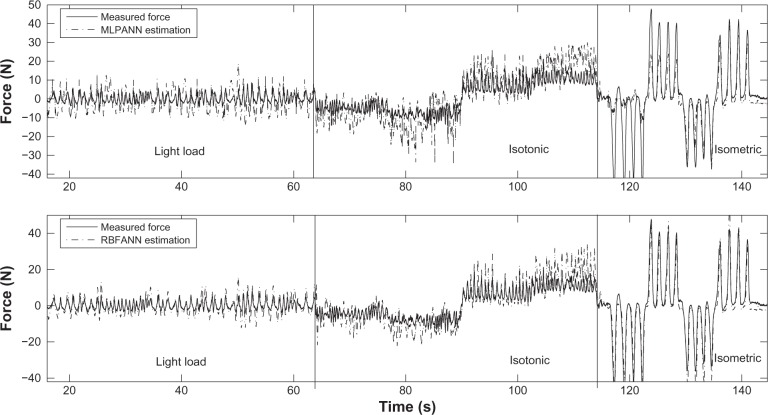
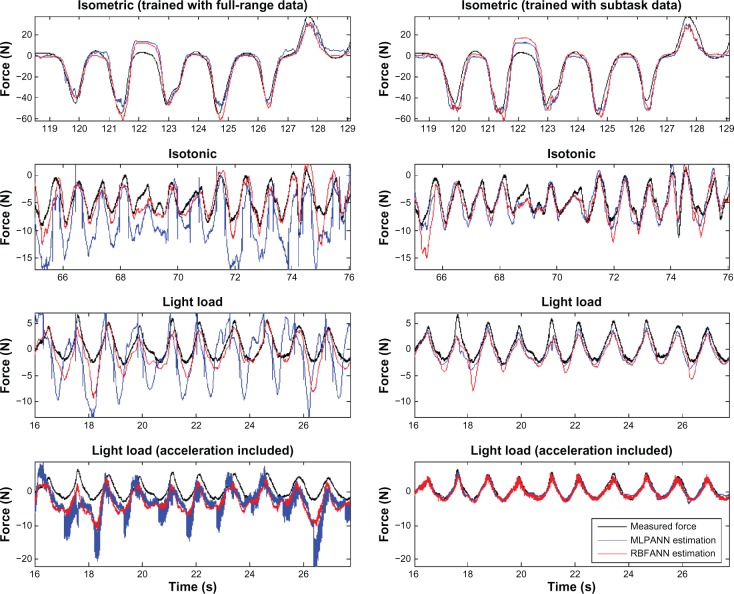
The validation results for the isometric condition for both networks trained with full-length data are significantly better than those obtained under isotonic and light load conditions. This can also be seen for subject F1 in Figure 7. In the light load condition, since the measured forces are significantly smaller, the RMSE values are very large. Therefore, the AAE serves as a better performance measure. In general, looking at the RMSE and CC values, both networks are unable to provide accurate estimation of hand force in light load. This is because under the light load condition the recorded EMG signals are small and as such not rich enough for training. The trained network with task subset data performs better since they are trained for the specific condition for which they are validated. This performance improvement can be observed by comparing the sub-figures in the left and the corresponding right-hand columns in Figure 8.

Figure 7.

MLPANN and RBFANN validation results for subject F1 after training on full-length data.

Figure 8.

MLPANN and RBFANN validation results for subject F1 after training on full-length data (left) and subtask data (right).

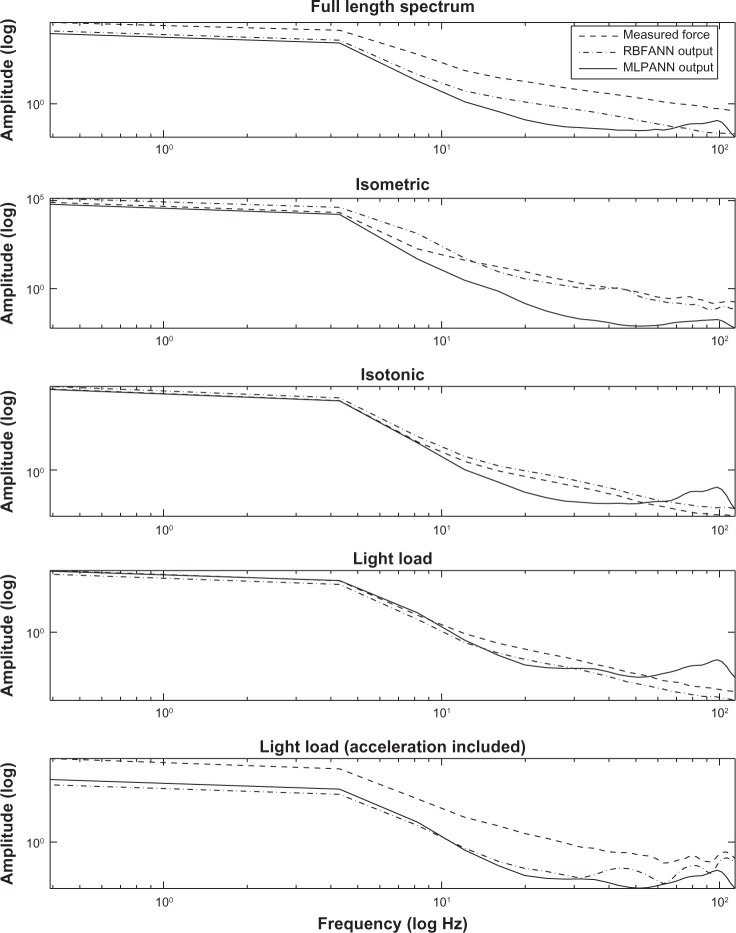
Comparing the performance of the two ANN architectures, RBFANN provides a better estimation for each subtask or all three tasks after full-length data training. However, MLPANN performs better when training is done for a specified subtask such as isotonic and isometric tasks. Adding acceleration as an input to ANN improves the RMSE and CC in the light load condition after training with subtask data, as shown in Figure 8 for RBFANN. The frequency domain analysis results in Figure 9 verify the above results. It can be observed that RBFANN and MLPANN have close performance in isotonic and isometric conditions, whereas RBFANN has superior performance after training with full-length data and when acceleration signal is used as an input in the light load condition.

Figure 9.

Frequency domain analysis of MLPANN and RBFANN validation results after training with full-length data and subtask data.

The results pertaining to the best performing architecture for each subject, trained with full-length and subtask data, are emphasized in Table 4. For the best performing network, validation for full-length data training was RMSE < 32% (CC > 86%), for isometric training RMSE < 18% (CC > 91%), and for isotonic training RMSE < 26% (CC > 84%). For light load training, RMSE < 40%, AAE [the actual indicative in this case] < 1.6 N (CC > 76%).

It is observed that none of the examined architectures is dominant in terms of performance. Moreover, the networks provide better performance when trained with subtask data. Therefore, authors suggest a switching scheme that chooses the best network out of a bank of subtask-trained networks based on the current operating condition. The switching decision can be made by a neural network or a neurofuzzy classifier that detects isometric, isotonic and light load states in real-time.

Discussion

As stated in the Introduction section, MLPANN has been reported for joint torque estimation.22–26 Although the anatomies or experimental conditions are different from ours, in most of the cases, a general comparison of the networks in terms of methodology, network structure and performance would better put our approach and results into perspective. Almost all methods, including ours, use feedforward networks with error backpropogation learning algorithm due to their simplicity. Song et al.26 however, use recurrent MLPANN to account for dynamic situations. The above models relate the EMG and/or joint kinematics to the joint torque. The methods that use single hidden layer22,24 has reported a large number of nodes from 10 to 32 in their hidden layer, and also large number of epochs in the order of 60,000 to reach RMSE% or AAE comparable to the results that we have reported. Two hidden layer networks use in the order of or less than 10 nodes and require significantly lower number of epochs (about 1,000) for training to avoid over-fitting and under-fitting. In terms of inputs, Sepulveda et al. use only the EMG signals to predict joint torque. However, it has been established that joint dynamics is also dependent on joint angular position and velocity. In fact, Song et al. demonstrate torque prediction improvement by up to three folds under dynamic conditions when kinematic data incorporated. Recent research, including ours, has reported the use of joint kinematic data as well. Savelberg et al. has argued that under dynamic conditions the relationship between EMG and force is history dependent.25 Therefore, they use an array of 10 to 30 data points preceding the instant of interest; As such the input layer in their networks contain up to 40 nodes. They have also argued that the number of nodes and the length of the EMG array depend on the desired level of generalization, whether it is intra-session or inter-session.

To improve the quality and reliability of the results we have taken a few measures as discussed in below. MAL is a function of excitation signal firing rate and recruitment of muscle fibers. The measured EMG is an ensemble of the Motor Unit Action Potentials (MUAPs) under the electrode and is heavily dependent on the electrode configuration, placement and signal pre-conditioning. Therefore, the recorded EMG is not an accurate representation of MAL. This factor and the stochastic property of EMG signals affects the repeatability of force estimation based on EMG data. The position of electrodes and the fidelity of the EMG/MAL relation play an important role in the accuracy of estimations based on ANN.24 This is caused by existing crosstalk readings from adjacent muscles. Therefore, active sensor locations should be selected to minimize the crosstalk effect.22 Towards this purpose, as reported in Section 5, multiple electrodes were utilized to record EMG signals from the biceps and triceps muscles. The results showed an improvement between 10% and 70% in estimation accuracy.

To further improve the fidelity of the EMG/MAL relation, a whitening filter.41 was employed. However, since the filter amplifies the higher frequency component of the EMG signals, no significant improvement in estimation performance was observed. The history of EMG data (up to 10 samples) was also employed as input to the networks, but the results were inconclusive and no consistent improvement was observed.

Another significant issue is muscle fatigue which has not been taken into consideration as the experiments were all conducted under non-fatiguing conditions. In addition, in anisometric motion, artifacts, caused by the movement of muscle under the electrode are often a problem. Since part of the hand force in motion is generated by hand dynamics and the dynamics of the grasped object, the inclusion of acceleration in the ANN inputs improves the performance (especially in free motion) as it has been observed in the results presented in Section 5.

In terms of applications, although the use of ANN for force estimation does not provide any insight on the joint dynamic model, it is suitable for applications that only require joint torque or hand force for monitoring purposes, such as in the analysis of athletes activities, and for the control of prosthetic arms.

Conclusion

This paper investigates the use of two artificial neural network architectures RBFANN and MLPANN for force estimation, and compares the performance of the two methodologies for human hand force estimation under an ensemble of operational conditions; isometric, isotonic and light load. A new EMG normalization method was employed as an alternative approach for MVC. The trained ANNs were able to predict the highly nonlinear relation between the joint parameters (EMG, angle and velocity) and the hand generated force. Use of multiple-electrode EMG reading from major muscles improved force estimation accuracy.

It was observed that both networks provide better performance when trained with subtask data. The experiments with three subtasks showed that the best performing architecture for each subject can generalize intra-session force estimation to a maximum RMSE of 40%, 26% and 18% for light load, isotonic and isometric conditions, respectively. Moreover, ANN is able to estimate the full-length data to a maximum RMSE of 40%. The experiments also showed that the performance of neither MLPANN nor RBFANN was dominant for all operating conditions. The training and validation results for both architectures for the isometric condition were significantly better than those for isotonic and light load conditions. RBFANN provided better estimation performance in the light load condition and MLPANN in the isotonic condition. The performance in light load condition improved significantly by including joint angular acceleration in the network inputs.

As none of the examined architectures proved to be dominant in terms of performance across all subtasks, a switching scheme that chooses the best RBF or MLP network out of a bank of subtask-trained networks can be considered as an attractive alternative for enhanced force prediction. An alternative solution can be to combine the MLP and RBF for an assemble network to predict the joint torque, which may result in improved estimation by utilizing different features of the two networks.