Structure-Based Simulations Reveal Concerted Dynamics of GPCR Activation

Abstract

G protein-coupled receptors (GPCRs) are a vital class of proteins that transduce biological signals across the cell membrane. However, their allosteric activation mechanism is not fully understood; crystal structures of active and inactive receptors have been reported, but the functional pathway between these two states remains elusive. Here, we employ structure-based (Gō-like) models to simulate activation of two GPCRs, rhodopsin and the β₂ adrenergic receptor (β₂AR). We used data-derived reaction coordinates that capture the activation mechanism for both proteins, showing that activation proceeds through quantitatively different paths in the two systems. Both reaction coordinates are determined from the dominant concerted motions in the simulations so the technique is broadly applicable. There were two surprising results. First, the main structural changes in the simulations were distributed throughout the transmembrane bundle, and not localized to the obvious areas of interest, such as the intracellular portion of helix 6. Second, the activation (and deactivation) paths were distinctly non-monotonic, populating states that were not simply interpolations between the inactive and active structures. These transitions also suggest a functional explanation for β₂AR’s basal activity: it can proceed through a more broadly defined path during the observed transitions.

1 Introduction

G protein-coupled receptors (GPCRs) are a class of biomedically important membrane proteins with roles in diverse functions such as sight, muscle contraction, and gene transcription. They are also targeted by an estimated 25–50% of FDA approved drugs^1–3. These membrane proteins function as allosteric transducers, responding to environmental stimuli and activating signal pathways inside the cell.

Many class A GPCRs are hypothesized to contain a number of microswitches comprised of conserved structural motifs^4–10. These include the CxWP motif in the protein’s hydrophobic core, the E/DRY region on transmembrane helix 3 (TM3), and the NPxxY motif on helix 7 (TM7). The latter two features are both on the intracellular side of the receptor, adjacent to the G protein binding site. It has been suggested that these conserved regions play key roles in GPCR activation. The CxWP region is hypothesized to act as a toggle, or “transmission” switch, interacting directly with the ligand and coupling the binding pocket to the protein at large^8,11.

The outstanding efforts of many labs have yielded high resolution structures of these proteins, revealing the dominant conformations of both the active and inactive states for rhodopsin and the β₂ adrenergic receptor (β₂AR)^12–20. These structures are vital to understanding GPCR signaling, and together with dynamics studies are advancing our understanding of GPCR function^8,9,21–31. The emerging image is that functionally important regions of the protein are allosterically coupled to one another loosely^6,9,32, rather than in a specific, ordered, and linear cascade. While the end states of these motifs are experimentally characterized at high resolution^{4–8,16,33–35}, there is still much to learn about how these states interconvert.

Molecular simulation can provide insights into protein dynamics at unparalleled resolution; no experimental method can track the position and interactions of every atom with angstrom and picosecond resolution. However, current computational resources limit the amount of data that can be collected, often resulting in a paucity of sampling^22,36–38. In order to obtain a statistically representative ensemble, a number of methods have been developed to allow faster sampling, such as replica exchange and metadynamics^39,40.

Alternatively, one can use a simpler, less computationally expensive model to describe the system. One such group of methods bases the forcefield itself on structural data. Structure-based models of dynamics construct a potential based on a particular set of initial coordinates. These models were pioneered by Gō and coworkers to study protein folding^41,42. Since then, they have undergone many refinements aimed at better-characterizing biomolecules and extending their resolution^43–45. These and similar models have also been used for studying functional transitions^46–54.

In the current study, we model the activation of two canonical GPCRs, rhodopsin and β₂AR, using the structure-based potential described by Whitford et al ^44,45. We use both experimentally motivated and data-derived reaction coordinates to describe the structural transitions. The biological meaning of the data-derived coordinates is discussed and these coordinates are used to quantify the differences between β₂AR and rhodopsin activation pathways.

2 Methods

2.1 Structure-based models

These simulations use a Gō-like force field, where the only favorable long-range interactions are those present in the native structure. As a result, the native state is stable even in the absence of water or lipids. In this study, we used an atomistic variant of this method developed by Onuchic and coworkers^44,45 utilizing the web-based parametrization tools⁵⁵. The Hamiltonian was described using the “Shadow Map” algorithm developed in Noel et al⁵⁶. This model provided all-heavy-atom resolution and made extensive sampling feasible, allowing us to carefully quantify the statistical error in our dataset. We performed these calculations using two proteins, rhodopsin and β₂AR, each in both the active and inactive states; the structures used are identified in Table I. All coordinates were obtained from the protein data bank (www.pdb.org). There are several different structures of both proteins to choose from, so we chose active/inactive pairs that were most similar in terms of mutations and the regions experimentally resolved. In these simulations no attempt was made to model the membrane; rather, we relied solely on the conformation present in the crystal structures. The Hamiltonian was defined by the starting structure, as expected with a Gō-model and the protein did not unfold in any simulations.

Table I.

PDB accession numbers of structures used.

Protein	Inactive	Active
Rhodopsin	1U1913	3PXO15
β2AR	3NY818	3P0G19

2.1.1 Simulating structural transitions with Gō models

To simulate a structural transition, we began by parametrizing a Gō-like potential for the target state, e.g. the active form of rhodopsin. We ran simulations using that potential but starting from the other state, in this case the inactive structure. As a result, the protein efficiently undergoes a transition from the inactive to the active form. One important caveat is that these simulations are not in equilibrium, since the starting structure is unlikely and thus over represented statistically. This strategy is similar to that used by Sanbonmatsu, Onuchic, and coworkers in their work on the ribosome⁵⁷.

2.1.2 Simulation protocol

After the initial system setup, the protein underwent an energy minimization scheme using the steepest decent and then conjugate gradient methods, in order to reduce forces sufficiently and allow stable dynamics; this typically required 1500–3000 steps of minimization in total. We then ran 300,000 steps of dynamics using a timestep of 0.0001 and a temperature of 50; as previously noted,^44,45 the potential defined by SMOG does not use conventional units. Simulations were performed using gromacs 4.5.4⁵⁸. For each system (β₂AR and rhodopsin) and each simulation type (activation and deactivation) an ensemble of 1,000 trajectories was produced, for a total of 4,000 trajectories.

2.2 Simulation analysis

Custom analysis tools were written using the LOOS framework (version 2.0.5, http://loos.sourceforge.net). LOOS is an extensible, object-oriented analysis toolkit designed to interface with the native file formats of all major simulation packages⁵⁹. Principal components were calculated using singular value decomposition⁶⁰. Data was plotted with gnuplot (version 4.6, http://www.gnuplot.info), structures and movies were made with LOOS and rendered in PyMol (version 1.6, http://www.pymol.org).

2.2.1 Comparing two eigensets

To quantify the similarity between two PCA results, we used the covariance overlap method (Equation 1), first derived by Hess⁶¹. This is a normalized metric for comparing two eigensets, where 0 indicates complete orthogonality and 1 indicates the data is identical. Importantly, the covariance overlap takes both the eigenvectors (directions of motion) and the eigenvalues (amplitudes of motion) into account and has been used to compare long-timescale conformation changes^38,62–66. It is defined here as Ω_A,B where A and B represent the two eigensets being compared:

$${\mathrm{\Omega }}_{A,B}=1-{\left[\frac{{\displaystyle \sum _i^N}({\lambda }_i^A+{\lambda }_i^B)-{\displaystyle \sum _i^N}{\displaystyle \sum _j^N}\sqrt{{\lambda }_i^A{\lambda }_j^B}{({\overrightarrow{\nu }}_i^A·{\overrightarrow{\nu }}_j^B)}^2}{{\displaystyle \sum _i^N}({\lambda }_i^A+{\lambda }_i^B)}\right]}^{1/2}$$ (1)

Here, λ represents a single eigenvalue associated with the eigenvector, ν. This value is summed over all N normal modes.

2.2.2 Contact-based reaction coordinate

In order to define a reaction coordinate, we looked specifically to the unique set of contacts that changed between the active and inactive crystal structures. A unique contact is defined as one that is present in one state but not the other. For the current study, we defined two residues to be in contact when the centroids of their sidechains were within 8 Å of each other. This analysis included all residues in the transmembrane bundle that were resolved in both the active and inactive crystal structures (see Table II). This set of contacts—both those broken and those formed—was monitored throughout each simulation. We constructed a matrix made from the timeseries of each contact throughout the simulation. The value of each cell was defined by:

$$u_{ij}(t)=\frac{1}{2}tanh(r_{ij}(t)-8)+\frac{1}{2}$$ (2)

where r_ij is a the distance between residues i and j, at time t. The tanh function makes a smooth transition between formed (value ≈ 0) and broken (value ≈ 1) states. By contrast, if a simple binary function is used, the variance of the contact matrix is dominated by the fluctuations of residue pairs that sit near the 8 Å cutoff in one of the crystal structures. We then performed principal component analysis (PCA) in contact space using singular value decomposition, and used the first two principal components as our reaction coordinate.

Table II.

GPCR transmembrane regions used in calculations. Superscripts use the notation developed by Ballestoros and Weinstein⁸².

Protein	TM1	TM2	TM3	TM4	TM5	TM6	TM7
β2AR	W1.31-Q1.59	V2.38-M2.67	N3.22-I3.54	N4.40-Q4.62	N5.35-K5.66	K6.29-I6.60	E7.33-R7.55
rhodopsin	W1.29-K1.59	P2.38-H2.67	P3.22-V3.54	N4.40-V4.62	N5.35-Q5.71	T6.25-T6.60	I7.33-M7.56

2.3 Statistical convergence

Using the principal components as reaction coordinates is only reasonable if they are robust across the dataset. In order to assess how many transition trajectories are required to confidently describe the pathway, we employed a bootstrap estimate of the variance in principal components. This was done by first varying the sample size from 5 to all 1,000 trajectories for a given system (see Section 2.1.2). For each sample, a set of 30 independent bootstrap datasets were created. Cartesian space PCA (using the alpha-carbons of the transmembrane helices) and contact space PCA were then performed on each of these sets. We then assessed the self-consistency of the modes produced as a function of data set size. This was done by computing the average absolute dot product of a single mode across all 30 bootstrap samples. The results, plotted in Supplementary Figures S1 and S3, show that PC1 was extremely well-defined in both the cartesian space and the contact space results; however, PC2 was heterogeneous in the cartesian space PCA, suggesting noise or degeneracy in the paths. By contrast, both PCs were well-defined when using contact space PCA.

3 Results and Discussion

3.1 Dynamics of biologically conserved regions tell a conflicting story

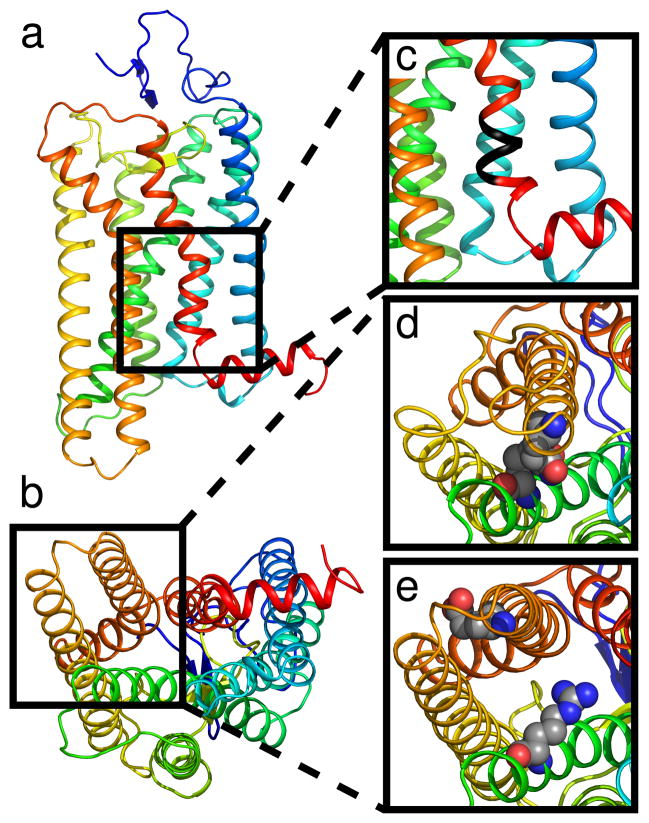
We first set out to find a suitable reaction coordinate for activation by following the approach used by Dror et al.⁶⁷, analyzing the dynamics of two highly conserved regions: the NPxxY motif in transmembrane helix 7 (TM7), and the ionic lock (between TM3 and TM6). These regions are illustrated in Figure 1. Briefly, the tyrosine residue in the former motif is thought to disrupt the inter-helical hydrogen bonding network and stabilize the active conformation^{4,15,16,19,68,69}, while it has been suggested that R3.50 forms a salt bridge with E6.30 (the so-called ionic lock) that stabilizes the inactive state^70,71. Both of these regions differ between the active and inactive forms of the receptor and have been implicated in the GPCR activation mechanism; however, their connection in the allosteric cascade is not fully understood^{5–8,33,69,70}.

Figure 1.

Overview of conserved regions. Rhodopsin is shown as a cartoon using rainbow coloring (a) in the plane of the membrane and (b) from the cytoplasmic side. (c) Location of the NPxxY motif in TM7 is highlighted in black. The ionic lock between TM3 and TM6 is shown in its (d) closed and (e) opened state.

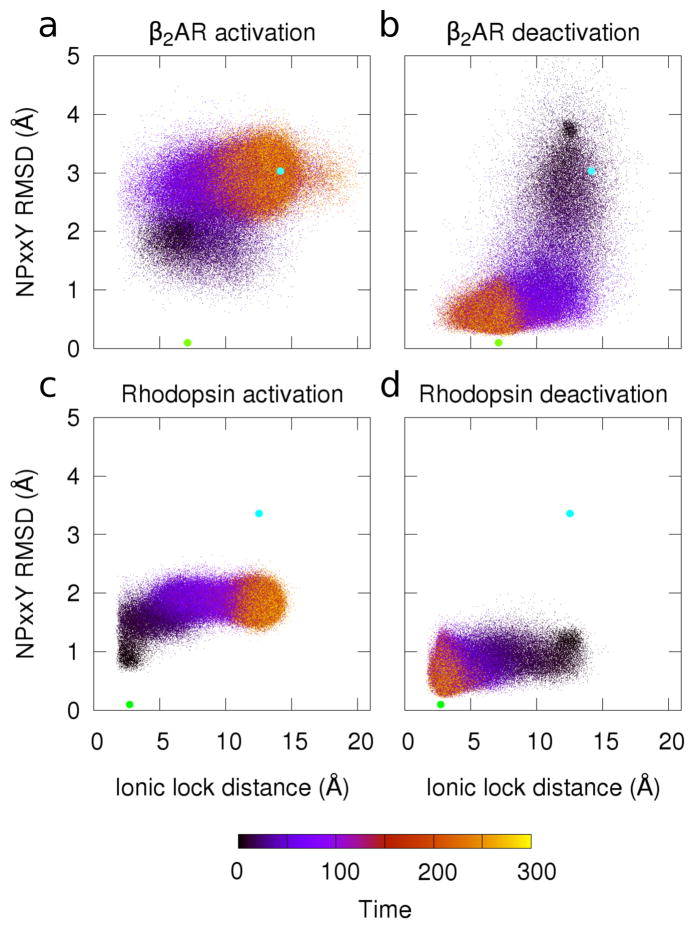
Recently, Dror et al.⁶⁷ used analyses of these two regions as a reaction co-ordinate to describe β₂AR deactivation. They suggested deactivation occurs by a two-stage process, where the NPxxY region transitions to a more inactive-like structure first, followed by the ionic lock closing as TM6 moves toward the rest of the helical bundle. We performed a similar analysis on our structure-based simulations (Figure 2). Here, we measured both the NPxxY region RMSD from the inactive crystal structure and the distance between ionic lock residues as a function of time. The path taken by β₂AR during activation (Figure 2a) shows the NPxxY region beginning to deviate from its inactive form before the lock is fully open. This order was actually the opposite of that reported for β₂AR deactivation ⁶⁷, but matched simulations of M2 muscarinic receptor activation performed using accelerated MD⁷². By contrast, the path taken in our structure-based simulationsof β₂AR deactivation (Figure 2b) is similar to that reported by Dror et al ⁶⁷. During deactivation, the NPxxY motif assumed a more inactive-like conformation before the ionic lock is formed. This was an encouraging result suggesting that this simple model produces dynamics similar to state-of-art all-atom results.

Figure 2.

Transitions in cytoplasmic motifs during activation and deactivation. Plots show the RMSD to the inactive NPxxY region (using the inactive structures in Table I). RMSD was calculated using backbone heavy atoms (y-axis). This is plotted with the distance between ionic lock residues (R3.50 to E6.30) using the minimum distance between heavy atoms (x-axis). Data color indicates the trajectory time (arbitrary units). The active (cyan circle) and inactive (green circle) crystal structures are plotted for reference. 1,000 simulations are shown for each of the four systems studied: (a) β₂AR activation, (b) β₂AR deactivation, (c) rhodopsin activation, and (d) rhodopsin deactivation.

The difference in transition order (as seen between Figures 2a and 2b) suggests that the paths of activation and deactivation are not necessarily the same. There are two likely explanations for this difference. One may be a simple kinetic issue; the NPxxY transitions are local rearrangements and thus can occur quickly, while the ionic lock reports on the larger structural transition of a whole helix, and thus proceeds more slowly. Since our simulations begin in a non-equilibrium state, relaxation kinetics (as opposed to equilibrium fluctuations) control the pathway, and as such the paths can be different. Alternatively, it is possible that the activation and deactivation paths differ because different potentials are used in the two sets of simulations.

The results were quite different for rhodopsin (Figure 2c, d). The ionic lock made a clear transition in both activation and deactivation simulations (Panels c and d), but there was no notable transition in the RMSD of the NPxxY region; in both the activation and deactivation simulations, the NPxxY motif prefers to stay near the inactive conformation.

The fact that this coordinate does not better capture the activation mechanism of rhodopsin was quite intriguing. While β₂AR and rhodopsin have similar structures, and this region is well-conserved, they perform diverse tasks and are activated in distinct ways. That these two regions worked well as a reaction coordinate for β₂AR, but not rhodopsin, and that β₂AR’s activation path is qualitatively different from its deactivation path emphasizes the importance of choosing a reaction coordinate carefully and quantitatively analyzing the paths described. Proteins are high-dimension objects, and projecting their motions into a small number of reaction coordinates is both necessary and risky; a good choice will allow intuitive understanding of the results, while a poor choice may be actively misleading.

3.2 Principal component-based reaction coordinate reveals non-monotonic transition pathway

3.2.1 Transitions identified by cartesian PCA

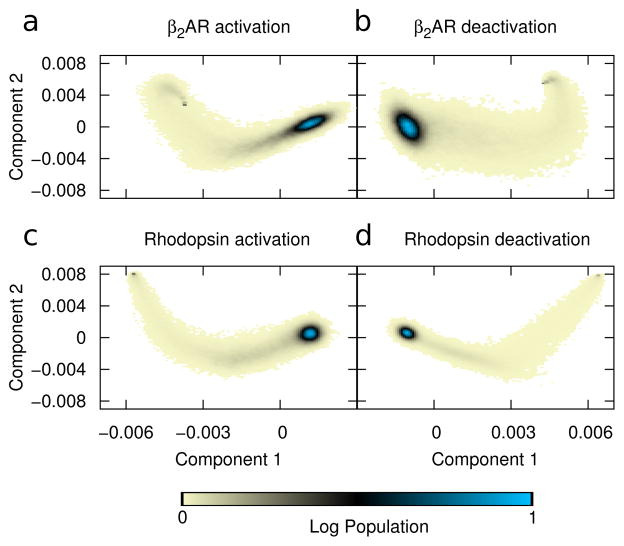
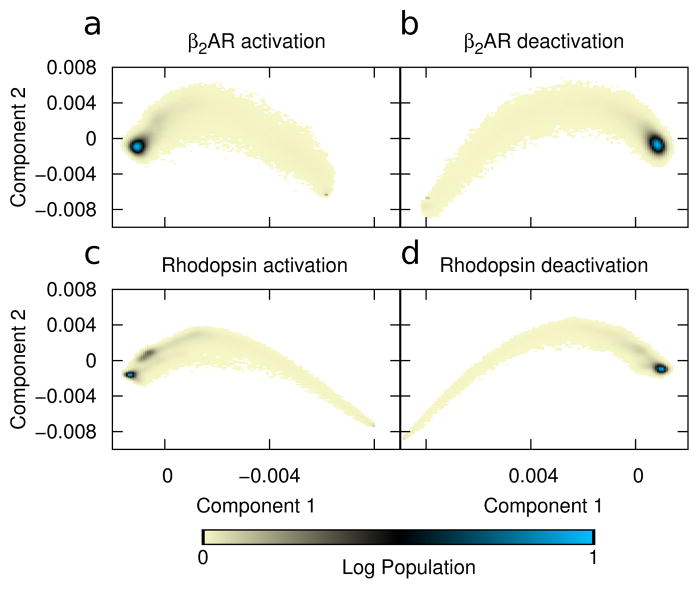
Arguably the best way to be sure the reaction coordinate captures the information from the simulation is to derive the coordinate directly from the data. In this case, we used principal component analysis (PCA) to extract the most concerted motions in the simulations. We first applied PCA to the cartesian coordinates of the transmembrane c_α’s^60,73–77. Figure 3 shows the result of projecting the trajectories along the first two principal components with axes showing the unscaled displacement along those modes.

Figure 3.

Principal component-based reaction coordinate. PCA of the covariance matrix in cartesian space is used to define the principal axes. Color shows the log-scale population from all simulations projected onto principal components one (x-axis) and two (y-axis) for all 1,000 trajectories in each ensemble. Displacement units are arbitrary. Data is shown for simulations of (a) β₂AR activation, (b) β₂AR deactivation, (c) rhodopsin activation, and (d) rhodopsin deactivation. In all cases the peak population density indicates the final structure.

These results indicate that even when using a data-driven coordinate system —one designed to pick up only the largest concerted motions—the transition path is not a simple linear interpolation between the two crystal structures. Rather, in all cases PC2 overshoots the average value and then must backtrack as the protein progresses in PC1. This in turn shows the value of the simulations, revealing that structures populated during the transition may have characteristics that are not obvious from the end states alone.

One crucial question that must be answered is whether the data set is sufficiently large to allow reliable interpretation; while 1000 independent transitions seems like a large dataset, it is still important to test convergence quantitatively. We show the results in Supplementary Figure S1, where we used a bootstrap procedure to estimate how many trajectories are needed to produce consistent PCA results that can be used as meaningful reaction coordinates. Specifically, we randomly selected sets of trajectories (with replacement), computed the PCA for each set, and measured the mean absolute dot product between their first or second principal components. By tracking this quantity as a function of data set size, we can assess the reliability of the principal axes. For example, Figure S1a shows that for the β₂AR activation system, the absolute dot product converges (to ≈ 1) with fewer than 200 trajectories, indicating both eigenvectors are very well converged; similarly, Panel e shows that that variance has dropped below 10⁻⁴; rhodopsin deactivation (Panels d and h) behaves similarly, while β₂AR deactivation (Panels b and f) converges somewhat more slowly. By contrast, the rhodopsin activation converges very slowly (Panels c and g), with the dot product remaining low and the variance high even for sets with 1000 trajectories. The poor convergence, specifically in rhodopsin activation, is possibly due to the fact that the active structure is more open, and fluctuations after this transition are less well-defined. Thus, this reaction coordinate, while intuitive, may not be the best possible choice; we will explore a contact-based alternative in section 3.3.

3.2.2 Visualizing modes of motion

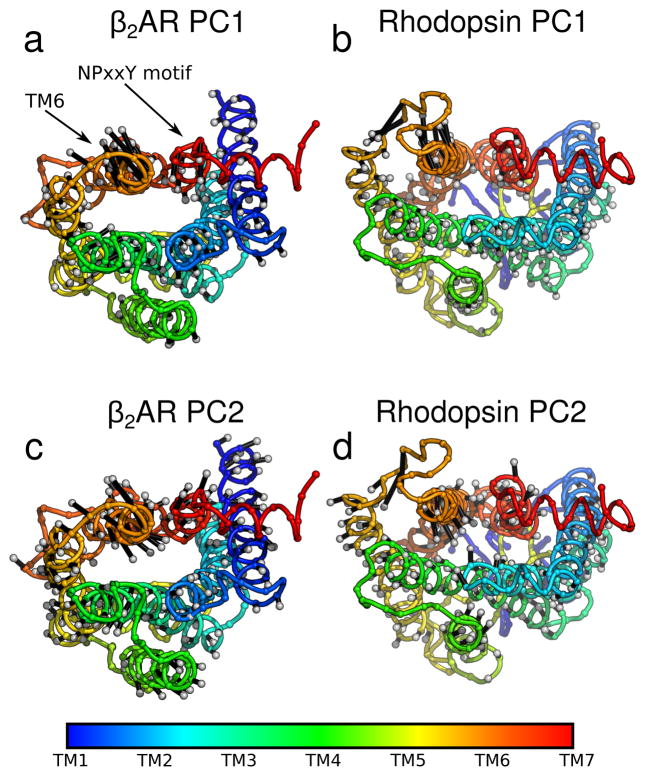
In order to better understand the PCA results, we mapped the first two modes back onto the protein structures for simulations of activation (Figure 4) and deactivation (Supplementary Figure S2); the arrows on the structure indicate the direction and relative magnitude of motion. PC1 (Figure 4a, b) showed a large displacement of helix 6 (orange helix in the upper left of each panel) outward in both proteins, as expected. By contrast, in PC2 (Figure 4c, d) TM6 makes a rotating motion in both β₂AR and rhodopsin, reminiscent to what was seen in previous all-atom work⁶⁰. The amplitude of motion around the NPxxY region was markedly greater in β₂AR (Panels a and c) compared to rhodopsin (Panels b and d) for both PC1 and PC2. TM5 also made appreciable changes during rhodopsin activation, extending the intracellular portion of TM5 (Panels b and d, yellow helix). It is worth noting that all regions of the protein are affected. Results for deactivation were largely similar (as illustrated in Supplementary Figure S2).

Figure 4.

Direction of the most concerted motions in activation. Principal components (from the analysis described in Section 3.2.1) are plotted as silver-tipped black vectors extending from c_α’s on protein cartoons. Vector length is proportional to each residue’s contribution to the principal component. The initial protein structure (the inactive state) is shown with the NPxxY motif and TM6 labeled. The spectrum bar shows the residues sequence number. Data is shown for (a) PC1 ofβ₂AR, (b) PC1 of rhodopsin, (c) PC2 of β₂AR, and (d) PC2 of rhodopsin.

3.3 Contact-based reaction coordinate reveals putative allosteric network

3.3.1 Transitions identified by contact space PCA

Because PC2 was poorly defined for rhodopsin activation when using standard cartesian-space PCA, we also applied an alternative procedure that is outlined in Section 2.2.2, performing PCA on time series of inter-residue contacts as instead of the coordinates. This analysis focuses on changes in topology as opposed to simply structure, and thus converges faster for flexible systems. Specifically, we calculated the time-progression of each unique contact to make a “transition matrix” where each cell is built using Equation 2. We then computed the principal components of this matrix using singular value decomposition and used the first two components as a reaction coordinate for each of the trajectories (Figure 5). As expected, this produced well-defined principal components; Supplementary Figure S3 shows that fewer than 200 trajectories would be necessary in all cases.

Figure 5.

Contact-based general reaction coordinate. Displacement along PC1 and PC2 of the “transition matrix” (Section 2.2.2) is shown. Color indicates the relative population of these displacements (log scale) across all trajectories. Displacements are given in arbitrary units. Data is shown for simulations of (a) β₂AR activation, (b) β₂AR deactivation, (c) rhodopsin activation, and (d) rhodopsin deactivation.

The contact-based reaction coordinates yielded similar results to those found using cartesian-space PCA. They identified a single, highly populated transition path for all four systems, characterized by deviations in the first two principal components. Here, we again observe that the trajectory of PC2 was non-monotonic for both proteins (Figure 3). In order to better understand why the system did not proceed directly to the final structure we analyzed the individual contacts more carefully.

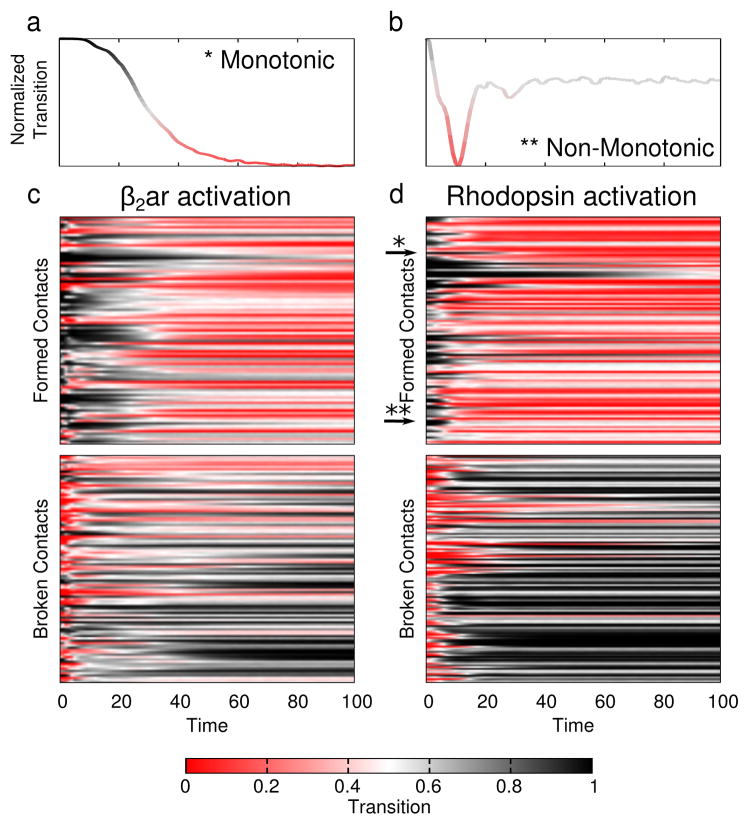
3.3.2 Individual residues make non-monotonic transitions

Both PCA-based reaction coordinates revealed a path that was non-monotonic; the system “overshot” the minimum energy structure, particularly in PC2. This fact was especially evident in the contact-based reaction coordinate (Figure 5 and Supplementary Figure S4). The physical interpretation of this path is that some contacts that form (or break) during activation have a higher (lower) probability of being formed during the transition than they do in the end state. Such “backtracking” was noted before by Gosavi et al.^78,79 In any given trajectory, these contacts regularly break and re-form (Supplementary Movie 1), so an average over many separate transitions is needed to reveal the pattern (Figure 6).

Figure 6.

Contact transitions during activation. The average transition value (color) across all 1,000 trajectories is plotted using Equation 2. Red indicates a formed contact and black one that is broken. (a and b) Single contacts selected from rhodopsin activation illustrate monotonic and non-monotonic transitions. (a) Example of a monotonic transition. (b) An example contact that makes a backward transition. (c and d) Each unique contact (y-axis) is shown as a separate row. The first 100 frames (x-axis) are shown for (c) β₂AR activation and (d) rhodopsin activation.

The non-monotonic motion in PC2 was most pronounced early in the trajectories — within the first 50,000 integration steps (or $\frac{1}{6}$^th of the trajectory) (Supplementary Figure S4). This backtracking in PC2 suggests that there was some steric hindrance preventing the main transition identified by PC1. In this view PC2 serves primarily to relieve strain in the molecule by moving atoms out of the way and thus facilitating activation. This is most clear in Supplementary Figure S4A, which shows that PC2 in β₂AR activation has roughly the same value at the beginning and end of the simulation.

To better understand these transitions, we plot the state (formed or broken) of individual contacts for the first third of each trajectory; after that, nearly all trajectories had reached their target state and were fluctuating about it. To reduce noise, we present the average time series for each unique contact in Figure 6, considering all 1000 activation trajectories (results for deactivation are plotted in Supplementary Figure S5).

Figure 6a, b highlights two contacts randomly chosen from our rhodopsin activation simulations. Panel a shows a contact that transitions monotonically: once that contact forms it remains formed throughout the simulation. By contrast, the plot in Figure 6b shows a contact that forms only briefly and is then re-broken. The curves are colored by transition value (Equation 2), where formed contacts are red and broken contacts are black. In Figure 6c, d this analysis is expanded to all contacts (with color still representing transition value), but here the y-axis contains the set of all unique contacts formed (top plot) or broken (bottom plot). In both β₂AR and rhodopsin activation, there is “checkering” in the x-axis, indicating multiple contacts make “backtracking” transitions to their starting orientation (similar to those contacts plotted in 6b). These contacts were spread throughout the protein and not localized to any specific region as can be seen in Supplementary Figure S6. Details for deciding which contacts are non-monotonic, or backtrack are provided in the Supplementary Information. That residue contacts re-form and re-break shows there is some topological frustration⁸⁰ in the transitions, despite the fact that no such frustration is built into the model itself. This underscores the need for dynamics data to complement structural information.

To better understand the complex mechanisms underlying protein function, it will likely be necessary to study their dynamic properties directly. This is particularly important for GPCRs, where many allosteric ligands modulate activity in different ways; recent simulations suggest that activation occurs via distinct pathways when different ligands are bound^28,31. The method presented here not only identified a non-trivial reaction coordinate, but it also resulted in a putative network of interactions that are vital to activation. This network was defined in terms of a reduced dataset that allowed quantitative comparison between the four different systems studied (see Section 3.4). The problem that remains is how to biologically interpret the reduced set of motions described in contact space.

3.3.3 Interpreting the contact-based coordinate

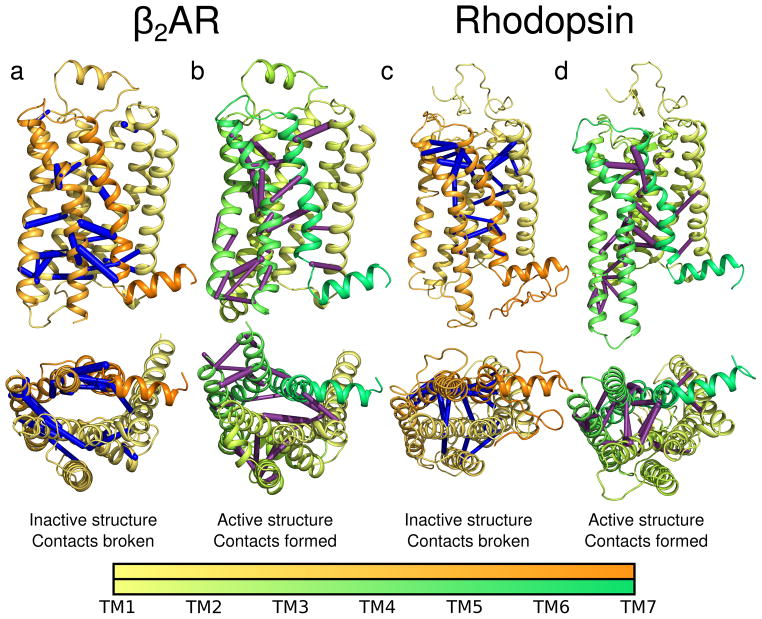
To visualize changes in contact space, we mapped the principal components back onto the structures themselves, with bonds showing those contacts crucial to activation. Specifically, we drew bonds between the c_α’s of residues making unique contacts, using the thickness of the bonds to indicate the variance of that contact within the component shown. For clarity, we only show those contacts that cumulatively constitute half of the amplitude of each principal component. In addition to activation (Figure 7), results obtained for deactivation (Supplementary Figure S7) and for PC2 (Supplementary Figures S8 and S9) are available in the supplementary information.

Figure 7.

Contacts characterizing activation. The contacts whose transitions contributed the most to PC1 (i.e. those accounting for 50% of PC1 displacement) are mapped onto cartoons of β₂AR and rhodopsin as bonds between c_α’s. The bond thickness is proportional to the contribution made to the principal component. Bonds broken during a activation are shown in blue, those formed are shown in purple. Cartoons of inactive protein are colored yellow to orange, the active proteins are colored yellow to green. The spectrum bars indicate residue numbers. Panels (a) and (b) show data for β₂AR activation simulations. Panels (c) and (d) show data for rhodopsin activation simulations.

Interestingly, these contacts were spread throughout the proteins and not limited to the obvious areas of change, such as the cytoplasmic face and TM6. Figure 7 revealed a network of contacts that may be fundamentally important to GPCR signaling. These bonds show how the whole protein is linked in contact-space, and their presence in the most concerted principal component suggests that an allosteric connection exists between the hydrophobic ligand binding pocket and the cytoplasmic G protein binding site. This demonstrates the power of letting the data speak for itself, rather than constraining analysis to a preconceived reaction coordinate.

In β₂AR, we identified a cluster of contacts near the G protein binding site that is broken on activation (Figure 7a). This included contacts between TM6 and the NPxxY motif in TM7. However, contacts are simultaneously formed between the more extracellular portions of TM6 and TM7. At the same time, multiple contacts between the intracellular portions of TM5 and TM6 form (Figure 7b). This mode gives a potential mechanism explaining how the ligand, located in a pocket toward the extracellular portion of the protein, can alter the structure and dynamics of the intracellular face.

In rhodopsin, the contacts were also spread over the whole surface of the protein. A cluster on the extracellular side of helices 5, 6 and 7 was identified with contacts both breaking and forming (Figure 7c, d). Notably, there is precedent for extracellular motion in rhodopsin, and others have suggested this motion may impact the conformation of the extracellular loops, specifically during activation⁸¹. In the future, it would be interesting to experimentally test the importance of these contacts using mutagenesis or crosslinking experiments.

Another surprising result was that there were many more contacts contributing to the first principal component in rhodopsin than in β₂AR (Supplementary Table Si). This corroborates an observation we noted previously: although dark-state rhodopsin has a vanishingly small basal activity, it was much more flexible than β₂AR in all-atom simulations⁶⁰. In the current study, rhodopsin transitions involved more contacts than β₂AR, but β₂AR populated a broader range of structures during transitions (Figure 5a, b vs. 5c, d).

3.4 Proteins activate via quantitatively different pathways

In both cartesian and contact-based results, the path traversed by rhodopsin was narrower than in β₂AR; this can be seen by visual inspection of Figures 3 and 5. The highly-populated endpoint was also broader in β₂AR than in rhodopsin. Together, this suggests that β₂AR activation may proceed through a more diverse ensemble of states and that its active ensemble may be more expansive. This makes functional sense as β₂AR has detectable basal activity, while rhodopsin acts like a switch, with essentially no activity when its ligand is bound in the 11-cis form. Using both data-derived PCA-based reaction coordinates, we quantitatively compared the transition paths using previously established methods for comparing eigensets from biomolecular covariance matrices^36,38,61,62.

To make this comparison we used the covariance overlap (Equation 1). For each iteration two trajectories were selected at random and compared. This process was repeated 100 times for each data point in figures 8 and 9. In those figures we report the average value ± standard deviation. These samples were also used to test for statistical significance in the difference between pathways using a Welch’s T-test.

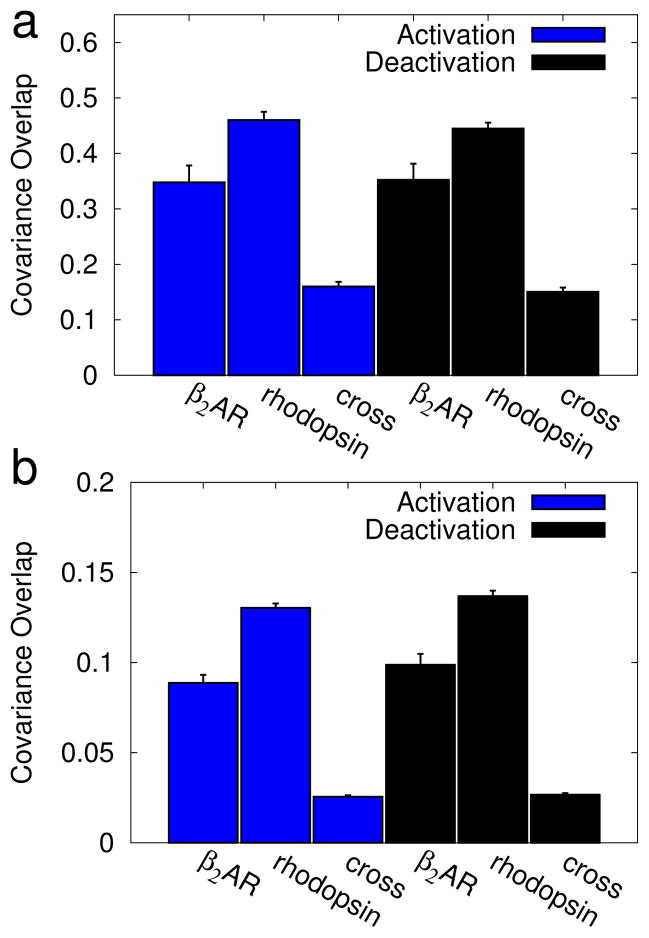
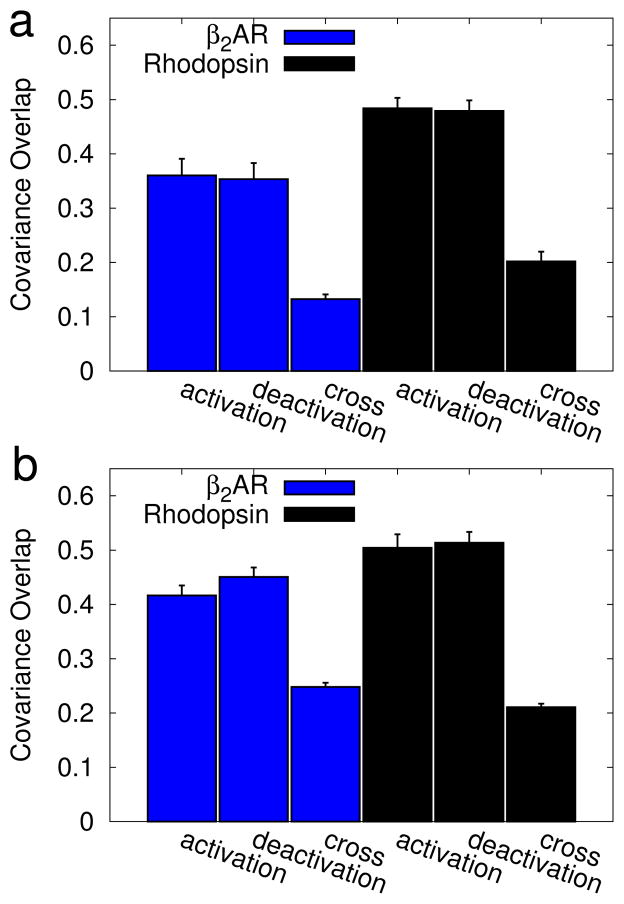
Figure 8.

Similarity between β₂AR and rhodopsin transitions. The average covariance overlap⁶¹ is shown for a random subset of 100 trajectories to compare the pathway taken by β₂AR to that taken by rhodopsin. The error bars represent the standard deviation. Data is shown for overlaps between (a) cartesian-space PCA and (b) contact-based PCA. Within each panel results are split into activation simulations (blue bars) and deactivation simulations (red bars). The average overlaps were calculated between: a pair of β₂AR simulations (β₂AR), a pair of rhodopsin simulations (rhodopsin), and from a β₂AR simulation to a rhodopsin simulation (cross). The difference in overlap between β₂AR simulations and a cross-comparison, and between rhodopsin simulations and a cross-comparison were found to be statistically significant (p < 0.05); p-values are listed in Table Sii.

Figure 9.

Similarity between activation and deactivation pathways. The average covariance overlap⁶¹ is shown for a subset of 100 trajectories, chosen randomly. The error bars represent the standard deviation. Results are shown for (a) covariance-based PCA and (b) contact-based PCA. Data is split into β₂AR simulations (blue bars) and rhodopsin simulations (red bars). The bars represent overlaps between: a pair of activation simulations (activation), a pair of deactivation simulations (deactivation), and from an activation simulation to a deactivation simulation (cross). The difference in overlap between activation simulations and a cross-comparison, and between deactivation simulations and a cross-comparison were found to be statistically significant (p < 0.05); p-values are listed in Table Siii.

3.4.1 How similar are the paths taken by β₂AR and rhodopsin?

First, we compared transition paths taken by β₂AR to those taken by rhodopsin (Figure 8), for both activation (blue) and deactivation (red) simulations. For each dataset, trajectories were randomly chosen and compared using the covariance overlap (Equation 1). This analysis was performed using cartesian PCA results (contact-based results (8b). Additional details of this analysis are provided in the Supplemental Methods (Section S1.3). Both panels follow the same format, with comparisons between activation simulations in blue and comparisons between deactivation simulations in red. We first compared sets of β₂AR simulations to themselves (β₂AR) by selecting 100 pairs of β₂AR activation eigensets and computing the covariance overlap for each pair. Similarly, the second bar shows a comparison of eigensets obtained from rhodopsin activation simulations (rhodopsin). Finally, we compared the paths from these two proteins to one another, creating pairs by pulling an eigenset from each ensemble (cross). The cross comparison was significantly lower than either self comparison (as measured using Welch’s T-test, at a significance level of 0.05). This demonstrates that the proteins take statistically different paths. The p-values between the overlaps are listed in Supplementary Table Siii).

We also found that β₂AR-β₂AR overlaps were lower than the rhodopsin-rhodopsin overlaps, suggesting more variance in β₂AR pathways. This correlates well with the broader β₂AR transition as seen in Figure 5, reinforcing the idea that there is a larger variance in β₂AR paths. As mentioned before, this larger variance may be indicative of β₂AR’s ability to activate spontaneously.

The covariance overlaps are systematically lower for the contact-space PCA (Figure 8b) than for cartesian-space (Figure 8a). This is expected, because the dimensionality of the contact-space analysis is significantly higher, and our previous work showed that the covariance overlap decreases systematically with increased matrix size⁶⁵; this is discussed further in the supplementary information (Section S1.3).

3.4.2 How similar are activation and deactivation?

Next, we compared the pathways of activation and deactivation for each pro-tein (Figure 9). This was done separately for β₂AR (blue) and rhodopsin (red). When comparing two β₂AR activation simulations (activation) or two deactivation simulations (deactivation) the calculated overlap was similar, indicating that the activation and deactivation paths have similar heterogeneities. However, when comparing an activation simulation to a deactivation simulation (cross), the drop in covariance overlap was statistically significant for both proteins; thus, in these calculations, deactivation is not a simple reversal of the activation path. This is consistent with our previous qualitative analysis in Section 3.1 and Figure 2.

As experimental structures for other GPCRs become available it will be important to quantitatively identify their activation pathways, especially in the context of related proteins. Also, as more computational resources become available similar analyses should be performed using more rigorous models. In particular, the quantitative assessments of statistical error discussed above will be critical in figuring out precisely how much sampling is needed to get reliable results. Our data indicates that using the contact-space PCA requires roughly 200 trajectories to be fully converged, so at present this is probably beyond the reach of even the most powerful brute-force calculation⁶⁷, although alternative sampling strategies may be plausible³¹.

4 Conclusion

We used Gō-like models to simulate activation of two model GPCRs, rhodopsin and the β₂ adrenergic receptor. While an experimentally motivated reaction coordinate captured β₂AR transitions, it proved inadequate when applied to rhodopsin. We therefore introduced a novel data-derived coordinate based on the unique set of contacts that change between two states of a molecule. Using this coordinate, we were able to track the changes in activation of both proteins. These results were corroborated by a standard cartesian-based PCA analysis. We showed that transition paths taken by the two proteins were statistically different, indicating the diversity of GPCR activation. In addition, β₂AR transitions were more heterogeneous, suggesting a possible explanation for β₂AR’s basal activity. In the future, it will be important to test this observation on other GPCRs as more active-state crystal structures are published. Using a general reaction coordinate that does not assume biological knowledge a priori will likely be an important means to differentiate the ensemble dynamics of proteins, and will be important for fully understanding the mechanism of their activation.