Highly anisotropic metasurface: a polarized beam splitter and hologram

Abstract

Two-dimensional metasurface structures have recently been proposed to reduce the challenges of fabrication of traditional plasmonic metamaterials. However, complex designs and sophisticated fabrication procedures are still required. Here, we present a unique one-dimensional (1-D) metasurface based on bilayered metallic nanowire gratings, which behaves as an ideal polarized beam splitter, producing strong negative reflection for transverse-magnetic (TM) light and efficient reflection for transverse-electric (TE) light. The large anisotropy resulting from this TE-metal-like/TM-dielectric-like feature can be explained by the dispersion curve based on the Bloch theory of periodic metal-insulator-metal waveguides. The results indicate that this photon manipulation mechanism is fundamentally different from those previously proposed for 2-D or 3-D metastructures. Based on this new material platform, a novel form of metasurface holography is proposed and demonstrated, in which an image can only be reconstructed by using a TM light beam. By reducing the metamaterial structures to 1-D, our metasurface beam splitter exhibits the qualities of cost-efficient fabrication, robust performance, and high tunability, in addition to its applicability over a wide range of working wavelengths and incident angles. This development paves a foundation for metasurface structure designs towards practical metamaterial applications.

Introduction

Metamaterials with metallic structures have been demonstrated to exhibit unique electromagnetic properties that are not available naturally, such as extraordinary transmission beyond the diffraction limit¹,², efficient light-harvesting ability³,⁴, plasmonic color filtering⁵,⁶,⁷, and, most notably, controlling the reflection or transmission direction of a light beam⁸,⁹,¹⁰. However, multi-layered three-dimensional (3-D) metamaterials suffer from complicated and costly fabrication, a narrow usable bandwidth due to their resonant character, and low optical efficiency due to the inherent metal absorption. Recently, metasurfaces have been proposed to overcome these issues by reducing the dimensionality to a two-dimensional (2-D) meta-platform. With this newly proposed meta-platform, applications of the photonic spin-Hall effect¹¹, polar metalensing¹², and light bending¹³,¹⁴,¹⁵, previously observed in 3-D metamaterials, have been successfully demonstrated. However, these 2-D metasurfaces still require precise arranging of the directions and shapes of their resonant antenna units to obtain a gradient refractive index. In this work, we further simplify the metastructure to a one-dimensional (1-D) metasurface using a type of bilayer metallic nanowire grating, which leads to not only much easier fabrication, but also better performance in producing polarized negative reflection, as reported for some 2-D metasurfaces¹³,¹⁴,¹⁵. Here, we refer to reflection into the negative first diffractive order as “Negative reflection (NR)” and reflection into the zero diffractive order as “Reflection (R)”. Consequently, an efficient approach for fabricating novel polarized beam splitters (PBSs) is presented here.

Previously, metallic nanowire gratings have been demonstrated as PBSs in liquid crystal displays (LCDs)¹⁶,¹⁷,¹⁸,¹⁹, having the advantages of high optical efficiencies and large extinction ratios compared with conventional PBSs fabricated from absorptive dichroic polymer films²⁰, bulky birefringent crystals²¹, multilayer interference laminas²², and dielectric gratings²³. However, thus far, these studies have only focused on the transmission and reflection properties, while polarized diffraction has not been considered. In this work, we propose the use of bilayer metallic nanowire gratings with nano-slits as 1-D metamaterials to realize both polarized negative reflection and reflection. The dispersion curves of the periodical nano-slit-waveguided modes are calculated based on waveguide theory²⁴,²⁵,²⁶ to reveal their TM-dielectric-like/TE-metallic-like character and thus the polarized negative reflection and reflection properties of the nano-optical material structures. We refer to this feature as “metasurface beam splitting”. Metasurface beam splitting does not rely on a resonant coupling mechanism and therefore enables a broad range of useable wavelengths and incident angles, with flexible tunability in operation.

Furthermore, as an example of a potential application, by combining the intrinsically fringed structure of a hologram and the anisotropic character of metasurface beam splitter, a metasurface holograph, ‘decodable’ only by TM light, is proposed and presented. Thus, a higher-security anti-counterfeit hologram is produced by adding the additional criterion of polarization dependence.

Structure design and fabrication

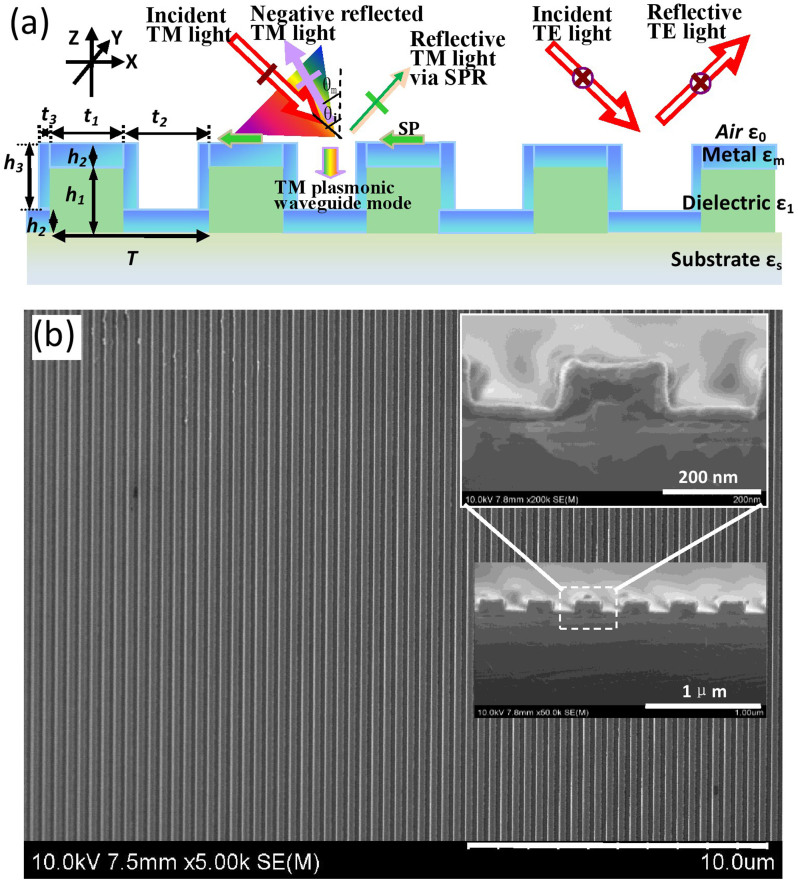
A schematic of the proposed metasurface beam splitter is presented in Fig. 1(a), where the effects of polarized beam splitting are illustrated. The longitudinal plasmonic slit-waveguide mode is denoted by a perpendicular arrow, which represents the primary physical component responsible for the splitting function. The lateral surface plasmon resonance (SPR) is denoted by the horizontal arrows, which leads to reflection peak for TM light.

Figure 1. Structure of the metasurface beam splitter.

(a) Schematic diagram. TM light enters the slits in plasmonic waveguide mode and is reflected by the bottom Al layer. The light is strongly negatively reflected, as indicated by the chromatic sector. The reflection includes light corresponding to lateral SPR, as shown by green arrow, and light in the non-diffraction zone shown in Fig. 2(b1) and Fig. 3(b1). TE light cannot enter the slits and is primarily reflected. (b) SEM images of the top and side views (insets) of the fabricated device. The grating pitch is T = 420 nm, the width of the dielectric PMMA is t₁ = 170 nm, and the width of the metal Al in the bottom PMMA-Al grating layer is t₂ = 250 nm. The thicknesses of the PMMA and Al are h₁ = 110 nm and h₂ = 30 nm, respectively. The size of the Al on the sidewalls of the PMMA grating lines is t₃ × h₃ = 20 nm × 110 nm. The substrate is silicon.

Scanning electron microscopy (SEM) images of the top and side views of the fabricated device are shown in Fig. 1(b). A polymethyl methacrylate (PMMA) grating with a pitch of 420 nm and 170-nm-wide bars was fabricated by nano-imprinting on a silicon substrate. The height of the PMMA reliefs was h₁ = 110 nm. Then, the nano-imprinted grating was deposited with an aluminum (Al) film of thickness h₂ = 30 nm by electron beam (E-beam) evaporation. In addition to the two layers of Al formed on the top of the PMMA ridges and in the grooves, the sidewalls of the PMMA bars were also coated with Al, as shown in Fig. 1(a).

Metasurface beam splitter

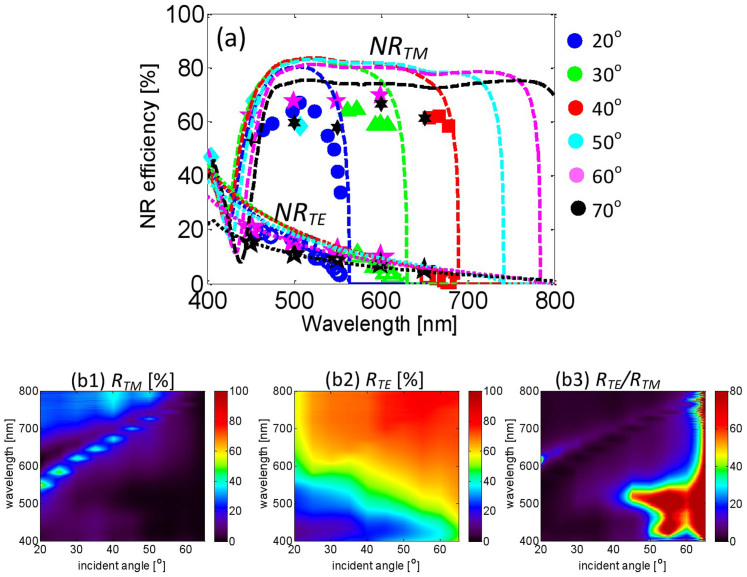
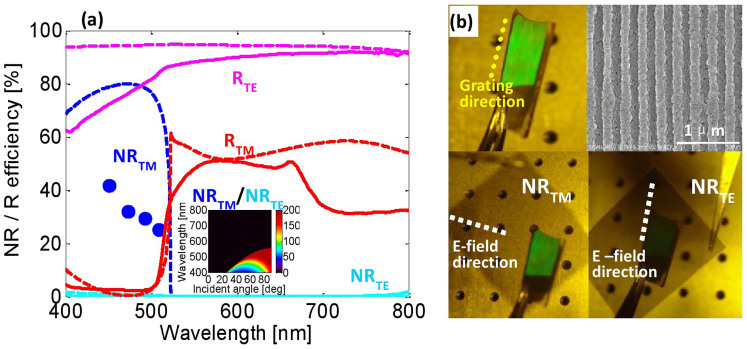
The NR spectra, as shown in Fig. 2(a) for experiments and Figs. 3(a1–a2) for simulations, clearly show a range termed diffraction zone, where TM light is strongly negatively reflected and the TE negative reflection is weak and decreases sharply with increasing wavelength. The distinct boundaries of the diffraction zone are the maximum negative first-order diffraction wavelengths of the grating, with  _G = T*(1+sin _i), where T is the grating pitch and  _i is the incident angle of the light beam. As the incident angle increases, the diffraction zone extends to longer wavelengths; consequently, the working spectral band can be tuned. The TM reflection spectra, as shown in Fig. 2(b1) for experiments and Fig. 3(b1) for simulations, exhibit a single peak arising from lateral SPR at the Al/air interface. Only TM light with a wavelength longer than the SPR peak wavelength is notably reflected, while TE light is strongly reflected throughout the entire visible light region at all incident angles for both experiments and simulations, as shown in Fig. 2(b2) and Fig. 3(b2). Thus, the device functions as a TM-NR/TE-reflection PBS for light in the diffraction zone. For example, for light with a wavelength of 500 nm and an incident angle of 55°, the measured NR efficiencies for TE and TM light, NR_TM and NR_TE, are 82% and 15%, respectively. The measured reflection efficiencies for TE and TM light, R_TE and R_TM, are 55% and 0.4%, respectively. As the incident angle increases, the PBS exhibits reflectivity over a broader band of wavelengths. In particular, at incident angles larger than 70°, PBS reflectivity can be achieved throughout the entire visible light range.

Figure 2. NR and reflection spectra.

(a) NR spectra for incident angles from 20° to 70°. The different colors denote different incident angles. The solid and hollow markers indicate measured results for TM and TE light, respectively. The dashed and dotted lines correspond to simulated results for TM and TE light, respectively, which are selected from Fig. 3(a1–a2). (b1–b3) Measured reflection spectra of (b1) TM light and (b2) TE light and (b3) the corresponding extinction ratios of R_TE/R_TM. The colors in (b1) and (b2) are the fraction of incident power going into NR or R in percentage. These results show that NR_TM is much larger than NR_TE, while R_TE is larger than R_TM. The operational spectrum expands to the entire visible light range for an incident angle of 70°. The TM reflection exhibits a single peak arising from SPR at the interface of Al and air.

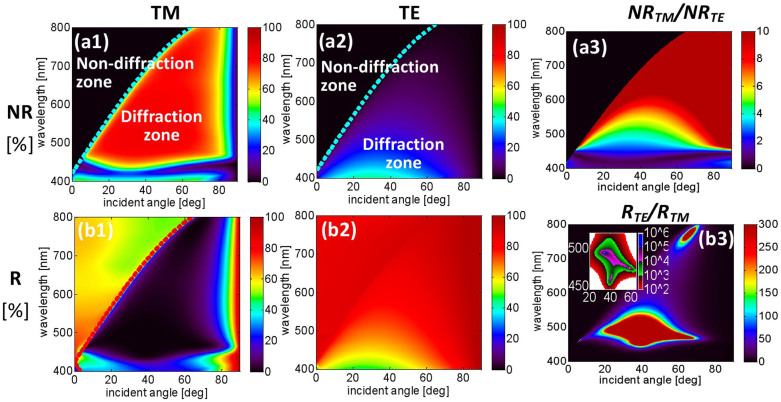
Figure 3. Simulated spectra.

(a1) – (a3) The simulated NR spectra for (a1) TM light and (a2) TE light and (a3) the extinction ratio of NR_TM/NR_TE, (b1–b3) The simulated reflection spectra for (b1) TM light and (b2) TE light and (b3) the extinction ratio of R_TE/R_TM. The colors in (a1–a2) and (b1–b2) are the fraction of incident power going into NR or R in percentage. The cyan dashed lines in (a1) and (a2) represent the boundary between the diffraction zone and the non-diffraction zone. The red dotted line in (b1) represents the SPR wavelengths. The inset in (b3) shows the high extinction ratio zone in detail. The structure used in this simulation is the same as that of the fabricated device shown in Fig. 1.

An extinction ratio of R_TE/R_TM > 80 was measured for wavelengths from 420 nm to 520 nm and incident angles from 50° to 65°, as shown in Fig. 2(b3). For the simulations shown in Fig. 3(b3), the extinction ratio of R_TE/R_TM is greater than 300 for a wide range of incident angles (20°–70°) and for a bandwidth of approximately 100 nm. Furthermore, the ratio reaches 10⁶ at a wavelength of 500 nm and an incident angle of 45°. Although the extinction ratios NR_TM/NR_TE, as shown in Fig. 3(a3), are just above 10 for wavelengths larger than 550 nm, higher extinction ratios can be obtained, for example, by reducing the slit width, as demonstrated in Supplementary Fig. 1.

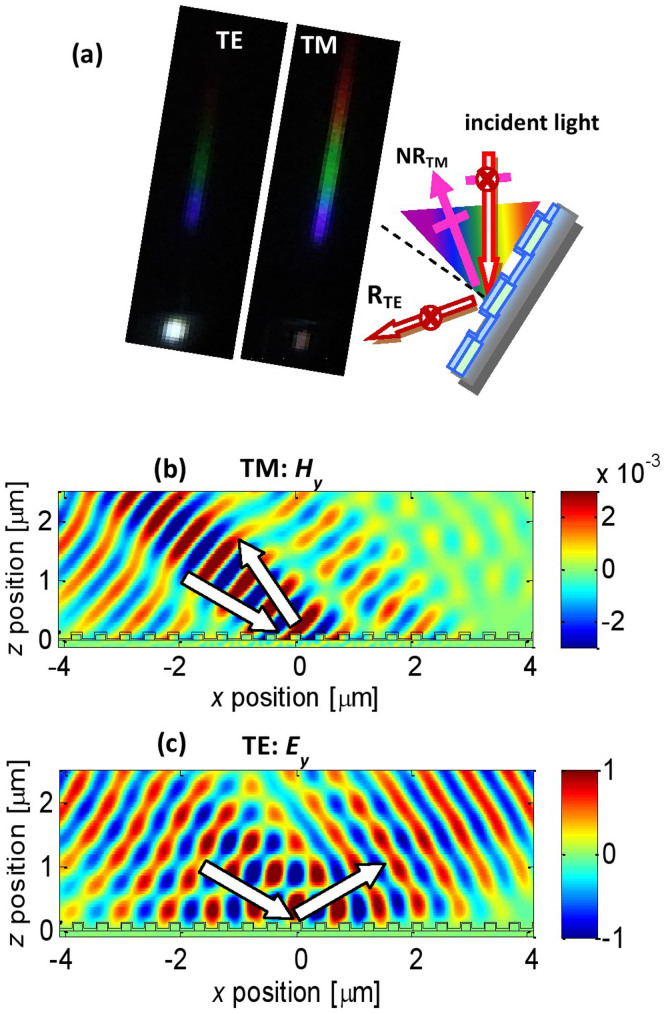
Figure 4(a) shows the experimental far-field patterns of NR and reflection for an incident angle of 55°, providing a visualization of the metasurface beam splitting characteristics. The reflected TE light is bright white light, indicating intense broadband reflectance, while the reflected TM light is faint dark red, implying low narrowband reflectance. Data for other incident angles and corresponding videos are available online (Supplementary Fig. 2 and Videos 1–3), which demonstrate the alternating intensity and color shifts of the NR and reflection as the incident light polarization is rotated. The near-field distributions shown in Figs. 4(b) and 4(c), obtained by using the finite-difference time-domain method (FDTD Solutions, Lumerical), clearly show the metasurface beam splitting. Supplementary Videos 4–5 vividly display these two processes.

Figure 4. Far- and near-field distributions.

(a) Images of NR and reflection for TE and TM white light, respectively, for an incident angle of 55° in the experiment. The TM light is strongly negatively reflected as a rainbow of colors while the TE light is primarily reflected as white light. Panels (b) and (c) display the time snapshots of the simulated magnetic field H_y for TM light and the electric field E_y for TE light, respectively, for a wavelength of 500 nm and an incident angle of 55°. The incident, NR, and reflected light are depicted by the white arrows, respectively. The black lines schematically depict the profile of the bilayer grating. The structure used in the simulation is the same as that of the fabricated device shown in Fig. 1. The magnitude of the incident electric field is 1.0.

To further demonstrate the flexible tunability of the devices, the measured and simulated results of a bilayer metallic nanowire grating fabricated by laser interference lithography on a BK7 glass substrate with a pitch of 280 nm and a PMMA line width of 140 nm are presented in Fig. 5. For this device, the thickness h₂ of the deposited Al is 50 nm, and the sidewall width t₃ is approximately 30 nm. It is clear that compared with above case, the upper and lower limits of the diffraction zone are blue-shifted and that NR_TE is reduced because the slit width is only 80 nm. Extinction ratio values of NR_TM/NR_TE = 150 and R_TE/R_TM = 30 at a wavelength of 450 nm were obtained in the experimental measurements. In the simulations, the extinction ratios for both reflection and NR exceeded 100 over a broad wavelength range, as shown in the insets of Fig. 5(a) and Supplementary Fig. 3. The polarized NR is clearly shown in the photos in Fig. 5(b).

Figure 5. Spectra and photos of a 280-nm-pitch grating.

(a) Measured (solid lines) and simulated (dashed lines) NR (blue and cyan lines) and reflection (red and magenta lines) spectra for TM (blue and red lines) and TE (cyan and magenta lines) light with an incident angle of 60°. The inset is the simulated extinction ratio of NR_TM/NR_TE. (b) Photos of the device irradiated by un-polarized white light with an incident angle of approximately 60° and filtered by a polyvinyl alcohol (PVA) plastic polarizer (extinction ratio of 300). The yellow dotted line indicates the direction of the grating lines. The white dashed lines illustrate the electric field direction of the light passing through the polarizer. An SEM image of the device is also presented. The dielectric grating in the device was fabricated by laser interference, with an Al thickness of 50 nm.

Using the Bloch theory of periodic waveguides, the TM and TE dispersion curves²⁸ of the dominant first-order waveguide mode for an Al-air grating with a 420-nm pitch and a slit width of 60–210 nm were calculated, as shown in Figs. 6(a) and 6(b), respectively. It is clear that for TM light, plasmonic waveguide modes (blue lines) exist below the light cone (black solid line), with a negligible imaginary part of the wave vector along the z-axis k_z (red lines). By contrast, for TE light, the first-order mode is above the light cone with a significant imaginary component of k_z, increasing with decreasing frequency  . The frequency (wavelength) at which the imaginary part of k_z is equal to the real part is called the cut-off frequency (wavelength) and represents the dissipation strength. The solid line represents the result for our experiments and corresponds to the simulation with a cut-off wavelength  _c = 480 nm. For shorter-wavelength light, the normal waveguide mode exists in the air slits; therefore, some diffraction is obtained, as shown in Figs. 2(a) and 3(a2), which fades rapidly with increasing wavelength. As the slit width is reduced, the TE cut-off wavelength  _c is blue-shifted, indicating a stronger dissipation effect. Figure 6(b) shows that for a slit narrower than 160 nm, all visible light with a wavelength longer than 400 nm can barely enter the slits.

Figure 6. Dispersion curves.

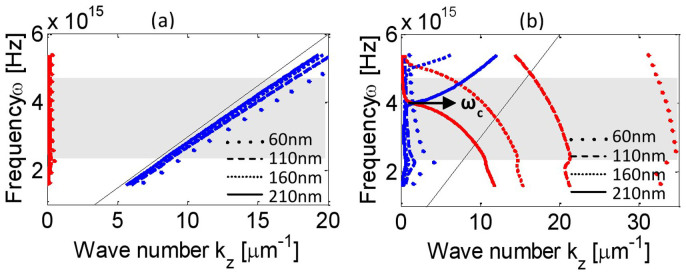
(a) Dispersion curves of the first-order longitudinal Bloch plasmonic waveguide modes in Al-air-Al slits for (a1) TM and (a2) TE light. The blue and red lines of various line types represent the real and imaginary parts of the wave vector k_z for slit widths of 60 nm to 210 nm, respectively. The black solid line represents the light cone.

In accordance with the plasmonic waveguide model, it is clear from Fig. 4(c) that the TE light is mostly reflected, with little penetration into the slits due to the cut-off effect of the slits. By contrast, as shown in Fig. 4(b), TM light can efficiently pass through the first layer of the metal grating and is then reflected by the bottom Al layer. Although the TM reflectance will be increased by the bottom Al grating in our bilayer structure metasurface, by utilizing destructive Fabry-Perot (F-P) resonance between the two metal films to inhibit the TM reflection, most of the TM light is diffracted, and high values of R_TE/R_TM and NR_TM/NR_TE can still be obtained. The field distribution in Fig. 4(b) clearly shows these two aspects: the low reflection of the first layer of the metal grating and the destructive interference of the F-P resonance between the two layers of the metal grating, which result in the overall low TM reflection. The simulated results presented in Fig. 3(b3) show the minimum R_TM and maximum R_TE/R_TM at resonant wavelength of 485 nm. This resonant wavelength can be tuned by changing the values of the slit width and thickness h₁. An example with a slit width of 100 nm and h₁ = 125 nm is shown in Supplementary Fig. 1, where R_TE/R_TM reaches 10⁶ at a resonant wavelength of 620 nm. Furthermore, for this narrower slit, the TE diffraction is further reduced and the reflection increased. This case results in both extinction ratios NR_TM/NR_TE and R_TE/R_TM being over 100 in the simulations, as shown in Supplementary Fig. 1.

Metasurface holography

Using SPR based on a diffraction grating and the metallic antenna effect, several plasmonic holograms have been demonstrated²⁹,³⁰. However, for such reported resonant-type devices, the incident angle or laser wavelength is limited to a narrow working range. However, using a non-resonant metasurface beam splitter, we can produce holograms that operate over a broad range of wavelengths and incident angles. A photoresist hologram of Shanghai Jiao Tong University's school badge “” was produced by laser interference lithography, as shown in Fig. 7(a). The hologram was then coated with a 50-nm-thick Al layer. The microscopy images in Fig. 7(b) show that the sample consists of randomly distributed bilayer metallic nanowire gratings with a pitch of 300 nm. The photos in Fig. 7(c) clearly show that only TM light can reconstruct the real image of “” which corresponds to the negative first-order diffraction mode (NR) of the bilayer metallic nanowire grating. Supplementary Videos 6 and 7 vividly display the clarity of the reconstructed image upon changes in the incident light polarization. Thus, a novel metasurface hologram with an inherent anti-counterfeiting quality is achieved with the additional verification of its polarization dependence.

Figure 7. Metasurface hologram.

(a) Photoresist hologram fabrication scheme: The badge was placed perpendicularly to the photoresist film, and both were illuminated by a large cross-section collimated laser beam with an incident angle of 49° to the photoresist film. (b) Microscopy and SEM images of the top views of the metasurface hologram film at different scales. The film consists of randomly distributed B-MNGs with a pitch of 300 nm. The width of the dielectric PMMA is t₁ = 150 nm, and the thicknesses of the PMMA and Al are h₁ = 110 nm and h₂ = 50 nm, respectively. (c) Real images reconstructed using TM and TE laser light, respectively. The metasurface hologram was illuminated by a TM or TE laser with a wavelength of 532 nm and an incident angle of 75°. The reconstructed real 3-D image was formed by the negative first-order diffraction mode with a diffractive angle of 55° and was imaged onto a black screen, as presented in the bottom left pictures. The image was also viewed with a camera, as presented in the top right pictures, or directly by eye.

Discussion

In general, diffraction occurs when the incident wavelength is comparable to the pitch of a grating. However, this is not the case for metallic gratings. It has been found that the cut-off effect of plasmonic waveguide arrays not only prohibits the transmission of TE light, but also causes the disappearance of TE diffraction. By contrast, the TM light remains and is even highly diffracted beyond the diffraction limit for a slit. The large anisotropy resulting from this TE-metal-like/TM-dielectric-like feature can be explained by the dispersion curve based on the Bloch theory of periodic metal-insulator-metal waveguides. We have demonstrated an ultra-compact TM-NR/TE-reflection metasurface beam splitter with excellent performance characteristics such as high efficiency and compatibility over a broad range of wavelengths and incident angles. In general, such a beam splitter can be designed using the following guidelines: (1) The slit width determines the lower wavelength limit due to the cut-off effect on TE light. (2) The grating pitch determines the upper wavelength limit of the diffraction zone. For wavelengths between the cut-off and the upper limit, TE diffraction is very weak and rapidly decreases for longer wavelengths, while TM light is substantially negatively reflected. (3) With proper slit height selection, TM reflection can be further inhibited by destructive F-P resonance of the plasmonic slit-guided mode, significantly enhancing the reflective polarization extinction ratio R_TE/R_TM.

In summary, by integrating diffraction, waveguide, and plasmonic effects, we propose a novel method for controlling photons with a 1-D metasurface, which is fundamentally different from methods previously proposed for 2-D or 3-D metastructures. A unique and robust PBS with a 1-D metasurface has been demonstrated, which is applicable over a wide range of working wavelengths and incident angles, making it ideal for practical beam splitting devices. As an application, we have demonstrated for the first time a unique metasurface hologram, which can be reconstructed only with TM light, thereby increasing the difficulty of producing a counterfeit. As a cost-efficient and robust metastructure, the 1-D device has the potential to be used in a broad range of applications including displays, holograms, and laser optics.

Methods

Device fabrication

PBS-1

A PMMA (Allresist, German) dielectric grating with a pitch of 420 nm and a bar width of 170 nm was fabricated by nano-imprinting on a silicon substrate. The grating was subsequently coated with a 30-nm-thick Al film by E-beam evaporation.

PBS-2

A PMMA dielectric grating with a pitch of 280 nm and a bar width of 140 nm was fabricated by laser interference using a He–Cd laser (442 nm, KIMMON) with a cross angle of 52° on a BK7 glass substrate. The grating was then coated with a 50-nm-thick Al film by E-beam evaporation.

Metasurface hologram

A photoresist hologram of Shanghai Jiao Tong University's school badge “” was produced by laser interference lithography. The badge was placed perpendicularly to the photoresist film, and both were illuminated by a large cross-section collimated laser beam with an incident angle of 49.7° to the photoresist film. The photoresist hologram was subsequently coated with a 50-nm-thick Al film by E-beam evaporation.

Diffraction images and spectral measurement

PBS characterization

Unpolarized white light from a white light LED was focused by a 20X objective lens and then collimated and polarized by a convex lens and a Glan-Thomson prism, respectively. Finally, the light was directed to a device fixed on a motor-driven rotating stage. The diffracted and reflected light was collected by a fiber mounted with a collimating lens connected to a spectrometer (QE65-PRO, Ocean Optics). As the diffraction and reflection patterns were displayed on a white screen, the Glan-Thomson prism was continuously rotated to change the polarization state of the incident light.

Metasurface hologram reconstruction

The metasurface hologram was illuminated by a TM or TE laser with a wavelength of 532 nm and an incident angle of 75°. The reconstructed real 3-D image was formed by the negative first-diffraction order (NR) with a diffractive angle of 55°. The image was either displayed on a black screen or viewed directly by eye or through a camera.

Simulation methods

The simulated spectra in Figs. 2, 3, and 5 were obtained using 2-D rigorous coupled-wave analysis (Diffract MODE, RSOFT). TM or TE light was incident from top to bottom with an incident angle of 0° to 90° in steps of 0.2°. The incident light had wavelengths of 400 nm to 800 nm in steps of 2 nm. Five harmonics were used in representing the eigen-mode expansion of the slits. The grid size was 1 nm. The permittivity of PMMA is ε₁ = 2.56. The permittivity of Al and the permittivity of Si substrate are taken from this software's material library. The permittivity of glass substrate in Fig. 5 is 2.25.

The simulated electromagnetic field distributions in Fig. 4 and Videos 4–5 in the Supplementary Material were produced using the finite-difference time-domain method (FDTD Solutions, Lumerical), where 21 periods of the grating were taken and the absorbed boundary condition was set in both the x and z directions. The grid step size was 2 nm. The incident wavelength was 500 nm, and the incidence angle was 55°. The permittivity of PMMA is ε₁ = 2.56. The permittivity of Al ε_m and the permittivity of Si substrate ε_s are taken from this software's material library. The dispersion curves of the longitudinal waveguide modes in the air slits, as shown in Fig. 6(a) and 6(b), are obtained from the following equation according to the theory of periodic waveguides:

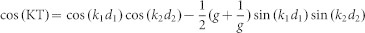Where, K denotes the Bloch wave number; the grating pitch T = d₁ + d₂; d₁ = 210 nm and d₂ = 210 nm are the width of the aluminum and air in one pitch, respectively; k₁ = (k₀ε₁-k_{z_1})^1/2 and k₂ = (k₀ε₂-k_{z_2})^1/2 are the wave number of the waveguide mode in the aluminum and air long the x-axis, respectively; k_z is the wave number along the z-axis; k₀ is the wave number of the light in air; g = k₁ε₂/(k₂ε₁) for TM light and k₁/k₂ for TE light, respectively. The permittivity of air ε₁ = 1. The permittivity of Al ε₂ is calculated the equation induced by the Lorantz-Drude mode in Ref. 27:

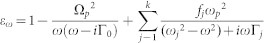where ω is the light frequency, ω_p is the plasma frequency, k is the number of oscillators with frequency ω_j, strength f_j, and lifetime 1/Γ_j, while Ω_p = (f₀)^0.5ω_p is the plasma frequency associated with intraband transitions with oscillator strength f₀ and damping constant Γ₀. These parameters are also taken from this reference: ω_p = 14.98*2πh, f _0-4 = [0.523, 0.227, 0.050, 0.166, 0.030]; Γ_0-4 = [0.047, 0.333, 0.312, 1.351, 3.382]* 2πh, ω_0-4 = [0.000, 0.162, 1.544, 1.808, 3.473]*2πh.

Author Contributions

J.Z. performed the device measurement, conducted the simulations, and wrote the main manuscript text. Z.C.Y. was responsible for project management, fabricated the samples, performed the device measurement and wrote the main manuscript text. N.L.S. and R.Z. developed the measurement setup and performed the measurements. Z.M.S., H.P.D.S., and J.Z. contributed to analyze the results and write the manuscript. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Video 1

Supplementary Information

Video 2

Supplementary Information

Video 3

Supplementary Information

Video 4

Supplementary Information

Video 5

Supplementary Information

Video 6

Supplementary Information

Video 7

Supplementary Information

Supplementary Figures