Structure–activity analysis of a CFTR channel potentiator: Distinct molecular parts underlie dual gating effects

The head and tail regions of 5-nitro-2-(3-phenylpropylamino)benzoate increase CFTR open probability through distinct mechanisms.

Abstract

The cystic fibrosis (CF) transmembrane conductance regulator (CFTR) is a member of the ATP-binding cassette transporter superfamily that functions as an epithelial chloride channel. Gating of the CFTR ion conduction pore involves a conserved irreversible cyclic mechanism driven by ATP binding and hydrolysis at two cytosolic nucleotide-binding domains (NBDs): formation of an intramolecular NBD dimer that occludes two ATP molecules opens the pore, whereas dimer disruption after ATP hydrolysis closes it. CFTR dysfunction resulting from inherited mutations causes CF. The most common CF mutation, deletion of phenylalanine 508 (ΔF508), impairs both protein folding and processing and channel gating. Development of ΔF508 CFTR correctors (to increase cell surface expression) and potentiators (to enhance open probability, P_o) is therefore a key focus of CF research. The practical utility of 5-nitro-2-(3-phenylpropylamino)benzoate (NPPB), one of the most efficacious potentiators of ΔF508 CFTR identified to date, is limited by its pore-blocking side effect. NPPB-mediated stimulation of P_o is unique in that it involves modulation of gating transition state stability. Although stabilization by NPPB of the transition state for pore opening enhances both the rate of channel opening and the very slow rate of nonhydrolytic closure, because of CFTR’s cyclic gating mechanism, the net effect is P_o stimulation. In addition, slowing of ATP hydrolysis by NPPB delays pore closure, further enhancing P_o. Here we show that NPPB stimulates gating at a site outside the pore and that these individual actions of NPPB on CFTR are fully attributable to one or the other of its two complementary molecular parts, 3-nitrobenzoate (3NB) and 3-phenylpropylamine (3PP), both of which stimulate P_o: the pore-blocking 3NB selectively stabilizes the transition state for opening, whereas the nonblocking 3PP selectively slows the ATP hydrolysis step. Understanding structure–activity relationships of NPPB might prove useful for designing potent, clinically relevant CFTR potentiators.

INTRODUCTION

The cystic fibrosis (CF) transmembrane conductance regulator (CFTR; Riordan et al., 1989) is the epithelial chloride ion channel mutated in CF patients. CFTR belongs to the family of ATP-binding cassette (ABC) proteins, most of which function as active transporters to move a diverse range of substrates across biological membranes at the expense of ATP hydrolysis (Dean and Annilo, 2005). Typical ABC protein architecture comprises two transmembrane domains (TMDs), which during a transport cycle alternate between inward- and outward-facing conformations, and two cytosolic nucleotide-binding domains (NBDs), which bind and hydrolyze ATP to power TMD movements required for unidirectional substrate transport (Hollenstein et al., 2007). Upon ATP binding the two NBDs of ABC proteins form a stable head-to-tail dimer that occludes two molecules of ATP at the interface. Both ATP-binding sites are formed by structural contributions of both NBDs: one contributes the conserved Walker A and B motifs, complemented by the conserved ABC “signature” motif of the other. Dissociation of this extremely stable dimer is facilitated by ATP hydrolysis, allowing ADP–ATP exchange and initiation of a new cycle. For ABC exporters, the closest relatives of CFTR, NBD dimer formation flips the TMDs from inward to outward facing, whereas NBD dimer dissociation resets the TMDs to inward facing (Hollenstein et al., 2007).

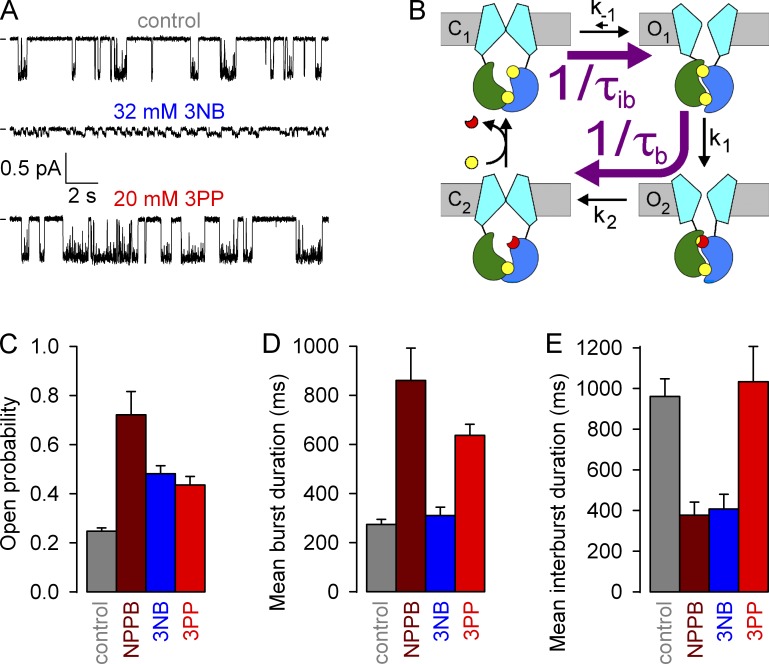
CFTR employs analogous structural elements to gate its transmembrane chloride ion pore, which is believed to be open and conducting in the outward-facing but closed in the inward-facing TMD conformation (Vergani et al., 2005; Gadsby et al., 2006; Hwang and Sheppard, 2009). In CFTR the ATP-binding site formed by NBD1 Walker motifs + NBD2 signature motif (“site 1”) is catalytically inactive (Aleksandrov et al., 2002; Basso et al., 2003), and only “site 2” (NBD2 Walker motifs + NBD1 signature) functions as an active ATPase (Ramjeesingh et al., 1999). Therefore, during each gating cycle (see cartoons in Figs. 6–8 and 10) site 2 cycles between dimerized prehydrolytic (open state O₁), dimerized posthydrolytic (open state O₂), and dissociated (closed states C₁ and C₂) conformations in a unidirectional manner, whereas site 1 remains ATP bound for several gating cycles (Basso et al., 2003; Tsai et al., 2010). In single-channel recordings, CFTR channels show bursting behavior: bursts of openings interrupted by brief (∼10 ms) “flickery” closures are flanked by longer (∼1 s) “interburst” closures. The above large conformational transitions that are powered by the evolutionarily conserved ATP hydrolysis cycle, i.e., formation and disruption, respectively, of the NBD dimer, coincide with entering and exiting a burst of openings, whereas the durations of flickery closures are insensitive to [ATP] (Vergani et al., 2003). Therefore, in this study, “opening” and “closing” will be used to mean entering and exiting a burst and open probability (P_o) to mean bursting probability (P_burst, the fraction of time the channel spends in the bursting state; note P_o∼P_burst in physiological salt solutions). In addition to the canonical ABC domains, CFTR possesses a unique cytosolic regulatory (R) domain, phosphorylation of which by cyclic AMP-dependent protein kinase (PKA) is a prerequisite for CFTR channel gating (Gadsby et al., 2006) and is the means of physiological regulation of CFTR activity in the context of living cells.

Figure 6.

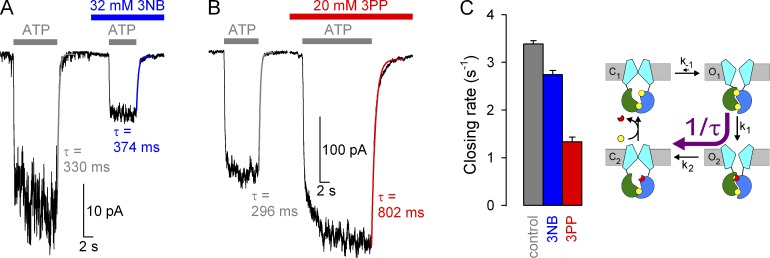
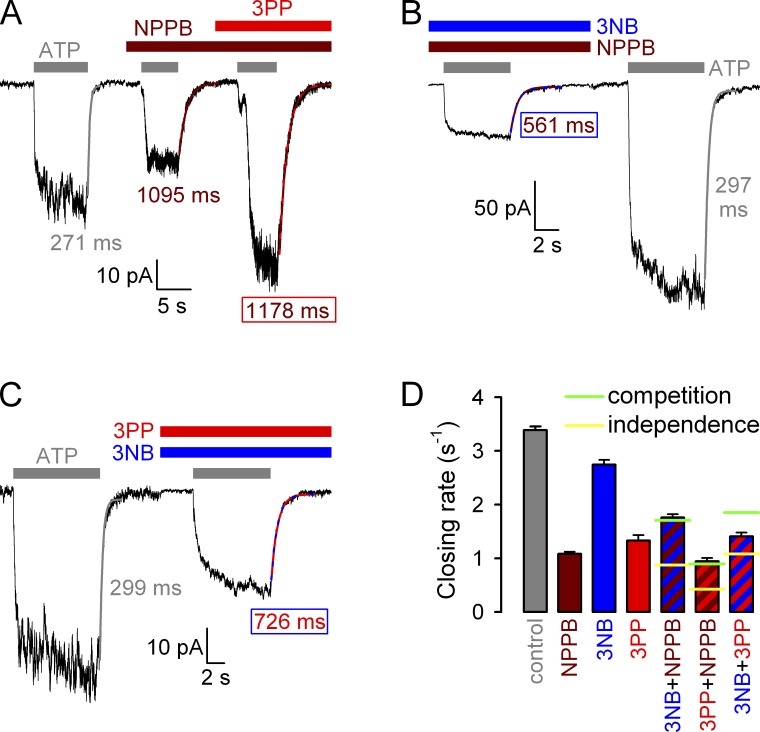
Effects of 3NB and 3PP on macroscopic closing rate of WT CFTR. (A and B) Macroscopic WT CFTR currents at −80 mV, elicited by brief applications of 2 mM ATP (gray bars) in the absence of drug or in the presence of either 32 mM 3NB (A, blue bar) or 20 mM 3PP (B, red bar). All four current decay time courses after ATP removal were fitted by single exponentials (colored lines), and time constants are indicated. (C) Macroscopic closing rates, obtained as the inverses of fitted time constants (see Materials and methods), under control conditions (gray bar) or in the presence of either 32 mM 3NB (blue bar) or 20 mM 3PP (red bar). Mean ± SEM is shown. Cartoon in C (also in Fig. 7 B; Fig. 8, C and G; and Fig. 10) depicts simplified cyclic CFTR gating model: cyan, TMDs; green, NBD1; blue, NBD2; yellow, ATP; red, ADP. Purple arrow highlights the pathway under study.

Figure 8.

Effects of 3NB and 3PP on gating rates under nonhydrolytic conditions. (A and B) Macroscopic K1250A CFTR currents at −20 mV, elicited by exposures to 10 mM ATP (gray bars) in the absence of drug or in the presence of either 32 mM 3NB (A, blue bar) or 20 mM 3PP (B, red bar). All current decay time courses after ATP removal were fitted by single exponentials (colored lines), and time constants are indicated. (C) Macroscopic closing rates (bars; 1/τ; see Materials and methods) in the absence (gray bar) or presence of 32 mM 3NB (blue bar) or 20 mM 3PP (red bar) quantify effects on rate k₋₁ (cartoon, purple arrow). The K1250A mutation (cartoon, red stars) disrupts ATP hydrolysis in site 2 (red cross). (D and E) Macroscopic K1250A CFTR currents elicited by 10 mM ATP at −20 mV and prolonged exposures to 32 mM 3NB (D, blue bars) or 20 mM 3PP (E, red bars) of channels gating at steady-state. Zero-current levels (dotted lines) were estimated from final segments. In D, brief exposure to 3NB of surviving locked-open channels after ATP removal (20-s yellow box, expanded in inset) measures fractional pore block (see Fig. 3). (F) Fractional K1250A CFTR currents at −20 mV in 32 mM 3NB (left pair of bars) or 20 mM 3PP (right pair of bars) applied during steady-state gating (gray bars) or in the locked-open state (yellow bars). (G) Effects of 3NB (blue bar) and 3PP (red bar) on the closed-open equilibrium (cartoon, purple double arrow). Fractional effects on P_o for K1250A CFTR were calculated as in Fig. 5 (D and H). Mean ± SEM is shown.

Figure 10.

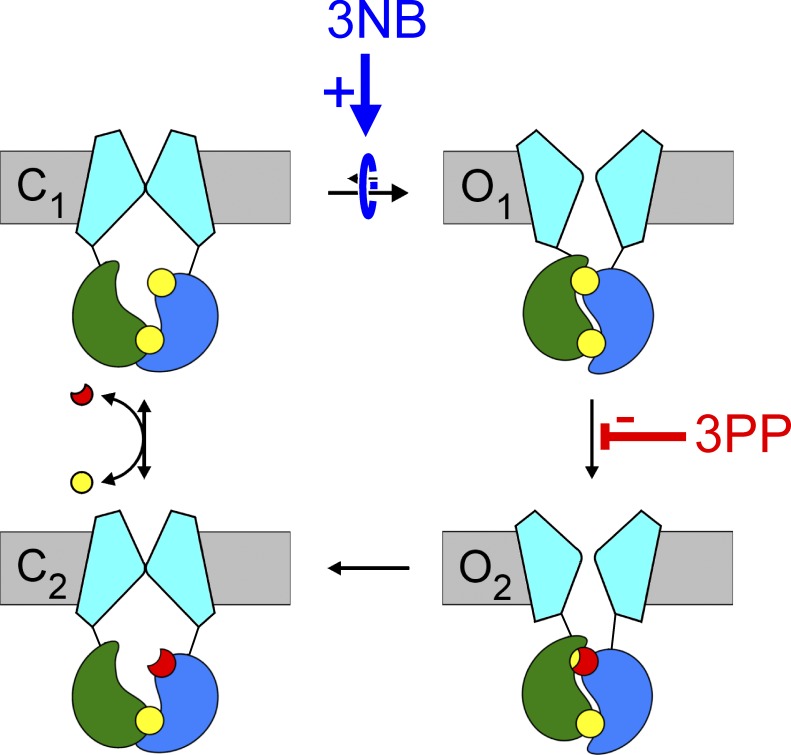
Cartoon summary of 3NB and 3PP gating effects. 3NB acts as a pure catalyst for the C₁↔O₁ transition (blue arrow), thereby increasing channel opening rate and nonhydrolytic closing rate. 3PP acts to inhibit the ATP hydrolysis step (red line). Both effects independently stimulate P_o for WT CFTR, but neither effect changes P_o for a nonhydrolytic mutant. NPPB exerts both effects at the same time, resulting in extremely efficacious stimulation of P_o for WT (and ΔF508) CFTR (Csanády and Töröcsik, 2014).

The most prevalent CF mutation, deletion of phenylalanine 508 of CFTR, is found in at least one allele of ∼90% of CF patients. The ΔF508 mutation primarily causes a folding/processing defect that diminishes CFTR surface expression (Cheng et al., 1990), but it also causes a functional defect resulting in a dramatically lowered P_o even for the minute fraction of mutant channels that do reach the cell surface (Miki et al., 2010). Much effort is therefore focused on finding chemical chaperones that enhance processing of ΔF508 CFTR (correctors) and small molecules that increase ΔF508 open probability (potentiators). The first CFTR potentiator to enter clinical use, VX-770 (Ivacaftor; Vertex Pharmaceuticals [Van Goor et al., 2009]), was recently approved for the treatment of CF patients carrying the G551D (Ramsey et al., 2011) and other rare CFTR mutations. Interestingly, VX-770 was also reported to stimulate ΔF508 CFTR currents in vitro (by ∼5-fold [Van Goor et al., 2009] or even by 10–20-fold [Kopeikin et al., 2014]), prompting hope for its usefulness in the treatment of the most common form of CF. However, the need for developing novel pedigrees for CFTR potentiators is underscored by the recent demonstration that VX-770 counteracts the beneficial effect of the corrector compound VX-809 (Lumacaftor; Vertex Pharmaceuticals [Van Goor et al., 2011]) on ΔF508-CFTR surface expression (Cholon et al., 2014; Veit et al., 2014), which might explain the very low level of synergy between these two compounds reported in recent clinical trials (Boyle et al., 2014).

Apart from VX-770, the most efficacious potentiating effect on ΔF508 CFTR documented to date (15–20-fold stimulation of P_o) is that of 5-nitro-2-(3-phenylpropylamino)benzoate (NPPB; Wang et al., 2005; Csanády and Töröcsik, 2014). Although NPPB itself is not clinically useful because its anionic carboxylate group blocks the pores of most anion channels including that of CFTR (Wangemann et al., 1986), previous work showed that gating stimulation by NPPB, unlike the pore block, is largely voltage independent, prompting the conclusion that the pore block and gating effects must happen through distinct binding sites on CFTR (Csanády and Töröcsik, 2014). If true, then identifying the NPPB gating site on CFTR might define a promising new drug target and allow development of pure potentiator compounds with an efficacy as high as that of NPPB, but without nonspecific side effects (compare with Wang et al. [2005]).

A detailed study of CFTR stimulation by NPPB identified a unique molecular mechanism, which involves effects on transition-state stabilities, rather than energetic stabilization of open states (Csanády and Töröcsik, 2014). NPPB exerted dual effects on CFTR gating. First, it prolonged WT CFTR open times by approximately fourfold, as a result of allosteric slowing of ATP hydrolysis at site 2 of the NBD dimer (step O₁→O₂; compare with Fig. 6 C, inset). Second, it increased by approximately threefold both the rate of opening of WT channels (step C₁→O₁) and the slow rate of nonhydrolytic closure (step O₁→C₁) of catalytically inactive mutants, such as K1250A CFTR in which lack of the conserved NBD2 Walker A lysine side chain abrogates ATP hydrolysis at site 2 (Ramjeesingh et al., 1999). Together, these latter actions imply a true catalyst effect for the C₁↔O₁ step, suggesting that NPPB binding to the gating site stabilizes the transition state for this conformational change: i.e., it decreases the height of the energetic barrier separating C₁ and O₁ ground states. Such a mechanism can lead to an increase in open probability only in the case of a nonequilibrium gating cycle: because for WT CFTR pore closure is rate limited by the O₁→O₂ step, a threefold acceleration of the very slow O₁→C₁ step has no appreciable effect on channel closing rate. Thus, the result is a selective enhancement of opening rate, and therefore of P_o. Importantly, for channels that gate with low P_o, such as ΔF508 (or poorly phosphorylated WT) channels, the above two effects on opening and closing rate enhance P_o in a multiplicative manner (Csanády and Töröcsik, 2014), explaining the very high efficacy of NPPB stimulation of ΔF508 CFTR.

The recently observed negative influence of VX-770 on ΔF508 CFTR stability, suggested to involve a direct CFTR–drug interaction (Cholon et al., 2014; Veit et al., 2014), raises concerns about the practical usefulness of potentiators that bind to that same binding site. Because the molecular mechanisms of stimulation by NPPB and VX-770 clearly differ from each other (Jih and Hwang, 2013; Csanády and Töröcsik, 2014; Kopeikin et al., 2014), it seems likely that NPPB exerts its gating effects at a distinct site. This offers hope for independent effects of NPPB-based potentiators on gating of ΔF508 CFTR and of VX-809 on its surface expression, underscoring the relevance of mechanistic studies of NPPB effects on CFTR.

In the present study we first reexamine the question of whether gating stimulation and pore block by NPPB indeed happen through distinct binding sites by exploiting competition for pore block between NPPB and MOPS, a blocker with no gating effects (Csanády and Töröcsik, 2014). Furthermore, to better understand the structural requirements of the complex gating effects of NPPB and whether perhaps distinct effects on gating might be attributable to distinct parts of the whole molecule, we undertook structure–activity relationship analysis on this drug. NPPB is a complex, long linear molecule flanked by two aromatic rings (Fig. 1), suggesting extended interactions with a relatively large binding surface on CFTR. We therefore examine here the functional effects on CFTR of two complementary parts of NPPB: the NPPB head 3-nitrobenzoate (3NB; Fig. 1, blue) and the NPPB tail 3-phenylpropylamine (3PP; Fig. 1, red).

Figure 1.

Structures of NPPB, 3NB, and 3PP. NPPB structure and its division into head (3NB, blue) and tail (3PP, red) parts.

MATERIALS AND METHODS

Molecular biology

WT and K1250A CFTR cDNA subcloned into the pGEMHE plasmid (Vergani et al., 2003) was linearized using NheI and transcribed in vitro using T7 polymerase (mMESSAGE kit; Ambion). Purified cRNA was quantitated on formaldehyde-agarose gels and stored at −80°C.

Isolation and injection of Xenopus laevis oocytes

Stage V–VI oocytes were obtained from Xenopus by partial ovariectomy, collagenase digested, and stored at 18°C in a modified Ringer’s solution supplemented with 1.8 mM CaCl₂ and 50 µg/ml gentamycin (Chan et al., 2000). To obtain adequate expression levels for single-channel and macroscopic recordings, respectively, 0.1–10 ng of cRNA was injected in a fixed 50-nl volume, and recordings were performed 1–3 d after injection.

Excised inside-out patch-clamp recordings

For excised inside-out patch-clamp recordings, patch pipettes were pulled from borosilicate glass to tip resistances of ∼3 MΩ. Pipette solution contained (mM) 136 NMDG-Cl, 2 MgCl₂, and 5 HEPES, pH 7.4 with NMDG, and bath solution contained (mM) 134 NMDG-Cl, 2 MgCl₂, 5 HEPES, and 0.5 EGTA, pH 7.1 with NMDG. After gigaseal formation (R_seal > 100 GΩ) patches were excised in the inside-out configuration and transferred into a flow chamber in which the continuously flowing bath solution could be exchanged with a time constant of <50 ms. MgATP (Sigma-Aldrich) was made up at 400 mM (adjusted to pH 7.1 with NMDG) and diluted into the bath solution at 2 and 10 mM final concentrations, respectively, for recordings on WT and K1250A CFTR (the higher [ATP] for K1250A was used to compensate for its reduced ATP-binding affinity [Vergani et al., 2003]). CFTR channels were prephosphorylated by 1–2-min exposure to 300 nM catalytic subunit of bovine PKA (Sigma-Aldrich); recordings were performed after PKA removal, in the stable partially dephosphorylated state, as described previously (Csanády et al., 2000). For macroscopic pore-block measurements on E1371S (see Fig. 2 A) or K1250A CFTR (see Figs. 3 and 4), surviving currents of channels opened in resting oocytes as the result of endogenous phosphorylation were also used (Csanády and Töröcsik, 2014). 3-nitrobenzoic acid, titrated to pH 7.1 using NMDG (∼1 mol/mol), was made up at 1 M and diluted into the bath from this stock solution. 3PP was dissolved at 50 mM in our bath solution and titrated to pH 7.1 using sulfuric acid (∼0.45 mol/mol), and further dilutions were made from this stock. Sulfuric acid (1, 2, 5, 10, and 20 mM) was added to the bath solution and pH adjusted to 7.1 using NMDG (∼2 mol/mol). Solutions containing MOPS were adjusted to pH 7.2; thus, [MOPS⁻] was ∼50% of total [MOPS] (pK_a = 7.2). All recordings were performed at 25°C. Currents were amplified (Axopatch 200B; Molecular Devices), Gaussian-filtered at 2 kHz, and digitized at 10 kHz (Digidata 1322A, pCLAMP 9 software; Molecular Devices).

Figure 2.

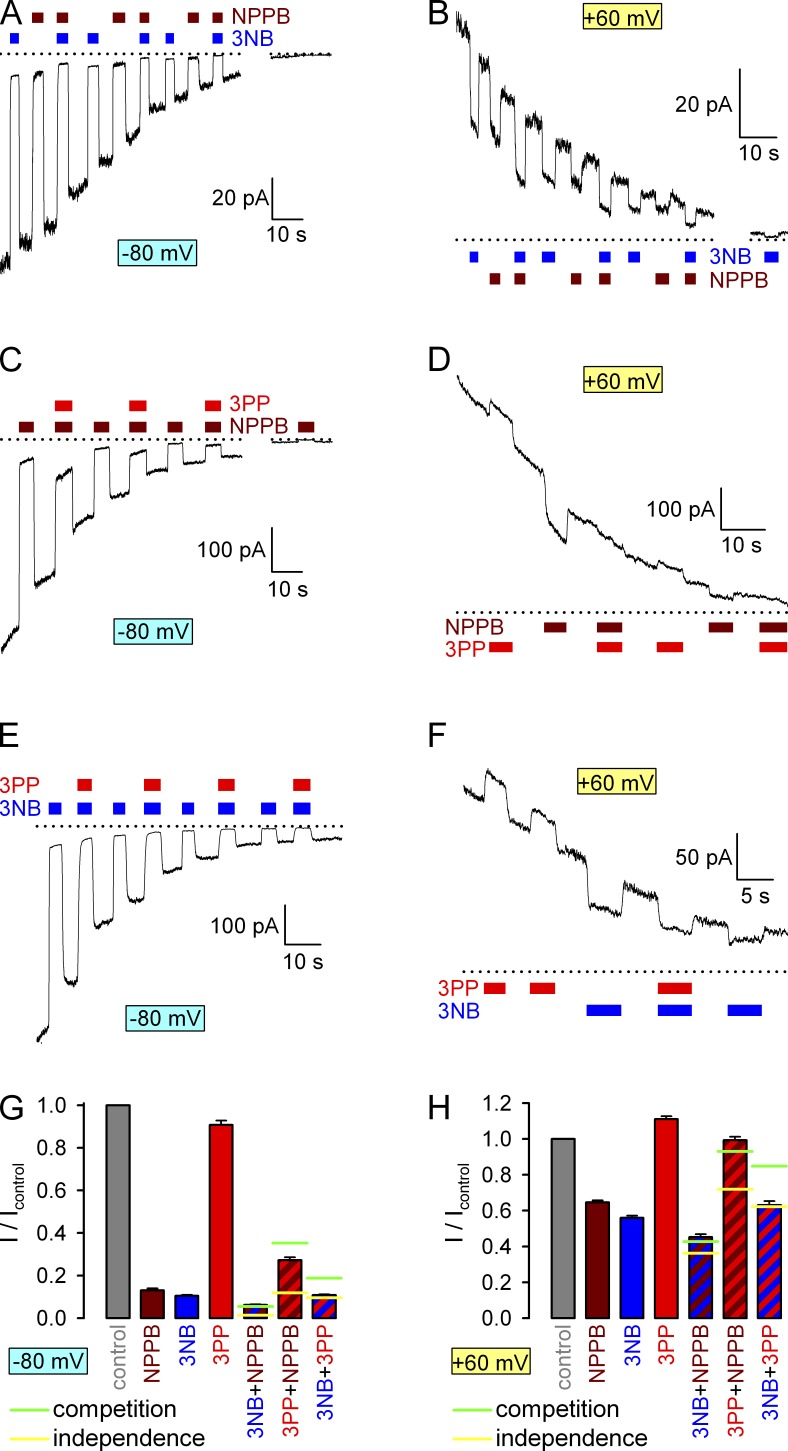
MOPS⁻ competes with NPPB for binding in the pore but not at the gating site. (A) Macroscopic locked-open E1371S CFTR current at −120 mV after removal of ATP from the bath; exposures to various NPPB concentrations (brown bars) in the continued presence of 80 mM MOPS⁻ (green bar; magnified in yellow inset). Dotted line marks zero-current level. (B) Dose–response curves for NPPB block at −120 mV in the absence (open symbols; replotted from Csanády and Töröcsik [2014]) and presence (green-filled symbols) of 80 mM MOPS⁻. Leftmost symbols in these and all other dose–response plots represent zero drug concentration. Fits to the Michaelis-Menten equation (dotted and solid line) reveal an approximate ninefold increase in the apparent K_I of NPPB in the presence of 80 mM MOPS⁻ (K_I = 8.3 mM for MOPS⁻; compare with Csanády and Töröcsik [2014]). (C) Macroscopic WT CFTR currents at −120 mV elicited by brief exposures to 2 mM ATP in the absence or presence of blockers. Current relaxations after ATP removal were fitted by single exponentials (colored lines), and colored numbers are time constants (in milliseconds). (D) Macroscopic closing rates of WT CFTR in the absence of blocker (gray) and in the presence of 100 µM NPPB (brown), 80 mM MOPS⁻ (green), or 100 µM NPPB + 80 mM MOPS⁻ (striped). (E) Macroscopic K1250A CFTR currents at −40 mV elicited by brief exposures to 10 mM ATP in the absence or presence of blockers. Current relaxations after ATP removal were fitted by single exponentials with time constants indicated. (F) Macroscopic K1250A closing rates in the absence of blocker (gray) and in the presence of 100 µM NPPB (brown), 80 mM MOPS⁻ (green), or 100 µM NPPB + 80 mM MOPS⁻ (striped). Mean ± SEM is shown.

Figure 3.

Effects of 3NB, 3PP, and sulfate on CFTR permeation. (A, B, F, G, I, and J) Decaying macroscopic currents of locked-open K1250A CFTR channels after removal of ATP, recorded at membrane potentials of −80 (A, F, and I) or 60 mV (B, G, and J) and responses to brief applications of various concentrations of 3NB (A and B, blue bars), 3PP-sulfate (F and G, red bars), or sulfate (I and J, green bars). Zero-current levels (dotted lines) were estimated from the responses of final current segments to application of 32 mM 3NB (blue bars in all panels). (C and H) Dose–response curves at −80 (cyan-filled symbols) and 60 mV (yellow-filled symbols) of fractional currents as a function of [3NB] (C), [3PP-sulfate] (H, red), and sulfate (H, green). The two alternative abscissae in H were scaled to reflect the presence of 0.45 mol/mol sulfate ions in 3PP-sulfate; i.e., the green abscissa correctly reflects sulfate concentrations for all four plots. The plots in C were fitted by the Michaelis-Menten and the yellow–red plot in H to the Hill equation, and midpoints are printed in the panels. (D) Responses of decaying macroscopic locked-open K1250A CFTR current to brief applications of 32 mM 3NB (blue bars) at various membrane potentials. Zero-current level (dotted line) was estimated from the final current segment after subtraction of the small (∼2 pA/60 mV) linear seal current. (E) Voltage dependence of macroscopic current block by 32 mM 3NB (symbols) and Boltzmann fit (solid line) yielding parameters z = 0.49 ± 0.02 mV and V_1/2 = 41 ± 2 mV (calculated K_d(0) = 14.7 mM). Mean ± SEM is shown.

Figure 4.

Competition for CFTR pore block between NPPB, 3NB, and 3PP. (A–F) Responses of decaying macroscopic locked-open K1250A CFTR currents, recorded at membrane potentials of −80 (A, C, and E) or 60 mV (B, D, and F), to brief exposures to the following drug combinations: (A and B) 32 mM 3NB (blue bars) and/or 210 µM NPPB (brown bars), (C and D) 20 mM 3PP (red bars) and/or 210 µM NPPB (brown bars), and (E and F) 32 mM 3NB (blue bars) and/or 20 mM 3PP (red bars). Zero-current levels (dotted lines) were estimated from the responses of final current segments to application of either 32 mM 3NB or 210 µM NPPB. (G and H) Fractional currents, normalized to control (gray bars), recorded at −80 mV (G) or 60 mV (H) membrane potentials in the presence of 210 µM NPPB (brown bars), 32 mM 3NB (blue bars), 20 mM 3PP (red bars), or their combinations (striped bars, same color coding). Horizontal lines illustrate fractional currents predicted for mixtures (see Materials and methods), assuming either completely independent (yellow lines) or mutually exclusive (green lines) binding of the two drugs in the pore. Mean ± SEM is shown.

Macroscopic data analysis

Fractional currents in the presence of drugs (see Figs. 2 A and 3–5) were calculated by dividing average steady (or quasi-steady, for Figs. 2 A, 3, and 4) current during brief drug application by the mean of the steady currents measured before and after drug exposure. Macroscopic current relaxations upon ATP removal were least-squares fitted to single exponentials, and closing rate was defined as the inverse of the fitted time constant. For better comparability, closing rates in the presence of various drugs or drug combinations were normalized to those measured under control conditions in the same patch, and average normalized closing rates were then scaled up using the pooled average from all control measurements.

Figure 5.

Voltage-independent stimulation of CFTR open probability by both 3NB and 3PP. (A and E) Macroscopic WT CFTR currents in 2 mM ATP (gray bars) at −80 (left traces) and 60 mV (right traces) and brief exposures to 32 mM 3NB (A, blue bars) or 20 mM 3PP (E, red bars). (B) Responses of macroscopic WT CFTR currents, elicited at −80 mV by repeated exposures to 2 mM ATP (gray bars), to applications of increasing concentrations of 3NB (blue bars). (F) Macroscopic WT CFTR currents elicited at −80 mV by exposures to 2 mM ATP (gray bars) either in the absence or in the presence (red bars) of various concentrations of 3PP. (C and G) Dose dependence of fractional currents on 3NB (C) and 3PP (G) concentrations at −80 mV (closed symbols) and Hill fits (solid lines; midpoints printed in the panels); open symbols and dotted lines show dose dependence of pore block, replotted from Fig. 3 (C and H). (D and H) Gating stimulation by 3NB (D) and 3PP (H) at −80 mV; P_o/P_o;control was calculated as the ratio (I/I_control)/(i/i_control). Control P_o (dotted lines), estimated for single WT channels under identical conditions (see Fig. 7 C), is ∼0.2. Mean ± SEM is shown.

Single-channel kinetic analysis

Gating kinetics in 32 mM 3NB was studied only in patches containing a single active channel, whereas patches with one to four active channels were used for characterizing the effects of 20 mM 3PP. For single-channel kinetic analysis under control conditions or in 20 mM 3PP, currents were digitally filtered at 100 Hz and idealized using half-amplitude threshold crossing. For recordings in the presence of 32 mM 3NB, the small unitary amplitudes (∼0.06 pA at −80 mV) required filtering at 50 Hz, and the closed-open threshold was set in between the zero-current and the lower subconductance level. Events lists were fitted to a closed-open-blocked scheme by maximum likelihood using an algorithm that accounts for the time resolution (fixed dead times of 4 and 6 ms, respectively, were imposed for bandwidths of 100 and 50 Hz) of the recording (Csanády, 2000). The closed-open-blocked scheme separates slow ATP-dependent and brief ATP-independent closures and allows calculation of mean burst (τ_b) and interburst (τ_ib) durations as described previously (Csanády et al., 2000).

Calculation of standard free enthalpies of binding

The dissociation constants for the gating site (K_d; see Table 2) were assumed voltage independent (see Csanády and Töröcsik [2014]; also compare with Fig. 5, A and E). The zero-voltage dissociation constant for the pore-binding site (K_d(0); see Table 1) was taken from Csanády and Töröcsik [2014] for NPPB, but calculated for 3NB from the apparent K_d(V_m) values measured at V_m = −80 and 60 mV (see Fig. 3 C) assuming K_d(V_m) = K_d(0)·exp(−zFV_m/(RT)) (F = 96500 C/mol, R = 8.31 J/mol/K, T = 298 K); the set of two equations for the two voltages allows solving for the two unknown parameters K_d(0) and z. For 3PP, K_d was assumed voltage independent and estimated from its value measured at 60 mV (see Fig. 3 H). Molecular standard free enthalpies of binding (see Tables 1 and 2) were calculated as ΔG^o_binding = kT·ln(K_d(0)) (k, Boltzmann’s constant).

Table 2.

Estimated free enthalpies of binding at the gating site for NPPB, 3NB, and 3PP

Drug	Kd	ΔGobinding
		kT
NPPB	80 µM	−9.4
3NB	9 mM	−4.7
3PP	6 mM	−5.1

For NPPB, K_d was taken from Csanády and Töröcsik (2014). For 3NB and 3PP, K_d was estimated as the apparent K_1/2 for stimulating open probability at −80 mV (Fig. 5, D and H), assuming voltage-independent binding at the gating site.

Table 1.

Estimated free enthalpies of binding in the pore for NPPB, 3NB, and 3PP

Drug	Kd(0 mV)	ΔGobinding
		kT
NPPB	150 µM	−8.8
3NB	12 mM	−4.4
3PP	10 mM	−4.6

For NPPB, K_d(0) was taken from Csanády and Töröcsik (2014). For 3NB, K_d(0) was calculated (see Materials and methods) from the apparent K_d values measured at −120 and 60 mV (Fig. 3 C). For 3PP, K_d(0) was estimated from the value measured at 60 mV (Fig. 3 H), assuming voltage-independent binding (z = 0) in the pore. (Assuming z values of 0.1, 0.2, and 0.5 for 3PP would yield K_d(0) estimates of 12.6, 16, and 32 mM and ΔG^o_binding values of 4.4, 4.1, and 3.4 kT, respectively.)

Inferring independent versus competitive binding from fractional effects of mixtures

Let ${\hat{x}}_0$, ${\hat{x}}_{\text{A}}$, and ${\hat{x}}_{\text{B}}$ denote the values of some functional parameter x of the channels (e.g., unitary conductance, Fig. 4 [G and H]; closing rate, Fig. 9 D) measured under control conditions and in the presence of fixed (reference) concentrations of compounds A or B, respectively, all normalized to the parameter’s control value (i.e., ${\hat{x}}_0=1$). Let ${\hat{x}}_{\text{AB}}$ denote the normalized value of x in the combined presence of compounds A and B, both applied at their reference concentrations ([A] and [B]). Furthermore, let ${\hat{x}}_{\text{A}\infty }$ and ${\hat{x}}_{\text{B}\infty }$, respectively, denote the normalized values of x in the presence of saturating concentrations of the two compounds. Finally, let K_A and K_B denote the dissociation constants of the two compounds for their respective binding sites.

Figure 9.

Competition between NPPB, 3NB, and 3PP for affecting hydrolytic closing rate. (A–C) Macroscopic WT CFTR currents at −80 mV, elicited by brief applications of 2 mM ATP (gray bars) in the absence of drug, or in the presence of either 210 µM NPPB (A, brown bar) or the following drug combinations: (A) 20 mM 3PP (red bar) plus 210 µM NPPB (brown bar), (B) 32 mM 3NB (blue bar) plus 210 µM NPPB (brown bar), and (C) 32 mM 3NB (blue bar) plus 20 mM 3PP (red bar). Current decay time courses after ATP removal were fitted by single exponentials (colored lines), and time constants are indicated. (D) Macroscopic closing rates, obtained as the inverses of fitted time constants (see Materials and methods), under control conditions (gray bar) or in the presence of 210 µM NPPB (brown bar), 32 mM 3NB (blue bar), or 20 mM 3PP (red bar), or their combinations (striped bars, same color coding). Horizontal lines illustrate the predicted closing rates in mixtures (see Materials and methods), assuming either completely independent (yellow lines) or mutually exclusive (green lines) binding of the coapplied drugs at their respective gating sites. Blue and red bars were replotted from Fig. 6 C. Mean ± SEM is shown.

If A and B bind to two distinct, nonoverlapping binding sites that are energetically not coupled, then independent action might be expected: ${\hat{x}}_{\text{AB}}={\hat{x}}_{\text{A}}{\hat{x}}_{\text{B}}$ (yellow lines in Fig. 4, G and H; and Fig. 9 D; in Fig. 9 D, ${\hat{x}}_{\text{AB}}$ has been rescaled by the control value). In contrast, if A and B compete with each other for overlapping binding sites, then in the combined presence of reference concentrations of A and B the fractions of channels that are free, A bound and B bound, respectively, are given by 1/(1+[A]/K_A+[B]/K_B), ([A]/K_A)/(1+[A]/K_A+[B]/K_B), ([B]/K_B)/(1+[A]/K_A+[B]/K_B), and

$${\hat{x}}_{\text{AB}}=\frac{{\hat{x}}_0+\left(\right[\text{A}]/K_{\text{A}}){\hat{x}}_{\text{A}\infty }+\left(\right[\text{B}]/K_{\text{B}}){\hat{x}}_{\text{B}\infty }}{1+\left(\right[\text{A}]/K_{\text{A}})+\left(\right[\text{B}]/K_{\text{B}})}$$

(green lines in Fig. 4, G and H; and Fig. 9 D; in Fig. 9 D, ${\hat{x}}_{\text{AB}}$ has been rescaled by the control value). Reference concentrations used were 210 µM for NPPB, 32 mM for 3NB, and 20 mM for 3PP. The parameter estimates used for NPPB, 3NB, and 3PP, respectively, in the various figure panels were as follows: 39 µM, 2.6 mM, and 10 mM for the K values and 0, 0, and 0.91 for the ${\hat{x}}_{\infty }$ values in Fig. 4 G; 420 µM, 38 mM, and 10 mM for the K values and 0, 0, and 1.13 for the ${\hat{x}}_{\infty }$ values in Fig. 4 H. In Fig. 9 D, all three reference concentrations were assumed to be ∼3K (compare, K estimates are 80 µM, 9.2 mM, and 6 mM, respectively), and ${\hat{x}}_{\infty }$ values of 0.093, 0.75, and 0.19 were estimated from the $\hat{x}$ values of 0.32, 0.81, and 0.39, respectively, measured at the reference concentrations of ∼3K.

Statistics

Symbols/bars and error bars represent mean ± SEM of at least five measurements.

Online supplemental material

Fig. S1 illustrates the effects of 10 mM sulfate on steady-state macroscopic currents and macroscopic closing rates of WT CFTR. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201411246/DC1.

RESULTS

The NPPB gating site is located outside the CFTR channel pore

To verify whether NPPB gating and pore-block sites are indeed physically distinct protein regions, we investigated whether NPPB gating effects can be mitigated by competing the drug out of the CFTR pore using the pore blocker MOPS⁻, which does not affect CFTR gating (Csanády and Töröcsik, 2014). To confirm that the pore-blocking sites of NPPB and MOPS⁻ indeed overlap, we first studied competition for pore block between the two compounds: at −120 mV the apparent K_I for pore block is ∼20 µM for NPPB, but 8.3 mM for MOPS⁻ (Csanády and Töröcsik, 2014). A convenient macroscopic assay for measuring fractional effects on average ion flux rates through bursting channels is provided by nonhydrolytic mutant CFTR channels such as E1371S (Vergani et al., 2003) or K1250A. Once opened by ATP, such channels are locked in the bursting state for tens of seconds, yielding macroscopic currents that decay over the time course of minutes after ATP removal. Because the channels contributing to these decaying currents after ATP removal are not gating (P_o∼1), fractional changes in macroscopic current upon brief exposures to various compounds (I/I_control) reflect fractional changes in average unitary current amplitude (i/i_control) under these conditions (compare with Csanády and Töröcsik [2014]). As expected, application of MOPS⁻ at a concentration of 80 mM, approximately ninefold its own K_I (Fig. 2 A, green bars), reversibly reduced macroscopic current through locked-open E1371S channels by almost 90% (Fig. 2 A). In the presence of 80 mM MOPS⁻, addition of NPPB (Fig. 2 A, brown bars) further suppressed locked-open E1371S currents in a dose-dependent manner; however, further fractional reduction by 210 µM NPPB (∼10-fold its own K_I) was only ∼50% (Fig. 2 A, yellow box magnified in inset). Accordingly, the dose–response curve for fractional reduction of locked-open currents by NPPB in the presence of 80 mM MOPS⁻ (Fig. 2 B, green-filled symbols) yielded an apparent K_I value for NPPB of 177 ± 4 µM (Fig. 2 B, solid fit line), approximately ninefold higher than the control K_I obtained under identical conditions but in the absence of MOPS⁻ (Fig. 2 B, open symbols and dotted fit line; replotted from Csanády and Töröcsik [2014]), confirming competition between NPPB and MOPS⁻ for the pore-blocking site. We therefore next compared gating effects of subsaturating, 100 µM, NPPB in the absence or presence of 80 mM MOPS⁻.

We first studied NPPB effects on normal hydrolytic closing rate of WT CFTR channels (Fig. 2 D, gray bar), assayed as the rate of decay of macroscopic current after sudden removal of ATP (Fig. 2 C, gray exponential fit lines and time constants). This rate was slowed by approximately twofold in the presence of 100 µM NPPB (Fig. 2, C [bottom trace, brown fit lines and time constants] and D [brown bar]), but little affected by 80 mM MOPS⁻ (Fig. 2, C [top trace, green fit lines and time constants] and D [green bar]). Importantly, the presence of 80 mM MOPS⁻ did not prevent slowing of WT-CFTR closing rate by 100 µM NPPB (Fig. 2, C [bottom trace, second application of NPPB] and D [striped bar]).

We next probed acceleration by NPPB of the slow nonhydrolytic closing rate of K1250A CFTR channels (Fig. 2 F, gray bar) upon removal of ATP (Fig. 2 E, gray fit lines and time constants). (Because NPPB gating effects are voltage independent and pore block by NPPB and MOPS⁻ are identically sensitive to voltage [Csanády and Töröcsik, 2014], these long experiments could be equivalently performed at −40 mV.) In the presence of 100 µM NPPB, K1250A closing rate was accelerated by approximately twofold (Fig. 2, E [top and bottom traces, brown fit line and time constant] and F [brown bar]). In contrast, 80 mM MOPS⁻ neither affected K1250A closing rate (Fig. 2, E [top trace, green fit line and time constant] and F [green bar]), nor prevented the accelerating effect of 100 µM NPPB (Fig. 2, E [bottom trace, second application of NPPB] and F [striped bar]). Thus, whereas MOPS efficiently competes off NPPB from the pore-blocking site, it cannot prevent NPPB gating effects, confirming that the NPPB gating site is indeed located outside the CFTR pore.

Pore block by NPPB is mediated by the head part, but head and tail contribute equally to the free enthalpy of binding in the pore

To better understand the structural requirements for the complex functional effects of NPPB on CFTR, we next studied individual contributions to these effects by the NPPB head and tail moieties. To dissect potential effects of 3NB (the NPPB head) and 3PP (the NPPB tail) on permeation and gating, we first characterized effects on permeation using locked-open macroscopic K1250A CFTR currents at two different voltages (−80 and 60 mV).

As expected, 3NB, which contains the pore-blocking carboxylate, dose-dependently suppressed currents through locked-open K1250A channels, and pore block was more pronounced at negative voltages, attesting to its voltage dependence (Fig. 3, A and B). Apparent K_I values, from fits to the dose–response curves (Fig. 3 C, solid lines), were 2.6 ± 0.2 and 38 ± 1 mM, respectively, at −80 and 60 mV. Based on these values the estimated (see Materials and methods) K_d at 0 mV is ∼12 mM (Table 1), and the apparent valence is z = −0.49. Similar parameters were obtained when pore block by a fixed concentration of 32 mM 3NB was tested at various voltages (Fig. 3 D); fitting the normalized current-voltage relationship (Fig. 3 E, symbols) by the Boltzmann equation (solid line) yielded z = −0.49 ± 0.02. This very similar z value to that of NPPB (Csanády and Töröcsik, 2014) is consistent with 3NB blocking the CFTR pore at a similar location as NPPB, ∼50% across the transmembrane electrical field. In contrast, the ∼100-fold reduced affinity of 3NB for binding in the pore suggests that the tail part of NPPB also contributes to its free enthalpy of binding (ΔG^o_binding; Table 1).

Considering the lack of an anionic moiety in the tail part of NPPB, 3PP was not expected to cause pore block. Indeed, at positive voltages only a small (∼10%) enhancement (rather than impairment) of the rate of ion flow through locked-open K1250A channels was observed at high 3PP concentrations (Fig. 3 G); a tentative fit to its dose–response curve yielded a K_1/2 of ∼10 mM (Fig. 3 H, red–yellow symbols and red fit line). However, we were surprised to see substantial block by our 3PP solution at −80 mV, especially in the lower (5–10 mM) 3PP concentration range (Fig. 3, F and H [red–cyan symbols and red abscissa]). Because 3PP was applied as a sulfate salt, we suspected that the observed pore block might be caused by the latter anions. Indeed, at −80 mV, exposure of locked-open K1250A CFTR channels to sulfate caused substantial pore block (Fig. 3 I) with similarly anomalous dose dependence, yielding maximal block at ∼5 mM sulfate (Fig. 3 H, green–cyan symbols and green abscissa). Taking into account the 0.45 mol/mol sulfate/3PP ratio (see Materials and methods) of our 3PP solution (Fig. 3 H, compare red and green abscissae), the block by sulfate ions fully accounts for the current reduction observed at negative voltages in the presence of our 3PP solution (Fig. 3 H, compare green–cyan and red–cyan symbols). In contrast, the slight enhancement of ion throughput rate by 3PP at 60 mV is attributable to the 3PP cation itself, as sulfate ions did not affect locked-open channel currents at this positive voltage (Fig. 3, H [green–yellow symbols] and J). The confounding effect of the sulfate ions precludes characterization of potential small stimulatory effects of the 3PP cations on permeation at −80 mV, and hence exact estimation of its binding affinity at that voltage. However, based on a homology model of CFTR with NPPB docked in the pore (Dalton et al., 2012), the 3PP moiety occupies a superficial position relative to 3NB, suggesting relatively little voltage dependence for its binding. For the purpose of describing 3PP binding energetics, a relatively voltage-independent K_d of ∼10 mM is therefore a reasonable first approximation: even if the true z value for 3PP is not exactly zero, the error in our estimation of ΔG^o_binding should be small (compare with Table 1). Thus, although pore block by NPPB is mediated by its head part, the comparable K_d(0) values of head and tail parts (∼12 and ∼10 mM, respectively; Table 1) indicate that both contribute about equally to its free enthalpy of binding in the pore.

Permeation effects of NPPB head and tail involve binding sites that both overlap with the NPPB pore-block site

The similar effective valences for pore block by NPPB and 3NB and the fact that ΔG^o_binding for 3NB and 3PP sums up to that of NPPB (Table 1) are consistent with both 3NB and 3PP occupying invariant positions in the pore, regardless of whether they are applied in isolation or linked to each other in the form of NPPB. To test this idea we performed pairwise competition experiments for the three compounds. Thus, using macroscopic locked-open K1250A CFTR currents elicited at either −80 (Fig. 4, A, C, and E) or 60 mV (Fig. 4, B, D, F), we compared fractional effects of coapplying 32 mM 3NB with 210 µM NPPB (Fig. 4, A and B, blue and brown bars), 20 mM 3PP with 210 µM NPPB (Fig. 4, C and D, red and brown bars), or 32 mM 3NB with 20 mM 3PP (Fig. 4, E and F, blue and red bars) with the fractional effects of the same three compounds when applied in isolation at the respective concentrations.

Fractional currents in NPPB, 3NB, and 3PP were ∼0.13, ∼0.11, and ∼0.91, respectively, at −80 mV, but ∼0.65, ∼0.56, and ∼1.11, respectively, at 60 mV (Fig. 4, G and H, brown, blue, and red bars). As one extreme possibility, if two compounds can bind in the pore independently of each other, then the fractional effect of coapplying both is expected to be the product of the two individual effects (Fig. 4, G and H, yellow horizontal lines); i.e., the fractional effect of one compound should be identical regardless of whether it is applied in the absence or presence of the other. Deviations from such multiplicative behavior signify nonindependent binding. At the other extreme, if binding of two compounds is mutually exclusive, then the expected effect of coapplying both will be milder and can be calculated from the equilibrium equations for pure competition (see Materials and methods; Fig. 4, G and H, green horizontal lines). Accordingly, both at −80 and 60 mV, pore block by coapplication of 3NB plus NPPB was consistent with pure competition between the two compounds (Fig. 4, G and H, blue–brown striped bars and green horizontal lines). For example, at −80 mV, current reduction by 3NB was ∼10-fold when the compound was applied on its own (Fig. 4 G, blue vs. gray bar), but only ∼2-fold (from 13 to 6.2% of control) when applied in the presence of NPPB (Fig. 4 G, blue–brown striped vs. brown bar). Similarly, coapplication of 3PP plus NPPB suggested pure competition between these two compounds (Fig. 4, G and H, red–brown striped bars and green horizontal lines); the slightly larger fractional block by this mixture at −80 mV, as compared with that predicted by pure competition (Fig. 4 G), likely reflects additional block by sulfate ions because such a deviation was not apparent at 60 mV (Fig. 4 H), at which voltage sulfate ions do not affect permeation (Fig. 3, H and J). In contrast, the multiplicative effects of 3NB and 3PP at both voltages attested to their ability to bind in the pore independently of each other (Fig. 4, G and H, red–blue striped bars and yellow horizontal lines). These results are consistent with 3NB and 3PP pore-binding sites that both overlap with the NPPB pore-block site but not with each other.

Head and tail parts of NPPB both stimulate gating and contribute equally to the free enthalpy of binding to the gating site

Detailed knowledge of 3NB and 3PP permeation effects allowed us to use macroscopic patches to investigate whether stimulation of CFTR open probability by NPPB can be elicited by either of its two component parts. This is because fractional stimulation of P_o (P_o/P_o;control) can be simply quantitated by comparing fractional effects on macroscopic (I/I_control) and average unitary (i/i_control) currents: because I = N·i·P_o (where N is the number of channels in the patch), any fractional change in P_o is obtained as P_o/P_o;control = (I/I_control)/(i/i_control). (Average unitary current [i] in the presence of a blocker is equivalent to the apparent unitary current as observed in heavily filtered current traces [Csanády and Töröcsik, 2014].)

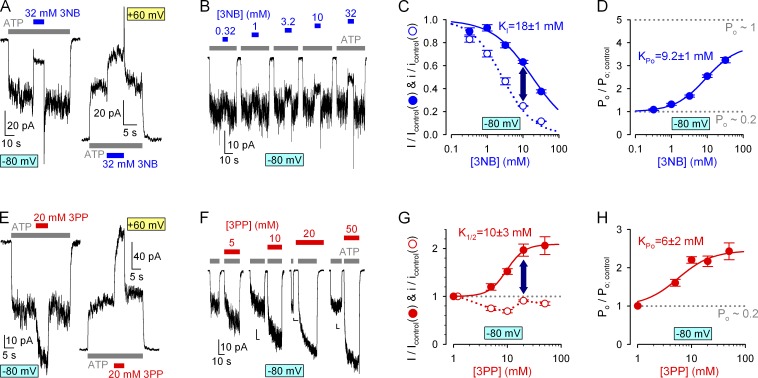
Indeed, at −80 mV, in macropatches containing WT CFTR channels gating at steady-state, both application and removal of 32 mM 3NB elicited biphasic current responses (Fig. 5 A, left trace), just as reported for NPPB (Csanády and Töröcsik, 2014). Upon 3NB addition, instantaneous pore block was followed by a slower partial current recovery, reflecting accumulation of a larger fraction of channels in the bursting state; and upon 3NB wash-off, instantaneous relief from pore block uncovered this larger fraction of bursting channels in the form of a current overshoot, followed by a relaxation back to the pre-application steady-state current level (Fig. 5 A, left trace). These obvious signs of P_o stimulation by 3NB were even more evident at 60 mV, at which voltage the milder pore block effect was overpowered by the P_o increase, resulting in net stimulation of WT CFTR current by 3NB (Fig. 5 A, right trace). Thus, similarly to NPPB (Csanády and Töröcsik, 2014), 3NB stimulates P_o of WT CFTR in a largely voltage-independent manner. To quantitate the effect of 3NB on P_o, we systematically compared fractional effects of increasing concentrations of 3NB on steady-state macroscopic WT CFTR currents at −80 mV (Fig. 5, B and C [solid symbols]) with the fractional effects of the same concentrations of 3NB on unitary currents (Fig. 5 C, open symbols; replotted from Fig. 3 C). Indeed, at any given concentration, reduction of steady-state macroscopic current was milder than reduction of unitary conductance (Fig. 5 C, dark blue vertical arrow), suggesting more than threefold stimulation of open probability for WT CFTR by high concentrations of 3NB (Fig. 5 D, symbols).

Intriguingly, macroscopic WT CFTR currents were also robustly stimulated by 20 mM 3PP, the NPPB tail (Fig. 5 E). Considering the small (∼10%) effects of 20 mM 3PP-sulfate on unitary currents (Fig. 3 H) this voltage-independent effect on macroscopic steady-state currents (Fig. 5 E, compare left and right current traces) again suggests a largely voltage-independent stimulation of P_o, and this stimulation cannot be attributed to the presence of the ∼9 mM sulfate because careful control experiments revealed little effect of 10 mM sulfate on WT CFTR open probability (Fig. S1, A–C). At −80 mV, systematic comparison of the fractional effects of increasing [3PP] on steady-state macroscopic WT CFTR currents (Fig. 5, F and G [solid symbols]) and on unitary conductances (Fig. 5 G, open symbols; replotted from Fig. 3 H) revealed dose-dependent stimulation by 3PP of WT CFTR open probability (Fig. 5 H, symbols) by as much as two- to threefold at high concentrations.

Thus, both the head and the tail parts of NPPB retain a significant fraction of its stimulatory efficacy (for WT, CFTR maximal stimulation of P_o by NPPB is approximately fourfold [Csanády and Töröcsik, 2014]), although the apparent affinities of 3NB (K_Po∼9 mM) and 3PP (K_Po∼6 mM) for the gating site, estimated from Hill-fits to the P_o dose–response curves (Fig. 5, D and H, solid lines), are greatly reduced relative to NPPB. These lower affinities of the head and tail parts are actually expected and suggest that the free enthalpy of binding of NPPB to the gating site is also relatively evenly distributed between its two complementary moieties (Table 2).

NPPB tail, but not head, slows macroscopic closing rate of WT CFTR channels

NPPB effects on CFTR gating are complex and affect two distinct gating transitions (Csanády and Töröcsik, 2014). To dissect which of its microscopic effects are recapitulated by its two complementary moieties, we first studied potential effects of 3NB and 3PP on macroscopic closing rate of WT CFTR, measured as the rate of current relaxation after ATP removal (Fig. 6, A and B): this rate of normal hydrolytic closure (Fig. 6 C, cartoon, pathway marked by purple arrow), which is limited by ATP hydrolysis at site 2 (Fig. 6 C, cartoon, step O₁→O₂; compare with Csanády et al. [2010]), is defined as the inverse of the time constant of a single exponential fitted to the current decay time course (Fig. 6, A and B, colored lines). 32 mM 3NB caused only a small (∼20%) decrease in WT CFTR closing rate (Fig. 6, A and C [blue vs. gray bar]): because this effect is insufficient to account for its more than threefold stimulation of P_o (Fig. 5 D), it inevitably follows that 3NB must robustly stimulate WT CFTR opening rate. In contrast, 20 mM 3PP-sulfate slowed hydrolytic closing rate by ∼2.5-fold (Fig. 6, B and C [red vs. gray bar]), and this effect was not caused by the presence of the ∼9 mM sulfate ions because in control experiments 10 mM sulfate did not affect WT CFTR closing rate (Fig. S1, D and E). Of note, the extent of slowing of WT-CFTR closing rate by 3PP is sufficient to fully account for its stimulation of P_o (Fig. 5 H).

NPPB head accelerates opening, whereas NPPB tail delays closure of single WT CFTR channels

The findings and predictions of macroscopic kinetic measurements can be independently verified in steady-state recordings of single WT CFTR channel currents, from which microscopic channel opening and closing rates (Fig. 7 B, purple arrows) can be extracted as the inverses of the mean interburst (τ_ib) and burst (τ_b) durations, respectively. We therefore compared the patterns of steady-state gating of single WT CFTR channels at −80 mV under control conditions (in 2 mM ATP; Fig. 7 A, top) or in the presence of either 32 mM 3NB (Fig. 7 A, middle) or 20 mM 3PP (Fig. 7 A, bottom).

Figure 7.

Effects of NPPB, 3NB, and 3PP on WT CFTR microscopic steady-state gating parameters. (A) Currents from single WT CFTR channels at −80 mV in 2 mM ATP (top), 2 mM ATP + 32 mM 3NB (middle), and 2 mM ATP + 20 mM 3PP (bottom); bandwidth, 50 Hz. (B) Cartoon gating model; opening rate (top purple arrow) and closing rate (bottom purple arrow) are given by 1/τ_ib and 1/τ_b, respectively. (C–E) Open probabilities (C) and mean burst (τ_b; D) and mean interburst (τ_ib; E) durations in 2 mM ATP (gray), 2 mM ATP + 210 µM NPPB (brown), 2 mM ATP + 32 mM 3NB (blue), and 2 mM ATP + 20 mM 3PP (red). The data for NPPB (brown bars) are replotted from Csanády and Töröcsik (2014) and reflect values measured at 60 mV. Mean ± SEM is shown.

The effects on average unitary conductance of WT CFTR, as observed in heavily (at 50 Hz) filtered current traces (Fig. 7 A), were consistent with the predictions of the macroscopic pore-block assays performed on locked open K1250A channels (Fig. 3, C and H). Thus, 20 mM 3PP little affected unitary current amplitude, whereas 32 mM 3NB reduced it by ∼10-fold (from ∼0.6 to ∼0.06 pA; also note a markedly asymmetrical subconductance pattern indicative of nonequilibrium gating; compare with Gunderson and Kopito [1995] and Jih et al. [2012]).

Kinetic analysis of channel gating (see Materials and methods) confirmed an approximate twofold stimulation of P_o by both 3NB and 3PP (Fig. 7 C, blue and red bar, respectively, vs. gray bar), which is more modest than that reported for NPPB (Fig. 7 C, brown bar; replotted from Csanády and Töröcsik [2014]). The reduced efficacies of the head and tail parts were explained by their partial kinetic effects. Whereas 3NB robustly shortened τ_ib (Fig. 7 E, blue bar) but did not affect τ_b (Fig. 7 D, blue bar), 3PP prolonged τ_b (Fig. 7 D, red bar) but did not affect τ_ib (Fig. 7 E, red bar), unlike NPPB which elicited both effects simultaneously (Fig. 7, D and E, brown bars). Considering the technical limitations associated with dwell time analysis in the presence of 3NB (see Materials and methods), these fractional effects on single-channel P_o (Fig. 7 C) are roughly consistent with those estimated from macroscopic recordings (Fig. 5, D and H). Moreover, the kinetic results (Fig. 7, D and E) are consistent with the macroscopic kinetic predictions (Fig. 6) and confirm that 3NB stimulates WT CFTR channels mainly by accelerating opening rate, whereas 3PP mainly acts by slowing closing rate.

In a nonhydrolytic CFTR mutant, NPPB head speeds gating but does not affect P_o

Acceleration of channel opening rate by NPPB is accompanied by a similar acceleration of nonhydrolytic closing rate, interpreted as a true catalyst effect on the C₁↔O₁ transition (Csanády and Töröcsik, 2014). Because the head part (3NB) also accelerated opening rate of WT CFTR (Fig. 7 E), we examined its effect on nonhydrolytic closing rate (Fig. 8 C, cartoon, purple arrow), measured as the very slow rate of macroscopic current decay after ATP removal in patches containing K1250A CFTR channels; the K1250A mutation (Fig. 8 C, cartoon, red stars) disrupts ATP hydrolysis (Fig. 8 C, cartoon, red cross; compare with Ramjeesingh et al. [1999]). Indeed, the presence of 32 mM 3NB accelerated K1250A closing rate by two- to threefold (Fig. 8, A [blue vs. gray fit lines and time constants] and C [blue vs. gray bar]), to a similar extent as reported for NPPB (Fig. 8 C, brown bar; replotted from Csanády and Töröcsik [2014]). In contrast, 20 mM 3PP, which did not significantly stimulate WT CFTR opening rate (Fig. 7 E), accelerated K1250A closing rate only slightly, by ∼20% (Fig. 8, B and C [red vs. gray bar]).

If 3NB indeed acted as a catalyst for the C₁↔O₁ step, then the equilibrium between those two states (Fig. 8 G, cartoon, purple double arrow), as reflected by the open probability of the K1250A mutant (K_eq = P_o/(1 − P_o)), should remain unaffected by 3NB. To test this, we compared fractional effects of 3NB on steady-state macroscopic (I/I_control) and average unitary (i/i_control) K1250A currents by applying 32 mM 3NB for extended time periods to channels gating at steady-state (in 10 mM ATP; Fig. 8 D, first and second 3NB applications) or briefly to locked-open channels after ATP removal (Fig. 8 D, third 3NB application, expanded in inset; this maneuver measures i/i_control; compare with Fig. 3). (Note that to increase the success rate of very long recordings, all experiments on K1250A gating shown in Fig. 8 were performed at −20 mV.) Both application and removal of 3NB to K1250A channels, which are gating at steady-state, evoked simple monophasic current responses (Fig. 8 D; in contrast with Fig. 5 A), and the fractional current reduction under such conditions (Fig. 8 F, left gray bar) was well matched by the fractional effect on unitary current (Fig. 8 F, left yellow bar), indicating little change in P_o (Fig. 8 G, blue bar). Similarly, the small fractional effect of 20 mM 3PP on steady-state K1250A currents (Fig. 8, E and F [right gray bar]) was well explained by a similar small fractional increase in unitary conductance at this voltage (Fig. 8 F, right yellow bar), revealing no change in P_o (Fig. 8 G, red bar). Thus, neither 3NB nor 3PP substantially affects the C₁↔O₁ equilibrium, although 3NB clearly stabilizes the transition state between them.

Gating effects of NPPB head and tail involve binding sites that both overlap with the NPPB gating site

The recovery of all the NPPB gating effects by either one or the other of its two complementary parts suggests that the NPPB gating site encompasses the two binding sites at which 3NB and 3PP exert their (partial) gating effects. However, the large (millimolar) concentrations at which 3NB and 3PP had to be applied, because of largely reduced apparent affinities, left room for the alternative interpretation of potential nonspecific effects unrelated to the NPPB gating site. We therefore tested whether gating effects of 3NB and 3PP could be completed by NPPB, as expected for overlapping binding sites. To this end we compared macroscopic closing rates of WT CFTR under control conditions, in the presence of 32 mM 3NB, 20 mM 3PP, or 210 µM NPPB, or in the combined presence of any two of the aforementioned compounds (Fig. 9). In contrast to the marked slowing of closing rate by 3PP observed when the compound was added alone (Fig. 9 D, red vs. gray bar; compare with Fig. 6 B), little further slowing was observed when 3PP was added in the presence of NPPB (Fig. 9, A and D [red–brown striped vs. brown bar]), exactly as expected for pure competition (Fig. 9 D, horizontal green line across red–brown striped bar). Similarly, whereas 3NB slightly slowed closing rate when added alone (Fig. 9 D, blue vs. gray bar; compare with Fig. 6 A), it actually accelerated closing rate when applied in the presence of NPPB (Fig. 9, compare B with A; and D, blue–brown striped vs. brown bar), again exactly as predicted by pure competition (Fig. 9 D, horizontal green line across blue–brown striped bar). In contrast, 3PP could slow closing rate even when applied in the presence of 3NB (Fig. 9 C), which is inconsistent with pure competition (Fig. 9 D, horizontal green line over red–blue striped bar). However, the fractional effect of 3PP in the presence of 3NB (Fig. 9 D, red–blue striped vs. blue bar) was less robust than under control conditions (Fig. 9 D, red vs. gray bar), which is a deviation from the expectation for completely independent binding (Fig. 9 D, horizontal yellow line across red–blue striped bar), as expected for two compounds that bind very close to each other.

DISCUSSION

In the first part of this study we investigated the location of the NPPB gating site on the CFTR chloride channel. Largely voltage-independent gating effects reported for NPPB in an earlier study were interpreted to suggest that these involve binding to a site (the gating site) distinct from the pore-blocking site (Csanády and Töröcsik, 2014). However, those results did not exclude the possibility that the two binding sites might overlap with each other: gating effects might be caused by voltage-independent binding of NPPB to a shallow site in the inner vestibule, from which the carboxylate of the head group could reach, and occlude in a voltage-dependent manner, the deeper narrow part of the pore. Because the anionic form of MOPS blocks the CFTR pore at an electrical distance similar to NPPB (Csanády and Töröcsik, 2014), it seemed likely that their pore-blocking sites should overlap. Indeed, by comparing fractional effects of NPPB, MOPS⁻, and mixtures of the two drugs on locked-open CFTR channel currents (Fig. 2 A), we confirm here pure competition between NPPB and MOPS⁻ for pore block (Fig. 2 B). Thus, given the dimensions of these blockers and of the intracellular vestibule of CFTR in homology models (Dalton et al., 2012), NPPB is unlikely to have access to the intracellular vestibule as long as MOPS⁻ is bound in the pore. In contrast, we also show here that the effects of NPPB on both of two distinct gating steps remain unaffected by the presence of MOPS⁻ (which itself does not affect gating). Thus, neither slowing of hydrolytic closure (Fig. 2, C and D; rate-limited by step O₁→O₂ [Csanády et al., 2010]), nor acceleration of nonhydrolytic closure (Fig. 2, E and F; transition O₁→C₁) by NPPB (the latter reflects its catalyst effect on step C₁↔O₁ [Csanády and Töröcsik, 2014]) is prevented by binding of MOPS⁻ in the pore. These results clearly indicate that the NPPB gating site cannot be located within the intracellular pore vestibule and must therefore be located elsewhere on CFTR.

In the second part of this study we dissected functional contributions of the head (3NB) and tail (3PP) parts of the NPPB molecule to its complex effects on both CFTR permeation and gating. Both parts can evidently bind in the pore, but, as expected, the voltage-dependent block by NPPB is attributable to the 3NB headgroup (Fig. 3 C). In contrast, 3PP slightly stimulated the rate of ion flow through locked-open channels (Fig. 3 H), possibly as a result of an electrostatic effect of its positively charged amino group, attracting anions into the pore. Although unlikely to happen in the context of NPPB, in which the amino group is neutral at physiological pH (Csanády and Töröcsik, 2014), this small effect allowed rough estimation of the binding affinity of 3PP for the pore; based on a computational study in which the NPPB structure was docked into the intracellular vestibule of a CFTR homology model (Dalton et al., 2012), the 3PP moiety may be expected to bind in a superficial location, suggesting little voltage dependence for its binding. 3NB and 3PP pore-binding sites both overlap with the NPPB pore-binding site, but not with each other (Fig. 4, G and H), consistent with binding of 3NB and 3PP to the same pore positions that they also occupy when they are applied in the context of NPPB, i.e., linked covalently to each other. Comparison of estimated K_d(0) values for pore binding of 3NB, 3PP, and NPPB revealed a relatively even distribution of the binding free enthalpy of NPPB along its molecular axis, with about equal contributions from both head and tail parts (Table 1). This is consistent with the predictions of the study by Dalton et al. (2012), which confirmed an electrostatic interaction of the 3NB carboxylate with the side chain of lysine 95 of CFTR (already shown by earlier experimental work [Linsdell, 2005]), but also suggested significant interactions of the 3PP phenyl group with the CFTR pore, including an aromatic interaction with tryptophan 1145 and a cation-π interaction with the guanidino group of arginine 352.

Unexpectedly, we discovered an anomalous mole fraction behavior for CFTR pore block by sulfate ions (Fig. 3 H), a finding indicative of a multi-ion pore. Such behavior was demonstrated earlier for SCN⁻ ions (Linsdell et al., 1997), but to our knowledge not so far for sulfate. Although further investigation of this phenomenon was outside the scope of the present study, closer examination of this behavior in the future might contribute to a better understanding of CFTR permeation properties.

Intriguingly, both the head and tail parts of NPPB contribute to its stimulation of CFTR gating (Fig. 5, A and E). Moreover, the overlapping gating sites of 3NB and NPPB (Fig. 9 D, blue–brown striped bar and green line) or of 3PP and NPPB (Fig. 9 D, red–brown striped bar and green line), confirm that the two complementary parts of NPPB exert their gating effects at binding sites that together form the NPPB gating site. Comparison of apparent affinities for affecting P_o (Fig. 5, D and H) suggests that both parts of NPPB contribute similarly to its overall binding enthalpy at the gating site (Table 2).

How do we interpret the finding that 3PP and 3NB binding to their respective gating sites are not mutually exclusive events, but do affect each other (Fig. 9 D, compare red–blue striped bar with green and yellow lines)? Pure competition and complete independence are two extreme possibilities. The former arises when the two binding sites sterically overlap: this is clearly not the case for 3NB and 3PP. In contrast, complete independence is observed when the two binding sites are sufficiently separated, so that the two bound ligands do not energetically interact with each other. Between these two extreme cases, a continuum of possible intermediate situations suggests either that (a) the two binding sites are near, such that the two bound ligands interact with (attract or repel) each other or that (b) binding of one ligand allosterically affects the conformation of the other binding site. For 3NB and 3PP the binding sites are in immediate proximity of each other (both overlap with the NPPB gating site), hence some mutual repulsion (option (a)) seems more likely, and could result from an “edge-on” cation-π interaction (Ahern et al., 2009) between the 3NB phenyl group and the cationic amino group of 3PP.

The dual gating effects of NPPB are attributable to distinct parts of the molecule. The tail moiety, 3PP, predominantly acts to slow hydrolytic closure (Figs. 6 and 7). Just as shown for NPPB (Csanády and Töröcsik, 2014), slowing of WT CFTR single-channel steady-state closing rate by 3PP (Fig. 7 D) is matched by a similar slowing of nonstationary macroscopic closing rate upon ATP removal (Fig. 6, B and C). Because the latter measures closing rate in the absence of bath ATP, the delayed closure in 3PP cannot be caused by facilitation of a proposed mechanism that would allow rebinding of ATP at site 2 after the release of hydrolysis products, but before pore closure (Jih et al., 2012). Rather, the most likely explanation is that 3PP binding at the gating site slows ATP hydrolysis at site 2 of the NBD dimer (Fig. 10, red line), as shown before for NPPB (Csanády and Töröcsik, 2014). Such an allosteric effect implies that the part of the NPPB gating site to which the 3PP tail binds participates in the TMD conformational change suggested to occur concomitant with ATP hydrolysis (Gunderson and Kopito, 1995; Jih et al., 2012; Csanády and Töröcsik, 2014).

3NB little affects hydrolytic closing rate (Figs. 6 and 7), but instead acts as a pure catalyst for the C₁↔O₁ step (Fig. 10, blue arrow) by stabilizing its transition state. This “activated” high-enthalpy conformation was suggested to represent a structure in which the NBD dimer has already formed but the pore is still closed. Because in such a structure molecular strain is expected to arise predominantly at the NBD–TMD interface (Csanády et al., 2006), the latter region is a likely candidate for the 3NB gating site. The mere fact that stabilization of a transition state enhances P_o for WT, but not for nonhydrolytic mutant, CFTR is a unique phenomenon that provides further evidence for a nonequilibrium CFTR gating cycle driven by ATP hydrolysis (compare with Csanády and Töröcsik [2014]).

In the broader context of ABC proteins, the catalyst effect of 3NB prompts further speculation. For CFTR the C₁→O₁ step is the slowest step of the entire gating cycle, and its rate therefore has a large impact on overall cycle time. If this feature is conserved between CFTR and related ABC exporters, then stabilizing the analogous transition state, i.e., in which the NBD dimer is already formed but the TMDs are still inward facing, is the most efficient way for regulating the cycle time, in other words the ATPase turnover rate. Many ABC exporters possess an intrinsic low level of ATPase activity, which is stimulated severalfold by transport substrate or allocrite (e.g., Al-Shawi [2011]). Because 3NB, like allocrites, likely binds to the TMDs in the vicinity of their cytoplasmic extensions, we speculate that the catalyst effect of 3NB on the CFTR pore-opening step (Fig. 10, blue arrow) might be equivalent to allocrite-mediated stimulation of ATPase activity in exporters.

In conclusion, we have provided a detailed description of the structure–activity relationship in NPPB, one of the most efficacious potentiators of ΔF508 CFTR known to date. This information might prove valuable both for tracing out the gating modulation site, an attractive candidate drug target site, and for the future development of practically useful CFTR potentiators that retain the full efficacy of NPPB (15–20-fold stimulation of P_o for ΔF508 CFTR), but display a higher affinity for the gating site, and do not block the anion pore.