Mean Scatterer Spacing Estimation Using Multi-Taper Coherence

Abstract

It has been hypothesized that estimates of mean scatterer spacing are useful indicators for pathological changes to the liver. A commonly employed estimator of the mean scatterer spacing is the location of the maximum of the collapsed average of coherence of the ultrasound radio-frequency signal. To date, in ultrasound, estimators for this quantity have been calculated with a single taper. Using frequency-domain Monte Carlo simulations, we demonstrate that multi-taper estimates of coherence are superior to single-taper estimates for predicting mean scatterer spacing. Scattering distributions were modeled with Gamma-distributed scatterers for fractional standard deviations in scatterer spacings of 5, 10, and 15% at a mean scatterer spacing of 1 mm. Additionally, we demonstrate that we can distinguish between ablated liver tissue and unablated liver tissue based on signal coherence. We find that, on the average, signal coherence is elevated in the liver relative to signal coherence of received echoes from thermally ablated tissue. Additionally, our analysis indicates that a tissue classifier utilizing the multi-taper estimate of coherence has the potential to distinguish between ablated and unablated tissue types better than a single-taper estimate of coherence. For a gate length of 5 mm, we achieved an error rate of only 8.7% when sorting 23 ablated and 23 unablated regions of interest (ROIs) into classes based on multi-taper calculations of coherence.

I. Introduction

As an acoustic wave propagates through a medium, energy is absorbed and reradiated by spatial fluctuations in compressibility and density in a process referred to as acoustic scattering [1]. The fundamental assumption in quantitative ultrasound (QUS) is that information about acoustic scattering may be gleaned from the received and beamformed RF echo signals, and QUS parameters may thereby be related to pathological changes in tissue. In many applications, the spatial variations are approximated by a stationary process [2]–[8]. However, in the liver it has been shown that a nonstationary two-component scattering model may be more appropriate [9]–[11]. This two-component model contains pseudo-periodically arranged scatterers and diffuse scatterers with a uniform spacing distribution [9]–[11]. The periodically arranged scatterers are hypothesized to correspond to the portal triads, which have a spacing of approximately 1 mm on the average, and encircle the periphery of the liver lobule [9]. The mean scatterer spacing (MSS) of these periodically arranged scatterers has been proposed as an useful biomarker to evaluate pathological changes in the liver, such as cirrhosis [9], [10], [12], or infiltration of primary or secondary liver tumors [13].

One of the earliest attempts to characterize liver tissue in terms of MSS was by Fellingham and Sommer [9]. For a regular array of scatterers with a separation of d, Fellingham and Sommer demonstrated that peaks in the power spectrum would occur at frequency intervals, Δf = c/2d, where c is the sound speed of the medium [9]. They performed peak detection using the autocorrelation of the power spectrum and made MSS measurements in healthy and cirrhotic livers of human subjects [9]. With a 5-MHz broadband transducer, they found an MSS of 1.07 ± 0.16 mm across 14 healthy livers and an MSS of 1.48 ± 0.24 mm across 15 cirrhotic livers [9]. The cepstrum has also been used for making MSS measurements because it transforms the multiplicative relationship between the system response and tissue response to an additive relationship [11], [14]. Kuc et al. showed that the maximum value of the cepstrum was related to the most probable spacing of a unimodal scatterer spacing distribution [14].

The generalized spectrum (GS), referred to as the spectral autocorrelation initially, was introduced by Varghese and Donohue to measure MSS [15], [16] and as a QUS biomarker. In [15], using computer simulations, they compared MSS measurements from the GS with MSS measurements from the cepstrum. In their simulations, two types of point-like scatterers were randomly incorporated: uniformly distributed scatterers, referred to as diffuse scatterers, and Gamma-distributed scatterers, referred to as quasi-periodic scatterers. The Gamma distribution is frequently used to model the arrangement of randomly but regularly spaced scatterers, and this distribution’s first use for modeling scatterer spacing can be attributed to Landini and Verrazini [10]. In Varghese and Donohue’s simulations, the randomly placed scatterers were convolved with a point spread function representing tissue attenuation and an ultrasound imaging system. It was shown that peaks in the GS predict MSS more reliably than peaks in the cepstrum as the concentration of diffuse scatterers increases or the regularity of the coherent scatterers decreases. Additionally, the GS offers the theoretical advantage that, when considering expectations computed over many realizations of the scattering process, the energy from diffuse scattering and the energy from periodic scattering appear in different regions of the GS [15]. Concerning separation of tissue properties from the imaging device, normalization has been proposed to remove the effects of the imaging device from the measurement of the GS [15].

In addition to frequency-domain techniques, MSS may be measured through time-domain measurements of the autocovariance function. Using singular spectrum analysis (SSA), Pereira et al. have decomposed the autocovariance of the RF echo envelope into a component resulting from diffuse scattering and a component resulting from periodic scattering [17], [18]. In SSA, the covariance matrix of the signal is diagonalized. Pairs of eigenvalues whose eigenvectors have a normalized correlation coefficient above a threshold, and whose eigenvectors have frequency content with sufficiently close peaks are identified. These eigenvectors are deemed to be due to a periodic component in the signal. The periodic component of the signal can then be found by projecting the signal onto the periodic basis vectors.

Rather than model the signal as nonstationary in its second moment, some authors have tried to model the ultrasound signal as a wide-sense stationary (WSS) signal and attribute coherent scattering to its higher order moments [19]–[22]. In [19]–[21], the authors use the Wold decomposition theorem to write the RF echo signal as a sum of a coherent and a diffuse component. In [19]–[21], the diffuse component of the signal is modeled as a zero-mean autoregressive process driven by a zero-mean white noise sequence. In [19], the coherent component is modeled as a periodic sequence; the authors use this model to measure an MSS of approximately 1 mm in the livers of three healthy subjects using a clinical transducer with a center frequency of 3.5 MHz. Meanwhile, an MSS of 1.5 mm was measured in liver tumors of 3 other volunteers using the same computational model and ultrasound system. In [22], Abeyratne et al. also measured an MSS of approximately 1 mm in the livers of two subjects based on higher order statistics of the RF signal from a 3.5-MHz clinical array transducer.

In this work, we compare MSS estimates using single-taper (ST) and multi-taper (MT) methods of estimation of the GS. First, we describe the GS theoretically. We then perform frequency domain simulations with scatterers modeled by monopole scatterers with a known diameter distribution. Finally, we demonstrate results for a tissue classification problem in the liver ex vivo.

II. Generalized Spectrum

A. The Generalized Spectrum

We model the ultrasound signal as a random time series with correlated frequency components. This type of signal falls under the general class of signals referred to as harmonizable processes [23]. Harmonizable processes include stationary time series, periodically correlated time series, and other types of time series [23]. A harmonizable process, X(t), has a Cramèr representation given by [24]

$$X(t)={\int }_{-1/2}^{1/2}exp(i2\pi ft)\text{d}Z(f).$$ (1)

In (1), the sampling frequency is assumed to be 1, making the Nyquist frequency equal to 1/2. The equation states that X(t) is the inverse Fourier transform of an increment process, dZ(f). The Cramèr spectral representation was originally developed for stationary processes, where the increments are orthogonal. The Cramèr representation was later extended to include nonstationary but harmonizable processes by Loève [25]. For stationary processes, the autocovariance function may be related to the power spectrum through the Wiener–Khintchine theorem [26]. For a zero-mean, harmonizable process the autocovariance function may be related to the Loève spectrum by

$$\begin{array}{l}{\mathrm{\Gamma }}_{\text{L}}(t_1,t_2)=E[X(t_1)X^{\ast }(t_2)]\\ {\int }_{-\infty }^{\infty }exp(i2\pi (t_1{f}_1-t_2{f}_2)){\gamma }_{\text{L}}(f_1,f_2){\text{d}f}_1\text{d}{f}_2.\end{array}$$ (2)

In the field of QUS, the Loève spectrum has been referred to as the spectral autocorrelation [15], [27] or the GS [28]–[30]. The GS may also be defined in terms of the increment process [24] as

$${\mathrm{\Gamma }}_{\text{L}}(f_1,f_2){\text{d}f}_1{\text{d}f}_2=E[\text{d}Z(f_1){\text{d}Z}^{\ast }(f_2)].$$ (3)

As demonstrated by Haykin in [31], it is easier to interpret the frequency and time variables if the coordinate system is rotated by 45°. We define an average time t₀, a time lag τ, an average frequency f, and a frequency difference g by

$$\begin{array}{l}{t}_1+t_2=2t_0\\ t_1-t_2=\tau \\ f_1+f_2=2f\\ f_1-f_2=g.\end{array}$$ (4)

By doing so, the autocovariance and GS may be rewritten in terms of the rotated time and frequency variables, yielding

$$\mathrm{\Gamma }(t_0,\tau )={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }exp(i2\pi (\tau f+{\text{t}}_{0}g))\gamma (f,g)\text{d}f\text{d}g.$$ (5)

With this equation, the rotated GS, γ, is the Fourier transform of the rotated autocovariance function, Γ; the time lag and average frequency may be considered conjugate variables; and the average time and frequency difference may be considered conjugate variables. Along the line g = 0, the GS is identical to the power spectrum. Any energy outside the line g = 0 is an indication that a time series is not stationary.

To date in ultrasound, the most commonly employed estimator for the GS is a synchronized, time-averaged estimate [15], [28], [30], [32]:

$$\begin{array}{l}{\widehat{\gamma }}_{\text{WB},i}(f_1,f_2)=\frac{1}{N_{\text{S}}}\sum _{i=1}^{N_{\text{S}}}{Y}_i(f_1){\phi }_i(f_1)Y_i^{\ast }(f_2){\phi }_i^{\ast }(f_2)\\ {\gamma }_{\text{WB}}(f_1,f_2)=\frac{1}{N_{\text{A}}}\sum _{i=1}^{N_{\text{A}}}{\widehat{\gamma }}_{\text{WB},i}(f_1,f_2).\end{array}$$ (6)

The Y_i in (6) refer to windowed DFTs of RF A-lines. For Welch–Bartlett averaging, each of these A-lines are broken up into N_S overlapping segments, where typically N_S = 3 [15]. The ϕ_i(f) are phase factors that account for the fact that arbitrarily dividing a segment into different sections produces phase offsets between those segments. The phase factor for a segment is given by ϕ (f) = exp(j2πfτ_i), where τ_i is the time delay between the beginning of the A-scan segment and the position of the dominant periodic scatterer [30]. This is typically approximated as the location of the maximum value of the envelope of the RF data. The averages across overlapped A-line segments are then averaged over N_A A-lines. This type of estimate for the GS effectively decreases the resolution in the nonstationary direction to decrease the variance of the GS estimate.

In addition to a Welch–Bartlett average for the GS, a diagonally smoothed estimate has been proposed by Varghese and Donohue [27]. The diagonal smoothing acknowledges that for a signal with periodically correlated frequency components we expect the GS to be continuous along lines corresponding to a constant scatterer spacing and discontinuous along lines perpendicular to this. A diagonally smoothed GS estimate is given by

$$\begin{array}{l}{\widehat{\gamma }}_{\text{ST},i}(f_1,f_2)=\sum _{f_1^{\prime }=-R}^{f_1^{\prime }=R}\sum _{f_2^{\prime }=-R}^{f_2^{\prime }=R}Y(f_1-f_1^{\prime })Y_i^{\ast }(f_2-f_2^{\prime })H(f_1^{\prime },f_2^{\prime })\\ {\widehat{\gamma }}_{\text{ST}}(f_1,f_2)=\frac{1}{N}\sum _{i=1}^{N_{\text{A}}}{\widehat{\gamma }}_{\text{ST},i}(f_1,f_2)\phi (f_1){\phi }^{\ast }(f_2),\end{array}$$ (7)

where R is the radius of nonzero elements of the smoothing kernel, H, and i indexes individual A-lines. Diagonal smoothing is implemented by allowing H(f₁, f₂) = δ(f₁ − f₂).

The GS depends on the spatial arrangement of the scatterers, overlying tissue attenuation, diffraction, and the transducer bandwidth [28], [30]. It has been shown that measuring coherence, as opposed to the GS, approximately deconvolves the effects of overlying tissue attenuation, diffraction, and transducer bandwidth [28]. Coherence is calculated by dividing an estimated GS for a given segment or A-line by its magnitude before averaging:

$$\widehat{C}(f_1,f_2)=\frac{1}{N_{\text{S}}}\sum _{s=1}^{N_{\text{S}}}\frac{{\widehat{\gamma }}_s(f_1,f_2)}{\mid {\widehat{\gamma }}_s(f_1,f_2)\mid },$$ (8)

where γ_s could be a diagonally smoothed estimate or a time-averaged estimate. In prior works, this has been referred to as a system-normalized GS. In addition to coherence, the collapsed average (CA) is frequently calculated. The CA is an average along diagonal lines in the stationary direction. It is given by

$${\widehat{\gamma }}^c(\mathrm{\Delta }f)=\frac{1}{M(g)}\sum _{f_1-f_2=g}\mid \widehat{C}(f_1,f_2)\mid ,$$ (9)

where M is a normalization constant that is equal to the number of discrete entries in a diagonal band corresponding to a single frequency difference.

B. Multi-Taper (MT) Estimation

To discuss the MT method, we begin by substituting the Cramèr representation for a discrete time process into the equation for a discrete Fourier transform. We note that (1)–(5) were valid for both discrete and continuous time. We use the index n to denote discrete time samples. Using this notation, and the convention that the sampling frequency is equal to one, a discrete Fourier transform is given by

$$y(f)=\sum _{n=0}^{N-1}X(n)exp(-i2\pi fn).$$ (10)

Inserting the Cramèr representation for a stochastic process into this equation yields

$$\begin{array}{l}y(f)={\int }_{-1/2}^{1/2}{K}_{\text{N}}(f-f^{\prime })\text{d}Z(f^{\prime })\\ K_{\text{N}}(f)=\frac{sin(N\pi f)}{sin(\pi f)}exp(-i2\pi f(N-1)/2).\end{array}$$ (11)

This equation is often referred to as the fundamental equation for spectral estimation [33]. It describes the blurring in the frequency domain that results from using a finite Fourier transform. The integral kernel K_N is similar to a sinc function and is known as the Dirichlet kernel.

Estimating the statistical properties of Z(f) could be considered an inverse problem. To solve it, Thomson advocated the use of a local least-squares eigenfunction approximation to the solution of the fundamental equation of spectrum estimation [33]. In the approximation, the meaning of local is defined by a user-selected bandwidth parameter, W. The majority of the energy of the eigenfunctions is concentrated in a band from −W to W. An eigenfunction approximation is possible because the eigenfunctions of the Dirichlet kernel are well known. They are the discrete prolate spheroidal sequences (DPSS). We will denote the kth DPSS by v_k(t) and the Fourier transforms of the DPSS as V_k(f); the eigenvalue of the kth DPSS will be denoted λ_k.

To solve the integral equation, Z is projected onto the DPSS over the bandwidth −W to W, yielding Z_k, where the Z_k are the unobservable, ideal eigencoefficients for the expansion. They are given by

$$Z_k(f)=\frac{1}{\sqrt{{\lambda }_k}}{\int }_{-W}^W{V}_k(f^{\prime })\text{d}Z(f-f^{\prime }),$$ (12)

where Z_k are unobtainable with the data. However, Thomson showed the following in his seminal paper on MT estimation [33]:

$$\begin{array}{l}{y}_k(f)={\int }_{-1/2}^{1/2}{V}_k(f^{\prime })\text{d}Z(f-f^{\prime })\\ y_k(f)=\sum _{t=0}^{N-1}exp(-i2\pi fn)v_k(n)x(n)\end{array}$$ (13)

These equations demonstrate two things. First, the eigen-coefficients can be approximated by the DFT of the data segment windowed with one of the DPSS. Second, the difference between the ideal eigencoefficients and the estimated eigencoefficients is given by the integral outside the bandwidth (−W, W). This difference between the ideal and estimated eigencoefficients can introduce bias in the spectral estimate. We define the bias for the estimate of the kth eigencoefficient, b_k(f) as

$$b_k(f)={\int }_{-1/2}^{1/2}{V}_k(f^{\prime })\text{d}Z(f-f^{\prime })-{\int }_{-W}^W{V}_k(f^{\prime })\text{d}Z(f-f^{\prime }).$$ (14)

Thomson proposed an adaptive weighting procedure for reducing the bias due to energy outside the local interval (−W, W) [33]. This is based on the fact that the amount of leakage for a given taper increases with the order of the taper. The data-adaptive method weights the higher order eigencoefficients less in regions where the spectrum is changing more rapidly. A derivation of the adaptive weighting scheme is also given by Percival and Walden [26]. These weights are derived assuming that x(t) is a realization of a stationary process, with a power spectrum S(f) [33]. To find the adaptive weights, the mean-square error between the ideal eigencoefficients and the estimated eigencoefficients is minimized for each of the k eigencoefficients. This yields

$$\begin{array}{l}{d}_k(f)=\frac{S(f)}{{\lambda }_{k}S(f)+(1-{\lambda }_k){\sigma }^2}\\ {\sigma }^2={\int }_{-1/2}^{1/2}S(f)\text{d}f,\end{array}$$ (15)

where S(f) is the true, but unknown value of the power spectrum.

To determine the data-adaptive weights, an iterative procedure is used. To begin the iteration, the true value of the spectrum is estimated to be the average of the spectrum calculated from the two lowest-order windowed Fourier transforms of the data. After each iteration, the spectrum is recalculated with the set of weights from the previous iteration. Generally, the procedure terminates after only a few iterations. Though this estimate for the data-adaptive weights was originally derived assuming a stationary time series, the weighted eigencoefficients have been successfully used for coherence estimation for non-stationary time series [34]. For nonstationary time-series, the following estimator for the GS has been used [24], [34]:

$${\widehat{\gamma }}_{\text{MT}}(f_1,f_2)={\int }_{-W}^W{\int }_{-W}^W\text{d}\widehat{Z}(f_1-f_{1^{\prime }})\text{d}\widehat{Z}(f_2-f_{2^{\prime }})H(f_{1^{\prime }},f_{2^{\prime }}){\text{d}f}_{1^{\prime }}{\text{d}f}_{2^{\prime }},$$ (16)

where H(f₁, f₂) is a smoothing function that considers the continuity properties of the GS. As demonstrated by Varghese et al. [27], for an RF signal from periodic scatterers, we expect the GS to be smooth along the diagonal lines f₁ − f₂ = c or along the horizontal line g = c in the rotated bifrequency plane. Letting $H(f_1^{\prime },f_2^{\prime })=\delta (f_1^{\prime }-f_2^{\prime })$, the estimate is smoothed over the bandwidth (−W, W) on a diagonal line. This yields the following estimator for the GS for the ith A-line in a 2-D ROI [34]:

$$\begin{array}{l}{\widehat{\gamma }}_{\text{MT},i}(f_1,f_2)=\frac{A}{K}\frac{{\displaystyle \sum _k}{\lambda }_k{d}_k(f_1)y_k(f_1)d_k(f_2)y_k^{\ast }(f_2)}{\sqrt{{\displaystyle \sum _k}{d}_k(f_1)}\sqrt{{\displaystyle \sum _k}{d}_k(f_2)}}\\ A=\sum _{k=0}^{K-1}\frac{1}{{\lambda }_k}.\end{array}$$ (17)

To estimate the GS of a block of ultrasound data containing N_A A-lines, we multiplied each estimate by the appropriate phase factor ϕ_i(f) and averaged them:

$${\widehat{\gamma }}_{\text{MT}}(f_1,f_2)=\frac{1}{N_{\text{A}}}\sum _i{\widehat{\gamma }}_{\text{MT},i}(f_1,f_2)\phi (f_1){\phi }^{\ast }(f_2).$$ (18)

In this paper, calculations of the eigencoefficients were performed with a Fortran code made available by Prieto et al. in [35]. All other computations were performed using Numpy [36].

III. Simulations

A. Pressure Field Calculation

Simulations were performed by computing the pressure field in the frequency domain as described by Li and Zagzebski [37]. We summarize the salient features of the simulation in the following paragraphs. The pressure at field point r emitted from a single rectangular element of a linear array transducer, vibrating so that the velocity of the surface is v(t) = u(ω)exp(iωt), is given by

$$\begin{array}{l}{p}_i(\mathbf{r},\omega )=-\frac{i\rho \mathit{kcu}(\omega )}{4\pi }{A}_0(\mathbf{r},\omega )\\ A_0(\mathbf{r},\omega )={\int }_{-b/2}^{b/2}{\int }_{-a/2}^{a/2}\frac{exp(ik\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid )}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }{\text{d}x}^{\prime }{\text{d}y}^{\prime },\end{array}$$ (19)

where c is the speed of sound in the medium, ρ is the density of the medium, k is the wavenumber, and r′ is the field point on the surface of the transducer. The width of the element laterally is b, and elevationally is a. Accurate approximation of this integral by truncating a Taylor series expansion for the term |r − r′| is discussed in [37]. Attenuation was taken into account by letting the wave number be complex with an imaginary part equal to the attenuation. Linear attenuation with frequency was used for these simulations, with an attenuation coefficient equal to 0.65 dB/cm·MHz.

For a focused linear-array transducer, the field from each element is summed and appropriate time-delays are applied to achieve a focused ultrasound beam. A 128-element array with element sizes of 0.15 mm laterally and 10 mm elevationally was simulated. Approximation of the time delays is discussed in [37]. The simulated transducer had an f-number of 2. The simulations assume the Born approximation of no multiple scattering, and that locally the incident pressure wave looks planar. Under these assumptions, the scattered pressure at a point r″ from a single scatterer is given by

$$p_s({\mathbf{r}}^{″},\omega )=p_i(\mathbf{r},\omega )\frac{exp(ik\mid \mathbf{r}-{\mathbf{r}}^{″}\mid )}{\mathbf{r}-{\mathbf{r}}^{″}}\mathrm{\Phi }(\omega ,\theta ).$$ (20)

The quantity Φ (ω, θ) denotes the scattering amplitude in the azimuthal direction. It describes the angular distribution of the scattered sound energy, and is discussed in Morse and Ingard [38].

The force on the face of the transducer caused by a single scatterer was given by integrating over the face of the transducer. We summed the contributions from all the scatterers, and assumed the scatterers were monopole scatterers. The scattering amplitude at all angles over the transducer face could then be approximated by the scattering amplitude at 180°. A uniform force-to-voltage transfer function for the transducer was assumed. The time-domain signal was generated by multiplying the scattered pressure in the frequency domain by a bandpass filter corresponding to a transducer with a particular bandwidth, BW, and center frequency, f_c; then performing the inverse Fourier transform:

$$V(t)={\int }_0^{\infty }V(\omega )exp\left(-\frac{{(f-f_{\text{c}})}^2}{{(f_{\text{c}}\text{BW})}^2}\right)exp(-i\omega t)\text{d}\omega .$$ (21)

A center frequency of 3.5 MHz with a fractional bandwidth of 70% was used in these simulations. The pressure field was calculated over a discrete grid with a spacing of Δx = 0.2 mm, Δy = 0.2 mm, Δz = 0.01 mm. We use the same convention as [37] for our coordinate system: x is the elevational direction, y is the lateral direction, and z is the axial direction. The pressure from scatterers located at arbitrary locations was found by multiplying the pressure at the closest grid point by a phase factor, φ, that accounted for the difference in phase and attenuation:

$$\phi (\mathrm{\Delta }z)=exp(i2\pi (2\mathrm{\Delta }z)k).$$ (22)

B. Scatterer Distribution

In Fig. 1(a) we show a schematic approximation of the liver tissue model containing multiple lobules. In the model, a lobule is made up of 7 periodic scatterers corresponding to 6 hexagonally arranged portal triads and the central vein, along with a collection of diffuse scatterers. In simulation, each A-line was a signal generated by an independent realization of a medium containing randomly placed scatterers. The simulated medium had dimensions of 44 mm axially, 5 mm laterally, and 10 mm elevationally. Two types of scatterers were created in each computational phantom: diffuse and periodic. They differed in the intensity of the reflected sound wave and their spatial arrangement. Diffuse scatterers were simulated by creating uniformly randomly distributed scatterers with a number density of 10/mm³. To ensure sufficient signal intensity, periodic scatterers were placed in the center of the beam laterally and elevationally and any reflected pressure from a periodic scatterer was amplified by a factor of 5. Axially, we used an MSS of 1 mm, or (2.27 wavelengths relative to the center frequency), for each column of periodic scatterers. However, we allowed a random offset between the start of each series of periodic scatterers from one beam-line to the next. This was captured in the simulations by drawing the position of the first periodic scatterer from a uniform distribution with a maximum value of 1 mm. Subsequent periodic scatterers were arranged according to a Gamma distribution. A diagram of a computational phantom is shown in Fig. 1(b).

Fig. 1.

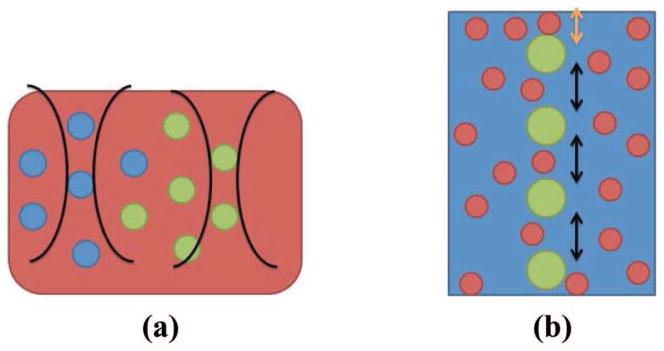
(a) Diagram showing idealized liver tissue insonified by two focused ultrasound beams. (b) Simplified periodic and diffuse scattering model used in simulation of an A-line. Large green circles represent regularly spaced scatterers which had initial position determined by a uniform distribution (orange arrow) and subsequent spacing determined by a gamma distribution (black arrow). Small red circles represent diffuse scatterers.

To calculate the scattering amplitude at 180°, we modeled the diffuse scatterers as glass beads 45 μm in diameter and the periodic scatterers as glass beads 85 μm in diameter. This was done because the scattering amplitude of glass beads is easily calculated based on Faran theory [39]. The medium was assumed to be tissue equivalent with a sound speed of 1540 m/s and a density of 1.02 g/ cm³. The glass beads were assumed to have a sound speed of 5570 m/s, a shear wave speed of 3375 m/s, and a density of 2.54 g/cm³.

The Gamma distribution is typically defined in terms of a shape parameter, k, and a scale parameter, θ. The distribution, f(x; k, θ) is given by

$$f(x;k,\theta )=\frac{x^{k-1}exp(x/\theta )}{{\theta }^k\mathrm{\Gamma }(k)}.$$ (23)

The symbol Γ denotes the Gamma function in this context. For our purposes, we discuss results in terms of the MSS, μ, the variance of the distribution, σ², and the fractional standard deviation of the scatter spacing, η = σ/μ. The mean and the variance are related to the shape and scale by μ = kθ and σ² = kθ².

IV. Materials and Methods

Five bovine livers were acquired from a slaughterhouse and 23 samples were taken. All procedures were performed within three days of acquiring the bovine liver. Samples were created by cutting a liver into small pieces approximately 3.5 × 6 × 6 cm. A sample was then placed on the holder shown in Fig. 2(a) and immersed in physiological saline solution. Following this, the sample was placed in a vacuum chamber for 15 min. After degassing, the tissue was placed in a water bath maintained at a constant temperature of 37°C for 30 min. An RF data set of the liver was then acquired.

Fig. 2.

(a) Tissue holder. (b) Tissue holder in water bath.

The sample holder locked the specimen in place by the insertion of two metal rods through the sample vertically. The sample holder also provided fiducial markers to ensure the imaging of the same plane, within the elevational resolution of the transducer, by allowing the insertion of two staggered metal cylinders through its sides. Each tissue sample was placed on top of a piece of rubber to avoid reverberations from the bottom of the container.

Following initial imaging of a sample, one RF ablated region was created in the imaging plane using an internally cooled CoolTip antenna (ValleyLab, Boulder, CO) with a 1-cm active region powered by a ValleyLab CoolTip RF generator. For each ablation, the power was set to 12 W for 8 min in a manual mode. These settings produced ablations that were roughly spherical and approximately 1 to 1.5 cm in diameter. Following ablation, the RF applicator was removed; tissue was again placed in physiological saline solution and degassed in a vacuum chamber for 15 min. Following the degassing the sample holder was placed in the same water bath maintained at 37°C for 30 min. The samples remained in saline solution; a transducer was placed in a clamp and partially submersed in the saline solution while imaging was performed. The experimental setup used is shown in Fig. 2(b).

For the classification task, this yielded 46 RF data sets. Twenty-three data sets were of the liver before RF ablation. The other 23 data sets were of identical imaging planes in the same sample of liver, but following RF ablation. One pair of ablated and unablated data sets was acquired from each bovine liver sample. Data sets were acquired using a clinical linear array transducer, the 9L4, on the Siemens S2000 scanner (Siemens Medical Solutions, Mountain View, CA), at a transmit frequency of 6 MHz.

Identical imaging settings were used for each pair of data sets collected. In all data sets, the TGC was uniformly set to the minimum setting across the whole imaging depth. The focal depth was set such that the ablation was slightly deeper than the focus of the transducer. Across all cases, this was a setting of 1 cm. The ablation was identified in B-mode imaging by locating the fiducial markers. The presence of the ablation in the imaging plane was then confirmed using acoustic radiation force imaging (ARFI), available on the ultrasound system, and gross pathology images.

V. Results and Discussion

A. Simulation Results and Discussion

Simulation results are presented for estimates of the GS for a specified number of gated A-line segments, gate length, and fractional standard deviation in spacing in Figs. 3 and 4; Monte Carlo simulations of MSS estimates for a variable number of A-lines or a variable gate length are shown in Figs. 5 and 6. In Figs. 3 and 4, the window that was used for the ST method was the Hann window; for Monte Carlo simulation results in Figs. 5 and 6 we used several different windows, i.e., Hann, Hamming, and Blackman–Harris. All windows are given by the formulae in Table I. For all Monte Carlo simulations, 150 ensembles of independent A-lines were used. To compute the MSS, the maximum of the CA of the coherence was computed. The CA was filtered, such that any values within 0.5 MHz of the diagonal corresponding to the power spectrum were set to zero. MSS was computed from the maximum value of the filtered CA. For all results shown, we fixed the smoothing bandwidth at 0.642 MHz, and gated the data starting at a depth of 25 mm.

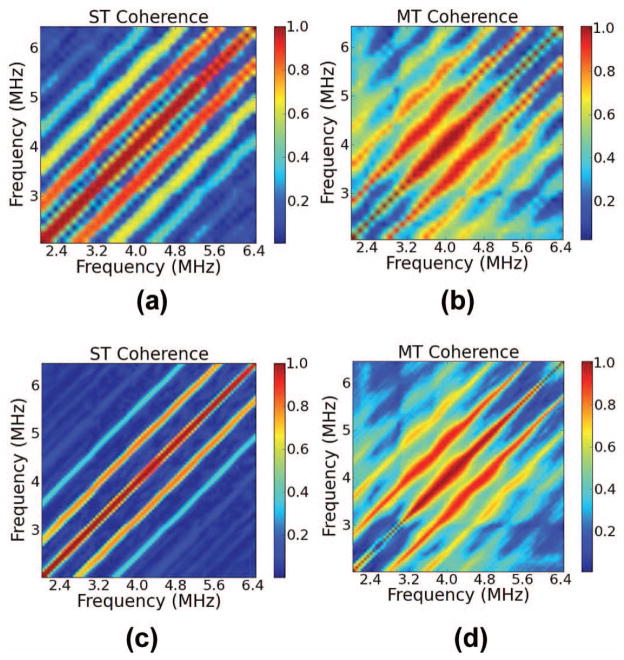
Fig. 3.

(a and c) Single-taper (ST) and (b and d) multi-taper (MT) estimates of the coherence averaged over 200 data segments when η = 5% and the gate length is either (a and b) 6 mm or (c and d) 13 mm.

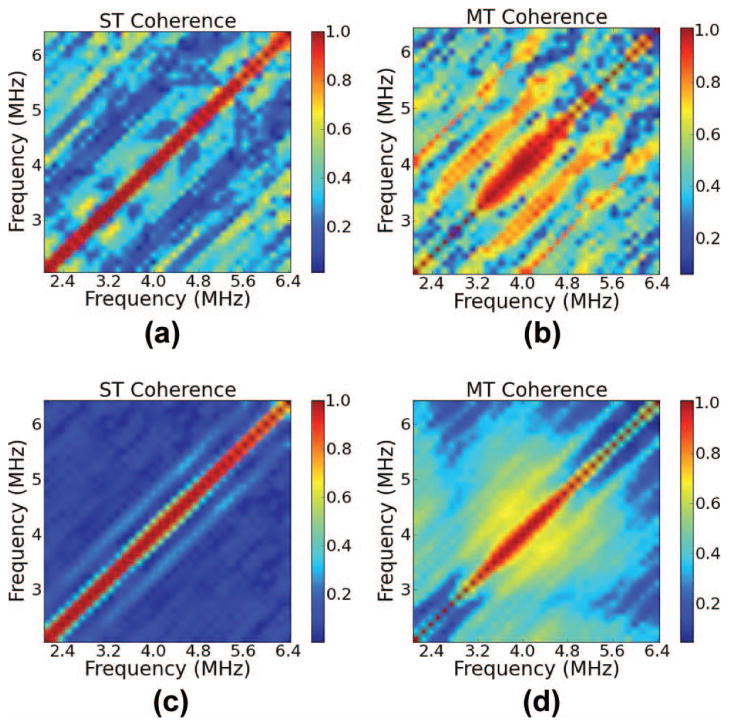
Fig. 4.

(a and c) Single-taper (ST) and (b and d) multi-taper (MT) estimates of the coherence with a gate length of 6 mm, η = 20%, and averaged over (a and b) 10 or (c and d) 200 data segments.

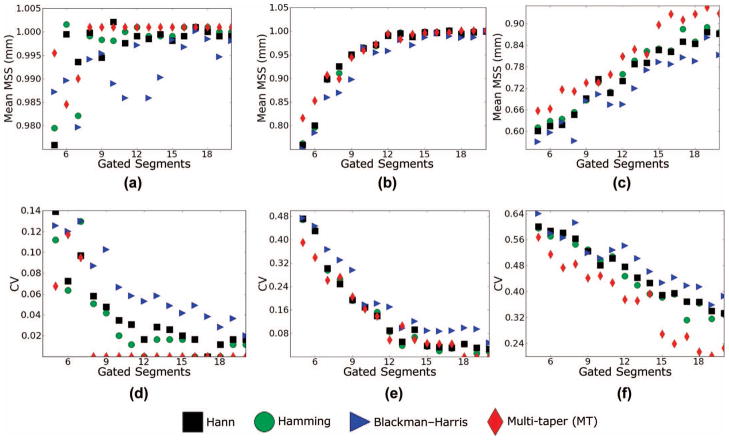
Fig. 5.

(a–c) Mean scatterer spacing (MSS) estimates and (d–f) coefficient of variation for a variable number of gated data segments in the estimate and a fixed gate length (6 mm). (a and d) η = 5%, (b and e) η = 10%, (c and f) η = 15%.

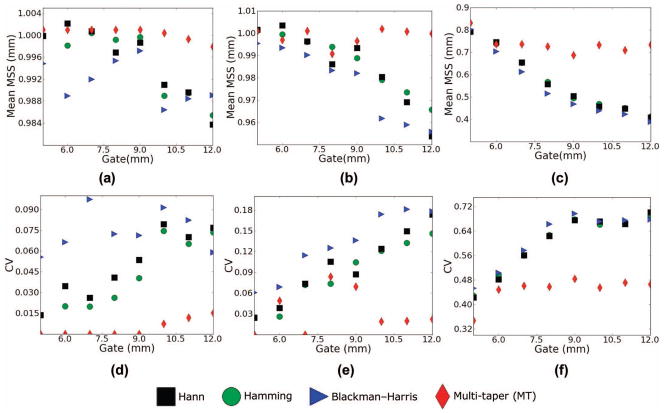
Fig. 6.

(a–c) Mean scatterer spacing (MSS) estimates and (d–f) coefficient of variation for a variable gate length in the estimate and a fixed number of gated data segments (N = 10). (a and d) η = 5%, (b and e) η = 10%, (c and f) η = 15%.

TABLE I.

Analytical Formulae For Windows Used in Generalized Spectrum Calculations.

Window	Formula
Hann	W(n) = 0.5(1 − cos(2πn/(N − 1)))
Hamming	W(n) = 0.54 − 0.46cos(2πn/(N − 1))
Blackman–Harris	W(n) = a0 − a1cos(2πn/(N − 1)) + a2cos(4πn/(N − 1)) − a3cos(6πn/(N − 1));
	a0 = 0.3635819; a1 = 0.4891775
	a2 = 0.1365995; a3 = 0.0106411

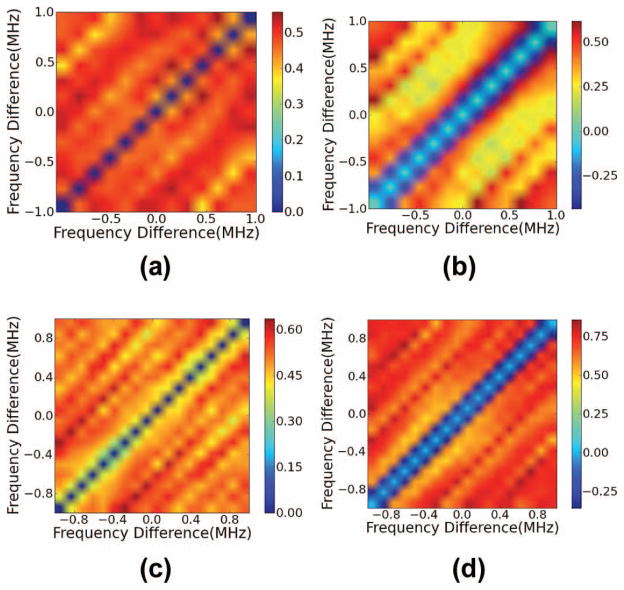
The simulation results shown in Figs. 3(a) and 3(b) demonstrate ST and MT calculations of the coherence for a large number of gated data segments in the ensemble (N = 200) for phantoms with η = 5%, using a short gate length of 6 mm. Figs. 3(a) and 3(b) illustrate the advantage of the MT calculation in reducing spectral leakage. The location of the peaks in the MT calculation is precise, with a maximum occurring along a single diagonal line. There is some leakage visible in the MT calculation, but the peak is identified more precisely for the MT than the ST calculation. In the limiting case of many independent data segments in the ensemble, note that the peaks of the ST calculation are centered in the correct diagonal band of the coherence estimate. They are simply smeared across a broad region of the bifrequency plane because of spectral leakage.

The effect of increasing the gate length on the coherence calculation under the particular conditions of our image formation and scattering model is shown in Figs. 3(c) and 3(d). In this figure, a loss of the higher order peaks is visible in both MT and ST calculations. Peaks are visible across three diagonal lines corresponding to a 1 mm spacing, two times this frequency difference, and three times this frequency difference with a short gate length. With a longer gate length the third peak is no longer discernible, and the first two peaks in the bifrequency plane have a reduced intensity. The reason for this is the periodic SNR was variable over the depth of the simulated phantom. As the simulated ultrasound beam propagated a resolution cell became larger. As the resolution cell became larger, the ratio of diffuse signal energy to coherent signal energy increased. This is because the periodic scatterers were distributed in one dimension, along a column, whereas the diffuse scatterers were distributed three-dimensionally and uniformly throughout the volume.

In Fig. 4, a phenomenon that was observed for larger fractional standard deviations in the spacing is demonstrated. This figure shows coherence calculations for a small and a large number of gated data segments when η is high (20%). At a high fractional standard deviation in the scatterer spacing, the sub-harmonic spacing peak in the coherence calculation starts to dominate over the peak corresponding to a spacing of 1 mm. This seems counterintuitive, but it has also been observed by Huang et al. in [29]. We can see, though, that the effect is less severe for the MT calculation than it is for the ST calculations.

The Monte Carlo results shown in Figs. 5 and 6 provide statistical confirmation of what we infer from the calculations in Figs. 3 and 4. For the parameters explored, the MT calculation outperforms any of the ST calculations in variance and bias simultaneously. For the GS calculated for a low fractional standard deviation in the spacing of 5%, the peak of the CA for the MT calculation corresponds precisely to 1.0 mm, whereas there is some variance and bias in the ST calculation when the number of gated data segments averaged is smaller than 8. As η increases to 10%, there is some variance and a small amount of bias in the MT calculation, but this rapidly falls off as more than 10 gated data segments are used in the calculation. At an η equal to 15%, a large amount of bias is visible in the MSS estimate for a small number of gated A-lines, but considerably less for the MT than for any of the ST calculations. The bias toward smaller scatterer spacings that is visible when η = 15% is a result of the prominence of the sub-harmonic spacing peak. Of the 3 ST estimators, the Hann and the Hamming windows seem to perform the best, with the Blackman–Harris window exhibiting slightly poorer performance.

B. Ex Vivo Results

In this section, we display the results of measurement of the GS in the liver. We hypothesize that thermal ablation results in destruction of the portal triads, and therefore a decrease in the periodic component of the ultrasound signal. We also hypothesize that an MT estimator has the potential to detect coherent scattering more consistently than an ST estimator of coherence. To demonstrate this, we constructed a tissue classifier and performed an ROC analysis with some limitations. We utilized a small number of tissue samples from four independent livers because of time constraints on making the measurements. The correlation between the coherence measurements made within the same liver was unknown. Because the correlation between coherence measurements of different samples from the same liver was unknown, techniques for assessing statistical significance were not used. Therefore, the results of the ROC analysis do not constitute a rigorous statistical test.

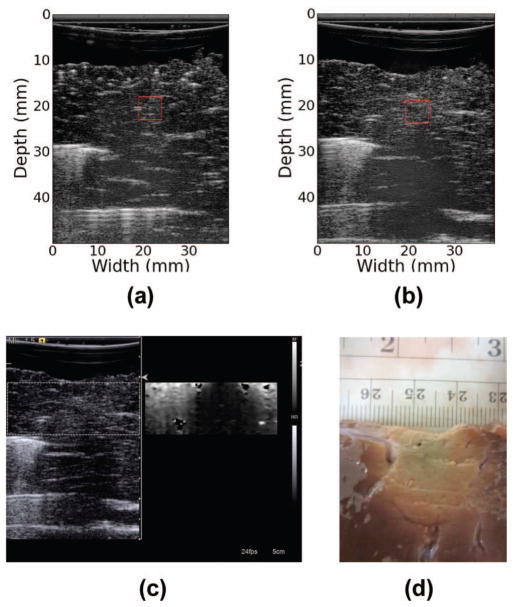
For the analysis, we selected one ROI from each of the 23 RF data sets before RF ablation and one ROI from each of the 23 ROIs following RF ablation to perform the ROC analysis with. Figs. 7(a), 7(b), 8(a), and 8(b) demonstrate the selection of ROIs. The fiducial markers are clearly visible across the B-mode image as bright streaks. These markers were located before and following ablation within a sample. The ablation presented on the B-mode image as a slightly hyperechogenic region showing a large amount of shadowing. In Fig. 7(b) the shadowing is so extreme as to obscure the tip of the fiducial marker following ablation. We note that attenuation is elevated to the point of obscuring the reflections that result from the huge impedance mismatch between the distal metal rod and the surrounding tissue. In addition to acoustic shadowing, we also confirmed the presence of the ablated region using ARFI and gross pathology, as delineation of the exact extent of the thermal ablation was difficult to determine from B-mode image alone.

Fig. 7.

B-mode image of liver sample reconstructed from RF data (a) before ablation and (b) following ablation. Red box shows the region of interest (ROI) used in calculations. (c) Clinical B-mode and acoustic radiation force imaging (ARFI) images of thermal ablation. (d) Optical (gross pathology) image of sample following thermal ablation.

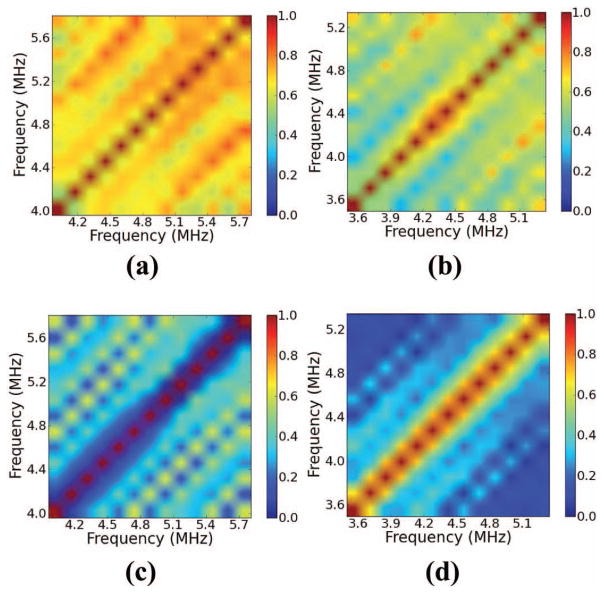
Fig. 8.

Coherence in the region of interest (ROI) in Fig. 7 calculated using the multi-taper (MT) method (a) before and (b) following ablation. Coherence obtained by the single-taper (ST) method using a Hann window (c) before and (d) following ablation.

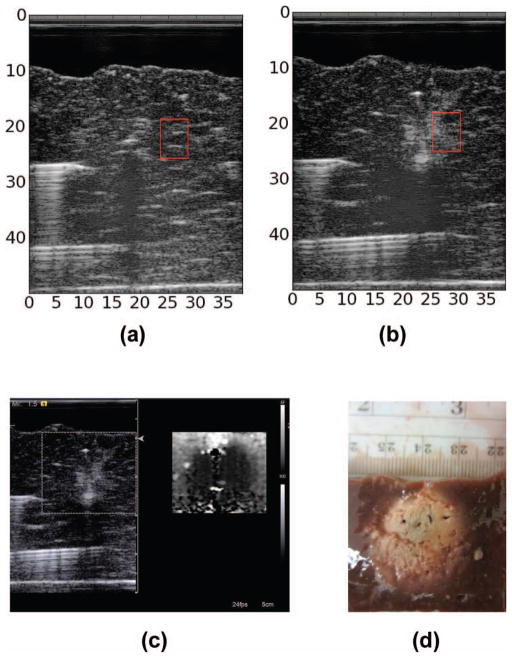
Analysis was performed for ROIs with two sizes: 5 mm axially by 5 mm laterally, and 7 mm axially by 5 mm laterally. The longer gate length was chosen as 7 mm because this was approaching the largest ROI that could be centered in an ablation having a diameter of 1 cm. Creating larger ablations to use a larger ROI at this center frequency was not feasible, because the signal would have been too attenuated to image the full extent of a larger ablation with a sufficient SNR. We make this claim based on the shadowing present at the bottom edge of the ablation and deeper, as shown in Figs. 7(b) and 9(b). The smaller ROI was chosen to be as small as possible while still containing enough periodic scatterer pairs to generate a convergent GS calculation. Each ROI was selected such that for a pair of images obtained before and after ablation, the tissue region being analyzed was identical within the elevational width of an imaging plane, and within the tissue volume changes caused by the ablation process. The 5-mm-long ROIs were manually selected, and the 7-mm-long ROIs were obtained by extending the 5-mm ROIs by 1 mm on either side.

Fig. 9.

B-mode image of liver sample reconstructed from RF data (a) before ablation and (b) following ablation. Red box shows the region of interest (ROI) used in calculations. (c) Clinical B-mode and acoustic radiation force imaging (ARFI) images of thermal ablation. (d) Optical image of sample following thermal ablation.

For each ROI, the center frequency of the received echoes was estimated by locating the maximum value of the GS along the diagonal corresponding to the power spectrum. At a 5 mm gate length, the mean estimated center frequency across all ROIs before ablation was 4.88 ± 0.34 MHz, and following ablation it was 4.66 ± 0.22 MHz. At a 7 mm gate length, the mean estimated center frequency across all ROIs before ablation was 4.73 ± 0.23 MHz and 4.61 ± 0.21 MHz following ablation. The GS was calculated for each ROI over a 2.0 MHz bandwidth about the center frequency. This analysis bandwidth was chosen by experimentally determining over what bandwidth the power spectrum had a magnitude over −6 dB.

Coherence was computed within each of the ROIs before and after ablation. The mean and standard deviation of coherence over all the ablated and unablated ROIs were computed in each frequency bin. The mean and standard deviation were computed in each frequency bin relative to the frequency difference with the estimated center frequency. The mean coherence before ablation was given by

$${\gamma }_{\text{pre}}^{\text{c}}(\mathrm{\Delta }{f}_1,\mathrm{\Delta }{f}_2)=\frac{1}{N}\sum _{i=1}^N\mid {\gamma }_i^{\text{c}}(f_{\text{c},i}-\mathrm{\Delta }{f}_1,f_{\text{c},i}-\mathrm{\Delta }{f}_2)\mid ,$$ (24)

where f_c,i is the estimated center frequency of the ith ROI, N = 23 was the number of ROIs, Δf ranged from −1.0 MHz to 1.0 MHz, and ${\gamma }_i^{\text{c}}$ is an estimate of coherence in the ith ROI. The mean following ablation was computed similarly; we denote it ${\gamma }_{\text{post}}^{\text{c}}$. The standard deviation was computed according to

$${\sigma }_{\text{pre}}(\mathrm{\Delta }{f}_1,\mathrm{\Delta }{f}_2)=\sqrt{\frac{1}{N-1}\sum _{i=1}^N{\left(\mid {\gamma }_i^{\text{c}}(\mathrm{\Delta }{f}_1,\mathrm{\Delta }{f}_2)\mid -{\gamma }_{\text{pre}}^{\text{c}}(\mathrm{\Delta }{f}_1,\mathrm{\Delta }{f}_2)\right)}^2}.$$ (25)

A tissue template was then constructed using Fisher’s linear discriminant:

$$T=\frac{{\gamma }_{\text{pre}}^{\text{c}}-{\gamma }_{\text{post}}^{\text{c}}}{{\sigma }_{\text{pre}}+{\sigma }_{\text{post}}}.$$ (26)

A score was then assigned to the speckle in each ROI by summing the coherence multiplied point-wise by the template. Symbolically, for the ith tissue sample we calculated the score S_i according to

$$S_i=\sum _{\mathrm{\Delta }{f}_1=-1.0}^{1.0}\sum _{\mathrm{\Delta }{f}_2=-1.0}^{1.0}\mid {\gamma }_i^{\text{c}}(\mathrm{\Delta }{f}_1,\mathrm{\Delta }{f}_2)\mid T(\mathrm{\Delta }{f}_1,\mathrm{\Delta }{f}_2).$$ (27)

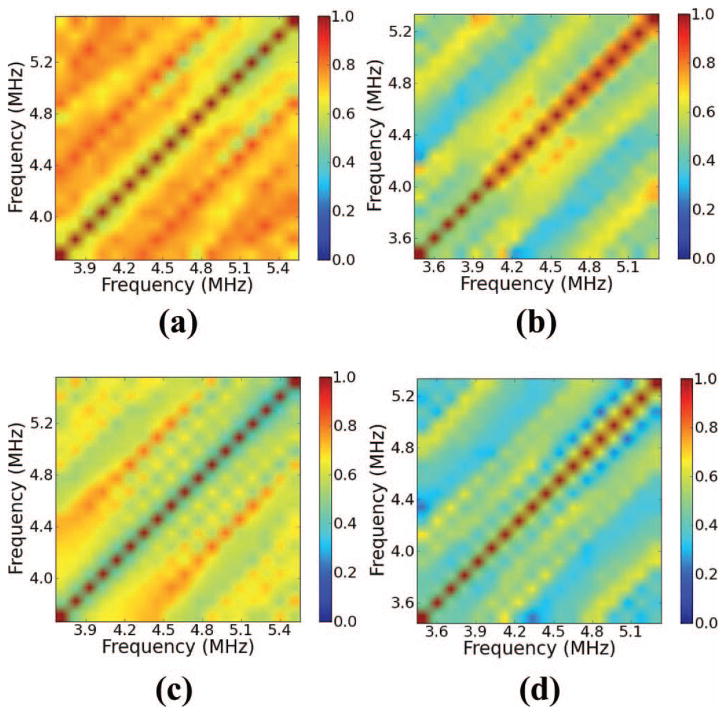
We first discuss the claim that the received signal from ablated liver tends to exhibit a decreased coherent component relative to a signal from unablated liver. In Figs. 8 and 10, we show examples of coherence calculations corresponding to the ROIs shown in Figs. 7 and 9. Fig. 8 demonstrates a calculation with a 5-mm ROI, whereas Fig. 10 demonstrates a calculation with a 7-mm ROI. In both figures, we show the coherence before ablation and following ablation. Across both ROIs shown, note that regardless of the calculation method, the coherence decreases throughout the bifrequency plane from its value before ablation. The tissue templates confirm this result across the ROIs investigated, as shown in Fig. 11. Across both gate lengths, all the calculated templates showed large positive values throughout the bifrequency plane, indicating that the unablated liver tissue tended to exhibit periodic scattering with a range of MSS values.

Fig. 10.

Coherence within the region of interest (ROI) in Fig. 9 calculated by the multi-taper (MT) method (a) before and (b) following ablation. Coherence obtained by the single-taper (ST) method using a Hann window (c) before and (d) following ablation.

Fig. 11.

Templates created by (a) the multi-taper (MT) method (b) Hann window at a gate length of 5 mm. Templates created by (c) MT method (d) Hann window at a gate length of 7 mm.

In Tables II and III, we display the minimum classification error achieved by a tissue classifier constructed from each tissue template. Classifiers were generated by varying a threshold on the score computed from (27), and labeling tissue as positive for liver and negative for ablation. A true positive in this case was liver before ablation exhibiting a large amount of coherence. A false positive was thermally ablated liver tissue whose received echoes possessed a large amount of coherence. The analysis indicates that the MT method has the potential to outperform ST calculations in applications in tissue, with a minimum error rate of only 8.7% for the 5 mm gate length and a minimum error rate of 10.9% for the 7 mm gate length. We note that increasing the gate length consistently improved the error rate for all ST calculation methods, whereas the MT calculation maintained roughly the same error rate at a long gate length. This is probably because at a longer gate length leakage is less pronounced, so increasing the gate length lessens the impact of the leakage improvement from multi-tapering, while increasing the chance that the scattering distribution is no longer the same throughout the gate length. Future work will also evaluate use of an improved estimate of MSS as a tissue classifier for diagnosing diffuse liver disease such as cirrhosis or fatty infiltration.

TABLE II.

Minimum Classification Error for Tissue Classifiers at a 5 mm Gate Length.

Method	FP	FN	Total errors (%)
Hann	5	10	32.6
Hamming	4	8	26.1
Blackman–Harris	1	15	34.7
Multi-taper (MT)	2	2	8.7

TABLE III.

Minimum Classification Error for Tissue Classifiers at a 7 mm Gate Length.

Method	FP	FN	Total errors (%)
Hann	1	7	17.4
Hamming	1	7	17.4
Blackman–Harris	3	10	28.3
Multi-taper (MT)	2	3	10.9

VI. Conclusion

We have shown that an MT estimate of coherence yields significant improvements over ST estimates of coherence with simulations and has the potential to yield improvements in calculations in tissue. Furthermore, we have shown that at a transmit center frequency of 6 MHz, scattering in the liver has a stronger coherent component than scattering from ablated tissue. Future work will evaluate whether or not this is true at other transmit center frequencies in the diagnostic range. Coherence at frequency differences corresponding to a well-chosen range of MSS may be a useful indicator for delineating thermal ablation.

Biographies

Nicholas Rubert was born in Sayre, PA, in 1985. He received the B.S. degree in physics from The Pennsylvania State University in 2008. In 2010, he received the M.S. degree in medical physics from the University of Wisconsin–Madison, where he is currently working toward his Ph.D. degree. He is a student member of the American Institute of Ultrasound in Medicine (AIUM), the American Association of Physicists in Medicine (AAPM), and the IEEE. His current research interests include quantitative ultrasound and ultrasound elastography.

Tomy Varghese received the B.E. degree in instrumentation technology from the University of Mysore, India, in 1988, and the M.S. and Ph.D. degrees in electrical engineering from the University of Kentucky, Lexington, KY, in 1992 and 1995, respectively. From 1988 to 1990, he was employed as an Engineer by Wipro Information Technology Ltd., India. From 1995 to 2000, he was a postdoctoral research associate at the Ultrasonics laboratory, Department of Radiology, University of Texas Medical School, Houston, TX. He joined the Department of Medical Physics at the University of Wisconsin–Madison, Madison, WI, in 2000 as an Assistant Professor. He is currently a Professor in the same department. His current research interests include elastography, ultrasound imaging, ultrasonic tissue characterization, detection and estimation theory, statistical pattern recognition and signal and image processing applications in medical imaging. Dr. Varghese is a fellow of the American Institute of Ultrasound in Medicine (AIUM), senior member of the IEEE, and a member of the American Association of Physicists in Medicine (AAPM) and Eta Kappa Nu.