Pulsatile Hemodynamics of Hypertension: Systematic Review of Aortic Input Impedance

Abstract

Objective

Input impedance is the frequency-dependent afterload to pulsatile blood flow. Studies of input impedance have been performed as early as the 1960s and have been applied to hypertension (HTN). However, to date, these studies have not been systematically evaluated. This systematic review aims to summarize the literature, interpret existing data from the perspective of impedance theory, and to discuss their potential for generating physiological insights into HTN.

Methods

We identified 11 studies where computed impedance moduli from both HTN and control (CNT) groups were reported. In addition, we performed bivariate analyses of raw data from 3 of these studies.

Results

Major findings include (1) HTN groups had consistently elevated impedance moduli at 0Hz (Z₀) and at heart rate frequency (Z₁), an increased frequency where impedance phase first crosses 0 (f₀), but no consistent pattern in characteristic impedance (Z_c), when compared to CNT groups; (2) systolic (SBP) and diastolic (DBP) blood pressure are highly correlated with Z₀ and Z₁, moderately correlated with f₀, less correlated with Z_c; and (3) the measurement and calculation methods for Z_c are varied and inconsistent, and (4) a not insignificant proportion of hypertensive subjects have “normal” Z₀, Z₁ and Z_c values. These findings are limited by the heterogeneous study populations and small sample sizes.

Conclusions

These findings suggest that Z₀, Z₁ and f₀ are significantly associated with hypertension, while the role of Z_c is less clear. Additional studies are needed to evaluate these input impedance variables in order to generate substantial implications in clinic settings.

Introduction

Despite the availability of multiple antihypertensive medications, surveys show that only half the patients with hypertension are able to adequately control their blood pressure¹. Although factors such as noncompliance, drug side effects, and poor access to health care are important contributors, our limited understanding of the dynamic and spectral features of hypertension may also play a role. Input impedance describes the frequency dependent opposition to blood flow and provides a more complex assessment of blood flow/pressure than peripheral resistance alone. By evaluating impedance across multiple frequencies, input impedance can capture underlying physiological processes - such as wave reflections and aortic (visco)elasticity – that may be important determinants for systemic blood pressure. Input impedance was suggested by McDonald and Taylor as early as in 1959², implemented by O’Rourke³, et al. and explained in detail in text books of Hemodynamics by Milnor⁴ and MacDonald’s blood flow in arteries by Nichols and O’Rourke⁵.

In general, the input impedance of the ascending aorta possesses the following characteristics: 1) the modulus (or amplitude) of the input impedance is greatest at zero frequency; 2) with increasing frequency, the modulus decreases in magnitude towards a minimal value which is commonly located between the 2^nd to 4^th harmonics (i.e. frequencies corresponding to two to four times the heart rate) and is approximately 5-10% of the input resistance (zero frequency impedance); 3) the input impedance moduli settle and fluctuate around a steady positive impedance value (Z_c, the characteristic impedance).

Past physiological studies have predominantly focused on two aspects of the aortic input impedance: Z₀ and Z_c. Z₀ is the peripheral vascular resistance and embodies impedance to flow as if the flow were steady and continuous. Z_c, on the other hand, is the impedance at higher frequencies and is generally attributed to the local aortic wall stiffness and diameter. Other reported impedance parameters include f_{0 -} the frequency where input impedance reaches its first minimum and its phase first crosses zero – and Z₁- the impedance modulus at the heart-rate frequency⁶. f₀ reveals information about wave reflections, with a higher f₀ indicating earlier reflections.

Studies of aortic input impedance have been specifically applied to hypertension populations. However, to date, these studies have not been systematically evaluated. This review aims to summarize the existing evidence, to interpret the data from the perspective of impedance theory, and to discuss their potential for generating physiological insights into hypertension.

Method

This systematic review includes 11 articles^7-17 from two electronic databases: PubMed and Scientific Citation Index for dates ranging from the database inception to May 2010. The searching keywords were “impedance”, “input resistance”, and “windkessel model” crossed with the keywords “hypertension”, “high blood pressure”, and “hypertensive”. Searches were limited to the English language. We also manually searched the references of all relevant publications. Articles were selected if the studies 1) contained in vivo human data; (2) had primary-collected data and were not review papers, commentaries, or editorials; (3) involved both control normotensive subjects and systemic hypertension subjects; (4) had central input impedance measured/calculated. Exclusion criteria were that the studies (1) had patients with effects of pharmacological drugs (we required the hypertensive patients were either never treated or withdrawn from the drug for at least a week); (2) had patients with other severe cardiovascular comorbidities.

Extracted data includes subjects, age, heart rate (HR), systolic blood pressure (SBP), diastolic blood pressure (DBP), Z₀, Z₁, Z_c and f₀. Other parameters such as input impedance phase, cardiac output, stroke volume, and total/mean work power were evaluated but ultimately excluded due to limited data availability from the papers for comparison. In cases where different units were employed, appropriate unit conversions were performed.

In a number of studies, the published raw data were employed for bivariate analysis. Primary authors of selected papers were also contacted to obtain additional raw data but with no success. Scatter plot matrix was computed from JMP (SAS Corporate, Cary, NC, USA) with Pearson correlation method and density ellipse was displayed with 95% as the confidential interval. Greater narrowing of the ellipse along the diagonal axis indicated greater correlations (coefficient r>0.5) while rounding of the ellipse and absence of a diagonal orientation suggested lack of correlation (r<0.5) between variables.

We also determined the receiver operating characteristic (ROC) curve with the raw data for Z₀, Z₁, Z_c and f₀ in regards to the diagnosis of hypertension.

Results

Table 1 summarizes the data extracted from the selected studies. Patients’ characteristics including gender and age are listed and categorized according to the group designations (control [CNT] vs. hypertension [HTN]) if the information was provided. In addition, the type of hypertension (essential/permanent vs. isolated systolic vs. mixed hypertension) is also listed. Overall, seven out of 11 studies^7-13 evaluated essential hypertension whereas two studies assessed isolated systolic^15,16, one investigated mixed hypertension¹⁷ and one study did not indicate the type of hypertension¹⁴. With the exception of Ferrier¹⁶ and Mitchell¹⁷ studies, study subjects were predominantly male. Mitchell’s study¹⁷ performed separate analyses according to gender. The HTN subjects within the isolated systolic and mixed hypertension studies were generally older, although two Merillon’s essential hypertension studies^7,8 had older hypertensive groups yet statistically younger control groups (bold fonts indicate statistically significant differences between HTN and CNT groups).

Table 1.

Extracted data including paper, subjects, age, heart rates (HR, beat/minute), systolic blood pressure (SBP, mmHg), diastolic blood pressure (DBP, mmHg), input impedance at 0Hz (Z₀, dyn·s·cm⁻⁵), first modulus of input impedance (Z₁, dyn·s·cm⁻⁵), characteristic impedance (Z_c, dyn·s·cm⁻⁵) and the frequency where input impedance reaches its first minimum and its phase first crosses zero (f₀).

paper	subjects	Age	HR	SBP	DBP	Z0	Z1	Zc	f0
Merillon JP 1982	CNTL (11M2F)	40	79	109.8	73.7	1140		90	4.3
	Essential HTN (12M)	51	83	174.4	100.8	1680		114	5.2
Merillon JP 1983	CNTL (10 M 1F)	38	81	112	73	1173		100
	Permant essential HTN (11M)	50	84	171	100	1677		104
Merillon JP 1985	CNTL (25M)	43	75	119	72	1270		101
	Essential HTN (19M1F)	47	85	171	101	1712		134
Ting CT 1986	CNTL (7M1F)	41.9	97.2	120.2	74.8	1713.3	165.1	93.9	2.97
	Essential HT (6M5F)	34.8	79.2	158.6	92.5	2294.9	300.7	145.7	4.15
Ting CT 1991	CNTL (7M3F))	34.5	87.4	115.7	77.3	1268	105	77.9	3.5
	essential HTN (8M4F)	33.8	86.8	162.4	102.5	1962	200	82.5	4.6
Ting CT 1993	CNTL (10M4F)	32.6	83.5	111.8	73.5	1239	110	75.5
	essential HTN (9M3F)	37	79.7	156.9	96.2	1612	185	60.4
Ting CT 1995	(CNT is same as Ting CT 1993)	32.6	83.5	111.8	73.5	1239	110	75.5	3.1
	Essential HTN (8M4F)	32.9	82.3	160.6	100.2	1863	220	71.9	4.3
Chang KC 1990	CNTL (5M2F)	46	75	122	74	1651	177	122	3.4
	HTN (7M2F)	49	79	180	100	2751	383	193	4.8
Nichols WW 1992	CNTL (9)	58	78	134	80	1395	210	89
	isolated systolic HTN (9)	58	76	166	84	2013	329	184
Ferrier KE 2001	CNTL (10M 10F)	64	62	119	<90		191.2	133.6
	isolated systolic HTN(10 M10 F)	64	64	154	<90		261.6	187.2
Mitchell GF 2003	CNTL (11F)	56	68	114	64	1686	236	185
	mixed HTN (50 F)	61	65	167	83	2415	444	268
	CNTL (19M)	60	62	125	69	1673	221	159
	mixed HTN (78 M)	60	63	162	88	2131	314	208

Table 1 also lists the mean values for the heart rate, blood pressure, and input impedance parameters for each of the studies. Across all studies, Z₀ and Z₁ are significantly increased in the HTN group compared to the CNT group. Z_c, however, did not display the same consistency and 5 of the 11 studies showed either no significant difference between the two groups or reduced Z_c values in the HTN group. The three studies^15-17 involving isolated and mixed hypertension and with older subjects, however, were consistent with relative increases in Z_c for HTN patients.

The magnitudes of Z₀ are six to twelve folds greater than that of Z₁ while Z_c amplitudes are generally smaller than that of Z₁. For the five studies reporting zero crossing frequencies, the mean f₀ was uniformly increased in HTN group as compared to the CNT group.

Figure 1 illustrates the aggregated results in graphical form. The HTN to CNT ratios of mean Z₀ magnitudes were generally 1.5 across studies and were comparable to the ratios of mean SBP and partially DBP amplitudes. The HTN to CNT ratio for Z₁ revealed a much greater range of ratios from 1.4 to 2.2. As noted previously, the ratios of Z_c were not consistent across studies, and although mean Z_c magnitudes were generally increased in hypertensive patients, some studies - notably Ting’s 1993 study¹² - demonstrated reduced Z_c.

Figure 1.

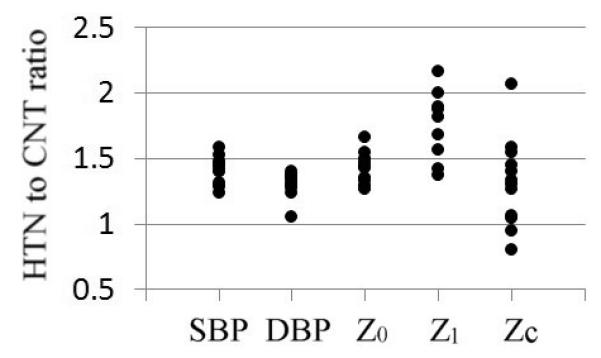
Plot of the variable ratios between hypertension (HTN) and control (CNT) groups. Variables include systolic blood pressure (SBP), diastolic blood pressure (DBP), input impedance at 0Hz (Z₀), first modulus of input impedance (Z₁) and characteristic impedance (Z_c).

Table 2 lists the devices and methods used to acquire blood pressure and flow measurements. In addition, the mathematical methods for calculating Z₀ and Z_c are also summarized. Most studies used intravascular catheter measurements, whereas Ferrier and Mitchell employed applanation tonometry at the carotid artery and Doppler imaging of the left ventricle outflow tract. Across the selected studies, four different methods were used to calculate Z_c: the average modulus of input impedance above 4Hz^7,8,10-13; averaged input impedance above 2 Hz^14-16; indirect derivation of Z_c from pulse wave velocity using the Waterhammer formula ${\mathrm{Z}}_{\mathrm{c}}=\frac{\rho \mathrm{C}}{\pi r^2}$ (where ρ is the density of blood, C is the wave velocity, r is the diastolic aortic radius) ⁹; and a time-domain approach where characteristic impedance was calculated as ΔP/ΔQ in early systole¹⁷. The methods for obtaining Z₁ were not included in Table 2 because Z₁ was derived as the ratio of 1^st blood pressure harmonic modulus to 1^st blood flow harmonic modulus in the seven studies where this information was detailed. No detailed description was provided in Mitchell’s study.

Table 2.

Locations and methods that the blood pressure and flow were measured and the method in the calculation of input impedance at 0Hz (Z₀) and characteristic impedance (Z_c).

Paper	Measurement	Device	Z0 calculation method	Zc calculation method
Merillon JP 1982	Ascending aorta pressure and blood flow	Catheters with micromanometer and flowmeter sensor	P0/Q0 (P0: pressure harmonic modulus at 0 Hz, Q0: flow harmonic modulus at 0 Hz)	Averaging of all moduli of input impedance above 4 Hz
Merillon JP 1983	Same as Merillon JP 1982	Same as in Merillon JP 1982	Same as Merillon JP 1982	Same as in Merillon JP 1982
Merillon JP 1985	Left ventricular and ascending aortic pressure and aortic flow velocity	Mcromanometer mounted on catheter	80×P/CO (P: mean aortic pressure, CO: cardiac output)	ρC/πr2 (r: diastolic aortic radius, C:pulse wave velocity, ρ: density of blood
Ting CT 1986	Left ventricular and ascending aortic pressure and aortic flow velocity	Catheter with pressure and velocity sensors	(Pv-Pa)/Q (Pv: average ventricular pressure; Pa: average atrial pressure; Q: mean blood flow)	Same as in Merillon JP 1982
Ting CT 1991	same as Ting CT 1986	Same as Ting CT 1986	Same as Ting CT 1986	Same as in Merillon JP 1982
Ting CT 1993	same as Ting CT 1986	Same as Ting CT 1986	Same as Ting CT 1986	Same as in Merillon JP 1982
Ting CT 1995	Same as Ting CT 1986	Same as Ting CT 1986	Same as Ting CT 1986	Same as in Merillon JP 1982
Chang KC 1990	Ascending aorta flow velocity and pressure	Multisensor catheter	Quotient of mean aortic pressure and cardiac output	Averaging of all moduli of input impedance above 2 Hz
Nichols WW 1992	Ascending aortic blood flow velocity and aortic and left ventricular pressure	Catheter mounted with multisensors	P/Q (P: mean pressure, Q: mean flow)	Averaging of all moduli of input impedance above 2 Hz
Ferrier KE 2001	Carotid artery pressure, volumetric aortic flow	Applanation tonometry and handheld doppler velocimeter	Cardiac output derived from velocity flow was used to calculate total peripheral resistance	Averaging of all moduli of input impedance above 2 Hz
Mitchell GF 2003	Carotid artery pressure and left ventricular outflow tract flow	Tonometry and pulsed doppler	Peripheral resistance (No method was mentioned)	ΔP/ΔQ (ΔP and ΔQ: pressure and flow difference in the early systolic period)

To further explore the detailed relationships between input impedance and blood pressure parameters (SBP, DBP, mean BP [MBP], and pulse pressure [PP]), the primary data from three of these 11 papers^7,10,14 were concatenated (Merillon’s paper⁷ lacked Z1 data) and are listed in Table 3. We also compared age distributions in the CNT (41.82±10.68) and HTN groups (44.97±12.68) which are not significantly different. The bivariate relationships are plotted in Figure 2. The figure shows scatter plots with coefficient correlations and an overlying density ellipse with 95% as the confidential interval. There are strong correlations (r>0.5) between Z₀ and SBP, MBP, PP and between Z₁ and SBP, MBP, PP. Weak correlations exist between Z_c and SBP, DBP, MBP, PP. The correlation between f₀ and blood pressure parameters are weak but otherwise strongest between f0 and Z₁.

Table 3.

Raw data from 3 of the 11 reviewed paper. MBP and PP were calculated from SBP and DBP as MBP=SBP/3+2*DBP/3, PP=SBP-DBP.

paper	subjects	age	SBP	DBP	MBP	PP	Z0	Z1	Zc	f0
Merillon JP 1982	N1	47	96.8	65.3	79.5	31.5	840	42	3.1
	N2	30	100.5	65.3	82.5	35.3	1140	90	3.9
	N3	22	106.5	69.0	87.8	37.5	1140	108	3.4
	N4	45	87.8	62.3	76.5	25.5	1260	126	3.6
	N5	41	126.0	81.8	102.0	44.3	1080	78	4.7	26
	N6	94.5	65.3	81.0	29.3	960	54	3.8
	N7	58	117.8	75.8	93.8	42.0	1200		60	5.8
	N8	25	114.0	84.8	100.5	29.3	1080		120	4.0
	N9	53	108.0	69.0	84.0	39.0		780	72	3.3
	N10	32	121.5	87.0	102.8	34.5	1260	72	5.7
	N11	56	120.8	78.8	97.5	42.0	1260	150	4.6
	N12	56	117.8	76.5	94.5	41.3	900		60	5.7
	N13	30	114.0	79.5	102.8	34.5		1620	138	3.7
Ting CT 1986	N1	30	126.9	76.0	100.7	50.9	2288	272	238	3.51
	N2	56	139.6	73.0	100.7	66.6	1741	234	68	1.96
	N3	37	106.1	72.2	88.2	33.9	1393	108	138	2.49
	N4	39	126.9	102.9	114.3	24.0	935	41	44	3.07
	N5	40	113.0	69.0	90.3	44.0	2168	243	147	2.89
	N6	37	115.2	75.4	93.9	39.8	1434	118	95	3.10
	N7	45	113.5	80.5	97.2	33.0	1794	121	56	2.92
	N8	51	125.9	77.5	100.6	48.4	1855	181	113	3.30
Chang KC 1990	N1	56	137	82	108	55	1994	234	147	3.9
	N2	37	118	79	98	39	1182	101	98	2.9
	N3	45	122	64	89	58	1358	204	116	4.1
	N4	40	111	66	88	45	1979	232	162	3.4
	N5	55	130	77	103	53	1824	238	119	2.5
	N6	36	111	67	89	44	1274	156	123	4.1
	N7	46	124	82	101	42	1949	74	87	2.7
Merillon JP 1982		H1	44	165.8	85.5	118.5	80.3	1260	60	6.1
	H2	58	176.3	105.8	139.5	70.5	1800	222	5.5
	H3	59	204.8	94.5	133.5	110.3	1680	42	4.4
	H4	53	243.8	117.0	164.3	126.8	2520	36	4.6
	H5	59	152.3	94.5	120.0	57.8	1680	48	5.1
	H6	52	162.8	96.8	126.0	66.0	1260	60	6.1
	H7	29	136.5	96.0	114.8	40.5	1440	102	4.9
	H8	51	170.3	111.8	135.0	58.5	1800	96	4.6
	H9	59	164.3	82.5	117.8	81.8	1680	126	5.7
	H10	36	192.8	112.5	144.8	80.3	1920	204	5.5
	H11	60	156.8	103.5	127.5	53.3	1320	162	4.7
	H12	52	163.5	103.5	129.8	60.0	1920	240	5.2
Ting CT 1986	H1	30	165.7	98.0	128.3	67.7	1379	160	113	4.05
	H2	25	142.8	93.6	118.8	49.2	2068	195	121	4.89
	H3	35	211.6	123.0	159.8	88.6	2721	377	154	4.41
	H4	34	151.8	92.3	122.1	59.5	1481	165	126	2.26
	H5	35	153.4	87.1	118.2	66.3	2968	425	173	3.98
	H6	44	160.8	90.9	121.6	69.9	4768	656	361	3.47
	H7	53	161.9	90.4	119.7	71.5	2127	278	145	3.86
	H8	46	167.1	92.1	123.2	75.0	2327	362	185	3.69
	H9	30	206.6	128.0	162.1	78.6	2774	349	169	4.11
	H10	25	172.3	95.3	129.7	77.0	3175	518	148	5.20
	H11	26	148.5	93.5	121.1	55.0	1797	199	128	4.53
Chang KC 1990	H1	31	151	90	120	61	3174	412	131	5.7
	H2	33	151	100	126	51	1942	219	154	4.4
	H3	58	176	88	125	88	2164	396	288	3.5
	H4	62	163	72	108	91	2567	516	279	4.9
	H5	65	203	100	146	103	3875	518	197	6.6
	H6	40	222	132	173	90	3817	459	157	5.4
	H7	56	177	90	125	87	2454	428	216	4.4
	H8	56	208	115	154	93	2424	299	218	4.5
	H9	43	165	117	137	48	2344	203	99	4.2

Figure 2.

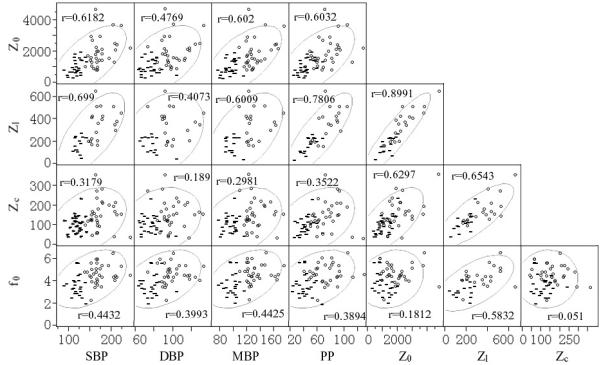
Scatter plot of the raw data with group designation markers. “-” denotes for the control subjects and “o” is for the hypertensive subjects. The figure also showed the density ellipses depicting the 95% of the confidential interval.

The scatter plots in the figure also have group designation markers: CNT in “-“ and HTN in “O”. A clear distinction is noted between CNT and HTN subjects with respect to SBP, DBP and MBP, since these parameters were used as inclusion/exclusion criteria. However, the differences in PP values between the two groups are less distinct and even much less so for the input impedance parameters Z₀, Z₁, Z_c, and f₀. For these latter variables, substantial overlap between the two groups exists – particularly for Z_c. A not insignificant proportion of hypertensive subjects have “normal” input impedance parameters (based on the ranges of values for the normal subjects). Conversely, some normal subjects have elevated input impedance values although such cases are comparatively less common.

With this subset of subjects, the area under Receiver Operating Characteristic (ROC) curves for Z₀, Z₁, Z_c and f₀ in regards to the diagnosis of hypertension were 0.80, 0.88, 0.72, and 0.80, respectively.

Discussion

This systematic review identified 11 studies that reported input impedance data for both normotensive (total N=147) and hypertensive patients (N=256). Collectively, the existing evidence suggests that (1) based on mean input impedance and blood pressure values, HTN groups had consistently elevated Z₀, Z₁, and f₀ values compared to the CNT groups but no consistent pattern with Z_c amplitudes, (2) based on individual, raw data analysis of three studies, SBP and DBP are highly correlated with input impedance parameters Z₀ and Z₁, somewhat correlated with f₀, but less correlated with Z_c, (3) the measurement and calculation methods for Z_c are varied and inconsistent, and (4) a not insignificant proportion of hypertensive subjects have “normal” Z₀, Z₁ and Z_c values. From a physiological standpoint, these data imply that peripheral vascular resistance (Z₀), input impedance at the heart beat frequency (Z₁), and wave reflection (f₀) are important factors associated with hypertension, while the role of aortic stiffness and aortic diameter (Z_c) is less clear in these hypertensive subjects.

The significant correlation between peripheral vascular resistance (Z₀) and hypertension is not a new finding and consistent with the understanding that vasoconstriction (possibly from enhanced sympathetic nervous activity) plays a prominent role in hypertension pathophysiology. Whether this vasoconstriction plays a causative, pathogenic role or is an abnormal response to persistently elevated blood pressure remains unclear^18,19.

In our raw data analyses, Z₁ demonstrated the strongest correlation with SBP and PP than any other reported input impedance parameter. Moreover, Z₁ was associated with greatest area under the ROC curve for the diagnosis of hypertension compared to Z₀, Z_c, and f₀. However, the total number of studies evaluating Z₁ in hypertension remains low, and the physiological implication of Z₁ is itself ambiguous. Based on the bivariate data, Z₁ also has the unique feature of being highly correlated with all other input impedance parameters reported here: Z₀ (peripheral resistance), Z_c (aortic stiffness and diameter), and f₀ (wave reflection). From a mechanistic standpoint, this may be observed because the frequency is low enough to be influenced by peripheral resistance and possibly high enough to be influenced by aortic stiffness. Additionally, Z₁ resides in the time domain where wave reflections have taken effect (1^st harmonic frequency [~1 Hz] < minimum modulus frequency [~2-4 Hz]). As a consequence, Z₁ may reflect the composite properties that personify the vascular system and thereby be a useful global marker for the impedance confronting the pulsating heart – particularly for hypertension. Naturally, additional studies should be performed before a definitive conclusion can be made.

The zero-crossing frequency (f₀) was significantly increased in hypertensive patients compared to normotensive controls in all 5 studies reporting this information. Furthermore, by the bivariate data, a moderate positive correlation (r>0.4) between f₀ and SBP is seen. An increased f₀ occurs when either the pressure/flow wave velocity increases or the effective distance to reflection sites are decreased. According to past studies, the former scenario is more likely and can be explained by the aortic distention resulting from elevated pressures and the accompanying increase in elastance (stiffness) which subsequently increases pulse wave velocities²⁰. This early reflection generates a temporal (earlier) shift in the retrograde wave at the ascending aorta to coincide with the outgoing systolic pressure wave, thus explaining for the moderate correlation between SBP and f₀.

According to the raw data, f₀ is not correlated with either Z₀ or Z_c. From a theoretical standpoint, f₀ and Z_c are expected to be correlated because earlier reflections (as indicated by increased f₀) result from an increase in aortic stiffness (which greatly determines Z_c). However, Z_c is also inversely related to the aortic radius to the power of 2.5, and the increase in radius accompanying hypertension may effectively nullify any increase in Z_c attributed to enhanced wall stiffness. As a consequence, wave reflection (f₀) appears to be an important, separable variable with respect to systolic hypertension.

As already made evident, characteristic impedance is a complicated variable influenced by not only arterial stiffness but also vessel radius. Its inverse relationship with aorta radius may partially explain for the inconsistencies in HTN to CNT ratios of Z_c seen across the selected studies and also for the relatively weak correlation between Z_c and blood pressure parameters in the aggregated raw data. This confounding factor has been mentioned by researchers before²¹. In addition, the data suggests an age-effect as well. The younger hypertension cohort for Ting’s three studies had reduced Z_c, whereas the older hypertension groups in Ferrier, Mitchell, and Nichols studies had significantly increased characteristic impedances compared to their respective control groups.

The inconsistencies in Z_c ratios across studies may also stem from the variable methods used to derive Z_c. As documented in Table 2, four different approaches were used to calculate Z_c. Two relied on the frequency-domain approach, albeit with different frequency cutoffs; one invoked a time-domain approach; and one calculated Z_c indirectly by using the Water-Hammer formula. Although the technical strengths and limitations for each approach are beyond the scope of this review, a more transparent and consistent approach is needed if Z_c is to be broadly applied to the clinical setting as some have advocated²². The need for consistency becomes more poignant in light of past studies showing how different characteristic impedance values can be obtained from the same data³. Moreover, hypertension may be particularly susceptible to variabilities in Z_c if Z_c is derived in the frequency domain. Due to the increased zero-crossing frequency, a frequency-domain cutoff of 2 Hz, for instance, will likely incorporate the impedance minimum and thus potentially distort the final characteristic impedance results (which should theoretically be without any reflection effects).

The raw bivariate data evaluated in this review were useful in identifying the overlap in input impedance variables between the HTN and CNT groups. The overlap did not occur due to increased incidences of elevated input impedance variables (particularly Z₀ and Z₁) in CNT subjects. Rather, there were more incidences of HTN subjects having “normal” ranges of input impedance values. Given the limited number of subjects within this raw data sample and the variable analytical methods, this observation will have to be confirmed with additional studies but, if true, will carry substantial implications for the clinician taking care of a hypertensive patient. The elevated pressure may originate from a specific physiological etiology (e.g., elevated peripheral vascular resistance vs. aortic stiffness vs. wave reflection effects), and a dynamic approach such as aortic input impedance may help clinicians determine which specific etiology is involved and subsequently what medication should be prescribed.

This review has identified some suggestive relationships between input impedance and blood pressure parameters, but the existing evidence for aortic input impedance in hypertension is still inadequate. Only 11 studies were identified in this review and the number of subjects per study was generally small (with the exception of Mitchell’s study¹⁷). These studies did not report data on body size (i.e. height, weight) – a known contributing factor to impedance measurement²³. In addition, the analyzed raw data were a composite of only 3 studies. The level of evidence is insufficient to conclude how input impedance may differ between the types of hypertension (i.e. isolated hypertension vs. essential hypertension), much less understand the effects of age and gender. Importantly, the majority of the studies involved younger subjects with essential hypertension who generally possess different pathophysiologies than older individuals with isolated systolic hypertension. Aside from the aforementioned need for consistent Z_c derivations methods, the methods for acquiring pressure and flow data needed for aortic input impedance are also varied (Table 2) and require some level of standardization.

Nevertheless, despite these limitations, aortic input impedance provides a comprehensive, frequency-dependent view of afterload encountered by the heart and may facilitate a more personalized approach to hypertension by delineating what pathophysiological factors are involved in each patient. Thus far, the existing literature lends support for the role of Z₀, Z₁, and f₀ in essential hypertension although additional studies and standardizations are needed before input impedance can be confidently applied to the clinical setting.