Abstract
Background
A condition to predict unbiased estimated breeding values by best linear unbiased prediction is to use simultaneously all available data. However, this condition is not often fully met. For example, in dairy cattle, internal (i.e. local) populations lead to evaluations based only on internal records while widely used foreign sires have been selected using internally unavailable external records. In such cases, internal genetic evaluations may be less accurate and biased. Because external records are unavailable, methods were developed to combine external information that summarizes these records, i.e. external estimated breeding values and associated reliabilities, with internal records to improve accuracy of internal genetic evaluations. Two issues of these methods concern double-counting of contributions due to relationships and due to records. These issues could be worse if external information came from several evaluations, at least partially based on the same records, and combined into a single internal evaluation. Based on a Bayesian approach, the aim of this research was to develop a unified method to integrate and blend simultaneously several sources of information into an internal genetic evaluation by avoiding double-counting of contributions due to relationships and due to records.
Results
This research resulted in equations that integrate and blend simultaneously several sources of information and avoid double-counting of contributions due to relationships and due to records. The performance of the developed equations was evaluated using simulated and real datasets. The results showed that the developed equations integrated and blended several sources of information well into a genetic evaluation. The developed equations also avoided double-counting of contributions due to relationships and due to records. Furthermore, because all available external sources of information were correctly propagated, relatives of external animals benefited from the integrated information and, therefore, more reliable estimated breeding values were obtained.
Conclusions
The proposed unified method integrated and blended several sources of information well into a genetic evaluation by avoiding double-counting of contributions due to relationships and due to records. The unified method can also be extended to other types of situations such as single-step genomic or multi-trait evaluations, combining information across different traits.
Electronic supplementary material
The online version of this article (doi:10.1186/s12711-014-0059-3) contains supplementary material, which is available to authorized users.
Background
Simultaneous use of all available data by best linear unbiased prediction (BLUP) is a condition to predict unbiased estimated breeding values (EBV) [1]. However, this condition is not often fully met. For example, in dairy cattle, while foreign bulls are often widely used, e.g. through artificial insemination, evaluating populations based only on internal phenotypic data (i.e. internal records) will lead to potentially biased and less accurate evaluations [2]. The reason is that external phenotypic data used to select these foreign bulls are not available at the internal level. Multiple across country evaluation (MACE), performed at an international level by International Bull Service (Interbull, Uppsala, Sweden), allows EBV, for each population scale, to be aggregated into a single ranking for international dairy sires. However, this has no influence on internal evaluations. These issues are also relevant in the setting of current developments of genomic multi-step or single-step prediction methods (e.g., [3-5]).
Because external phenotypic data are not available at the internal level, methods were developed to combine external information, i.e. external EBV and associated reliabilities (REL), with internal data to improve accuracy of internal genetic evaluations. A first type of approaches is based on performing, a posteriori, an additional step after the genetic evaluation at the internal level. These approaches combine external and internal EBV based on selection index theory (e.g., [6]), based on mixed model theory (e.g., [7]) or based on bivariate evaluations (e.g., [8]). One of the problems of a posteriori approaches is that external information used for selection will not contribute to the estimation of fixed effects at the internal level, which can create potential biases. A second type of approaches combines external information simultaneously with internal phenotypic data in genetic evaluations at the internal level. Simultaneous combination of external information and internal phenotypic data can be carried out using different methods. However, to our knowledge, the following two approaches are the most used. First, external information can be directly included by converting this information into pseudo-records for fictive daughters of external animals (e.g., [2]). Similar approaches were proposed to include external information into internal single-step genomic evaluations (e.g., [5,9]). Second, external information can be directly included by changing both the mean and (co)variance of the prior distributions of genetic effects in a Bayesian approach, as mentioned, for example, by Gianola and Fernando [10]. Quaas and Zhang [11,12] and Legarra et al. [13] proposed two Bayesian derivations to integrate external information into internal genetic evaluations in the context of multi-breed genetic evaluations for beef cattle. These two derivations consider external information as priors of internal genetic effects. Vandenplas and Gengler [14] compared these two derivations and proposed some improvements that concerned mainly double-counting of contributions due to relationships among external animals. Indeed, an EBV of an animal combines information from its own records (i.e., contributions due to own records) and from records of all relatives through its parents and its progeny (i.e., contributions due to relationships) [6,15]. Therefore, integration of EBV for relatives can cause the same contributions that are due to relationships to be counted several times, which can bias genetic evaluations at the internal level.
Both types of approaches i.e. that combine available information a posteriori or simultaneously, raise another issue if the external information results from an evaluation that combines external and internal records, which is that some contributions due to records will be considered several times when external information is combined with internal records. Although this is a major issue for common sources of external information (e.g., MACE information), to our knowledge, only a few studies have proposed solutions to the double-counting of contributions due to records (e.g., [5,16,17]). The proposed solutions were developed as an additional pre-processing step before integration of external information. Furthermore, in many situations, integration of several sources of external information into genetic evaluations at the internal level may be needed but this has not been studied to our knowledge. In such cases, double-counting of contributions due to records could be worse if external information from several evaluations were, at least partially, based on the same internal records, and/or on the same external records, and integrated into the same genetic evaluation.
Thus, the aim of this research was to develop a unified method to integrate and blend simultaneously several, potentially related, external sources of information into an internal genetic evaluation based on a Bayesian approach. In order to achieve this aim, methods were developed to avoid double-counting of contributions due to relationships and due to records generated by the integration of several sources of information. This resulted in modified mixed model equations (MME) that integrate and blend simultaneously several sources of information and avoid double-counting of contributions due to relationships and due to records. The performance of the developed equations was evaluated using simulated and real datasets.
Methods
Integration of several sources of external information
Assume an internal genetic evaluation (referred to with the subscript E0) based on internal data (i.e. a set of phenotypic records: 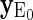 ) that provides internal information (i.e. EBV and associated REL obtained from the evaluation E0). Also, assume an ith external genetic evaluation (i = 1, 2, …, N, referred to with the subscript Ei) that is based on the ith source of external data (i.e. the ith set of phenotypic records not used by evaluation E0 and free of internal data:
) that provides internal information (i.e. EBV and associated REL obtained from the evaluation E0). Also, assume an ith external genetic evaluation (i = 1, 2, …, N, referred to with the subscript Ei) that is based on the ith source of external data (i.e. the ith set of phenotypic records not used by evaluation E0 and free of internal data: 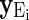 ) and that provides the ith source of external information, i.e., all available external EBV (EBVEi) and associated REL (e.g., EBV and associated REL obtained from evaluation E1 based only on external data E1, and EBV and associated REL obtained from evaluation E2 based only on external data E2). In addition to be free of internal data, it is also assumed that each ith source of external data was free of the other N-1 sources of external data. These assumptions lead to each ith source of external information to be free of internal data and information, as well as of the N-1 other external data and information.
) and that provides the ith source of external information, i.e., all available external EBV (EBVEi) and associated REL (e.g., EBV and associated REL obtained from evaluation E1 based only on external data E1, and EBV and associated REL obtained from evaluation E2 based only on external data E2). In addition to be free of internal data, it is also assumed that each ith source of external data was free of the other N-1 sources of external data. These assumptions lead to each ith source of external information to be free of internal data and information, as well as of the N-1 other external data and information.
Two groups of animals, hereafter called external and internal animals, are defined according to the ith source of external information. Therefore, for each ith source of external information, external animals (subscript Ai with i = 1, 2,…, N) are defined as animals that are associated with this ith source of external information and for which internal data and/or information is available or that have relationships with animals involved in the internal evaluation E0. All animals that are not defined as external animals for the ith source of external information are defined as internal animals (subscript 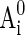 ). Internal animals are then defined as animals associated with only internal information when considering the ith source of external information. It is noted that external animals may be associated with different sources of external information and that an animal may be considered as external for the ith source of external information and internal for the N-1 other sources of external information because the definitions of external and internal animals depend only on the source of external information considered. Those definitions are summarized in Table 1. In addition, because pedigree information for animals can be easily integrated into a genetic evaluation, it is assumed that the same complete pedigree information could be used for all animals for each genetic evaluation. Concerning the notation of matrices in the following sections (e.g.,
). Internal animals are then defined as animals associated with only internal information when considering the ith source of external information. It is noted that external animals may be associated with different sources of external information and that an animal may be considered as external for the ith source of external information and internal for the N-1 other sources of external information because the definitions of external and internal animals depend only on the source of external information considered. Those definitions are summarized in Table 1. In addition, because pedigree information for animals can be easily integrated into a genetic evaluation, it is assumed that the same complete pedigree information could be used for all animals for each genetic evaluation. Concerning the notation of matrices in the following sections (e.g., 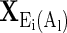 ), the subscript Ei refers to the ith source of external information and the subscript within brackets (Al) refers to the lth group of animals.
), the subscript Ei refers to the ith source of external information and the subscript within brackets (Al) refers to the lth group of animals.
Table 1.
Concepts related to the terminology of internal and external animals and information
| Data 1 | Pedigree | |
|---|---|---|
| Internal animals | External animals | |
| Internal data | Internal evaluation | Internal - external evaluations |
| Internal information2 | Internal - external information | |
| External data | - | External evaluation |
| External information | ||
1Data = set of phenotypic records; 2Information = estimated breeding values and associated reliabilities.
The N sources of external information must be integrated into the internal evaluation E0. For external animals associated with the ith source of external information, all EBVEi are summarized by the vector of external EBV, 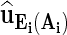 , and by the prediction error (co)variance matrix,
, and by the prediction error (co)variance matrix, 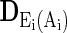 . Because
. Because 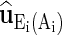 could be estimated with an equivalent external genetic evaluation that includes the internal animals in the pedigree through a genetic (co)variance matrix extended to all animals for the ith source of external information,
could be estimated with an equivalent external genetic evaluation that includes the internal animals in the pedigree through a genetic (co)variance matrix extended to all animals for the ith source of external information, 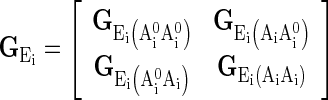 , the vector of external EBV for all internal and external animals for the ith source of external information is estimated as:
, the vector of external EBV for all internal and external animals for the ith source of external information is estimated as:
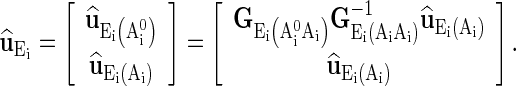 |
A modified set of multi-trait mixed model equations that integrate N sources of external information, each summarized by 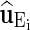 and its associated prediction error (co)variance matrix
and its associated prediction error (co)variance matrix 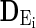 for the ith source of external information, can be written as [See Additional file 1 for the derivation of the equations]:
for the ith source of external information, can be written as [See Additional file 1 for the derivation of the equations]:
 |
1 |
where 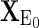 and
and 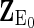 are incidence matrices relating records in
are incidence matrices relating records in 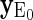 to the vector of fixed effects
to the vector of fixed effects 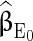 and the vector of random additive genetic effects
and the vector of random additive genetic effects 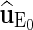 , respectively,
, respectively, 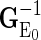 is the inverse of the internal additive genetic (co)variance matrix associated with the internal genetic evaluation E0 that includes all internal and external animals and
is the inverse of the internal additive genetic (co)variance matrix associated with the internal genetic evaluation E0 that includes all internal and external animals and 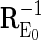 is the inverse of the residual (co)variance matrix.
is the inverse of the residual (co)variance matrix.
For the approximation of 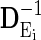 , it can be shown that [See Additional file 1]:
, it can be shown that [See Additional file 1]: 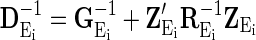 , where
, where 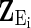 is the incidence matrix relating records of ith external data to internal and external animals and
is the incidence matrix relating records of ith external data to internal and external animals and 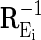 is the residual (co)variance matrix for the ith source of external information. Thereby,
is the residual (co)variance matrix for the ith source of external information. Thereby, 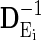 is approximated by
is approximated by 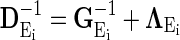 , where
, where 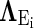 is a block diagonal variance matrix with one block per animal [12,14] and
is a block diagonal variance matrix with one block per animal [12,14] and 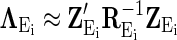 . Each diagonal block of
. Each diagonal block of 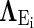 is equal to
is equal to 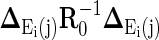 for j = 1, 2, …, J animals, where the matrix R0 is a matrix of residual (co)variance among traits and the jth matrix
for j = 1, 2, …, J animals, where the matrix R0 is a matrix of residual (co)variance among traits and the jth matrix 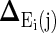 is a diagonal matrix with elements
is a diagonal matrix with elements 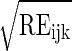 where k = 1,2,…, K traits. Element REijk is the effective number of records, i.e. record equivalents, for the jth animal for the kth trait associated with the ith source [14,15]. Record equivalents express the quantity of contributions due to relationships and/or due to records considered for the evaluation of an animal. For internal animals, REijk is equal to 0 because all contributions are only due to the relationships among external and internal animals. For external animals, if double-counting of contributions due to relationships among them is not taken into account,
where k = 1,2,…, K traits. Element REijk is the effective number of records, i.e. record equivalents, for the jth animal for the kth trait associated with the ith source [14,15]. Record equivalents express the quantity of contributions due to relationships and/or due to records considered for the evaluation of an animal. For internal animals, REijk is equal to 0 because all contributions are only due to the relationships among external and internal animals. For external animals, if double-counting of contributions due to relationships among them is not taken into account, 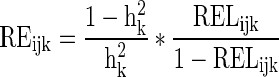 for the jth animal for the kth trait associated with the ith source, where
for the jth animal for the kth trait associated with the ith source, where 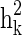 is the heritability of the kth trait [15,18]. If double-counting of contributions due to relationships among external animals is taken into account, REijk only expresses the amount of contributions due to records and can be estimated through a two-step algorithm (TSA) [14]. The first step of this TSA determines external animals associated with external information that includes only contributions due to relationships. The second step estimates the amount of contributions due to records (expressed as RE) for external animals associated with information that combines both contributions due to relationships and own records. Note that the proposed approximation of
is the heritability of the kth trait [15,18]. If double-counting of contributions due to relationships among external animals is taken into account, REijk only expresses the amount of contributions due to records and can be estimated through a two-step algorithm (TSA) [14]. The first step of this TSA determines external animals associated with external information that includes only contributions due to relationships. The second step estimates the amount of contributions due to records (expressed as RE) for external animals associated with information that combines both contributions due to relationships and own records. Note that the proposed approximation of 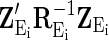 differs from the approximation proposed by Quaas and Zhang [12]. Indeed, they proposed to approximate each diagonal block of
differs from the approximation proposed by Quaas and Zhang [12]. Indeed, they proposed to approximate each diagonal block of 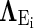 by
by 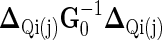 , where the matrix G0 is a matrix of genetic (co)variance among traits and ΔQi(j) is a diagonal matrix with elements:
, where the matrix G0 is a matrix of genetic (co)variance among traits and ΔQi(j) is a diagonal matrix with elements:
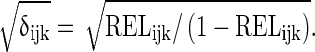 |
Also, the multi-trait MME (1) that integrate N sources of external information differ from the usual multi-trait MME only by the terms 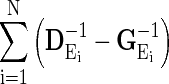 and
and 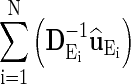 :
:
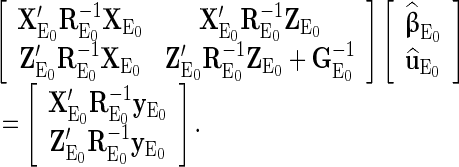 |
2 |
Furthermore, it was previously assumed that the whole pedigree is available for all genetic evaluations. The additive genetic (co)variance matrices that include all internal and external animals are then equal for all genetic evaluations (i.e., 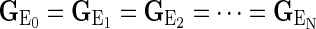 ). Nevertheless, each internal or external genetic evaluation could be performed as a single-step genomic evaluation (e.g., [3,4]) without modifications to the Bayesian derivation [See Additional file 1] because assumptions on the different matrices
). Nevertheless, each internal or external genetic evaluation could be performed as a single-step genomic evaluation (e.g., [3,4]) without modifications to the Bayesian derivation [See Additional file 1] because assumptions on the different matrices 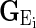 were not limiting. Such cases would lead to
were not limiting. Such cases would lead to 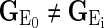 . For example, integration of external information provided by the usual MME into a single-step genomic evaluation would lead to
. For example, integration of external information provided by the usual MME into a single-step genomic evaluation would lead to 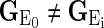 because
because 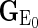 would include genomic information [3,4], unlike
would include genomic information [3,4], unlike 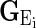 .
.
Integration of several sources of external information by avoiding double-counting of contributions due to records
Assumptions stated in the previous section led to each source of external information to be obtained from an external evaluation that was based only on external data and free of internal data and information, as well as of the N-1 other external data and information. In practice, this assumption is not necessarily valid because a source of external information may be obtained from an external evaluation based on external data and/or information and also on internal data and/or information (e.g., EBV and associated REL obtained in country E1 based on external data E1 and on internal data E0). Thus, double-counting of contributions due to records between internal and external information must be taken into account, as detailed below.
For the ith source of external information, internal information included into external information (subscript Ii) associated with the external animals can be summarized as 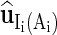 , i.e. the vector of internal EBV associated with external animals for which external information included both external and internal information, and by
, i.e. the vector of internal EBV associated with external animals for which external information included both external and internal information, and by 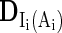 , the prediction error (co)variance matrix associated with
, the prediction error (co)variance matrix associated with 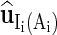 .
.
A modified set of multi-trait mixed model equations that integrate several sources of external information and take double-counting of contributions due to records between external and internal information into account, can be written as follows [See Additional file 2]:
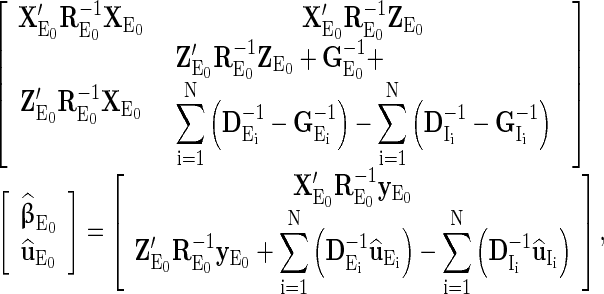 |
3 |
where 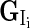 is a genetic (co)variance matrix for all animals for the internal information included into the ith source of external information,
is a genetic (co)variance matrix for all animals for the internal information included into the ith source of external information, 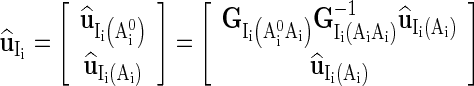 is the vector of internal EBV associated with the ith source of external information that includes internal information and
is the vector of internal EBV associated with the ith source of external information that includes internal information and 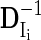 is the inverse of the prediciton error (co)variance matrix associated with
is the inverse of the prediciton error (co)variance matrix associated with 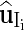 and approximated as detailed in the previous section.
and approximated as detailed in the previous section.
If the ith source of external information does not include internal information for external animals, the vector 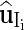 is undetermined and the matrix
is undetermined and the matrix 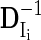 is equal to
is equal to 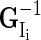 . This leads to the system of equations (1).
. This leads to the system of equations (1).
Blending several sources of external information by avoiding double-counting of contributions due to records
Equations to blend several sources of external information by avoiding double-counting of contributions due to records among internal and external data/information can be derived from the system of equations (3) by assuming that 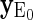 has no records (i.e. that
has no records (i.e. that 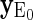 is an empty vector). Then, the equation can be written as follows:
is an empty vector). Then, the equation can be written as follows:
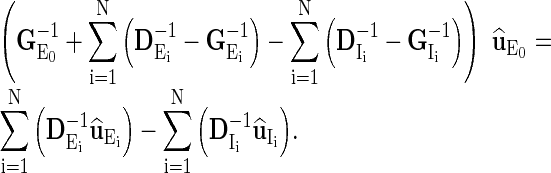 |
4 |
Simulated example
The system of equations (3) was tested using data simulated with the software package GNU Octave [19]. The context of the simulation was a country that imports sires from another country to generate the next generation of production animals and potential sires. Populations of the importing country (hereafter called the internal population) and of the exporting country (hereafter called the external population) were assumed to belong to the same breed. Each population included about 1000 animals distributed over five generations and was simulated from 120 female and 30 male founders. For both populations, milk yield in the first lactation was simulated for each female with progeny, following Van Vleck [20]. A herd effect nested within-population was randomly assigned to each phenotypic record. To obtain enough observations per level for the herd effect, each herd included at least 40 females. Phenotypic variance and heritability were assumed to be 3.24*106 kg2 and 0.25, respectively.
To simulate the internal and external populations, the following rules were applied to generate each new generation. First, from the second generation, both females and males older than one year old were considered as mature for breeding and a male could be mated during at most two breeding years. Second, 95% of the available females and 75% of the available males with the highest true breeding values were selected for breeding. Third, all selected females were randomly mated with the selected males. The maximum number of males mated to produce the next generation was set to 25. Furthermore, a mating could be performed only if the additive relationship coefficient between male and female was less than 0.5 and if the female had less than three progeny.
The external population was simulated first and additional rules were applied to this population. For this population, males that were selected for mating only originated from the external population and 60% of the external male offspring with the lowest true breeding values were culled in each generation. Then, the internal population was simulated. For this population, males were selected among all available internal males and a subset of selected external sires. This subset of external sires included the first 50 sires with the highest true breeding values in the external population. Also, 99% of internal male offspring with the lowest true breeding values were culled in each generation. No female offspring was culled in either population.
Using the simulated data, three genetic evaluations were performed (Table 2):
A joint evaluation (EVALJ) was performed as a BLUP evaluation using the system of equations (2) and based on external and internal pedigree and data. This evaluation was assumed to be the reference.
An internal evaluation (EVALI) was performed as a BLUP evaluation using the system of equations (2) and based on internal pedigree and data.
An external evaluation (EVALE) was performed as a BLUP evaluation using the system of equations (2) and based on external pedigree and data.
Table 2.
Genetic evaluations performed for the simulated example
| Genetic evaluations 1 | ||||||
|---|---|---|---|---|---|---|
| J | E | I | BE | BJ | BJ-I | |
| External pedigree | X | X | ||||
| Internal pedigree | X | X | X | X | X | |
| External data | X | X | ||||
| Internal data | X | X | X | X | X | |
| Integrated information (50 external sires) | ||||||
| External EBV and REL | X | |||||
| Joint EBV and REL | X | X | ||||
| Internal EBV and REL | X | |||||
1J = Joint; E = External; I = Internal; BE = Bayesian External; BJ = Bayesian Joint; BJ-I = Bayesian Joint minus Internal.
Three Bayesian evaluations that integrated information provided by EVALE or by EVALJ for the 50 external sires into EVALI were also performed. Because the external sires were related, double-counting of contributions due to relationships existed and this was taken into account for the three Bayesian evaluations through the TSA [14]. Double-counting of contributions due to records could also exist with the integration of information provided by EVALJ into EVALI because EVALJ and EVALI were partially based on the same data (i.e., internal data). The following three Bayesian evaluations were performed:
-
(d)
A Bayesian evaluation using the system of equations (1) and using EBV and PEV obtained from EVALE associated with the 50 external sires that were used inside the internal population as external information (EVALBE).
-
(e)
A Bayesian evaluation using the system of equations (1) and EBV and PEV obtained from EVALJ associated with the 50 external sires as external information (hereafter called joint information) (EVALBJ). Although EVALJ was based on external and internal data, double-counting of contributions due to records between joint and internal information was not taken into account.
-
(f)
A Bayesian evaluation integrating joint information by using the system of equations (3) and taking into account double-counting of contributions due records among internal and joint information (EVALBJ-I). Double-counting of contributions due to records among internal and joint information was taken into account by using EBV and PEV obtained from EVALI associated with the 50 external sires.
The simulation was replicated 100 times. Comparisons between EVALJ and EVALI, EVALBE, EVALBJ, or EVALBJ-I were performed separately for the 50 external sires and for the internal animals. Comparisons were based on:
Spearman’s rank correlation coefficients (r) of EBV obtained from EVALJ (EBVJ) with EBV obtained from EVALI (EBVI), EVALBE (EBVBE), EVALBJ (EBVBJ), and EVALBJ-I (EBVBJ-I),
regression coefficients (a) of EBVJ on EBVI, EBVBE, EBVBJ, and EBVBJ-I, and
coefficients of determination (R2) associated with the regressions,
the total amount of RE (REtot) associated with external information, joint information and joint information corrected for the included internal information, and
mean squared errors (MSE) of EBVI, EBVBE, EBVBJ, and EBVBJ-I, expressed as a percentage of MSE obtained for EBVI. For each replicate, the MSE obtained for EBVI was reported to a relative value of 100 before the different computations of MSE.
Because the TSA was applied before all three Bayesian evaluations, REtot were free of contributions due to relationships estimated by the Bayesian evaluations. For an easier understanding of the results and discussion, RE can be transformed into daughter equivalents (DE) through 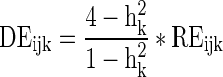 [18]. All results were the average of the 100 replicates.
[18]. All results were the average of the 100 replicates.
Walloon example
Even if MACE allows the aggregation of EBV for dairy sires, internal genetic evaluations for animals not associated with MACE information (e.g., cows, calves, young sires) are not influenced by external information considered by the MACE for dairy sires and may be still biased. Therefore, integration of MACE information into internal evaluations, as well as blending of MACE and internal information, could benefit those animals. The performance of equation (4) that blends MACE and internal information was evaluated in the context of the official Walloon genetic evaluation for Holstein cattle.
The Walloon example used information for milk, fat and protein yields for Holstein cattle provided by the official Walloon genetic evaluation [21,22]. The genetic variances were those used for the official Walloon genetic evaluation [21] and were equal to 280 425 kg2 for milk yield, to 522.6 kg2 for fat yield and to 261.5 kg2 for protein yield. The respective heritabilities were equal to 0.38, 0.43 and 0.41. The pedigree file was extracted from the database used for the official Walloon genetic evaluation (EVALW) and covered up to six known ancestral generations. The extraction was performed for a randomly selected group of 1909 animals (potentially genotyped) born after 1998. The selected group included sires, cows and calves that were used or were not at the internal level. After extraction, the pedigree file contained 16 234 animals.
Internal information included EBV and associated REL estimated from data provided by the Walloon Breeding Association (EBVW, RELW) for the EVALW for milk production of April 2013 [21,22]. A total of 12 046 animals were associated with an available EBVW. External information included EBV and REL for 1981 sires provided with the official release for the April 2013 MACE performed by Interbull (EVALMACE, EBVMACE, RELMACE) [23]. It should be noted that the Walloon region in Belgium participated in the April 2013 MACE. Internal and external information were harmonized between the Walloon and MACE evaluations by adjusting scales and mean differences towards the original expression of the trait in the Walloon genetic evaluations. External information was then considered to be the same trait as the internal phenotype trait.
Unlike the simulated example, no joint evaluation based on Walloon and external records was available for both external and internal animals. Because EVALMACE aggregated EBV from several national genetic evaluations for sires, it was considered as the reference for the evaluated sires. Walloon and MACE information were blended by using equation (4) for the following four cases: with or without consideration of double-counting of contributions due to relationships and with or without consideration of double-counting of contributions due to records (Table 3). Double-counting of contributions due to relationships was possible because all animals associated with Walloon and/or MACE information were related. Double-counting of contributions due to records was also possible because MACE information associated with the 1981 sires included contributions provided by EVALW. Thus, to test the importance of both double-counting issues, the following four cases were evaluated:
Walloon and MACE information were blended without considering double-counting of contributions due to records and due to relationships (EVALBLNN, EBVBLNN, RELBLNN).
Walloon and MACE information were blended by considering only double-counting of contributions due to records (EVALBLRE, EBVBLRE, RELBLRE). To achieve this goal, the contribution of Walloon information into MACE information was determined based on the domestic effective daughter equivalents (EDC) associated with EBVMACE and RELMACE and provided with the official release for the 2013 April MACE by Interbull. MACE information free of Walloon information was reported by a domestic EDC equal to 0. A total of 601 sires were associated with an EDC greater than 0. For these 601 sires, EBV and associated REL estimated from Walloon data and contributing to the April 2013 MACE routine-run (EBVWc, RELWc) were considered by EVALBLRE to take double-counting of contributions due to records into account. Double-counting of contributions due to relationships was not taken into account for either Walloon or MACE information.
Walloon and MACE information were blended by only considering double-counting of contributions due to relationships among all animals (EVALBLR, EBVBLR, RELBLR). The TSA was therefore applied for Walloon and MACE information. Double-counting of contributions due to records was not considered.
Walloon and MACE information were blended by considering both double-counting of contributions due to records and due to relationships (EVALBL, EBVBL, RELBL). Reliabilities for EBVBLNN, EBVBLRE, EBVBLR and EBVBL were computed using the equation
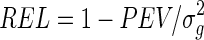 , where
, where 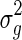 is the genetic variance for the corresponding trait and PEV is the prediction error variance obtained from the diagonal element of the inverted left-hand-side of the equation (4).
is the genetic variance for the corresponding trait and PEV is the prediction error variance obtained from the diagonal element of the inverted left-hand-side of the equation (4).
Table 3.
Bayesian evaluations performed for the Walloon example
| Bayesian evaluations | ||||
|---|---|---|---|---|
| BLNN | BLRE | BLR | BL | |
| Available estimated breeding values and reliabilities | ||||
| Official Walloon evaluation | X | X | X | X |
| Multiple Across Country Evaluation | X | X | X | X |
| Double-counting accounted | ||||
| Records | X | X | ||
| Relationships | X | X | ||
As explained previously, EVALMACE was considered as the reference for sires evaluated through EVALMACE. Comparisons between EVALMACE and EVALW, EVALBLNN, EVALBLRE, EVALBLR or EVALBL were performed based on:
Spearman’s rank correlation coefficients (r) of EBVMACE with EBVW, EBVBLNN, EBVBLRE, EBVBLR and EBVBL,
MSE of EBVW, EBVBLNN, EBVBLRE, EBVBLR, and EVALBL (i.e. mean squared errors expressed as a percentage of average MSE of EBVW),
regression coefficients (a) and,
R2 of the regressions of EVALMACE on the five other evaluations (i.e., EVALW, EVALBLNN, EVALBLRE, EVALBLR and EVALBL),
REtot and (6) average REL.
Comparisons concerned two groups of sires. A first group of sires included 1212 sires that were associated with both Walloon and MACE information and had daughters with records in the Walloon region dataset (hereafter called “internally used sires”). A second group of sires included 631 sires that were associated with both Walloon and MACE information but had no daughters with records in the Walloon region dataset (i.e. they had only foreign, or external, daughters; hereafter called “internally unused sires”). The REtot were free of contributions due to relationships that were estimated by the Bayesian evaluations but could include contributions due to relationships that resulted from the previous genetic evaluation if the TSA was not applied.
The effect of blending MACE and Walloon information was also studied for internal animals that were not associated with MACE information and that were sired by internally used sires by considering (1) r between EVALBL and EVALW, EVALBLNN, EVALBLRE or EVALBLR, (2) REtot and (3) average REL. Three groups of internal animals were defined depending on their RELW. The first group included internal animals that were associated with a RELW lower than 0.50, the second group included internal animals that were associated with a RELW between 0.50 and 0.75, and the third group included internal animals with a RELW equal or higher than 0.75.
All blending evaluations were performed using a version of the BLUPF90 program [24] modified to implement the equations (1), (3) and (4).
Results and discussion
Simulated example
On average, each of the 100 simulated internal and external populations included 1048 animals. Results for r, MSE, a and R2 for prediction of EBVJ are in Table 4 for the 50 external sires and for the internal animals.
Table 4.
Average (SD in parentheses) of parameters obtained for the simulated example over 100 replicates
| Concerned animals 1 | Genetic evaluation 2 | r 2 | MSE 3 | a 4 | R 2 4 | RE tot 5 |
|---|---|---|---|---|---|---|
| Internal animals | ||||||
| EVALI | 0.934 (0.021) | 100.00 (28.621) | 0.982 (0.042) | 0.896 (0.030) | - | |
| EVALBE | >0.999 (0.000) | 0.61 (0.58) | 0.997 (0.005) | 0.999 (0.001) | - | |
| EVALBJ | 0.979 (0.005) | 34.26 (7.92) | 0.977 (0.024) | 0.965 (0.008) | - | |
| EVALBJ-I | 0.996 (0.001) | 6.78 (3.02) | 1.021 (0.013) | 0.993 (0.002) | - | |
| External sires | ||||||
| EVALI | 0.571 (0.131) | 100.00 (32.31) | 0.712 (0.168) | 0.391 (0.146) | - | |
| EVALBE | 0.997 (0.001) | 0.35 (0.22) | 1.000 (0.011) | 0.998 (0.002) | 76.3 (5.1) | |
| EVALBJ | 0.956 (0.017) | 17.16 (4.18) | 0.821 (0.039) | 0.924 (0.030) | 141.5 (7.8) | |
| EVALBJ-I | 0.996 (0.002) | 0.60 (0.26) | 0.993 (0.012) | 0.996 (0.002) | 78.7 (5.1) |
1Internal animals = animals associated with only internal information; External sires: sires associated with external information; 2EVALI = BLUP evaluation based on internal pedigree and data; EVALBE = Bayesian evaluation using external EBV and PEV associated with the 50 external sires used in the internal population; EVALBJ = Bayesian evaluation using EBV and PEV obtained from the joint evaluation and associated with the 50 external sires; EVALBJ-I = Bayesian evaluation using EBV and PEV obtained from the joint and from internal evaluations and associated with the 50 external sires to avoid double-counting among internal and joint information; r2 = rank correlations between EBV estimated by EVALJ and by EVALI, EVALBE, EVALBJ or EVALBJ-I; 3MSE = mean squared errors expressed as a percentage of the average internal MSE between a joint evaluation and EVALI, EVALBE, EVALBJ or EVALBJ-I; 4a = regression coefficient and R2 = coefficient of determination of the regression of EBV estimated by the joint evaluation on EBV estimated by EVALI, EVALBE, EVALBJ or EVALBJ-I; 5REtot = total amount of record equivalents free of contributions due to relationships among external animals.
Compared to the rankings of EVALI, integration of external or joint information for the 50 external sires led to rankings of EVALBE, EVALBJ or EVALBJ-I that were more similar to those of EVALJ. Rank correlations r increased from 0.57 for EVALI to at least 0.95 for EVALBJ for the 50 external sires and from 0.93 for EVALI to at least 0.98 for EVALBJ for internal animals (Table 4). Furthermore, MSE, a and R2 also showed that the integration of external or joint information for the 50 external animals with EVALBE, EVALBJ or EVALBJ-I led to better predictions of EBVJ for both external and internal animals (Table 4). Therefore, the observations that internals animals related to the 50 external sires were also better predicted by EVALBE, EVALBJ and EVALBJ-I, compared to EVALI, revealed that the external information propagated from the 50 external sires to relatives.
The REtot associated with EVALBE was equal to 76.3 (which also corresponded to 381.6 DE), while the REtot associated with EVALBJ was equal to 141.5 (DE = 707.7, Table 4). The higher REtot associated with EVALBJ showed that double-counting of contributions due to records was present when joint information was integrated. Indeed, joint information contained both external and internal information. The REtot associated with EVALBJ-I was equal to 78.7 (DE = 393.3, Table 4). While this latter REtot is slightly higher (i.e. 3.1% on average) than the REtot associated with EVALBE, it showed that double-counting was almost avoided when internal information was considered for the 50 external sires. A total of 96.4% of contributions due to records of internal information on average was removed from the joint information (Table 4). The remaining 3.6% of contributions due to records of internal information was double-counted by the Bayesian evaluations and may result from the estimation of contributions due to relationships and/or from the estimation of contributions due to records among joint and internal information.
Because double-counting of contributions due to records between joint and internal information was almost avoided, breeding values that were estimated by EVALBJ-I for all animals led to better predictions of EBVJ than EVALBJ, based on r, MSE, a and R2 (Table 4). Rank correlations of EBVJ with EBVBJ and EBVBJ-I increased from 0.979 for EVALBJ to 0.996 for EVALBJ-I for the internal animals and from 0.956 for EVALBJ to 0.996 for EVALBJ-I for the 50 external animals. The MSE decreased on average from 34.3% for EVALBJ to 6.8% for EVALBJ-I for the internal animals and from 17.2% for EVALBJ to 0.6% for EVALBJ-I for the external animals. These results again showed that integration of external/joint information for the 50 external sires influenced the prediction of internal relatives through the propagation of information from the external sires to relatives. These results show that the double-counting of contributions due to records also affected predictions of internal animals. Furthermore, as expected, EVALBE predicted EBVJ slightly better than EVALBJ-I for both external sires and internal animals, based on the corresponding r, MSE, a and R2 (Table 4). The low difference in accuracy of prediction between EVALBE and EVALBJ-I could be attributed to the estimation of contributions due to relationships and due to records.
Based on these results, double-counting of contributions due to records was almost avoided. Thus, the integration of information into a genetic evaluation by avoiding both contributions due to relationships and due to records performed well for external animals. Internal animals also benefited of the integration of information thanks to their relationships with external animals.
Walloon example
Of the 12 046 animals associated with available Walloon information for the three traits, 6232 animals for milk yield, 6209 animals for fat yield, and 6212 animals for protein yield were associated with information that was based only on contributions due to relationships, as estimated by the TSA. In terms of RE, contributions due to relationships represented from 14.9% for fat yield to 16.3% for milk yield of the contributions associated with Walloon information (Figure 1). Among the 1981 sires associated with MACE information, two sires were associated with information that includes only contributions due to relationships for the three traits. Both these sires had several sons among all the sires associated with an EBVMACE, which explains that the contributions were considered as only due to relationships. In terms of RE, all contributions due to relationships represented on average 5.1% of the contributions associated with MACE information for the three traits. Of the 601 sires with an EBVWc, all sires were associated with information that included both contributions due to relationships and due to records. This latter observation for the 601 sires was expected because these 601 sires must have at least 10 daughters with records within 10 herds in the Walloon region to participate in the MACE evaluation.
Figure 1.
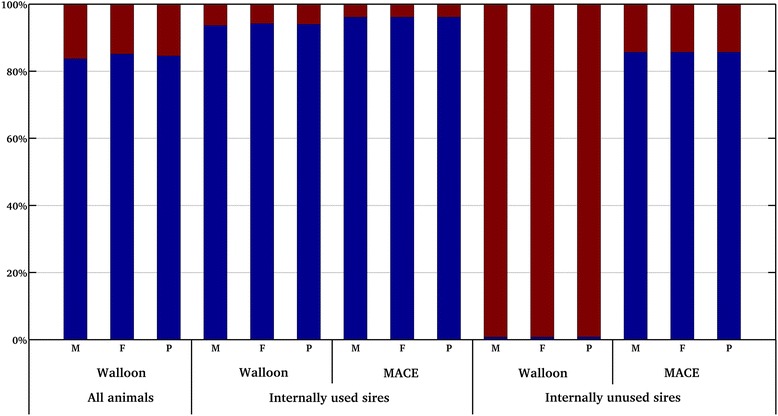
Percentage of contributions due to records and due to relationships for the Walloon example. Percentage of contributions due to records (blue squares) and due to relationships (red squares) associated with Walloon information for all animals, internally used and unused sires and associated with MACE information for internally used and unused sires for milk (M), fat yield (F) and protein (P) yields.
Internally used sires
Of the internally used sires, 1212 had Walloon and MACE information and had both internal and external daughters with records. On average, each sire had 143.1 internal daughters with records. The average RELW ranged from 0.74 to 0.76 (Table 5) and the average RELMACE was equal to 0.88 for the three traits. Results for r, MSE, a and R2 for prediction of EBVMACE by EVALBL are in Table 6 for the 1212 sires for milk, fat and protein yields. For the three traits, blending of Walloon and MACE information by taking double-counting of contributions due to records and due to relationships into account (i.e. EVALBL) led to a ranking that was more similar to the MACE ranking than to the internal ranking (i.e. EVALW), although these internally used sires sired a large number of cows with records in the Walloon region. Rank correlations increased by 0.104 points for milk yield to 0.125 points for fat yield to achieve a rank correlation between EBVMACE and EBVBL that ranged from 0.987 to 0.990 (Table 6). The MSE, a and R2 showed that accuracy of predictions of EBVMACE by EBVW or by EBVBL increased when external information was integrated. Integration of MACE information also increased the average REL by 0.14 points for fat yield to 0.16 points for milk yield (Table 5). This increase of average REL corresponded to an increase of 57.5, 51.4, and 50.9 DE per sire on average for milk, fat and protein yields, respectively. Also, the average RELBL for the 1212 sires was 0.02 points higher than the average RELMACE (Table 6). This difference in average REL, as well as the differences between EBVMACE and EBVBL based on MSE, a and R2 (Table 6), can be explained by the fact that MACE did not include all information available for animals in the Walloon region. Indeed, EBVW of a sire was included into MACE if it had at least10 daughters with records within 10 herds at the internal level. Therefore, EBVW for sires that did not fulfill this requirement were not considered by MACE, but were taken into account by the four Bayesian evaluations, which provided additional information compared to MACE information. Approximations based on estimation of contributions due to relationships and theoretical assumptions of the model may also explain some of the differences between EBVMACE and EBVBL. For example, MACE was considered as a national genetic evaluation. These results indicate that EVALBL, i.e. a Bayesian evaluation that blended internal information and external information and avoided most double-counting of contributions due to records and due to relationships, was successful in integrating MACE information for internally used sires.
Table 5.
Average reliabilities (REL; SD in parentheses) associated with Walloon estimated breeding values for internally used and unused sires
| Considered animals | Milk yield | Fat yield | Protein yield |
|---|---|---|---|
| Internally used sires | 0.74 (0.22) | 0.76 (0.21) | 0.75 (0.22) |
| Internally unused sires | 0.22 (0.10) | 0.23 (0.10) | 0.22 (0.10) |
Table 6.
Parameters obtained for the Walloon example for 1212 internally used sires
| Genetic evaluations | Milk yield | |||||
|---|---|---|---|---|---|---|
| r 1 | MSE 2 | a 3 | R 2 3 | RE tot 4 | REL 5 | |
| EVALW | 0.886 | 100.00 | 0.87 (0.013) | 0.78 | 21 934.6 | 0.74 (0.22) |
| EVALBLNN | 0.987 | 11.68 | 0.993 (0.005) | 0.97 | 55 038.2 | 0.92 (0.05) |
| EVALBLRE | 0.989 | 10.01 | 0.984 (0.004) | 0.98 | 37 487.1 | 0.91 (0.05) |
| EVALBLR | 0.988 | 10.57 | 1.004 (0.004) | 0.98 | 52 313.0 | 0.91 (0.06) |
| EVALBL | 0.990 | 8.87 | 0.995 (0.004) | 0.98 | 34 141.2 | 0.90 (0.06) |
| Fat yield | ||||||
| r 1 | MSE 2 | a 3 | R 2 3 | RE tot 4 | REL 5 | |
| EVALW | 0.862 | 100.00 | 0.815 (0.014) | 0.74 | 20 016.8 | 0.76 (0.22) |
| EVALBLNN | 0.983 | 12.22 | 0.989 (0.005) | 0.97 | 46 144.6 | 0.92 (0.05) |
| EVALBLRE | 0.985 | 10.69 | 0.977 (0.005) | 0.97 | 32 320.9 | 0.92 (0.05) |
| EVALBLR | 0.985 | 11.12 | 1.004 (0.005) | 0.97 | 43 943.6 | 0.91 (0.06) |
| EVALBL | 0.987 | 9.54 | 0.991 (0.005) | 0.97 | 29 631.1 | 0.90 (0.06) |
| Protein yield | ||||||
| r 1 | MSE 2 | a 3 | R 2 3 | RE tot 4 | REL 5 | |
| EVALW | 0.882 | 100.00 | 0.851 (0.013) | 0.79 | 20 851.6 | 0.75 (0.22) |
| EVALBLNN | 0.985 | 12.38 | 0.985 (0.005) | 0.97 | 49 589.7 | 0.92 (0.05) |
| EVALBLRE | 0.987 | 10.79 | 0.975 (0.004) | 0.98 | 34 372.9 | 0.91 (0.05) |
| EVALBLR | 0.986 | 11.26 | 0.996 (0.005) | 0.98 | 47 189.5 | 0.91 (0.06) |
| EVALBL | 0.988 | 9.56 | 0.986 (0.004) | 0.98 | 31 434.7 | 0.90 (0.06) |
1r = rank correlation between EVALMACE and EVALW, EVALBLNN, EVALBLRE, EVALBLR or EVALBL; 2MSE = mean squared error expressed as a percentage of the average internal mean squared error; 3a = regression coefficient (SE in parentheses) and R2 = coefficient of determination of the regression of MACE EBV on EBV estimated by EVALW, EVALBLNN, EVALBLRE, EVALBLR or EVALBL; 4REtot = total amount of record equivalents; 5REL = average reliability (SD in parentheses).
Double-counting of contributions due to records and due to relationships were also not considered (i.e. EVALBLNN) or were considered separately (i.e. EVALBLRE and EVALBLR) to study their influences on prediction of EVALMACE for internally used sires. Parameters r, a and R2 associated with EVALBLNN, EVALBLRE and EVALBLR for the 1212 sires were similar to the r, a and R2 of EVALBL, although a slight advantage was observed for EVALBL. Therefore, the four blending evaluations led to similar rankings as MACE for the 1212 internally used sires (i.e., rank correlations equal to 0.99 on average; Table 6).
However, double-counting can be observed based on MSE, REtot and REL (Table 6). With regard to double-counting of contributions due to relationships for the 1212 internally used sires, RE that were free of contributions due to relationships (i.e. RE that included only contributions due to records) for EBVMACE were equal to 30 378 (DE = 176 578) for milk yield, 23 927 (DE = 150 772) for fat yield, and 26 338 (DE = 160 416) for protein yield. These amounts of RE free of contributions due to relationships represented 96.1% of the RE that contributed to MACE information. Considering the Walloon information for the 1212 sires, RE that included only contributions due to records represented from 93.6% of all Walloon contributions for milk yield to 94.2% for fat yield. For both Walloon and MACE information associated with the internally used sires and for the three traits (i.e. for milk, fat and protein yields), less than 6.4% of all contributions were attributed to relationships (Figure 1). Such low percentages of contributions due to relationships are in agreement with selection index theory [25]. While double-counting of contributions due to relationships was present for EVALBLRE (i.e. the blending evaluation that considered only double-counting of contributions due to records), the contributions due to relationships were small and their double-counting had little effect on the prediction of EBVMACE for the internally used sires, compared to EVALBL, based on parameters r and MSE. However, as expected, an average increase of 1% in RELBLRE was observed, compared to RELBL. Thus, the RELBLRE were, on average, slightly overestimated.
With regard to double-counting of contributions due to records, based on RE, Walloon information represented from 64.3% of the total information free of contributions due to relationships associated with EVALBL for milk yield to 67.6% for fat yield (Table 6). Thus, integrated information free of contributions due to relationships and due to records (i.e. MACE information from which Walloon information was subtracted) represented 32.5% of the total information associated with EVALBL for fat yield to 35.8% for milk yield. If double-counting of contributions due to relationships was considered only, REtot associated with EVALBLR ranged from 43 944 RE for fat yield to 52 313 RE for milk yield, while REtot associated with EVALBL ranged from 29 631 RE for fat yield to 34 141 RE for milk yield. Thus, between 14 313 and 18 172 RE were considered twice by EVALBLR. However, double-counting of contributions due to records affected the prediction of EBVMACE for internally used sires only slightly according to all parameters evaluated (Table 5). The RELBLR were overestimated by 1% on average for the internally used sires, compared to RELBL. Furthermore, no preference was observed between EVALBLRE and EVALBLR based on r, MSE, a and R2 for the three traits. Indeed, r and R2 were similar for these two evaluations, while EVALBLRE was more reliable based on MSE, but parameter a indicated that EVALBLR was more reliable. However, EVALBLRE had the greatest under- and overestimation of true breeding values based on parameter a. Based on these results, it can be stated that double-counting of contributions due to relationships and due to records had little effect on EBV for internally used sires.
Internally unused sires
Of the internally unused sires (i.e. that had only external daughters with records), 631 sires were associated with Walloon and MACE information. Their average RELW ranged from 0.22 to 0.23 for the three traits (Table 7) and the average RELMACE was equal to 0.77. Because they had only external daughters, Walloon contributions only included contributions due to relationships and no contributions due to records. Based on REtot (Table 7), Walloon contributions due to records for all 631 sires were in general well estimated by the TSA, ranging from 0.79% of the Walloon total contributions for milk yield to 0.80% for protein yield (Figure 1). The small non-zero percentage could be attributed to approximations involved in estimating the contributions due to relationships and due to records by the TSA, such as the consideration of an unknown fixed effect [14]. The nearly correct estimation of contributions due to relationships led to similar average RELMACE and average RELBL for the three traits (Table 7). Integration of MACE information also increased the average RELW by at least 0.54 points, resulting in an average RELBL equal to 0.77 for the three traits. These results for the 631 internally unused sires confirmed that MACE information already contained the main contributions due to relationships that were expressed in the Walloon information and that double-counting of contributions due to relationships was mostly avoided. Not considering contributions due to relationships (i.e. EVALBLNN and EVALBLRE) led to overestimation of average REL by at least 3% (Table 7).
Table 7.
Parameters obtained for the Walloon example for 631 internally unused sires
| Genetic evaluations | Milk yield | |||||
|---|---|---|---|---|---|---|
| r 1 | MSE 2 | a 3 | R 2 3 | RE tot 4 | REL 5 | |
| EVALW | 0.725 | 100.00 | 0.667 (0.024) | 0.56 | 2.5 | 0.22 (0.10) |
| EVALBLNN | 0.994 | 3.09 | 0.953 (0.004) | 0.99 | 4021.7 | 0.81 (0.05) |
| EVALBLRE | 0.994 | 3.06 | 0.952 (0.004) | 0.99 | 4021.7 | 0.81 (0.05) |
| EVALBLR | 0.994 | 2.68 | 0.978 (0.004) | 0.99 | 3172.9 | 0.77 (0.06) |
| EVALBL | 0.994 | 2.68 | 0.977 (0.004) | 0.99 | 3172.9 | 0.77 (0.06) |
| Fat yield | ||||||
| r 1 | MSE 2 | a 3 | R 2 3 | RE tot 4 | REL 5 | |
| EVALW | 0.571 | 100.00 | 0.506 (0.024) | 0.40 | 2.0 | 0.23 (0.10) |
| EVALBLNN | 0.992 | 2.28 | 0.95 (0.005) | 0.99 | 3172.5 | 0.81 (0.05) |
| EVALBLRE | 0.992 | 2.28 | 0.949 (0.005) | 0.99 | 3172.5 | 0.81 (0.05) |
| EVALBLR | 0.992 | 2.09 | 0.987 (0.005) | 0.99 | 2499.1 | 0.77 (0.06) |
| EVALBL | 0.992 | 2.08 | 0.986 (0.005) | 0.99 | 2499.1 | 0.77 (0.06) |
| Protein yield | ||||||
| r 1 | MSE 2 | a 3 | R 2 3 | RE tot 4 | REL 5 | |
| EVALW | 0.717 | 100.00 | 0.684 (0.025) | 0.54 | 2.3 | 0.22 (0.10) |
| EVALBLNN | 0.993 | 2.96 | 0.952 (0.004) | 0.99 | 3490.3 | 0.81 (0.05) |
| EVALBLRE | 0.993 | 2.95 | 0.951 (0.004) | 0.99 | 3490.3 | 0.81 (0.05) |
| EVALBLR | 0.993 | 2.75 | 0.978 (0.005) | 0.99 | 2751.0 | 0.78 (0.06) |
| EVALBL | 0.993 | 2.75 | 0.977 (0.005) | 0.99 | 2751.0 | 0.77 (0.06) |
1r = rank correlation between EVALMACE and EVALW, EVALBLNN, EVALBLRE, EVALBLR or EVALBL; 2MSE = mean squared error expressed as a percentage of the average internal mean squared error; 3a = regression coefficient (SE in parentheses) and R2 = coefficient of determination of the regression of MACE EBV on EBV estimated by EVALW, EVALBLNN, EVALBLRE, EVALBLR or EVALBL; 4REtot = total amount of record equivalents; 5REL = average reliability (SD in parentheses).
Results for r, MSE, a and R2 for the prediction of EBVMACE by the four blending evaluations are in Table 7 for the 631 internally unused sires for the three traits. Blending of Walloon and MACE information led to similar rankings of the 631 sires for the four blending evaluations. Rank correlations between EBVMACE and EBV for the four blending evaluations increased from 0.73 to 0.99 for milk yield, from 0.57 to 0.99 for fat yield and from 0.72 to 0.99 for protein yield. These rank correlations indicated that the blending method was also successful for sires with only external information for all three traits. These results were confirmed by a decrease of MSE by at least 96.9% and by regression coefficients close to 1.0, with an R2 equal to 0.99 for all three traits (Table 7). Because double-counting can be only attributed to contributions due to relationships for the 631 internally unused sires, EVALBLNN and EVALBLRE led to similar parameters. This was also observed for EVALBL and EVALBLR (Table 7). Differences between these two groups of evaluations were only observed based on MSE and a (Table 7). These two parameters showed that EBVMACE for the 631 sires were slightly better predicted when contributions due to relationships were considered. However, all these results showed that contributions due to relationships had little effect on the prediction of EBVMACE.
VanRaden and Tooker [17] found similar correlations between EBVMACE and combined EBV for sires with only external daughters (i.e. between 0.991 and 0.994 for yield traits). Their strategy consisted of computing external deregressed proofs (DRP) from EBVMACE and including one extra record based on these DRP, weighted by the associated DE for the sire. Internal contributions in MACE information for sires with internal and external daughters were considered by subtracting the number of internal DE from the total and by using internal EBV instead of parent averages from EBVMACE to compute external DRP. Based on Legarra et al. [13], Gengler and Vanderick [16] integrated MACE information into the official Walloon genetic evaluation for milk production. External EBV were estimated by selection index theory and internal contributions were considered as in VanRaden and Tooker [17]. Thus, while these two latter approaches and the approach proposed in this study consider internal contributions to MACE information in a similar manner [See Additional file 2], the main advantage of the proposed approach is to avoid a pre-processing deregression step or computation of external EBV.
Internal animals
The effect of the integration of MACE information on predictions was also studied for internal animals that were not associated with MACE information and that were sired by internally used sires. A total of 3331 internal animals was considered. If double-counting of contributions due to relationships and due to records were avoided (i.e. EVALBL), integration of MACE information led to an increase of the REL from 0.32 to 0.42 for milk yield and from 0.31 to 0.42 for fat and protein yields for internal animals that had a RELW less than 0.50 (Table 8). These increases were equivalent to 2.4 DE for milk yield, 2.3 DE for fat yield and 2.4 DE for protein yield. On average, no increase in REL was observed for internal animals with RELW greater than 0.50 (Tables 9 and 10; Figure 2). Therefore, integration of MACE information was mostly relevant for external animals that were associated with this information and for internal animals with a low RELW sired by external animals.
Table 8.
Parameters for internal animals with a Walloon reliability less than 0.50 and sired by internally used sires
| Traits | N 1 | Parameters 2 | Genetic evaluation | ||||
|---|---|---|---|---|---|---|---|
| EVAL W | EVAL BLNN | EVAL BLRE | EVAL BLR | EVAL BL | |||
| Milk yield | 1948 | r | 0.944 | 0.995 | 0.995 | 0.999 | 1.000 |
| REtot | 245.1 | 1655.2 | 1655.2 | 245.1 | 245.1 | ||
| REL | 0.32 (0.10) | 0.57 (0.06) | 0.56 (0.06) | 0.43 (0.07) | 0.42 (0.07) | ||
| Fat yield | 1694 | r | 0.923 | 0.994 | 0.994 | 0.999 | 1.000 |
| REtot | 102.6 | 1254.9 | 1254.9 | 102.6 | 102.6 | ||
| REL | 0.31 (0.09) | 0.56 (0.06) | 0.56 (0.06) | 0.42 (0.08) | 0.42 (0.08) | ||
| Protein yield | 1786 | r | 0.938 | 0.995 | 0.995 | 0.999 | 1.000 |
| REtot | 148.4 | 1243.5 | 1243.5 | 148.4 | 148.4 | ||
| REL | 0.31 (0.09) | 0.56 (0.06) | 0.56 (0.06) | 0.42 (0.08) | 0.42 (0.08) | ||
1N = Number of internal animals; 2r = rank correlation between EVALBL and EVALW, EVALBLNN, EVALBLRE or EVALBLR; REtot = Total amount of record equivalents; REL = average reliability (SD in parentheses).
Table 9.
Parameters for internal animals with a Walloon reliability between 0.50 and 0.74 and sired by internally used sires
| Traits | N 1 | Parameters 2 | Genetic evaluation | ||||
|---|---|---|---|---|---|---|---|
| EVAL W | EVAL BLNN | EVAL BLRE | EVAL BLR | EVAL BL | |||
| Milk yield | 1360 | r | 0.999 | >0.999 | >0.999 | >0.999 | 1.000 |
| REtot | 1205.7 | 2759.1 | 2759.1 | 1205.7 | 1205.7 | ||
| REL | 0.55 (0.04) | 0.67 (0.02) | 0.67 (0.03) | 0.55 (0.03) | 0.55 (0.03) | ||
| Fat yield | 1607 | r | 0.999 | >0.999 | >0.999 | >0.999 | 1.000 |
| REtot | 1322.0 | 3125.6 | 3125.6 | 1322.0 | 1322.0 | ||
| REL | 0.57 (0.04) | 0.68 (0.03) | 0.68 (0.03) | 0.57 (0.04) | 0.57 (0.04) | ||
| Protein yield | 1516 | r | 0.999 | >0.999 | >0.999 | >0.999 | 1.000 |
| REtot | 1252.0 | 2787.7 | 2787.7 | 1252.0 | 1252.0 | ||
| REL | 0.56 (0.04) | 0.68 (0.03) | 0.68 (0.03) | 0.56 (0.04) | 0.56 (0.04) | ||
1N = Number of internal animals; 2r = rank correlation between EVALBL and EVALW, EVALBLNN, EVALBLRE or EVALBLR; REtot = Total amount of record equivalents; REL = average reliability (SD in parentheses).
Table 10.
Parameters for internal animals with a Walloon reliability greater than 0.74 and sired by internally used sires
| Traits | N 1 | Parameters 2 | Genetic evaluation | ||||
|---|---|---|---|---|---|---|---|
| EVAL W | EVAL BLNN | EVAL BLRE | EVAL BLR | EVAL BL | |||
| Milk yield | 23 | r | 0.998 | 0.999 | 1.000 | 0.999 | 1.000 |
| REtot | 132.6 | 156.9 | 156.9 | 132.6 | 132.6 | ||
| REL | 0.80 (0.04) | 0.82 (0.03) | 0.82 (0.03) | 0.80 (0.04) | 0.80 (0.04) | ||
| Fat yield | 30 | r | 0.999 | 1.000 | >0.999 | 1.000 | 1.000 |
| REtot | 158.8 | 190.6 | 190.6 | 158.8 | 158.8 | ||
| REL | 0.81 (0.04) | 0.83 (0.03) | 0.83 (0.03) | 0.81 (0.04) | 0.81 (0.04) | ||
| Protein yield | 29 | r | 0.999 | >0.999 | >0.999 | 1.000 | 1.000 |
| REtot | 147.7 | 174.6 | 174.6 | 147.7 | 147.7 | ||
| REL | 0.80 (0.04) | 0.83 (0.03) | 0.83 (0.03) | 0.80 (0.04) | 0.80 (0.04) | ||
1N = Number of internal animals; 2r = rank correlation between EVALBL and EVALW, EVALBLNN, EVALBLRE or EVALBLR; REtot = Total amount of record equivalents; REL = average reliability (SD in parentheses).
Figure 2.
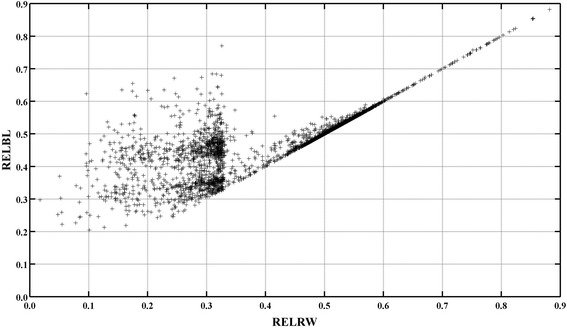
Reliabilities for internal progeny. Reliabilities associated with the Bayesian evaluation that considers double-counting of contributions due to relationships and due to records (RELBL) as a function of reliabilities associated with the official Walloon evaluation (RELRW) for the 3331 internal animals sired by internally used sires (i.e., having daughters with records in the Walloon Region) for milk yield.
The effect of double-counting was also studied in comparison to EVALBL for the 3331 internal animals that were only associated with Walloon information and that were sired by internally used sires. Own contributions due to relationships for internal animals with RELW less than 0.50 represented from 85.2% of the total contributions for milk yield to 91.8% for fat yield (Table 8). These percentages ranged from 55.1% for protein yield to 57.7% for fat yield for internal animals with RELW between 0.50 and 0.75, and from 15.4% for protein yield to 16.7% for fat yield for internal animals with RELW greater than 0.75 (Tables 9 and 10). As stated before, these observations were as expected based on selection index theory [25], and double-counting of own contributions due to relationships was mostly present for internal animals with low RELW. However, internal animals were also affected by double-counting of contributions due to relationships and due to records that originated from their sires (and relatives) through the contributions due to relationships. Double-counting that originated from their own contributions and from their sires (and relatives) could be observed based on a comparison of RELBLRE, RELBLR and RELBL and of r between EBVBL and EBVBLRE or EBVBLR (Tables 8, 9 and 10). Double-counting of contributions due to records that originated from sires of internal animals had minor effects on the average RELBLR associated with internal animals (at most 1%) and rankings of internal animals (r ≥ 0.999; Tables 8, 9 and 10). However, double-counting of contributions due to relationships led to an increase of average REL by at least 0.14 points for internal animals with RELW less than 0.50 and by at least 0.11 points for internal animals with RELW ranging from 0.50 to 0.74. The increase of average REL was lower for internal animals with RELW greater than 0.75 (>0.02 points; Tables 8, 9 and 10). Although the average RELBLR and RELBLRE were (slightly) overestimated for both evaluations, double-counting of contributions due to records and due to relationships had little effect on the ranking of internal animals compared to the ranking of EVALBL, regardless of the group of internal animals or trait considered. Indeed, rank correlations between EVALBL and EVALBLR or EVALBLRE were greater than 0.99 (Tables 8, 9 and 10). All these results show that double-counting of contributions due to relationships and due to records can be ignored for the prediction of EBV for internal animals that are sired by external animals. However, all double-counting must be taken into account to estimate REL accurately.
On the implementation
Considering all groups of animals, i.e. internally used and unused sires, as well as internal animals sired by internally used sires, our results for the Walloon example suggest that contributions due to relationships can be ignored. Indeed, the different rank correlations for EVALBLRE (i.e. the Bayesian evaluation that took only double-counting of contributions due to records into account) were similar to the rank correlations of EVALBL. Furthermore, in practice, the TSA could be difficult to apply if a high number of animals is associated with external information because it requires the inversion of a, potentially, dense matrix for each iteration. However, effects of double-counting of contributions due to relationships should be tested before ignoring it. For example, overestimation of REL could occur especially for traits for which contributions due to relationships would be at least as significant as contributions due to records (e.g., if the phenotypes are expensive to obtain). Furthermore, REL associated with the modified MME were estimated based on the inverted LHS. Although this was feasible for the simulated and Walloon data, this may not be feasible in most cases, and approaches that estimate REL (e.g., [15,18]) could be modified to take into account RE (or DE) associated with external information.
The Walloon example was considered as an evaluation that blends MACE and Walloon (internal) information in the context of official Walloon genetic evaluations for Holstein cattle. However, the Walloon example can also be considered as a particular case of an internal evaluation that has no internal data and blends only sources of external information, i.e. MACE and Walloon information, that are partially based on the same information, i.e. the Walloon information. This case can be extended to more general cases for which internal data may exist and external animals are associated with at least two sources of information (e.g., E1 and E2) that are partially based on the same external records or information. Double-counting of external information that is shared by the sources of external information, e.g. E1 and E2, can be avoided by the proposed approach thanks to the knowledge and availability of EBV and associated REL that are based only on external information that is shared by the sources of external information. Nevertheless, although taking external information that is shared by different sources of external information into consideration seems to be possible with the proposed approach, this may be difficult in practice because it requires that EBV and associated REL based on shared external information are known and available.
Conclusions
The proposed unified method integrated and blended several sources of information into an internal genetic evaluation in an appropriate manner. The results also showed that the proposed method was able to avoid double-counting of contributions due to records and due to relationships. Furthermore, because all available external sources of information were correctly propagated, relatives of external animals benefited from integrated information and, therefore, received more reliable EBV. The unified method could also be used in the context of single-step genomic evaluations to integrate external information to indirectly recover a large amount of external phenotypic information [26]. While the simulated and Walloon examples were univariate, the unified method was developed for multi-trait models that, e.g., allow evaluation of only internally available traits (e.g., methane emissions, fine milk composition traits, such as fatty acids, milk proteins and other minor components), using additional external information from correlated traits (e.g., traits evaluated by Interbull).
Acknowledgments
J Vandenplas, as a research fellow, and N Gengler, as a former senior research associate, acknowledge the support of the National Fund for Scientific Research (Brussels, Belgium) for these positions. Additional financial support was provided by the Ministry of Agriculture of the Walloon region of Belgium (Service Public de Wallonie, Direction Générale opérationnelle “Agriculture, Ressources Naturelles et Environnement” – DGARNE) through research projects D31-1207, D31-1224/S1, D31-1274, D31-1304 and D31-1308. Financial support for scientific visits was also provided by Wallonie Brussels International. J Vandenplas acknowledges I Misztal for hosting him at the Animal and Dairy Sciences Department of University of Georgia, G Gorjanc for hosting him at the Animal Science Department of University of Ljubljana, P Faux for helpful discussions and editing help, S Tsuruta and I Aguilar for their help concerning the BLUPF90 programs. Computational resources have been provided by the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the National Fund for Scientific Research (Brussels, Belgium) under Grant No. 2.5020.11. The authors thank the two anonymous reviewers for the useful comments.
Additional files
Integration of two sources of external information into a genetic evaluation. This file describes a derivation that integrates two sources of external information into a genetic evaluation, based on a Bayesian view of the mixed models [27] and similar to the Bayesian derivation of Legarra et al. [13] that integrates one source of external information into a genetic evaluation.
Double-counting between internal and external information. This file describes the development to avoid double-counting of contributions due to records between internal and external information.
Footnotes
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
JV developed the algorithms and the equations, conceived the experimental design, ran the tests and wrote the first draft. FC prepared data for the Walloon example. NG initiated and directed the research. All authors participated in writing the manuscript. All authors read and approved the final manuscript.
Contributor Information
Jérémie Vandenplas, Email: jvandenplas@ulg.ac.be.
Frederic G Colinet, Email: frederic.colinet@ulg.ac.be.
Nicolas Gengler, Email: nicolas.gengler@ulg.ac.be.
References
- 1.Henderson CR. Applications of Linear Models in Animal Breeding. 2. Guelph: University of Guelph; 1984. [Google Scholar]
- 2.Bonaiti B, Boichard D. Accounting for foreign information in genetic evaluation. Interbull Bull. 1995;11:4pp. [Google Scholar]
- 3.Aguilar I, Misztal I, Johnson DL, Legarra A, Tsuruta S, Lawlor TJ. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J Dairy Sci. 2010;93:743–752. doi: 10.3168/jds.2009-2730. [DOI] [PubMed] [Google Scholar]
- 4.Christensen OF, Lund MS. Genomic prediction when some animals are not genotyped. Genet Sel Evol. 2010;42:2. doi: 10.1186/1297-9686-42-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.VanRaden PM. Avoiding bias from genomic pre-selection in converting daughter information across countries. Interbull Bull. 2012;45:29–33. [Google Scholar]
- 6.VanRaden PM. Methods to combine estimated breeding values obtained from separate sources. J Dairy Sci. 2001;84:E47–E55. doi: 10.3168/jds.S0022-0302(01)70196-8. [DOI] [Google Scholar]
- 7.Täubert H, Simianer H, Karras K. Blending Interbull breeding values into national evaluations A new approach. Interbull Bull. 2000;25:53–56. [Google Scholar]
- 8.Mäntysaari EA, Strandén I. Proceedings of the 9th World Congress on Genetics Applied to Livestock Production: 1–6 August 2010; Leipzig. 2010. Use of bivariate EBV-DGV model to combine genomic and conventional breeding value evaluations. [Google Scholar]
- 9.Přibyl J, Madsen P, Bauer J, Přibylová J, Šimečková M, Vostrý L, Zavadilová L. Contribution of domestic production records, Interbull estimated breeding values, and single nucleotide polymorphism genetic markers to the single-step genomic evaluation of milk production. J Dairy Sci. 2013;96:1865–1873. doi: 10.3168/jds.2012-6157. [DOI] [PubMed] [Google Scholar]
- 10.Gianola D, Fernando RL. Bayesian methods in animal breeding theory. J Anim Sci. 1986;63:217–244. [Google Scholar]
- 11.Quaas RL, Zhang ZW. Incorporating external information in multibreed genetic evaluation. J Anim Sci. 2001;79:S342. [Google Scholar]
- 12.Quaas RL, Zhang Z. Proceedings of the 8th World Congress Applied to Livestock Production: 13–18 August 2006; Belo Horizonte. 2006. Multiple-breed genetic evaluation in the US beef cattle context: methodology; pp. 12–24. [Google Scholar]
- 13.Legarra A, Bertrand JK, Strabel T, Sapp RL, Sanchez JP, Misztal I. Multi-breed genetic evaluation in a Gelbvieh population. J Anim Breed Genet. 2007;124:286–295. doi: 10.1111/j.1439-0388.2007.00671.x. [DOI] [PubMed] [Google Scholar]
- 14.Vandenplas J, Gengler N. Comparison and improvements of different Bayesian procedures to integrate external information into genetic evaluations. J Dairy Sci. 2012;95:1513–1526. doi: 10.3168/jds.2011-4322. [DOI] [PubMed] [Google Scholar]
- 15.Misztal I, Wiggans GR. Approximation of prediction error variance in large-scale animal models. J Dairy Sci. 1988;71:27–32. doi: 10.1016/S0022-0302(88)79976-2. [DOI] [Google Scholar]
- 16.Gengler N, Vanderick S. Bayesian inclusion of external evaluations into a national evaluation system: application to milk production traits. Interbull Bull. 2008;38:70–74. [Google Scholar]
- 17.VanRaden PM, Tooker ME. Methods to include foreign information in national evaluations. J Dairy Sci. 2012;95:S446. [Google Scholar]
- 18.VanRaden PM, Wiggans GR. Derivation, calculation, and use of national animal model information. J Dairy Sci. 1991;74:2737–2746. doi: 10.3168/jds.S0022-0302(91)78453-1. [DOI] [PubMed] [Google Scholar]
- 19.Eaton JW, Bateman D, Hauberg S, Wehbring R. GNU Octave. A High-Level Interactive Language for Numerical Computations. 3. Boston: Free Software Foundation, Inc.; 2011. [Google Scholar]
- 20.Van Vleck LD. Algorithms for simulation of animal models with multiple traits and with maternal and non-additive genetic effects. Braz J Genet. 1994;17:53–57. [Google Scholar]
- 21.Auvray B, Gengler N. Feasibility of a Walloon test-day model and study of its potential as tool for selection and management. Interbull Bull. 2002;29:123–127. [Google Scholar]
- 22.Croquet C, Mayeres P, Gillon A, Vanderick S, Gengler N. Inbreeding depression for global and partial economic indexes, production, type, and functional traits. J Dairy Sci. 2006;89:2257–2267. doi: 10.3168/jds.S0022-0302(06)72297-4. [DOI] [PubMed] [Google Scholar]
- 23.Interbull routine genetic evaluation for dairy production traits. April 2013. [http://www.interbull.org/web/static/mace_evaluations_archive/eval/prod-apr13.html]
- 24.BLUPF90 family of programs. [http://nce.ads.uga.edu/wiki/doku.php]
- 25.Van Vleck LD. Selection Index and Introduction to Mixed Model Methods. Boca Raton: CRC Press; 1993. [Google Scholar]
- 26.Colinet FG, Vandenplas J, Faux P, Vanderick S, Renaville R, Bertozzi C, Hubin X, Gengler N. Walloon single-step genomic evaluation system integrating local and MACE EBV. Interbull Bull. 2013;47:203–210. [Google Scholar]
- 27.Sorensen D, Gianola D. Likelihood, Bayesian and MCMC Methods in Quantitative Genetics. New York: Springer; 2002. [Google Scholar]


