Utilizing movement synergies to improve decoding performance for a brain machine interface

Abstract

A major challenge facing the development of high degree of freedom (DOF) brain machine interface (BMI) devices is a limited ability to provide prospective users with independent control of many DOFs when using a complex prosthesis. It has been previously shown that a large range of complex hand postures can be replicated using a relatively low number of movement synergies. Thus, a high DOF joint space, such as the one the hand resides in, may be decomposed via principal component analysis (PCA) into a lower DOF (eigen-reach) space that contains most of the variance of the original movements. By decoding in this eigen-reach space, BMI users need only control a few eigen-reach values to be able to make movements using all DOFs in the arm and hand. In this paper we examine how using PCA before decoding neural activity may lead to improvements in decoding performance.

I. Introduction

Brain machine interfaces (BMIs) aim to allow users to control devices such as a cursor on screen or a prosthetic arm and hand via neural signals. Current state-of-the-art devices have progressed to allow subjects to accurately control a cursor for use in rudimentary point and click applications [1], [2], as well as seven degree of freedom (DOF) control over a robotic arm and hand for reaching and grasping of objects [3], [4].

For cursor applications, users are now able to control with some success all the degrees of freedom necessary for the task. However, for applications that involve the control of a prosthetic arm or hand that may contain over 20 independent actuators, current neural interfaces do not allow control of the necessary number of DOFs.

To overcome this, it has been proposed that decomposition of the complete upper limb DOF space to a lower DOF space would result in a more manageable interface for users of a high-DOF prosthetic [5]. Such mappings may take advantage of movement synergies that arise in natural reach and grasp movements. While many different hand postures are used when grasping to various objects, many of the joint angles between the digits of the hand do not vary independently. In fact, these movements can be projected into a space in which the first two components account for more than 80 % of the variance in the grasps [6].

In this paper we examine the effects on decoding performance when joint angles are first decomposed via principal component analysis (PCA) into an eigen-reach space. We also compare the decoding performance of a kernel-based autoregressive moving average (KARMA) model, which nonlinearly maps population neural activity to dimensions of joint angles against traditional Kalman filter decoders. KARMA has been previously shown to outperform Kalman filter decoders in three-dimensional cursor tasks [7]. In this paper we compare the performance of both decoders across joint angles in a reach and grasp task.

II. Methods

A. Experimental Procedures

Four thirty-two electrode microdrives (SC32, Gray Matter Research, USA) were implanted in one adult Rhesus macaque (Maccaca mulatta). The microdrives were placed via an MRI guided stereotax (Brainsight, Rogue Research Inc., Ca) over dorsal premotor cortex (PMd) and ventral premotor cortex (PMv) of both hemispheres. Each electrode was individually controllable and had an initial impedance between 0.6 – 1.5 MΩ at 1 kHz.

All surgical and animal care procedures were approved by the New York University Animal Care and Use Committee and were performed in accordance with the National Institute of Health guidelines for care and use of laboratory animals.

B. Behavioral Task

The subject was trained to perform a reach and grasp task to objects of various sizes and shapes for liquid reward. Objects were variably presented to the subject in a workspace that was approximately 50 cm × 50 cm × 50cm (Fig. 1a). While performing the task, the position of each bone segment from the subjects shoulder to hand was tracked through localization of reflective markers placed on the subject’s skin via infrared and near-infrared cameras (Osprey Digital RealTime System, Motion Analysis Corp., USA; for more information please see [8], [9]; Fig. 1b,c). A total of 23 markers were used (three on each finger, one on the back of the hand, three on the wrist, two on the elbow and three on the chest; the subject was missing the distal phalange of the middle finger). These markers were tracked at 100 frames/sec and identified in real-time (Cortex, Motion Analysis Corp.).

Figure 1.

Behavioral task setup. A) Various grasping objects with reflective markers placed on unique locations to allow tracking. B) Reflective markers fixated to the subject’s skin. C) Infrared and near-infrared cameras surrounding the workspace.

For offline analysis, 26 joint angles were solved using a Rhesus macaque musculoskeletal model [10] (SIMM, MusculoGraphics Inc., USA). This model was scaled to fit the subject’s right arm and hand via an MRI reconstruction of bone segments and aligned to the tracked marker locations via x-rays of the subject’s hand and arm while the reflective markers were in place.

C. Offline decoding

Joint angles were decoded offline from spiking activity in a cross-validated manner. Spike waveforms were extracted by first band-pass filtering the raw neural waveforms from 0.3 – 6.6 kHz, and then finding threshold crossings 3.5 standard deviations below the mean filtered signal. Threshold-crossing events were not further clustered to identify and extract single units. Once spike times were identified, joint angles were decoded using three different methods: a Kalman filter [11], [12], a kernel-based autoregressive moving average (for more information the reader is directed to [7], [9], [13], and a PCA transformation before performing the KARMA decoding (PCA-KARMA). KARMA parameters were fit using a grid search technique. The PCA analysis inputs were vectors of joint angles in time, which had the circular mean subtracted and were then arctan transformed. Joint angles were decomposed into 24 components.

To compare performance of each decoding algorithm, the correlation coefficient between the actual and decoded values were calculated for each joint angle. All decoded sessions were cross-validated by dividing each session in half, and then training on one section and decoding on the other.

III. Results

One subject performed in 42 behavioral sessions. We first present an example session of decoding performance and then show differences across sessions for each of the decoding algorithms.

A. Offline decoding

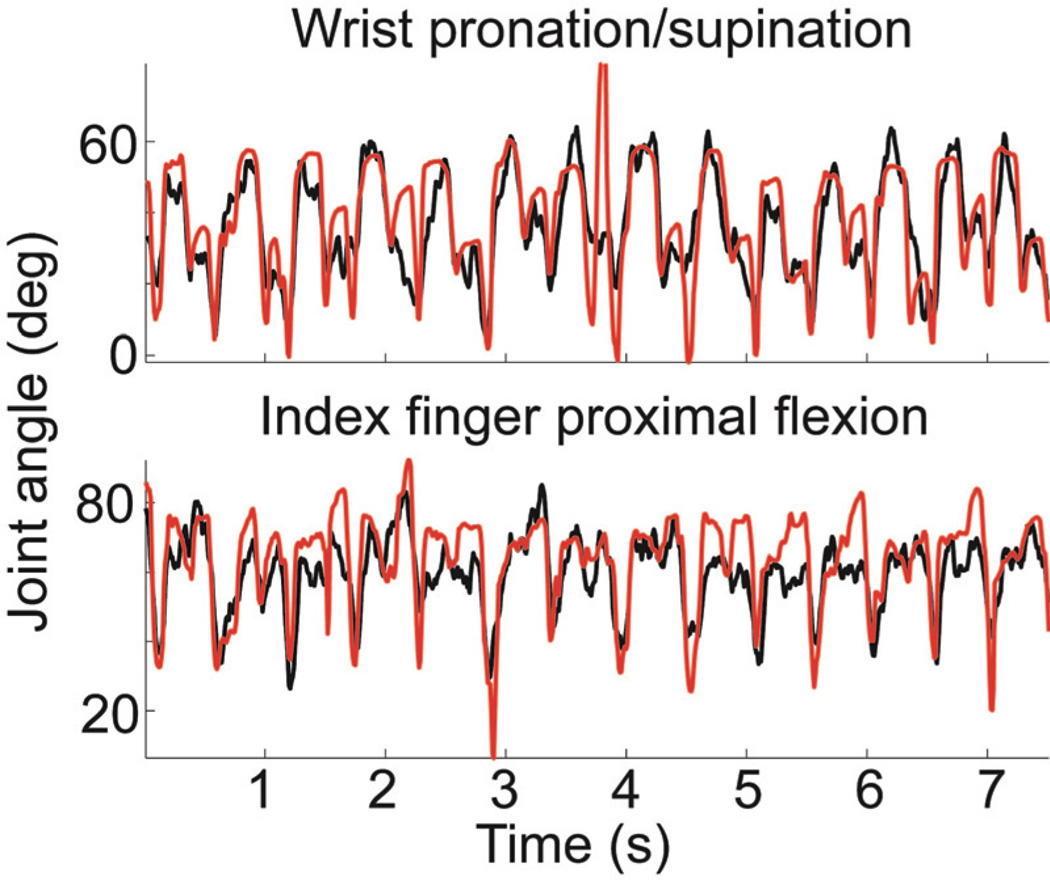
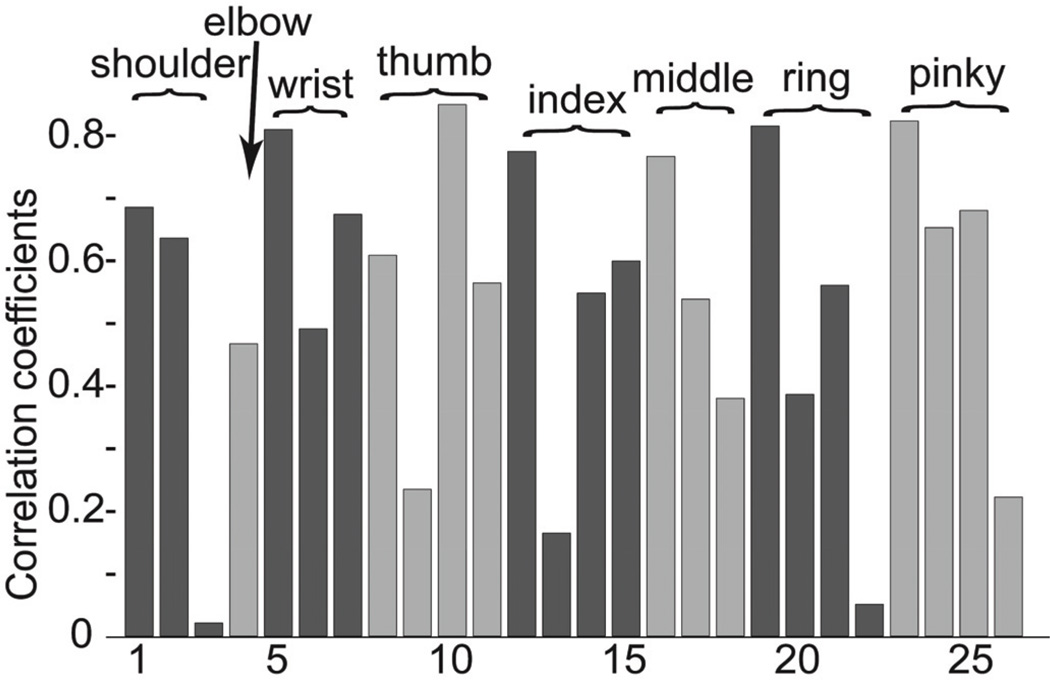
Joint angles were decoded and reconstructed from neural data after the completion of each session. Reconstructed joint angles from the index finger and wrist using the PCA-KARMA method for a single session are shown in Figure 2. The decoded joint angles followed the actual joint angle closely. To quantify this, Figure 3 presents the correlation coefficients for all 26 joint angles measured in the behavioral session. The overall average cross-validated correlation coefficient was 0.54 ± 0.23 (mean ± std).

Figure 2.

Actual (black) and decoded (red) joint angle data for the proximal joint in the index finger and the wrist.

Figure 3.

Decoding performance for a single session multiple joint angles. 1- shoulder elevation; 2 – shoulder angle; 3 – shoulder rotation; 4 – elbow flexion; 5 wrist pro/supination; 6 – wrist flexion; 7 – wrist deviation; 8, 12, 16, 19, 23 – finger proximal flexion; 9, 13, 17, 20, 24 – proximal abduction; 10, 14, 18, 21, 25 – mid flexion; 11, 15, 19, 26 – distal flexion.

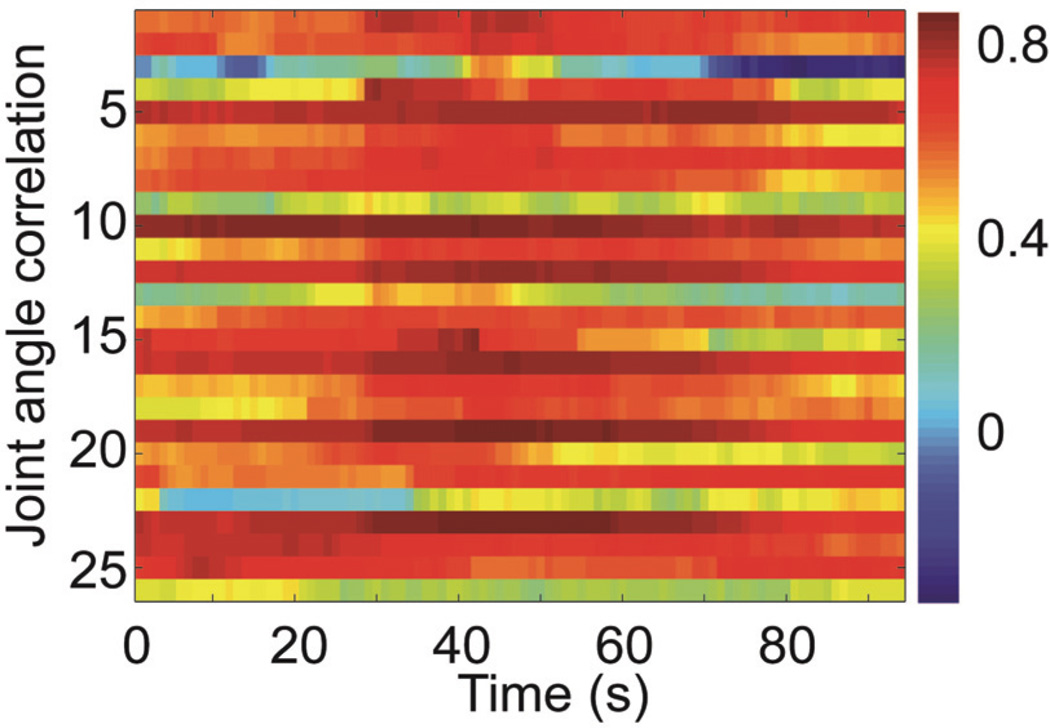
As the electrodes were moved individually between behavioral sessions the decoding performance of each joint angle varied with electrode position. We also found that as we decoded large segments of time (that did not sub-select for behavioral events), the decoding performance also varied significantly with time (Figure 4).

Figure 4.

Joint angle correlation coefficients calculated over a 30 second sliding window from KARMA decoding for a segment in time.

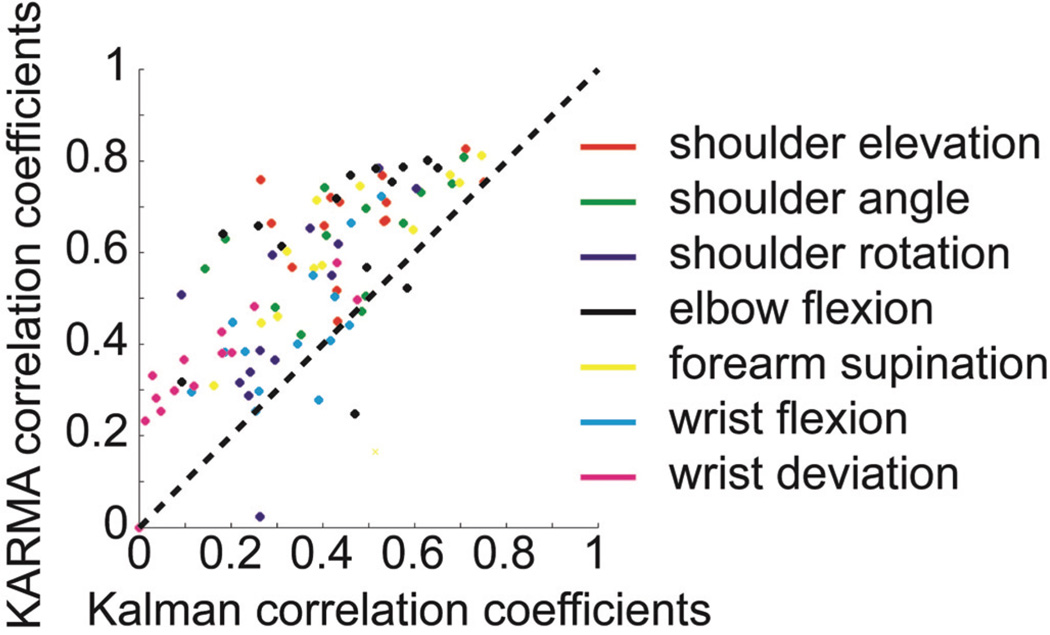
B. KARMA vs. Kalman filter decoding

Similar to the 3D cursor results presented by Shpigelman et al. [7], KARMA outperformed the Kalman filter decoder for the majority of the decoded sessions. Figure 5 presents the correlation coefficients over a sliding window for seven of the proximal joint angles for both decoding algorithms across multiple sessions.

Figure 5.

Correlation coefficients of actual and decoded joint angles for KARMA decoding and Kalman filter decoding.

C. Decoding synergistic movements

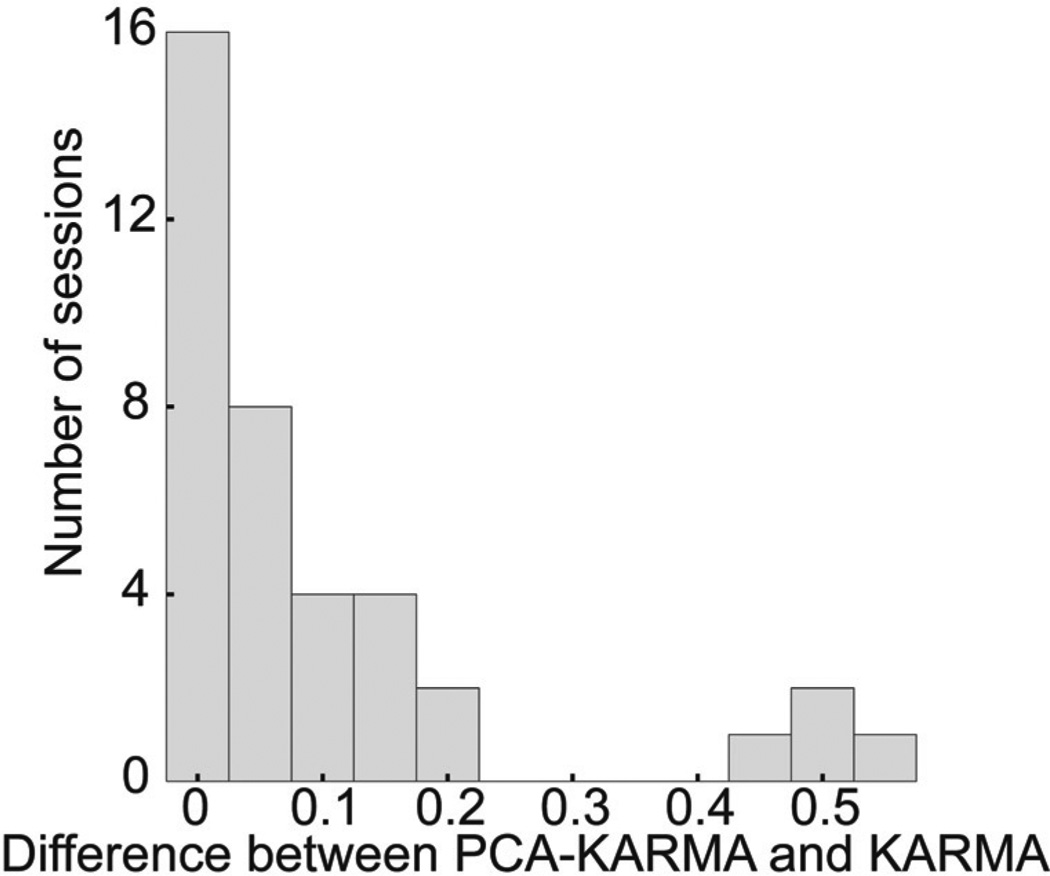
When joint angles are first decomposed into their principal components and then decoded via KARMA, decoding performance as characterized by the correlation coefficients improved or stayed the same for each session (Fig. 6). Across all sessions, the average correlation coefficient increased by 0.09 ± 0.2 (mean ± std).

Figure 6.

Histogram of the differences in average correlation coefficients per behavioral session when PCA is performed on the joint angles before KARMA decoding.

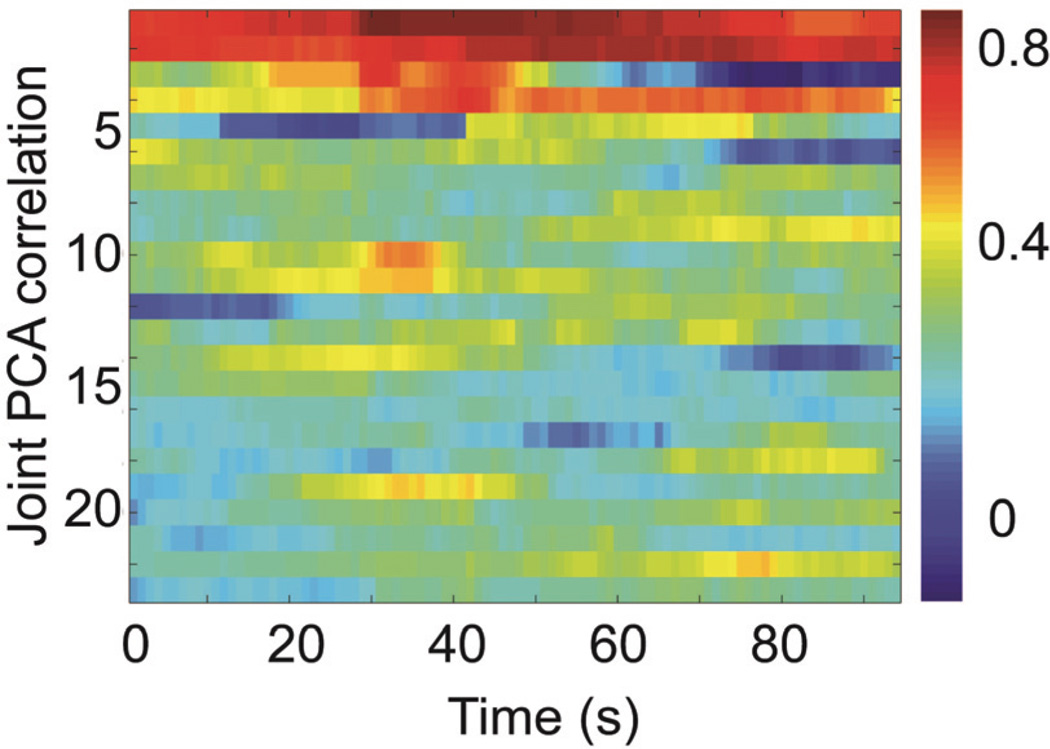
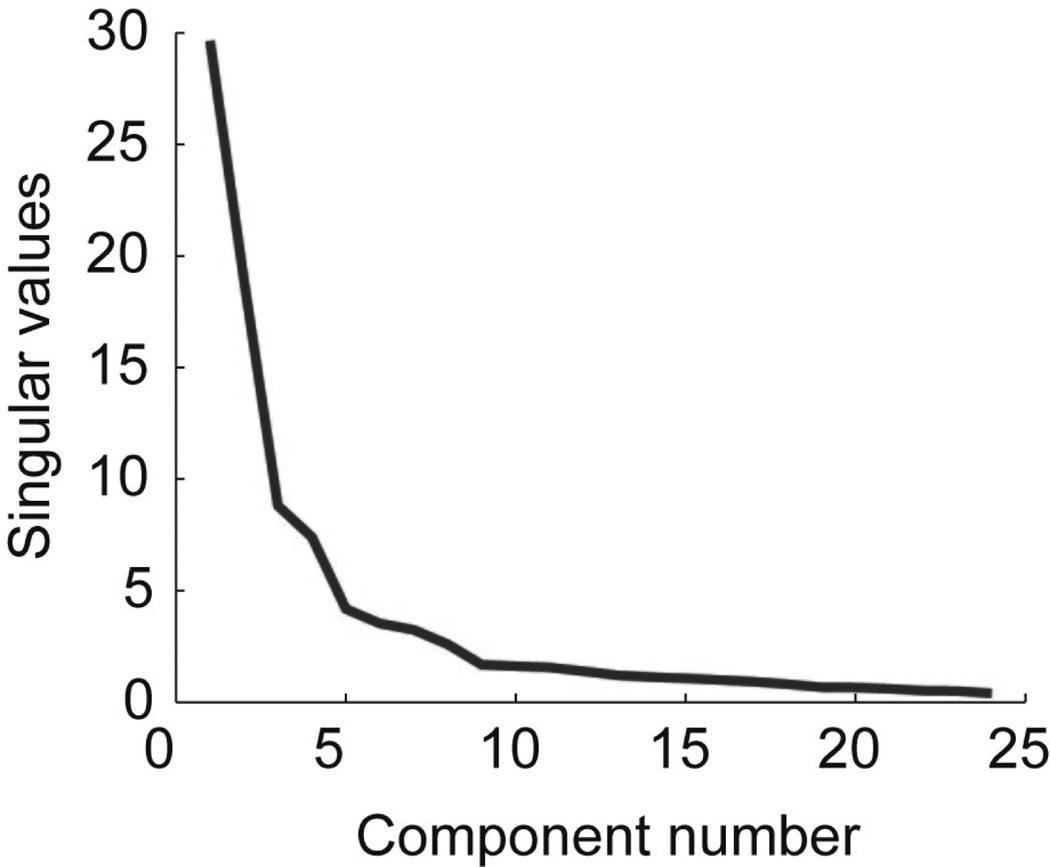
When the correlation coefficients for the eigen-reaches (components of the PCA decomposition) are analyzed for an example session, only three of the components have correlation coefficients greater than 0.4, with seven of the coefficients greater than 0.2. Figure 7 presents these correlation coefficients calculated over a sliding window of 30 s while Figure 8 shows the singular values associate with the principal components. Most variance is captured by the lower components which are decoded with higher precision.

Figure 7.

Correlation coefficients calculated over a 30 second sliding window of the decoded joint angles in the PCA space.

Figure 8.

Singular values for all PCA components from an example session. As expected the lower components capture the majority of the variance of the original joint data.

IV. Discussion

Our results show that KARMA outperforms the Kalman filter decoder, suggesting a nonlinear mapping of neural activity to the joint angles. By using these nonlinear techniques significant improvements may be made in joint decoding. However, this may be at the cost of increased decoding time. For a three-DOF task, this has been shown not to be an issue for real-time control [7].

In the second section of the paper, performing PCA was shown to provide two benefits to decoding. The first is that for offline decoding, the performance increased significantly for each session tested. The second benefit is that it allows a transformation from a low-DOF controllable input signal to a high-DOF motor/robotic output. This has implications for online decoding and control.

For offline decoding, performing the PCA decomposition may result in improved decoding performance due to the synergistic relationship in the joint angles of reaches and grasps. As 3–4 eigen-reach components capture the most variance in the movements, PCA may also increase the decoding power of the neural activity by denoising the data. Highly random or noisy movements will be captured by higher order components, which are not decoded well. This may result in improved decoding of the lower order components which contain the majority of the meaningful joint information.

For online decoding, utilizing the synergies in movements will allow users substantial control over a high-DOF prosthetic without the need to provide high-DOF readouts from neural interfaces. While this is highly desirable, a method to train a user on how to individually control and add multiple eigen-reaches to perform daily tasks will be required.

V. Conclusion

In this paper we have show that KARMA can outperform a Kalman filter decoder for joint angles in a reach and grasp task. Performing PCA on the joint angles before using KARMA was also shown to increase performance. Finally, the relatively low-DOF control needed in the decomposed space may provide an easier route towards controlling high-DOF prosthetics.