Atlas-Based Probabilistic Fibroglandular Tissue Segmentation in Breast MRI

Abstract

In this paper we propose an atlas-aided probabilistic model-based segmentation method for estimating the fibroglandular tissue in breast MRI, where a novel fibroglandular tissue atlas is learned to aid the segmentation. The atlas represents a pixel-wise likelihood of being fibroglandular tissue in the breast, which is derived by combining deformable image warping, using aligned breast contour points as landmarks, with a kernel density estimation technique. A mixture multivariate model is learned to characterize the breast tissue using MR image features, and the segmentation is subsequently based on examining the posterior probability where the learned atlas is incorporated as the prior probability. In our experiments, the algorithm-generated segmentation results of 10 cases are compared to the manual segmentations, verified by an experienced breast imaging radiologist, to assess the accuracy of the algorithm, where the Dice’s Similarity Coefficient (DSC) shows a 0.85 agreement. The proposed automated segmentation method could be used to estimate the volumetric amount of fibroglandular tissue in the breast for breast cancer risk estimation.

1 Introduction

Breast magnetic resonance imaging (MRI) provides 3D scanning and has emerged as an effective modality for breast cancer risk assessment for high-risk population [1, 2]. Studies indicate that the percentage of fibroglandular tissue (FT%) computed in breast MRI is related to breast cancer risk [2, 3]. To estimate the FT% in breast MRI, accurate segmentation of the fibroglandular tissue from the breast is a fundamental step. Fibroglandular tissue segmentation is challenging in several aspects. First, segmenting the breast as an organ from the remaining parts of the MR image is critical [4]. Second, fibroglandular tissue may be present anywhere in the breast with varying amounts, shapes, and patterns, which is challenging to model by simple geometric descriptors. In addition, the bias field is common in breast MRI where the intensity inhomogeneity may considerably affect the appearance of tissue properties.

The problem of automated fibroglandular tissue segmentation has received little attention in the literature to date [4, 5]. In addition to the qualitative estimation of the fibroglandular tissue by visual assessment [3], most previous studies rely on semi-automated segmentation methods such as interactive thresholding [1] or clustering [2, 6]. Fuzzy C-means (FCM) has been used where usually the number of clusters either relies on user’s determination [2] or based on intensity range assumptions followed by interactive adjustments [6]. Visual assessment and interactive methods are subjective and introduce inter- and intra-reader variability [1–3, 6]. An automatic method is reported in [4] to simultaneously segment heart, pectoral, lung, and breast, in which the fibroglandular tissue is also processed in the axial view of breast MRI. In dealing with intensity inhomogeneity, FCM, N3 [7], and CLIC [8] have been recently tested for breast MRI [5], where segmentation performance of different combinations of these algorithms is reported based mainly on the visual evaluation by radiologists.

We propose an atlas-aided probabilistic model-based method for fibroglandular tissue segmentation, where a likelihood atlas is constructed to aid the segmentation. The breast tissue is characterized by a mixture model and segmentation is based on posterior probability evaluation by incorporating the likelihood atlas as a prior. Our major contributions include i) constructing the novel fibroglandular tissue likelihood atlas and ii) proposing an atlas-aided probabilistic model-based method to address the challenging problem of fibroglandular tissue segmentation in breast MRI.

2 Methods

The proposed segmentation method includes two preprocessing steps. First, the outline of the breast is segmented in the breast MR images, implemented based on [9]. This step is critical to the fibroglandular tissue estimation because it precludes the interferences coming from the non-breast regions. Second, we further process the segmented breast by applying the nonparametric non-uniform intensity normalization (N3) algorithm [7] to reduce bias field. After that, our atlas-aided model-based segmentation method consists of three major modules, i.e., 1) likelihood atlas construction, 2) model learning, and 3) segmentation, as described in the following.

2.1 Fibroglandular Likelihood Atlas Learning

We construct a fibroglandular tissue likelihood atlas to aid the segmentation. The atlas represents a statistical likelihood of being fibroglandular tissue for each pixel on a standard breast template and it is derived by deformable breast image warping and kernel density estimation techniques. Our atlas is similar in principle to shape/organ atlases in the notion of “statistical atlas” but differs in that it describes the likelihood of breast tissue type rather than the anatomy/structure of a shape or organs [4, 10]. In our approach, we choose not to treat fibroglandular tissue as a well-defined structure in the image (e.g., the shape of the fibroglandular tissue can vary largely between cases), but rather model its spatial distribution to construct the likelihood atlas.

The likelihood atlas is derived based on “ground truth” segmented fibroglandular tissue (e.g., provided by an expert), from a set of training samples of 3D breast MRI scans, and processing is performed separately at the intra-case and inter-case levels.

Intra-case Learning

For a given 3D scan, the first step is to create a case-specific 2D breast template in the form of a closed contour of the breast. To do so, the slices of the given scan are aligned via rigid registration [11] to the center slice. Then, the breast contour for each slice is extracted [9] and interpolated into equidistantly distributed points of a fixed number (200 in our settings) (Fig. 1(a)(b)). The points of breast contours across the different slices are then matched by the non-linear dynamic time warping (DTW) algorithm [12] to establish point-correspondence (Fig. 1(c)), from which a breast contour is produced by averaging the corresponding matched-points across different slices. The averaged contour delineates a 2D mean shape of the breast defined as the case-specific 2D breast template for the given scan (Fig. 1(c)).

Fig. 1.

Intra-case fibroglandular likelihood atlas construction. (a) (b) Two representative slices of a 3D MRI scan where the breast contours are plotted in red. (c) The DTW-based matching of the breast contours between (b) (red) and the generated case-specific 2D breast template (blue). (d) Based on the built point-correspondence in (c), the breast in (b) is deformed to the breast template (blue). (e) The learned case-specific 2D likelihood atlas where the colorbar indicates pixel-wise likelihood of being fibroglandular tissue within the breast template.

Next, pixel-wise likelihood is learned for each point in the case-specific 2D breast template. For each of the training slice, we take its breast contour points as original landmarks and warp the whole slice to align it with the case-specific breast template whose breast contour points are taken as the corresponding target landmarks (Fig. 1(d)). Here the warping is implemented in a deformable manner by the Delaunay triangulation and cubic interpolation [13]. In this way we transfer all slices and the associated segmented fibroglandular tissues into the same coordinate space. Subsequently, we project the segmented fibroglandular tissues for each slice into the case-specific breast template space where a 2D spatial distribution of the accumulated projected points is formed. Let ${\left\{Z_i\right\}}_{i=1}^N$ represent the N accumulated points where Z_i = [x_i, y_i] encodes the 2D coordinates for point i, we apply the following 2D kernel density estimation [14] to derive a continuous distribution function,

$$f_H(Z)=\frac{1}{N}{\sum }_{i=1}^N{G}_H(Z-Z_i),$$ (1)

where Gaussian kernel is selected for G_H and the bandwidth H is automatically determined according to [14]. Function f_H(Z) represens a pixel-wise likelihood of being fibroglandular tissue in the breast template, which yields the case-specific fibroglandular likelihood atlas for the given MRI scan (Fig. 1(e)).

Inter-case Learning

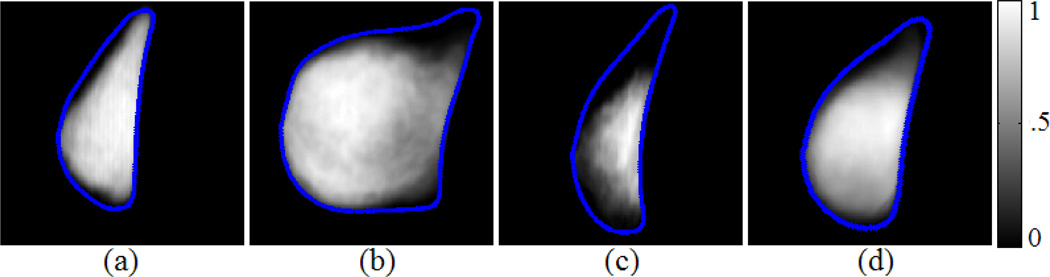
By repeating the above intra-case processing for multiple 3D scans we obtain multiple case-specific likelihood atlases (Fig. 2(a)-(c)). At the inter-case level, we apply similar processes as described above to generate the likelihood atlas over the entire training set. First, an overall 2D breast template is generated from averaging the DTW-matched contour points extracted from multiple case-specific 2D atlases. Then all the case-specific atlases are deformed by the Delaunay triangulation and cubic interpolation [13] to the overall breast template space to average out an overall fibroglandular likelihood atlas (denoted by A₁ ; Fig. 2(d)). Since a breast primarily consists of fibroglandular tissue and fat, a fat likelihood atlas A₂ can be obtained simultaneously as A₂ = 1 − A₁. The two atlases will be used in Section 2.3.

Fig. 2.

Inter-case fibroglandular likelihood atlas construction. Three case-specific likelihood atlases derived from three different cases are shown in (a), (b), and (c), respectively, and (d) shows an overall atlas (denoted by A₁) learned over 9 different cases. The colorbar for (a)-(d) indicates pixel-wise likelihood of being fibroglandular tissue.

2.2 Fibroglandular Tissue Model Learning

A mixture model of Gaussian distribution is employed to model the fibroglandular tissue and fat, respectively, using image-derived features of the tissue appearance. For more efficient model learning, we choose to work at the superpixel [15] rather than pixel level (note here a pixel essentially represents a voxel). We adapt a publicly available code in [15] to over-segment to a set of superpixels (superpixel number is initially set to 300 by referring to [16]) in which the superpixels in the non-breast regions are filtered out (Fig. 3(a)). Then tissue feature vectors (X) are computed at the superpixel level including, mean intensity, intensity variance, skewness, and kurtosis [17]. For each class of tissue, the following multivariate mixture model Θ is learned,

$$P(X|\Theta )={\sum }_{k=1}^K{\omega }_k\cdot \frac{1}{{(2\pi )}^{d/2}|{\mathrm{\Sigma }}_k{|}^{1/2}}\cdot e^{[-1/2\cdot {(X-{\mu }_k)}^T{{\mathrm{\Sigma }}_k}^{-1}(X-{\mu }_k)]},$$ (2)

where d = 4, ω_k, μ_k and Σ_k represent the weight, mean, and covariance matrix of the k-th Gaussian component, respectively. The integrated expectation–maximization (EM) and iterative pairwise replacement algorithm (IPRA) [12] are adapted to learn the model, in which the mixing component number K is automatically determined. Briefly, the EM algorithm performs an initial estimation of the components and a refinement process is followed by the IPRA algorithm. The learned two models are denoted by ${\Theta }_m={\left\{{\{{\omega }_k,𝒩({\mu }_k,{\Sigma }_k)\}}_{k=1}^K\right\}}_{m=1}^2$ where Θ₁ is for fibroglandular tissue and Θ₂ for fat, respectively.

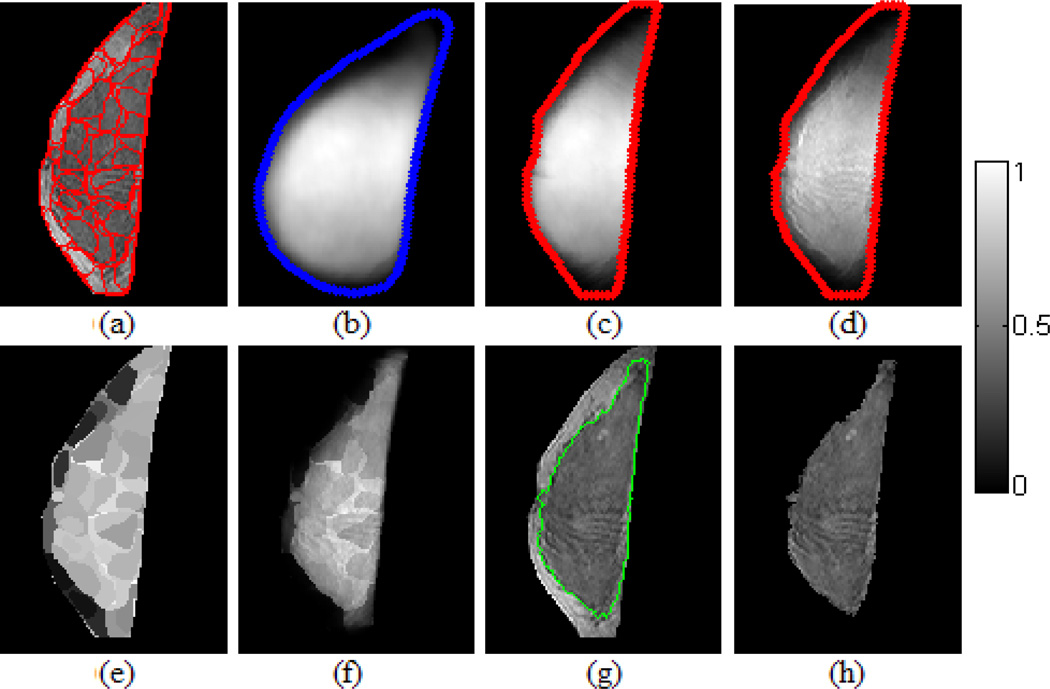
Fig. 3.

Fibroglandular tissue segmentation by examining posterior probability. The colorbar is for (b)-(f) and indicates the likelihood of being fibroglandular tissue. (a) Test slice in terms of superpixel representation. (b) A training-set learned fibroglandular likelihood atlas (A₁). (c) The atlas in (b) is warped to align with the test slice. (d) Regularized atlas (P(Θ₁(q))). (e) Superpixel-wise probability profile of P(S|Θ₁). (f) Pixel-wise posterior probability profile P(Θ₁|q). (g) Segmentation contour. (h) Segmented fibroglandular tissue.

2.3 Fibroglandular Tissue Segmentation

We formulate the segmentation of a test breast (i.e., the set of 2D slices) as the atlas-aided posterior probability assessment after incorporating the likelihood atlases as prior probability. To do so, the correspondence between each of the test slices (Fig. 3(a)) and the atlas (i.e., the breast template; Fig. 3(b)) needs to be established. We utilize a similar warping process as described in the atlas construction to deform the likelihood atlas to align with a test slice by the Delaunay triangulation and cubic interpolation [13] (Fig. 3(c)). For segmenting a single test slice, we compute pixel-wise posterior probability. Note that the atlas gives pixel-wise likelihood but the test image features are extracted in terms of superpixels. Therefore, in computing the pixel-wise posterior probability for each pixel within a superpixel region, the same set of image features is repeatedly used for each pixel belonging to that superpixel (refer to equation (4)). This way the segmentation can benefit both from the robustness of superpixels to noise and the sensitivity to small blobs of fibroglandular tissue. For each pixel q of a superpixel S in the test slice I (assume _I is a gray level image and I(q) ∈ [0,255]), the posterior probability (Fig. 3(f)) w. r. t the learned models ${\left\{{\Theta }_m\right\}}_{m=1}^2$ is computed by:

$$P({\Theta }_m|q)\propto P(q|{\Theta }_m)\cdot P({\Theta }_m(q)),$$ (3)

where P(q|Θ_m) (Fig. 3(e)) is calculated at its superpixel level using equation (2):

$$P(q|{\Theta }_m)=P(S|{\Theta }_m)={[-\text{log}{\sum }_{k=1}^K{\omega }_k\cdot 𝒩(S;{\mu }_k,{\Sigma }_k)]}^{-1},$$ (4)

and P(Θ_m(q)) (Fig.3d) is based on atlas A_m weighted by a regularization item R_m:

$$P({\Theta }_m(q))=R_m(q)\cdot A_m(q),\text{where}{R}_1(q)=1-\frac{I(q)}{255};R_2(q)=1-R_1(q).$$ (5)

In equation (5), A_m(q) is the corresponding likelihood value of the aligned atlas and R_m(q) (R₁ for fibroglandular tissue and R₂ for fat) is a regularization/weighting coefficient based on the intensity properties of the test slice. The term R_m is considered as a further regularization to the magnitude of the a priori learned atlas to better fit the given test case for improved segmentation. Fibroglandular tissue is segmented (Fig. 3(g)(h)) as the pixels that satisfy P(Θ₁|q) > P(Θ₂|q).

3 Results

In our experiments we use 10 3D bilateral MRI cases randomly selected from a high-risk screening population [18], with cancer-unaffected, T1-weighted, non-fat-suppressed imaging in the sagittal view. Three cases fall in the Breast Imaging-Reporting and Data System (BI-RADS) density category III and 7 in category IV. There are 56 slices for each scan, resulting in a total of 10×56=560 2D MRI slices used in our experiments. Women were imaged prone in a 1.5T scanner with dedicated surface breast coil; matrix size: 256×256; slice thickness: 2-3.5mm; flip angle: 20°. The fibroglandular tissue for each case (after bias correction) is manually segmented by a 10-year experienced breast imaging radiologist, who estimates the fibroglandular regions in the breast by adapting a previously-suggested intensity thresholding approach [1]. The radiologist has the option to first select a rough region of fibroglandular tissue by outlining a closed contour prior to operating the thresholding. This manual segmentation is considered as our ground truth for validation.

Our experiments are based on leave-one-out cross validation: in each loop 9 cases are used for model training and atlas learning and the left one is used for testing. The segmentation accuracy is based on assessing agreement of the 3D volume between the algorithm- and manual-generated segmentation by the Dice's Similarity Coefficient (DSC). We also compare our segmentation against the intensity-based FCM clustering algorithm [19], which has previously been used for fibroglandular tissue segmentation in breast MRI. In our implementation we also apply the two preprocessing steps (e.g., the breast boundary segmentation and bias field correction) and we fix the number of cluster to 2 to guide the FCM to divide the breast into two broad intensity-based clusters: fibroglandular tissue and fat. Finally, we also compare our proposed method to a conventional (e.g., without atlas prior) Gaussian mixture model (GMM) where P(Θ_m) is set to 0.5 for equal occurrence frequency for the two breast tissue classes.

Table 1 lists the volumetric DSC performance comparison for each of the 10 cases. Overall we achieved an average segmentation accuracy of DSC=0.85. As can be seen, our proposed atlas-aided method brings a significant improvement in segmentation accuracy over FCM and the conventional GMM method (the corresponding p values are 0.0009 and 0.004 for comparing our atlas-aided method against the GMM and FCM, respectively, using a paired t-test), which suggests a benefit from incorporating the constructed fibroglandular tissue likelihood atlases in the segmentation process. Segmentation examples are shown in Fig. 4 with the comparison to the corresponding manual segmentations.

Table 1.

Segmentation performance (DSC) comparison for the 10 cases

Case	#1	#2	#3	#4	#5	#6	#7	#8	#9	#10	Average
Atlas-GMM	0.80	0.81	0.82	0.89	0.88	0.87	0.88	0.83	0.84	0.85	0.85
GMM	0.57	0.47	0.62	0.79	0.73	0.71	0.79	0.74	0.70	0.77	0.69
FCM	0.66	0.68	0.73	0.87	0.79	0.80	0.82	0.70	0.79	0.79	0.76

Fig. 4.

Segmentation examples and the comparison to manual segmentation. Each row shows one case example. (a) Segmented and bias corrected breast. (b) Manual segmentation. (c) Atlas-aided GMM segmentation. (d) GMM segmentation (without atlas). (e) FCM segmentation.

As a preliminary validation of the dependency of our method on the pre-selected number of superpixels, we also experiment with initializing the superpixel algorithm [15] by 1000 superpixels. We observe that the atlas-aided segmentation accuracy remains relatively stable, with a slight increase of ~ 0.3% relative to 300 superpixels.

4 Discussion and Conclusion

We propose an atlas-aided probabilistic model-based approach for fibroglandular tissue segmentation in breast MRI. The constructed statistical atlases serve as an effective prior of fibroglandular tissue likelihood in posterior probability assessment for segmentation. Experiment results demonstrate superior segmentation accuracy for our approach, compared to other commonly used approaches, suggesting a benefit of incorporating the constructed atlases in the proposed segmentation method. This work is performed to establish proof-of-concept and feasibility for our algorithm. Based on the segmentation, it is straightforward to derive a volumetric percentage of the fibroglandular tissue (FT%), which could ultimately be used for breast cancer risk estimation. In addition, the computed posterior probabilities could essentially be translated into voxel-wise percentages of fibroglandular tissue to alleviate partial volume effects [2] and provide aggregated relative measures of fibroglandular tissue.

Future work will include further validation with a larger dataset including different vendors and protocols, extending the atlas construction in the 3D space, and employing additional image features (e.g., textures) to characterize the tissue properties. Multi-reader variability study on the manual segmentation will also be considered. Further testing of performance dependence on the number of superpixels is also warranted to fully validate our method’s robustness.