Sensory Gain Outperforms Efficient Readout Mechanisms in Predicting Attention-Related Improvements in Behavior

Abstract

Spatial attention has been postulated to facilitate perceptual processing via several different mechanisms. For instance, attention can amplify neural responses in sensory areas (sensory gain), mediate neural variability (noise modulation), or alter the manner in which sensory signals are selectively read out by postsensory decision mechanisms (efficient readout). Even in the context of simple behavioral tasks, it is unclear how well each of these mechanisms can account for the relationship between attention-modulated changes in behavior and neural activity because few studies have systematically mapped changes between stimulus intensity, attentional focus, neural activity, and behavioral performance. Here, we used a combination of psychophysics, event-related potentials (ERPs), and quantitative modeling to explicitly link attention-related changes in perceptual sensitivity with changes in the ERP amplitudes recorded from human observers. Spatial attention led to a multiplicative increase in the amplitude of an early sensory ERP component (the P1, peaking ∼80–130 ms poststimulus) and in the amplitude of the late positive deflection component (peaking ∼230–330 ms poststimulus). A simple model based on signal detection theory demonstrates that these multiplicative gain changes were sufficient to account for attention-related improvements in perceptual sensitivity, without a need to invoke noise modulation. Moreover, combining the observed multiplicative gain with a postsensory readout mechanism resulted in a significantly poorer description of the observed behavioral data. We conclude that, at least in the context of relatively simple visual discrimination tasks, spatial attention modulates perceptual sensitivity primarily by modulating the gain of neural responses during early sensory processing

Introduction

Spatial attention has been postulated to facilitate perceptual sensitivity via several mechanisms, including sensory gain (Moran and Desimone, 1985; Motter, 1993; Luck et al., 1997), noise modulation (Mitchell et al., 2007, 2009; Cohen and Maunsell, 2009) and the efficient “readout” of sensory representations (Palmer et al., 2000; Pestilli et al., 2011). However, it is unclear how much each of these mechanisms contributes to the relationship between attention-modulated changes in behavior and neural activity.

Sensory gain models (Fig. 1A) postulate that attention amplifies sensory signals evoked by attended stimuli. In a typical study, the magnitude of sensory responses is assessed as a function of stimulus contrast, yielding a contrast response function (CRF). Using this approach, attention has been shown to modulate the CRF in several ways: response gain, contrast gain, or a combination of both (Fig. 1B–D; Reynolds et al., 2000; Martínez-Trujillo and Treue, 2002; Williford and Maunsell, 2006; Buracas and Boynton, 2007; Kim et al., 2007; Murray, 2008; Lauritzen et al., 2010; Lee and Maunsell, 2010; Itthipuripat et al., 2014). The relationship between attention-related CRF and behavioral changes can then be assessed using simple linking hypotheses. For example, signal detection theory predicts that increasing the slope of CRFs, which would happen with multiplicative gain, should amplify the differential response evoked by stimuli rendered at slightly different contrast levels and lead to better discriminability (Fig. 1A). Similarly, regardless of the nature of gain modulations, a reduction in the trial-to-trial variability of neural responses should also lead to better discriminability (Fig. 1E).

Figure 1.

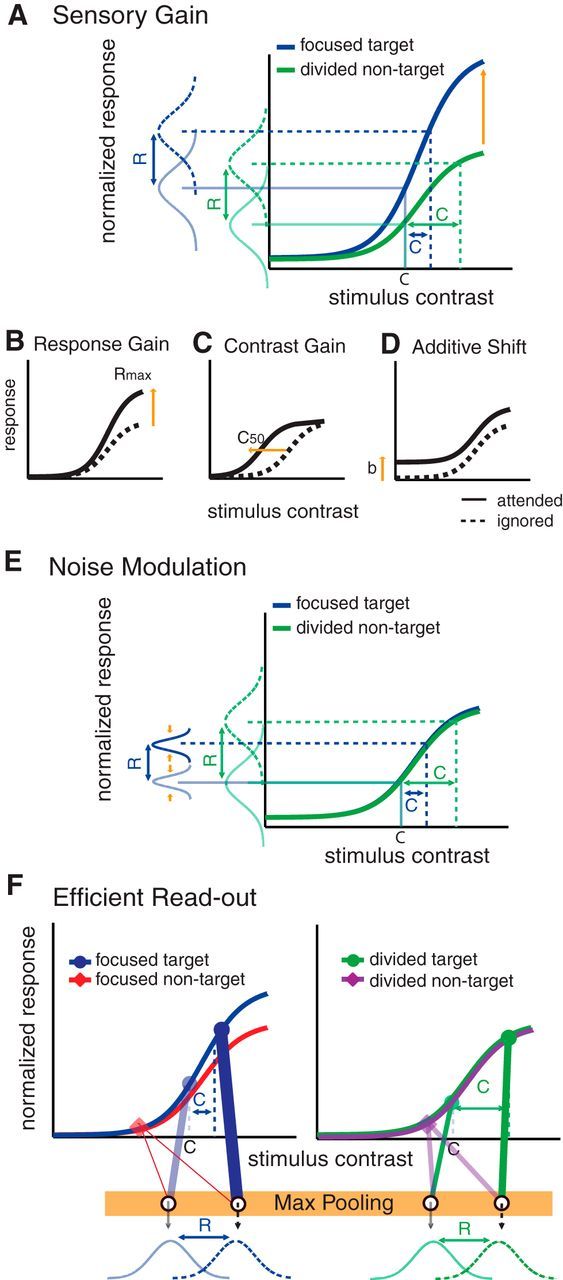
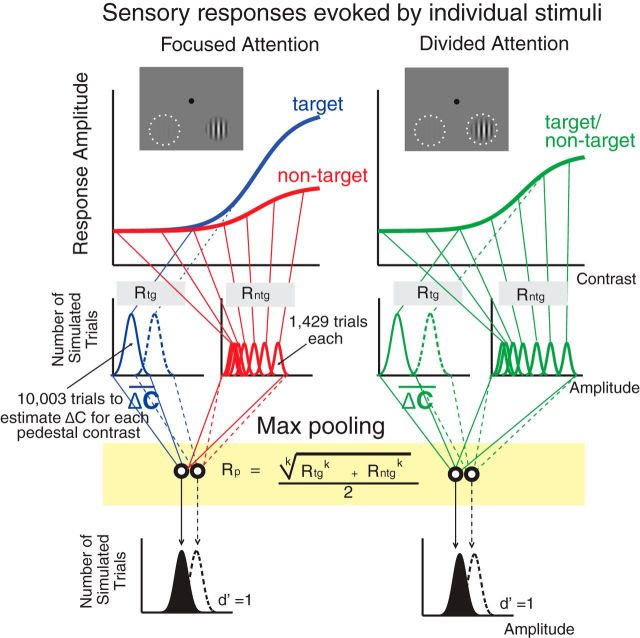
Competing theories of selective spatial attention. A, The sensory gain model predicts that focused spatial attention amplifies neural responses evoked by visual stimuli of differing contrasts. According to the sensory gain model, increasing the slope of neural CRFs with attention will result in a reduction of the contrast increment (ΔC) that is required in the focused-attention condition, compared with the divided-attention condition. Importantly, this model makes an explicit assumption that neural gain in early sensory areas is sufficient to account for attention-related improvements in perceptual performance. B–D, Note that many past studies have reported that spatial attention leads to a variety of gain patterns in the neural CRF: a multiplicative response gain (B), a contrast gain (C), or an additive baseline shift (D). Note that we use the term additive shift instead of additive gain here since gain is multiplicative by definition. E, The noise modulation model predicts that focused spatial attention reduces trial-by-trial variability of neuronal responses and/or decreases correlated noises across neuronal populations. Under this scenario, if sensory gain modulations are insufficient to explain changes in psychophysical thresholds, changes in the noise parameter could be estimated to account for the observed behavioral changes. F, The efficient readout model argues that attention does not strongly modulate responses in early sensory areas and neither sensory gain nor noise modulation could sufficiently account for attention-induced improvements in behavioral performance. Instead, attentional modulation is driven primarily by the efficient selection or readout of sensory signals in a manner that preferentially weights informative as opposed to noninformative sensory signals (Eq. 10, a max-pooling rule). In brief, the model will preferentially weight the stimulus that evokes a relatively large response compared with a stimulus that evokes a relatively small response, and consequently the stimulus evoking the larger response will increasingly influence downstream decision mechanisms.

In contrast to sensory gain and noise modulation accounts, a recent fMRI study reported that linking modulations of the fMRI response to behavior required an efficient readout mechanism that adaptively amplified the differential response evoked by target and nontarget stimuli (Fig. 1F). However, the generality of these findings is unclear as fMRI measures of attentional modulation are largely independent of stimulus intensity (Buracas and Boynton, 2007; Murray, 2008), and may be strongly influenced by the magnitude of top-down input to a region as opposed to changes in local spiking activity (Logothetis and Wandell, 2004).

Here, we quantitatively linked attention-related changes in contrast discrimination thresholds with changes in neural activity measured using electroencephalography (EEG). We focus on attention-related changes in the amplitude of two event-related potentials (ERPs): the P1, an early component thought to reflect sensory processing in early visual cortex (Van Voorhis and Hillyard, 1977; Woldorff et al., 1997), and the late positive deflection (LPD) component, which is thought to reflect decision-related processing (Hillyard et al., 1971; Squires et al., 1973, 1975a, 1975b). Consistent with sensory gain models, we found that increases in the amplitude of the P1 and LPD components were sufficient to explain attention-induced changes in psychophysical contrast discrimination thresholds, without a need to invoke noise modulation. In contrast, models that incorporated an efficient readout mechanism did not accurately capture the link between ERP modulations and behavior. The results suggest that, at least in relatively simple visual discrimination tasks, attention-related improvements in perceptual sensitivity are more closely linked to sensory gain.

Materials and Methods

Subjects.

Seventeen neurologically healthy human observers (18–31 years old, nine females, two left-handed) with normal or corrected-to-normal vision were recruited from the University of California, San Diego (UCSD). All participants provided written informed consent as required by the local institutional review board at UCSD. All participants first underwent a 2.5 h behavioral training session where contrast discrimination thresholds were estimated using a staircase procedure (see below). Next, each subject participated in multiple sessions of the main EEG experiment (4–6 d over a period of 2–3 weeks). Each EEG session lasted ∼3.5–4 h, including EEG preparation, data acquisition, and breaks. Data from one subject were discarded due to a failure to complete the experimental protocol (the subject withdrew after the second EEG session). Of the remaining 16 subjects, two subjects completed six EEG sessions (126 blocks, 7056 trials) and the rest completed four EEG sessions (84 blocks, 4704 trials).

Stimuli and task.

Stimuli were presented on a PC running Windows XP using Matlab (Mathworks) and the Psychophysics Toolbox (version 3.0.8; Brainard, 1997; Pelli, 1997). Participants were seated 60 cm from the CRT monitor (which had a gray background of 34.51 cd/m², 85 Hz refresh rate) in a sound-attenuated and electromagnetically shielded room (ETS-Lindgren).

Participants performed a two-interval forced-choice contrast discrimination task (Fig. 2) similar to a procedure described by Pestilli et al. (2011). Each trial started with a red, green, or blue cue that instructed the subject to either covertly attend to the lower left or the lower right quadrant, or to attend to both quadrants. The relationship between cue color and attention condition was counterbalanced across participants. Trials in which the subject attended to either the left or the right quadrant were termed focused-attention trials, and trials in which the subject attended to both quadrants were termed divided-attention trials. The precue was 100% valid for the focused-attention trials, whereas the target was equally likely to appear in the left or right hemifield on divided-attention trials. The attention cue was presented for 500 ms and followed by a 400–600 ms blank interstimulus-interval (ISI). This ISI was followed by two successive stimulus presentations, with each presentation consisting of two sinusoidal Gabor patches (spatial frequency, 1.04 cycles/°; SD of a Gaussian window, 1.90°) located in the lower left and right quadrants (±8.58 and −7.63° from the horizontal and vertical meridians, respectively). Each stimulus pair was presented for 300 ms, followed by a 600–800 ms ISI. The pedestal contrasts of the two Gabor patches in each interval were randomly selected from seven possible values (0, 2.04, 4.26, 8.90, 18.61, 38.90, and 81.13% Michelson contrast). The stimulus contrast at each pedestal contrast level, except for the 0% contrast value, was jittered ±0.01 log contrast from the mean contrast value. For each trial, the orientations of the left and right Gabor stimuli were yoked and the orientation value was randomly drawn from a uniform distribution. During one of the two stimulus intervals, a small contrast increment (Δc) was added to one of the Gabors for the entire interval. After the offset of the second stimulus array, a postcue appeared to inform subjects which of the two stimuli contained this increment, and subjects reported whether the increment occurred during the first or second stimulus interval. Participants were instructed to prioritize accuracy, and no response deadline was imposed.

Figure 2.

Experimental design. The two-interval forced-choice contrast discrimination task. Each trial started with an attention cue (a color cue, first column) instructing subjects to covertly attend to the lower left (a red cue) or right (a blue cue) quadrant (focused-attention conditions), or to both quadrants (a green cue, divided-attention condition). The white dotted rings in the second and third columns represent the spatial positions of the stimuli that the subjects were supposed to attend to (although they were not shown in the actual display). The attention cue was followed by two successive stimulus presentations, each consisting of two sinusoidal Gabor patches located in the lower left and right quadrants. The pedestal contrasts for each of the Gabor patches were randomly chosen from seven possible values (0–81.13% Michelson contrast). During one of the two stimulus intervals, a Gabor patch (either left or right) had a contrast increment (Δc) added to its pedestal contrast. After the second stimulus interval, a target cue appeared, informing subjects of the exact location of the target stimulus. Subjects reported whether the first or second stimulus presentation contained the target stimulus of higher contrast.

Each EEG session contained a total of 21 experimental blocks, which were broken up into three minisessions consisting of seven blocks each. Each minisession contained 392 trials across which all experimental conditions were counterbalanced—i.e., 2 (attention cues: focused, divided) × 2 (target locations: left, right) × 2 (target intervals: first, second) × 7 (pedestal contrast levels of target) × 7 (pedestal contrast levels of nontarget). Critically, Δc for each target pedestal contrast and each attention condition were adjusted after each minisession so that accuracy was maintained at 76% across all experimental conditions. Note that the contrast thresholds used in the first EEG minisession were obtained from the thresholds initially estimated in the 2.5 h behavioral training session using a staircase procedure that was applied independently for each attention condition and each pedestal contrast level. Specifically, three successive correct responses led to a 0.5% decrease in the Δc that defined the target stimulus, while one incorrect response led to a 0.5% increase in Δc. Trials from the first five reversals were excluded and the mean values of the contrast increments from remaining trials were used as contrast discrimination thresholds in the first EEG minisession.

Psychophysical analysis.

To examine relationships between stimulus contrast and attention condition (i.e., focused vs distributed) we generated a set of threshold-versus-contrast (TvC) functions by plotting Δc as a function of pedestal contrast separately for each attention condition. We focused on data from the first six pedestal contrasts (0–38.90%) as we could not obtain stable Δc estimates at the highest pedestal contrast, due to scaling factors (i.e., the maximum contrast cannot be increased beyond 100%, so Δc was too small at the highest pedestal value).

Following previous studies (Nachmias and Sansbury, 1974; Legge and Foley, 1980; Ross et al., 1993; Boynton et al., 1999; Gorea and Sagi, 2001; Huang and Dobkins, 2005; Pestilli et al., 2011), we assumed that perceptual sensitivity (indexed via d′) is limited by the differential neural response amplitude [R(c + Δc) − R(c), or ΔR] divided by the magnitude of sensory noise (σ), as expressed in the following equation (Eq. 1):

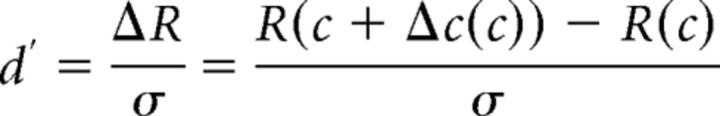where R is a hypothetical CRF that was estimated using the following Naka-Rushton equation (Eq. 2) (Geisler and Albrecht, 1997; Reynolds et al., 2000; Pestilli et al., 2011):

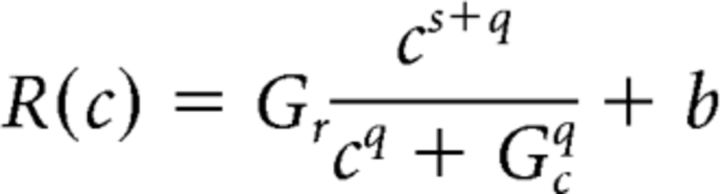Here, G_r is a multiplicative response gain factor that determines the highest response amplitude of the CRF, G_c is a contrast gain factor that determines the horizontal position of the CRF, b is the baseline offset at 0% contrast, and s and q are exponents controlling how quickly the CRF rises and reaches an asymptote. Since G_r, ΔR, and σ are codependent (i.e., they all control the vertical shift of the TvC), we set ΔR and σ to 1. We also set b to zero since changing b would not affect the shape of the TvC. With the combination of the d′ (Eq. 1) and Naka-Rushton (Eq. 2) equations, the contrast discrimination thresholds can be estimated based on the derivative (i.e., slope) of the hypothetical underlying CRF, as expressed in the following equation (Eq. 3):

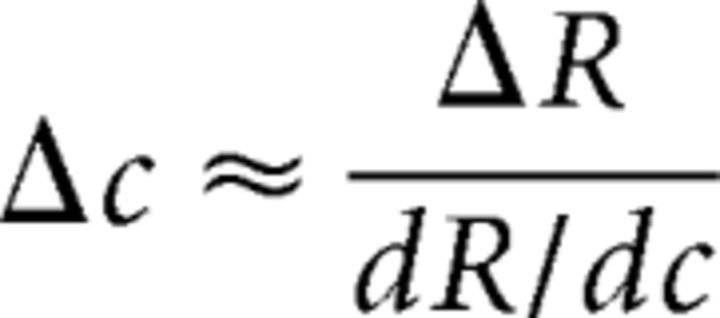where dR/dc is the derivative of the underlying CRF (Boynton et al., 1999).

We fit the TvC functions with Equations 1–3 with Matlab's fminsearch function (Nelder–Mead method; nonlinear least squares) to estimate a multiplicative response gain factor (G_r), a contrast gain factor (G_c), and two exponents (s and q) that describe the hypothetical CRF that best accounts for the observed TvC functions derived from the focused-attention and divided-attention conditions in each subject. Paired t tests were performed to examine the effects of focused and divided attention on the G_r, G_c, s, and q parameters. Note that this analysis attempts to recover the shape of the hypothetical CRF that best explains attention-related changes in contrast discrimination thresholds under the assumption that the behavioral data can be predicted by the differential response evoked by target and pedestal stimuli divided by the variability of responses at each pedestal level (and that variability is constant across all response levels).

EEG recording.

EEG data were recorded with a 64 + 8-channel Biosemi ActiveTwo system (Biosemi Instrumentation) at a sampling rate of 512 Hz. The 64 channels were equally spaced across the EEG cap and covered the whole head from above the eyebrows to slightly below the inion. Two reference electrodes were placed at the mastoids. Vertical eye movements and blinks were monitored via four extra electrodes placed below and above the eyes. Horizontal eye movements were detected by another pair of electrodes, placed near the outer canthi of the eyes. Electrode impedances were kept <20 kΩ, which is standard for this active-electrode system.

EEG preprocessing and analysis.

The EEG data were preprocessed using a combination of EEGlab11.0.3.1b (Delorme and Makeig, 2004) and custom Matlab scripts. The continuous EEG data were first rereferenced to the algebraic mean of the two mastoid electrodes and then filtered by applying 0.25 Hz high-pass and 55 Hz low-pass Butterworth filters (third order). The data were then segmented into epochs extending from 195 ms before to 3437 ms after the trial onset (i.e., the attention cue onset). Artifact rejection was performed off-line by discarding epochs contaminated by eye blinks and vertical eye movements (>±80–150 μV deviation from zero; exact thresholds were determined on a subject-by-subject basis due to differences in amplitudes of eye blink and vertical eye movement artifacts), horizontal eye movements (>±75 μV deviation from zero), excessive muscle activity, or drifts using threshold rejection and visual inspection on trial-by-trial basis, which resulted in the removal of 17.46% (SD, 6.44%) of trials across all subjects.

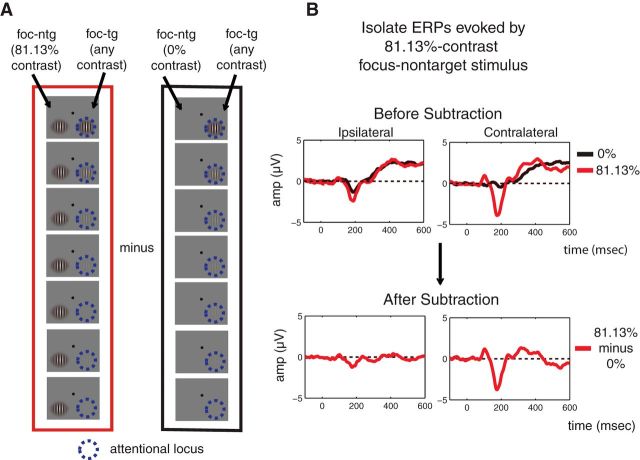
Next, the artifact-free data were time-locked to the onset of the first and second stimulus presentations and the algebraic mean of the prestimulus baseline (−100–0 ms preceding stimulus onset) was subtracted from each epoch. The data were then sorted into 112 different bins: 2 (attention conditions: focused, divided) × 2 (stimulus intervals: first, second) × 2 (types of the stimulus of interest: target, nontarget) × 2 (locations of the stimulus of interest: left, right) × 7 (pedestal contrast levels). We arranged the electrode labels so that the electrodes that were contralateral and ipsilateral to the stimulus of interest were on the right and left hemispheres of the head model, respectively. Accordingly, we collapsed trials across target position and averaged all epoched EEG data to obtain ERPs. To subtract out the evoked potentials associated with the stimulus that was paired with the stimulus of interest and to minimize the potential effects of anticipatory ERPs, we subtracted the ERP evoked by a contralateral 0%-contrast stimulus in each stimulus-cue condition (focused target, focused nontarget, divided target, divided nontarget) from the ERPs elicited by stimuli of all other contrast levels in each condition (Fig. 3, schematic illustrating all signal processing steps; Talsma and Woldorff, 2005). Finally, we collapsed across ERPs evoked by the first and second stimulus presentations.

Figure 3.

The ERP subtraction method. To isolate the ERP response evoked by stimuli in each experimental condition (i.e., each attention condition, each stimulus type, each stimulus location, and each stimulus interval), we subtracted the ERP evoked by the contralateral 0%-contrast stimulus from the ERP evoked by the stimulus of all other contrasts. In effect, this allowed us to use the response to a contralateral 0% stimulus as an index of how much effect a nonzero contrast ipsilateral stimulus had on the evoked response. A, B, An example of this subtraction method is presented in A where the ERP response contralateral to the focused-attention nontarget stimulus of 81.13% contrast on the left hemifield (termed the stimulus of interest) was to be extracted (B). In this case, the ERP response evoked by the left focused-attention nontarget stimulus of 0% contrast (A, right; B, top, black traces) was subtracted from the ERP response evoked by the left focused-attention nontarget stimulus of 81.13% contrast (A, left; B, top, red traces), resulting in the subtracted ERP response (B, bottom, red traces). Note that the stimulus paired with the stimulus of interest (in this case, the right target stimulus) could have any of seven contrast values. Therefore, the ERP response associated with the stimulus paired with the stimulus of interest should be subtracted out through this subtraction method.

Previous work has shown that attentional modulation of N1 amplitudes (an early negative-going waveform in ERPs) can be confounded by modulations of the nearby P1 and LPD components (especially when bilateral displays are used; Mangun et al., 1987; Heinze et al., 1990; Luck et al., 1990; Lange et al., 1999; Störmer et al., 2009). Thus, our analyses focus on attention-related modulations of P1 and LPD component amplitudes. The P1 component is thought to index sensory gain in early visual cortex based on its timing (∼80–130 ms poststimulus) and its putative origin in extrastriate visual cortex (Van Voorhis and Hillyard, 1977; Woldorff et al., 1997; Hillyard and Anllo-Vento, 1998). The LPD component, which is maximal above the parietal lobe, has been linked to the accumulation of sensory evidence and perceptual decision mechanisms (Hillyard et al., 1971; Squires et al., 1973, 1975a, 1975b; O'Connell et al., 2012). If early sensory gain is sufficient to explain attention-induced changes in behavior, we should be able to use signal detection theory to link attention-induced changes in P1 component amplitude with changes in psychophysical contrast discrimination thresholds. The predictive relationship between LPD component amplitude and behavior might also be expected if early sensory gain cascades to later processing stages.

To examine the pattern of attentional gain of the P1 component amplitude, we calculated the mean amplitude of the early positive P1 component across three contiguous contralateral posterior-occipital electrodes (PO3, P5, and P7 for right stimuli; PO4, P6, and P8 for left stimuli) across a 80–130 ms poststimulus window. These analyses were performed separately for each contrast level, attention condition, and stimulus type. We also identified and examined the mean amplitude of LPD components across three focal central posterior electrodes (P1, Pz, and P2) across a 230–330 ms poststimulus window. Next, the mean amplitudes of the P1 and LPD components for each attention condition were averaged across subjects and plotted as a function of stimulus contrast (for nontarget stimuli, the contrast value was the pedestal contrast; for target stimuli, the contrast value was the average between the pedestal contrast and the contrast value of the stimulus that contained the contrast increment, corresponding to the averaged physical contrast of the stimulus of interest across the two stimulus intervals). We then fit these functions with the Naka-Rushton equation (Eq. 2) to estimate the baseline (b), the maximum response (R_max), and the semisaturation [the contrast value at half the R_max (C₅₀)] parameters using Matlab's fminsearch function. In this fitting routine, there were a total of 28 observed data points (seven contrast levels times four attention/stimulus-type conditions) and 14 free parameters (four attention/stimulus-type conditions times three free parameters G_r, G_c, and b), plus s and q exponents that were identical across all conditions. Since the G_r and G_c parameters control the response and contrast gain of the function where the contrast axis ranges from zero to ∞, the G_r and G_c parameters could in principle exceed the realistic range of stimulus contrast (0–100% contrast). Thus, instead of directly comparing G_r and G_c parameters across conditions, we obtained R_max and C₅₀ parameters as they respectively capture response gain and contrast gain of the CRFs over the realistic range of stimulus contrast values.

Next, a bootstrapping procedure was used to assess differences between parameter estimates in each condition and to establish confidence intervals on the best fitting model parameters. First, we resampled subject labels with replacement. Next, we averaged the mean amplitudes of P1 and LPD components across the resampled subject labels to generate ERP CRFs for each experimental condition, and then we fit the grand-averaged ERP CRFs to estimate b, R_max, and C₅₀ parameters. This resampling and fitting procedure was then repeated 10,000 times to create bootstrap distributions from which confidence intervals associated with each parameter were computed. To evaluate the main effect of attention condition (focused/divided), we compiled the bootstrap distribution of the differences between the estimated fit parameters in the focused-attention and distributed-attention conditions—i.e., focused (target plus nontarget) minus divided (target plus nontarget)—and computed the percentage of values in the tail of this distribution that were <0. Similarly, we tested the main effect of stimulus type (target/nontarget) by compiling the bootstrap distributions of the differences between the estimated fit parameters in the target and the nontarget conditions—i.e., target (focused plus divided) minus nontarget (focused plus divided). The interaction between attention condition and stimulus type was examined by comparing the bootstrap distributions of focused (target minus nontarget) minus divided (target minus nontarget). Finally, post hoc comparisons were performed to test for additional differences between pairs of conditions by evaluating bootstrap distributions of differences and then computing the percentage of the values in the tails of these distributions that were >0 or <0. We used two-tailed statistical tests to be conservative and all p values associated with post hoc comparisons were corrected by the Holm-Bonferroni method.

Fit procedure for the sensory gain model.

To quantitatively evaluate whether gain in the ERP response amplitudes in the P1 and LPD component windows could sufficiently account for attention-induced changes in contrast discrimination thresholds, we simulated the P1 and LPD component CRFs using the combination of the d′ (Eq. 1) and Naka-Rushton (Eq. 2) equations (Fig. 4). The main parameters of interest were the baseline parameter of the simulated CRFs (b) and the noise parameter in the d′ equation (σ; see similar method in Pestilli et al., 2011). Specifically, the TvC functions in the focused-attention and divided-attention conditions were first estimated using Equations 1–3. Then, we estimated the P1 and LPD component CRFs for the divided condition based on the TvC function of the divided-attention condition. The fit routine started by setting the first point on the estimated CRF (c₀ = 0% contrast) to be a baseline parameter (b), for any given values of b and σ (Fig. 4A,B), as shown in the following equation (Eq. 4): R(c₀) = b.

Figure 4.

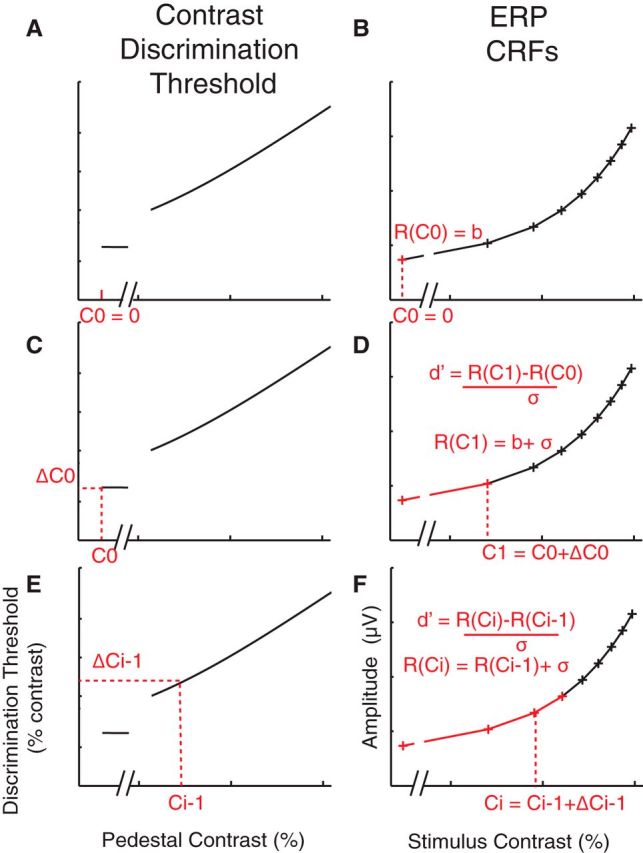
Testing the sensory gain model. To quantitatively evaluate whether the observed sensory gain in the ERP CRFs could sufficiently account for attention-induced changes in the contrast-discrimination thresholds, the TvC functions from the focused-attention and divided-attention conditions were interpolated (A, C, and E) and the ERP CRF (B, D, F) was estimated based on the interpolated TvC function using the combination of the signal-detection theory (Eq. 1) and Naka-Rushton functions (Eq. 2), given that d′ = 1 (accuracy, ∼76%; see step-by-step details in Materials and Methods).

The next contrast (c₁) for which a response was estimated was taken from the TvC function shown in the following equation (Eq. 5): c₁ = c₀ + Δc₀, where Δc₀ is the threshold at c₀ (Fig. 4C). Then, the response at c₁ was estimated using the d′ equation (Eq. 1) as shown in the following equation (Eq. 6): R(c₁) = b + σ, given that d′ = 1 (Fig. 4D). The next contrast was selected in the same way, shown in the following equation (Eq. 7): c_i = c_{i − 1} + Δc_{i − 1}, where i is the number of the current iteration that is >1. Accordingly, the response at c_i was estimated as the following equation (Eq. 8): R(c_i) = R(c_{i − 1}) + σ. This procedure was continued until the entire CRF was estimated (Fig. 4E,F). Finally, the b and σ parameters were optimized by minimizing the least-squares error between the simulated CRFs and the observed P1 and LPD component CRFs in the divided-attention condition (the average between divided-attention target and nontarget conditions) using Matlab's fminsearch function. To test whether the multiplicative response gain of the ERP CRFs alone could account for changes in the TvC function, we estimated the P1 and LPD component CRFs for the focused-attention target, using the modeling routine described above with the b and σ parameters that are identical to those obtained from in the divided-attention condition.

To test whether allowing changes in the noise (σ) and baseline (b) parameters across the focused-attention and divided-attention conditions could significantly improve the fit of the P1 and LPD component responses, we estimated the P1 and LPD component CRFs derived from the focused-attention condition as we did above except that we allowed σ and b parameters to vary freely to find the best fit. The R² value obtained from the model with fixed σ and b parameters (reduced model) was then compared with the R² value from the model with free σ and b parameters in the focused-attention condition (full model), using an F test statistic as shown in the following equation (Eq. 9):

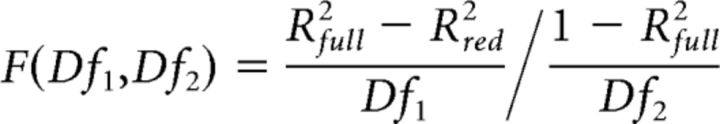where R_full² and R_red² are obtained from the best fits of the full and reduced models, respectively. Df₁ is the number of parameters in the full model (four free parameters: σ and b for the divided-attention condition, and σ and b for the focused-attention condition) minus the number of the parameters in the reduced model (two free parameters: σ and b, shared across the divided-attention and focused-attention conditions). Df₂ is the number of observations (seven contrast levels times two attention conditions) minus the number of the free parameters in the full model minus one. The F distribution was then used to estimate the probability that the full model differed significantly from the reduced model.

To determine whether allowing the optimization of σ and b in the focused-attention condition led to a significant change in these parameters in the divided-attention condition, we used a bootstrapping procedure to establish confidence intervals on the best fitting model parameters (σ and b for the divided-attention condition, and σ and b for the focused-attention condition). First, we resampled subject labels with replacement. Next, we averaged the psychophysical contrast discrimination thresholds and the mean amplitudes of P1 and LPD components across the resampled subject labels to generate new TvC and ERP CRF functions for each experimental condition. Then, the TvC functions were interpolated using Equations 1–3. In turn, the interpolated TvC functions were used to estimate the ERP CRFs via the model as described in Figure 4 and σ and b for each of the attention conditions were optimized using Matlab's fminsearch function. To test the difference between σ parameters obtained from the divided-attention and focused-attention conditions, we compiled the bootstrap distribution of the differences between the estimated fit parameters in the focused-attention and the distributed-attention conditions, and computed the percentage of values in the tail of this distribution that were different from zero. An identical analysis was then performed for b parameters.

In addition, to examine the variability of the P1 and LPD component amplitudes across focused-target and divided-target conditions, we resampled half of the trials for each pedestal contrast level and each attention condition (focused-target and divided-target conditions) separately for individual subjects. The ERP for each pedestal contrast and each attention condition was obtained by averaging the stimulus-locked EEG data across these resampled trials and applying the subtraction method (Fig. 3). This resampling method was repeated 1000 times and the SEM amplitudes of these resampled and subtracted ERPs (P1 component from 80 to 130 ms and LPD component from 230 to 330) was obtained for each subject.

Fit procedure for the efficient readout model.

First, we estimated the three CRFs (focused target, focused nontarget, and the average between divided target and nontarget) using the Naka-Rushton equation (Eq. 2), with G_r and G_c as free parameters for each of the three CRFs and q, s, and b parameters that were shared across the three CRFs. Since a max-pooling rule (Eq. 10; see below) requires overall response amplitudes to be positive values, the baseline values of the P1 and LPD component CRFs, which were slightly negative, were subtracted out from the CRFs so that all values on the CRFs were converted to positive numbers. This was done separately for the P1 and LPD component CRFs, and the resulting values formed the basis of the efficient readout model. Next, we simulated the performance of an ideal observer in 60,018 randomly generated trials (Fig. 5). These trials include 10,003 trials of each of the six trial types where the target contrast was 0, 2.04, 4.26, 8.90, 18.61, and 38.90% contrast, respectively (this ensures that the simulated performance of an ideal observer did not vary more than ∼0.01% for each pedestal contrast level). Note that we focused on these six contrast levels where the accuracy was successfully equated across subjects (Fig. 2B). From these 10,003 trials, there were 1429 trials each where the nontarget contrast was 0, 2.04, 4.26, 8.90, 18.61, 38.90, and 81.13%, respectively. Then, for each simulated trial, we set the response of each stimulus type (target or nontarget) and stimulus interval (the interval that contains the contrast increment target) as a random draw from a Gaussian distribution whose mean was given by the mean amplitude of the interpolated P1 and LPD component CRFs at the corresponding contrast value and whose SD was the σ parameter in the d′ equation (Eq. 1). The target (R_tg) and nontarget evoked responses (R_ntg) were then pooled into a single value (R_p) using the max-pooling equation expressed as follows (Eq. 10):

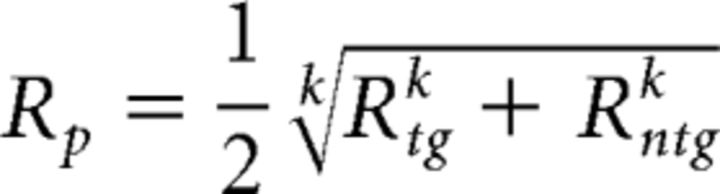where k is an exponent that weights each of the responses to individual stimuli (k ranges from 1 to ∞). Next, we searched for the contrast increment value (Δc) that yielded 76% (or d′ = 1) across the 10,003 simulated trials at each target contrast, assuming that an ideal observer would choose the interval that contained a larger pooled response as the interval that contained the target. To test how well we could estimate the TvCs based solely on the multiplicative response gain increase of the P1 and LPD component CRFs, we fixed k at 1 (i.e., equivalent to no differential weighting) and we optimized the σ parameter to find the best fit by minimizing the least-square error (this essentially amounts to the sensory gain model). To examine whether the max-pooling rule (k > 1) improves our ability to estimate attention-induced changes in behavior, we then allowed k to increase from 2 to 70 (the range of k used in this fitting routine is based on the best fit value (k = ∼68) recently reported by Pestilli et al. (2011).

Figure 5.

Testing the efficient readout model. Psychophysical contrast discrimination thresholds were estimated based on the CRFs measured by ERP responses (P1 and LPD components) using the max-pooling rule (Eq. 10; yellow box in the figure). The exponent of the max-pooling rule (k) determines the differential weight given to responses to target (R_tg) and nontarget stimuli (R_ntg) in each interval, which are later pooled into a single neural output (R_p). We used an ideal observer model that selected the interval with the highest R_p to determine the contrast increment value (Δc) that yielded 76% (or d′ = 1) across 10,003 simulated trials at each target contrast. We first set k = 1 to examine how well sensory gain alone can estimate changes in the observed contrast thresholds. Finally, k was allowed to increase from 2 to 70 to determine whether the increase in differential weighting as implemented by the max-pooling rule is better at predicting changes in the behavioral data.

Results

Focused attention reduces psychophysical contrast discrimination thresholds

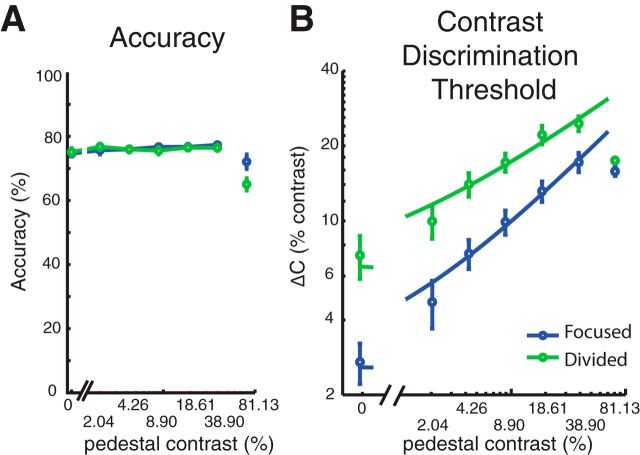
Figure 6A shows the mean response accuracy for each attention condition and each pedestal contrast level. By design, the Δc for each pedestal contrast and each attention condition were adjusted every seven blocks (i.e., the minimum number of blocks needed to ensure that all trial types were counterbalanced) to equate accuracy at a fixed level across attention conditions and pedestal contrast levels. As a result, accuracy did not deviate significantly from 76% for the first six pedestal contrast levels [accuracy, 76.11 ± 0.64% (mean ± SEM across subjects)]. A 2 × 6 repeated-measures ANOVA with attention condition and stimulus contrast as within-subject factors revealed no effect of the attention cue (F_(1,15) = 0.08, p = 0.78), a marginal effect of stimulus contrast (F_(5,75) = 2.28, p = 0.055), and no interaction between these two factors (F_(5,75) = 1.30, p = 0.27). While these results suggest that accuracy was successfully matched across the first six contrast levels, the contrast increment at the highest pedestal contrast reached ceiling in most subjects (14 of 16 subjects), which prevented us from accurately estimating contrast discrimination thresholds (that is, when the pedestal contrast plus Δc reached 100%, and we were unable to increase contrast further). Thus, overall accuracy was lower for the highest contrast pedestal compared with lower contrast pedestals (t₍₁₅₎ = 4.28, p < 0.0001). Because we were unable to equate the accuracy at the highest pedestal contrast, we focused all subsequent behavioral analyses on the first six pedestal contrast levels (0–38.90% contrast) for which task difficulty was successfully equated.

Figure 6.

Psychophysical results. A, Accuracy was successfully equated across attention conditions for the first six pedestal contrast levels by systematically changing Δc. Subjects performed poorly for the target of the highest contrast as we could not make Δc large enough at this pedestal (unconnected circles at 81.13% contrast). Thus, we focused the behavioral analysis on the first six pedestal contrast levels. B, Psychophysical contrast discrimination thresholds at different pedestal contrast levels across focused-attention (blue circles) and divided-attention conditions (green circles). Smooth curves represent the fits of the TvC functions using a combination of signal detection theory (Eq. 1) and a Naka-Rushton equation (Eq. 2). Focused attention reduced discrimination thresholds, leading to a downward shift of the TvC. In turn, this downward shift in the TvC curve is consistent with a change in the multiplicative response gain parameter or the slope of the underlying CRF. Error bars in all figures indicate ±SEM across subjects.

Given that accuracy was by design equated across the first six pedestal levels, the critical measure of the effects of attention on behavioral performance was the Δc required to achieve threshold performance at each pedestal contrast. We thus evaluated attention effects using a two-way repeated-measures ANOVA with attention condition and stimulus contrast as within-subject factors. Consistent with many previous studies (Nachmias and Sansbury, 1974; Legge and Foley, 1980; Ross et al., 1993; Gorea and Sagi, 2001; Huang and Dobkins, 2005; Pestilli et al., 2011), Δc significantly increased as a function of pedestal contrast (Fig. 6B; F_(5,75) = 106.15, p < 0.0001). Moreover, contrast discrimination thresholds were significantly lower in the focused-attention condition compared with the divided-attention condition (F_(1,15) = 30.98, p < 0.0001), demonstrating that subjects were more sensitive to small contrast changes in the focused-attention condition compared with the divided-attention condition. Post hoc t tests revealed that this pattern held across all six pedestal contrast levels that were considered in the analysis (all t₍₁₅₎'s ≥3.33, all p's ≤0.0045, Holm-Bonferroni corrected).

In addition, the combination of d′ and Naka-Rushton equations (Eqs. 1–3) accurately predicted the observed contrast discrimination thresholds (Fig. 6B) in both the focused-attention [blue curve; R² = 0.98 ± 0.0034 (mean ± SEM)] and the divided-attention conditions [green curve; R² = 0.98 ± 0.0034 (mean ± SEM)]. Importantly, the downward shift of the TvC curves with focused attention was selectively driven by an increase in the multiplicative response gain factor (G_r) of the Naka-Rushton equation (t₍₁₅₎ = 4.92, p < 0.001), which reflects an increase in the slope of the inferred CRFs in the focused-attention condition. Other parameters of the Naka-Rushton equation, including the contrast gain factor (G_c) and the exponents (q and s) did not differ across the focused-attention and divided-attention conditions (G_c: t₍₁₅₎ = 0.23, p = 0.82; q: t₍₁₅₎ = 0.72, p = 0.50; s: t₍₁₅₎ = 1.43, p = 0.17). These results suggest that the effects of focused attention on the shape of the behavioral TvC curves can be best explained via changes in the multiplicative response gain of the hypothetical CRF. However, it is important to note that this effect of focused attention that was inferred solely on the basis of behavior can also be explained by alternative neural models (Pelli, 1985; Palmer et al., 2000; Mitchell et al., 2007, 2009; Cohen and Maunsell, 2009; Pestilli et al., 2011).

Focused attention enhances multiplicative response gain of visually evoked responses

The grand average of stimulus-locked ERPs (see Materials and Methods; Fig. 3) are shown in Figure 7A for each contrast level and combination of attention condition and stimulus type. In the posterior-occipital electrodes, we observed the lateralized P1 and N1 components peaking at ∼80–130 and ∼150–200 ms, respectively. These early components are followed by the LPD component peaking at ∼230–330 ms over centroparietal electrodes. The timing (Fig. 7A) and topography (Fig. 7B) of each ERP component is consistent with previous reports of the P1, N1, and LPD components (Campbell and Kulikowski, 1972; Spekreijse et al., 1973; Van Voorhis and Hillyard, 1977; Wright and Johnston, 1982; Mangun and Hillyard, 1987, 1988, 1990, 1991; Heinze et al., 1990; Luck et al., 1990; Vassilev et al., 1994; Johannes et al., 1995; Hillyard and Anllo-Vento, 1998; Hillyard et al., 1998; Mangun and Buck, 1998; Lange et al., 1999; Noesselt et al., 2002; Schadow et al., 2007; Zimmer et al., 2010; Cravo et al., 2013). Note that previous work has shown that attentional modulation of N1 amplitudes can be confounded by modulations of the nearby P1 and LPD components (especially when bilateral displays are used; Mangun et al., 1987; Heinze et al., 1990; Luck et al., 1990; Lange et al., 1999; Störmer et al., 2009). Thus our analyses focus on attention-related modulations of P1 and LPD component amplitudes.

Figure 7.

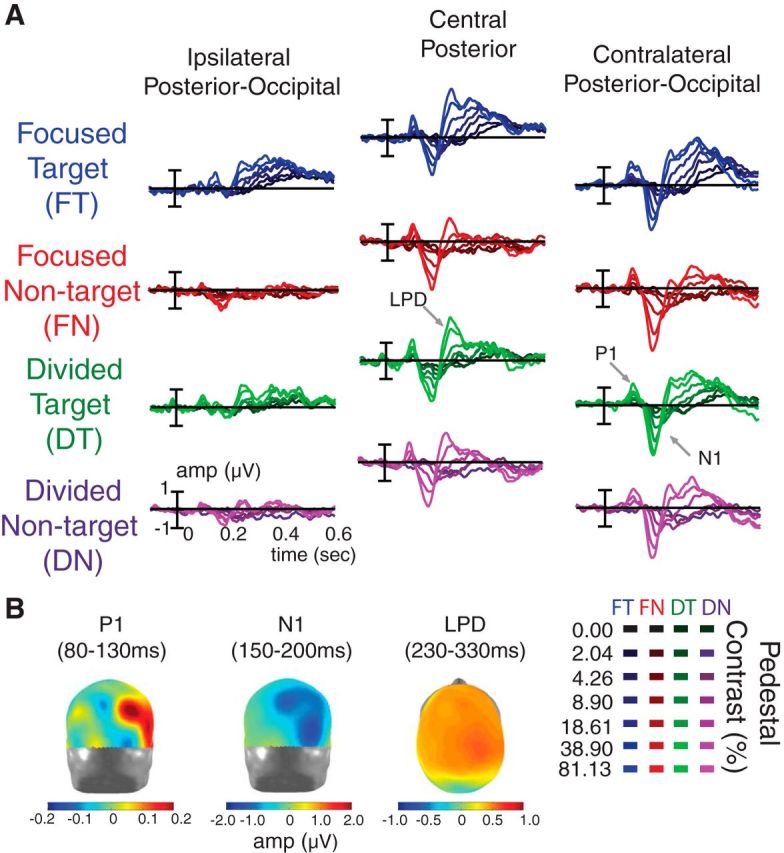
ERP responses and topographies. A, Stimulus-locked ERPs (collapsed across the first and second intervals). The data were sorted into four main conditions: focused-attention target (i.e., attended stimulus in the focused-attention condition, blue), focused-attention nontarget (i.e., ignored stimulus in the focused-attention condition, red), divided-attention target (green), and divided-attention nontarget (purple). Shading of ERP traces represents the pedestal contrast of the driving stimulus (dark and bright colors represent low-contrast and high-contrast stimuli, respectively). The ERPs evoked by contralateral 0%-contrast stimuli in each condition were subtracted from the ERPs evoked by contralateral stimuli of all other contrast levels (Fig. 3). This subtraction was done to subtract out the evoked potentials associated with variable contrast ipsilateral stimuli paired with all other contralateral stimuli. We found early sensory positive (P1) and negative potentials (N1) peaking at the contralateral posterior-occipital electrodes in ∼80–130 and ∼150–200 ms temporal windows, respectively. These early components were followed by an LPD component peaking at ∼230–330 ms in the central posterior electrodes. B, The topographical maps of P1 (posterior view), N1 (posterior view), and LPD (dorsal view) components collapsed across all experimental conditions and all pedestal contrast levels. The data were arranged so that the electrodes on the left and right sides of the head models represented the electrodes that are ipsilateral and contralateral to the stimulus of interest, respectively.

To assess the effect of attention on the gain pattern of neural CRFs, the mean amplitudes of the P1 and LPD components were plotted as a function of stimulus contrast (Fig. 8A,D). Overall, the Naka-Rushton equation explained a large proportion of the variance in the P1 (mean R², 0.92; 68% CI, 0.88–0.96) and LPD component CRFs (mean R², 0.95; 68% CI, 0.94–0.97). Neither attention (i.e., focused vs distributed) nor stimulus type (target vs nontarget) had an effect on the baseline or the C₅₀ parameters (nor did these factors interact; Fig. 8B,E, left, right; baseline: all p's ≥ 0.21; C₅₀: all p's ≥ 0.15; note that all p values reported here and elsewhere for the ERP data are based on bootstrapping at the subject level). However, we did find that attention significantly modulated the response gain of the P1 and LPD component CRFs (the R_max parameter; Fig. 8B,E, middle).

Figure 8.

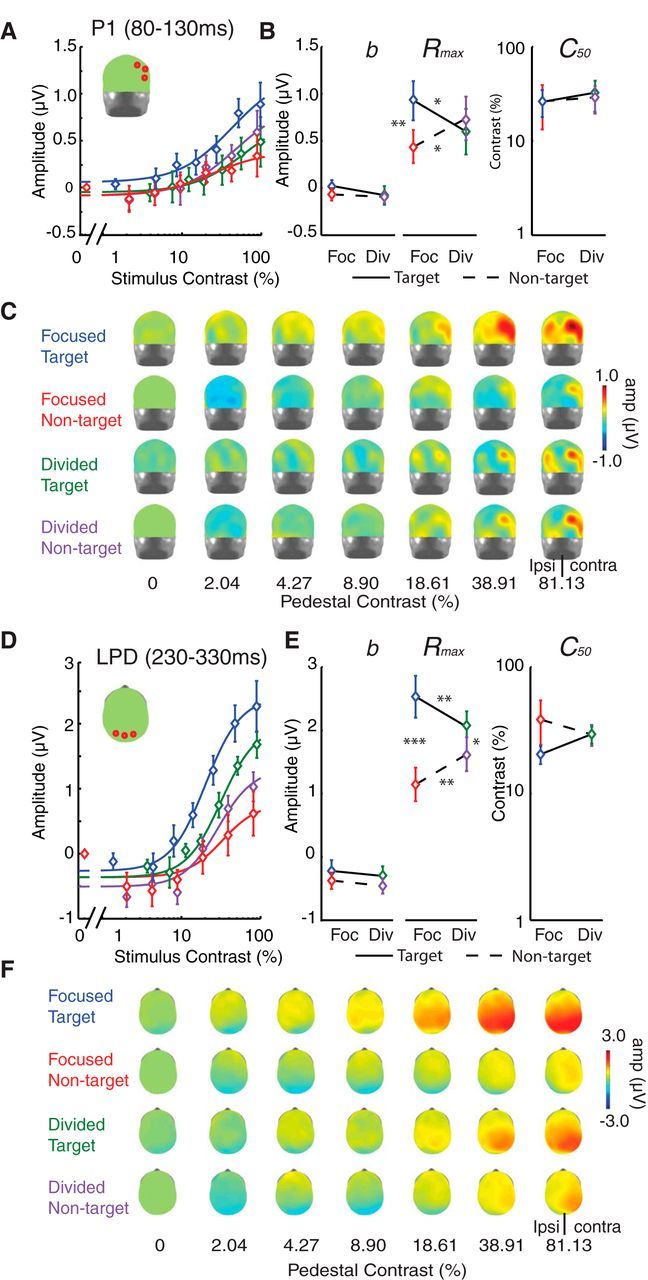
Multiplicative response gain increases with focused attention in ERP CRFs. A, C, D, F, The mean amplitudes of P1 (A) and LPD (D) components are plotted as a function of stimulus contrast (see corresponding topographical maps in C and F, respectively). The CRFs for focused-attention targets (blue), focused-attention nontargets (red), divided-attention targets (green), and divided-attention nontargets (purple) were fit with a Naka-Rushton equation (Eq. 2). B, E, A bootstrapping analysis showed that the attentional enhancement on the P1 and LPD components was selectively driven by changes in the response amplitude parameter (R_max; B, E, middle), and the baseline (b, left) and the semisaturation contrast parameters (C₅₀, right) did not significantly change. Error bars in A and D indicate ±SEM across subjects. Error bars in B and E represent 68% confidence intervals from the bootstrapping analysis. *, **, and *** Indicate significance based on post hoc pairwise comparisons corrected by the Holm-Bonferroni method at p < 0.05, p < 0.01, p < 0.001, respectively.

For the R_max for the P1 component CRF (Fig. 8A–C), there was a significant interaction between attention condition and stimulus type (p = 0.0022). Post hoc pairwise comparisons (two-tailed) with the Holm-Bonferroni correction revealed that this interaction was driven by a higher R_max for focused-attention targets compared with focused-attention nontargets (blue vs red lines; p = 0.0026) and compared with divided-attention targets (blue vs green lines; p = 0.015). In addition, the R_max for divided-attention nontargets was significantly higher than the R_max associated with focused-attention nontargets (purple vs red lines; p = 0.020). We did not find any difference in R_max between target and nontarget stimuli in the divided-attention condition (green vs purple lines; p = 0.35).

For the R_max for the LPD component CRF (Fig. 8D–F), we observed a significant main effect of stimulus type (target/nontarget; p < 0.0001) and a significant interaction between attention condition and stimulus type (p < 0.0001). Post hoc pairwise comparisons (two-tailed) with Holm-Bonferroni correction revealed that this interaction was driven by a higher R_max for focused-attention targets compared with focused-attention nontargets (blue vs red lines; p < 0.0001) and compared with divided-attention targets (blue vs green lines; p = 0.0086). In addition, R_max for divided-attention nontargets was significantly higher than R_max for focused-attention nontargets (purple vs red lines; p = 0.0018) and R_max for divided-attention targets was significantly higher than R_max for divided-attention nontargets (green vs purple lines; p = 0.017).

In sum, we observed that focused spatial attention primarily increased the slope of P1 and LPD component CRFs via a multiplicative response gain as indexed by R_max, and that there was no significant impact on other parameters, such as the baseline offset or the semisaturation constant. Importantly, the increases in multiplicative response gain of the P1 and LPD component CRFs with focused attention are qualitatively consistent with the effects of focused attention on the psychophysically measured TvC functions, which were also modulated in a manner that is suggestive of a multiplicative response gain in the hypothetical CRFs (see psychophysical results).

Sensory gain is sufficient to account for attention-related behavioral improvements

Although both the psychophysical and the ERP data are consistent with the sensory gain model depicted in Figure 1A, these two independent sources of information must be formally linked to directly test competing accounts of attentional selection. For example, the magnitude of sensory gain that we observe in the ERP data might be either too small or too large to accurately predict the magnitude of psychophysically measured attention effects (Cook and Maunsell, 2002; Cohen and Maunsell, 2009; Pestilli et al., 2011). If this turns out to be the case, then we might need to posit an additional readout mechanism to accurately characterize the behavioral data (Pestilli et al., 2011). In contrast, if the sensory gain model fits the data with a high degree of precision, then we may not need to invoke any additional readout mechanism.

Thus, we then tested a series of nested models that incorporate sensory gain and/or efficient readout to determine which model (or combination of models) most parsimoniously links the ERP-derived CRFs with the psychophysically measured TvC functions. To assess these models, we first estimated the contribution of pure sensory gain to behavioral performance using a quantitative framework based on signal detection theory, which assumes that behavioral contrast discrimination thresholds are directly related to the amplitude difference and the variability of stimulus-evoked responses in early visual cortex. Then, we combined this sensory gain model with a recently developed efficient readout model, which estimates the degree to which early sensory responses are differentially weighted by postperceptual decision mechanisms (Pestilli et al., 2011). This variant of a readout model is designed to ensure that responses evoked by attended stimuli contribute more to a decision variable than responses associated with irrelevant stimuli, even in situations where attention-related sensory gain is minimal.

To investigate the sensory gain model, we first fit the psychophysical contrast discrimination thresholds in the divided-attention condition using a combination of the d′ (Eq. 1) and the Naka-Rushton equations (Eq. 2) to obtain a continuous TvC function (Fig. 9A, green curve). Then, we optimized the sensory noise parameter (σ) in Equation 1 and the baseline (b) parameter in Equation 2 to find the value of each parameter that best fit the P1 and LPD component CRFs using only data from the divided-attention condition. This procedure resulted in an excellent fit for both the P1 (Fig. 9B, green curve; R² = 0.97, σ = 0.15 μV, b = −0.13 μV) and LPD component CRFs (Fig. 9C, green curve; R² = 0.89, σ = 0.44 μV, b = −0.57 μV). To examine how well changes in multiplicative response gain of the P1 and LPD component CRFs (Fig. 8) could account for the observed behavioral improvements with attention (i.e., the downward shift of the TvC curves; Fig. 6B), we then estimated the P1 and LPD component CRFs for the focused-attention target based on the continuous TvC function associated with the focused-attention condition (Fig. 9D, blue curve). Importantly, we used the σ and b parameters that were previously estimated using only the psychophysical TvC and ERP data from the divided-attention conditions (Fig. 9A–C). We observed an increase in the slope of the estimated ERP CRF in the focused-attention conditions (Fig. 8E,F, blue solid curves) compared with the divided-attention conditions (green dotted curves). This slope increase of the estimated CRFs led to an excellent fit to the real ERP CRFs in the focused-attention condition (Figs. 9E,F, blue curves; P1 R² = 0.93; LPD R² = 0.94). These findings strongly suggest that a simple change in multiplicative response gain can sufficiently account for a high degree of attention-induced changes in both the psychophysical and the ERP data.

Figure 9.

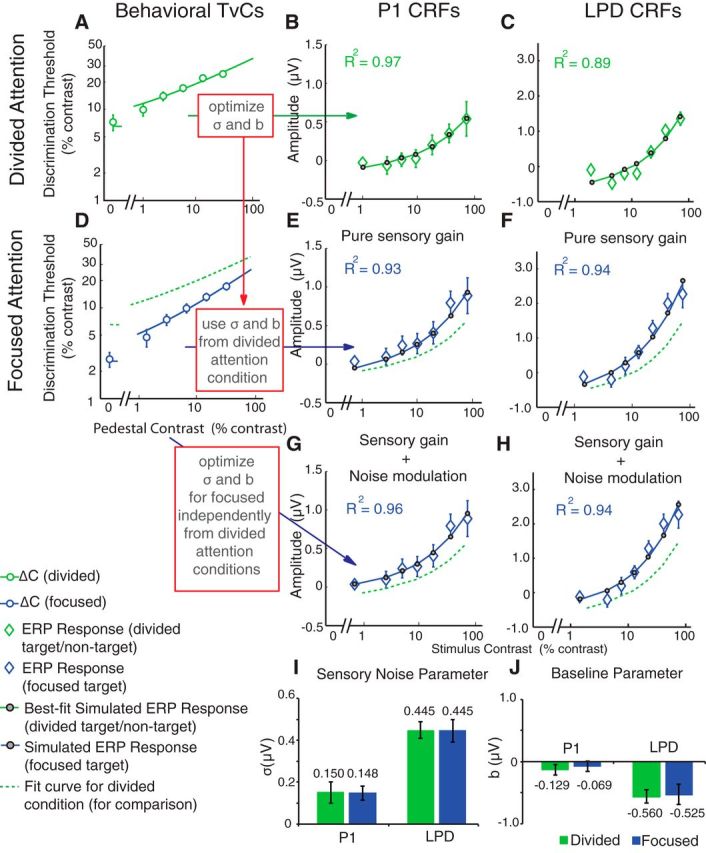
Sensory gain is sufficient to link neural and behavioral data. A–C, The psychophysical TvC function in the divided-attention condition (A, green curve) was used to estimate P1 and LPD component CRFs (B, C, green curves; Fig. 4, fitting procedure; see experimental procedures). Using the modeling routine in Figure 4, the sensory noise (σ) and baseline (b) parameters were optimized to yield the best fits for P1 and LPD component CRFs from the divided-attention condition, respectively. D–F, To examine whether the multiplicative response gain increase in the P1 and the LPD component CRFs could sufficiently account for behavioral improvements with attention, the TvC function from the focused-attention condition (D, blue curve) was then used to estimate the P1 and the LPD component CRFs in the focused-attention condition (E, F, blue curves) using the σ and b parameters obtained from the divided-attention condition (A–C). The simulation yielded excellent fits for both the P1 and the LPD component CRFs. To determine whether noise modulation improves the ability of the model to link neural and behavioral data, a similar analysis was also performed directly on data from the focused-attention condition by allowing the σ and b parameters in the divided-attention and focused-attention conditions to vary freely. G, H, This analysis yielded excellent fits for both the P1 (G) and the LPD (H) component CRFs. However, it did not significantly improve the fit. I, J, Moreover, a bootstrapping analysis on this later fitting procedure demonstrated there was no significant difference in σ (I) and b parameters (J) across divided-attention (green bars) and focused-attention conditions (blue bars). Error bars in A–H indicate ±SEM across subjects. Error bars in I and J indicate ±68% confidence intervals from the bootstrapping analysis.

In addition, we evaluated a more complex model in which the sensory noise (σ) and baseline parameters (b) were also allowed to vary freely between the divided-attention and the focused-attention conditions (yielding four free parameters: σ for divided attention, σ for focused attention, b for divided attention, and b for divided attention). We followed the same procedure outlined above in Figure 9D–F except that we now optimized the σ and b parameters to find the best fit to the P1 and LPD component CRFs obtained in the focused-attention condition. This more complex model led to a slight improvement in the fit to the P1 component CRF (Fig. 9G, blue curve; R² = 0.96, σ = 0.15 μV, b = −0.07 μV) and to the LPD component CRF (Fig. 9H, blue curve; R² = 0.94, σ = 0.45 μV, b = −0.52 μV). However, this improvement was not statistically significant (P1, F_(2,9) = 2.29, p = 0.16; LPD, F_(2,9) = 0.85, p = 0.92, nested F test) so the added complexity of the model with the increased number of free parameters was not justified. An additional bootstrapping analysis with resampled subject labels also revealed that this more complex model did not significantly change the values of the σ (Fig. 9I) or the b parameters (Fig. 9J) across the divided-attention and focused-attention conditions (σ of P1, p = 0.92; σ of LPD, p = 0.98; b of P1, p = 0.46; b of LPD, p = 0.83). This analysis suggests that changes in the sensory noise parameter and the baseline parameter are not necessary for explaining changes in behavior. Consistent with this notion, an additional analysis revealed no significant main effect of attention on the SD of the bootstrapping distribution of P1 (F_(1,15) = 1.19, p = 0.29) and LPD component amplitudes (F_(1,15) = 0.0040, p = 0.60; See Materials and Methods).

Sensory gain outperforms efficient readout

Thus far, a model in which only sensory gain varies between attention conditions can effectively link attention-related changes in behavioral TvCs and neural CRFs. However, we also asked whether a recently developed efficient readout model (Pestilli et al., 2011) could provide an even better account of the link between attention-related changes in neural CRFs and behavioral TvC curves. The model is based on the notion that the subject's task is to select the interval with the higher overall contrast. Thus, an ideal observer could compute the overall contrast across both stimuli in each interval and then select the interval associated with the higher mean contrast. To evaluate this model, we estimated the TvCs in the focused-attention and divided-attention conditions using a max-pooling equation (Eq. 10). In this equation, k is an exponent that weights each of the responses to individual stimuli (k ranges from 1 to ∞). When k = 1, the responses are unmodified and are equal to the magnitude of their evoked responses (simple mean) and the model reduces to the standard sensory gain model described in the previous section. However, when k > 1, the stimulus that evokes a relatively large response will be overweighted compared with a stimulus that evokes a relatively small response, and consequently the stimulus evoking the larger response will increasingly influence downstream decision mechanisms (and as k approaches ∞, only the stimulus that evokes the largest response will contribute). Therefore, if a target-evoked response on a given trial is higher than a nontarget-evoked response, the pooling model will exacerbate this differential response in favor of the target response, and the interval containing the target will tend to be selected correctly. However, if a nontarget-evoked response on a given trial is higher than a target-evoked response, then this model will overweight the nontarget-evoked response and the probability of a correct response will decrease.

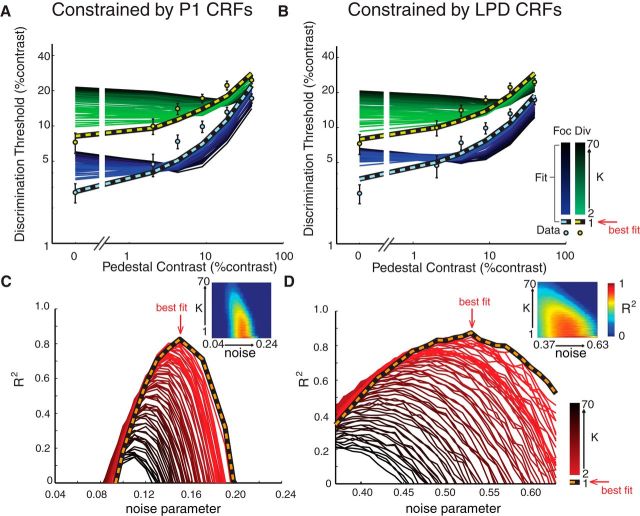
As shown in Figure 10A–D, without the max-pooling rule (i.e., k = 1), the model provided a good description of the observed behavioral data (striped curves) for both focused-attention and divided-attention conditions (R² of 0.82 and 0.87; σ of 0.15 and 0.53 μV for the P1 and LPD components, respectively). Conversely, the addition of the max-pooling rule (i.e., allowing k to adopt values >1) led to increasingly poor model performance that did not closely track the behavioral data (Fig. 10A–D; darker solid color curves for higher values of k). Under these circumstances (k > 1), the selection model overweights responses generated by any high-contrast stimulus in the display, and this degrades performance given that higher contrast stimuli may or may not be the target on a given trial.

Figure 10.

Direct comparison of the sensory gain and efficient readout models. A, B, To test whether the sensory gain model or efficient readout model is better at describing the relationship between the neural and behavioral data, we estimated the psychophysical contrast-discrimination thresholds with the max-pooling rule (Eq. 4), while constraining the fitting procedure with the P1 (A) and LPD (B) component CRFs. When the exponential weight in the max-pooling rule (k) was set to 1 (i.e., equivalent to the pure sensory gain model), the estimated TvC function fit very well with the observed psychophysical thresholds (light blue and black lines, focused-attention condition; light green and black lines, divided-attention condition). However, as k increased (i.e., implementing the max-pooling rule), the performance of the efficient readout model systematically declined. Specifically, the efficient readout model underestimated contrast thresholds when target stimuli had low pedestal contrasts and overestimated contrast thresholds when target stimuli had high pedestal contrasts. Error bars indicate ±SEM across subjects. The shading of the curves indicates the simulations at different k values (bright to dark colors for k of 2–70). C, D, Corresponding R² of the simulations shown in A and B, respectively. Orange and black lines represent the goodness of fit when k = 1. Shading of the curves indicates R² at different k values (bright to dark colors for k of 2–70). Red arrows point to the k and noise values that yield the best fit (k = 1). Insets in C and D show the 2D plots of R² where x and y axes represent noise and k parameters in the fitting routine.

Discussion

Several studies have demonstrated that spatial attention amplifies neural responses in early sensory areas (Haenny et al., 1988; Motter, 1993; Connor et al., 1997; Luck et al., 1997; McAdams and Maunsell, 1999; Reynolds et al., 2000; Martínez-Trujillo and Treue, 2002; Lee and Maunsell, 2009, 2010; Pooresmaeili et al., 2010; Sprague and Serences, 2013); however, very few of them have quantitatively linked these gain modulations with behavioral changes. As a result, almost all documented links between attention and behavior can be explained equally well by theories that invoke either noise modulation (Mitchell et al., 2007, 2009) or postsensory readout mechanisms (Pelli, 1985; Palmer et al., 2000; although see Cohen and Maunsell, 2009; Pestilli et al., 2011). Here, we examined the relative contributions of sensory gain, noise modulation, and readout to attention-dependent changes in perceptual sensitivity by simultaneously linking psychophysical and neurophysiological data using quantitative frameworks based on either signal detection theory or a combination of signal detection theory and efficient readout. We find that a model based solely on a multiplicative increase in the amplitude of the P1 and the LPD component-evoked potentials captures nearly all the variance in behavior, even in an absence of noise modulation. Moreover, this sensory gain model outperforms models that also incorporate an efficient readout mechanism.

Our results stand in contrast with a recent fMRI study (Pestilli et al., 2011), which found that attention induced an additive shift in hemodynamic CRFs. This additive shift cannot explain attention-related changes in TvCs via a sensory gain model, as changes in behavioral sensitivity are only predicted if the CRF slope changes. Note that we use the term additive “shift” instead of additive “gain” here since gain is multiplicative by definition. Alternatively, Pestilli et al. (2011) adopted a readout mechanism based on a max-pooling rule that uses exponentiation to increase differential responses evoked by pedestal and target stimuli. Unlike our study, the nontarget contrast values in Pestilli et al. (2011) by design were very close to the target contrast value. Thus, the additive shift in hemodynamic CRFs ensures that target-related responses will be higher than nontarget-related responses. As the exponent of the max-pooling rule increases, the contrast increment that defines the target will elicit a larger differential response and an ideal observer will more accurately discern the interval that contained the target. Accordingly, this max-pooling rule enabled them to accurately predict the relationship between attention-induced changes in TvCs and hemodynamic CRFs even without changes in slopes of the CRFs.

It is possible that a lack of quantitative evidence for sensory gain in Pestilli et al. (2011) may be due to the insensitivity of fMRI to detect attention-induced sensory gain changes. For example, it is known that attention-related additive increases in hemodynamic CRFs are independent of stimulus intensity (Buracas and Boynton, 2007; Murray, 2008), which is not typically observed in electrophysiological data (Reynolds et al., 2000; Di Russo et al., 2001; Martínez-Trujillo and Treue, 2002; but see Williford and Maunsell, 2006; Kim et al., 2007; Lauritzen et al., 2010; Lee and Maunsell, 2010; Itthipuripat et al., 2014). The stimulus-independent nature of hemodynamic responses is consistent with other reports showing large anticipatory/top-down effects of spatial attention on fMRI signals (Kastner et al., 1999; Ress et al., 2000; Serences et al., 2004; McMains et al., 2007; Sylvester et al., 2009) and this anticipatory/top-down modulation may not always be tightly associated with local neuronal activity (Sirotin and Das, 2009; Cardoso et al., 2012). Moreover, there is evidence from the clinical literature suggesting that fMRI may be insensitive to local changes in sensory gain, as presumed deficits in sensory gain in schizophrenic patients could be captured by EEG but not by fMRI (Calderone et al., 2013).

In contrast to fMRI studies (Buracas and Boynton, 2007; Murray, 2008; Pestilli et al., 2011), studies using EEG (Di Russo et al., 2001; Kim et al., 2007; Lauritzen et al., 2010; Wang and Wade, 2011; Itthipuripat et al., 2014) have shown various gain patterns resembling those measured using single-unit recording (Reynolds et al., 2000; Martínez-Trujillo and Treue, 2002; Lee and Maunsell, 2010). Among these studies, EEG does not typically exhibit an additive offset with attention and it appears to be sensitive to changes in sensory-evoked responses. This sensitivity to sensory responses enables us to assess the interaction of attention and stimulus-evoked responses to evaluate how well a model based on sensory gain can account for behavioral changes. We found that a multiplicative response gain of the ERP-based CRFs was sufficient to explain attention-related changes in behavior. As a result of this strong predictive relationship between ERP gain profiles and behavior, the implementation of a max-pooling rule impaired model fits, as little variance was left to be explained. Also note that by design, target and nontarget pedestal contrasts were fully crossed and independent. Thus a max-pooling rule would not always give more weight to the target-evoked response (e.g., when a low-contrast target paired with a high-contrast nontarget).

One resolution to the discrepancies between different measurements is offered by Hara et al. (2014), who argue that population-based metrics that index the activity from broadly tuned neurons will give rise to additive shifts with attention as observed in hemodynamic CRFs. In contrast, well-tuned cells, as is the case in most single-unit electrophysiology, will exhibit either response or contrast gain, which is thought to be determined by the relative size of the stimulus with respect to the scope of spatial attention as predicted by the normalization model of attention (Reynolds and Heeger, 2009; Herrmann et al., 2010; Itthipuripat et al., 2014). However, this possibility does not by itself offer a clear account for differences between fMRI and EEG, as EEG also provides a broad population-based activity. Further complicating matters, recent work using voltage-sensitive dye imaging (VSDI) also reported additive attention effects in monkey V1 (Chen and Seidemann, 2012). As suggested by Hara et al. (2014), each of these population-level measures (EEG, fMRI, and VSDI) might be differentially sensitive to well tuned and broadly tuned neurons, with EEG perhaps dominated more by responses from well tuned neurons. However, as mentioned above, it is also possible that EEG may be more sensitive to attentional modulations of local stimulus-evoked spiking activity, whereas fMRI and VSDI may be more sensitive to top-down signals. Consistent with this idea, fMRI has been suggested to be sensitive to capture synaptic inputs to particular cortical areas instead of spiking outputs from the areas (Logothetis, 2002, 2008; Logothetis and Wandell, 2004; Viswanathan and Freeman, 2007). Similarly, VSDI primarily captures the top-down inputs to V1 rather than the local modulations of spiking in V1 (Chen and Seidemann, 2012). In contrast to fMRI and VSDI, EEG has been closely associated with spiking activity in visual cortex (Whittingstall and Logothetis, 2009) and tightly linked to the perceived appearance of a stimulus (Campbell and Kulikowski, 1972; Störmer et al., 2009). Thus, it is possible that attentional modulation of stimulus-evoked spiking activity, which might be better captured by EEG, is more closely related to perceptual experience and its behavioral outcomes. Nonetheless, these attention-related changes in stimulus-evoked sensory responses are presumably being modulated by top-down attention signals, so understanding how different metrics of brain activity index different aspects of attentional modulation is crucial to develop a more complete understanding of cortical information processing.

Contrary to the sensory gain and efficient readout accounts, recent studies in monkeys have demonstrated that attention modulates neural noise. Attention has been shown to modulate the trial-by-trial variability of single neuron spike rates as well as pairwise correlations between neurons in early visual areas (Mitchell et al., 2007, 2009; Cohen and Maunsell, 2009; Niebergall et al., 2011; Herrero et al., 2013). These noise modulations have been hypothesized to lead to a larger improvement in the signal-to-noise ratio (SNR) of neural populations compared with pure changes in sensory gain (Cohen and Maunsell, 2009; Mitchell et al., 2009). In our study, we found that sensory gain in ERPs could satisfactorily account for the observed behavioral improvements, even under the assumption that the trial-by-trial variability of ERP amplitudes is unaltered across attention conditions. Note, however, that our results are not necessarily inconsistent with observations from monkey data showing that attention does modulate neural noise, because EEG measures do not provide direct estimates of single-unit variability or population-level covariance measures (and the same limitation also applies for fMRI measures). Indeed, it is possible that attention-related modulations in neural noise might contribute to changes in ERP amplitudes. For example, if sensory neurons fire more consistently, and if changes in noise correlation improve the SNR of pooled neuronal signals, then these noise modulations may strengthen the synchronization across local neural populations and thus amplify the electrical dipole that generates an ERP on the scalp (Cooper et al., 1965; Gloor, 1985; Makeig et al., 2002; Murakami and Okada, 2006). Therefore, it is also possible that changes in the noise characteristics of underlying neural generators might influence attentional modulation of the P1 and LPD components.