Abstract
It is desirable to predict the tumor growth rate so that appropriate treatment can be planned in the early stage. Previously, we proposed a finite element method (FEM)-based 3D kidney tumor growth prediction system using longitudinal images. A reaction-diffusion model was applied as the tumor growth model. In this paper, we not only improve the tumor growth model by coupling the reaction-diffusion model with a biomechanical model, but also take the surrounding tissues into account. Different diffusion and biomechanical properties are applied for different tissue types. FEM is employed to simulate the coupled tumor growth model. Model parameters are estimated by optimizing an objective function of overlap accuracy using a hybrid optimization parallel search package (HOPSPACK). The proposed method was tested with kidney CT images of eight tumors from five patients with seven time points. The experimental results showed the performance of the proposed method improved greatly compared to our previous work.
Index Terms: Tumor growth prediction, finite element method, biomechanical model, reaction diffusion model, kidney tumor
I. Introduction
Kidney cancer is among the ten most common cancers in both men and women. The lifetime risk for developing kidney cancer is about 1 in 75 (1.34%) [1]. It is desirable to predict the kidney tumor growth rate in clinical research so that appropriate treatment can be planned. “The accurate tumor growth prediction will provide a significant aid in the determination of the appropriate treatment modality, and also help for deciding the level of aggressiveness to undertake for each patient.”
During the last three decades, the methods for simulating tumor growth have been extensively studied. The representative methods include mathematical models [2, 3, 14], cellular automata [4], finite element [3, 5] and angiogenesis based methods [6]. However, most of these methods were focused on brain tumor. Only a few worked on organ tumors in the body region. Pathmanathan et al. [7] proposed to use the finite-element method to build a 3-D patient specific breast model and used it to predict the tumor location. However, their method was not intended for tumor growth prediction.
Previously, we proposed a tumor growth prediction system for kidney tumor based on a finite element method (FEM) [16]. The kidney tissues were classified into three main types: renal cortex, renal medulla and renal pelvis. However, surrounding tissues were not taken into consideration. Different diffusion properties are considered for the kidney: the renal cortex and renal pelvis were isotropic while renal medulla was anisotropic. The reaction-diffusion model was applied to model the tumor growth and the FEM was applied to simulate this diffusion process. In this paper, we improve our previous work by (1) coupling the reaction-diffusion model and biomechanical model; and (2) taking the surrounding tissues into account. We examined the kidney tumor data and found that non-kidney tissues surrounding tumors at the kidney surface are mostly visceral fat. Therefore, we add fat tissues in our new model. We assign different diffusion and biomechanical properties for different tissue types, and employ the FEM method to simulate the coupled tumor growth model. We tested the proposed method on a larger data set of kidney CT images, with eight tumors from five patients with seven time points (previously five tumors from two patients).
II. Coupling Model Based Tumor Growth Prediction
A. Overview of the proposed approach
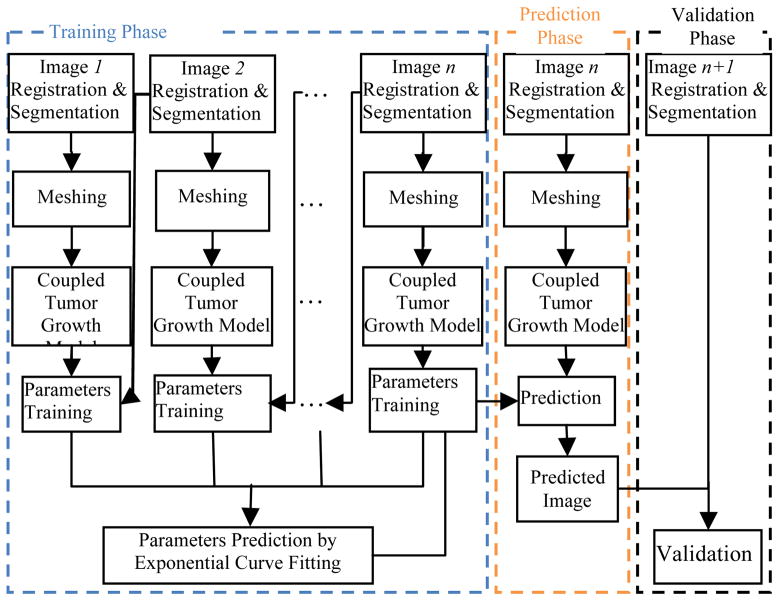
The flowchart of our tumor growth prediction system is shown in Fig. 1. The system consists of three main phases: training, prediction and validation. Suppose the longitudinal study has n+1 time points. We use the first n time point images for training. Fig. 2 shows the kidney tumor growth process on one patient with 7 time points. The training phase is composed of five steps. First, image registration and segmentation are conducted on the kidney images. Second, tetrahedral meshes are constructed for both the segmented kidney and tumors. Third, the coupling of reaction-diffusion with the biomechanical model is applied as the tumor growth model, and FEM is used to solve this coupled model. Fourth, the parameters of the tumor growth model are optimized by HOPSPACK. Fifth, after computing the parameters based on the first n images, the model parameters for prediction at the n+1th time point are estimated by exponential curve fitting using the non-linear least squares method. In the prediction phase, the estimated growth parameters are applied to the tumor growth model to compute the prediction result for time point n+1 using the image at time point n as reference. In the validation phase, the prediction result is validated by comparing it with image n+1.
Fig. 1.
The flowchart of the proposed tumor growth prediction system.
Fig. 2.

The kidney tumor growth process for one patient with 7 time points from 2004 to 2007, manually segmented boundaries are represented by red color contour.
B. Registration, Image segmentation and Meshing
The baseline study is used as the reference study and all other studies are registered to it via a rigid transformation. Then, the kidney is segmented using a combination of graph-cut and active appearance model [16]. This method segments the kidney into three types of tissues: renal cortex, medulla and pelvis. After the kidney is segmented, tumors and visceral fat tissues surrounding the tumors are manually segmented. Tetrahedral meshes are built for the segmented tissues using the ISO2Mesh method [9].
C. Coupling of Reaction-Diffusion and Biomechanical Models
During the tumor growth process, tumor cells can invade and infiltrate the surrounding healthy tissues. As the number of tumor cells increases, pressure internal to the tumor will increase unless the tumor pushes away the surrounding tissues (mass-effect). Based on this hypothesis, we propose to couple the reaction-diffusion model with the biomechanical model to simulate the tumor growing process.
The reaction-diffusion model [3] is adopted to model the proliferation and infiltration of tumor cells in the kidney. It was first proposed in chemistry, and widely applied in biology, geology, physics and ecology. The model is defined as follows:
| (1) |
where c represents the tumor cell density, D is the diffusion coefficient of tumor cells, S(c,t) represents the source factor function that describes the proliferation of tumor cells and T(c,t) is used to model the efficacy of the tumor treatment.
Since our purpose is to predict the tumor growth before treatment, the treatment term T(c,t) is omitted. The source factor S(c,t) can be modeled using Gompertz’s law [3], which is defined as follows,
| (2) |
where ρ is the proliferation rate of tumor cells and Cmax is the maximum tumor cell carrying capacity of the kidney. According to [3], Cmax is set to 3.5×104Cells mm−3.
Combining Equ. (1) and (2) and omitting T(c,t), we can get,
| (3) |
Based on [8], the diffusion in the renal cortex, pelvis and fat are considered to be isotropic, while that in renal medulla is anisotropic and the diffusion in the radial direction is faster than other directions. The diffusion properties are listed in Table 1. It is important to note that in the diffusivity matrix Dm of medulla, the diffusivity in the radial direction is set as λ (λ >1) times of those in other directions.
Table 1.
Diffusion properties (D), Young modules E and Poisson coefficients of different tissues. (D and E will be estimated in section 2.3.)
| Tissue | Diffusivity D (10−3mm2s−1) | Young modulus E (KPa) | Poisson coefficient |
|---|---|---|---|
| Renal cortex | Dc (isotropic) | Ec | 0.4 |
| Renal medulla | Dm (anisotropic) | Em | 0.45 |
| Renal pelvis | Dp (isotropic) | Ep | 0.4 |
| Visceral fat | Df (isotropic) | Ef | 0.45 |
We use the classical continuum mechanics formalism to describe the mechanical behavior of the kidney tumor. Since the deformation process is very slow, the static equilibrium equation is used,
| (4) |
where fexternal is the external force applied on the tissue (body force), σ is the internal stress tensor. Here fexternal is proportional to the tumor cell density:
| (5) |
The proliferation is assumed to slow down in regions where c approaches Cmax. Thus, f (c) is defined as,
| (6) |
where α, β are positive constants. This function has a maximum at c = Cmax.
Based on the constitutive equation, we have,
| (7) |
| (8) |
where K is the elasticity tensor (Pa, related to Young’s modulus and Poisson coefficient) and ε is the linearized Lagrange strain tensor expressed as a function of the displacement u.
Based on [13], in this paper, different Young modulus and Poisson coefficients are assigned to renal cortex, medulla, pelvis and visceral fat, as listed in Table 1.
The coupling model for simulating tumor growth is summarized as follows,
| (9) |
| (10) |
| (11) |
The finite element method (FEM) is used to solve the above coupled PDE equations. Based on the Galerkin method [11], the continuous problem can be converted to a discrete problem in a subvectorial space of finite dimension. In principle, it is the equivalent of applying the method of variation to a function space, by converting the equation to a weak formulation. The details of implementation of a reaction-diffusion model by FEM can be found in [11].
D. Tumor Growth Model Parameters Training
In our tumor growth model, α, β, Dc, Dm, Dp, Df, ρ, Ec, Em, Ep and Ef are the parameters to be estimated. It is important to notice that we assumed α and β are same for all patients. As for Poisson coefficients, we assume they do not change, so the values in Table 1 are used. The optimal set of tumor growth parameters for a particular patient is estimated using the patient’s image (image driven). The optimization of the tumor model parameters is based on the hypothesis that the optimal tumor parameters minimize the discrepancies between the simulated tumor image and the patient tumor image. It is achieved by solving the following optimization problem,
| (12) |
where θ ={α, β, Dc, Dm, Dp, Df, ρ, Ec, Em, Ep, Ef} and F is the objective function. Many criteria can be used to construct function F, such as the overlap accuracy, feature-based similarity and smoothness of the registration [14]. Here, we use only the overlap accuracy. In this paper, we assumed the tissue diffusion properties do not change over the tumor growing process, while the proliferation rate ρ could change. Suppose ρ1, ρ2, …, ρn-1 are the proliferation rates corresponding to time points t1, t2, …, tn-1, respectively, then the parameters that need to be estimated become:
As mentioned earlier, the first n studies are used for model parameters training. The parameters are trained by pairs, using consecutive studies i and i+1. Finally, our objective function is:
| (13) |
where Ii+1 is used as the validation image, Ii,θ is the predicted tumor image by applying parameter set θ on image Ii, and w is the weight for TPVF (true positive volume fraction [10]), w=0.5 in this paper. TPVF indicates the fraction of the total amount of tumor correctly predicted and FPVF (false positive volume fraction) denotes the amount of ‘tumor’ falsely identified. After a new tumor image is predicted, a thresholding method is applied to segment the tumor. We use the threshold of 8000 cell mm−3, as suggested in Tracqui et al. [12].
The optimization of Eq. (12) is not a trivial task, due to the discontinuities in the objective function. Pattern search methods such as HOPSPACK, proposed in [15], are suitable for such problems. HOPSPACK is a hybrid optimization search method and takes advantage of multi-threading and parallel computing platforms for efficient search. Due to the complicated form of our objective function, it is not guaranteed that a global optimum exists. We set the maximum iteration of 200 in the optimization process.
E. Tumor Growth Prediction
After the parameters are optimized, they are applied to the tumor growth model to compute the prediction result for time point n+1. For diffusion and biomechanical parameters, assumed not changing over time, the optimized values can be used directly. Since the proliferation rate ρ may change over time, it needs to be recalibrated for every time point n based on the previously optimized values ρ1, ρ2, …, ρn-1. Based on [12], we assume the tumor growth follows the exponential law, such that:
| (14) |
where, a, b, c, d are the growth coefficients. Curve-fitting based on the non-linear least squares method is used to fit ρ.
III. Experimental Results
We tested the proposed method on longitudinal studies of kidney tumors from five patients (2 male and 3 female, 40–61 years old). Contrast-enhanced CT images in arterial phase were used. All five patients had 7 time points images scanned at regular intervals over a period of 3 to 6 years. Three, two and one kidney tumors were monitored for patient #1, #2, and #3–5, respectively (eight tumors in total). The CT images were acquired from GE LightSpeed QX scanner. The slice spacing varies from 1.00 to 5.00 mm and pixel size varies from 0.70×0.70 to 0.78×0.78 mm2. All images were segmented manually by an expert to generate the reference standard.
The training of parameters in the tumor growth model was done using the first six time points and validated on the seventh one. The trained α =0.221 and β =0.015. Trained diffusivities and ρ are shown in Table 2 and Fig. 3. The average training time was about 30 hours using Matlab programs running on an Intel Xeon E5440 workstation with quad cores(2.83GHz), 8 threads, and 8 GB of RAM, which can be done off-line. Fig. 4 shows the prediction results for two different studies. The prediction process took about 100 seconds.
Table 2.
Trained diffusivities ((mm−2day−1)) and Young modulus (KPa) for each tissue in five studies.
| Diffusivity (mm−2day−1) | Study #1 | Study #2 | Study #3 | Study #4 | Study #5 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Tumor1 | Tumor2 | Tumor3 | Tumor1 | Tumor2 | Tumor1 | Tumor1 | Tumor1 | ||
| Dc (isotropic) | 0.085 | 0.088 | 0.098 | 0.083 | 0.071 | 0.062 | 0.082 | 0.102 | |
| Dm (anisotropic) | Dradical dir | 0.076 | 0.080 | 0.087 | 0.079 | 0.060 | 0.053 | 0.073 | 0.089 |
| Dother dirs | 0.065 | 0.066 | 0.074 | 0.063 | 0.053 | 0.045 | 0.061 | 0.073 | |
| λ | 1.169 | 1.212 | 1.175 | 1.253 | 1.132 | 1.177 | 1.196 | 1.119 | |
| Dp (isotropic) | 0.093 | 0.101 | 0.105 | 0.095 | 0.079 | 0.080 | 0.099 | 0.115 | |
| Df (isotropic) | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | |
| Ec | 233 | 215 | 221 | 231 | 201 | ||||
| Em | 116 | 132 | 125 | 136 | 102 | ||||
| Ep | 116 | 118 | 121 | 128 | 109 | ||||
| Ef | 10 | 15 | 18 | 25 | 8 | ||||
Fig. 3.
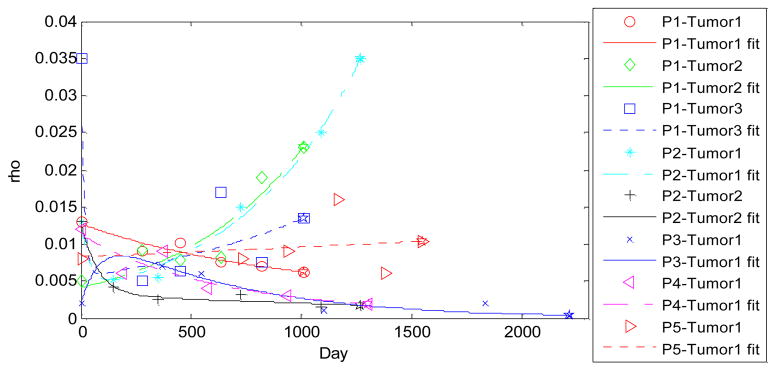
Parameter ρ curve fit by eq. (14) for all 8 tumors. The fit was based on the 5 estimated values, and the 6th value (overlap with ☆) was used for prediction. P2-Tumor1 was shown in Fig. 2.
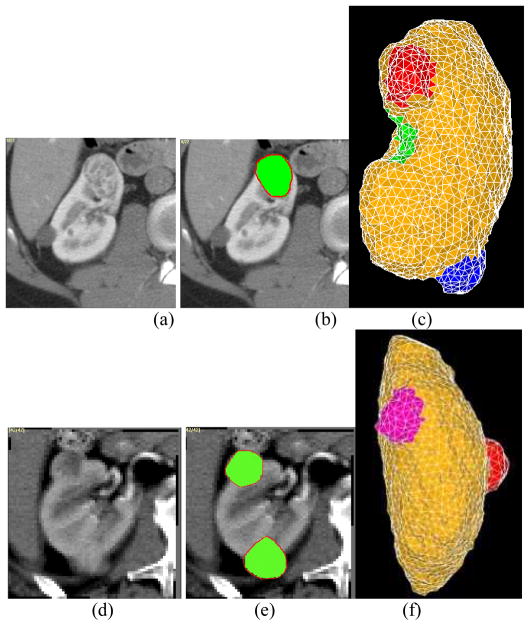
Fig. 4.
Results of the tumor growth prediction on two slices for two different studies. (a) and (d) are the images at time point 7. (b) and (e) shows the prediction results by green overlaid on (a) and (d), respectively. (c) and (f) show the meshes results. Red contour represents the manually segmented tumor results.
As for the quantitative evaluation, the volume difference, TPVF and FPVF [10] were used to show the accuracy of the proposed method. Our new method was compared with our previous method which only used the reaction-diffusion model. The results are shown in Table 3. We can see the performance was much improved (volume difference dropped from average 5.125% to 4.325%, TPVF increased from 90.825% to 92.725%, and FPVF dropped from 4.5% to 3.125%) by coupling the reaction-diffusion model and the biomechanical model. The paired t-test results showed these performance improvements are statistically significant (p<0.01).
Table 3.
Comparison of prediction performance based on reaction-diffusion model and the proposed coupling model: volume difference, TPVF and FPVF.
| Study #1 | Study #2 | Study #3 | Study #4 | Study #5 | Summary | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tumor1 | Tumor2 | Tumor3 | Tumor1 | Tumor2 | Tumor1 | Tumor1 | Tumor1 | |||
| VolDif | Reaction-diffusion model | 4.1% | 5.1% | 4.8% | 4.5% | 5.7% | 5.5% | 6.1% | 5.2% | 5.1% |
| Coupling model | 3.1% | 4.3% | 4.1% | 4.0% | 5.1% | 4.6% | 4.9% | 4.5% | 4.3% | |
| TPVF | Reaction-diffusion model | 91.5% | 90.9% | 91.6% | 92.1% | 90.8% | 90.1% | 89.3% | 90.3% | 90.8% |
| Coupling model | 93.2% | 92.5% | 93.5% | 93.8% | 92.8% | 91.9% | 91.6% | 92.5% | 92.7% | |
| FPVF | Reaction-diffusion model | 4.6% | 4.2% | 3.7% | 3.5% | 3.8% | 5.3% | 6.1% | 4.8% | 4.5% |
| Coupling model | 3.1% | 2.9% | 3.1% | 2.4% | 2.9% | 3.5% | 3.9% | 3.2% | 3.1% | |
IV. Conclusions and discussion
Different mathematical model has been employed to simulate growth of tumors of different types. Such as Gompertz model was successfully used to describe the growth rate of solid avascular tumors at the population level [17], reaction diffusion model was successfully applied to simulate growth of brain Glioblastomas tumor [3]. In this paper, we try to couples a reaction-diffusion model and biomechanical model to simulate the kidney tumor growth. The proposed method was tested on eight tumors from five patients’ longitudinal studies with seven time points. Compared to the prediction results based on only the reaction-diffusion model [16], the overall performance based on the coupling model has been improved: volume difference was decreased from 5.1% to 4.3%, TPVF was increased from 90.8% to 92.7%, and FPVF was decreased from 4.5% to 3.1%. The training time was increased from 260 minutes to 30 hours due to more parameters need to be estimated, however, this can be done off-line.
We include only visceral fat in the model in this study as we found that the tissues directly surrounding the kidney tumors are mostly visceral fat. However, this is not always true; sometimes kidney tumor may touch the liver. Taking more surrounding tissues into consideration is another important issue that will be investigated in our future work.
Contributor Information
Xinjian Chen, Email: xjchen@suda.edu.cn, School of Electronics and Information Engineering, Soochow University, Suzhou City, China 215006.
Ronald M. Summers, Email: rsummers@mail.nih.gov, Radiology and Imaging Sciences Dept., National Institute of Health, Bethesda, MD 20892, USA
Jianhua Yao, Email: jyao@mail.nih.gov, Radiology and Imaging Sciences Dept., National Institute of Health, Bethesda, MD 20892, USA.
References
- 1.American Cancer Society. http://www.cancer.org/docroot/cri/content/cri_2_4_1x_what_are_the_key_statistics_for_kidney_cancer_22.asp.
- 2.Swanson K, Bridge C, Murray JD, Alvord EC. Virtual and real brain tumors: Using mathematical modeling to quantify glioma growth and invasion. J Neurol Sci. 2003 Dec;216(1):1–10. doi: 10.1016/j.jns.2003.06.001. [DOI] [PubMed] [Google Scholar]
- 3.Clatz O, Sermesant M, Bondiau PY, Delingette H, Warfield SK, Malandain G, Ayache N. Realistic simulation of the 3-D growth of brain tumors in MR images coupling diffusion with biomechanical deformation. IEEE Trans Med Imaging. 2005 Oct;24(10):1334–46. doi: 10.1109/TMI.2005.857217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mallet DG, Pillis LGD. A cellular automata model of tumor-immune interactions. Journal of Theoretical Biology. 2006;239(3):334–350. doi: 10.1016/j.jtbi.2005.08.002. [DOI] [PubMed] [Google Scholar]
- 5.Mohamed A, Davatzikos C. Finite element modeling of brain tumor mass-effect from 3D medical images. In: Duncan JS, Gerig G, editors. MICCAI 2005 LNCS. Vol. 3750. pp. 400–408. [DOI] [PubMed] [Google Scholar]
- 6.Lloyd BA, Szczerba D, Székely G. A Coupled Finite Element Model of Tumor Growth and Vascularization. MICCAI. 2007:874–881. doi: 10.1007/978-3-540-75759-7_106. [DOI] [PubMed] [Google Scholar]
- 7.Pathmanathan P, Gavaghan DJ, Whiteley JP, Chapman SJ, Brady JM. Predicting tumor location by modeling the deformation of the breast. IEEE Trans Biomed Eng. 2008 Oct;55(10):2471–80. doi: 10.1109/TBME.2008.925714. [DOI] [PubMed] [Google Scholar]
- 8.Chandarana H, Hecht E, Taouli B, Sigmund EE. Diffusion Tensor Imaging of In Vivo Human Kidney at 3T: Robust anisotropy measurement in the medulla. Proc Intl Soc Mag Reson Med. 16(2008):494. [Google Scholar]
- 9.Fang Q. ISO2Mesh: a 3D surface and volumetric mesh generator for matlab/octave. http://iso2mesh.sourceforge.net/cgi-bin/index.cgi?Home.
- 10.Udupa JK, Leblanc VR, Zhuge, et al. A framework for evaluating image segmentation algorithms. Computerized Medical Imaging and Graphics. 2006;30(2):75–87. doi: 10.1016/j.compmedimag.2005.12.001. [DOI] [PubMed] [Google Scholar]
- 11.Hanhart Al MK, Izu LT. A memory-efficient finite element method for systems of reaction-diffusion equations with non-smooth forcing. Jonunal of Computational and Applied Mathematics. 2004;169:431–458. [Google Scholar]
- 12.Tracqui P, Cruywagen G, Woodward D, Bartoo G, Murray J, Alvord E., Jr A mathematical model of glioma growth: The effect of chemotherapy on spatio-temporal growth. Cell Proliferation. 1995 Jan;28(1):17–31. doi: 10.1111/j.1365-2184.1995.tb00036.x. [DOI] [PubMed] [Google Scholar]
- 13.Kallel F, Ophir J, Magee K, Krouskop T. Elastographic Imaging of Low-Contrast Elastic Modulus Distributions in Tissue. Ultrasound in Medicine & Biology. 1998;24(3):409–425. doi: 10.1016/s0301-5629(97)00287-1. [DOI] [PubMed] [Google Scholar]
- 14.Hoge Cosmina, Davatzikos Christos, Biros George. An image-driven parameter estimation problem for a reaction-diffusion glioma growth model with mass effects. J Math Biol. 2008;56:793–825. doi: 10.1007/s00285-007-0139-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gray GA, Kolda TG. Algorithm 856: APPSPACK 4.0: Asynchronous parallel pattern search for derivative-free optimization. ACM Transactions on Mathematical Software. 2006;32:485–507. [Google Scholar]
- 16.Chen X, Summers RM, Yao J. FEM Based 3D Tumor Growth Prediction for Kidney Tumor. IEEE Transactions on Biomedical Engineering. 2011;58(3):463–467. doi: 10.1109/TBME.2010.2089522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bajzer Z. Gompertzian growth as a self-similar and allometric process. Growth Dev Aging. 1999;63(1–2):3–11. [PubMed] [Google Scholar]