Mechanisms shaping cell membranes

Abstract

Membranes of intracellular organelles are characterized by large curvatures with radii of the order of 10–30nm. While, generally, membrane curvature can be a consequence of any asymmetry between the membrane monolayers, generation of large curvatures requires the action of mechanisms based on specialized proteins. Here we discuss the three most relevant classes of such mechanisms with emphasis on the physical requirements for proteins to be effective in generation of membrane curvature. We provide new quantitative estimates of membrane bending by shallow hydrophobic insertions and compare the efficiency of the insertion mechanism with those of the protein scaffolding and crowding mechanisms.

Introduction

Biological membranes serve as envelopes around cells and intracellular compartments and, are hence crucial for providing insulation of intracellular life from the environment and enabling the complexity of intracellular processes.

Most intracellular membranes have highly complex shapes characterized by a large ratio between the area and the enclosed volume. A biological reason for this is the necessity to facilitate or accelerate the molecular exchange between the luminal volume bounded by the membrane and the cytosol. Peripheral Endoplasmic Reticulum (ER) consists of 30–50nm thick tubules interconnected by three-way junctions into an elaborate three-dimensional network, and micron wide sheets with a thickness similar to that of the tubes [1,2]. The sheets can be stacked by peculiar helicoidal membrane connections [3], can have fenestrations [4] and their rims are connected to the tubes. The 10–20nm thick cisternae of the Golgi Complex (GC) are stacked, strongly fenestrated, and undergo constituent material exchange by fusion and fission with spherical vesicles and pleiomorphic traffic intermediates [5,6]. The inner membranes of mitochondria are compartmentalized into numerous cristae, the thin sheet-like structures similar in their dimensions to the ER sheets and GC cisternae [7,8]. A common feature of all these structures is the large membrane curvature seen in their cross-sections. The radii of these curvatures, varying in the range of 10–30nm, are only a few times larger compared to the 4–5nm thicknesses of the membranes. Similarly large curvatures characterise also other intracellular membranes such as endocytic vesicles [9–11] and caveolae [12,13].

A question arises whether generation of large membrane curvatures and the related intricate shapes of intracellular compartments is an easy task for cells, which can be completed using non-specific mechanisms based on thermal undulations of the membrane surface, or whether cells must utilize special molecular mechanisms consuming energy and employing specialized proteins. The answer to this question can be reduced to the physical and, more specifically, mechanical properties of membranes. From a physical point of view, membranes can be defined as nano-films consisting of a mixture of lipids and proteins. The structural basis of any biological membrane is a few nanometres thick lipid bilayer, which forms by self-organization of amphipathic molecules of phospholipids within aqueous solutions [14]. Proteins bind lipid bilayers by inserting their hydrophobic domains into the bilayer interior and/or through attraction of their hydrophilic domains to the bilayer surface mediated by such physical forces as electrostatic, Van-der-Waals or hydrogen bonding forces [15,16].

There are two competing physical properties of lipid bilayers, whose interplay enables the ability of the membranes to serve as universal biological wrappers and determines the shapes of the resulting membrane envelopes.

On one hand, a homogeneous lipid bilayer formed by individual lipids prefers to remain flat and is resistant to any deviation from this shape by bending. The tendency to flatness is dictated by the symmetry of its monolayers. The resistance to bending is determined by the intra-monolayer interactions between the lipid molecules. In spite of a common intuitive feeling that a 4nm thick film consisting of soft biological matter should be absolutely flexible, a typical lipid bilayer is characterized by bending rigidity of about κ = 20 k_BT (where k_BT ≈ 0.6 kcal/mole is a product of the Boltzmann constant and the absolute temperature). This rigidity is an order of magnitude larger than a characteristic energy of about 1 k_BT provided by thermal fluctuations, which means that the latter cannot determine membrane shapes.

On the other hand, any bilayer tends to be continuous, resisting all kinds of ruptures and structural defects and, particularly, it avoids having edges [17]. In order to get rid of its external edge, any initially flat bilayer has to adopt a closed shape, which is unavoidably accompanied by the bilayer bending [18]. Hence, the membrane bending rigidity and the tendency to prevent edge formation compete. This competition results in any bilayer fragment larger than 200nm in diameter adopting a closed spherical shape whose bending energy is about 8πκ = 500 k_BT ≈300 kcal/mole (which is independent of the sphere radius) [18].

In conclusion, according to their basic physical properties, homogeneous and symmetric lipid bilayers tend to adopt shapes of closed spheres. Deviations of the bilayer shape from the spherical one require either changes of the bilayer structural properties making it asymmetric or applications of forces to the bilayer surface providing energies in the range of tens to hundreds of kcal/mole, depending on the extent of deformation. The membrane asymmetry can be achieved by having different lipid compositions and/or different amounts of lipid molecules in the two monolayers [19]. Alternatively, asymmetry can be produced by asymmetric protein binding to the two membrane sides. The forces acting on intracellular membranes and deforming them can be produced only by proteins or protein machines.

By analogy to membrane remodelling by fusion, which is known for different fusion events to be driven by unrelated proteins [20–22], it is conceivable that a cell employs various molecular mechanisms for generation of membrane curvatures and shapes of different subcellular compartments. Below we list and discuss some of these mechanisms driven directly by proteins.

Ways in which proteins create membrane curvature

By molecular motors and cytoskeletal filaments

High membrane curvatures of cellular nanotubules or tubular components of the trans-Golgi Complex and ER could, in general, be produced by ensembles of polymerizing actin filaments or by groups of molecular motors such as kinesins or dyneins attached to the membranes and moving along the cytoskeletal filaments.

All these system must be able to develop forces sufficient for generation of the relevant membrane curvatures with radii of about ρ = 10nm. A required force f can be estimated by dividing the membrane bending rigidity κ by ρ, which gives $f=\frac{\kappa }{\rho }\approx 10\text{pN}$. A characteristic maximal force, which can be produced by one polymerizing actin filament or one molecular motor is of the order of 1pN [23,24]. Hence, ensembles of several molecular motors working in concert, or bundles keeping together tens of polymerizing actin filaments must have enough power to provide the required curvatures.

At the same time, a crucial question arises about the specific means by which these forces have to be transmitted to the membrane. The forces would be ineffective if applied tangentially to the membrane surface. The reason for this is that protein anchors connecting the polymerizing filament tips or the molecular motors to the membrane must be freely movable along the membrane plane due to the two-dimensional membrane fluidity. As a result, in the tangential direction only transient and weak viscous forces [25–27] but not the long lasting elastic forces needed for the generation of stable curvature can be transmitted. To be effective, the forces have to be directed normally to the membrane plane and applied to limited spots of the membrane area. At the same time the bulk of the membrane has to be under lateral tension counteracting the applied force. Such setup is realized, for example, in artificial systems where membrane tethers of large curvatures are pulled out of stressed giant vesicles by localized force application through beads attached to the membrane surface (see e.g. [28]). In vivo, actin filament bundles polymerizing against tensed plasma membranes must be the major driving force of filopodia formation[29], while molecular motors accumulating at the tips of microtubules and anchored in membranes must be able to drive intracellular membrane tube formation (see for review [30]).

Importantly, membrane tubes generated by the pulling or pushing force application are persistently stretched and, therefore, the tubule axes must appear as straight lines. While this is true for filopodia under normal conditions [31], the tubules of ER look loose, their axes being bent [1,2]. It is conceivable that the pulling mechanisms may be involved in the initial stages of formation of ER or trans-Golgi tubules, but the tube stabilization and maintenance have to be due to other mechanisms such as membrane bending by reticulon and/or DP1/Yop1p proteins [32–36] (see below).

By hydrophilic protein domains adhering to membrane surfaces: scaffolding and crowding

Binding of hydrophilic proteins to the surface of one membrane monolayer leads to membrane asymmetry and, hence, may produce membrane curvature.

Such proteins, referred to below as scaffolds, can most efficiently bend membranes if their membrane interaction faces are intrinsically curved or if they polymerize into multimolecular oligomers with a preferred curved architecture. Depending on their structure, the protein scaffolds can impose their curvature on membranes by moulding the membranes into spherical or cylindrical shapes. Well-documented examples of multimeric spherical scaffolds are protein coats such as COPI, COPII and clathrin coats that polymerize around nascent vesicles as the latter bud from donor compartments (see for recent review [37]). Candidates for acting as cylindrical multimeric scaffolds are oligomers of dynamin family proteins involved in endocytosis (see for recent review [38]), and, probably, oligomers of reticulons and DP1/Yop1p shaping ER tubules and sheets [32–36] and some BAR domain proteins. Other BAR domain proteins form monomeric cylindrical scaffolds having an intrinsic crescent-like shape (see for review [39,40]). We are not aware of any example of a spherical monomeric scaffold.

To be effective, a protein scaffold must bind the membrane surface with an energy exceeding the membrane bending energy and the scaffold rigidity has to be larger than the membrane bending rigidity. For monomeric scaffolds a curved shape, large rigidity and strong membrane affinity must characterize the individual protein domains. In the case of multimeric scaffolds, all three characteristics may result from the subunit polymerization. For example, while separate clathrin triskelia appear to be, approximately, as soft as a lipid bilayer [41,42], the clathrin baskets resulting from the triskelion self-assembly may be sufficiently rigid to bend membranes [43].

Protein scaffolds generate membrane curvature at the membrane contact surface and in their immediate vicinity. For monomeric scaffolds the larger the membrane area coverage by the scaffolds is, the closer the generated membrane curvature to the intrinsic curvature of the protein.

Besides scaffolding activity, monomeric hydrophilic protein domains bound to the membrane surface have been suggested to generate membrane curvature by a crowding mechanism [44]. The essence of this mechanism is that hydrophilic protein domains undergo a thermally driven lateral diffusion and collide with each other in a plane, which is parallel to, but remote from, the membrane plane by a distance equal, approximately, to the domain size. Similar to molecules of a hypothetical 2D gas, these protein domains are suggested to generate a 2D pressure in the plane of their collisions. The distance between this plane and the membrane plane serves as a lever by which the 2D pressure produces bending moment acting on the membrane. This effect is nonspecific in its nature since it could to be produced by any particles bound to the membrane that undergo lateral diffusion above the membrane surface.

A crucial question is whether the crowding mechanism can generate high membrane curvatures on its own or merely contributes to or interferes with [45] the action of more powerful mechanisms. Below we present a quantitative computational assessment of the curvature produced by crowding, predicting a relatively low efficiency of curvature generation in comparison to the mechanism based on insertion of protein domains into the membrane matrix. In any case, the biological relevance of a crowding mechanism is questionable given that crowding is a non-specific feature of all proteins with extra-membrane protruding domains. For common cell membranes protein crowding will be essentially equal on both sides of the membrane, so that the resulting bending moments should cancel each other. If one assumes that some areas of the membrane are more crowded on one side of the bilayer, then this has likely occurred by concentrating the given proteins, whether by oligomerization or by other protein-protein attractive interactions. In these circumstances the protein crowding would not work to generate curvature, as it requires free protein diffusion.

The relative ineffectiveness of the crowding mechanism is further supported by experimental results we obtained on membrane vesiculation by mutant ENTH domains where the amphipathic helix was replaced with an engineered hexa-his tag (hisENTH) (Fig. 1). Binding of hisENTH to the external membrane monolayer occurred through DOGS-NTA(Ni) incorporated in the membrane. While wild type protein effectively transformed the initial slightly curved membranes into strongly bent 30nm vesicles (Fig. 1A), the mutant hisENTH, although binding the membranes, did not (Fig. 1B) [46].

Fig. 1. Lipid binding and vesiculation by epsin ENTH domain.

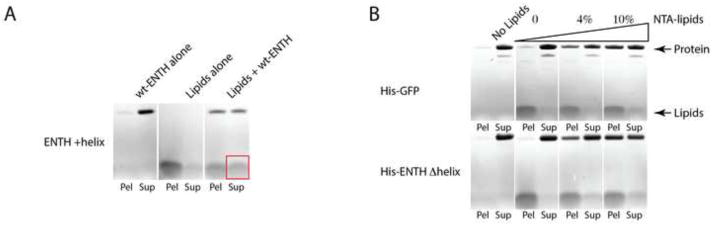
A. Epsin ENTH is a soluble domain and so is found in the supernatant (Sup) after centrifugation at 53664×g. In contrast, 200nm liposomes (Avanti Folch with 0.5% PI(4,5)P₂ added) largely pellet (Pel) on centrifugation. When both are present, epsin ENTH binds to the liposomes, and while some protein pellets with the liposomes, some of the liposomes move to the supernatant. This reversal of liposome pelleting is the result of generation by insertion of epsin amphipathic helices of smaller liposomes characterized by large curvatures, which bud off from the initial liposomes and cannot be pelleted (as in [46]). Thus this is a biochemical assay to show at a bulk level the consequences of epsin ENTH helix insertion on curvature generation and membrane fission. This differential centrifugation assay, which can biochemically distinguish between liposomes greater than 100nm diameter and small vesicles of 50nm diameter or less, has previously been published in [46].

B. A question arises as to whether curvature generation could equally be promoted by a crowding mechanism. So using the same assay conditions as in A, His₆-tagged GFP or His₆-tagged epsin ENTH domains with deleted amphipathic helices were attached to liposomes (using the protocol of [44]) via incorporated DOGS-NTA (Ni) lipids (presence of an additional 4% NTA lipids, and even more protein binds/pellets with 10% NTA lipids). Neither GFP nor epsin ENTH domain without its amphipathic helix result in vesiculation of liposomes, and thus if they are capable of curvature generation it is not on the same scale as the ENTH domain with an intact amphipathic helix.

These findings seem to disagree with a strong lipid bilayer bending by DGS-NTA(Ni)-anchored hisENTH seen in cryomicroscopy images in [44]. Note that in our experiments we used liposomes formed of the lipids usually found in cell membranes (Folch liposomes spiked with 5% PIP2) rather than liposomes formed mostly of diphytanoyl phosphatidylcholine used in [44]. This branched-chain lipid is known to strongly promote membrane tubulation [47], more generally, has very unusual properties compared with common biological phospholipids [48,49].

By embedding hydrophobic protein domains into the membrane matrix

Hydrophobic or amphipathic protein domains inserting into the membrane matrix generally perturb the membrane structure. If such perturbation is asymmetric, it must result in generation of local membrane curvature. To assess the effectiveness of this mechanism of membrane curvature generation, it is convenient to distinguish between shallow insertions, which are embedded only into the external part of a lipid monolayer, and integral insertions spanning the whole membrane thickness.

We know from structures of integral insertions such as trans-membrane domains (TMD) of ATPases or the acetylcholine receptor that they can have specific architectures with distinctive intrinsic shapes and that they will be most relaxed in a specific membrane environment. Even the side chains of single TMDs frequently show a bias for bulkier residues on one side over the other and thus would naturally have a preference for a specific curvature. Thus, because of their intrinsic trans-membrane architecture, many integral insertions are likely to generate some local membrane curvature. At the same time, to produce curvature radii of 10–20nm at reasonable protein concentrations corresponding to few tens of percents of the membrane area coverage, the integral insertions need to have effective shapes of truncated cones with characteristic radii of curvature of a few nanometres, comparable to the membrane thickness, which appears to be a rare feature, but may characterize such proteins as caveolins (see e.g. [13,50]).

Shallow protein insertions have been demonstrated [51] and predicted [52–56] to be much more powerful generators of membrane curvature than the integral insertions. A protein domain penetrating the external lipid monolayer only up to the interface between the lipid polar heads and the hydrocarbon tails push aside the polar heads while leaving the area underneath the insertion to be filled by splaying and tilting acyl chains. This has knock-on consequences for surrounding lipid molecules and results in a strong local asymmetry in the monolayer structure, which must generate considerable local membrane curvatures. If insertions are brought together in the membrane plane, e.g. by cross-linking, the locally induced curvatures sum up into an overall membrane curvature in the region of the insertion concentration. The more shallow insertions that are embedded per unit area of the membrane surface, the greater will be the overall membrane curvature in the region of the insertion concentration [52]. Importantly, curvature generation by the insertion mechanism is specific to a limited subset of proteins and so, in contrast to the crowding mechanism, it is unlikely to be cancelled due to a presence on both leaflets.

The high effectiveness of curvature generation by shallow insertions has been suggested by previous computational modelling of the embedding of N-terminal amphipathic helices of ENTH domains and of N-BAR domains [52,57]. To strengthen this point, we present here the results of more accurate computations based on a state-of-the art model of the elastic properties of lipid bilayer interior, which was recently developed [58] based on a coarse-grained level representation of lipids employing the Martini force field [59]. These computations were performed as described in [48].

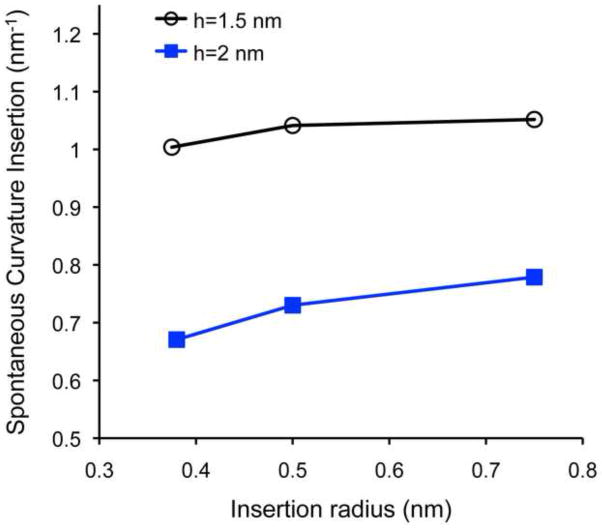
The ability of a shallow insertion to generate membrane curvature can be quantified by the spontaneous curvature, ζ_s, of an effective particle formed by the insertion and the adjacent lipid molecules [52]. The values of ζ_s computed for a rod-like insertion modelling an N-terminal amphipathic helix and presented in (Fig. 2) are larger than 0.7 nm⁻¹ meaning that such an insertion is a few times more powerful curvature generator than lysophosphatidylcholine, a lipid having a most pronounced asymmetric shape and characterized by a spontaneous curvature of about 0.25 nm⁻¹ [60]. The biological feasibility of the curvature generation by a protein can be evaluated by a relationship between the radius of a lipid tube emerging as a result of the protein addition to an initially flat membrane, and the percentage of the outer monolayer area covered by the protein projections on the monolayer surface [44]. Since this relationship was recently discussed within the context of the crowding mechanism for epsin 1 ENTH domain [44], we present here the computational predictions for this specific protein.

Fig. 2.

Effective spontaneous curvature of a rod-like hydrophobic insertion is represented as a function of the rod radius, r, for monolayer thicknesses of h = 1.5 nm(black) and h = 2 nm (blue).

An important parameter for this computation, whose value was challenged in [44], is the ratio λ between the membrane projection of the full ENTH domain and the footprint of the inserting helix. In Stachowiak et al [44] this ratio was suggested to be λ = 0.1. Here we present a molecular projection of an ENTH domain (Fig. 3A,B) demonstrating that the helix footprint including its hydrophobic side-chains constitutes approximately 30% of the total domain projection, λ = 0.3. The estimation of the helix embedding into the lipid monolayer is based on [54].

Fig. 3. Putative membrane binding footprint of epsin ENTH domain.

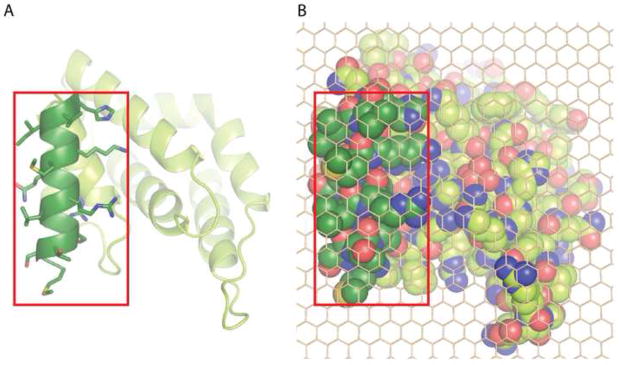
A. Membrane interaction surface of epsin1 ENTH domain viewed from the membrane. The amphipathic helix, which inserts into the membrane is shown in dark green with amino acid side chains included.

B. Space filled representation of (A) with side chains included for the whole protein, overlaid with a carbon atom lattice (to facilitate area calculations), showing that the amphipathic helix occupies approximately 1/3^rd of the total projection area.

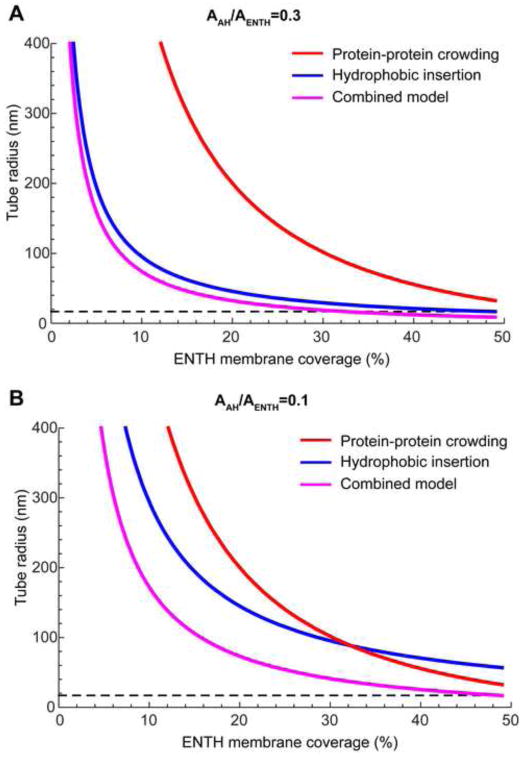
For completeness, the computed radius of a membrane tube, based on the results presented in (Fig. 2) [52,58], as a function of the membrane surface coverage by the full protein projections is presented in (Fig. 4 A,B, blue lines) for both λ = 0.1 and λ = 0.3. For comparison, the same figures show the radii of membrane tubes (the inverse of the tube curvature presented in [44]), which would be generated solely by crowding of the ENTH hydrophilic subdomains as computed in [44] (Fig. 4 A,B, red lines). The crowding effect is clearly predicted to be weaker than that of the insertions for the relevant coverage of the membrane surface by the protein (Fig. 4 A,B), which is especially obvious for our estimation of λ = 0.3 (Fig. 4 A). However, the insertion and crowding mechanisms are not mutually exclusive but rather complementary. If both mechanisms are acting at λ = 0.3, about 30% area coverage by ENTH domains is predicted to generate the biologically relevant and experimentally observed [51] tube radii of 17nm (Fig. 4 A).

Fig. 4.

Membrane curvature generated by epsin ENTH domains as predicted by different models. The membrane tube radius was calculated for the hydrophobic insertion model (blue line), the protein-protein crowding model (red line), and a combined model (pink line), and is represented as a function of the membrane area coverage by ENTH. The dashed black line represents the observed radius of tubes generated by epsin ENTH domains [51]. The relative area fraction of the amphipathic helices to the total surface area of the ENTH is taken to be: (A) A_AH/A_ENTH = 0.3, (B) A_AH/A_ENTH = 0.1. The monolayer thickness h = 2 nm and the insertion is modelled as a rigid cylinder of a radius r = 0.5nm which embeds to the depth d = 0.8 nm into the membrane. The crowding model line has been taken as in Fig. 3C of Ref. [44] with replacement of the spontaneous curvature, J_s, by the radius, R = 1/J_s. Specifically, the curve has been calculated using Eqs. (4–5) of the Supplementary note of Ref. [44] using the same parameter values as in Ref. [44].

It is important to note that the scaffolding mechanism of curvature generation is complementary to the insertion mechanism. At the same time, the relationship between the scaffolding and crowding mechanisms depends on the scaffolding mode. For monomeric scaffolds the two mechanisms are complementary, while formation of polymeric scaffolds must abolish the crowding effects.

In conclusion, shallow hydrophobic insertions and strongly curved protein scaffolds appear to be the most effective generators of membrane curvature of intracellular organelles. The interplay of both mechanisms will be a challenge to understand in the future. The combined action of shallow insertions and crescent-like scaffolds has been demonstrated to influence also the topological state of the membranes, i.e. to determine whether the resulting curvature is realized in shapes of long tubules or spherical vesicles [46]. However the interaction between the insertions and the ubiquitous spherical scaffolds, which may be of critical relevance for the processes of endocytosis and vesicle budding from the ER and Golgi Complex, remains to be understood.