What exactly do numbers mean?

Abstract

Number words are generally used to refer to the exact cardinal value of a set, but cognitive scientists disagree about their meanings. Although most psychological analyses presuppose that numbers have exact semantics (two means EXACTLY TWO), many linguistic accounts propose that numbers have lower-bounded semantics (AT LEAST TWO), and that speakers restrict their reference through a pragmatic inference (scalar implicature). We address this debate through studies of children who are in the process of acquiring the meanings of numbers. Adults and 2- and 3-year-olds were tested in a novel paradigm that teases apart semantic and pragmatic aspects of interpretation (the covered box task). Our findings establish that when scalar implicatures are cancelled in the critical trials of this task, both adults and children consistently give exact interpretations for number words. These results, in concert with recent work on real-time processing, provide the first unambiguous evidence that number words have exact semantics.

1. Introduction

Questions concerning the meaning of number words have sparked great attention in both psychology and linguistics. In psychology, this interest has centered on the observation that while 2-year-olds often produce number words in the context of a counting routine (Gelman & Gallistel, 1978; Wynn, 1990), their mapping of these words onto quantities occurs slowly and sequentially during the preschool years (Sarnecka, Kamenskaya, Yamana, Ogura, & Yudovina, 2007; Le Corre & Carey, 2007; Condry & Spelke, 2008; Huang, Spelke, & Snedeker, 2010). Children begin with a consistent and reliable interpretation of one; when asked for “one fish,” they give exactly 1 (Wynn, 1992). However, the same children are inconsistent in their interpretation of larger numbers. When asked for two or more they give more than 1 item, but the quantity produced is variable and not clearly related to the number requested. By 2.5 years, most children become “two-knowers”: they give exactly 2 fish when asked for two, but continue to grab a handful of 3 or more when asked for larger quantities. Several months later, they begin responding consistently to three (“three-knowers”) and by around 4-years of age, many master four along with the ability to apply their counting routine to enumerate even larger sets.

In linguistics, the puzzle of number word meaning has centered on the observation that these terms appear to have two distinct interpretations (Horn, 1972 & 1989; Gadzar, 1979; Levinson, 1983 & 2000). Although numbers are often interpreted as specifying exact cardinal values, they can be used in some contexts where the total quantity of items is greater (lower-bounded or “at least” interpretations). For example, in sentence (1) two is interpreted exactly. In contrast, in example (2), David uses two to mean something like TWO AND POSSIBLY MORE. His statement is true, and felicitous, even if there is a total of 5 chairs in his office.

• (1)A bicycle has two wheels, while a tricycle has three. (based on Horn, 1989: 251)
• (2)Bonnie: I need to borrow two chairs. Do you know where I could get them?

  David: Sure, I’ve got two chairs in my office. (adapted from Kadmon, 2001)

The fact that number words can be interpreted in both of these ways creates a challenge for accounts of number word semantics. Many linguists have suggested that utterances like (2) reveal the lower-bounded semantics of numbers and that exact interpretations only arise through pragmatic inferences (Horn, 1972 & 1989; Gadzar, 1979; Levinson, 1983 & 2000). In contrast, others have proposed the reverse: number words have an exact semantics and lower-bounded interpretations arise through pragmatic processes (Carston, 1998; Breheny, 2008). Both accounts argue that the mapping from semantics to ultimate interpretation is complex, suggesting that we cannot trust our pre-theoretical intuitions to guide us to the underlying meaning of these terms.

In the present paper, we examine what number words mean and suggest that the answers to the developmental and linguistic puzzles are intimately related. By examining interpretations in very young children who have mastered the meanings of some, but not all, of the words in their count list, we may be able to isolate the semantics of numbers in a population without the requisite knowledge for pragmatic inferencing. In the remainder of the Introduction, we flesh out the two accounts of number semantics and discuss reasons why data from children might be particularly revealing (see Musolino, 2004 for an earlier discussion of these issues). Next, we explain why previous studies exploring these issues have not sufficiently distinguished between the exact and lower-bounded accounts. Finally, we describe a novel task designed specifically to do so. The following experiments sought to uncover the semantics of number words by assessing interpretations in a context where pragmatic inferences are likely to be canceled.

1.1. Two means AT LEAST TWO: the proposal for lower-bounded semantics

The issue of number word semantics came to prominence when Horn (1972) argued that the interpretation of numbers closely parallels the interpretation of scalar terms: sets of words that can be arranged in an ordinal relationship with respect to the strength of the information they convey. For example, some is part of a scale that includes the stronger term all, and warm is part of a scale that also includes hot.¹ Scalar terms are typically interpreted as having both an upper and lower bound, giving rise to a reading which parallels the exact reading for number words. Thus (3) will generally be taken to imply that Henry ate some, but not all, of the ice cream.

• (3)Henry: I ate some of the ice cream.
• (4)Eva: Did anyone try the lutefisk?

  Karl: Yeah, Leif ate some of it. In fact, he ate all of it.

However, in certain contexts, scalar terms, like number words, also take on lower-bounded interpretations. Thus in (4), Karl asserts that Leif ate both some and all of the lutefisk (an infamous Norwegian dish made of fish soaked in lye), indicating that some in this context has a meaning which does not exclude the stronger term all.

Formal treatments of natural language have generally treated phenomena like these as examples of a pragmatic inference called scalar implicature (Horn, 1972; Gadzar, 1979). Following Grice (1957/1975), Horn argued that weak scalars like some do not have a semantically-encoded upper bound and therefore are compatible with stronger scalar terms like all. Scalars can receive an upper-bounded interpretation, as in (3) via a process of pragmatic inference. This inference is motivated by the listener’s implicit expectation that the speaker will make his contribution to the conversation “as informative as is required” (Maxim of Quantity). If Henry had polished off the ice cream, (5) would be a more informative utterance than (3).

• (5)Henry: I ate all of the ice cream.

However, since Henry did not use this stronger statement, the listener can infer that he does not believe it to be true. Although scalar implicatures are robust across many contexts, they are, by definition, not a part of the truth conditional content of the sentence and can be cancelled, resulting in overt lower-bounded utterances such as (4).

The lower-bounded account of number semantics capitalizes on these parallels, arguing that numbers are simply another set of scalar terms. Like other scalars, they have a lower-bounded semantics (two dogs means AT LEAST TWO DOGS) but receive an upper bound via scalar implicature. Since implicatures are calculated in most situations, listeners typically access the exact interpretation of the utterance. But when implicatures are cancelled, the true meaning of the number word is visible, yielding the marked lower-bounded interpretation as in (2).

Theories which posit a lower-bounded semantics for numerical phrases come in two kinds. Some accounts take the form described above: the lower-bounded meaning arises because the lexical item itself lacks an upper bound (Horn, 1972 & 1989; Gadzar, 1979; Levinson, 2000; Winter, 2001). In other theories, the lexical item may have an upper bound but the entire phrase (the determiner phrase or quantifier phrase) generates a mandatory lower-bound meaning as part of semantic composition (Fox & Hackl, 2004; van Rooy & Shulz, 2006; Ionin & Matushansky, 2006; Chierchia, Fox, & Spector, 2008; Barner & Bachrach, 2010; Foppollo, Guasti, & Chierchia, under review; Panizza, Chierchia, & Clifton, 2009). Our data and arguments will speak to both versions of this hypothesis. In all of our experiments, we examine interpretations of number words in count phrases that occur in argument positions. In these locations, both compositional theories and lexical theories posit a lower-bounded semantics.

1.2. Two means EXACTLY TWO: Theories of exact semantics

While the lower-bounded account neatly captures the parallels between cardinal numbers and scalar quantifiers, it flies in the face of the pre-theoretical intuition that numbers have exact meanings. Several theorists have pursued this intuition, arguing that numbers, unlike scalar quantifiers, have exact semantics that delimits both their upper and lower boundaries (Saddock 1984; Koenig, 1991; Horn, 1992; Scharten, 1997; Carston, 1998; Breheny, 2008). These accounts have gained support from evidence that numbers pattern differently from other scalar terms. For example, even in contexts in which other scalars systematically receive lower-bounded readings as in (6), the exact interpretation is favored for numbers as in (7).

• (6)Everyone who ate some of their berries felt fine.
• (7)Everyone who ate two of their berries felt fine.

In these examples, the scalar term appears in the restrictor of the quantifier. Calculating the scalar implicature (to obtain the SOME BUT NOT ALL and EXACTLY TWO readings) would narrow down the set of people who feel fine, thus resulting in a weaker statement. For this reason, most linguistic theories predict that implicatures are typically cancelled in these contexts (Levinson, 2000; Chierchia, Spector, & Fox, 2008; Noveck, Chierchia, Chevaux, Guelminger, & Sylvestre, 2002; Chierchia, Crain, Guasti, Gualmini, & Meroni, 2001; Panizza et al., 2009). Consistent with this prediction, the most natural reading of (6) is one in which some is lower bounded, allowing us to conclude that even the folks who ate all of their berries felt fine. In contrast, Breheny (2008) argues that in sentences like (7), the number word continues to get an exact interpretation (and thus those who ate 3 berries might be ill). This pattern of interpretation is surprising if number words receive their upper boundaries through scalar implicature but predictable if these upper boundaries are part of their meanings.

The challenge for an exact semantics account is to explain how exact meanings can give rise to sentences that appear to have lower-bounded interpretations such as (2). The most common answer is that these interpretations arise through another pragmatic process. For example, Breheny (2008) suggests that numbers refer to the exact numerosity of a set, but that pragmatic factors play a role in determining which set is under discussion. This is implemented by an implicit restrictor that specifies the domain over which quantification occurs. Such restrictors are necessary to explain a variety of phenomena. For example, we understand (8) as quantifying over a contextually-salient group of people.

• (8)Everybody came to Allison’s party.

Without this implicit restrictor, the sentence would quantify over all animate entities and thus be blatantly false. A similar logic could apply to our understanding of (2). Rather than quantifying over all the chairs in his possession, David’s response may have restricted interpretation to an exact subset that had been made salient by Bonnie’s request.

1.3. Why children’s interpretation of numbers might be particularly informative

Both lower-bounded and exact semantics accounts provide prima facie adequate explanations for the dominance of exact interpretations of number words and the occasional appearance of lower-bounded interpretations. Several researchers, however, have suggested that these hypotheses could be distinguished by examining how young children interpret number words. Children are notoriously poor at calculating scalar implicatures and tend to generate judgments in which the lower-bounded meanings of scalar terms are clearly visible (Paris, 1973; Smith, 1980; Braine & Rumain, 1981; Noveck, 2001; Papafragou & Musolino, 2003; Chierchia et al., 2001; Gualmini, Crain, Meroni, Chierchia, & Guasti, 2001; Barner, Chow, & Yang, 2009; Huang & Snedeker, 2009b; Foppollo et al., under review). Thus if the upper-bounds of numbers arise via scalar implicature, we might expect that children would accept lower-bounded interpretations, even in contexts where adults prefer exact interpretations.

This issue was first explored by Papafragou and Musolino (2003) who tested both 5-year-old children and adults using a pragmatic judgment task. Consistent with previous research, they found that children, but not adults, were content to accept weak scalar predicates (started) and weak scalar quantifiers (some) in situations where the stronger scalar term applied (finished or all). In contrast, children treated numbers in an adult-like manner, refusing to accept statements like “Two of the horses jumped over the fence,” in a context in which they saw exactly 3 horses jump. Similarly, in a study by Hurewitz, Papafragou, Gleitman, and Gelman (2006), 3- and 4-year-old children were asked to find pictures in which “The alligator took two of the cookies.” Children, like adults, selected only the picture in which the character had exactly 2 of the 4 cookies, rejecting the one in which he had all 4. However, these same children happily selected both pictures when asked a parallel question about some.

Both of these studies suggest that number word interpretation does not follow the same developmental trajectory as the interpretation of scalar quantifiers. However, evidence that children typically entertain exact interpretations of numbers does not, by itself, tell us how they reach these interpretations. As we saw earlier, both the exact and the lower-bounded theories can account for the existence of exact and lower-bounded interpretations, and both theories predict that the exact interpretation will frequently be favored. Thus the findings from prior studies can be understood in two different ways:

Account #1: exact semantics

On this proposal, children’s lower-bounded interpretation of true scalar terms like some is taken as evidence of a profound and global difficulty in calculating scalar implicatures. If children cannot calculate implicatures, then their exact interpretations of number words cannot be attributed to this pragmatic process, and so this strong preference must reflect the semantic properties of these terms. This interpretation is called into question, however, by the evidence that young children can calculate scalar implicatures when they are given instructions and training emphasizing pragmatic interpretation over literal truth (Papafragou & Musolino, 2003) and when experimental tasks more closely approximate the role of implicatures in communicative interactions (Papafragou & Tantalou, 2004; Pouscoulous, Noveck, Politzer, & Bastide, 2007; Katsos & Bishop, 2011).

Account #2: lower-bounded semantics

If implicature is variable in childhood rather than absent, then the discrepancy between true scalars and numbers could reflect differences in the pragmatic processing of these items rather than differences in their meanings. On this hypothesis, children learn to calculate upward-bounding implicatures for two earlier than for some or start. This precocity could be fueled by several factors: the frequency with which particular implicatures are suspended, greater contextual support for the upper-bounded interpretation of numbers, parental feedback about the correct use of number words, and the role of the counting routine in allowing children to generate and compare expressions using alternative numerical terms (Papafragou & Musolino, 2003; Barner & Bachrach, 2010; Foppolo et al., under review).

1.4. How can we discover what number words mean?

The arguments above suggest that in order to truly isolate the meaning of number words, we must use tasks and populations that allow us to disentangle the semantics of the terms from the contributions of pragmatic implicatures. Critically, because previous studies have used contexts in which adults typically calculate implicatures, it is not clear whether children’s exact number-word interpretations in these contexts reflect an exact semantics or a lower-bounded semantics supplemented by an upward-bounding implicature. Our experiments had two features that were designed to eliminate the possibility that children were calculating implicatures.

First, we examined number word interpretations in very young children who have mastered the meanings of some, but not all, of the numbers in their count list. As we noted earlier, previous research has shown that number words are acquired through a slow, sequential process (Wynn, 1992; Sarnecka et al., 2007; Le Corre & Carey, 2007; Condry & Spelke, 2008; Huang et al., 2010). Thus there is a period of a year or more during which children know the meanings of some of the number words on their count list but not others (e.g., a “two-knower” will produce 1 fish when asked for one and 2 fish when asked for two, but grabs a handful of fish when asked for three, four or five). Critically, because scalar implicature depends on knowledge of what the speaker might have said, children’s limited competence could have profound effects on their interpretation of known numbers. According to the lower-bounded account, we interpret two as EXACTLY TWO because we know that a cooperative speaker could have said three if the situation had warranted it. But it is not clear that a child who only knows the meanings of one and two has learned enough about the meaning of three to support such an inference. Levinson (2000) notes that, in the absence of a stronger term to drive the implicature, the lower-bounded theory predicts that the underlying semantics of the term would guide its use. Thus we might expect that children who have no stable mapping for three would allow two to refer to larger sets.

We recognize, however, that this prediction depends upon an assumption about how two-knowers interpret the word three, and what knowledge is required for a word to be a member of a scale (see section 6.1). Thus a second feature of these experiments is equally critical: We created a novel task that allowed us to assess how number words are interpreted in two contexts, one in which scalar implicatures should be calculated, and one in which those implicatures should be suspended. In the following experiments, this manipulation is validated by demonstrating its influence on the interpretation of some. Since upper-bounded interpretations of this perennial poster child for implicatures are unambiguously derived through inference (Horn, 1972; Gadzar, 1979), examining responses to some will allow us to assess whether we have succeeded in creating contexts in which scalar implicatures are suspended and calculated.

Theoretically, scalar implicatures are expected to occur in contexts where they would make the utterance more informative (Horn, 1972 & 1989; Gadzar, 1979; Fox & Hackl, 2004; van Rooy & Shulz, 2006; Chierchia et al., 2008; Barner & Bachrach, 2010). Typical comprehension tasks provide precisely this kind of context. Participants are shown two or more choices: one of which matches the lower-bounded reading of the scalar term (ALL in the case of some) and another which matches the exact reading (subset in the case of some). If participants calculate the scalar implicature and access the more informative interpretation, then they are left with a single correct response. However if they do not calculate the implicature, then the utterance is underspecified. Unsurprisingly, under these circumstances, most adults treat scalar terms as upper bounded (see e.g., Noveck, 2001; Papafragou & Musolino, 2003; Hurewitz et al., 2006; Papafragou & Tantalou, 2004; Pouscoulous et al., 2007; Katsos & Bishop, 2011).

Constructing a context that justifies the suspension of a scalar implicature is trickier. One obvious solution is to provide only a single alternative that is correct on the lower-bounded reading, making the inference redundant with the context. But which alternative should it be? If only the exact alternative is present, then it is impossible to know whether participants arrived at the lower-bounded or exact interpretation of the term (did they pick some as an example of SOME BUT NOT ALL or as an example of SOME AND POSSIBLY ALL?). If only the lower-bounded alternative is present, then it impossible to test whether the upper-bound of the term results from an implicature or is a necessary part of the meaning of the utterance. For example, if we asked participants for two and gave them a choice between 1 and 3, then anyone who interprets the term exactly has no valid response and must either protest or reconstrue the task in some way.

We resolved this dilemma by providing participants with a decoy that could be interpreted as an exact match, or not, as they saw fit. Participants were asked to “Give me the box with two fish” in the context of a visible mismatch (a box with 1 fish), a visible and salient lower-bounded target (a box with 3 or 5 fish) and a covered box with unknown contents. We predicted that this context would suspend scalar implicatures in the following ways. First, by embedding the number word in a singular definite noun phrase (“the box with two fish”), the instructions lead to a presupposition that there is one unique referent in the context that satisfies the description (Frege, 1892; Strawson, 1950). Critically, this presupposition makes it so that calculating the implicature would provide no additional information. Under these circumstances, if two has lower-bounded semantics, then the description would be satisfied by the visible lower-bounded match (box with 3 or 5 fish). However, if two has an exact semantics, this option would not be available and participants would have to conclude that the referent must be in the covered box. Second, to minimize the possibility of a lower-bounded interpretation arising from a pragmatic shift in the domain of reference (e.g., selecting 2 of the 5 chairs in David’s office in sentence (2); see Breheny, 2008), the boundary of each set was physically delineated using boxes. Since these boxes forced the participant to act upon each set as a whole rather than as a collection of individual units, this would make it difficult to decompose the set into smaller subsets.

In Experiment 1, we used this paradigm to explore the interpretation of some and two in a population that robustly calculates scalar implicatures, college undergraduates. In the critical condition for some, adults were asked to “Give me the box where Cookie Monster has some of the cookies” when presented with a box where he has none of the cookies within a set, a second box where he has all of them, and a third covered box (see Figure 1). If this task succeeds in canceling scalar implicatures, then adults should select the box where Cookie Monster has all the cookies. If however this task does not cancel implicatures, then adults should infer the presence of an upper-bounded match in the covered box. Similarly, in the critical condition for two, adults were asked to “Give me the box with two fish” when presented with a box with 1 fish, a box with 3 or 5 fish, and a covered box. If number words have lower-bounded semantics, then adults should select the box with 3 or 5 fish. If however they have exact semantics, then adults should select the covered box.

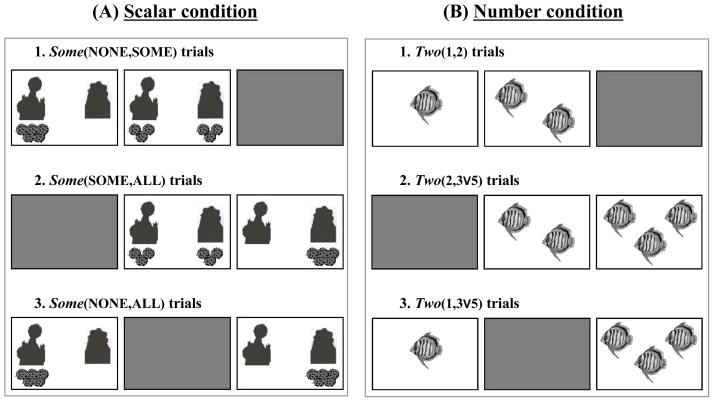
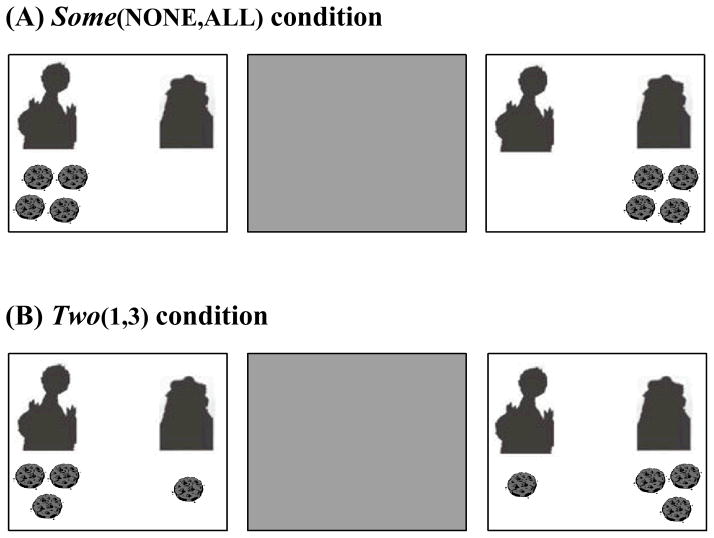
Figure 1.

Stimuli for Experiments 1 and 2. Each trial featured two open boxes and one closed box. (A) In the scalar condition, the open boxes depicted Big Bird (on the left), Cookie Monster (on the right) and a set of cookies. Participants were asked to “Give me the box where Cookie Monster has some of the cookies.” (B) In the number condition, the open boxes contained sets of fish. Participants were asked to “Give me the box with two fish.”

2. Experiment 1

2.1. Methods

2.1.1. Participants

Sixty English-speaking undergraduates from Harvard University participated in the experiment. Both the scalar and number conditions and all the trial type within each condition were manipulated between subjects. This ensured that adult responses reflected a naïve understanding of the sentences rather than any inferences about the study that might emerge by comparing different trials types.

2.1.1. Procedure and Materials

The study was composed of two parts. During the Familiarization phase, we introduced adults to the covered-box task. On each trial, they were presented with two open boxes containing toy animals and a third covered box and were asked to give the experimenter the box that contained a particular animal. The target animal was in one of the open boxes on two of the familiarization trials and hidden inside of the covered box on the remaining two. This sequence of four trials was repeated twice. The first time through, adults were given feedback after each choice and were allowed to open the covered box in their search for the target animal. The second time through, they were told not to open the covered box and they were not given any feedback. All adults selected correct boxes when the target animal was visible and selected the covered box when it was not and were therefore included in this experiment.

During the Test phase, adults were presented with three boxes. For the scalar condition, each box featured two characters (Cookie Monster and Big Bird) and a set of cookies that belonged to one of them or was split between them. Adults were asked to “Give me the box where Cookie Monster has some of the cookies” in three contexts (see Figure 1):

1. Some(NONE, SOME). In these trials, adults were presented with one subset match (a box with a picture where both Cookie Monster and Big Bird had some but not all of the cookies), one empty set match (where Cookie Monster had none of the cookies and Big Bird had all of them), and a third covered box.

2. Some(SOME, ALL). Adults were presented with one subset match (where both Cookie Monster and Big Bird had some but not all of the cookies), one total set match (where Cookie Monster had all of the cookies and Big Bird had none of them), and a third covered box.

3. Some(NONE, ALL). Adults were presented with one empty set match (where Cookie Monster had none of the cookies and Big Bird had all of them), one total set match (where Cookie Monster had all of the cookies and Big Bird had none of them), and a third covered box.

Similarly, for the number condition, adults were asked to “Give me the box with two fish” in the following contexts:

1. Two(1,2). In these trials, adults were given a box containing 2 fish (exact match), a box containing 1 fish (the less-than option), and a covered box. These trials corresponded to the some(NONE, SOME) trials in the scalar condition.

2. Two(2,3V5). Adults were given box containing 2 fish (exact match), a box containing either 3 or 5 fish (the more-than option), and a covered box. These trials corresponded to the some(SOME, ALL) trials in the scalar condition.

3. Two(1,3V5). During these critical trials the exact match was absent. Adults saw a box containing 1 fish (the less-than option), a box containing either 3 or 5 fish (the more-than option), and a third covered box. These trials corresponded to the some(NONE, ALL) trials in the scalar condition.

Across all trials, the three boxes were presented side-by-side in random linear order. There were three tokens of each trial type, featuring different characters/objects (e.g., Winnie-the-Pooh & Piglet with apples, Barney & Tinky-Winky with lollipops in scalar trials; sheep in number trials).

2.2. Results and Discussion

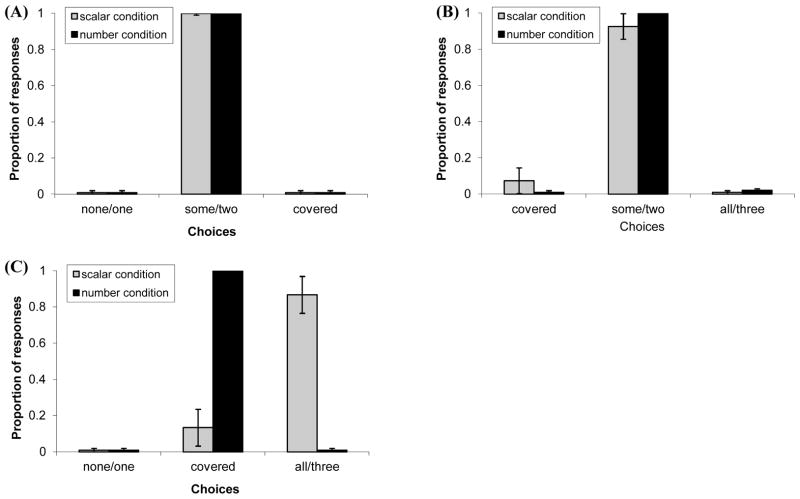
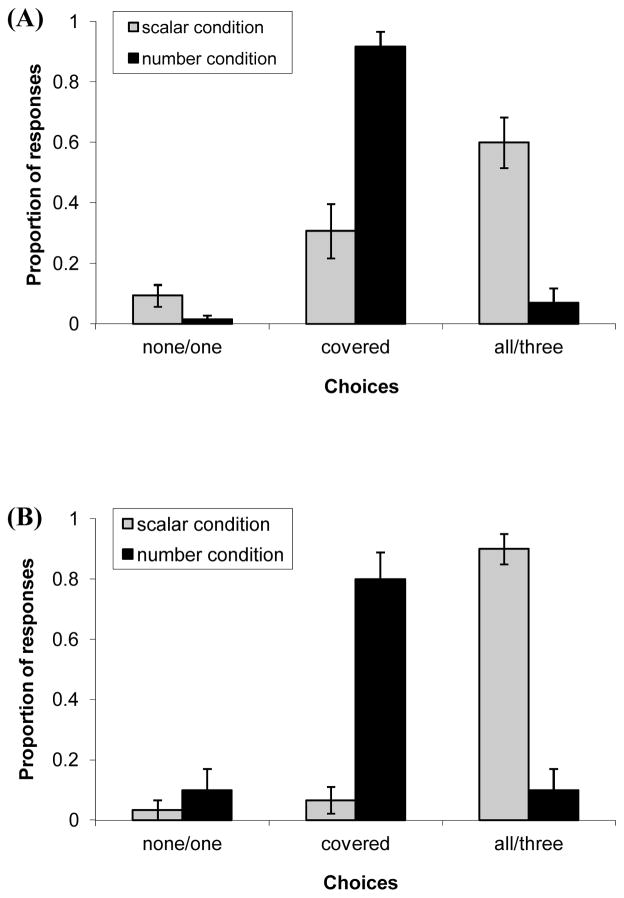
Figure 2 indicates that adult interpretations of some varied across the three types of trials. In the some(NONE, SOME) trials, adults always selected the box where Cookie Monster had a subset of the cookies (M = 100%). Similarly, in the some(SOME, ALL) trials, they overwhelmingly favored the box with the subset (M = 90%), demonstrating a robust ability to calculate the scalar implicature. Critically, on the some(NONE, ALL) trials, adults strongly favored the box containing the total set of cookies (M = 87%) and rarely selected the covered box (M = 13%).

Figure 2.

Results for Experiment 1. Light bars indicate adults’ responses when presented with (A) some(NONE, SOME) trials, (B) some(SOME, ALL) trials, and (C) some(NONE, ALL) trials. Dark bars indicate adults’ responses when presented with (A) two(1,2) trials, (B) two(2,3V5) trial, and (C) two(1,3V5) trials.

We compared the selection of the subset match and found a significant difference across the three scalar trial types (Kruskal–Wallis test, p < .001). Adults were as likely to select the subset when it was paired with a semantically-incompatible set (empty set) than when it was paired with a semantically-compatible one (total set) (Mann–Whitney U = 40.0, n₁ = n₂ = 10, p > .10). However, they rarely selected the subset when it was under the guise of the covered box, leading to fewer subset matches in the critical some(NONE, ALL) trials compared to both the some(NONE, SOME) trials (Mann–Whitney U = 5.0, n₁ = n₂ = 10, p < .001) and some(SOME, ALL) trials (Mann–Whitney U = 6.5, n₁ = n₂ = 10, p < .001). These results demonstrate that when no clear match for the scalar implicature is provided, adults interpret some as consistent with the lower-bounded quantity (all of the cookies). These findings support our conjecture that scalar implicatures are cancelled when the critical terms are used as part of a definite description, in the presence of a salient lower-bounded alternative, and the absence of a clear implicature match.

Figure 2 also indicates that when asked for two, adults unsurprisingly chose the box containing exactly two fish in both the two(1,2) trials (M = 100%) and the two(2,3V5) trials (M = 100%). Furthermore on the two(1,3V5) trials, when there was no exact match, adults consistently selected the covered box (M = 100%). We directly compared adults’ responses for two with their responses for some by focusing on their selection of the covered box in two critical trials of interest. First, we examined trials that featured a visible contrast between the subset/exact match and the lower-bounded match. Proportions were no different in the some(SOME, ALL) and two(1,3V5) trials (Mann–Whitney U = 50.0, n₁ = n₂ = 10, p = 1.0) because, in both cases, the adults rarely selected the covered box when the exact match was visible. Next we examined trials that featured no visible subset/exact match. We found that adults selected the covered box significantly more in the two(1,3V5) trials than in the some(NONE, ALL) trials (Mann–Whitney U = 5.0, n₁ = n₂ = 10, p < .001). Thus when asked for “two fish,” adults rejected the visible lower-bounded option and inferred that the covered box must have 2 fish in it. This pattern is strongly consistent with an exact semantics account for number words.

However, an alternate construal of these findings is that adults’ explicit knowledge of the number scale enabled them to retrieve the stronger alternative (three fish) when they heard the weaker expression. This robust knowledge led to the inference that the speaker’s avoidance of this alternative implies that his use of two excludes THREE and higher number. Any account of this kind would have to explain why the adult did not apply their knowledge of the quantifier scale (some implies not all) in a closely parallel task. For example, one may invoke differences in the accessibility of each scale. In Experiment 2, we attempt to rule out this possibility entirely by identifying children who have mastered two but not three (“two-knowers”) and assessing their interpretation of two. On the lower-bounded theory, children who lack knowledge of three should be unable to predict that a cooperative speaker would use three rather than two to designate sets with more than 2 members. Thus if number words have a lower-bounded semantics, then these children should select the box with 3 fish in the critical condition.

3. Experiment 2

3.1. Methods

3.1.1. Participants

Twenty English-speaking children between the ages of 2;6 and 3;5 (mean 3;0) participated in the experiment. Like Experiment 1, the scalar and number conditions were manipulated between subjects (10 children in each condition). However, unlike Experiment 1, the trial types within each condition were manipulated within subjects. Across all experiments, children were recruited from the database of the Laboratory for Developmental Studies at Harvard University.

3.1.1. Procedure and Materials

The study was composed of three parts. During the Pretest phase, we elicited knowledge of the relevant quantities using a Give-N task. For the scalar condition, children were presented with several small plastic fish and were simply asked to “Put some (all) of the fish” into a basket (“the pond”). All children who were tested demonstrated knowledge of these scalar terms by putting at least 1 fish in the basket when asked for some and by putting the entire quantity when asked for all. For the number condition, Wynn’s (1992) version of the Give-N task was used to determine the level of number word knowledge by asking children to put different quantities of fish into a basket. Children were classified as two-knowers if they gave 1 fish when asked one, 2 in response to two, and an arbitrary larger number in response to all other requests. The first ten children that we identified in this group participated in this study. We also elicited knowledge of the count list and found that all children were able to count up to ten.

The Familiarization phase was identical to Experiment 1. Only children who selected correct boxes when the target animal was visible and selected the covered box when it was not were included in this experiment. One child was excluded on this basis. The Test phase was similar to Experiment 1 but all three trial types were presented in pseudo-randomized order.

3.2. Results and Discussion

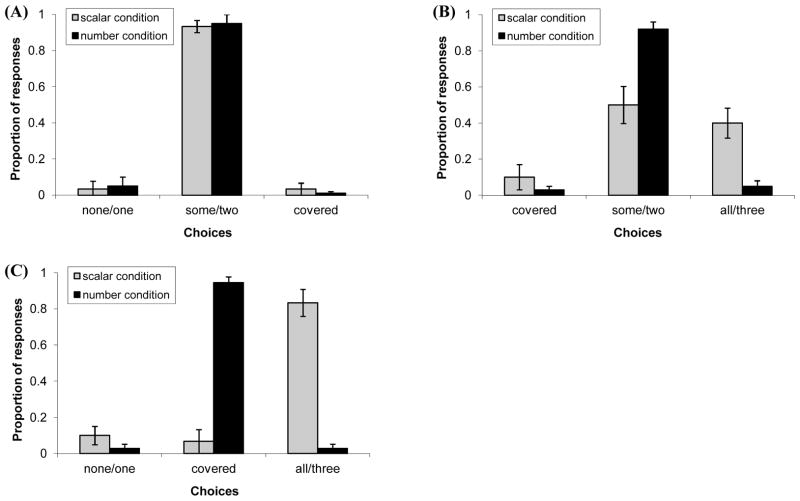
Figure 3 indicates that children’s responses to some varied across the three types of trials. In the some(NONE, SOME) trials, children overwhelmingly selected the box where Cookie Monster had a subset of the cookies (M = 93%). This demonstrates that they clearly understood the task and recognized that some is incompatible with none. In the some(SOME, ALL) trials, however, children were equally disposed to select the box containing the subset of cookies and the box containing the total set (M = 50% and M = 40% respectively). This demonstrates that they did not calculate a scalar implicature to restrict the reference of the quantifier (Hurewitz et al., 2006; Papafragou & Musolino, 2003; Foppollo et al., under review). Critically, on the some(NONE, ALL) trials, children strongly favored the box containing the total set of cookies (M = 83%) while very few selected the covered box (M = 7%). In the absence of a visible implicature match, children, like adults, accepted the box where Cookie Monster had all of the cookies, demonstrating a common semantic representation of the scalar term. We compared the selection of the subset match and found a significant difference across the three conditions (Friedman’s test, X²(2) = 18.17, p < .001). Children were more likely to select the subset when it was paired with a semantically-incompatible set (empty set) than when it was paired with a semantically-compatible one (total set) (W= 45.0, Z=2.74, p < .01). Furthermore, they rarely selected the subset when it was under the guise of the covered box, leading to fewer subset matches compared to the some(NONE, SOME) trials (W= 55.0, Z=2.91, p < .01) and the some(SOME, ALL) trials (W=28.0, Z=2.41, p < .05).

Figure 3.

Results for Experiment 2. Light bars indicate children’s responses when presented with (A) some(NONE, SOME) trials, (B) some(SOME, ALL) trials, and (C) some(NONE, ALL) trials. Dark bars indicate children’s responses when presented with (A) two(1,2) trials, (B) two(2,3V5) trial, and (C) two(1,3V5) trials.

Figure 3 also illustrates that when asked for two, children overwhelmingly preferred to select an exact match when it was visibly present (M = 95% in the two(1,2) trials and M = 93% in the two(2,3V5) trials). Performance in the two(2,3V5) trials is notable because it demonstrates a divergence between scalars and numbers in children: in the presence of larger quantity children did not generate an implicature in the scalar task but showed a strong preference for the exact interpretation of two (Papafragou & Musolino, 2003; Hurewitz et al., 2006; Foppollo et al., under review). However, as we noted above, it is unclear from these data whether children’s divergent preferences are a result of an exact semantics for numbers or a greater precocity with scalar implicatures along the number scale. The critical two(1,3V5) trials explore this issue directly. On these trials, where there was no visible exact match, children consistently selected the covered box (M = 95%). Comparisons of children’s covered box selections revealed a significant difference across the three conditions (Friedman’s test, X²(2) = 19.42, p < .001). Children were far more likely to select the covered box in the two(1,3V5) trials compared to the two(1,2) trials (W=55.0, Z =2.97, p < .01) and the two(2,3V5) trials (W=55.0, Z = 2.92, p < .01). In contrast, their selections in the latter two conditions did not differ from each other (W=1.0, Z=1.0, p>.30).

Overall the results from the number condition provide a stark contrast to children’s performance with the scalar condition. This was confirmed by comparisons across the two quantifiers in two trials of interest. First, we examined the proportion of subset/exact matches in the trials that featured a visible contrast between the subset/exact match and the lower-bounded match. Proportions were significantly greater in the two(2,3V5) trials than in the some(SOME, ALL) trials (Mann–Whitney U = 6.5, n₁ = n₂ = 10, p < .01). This is consistent with the notion that children did not restrict their interpretation for scalar quantifiers but did so for number words. Next we examined the proportion of covered box choices in the critical trials that featured no visible subset/exact match. We found that children, like adults, selected the covered box significantly more in the two(1,3V5) trials than in the some(NONE, ALL) trials (Mann–Whitney U = 0.5, n₁ = n₂ = 10, p < .001). These patterns are strongly consistent with an exact semantics account for number words. Since the task was to find one box that uniquely satisfies the description (“the box with two fish”), a theory of lower-bounded semantics most naturally predicts that children should select the visible box with more objects without ever needing to consider the covered box. Instead they rejected the visible lower-bounded option and inferred that the covered box must have 2 fish in it. In contrast, when there was a visible exact quantity match, children had no difficulty ignoring the covered box and selecting this item.

However, there are a couple features of this experiment that might lead one to a more conservative interpretation of the current results. While children’s preference for both the subset and total set in the some(SOME, ALL) trials is consistent with the prior studies on the interpretation of some, we considered the possibility that their response pattern reflected simpler strategies that were unique to this experiment. Children may have simply ignored the quantifier and picked a card in which the target character was associated with cookies. Another possibility is that children may have failed to understand that each box was to be evaluated in isolation and instead interpreted some as quantifying over the contents of all three boxes. Either of these strategies would be inconsistent with the notion that children canceled scalar implicatures in this task.

In Experiment 3, we tested which of these possibilities characterizes children’s selections in the scalar condition by presenting them with the same alternatives from Experiment 2 but now asking for “the box where Cookie Monster has all of the cookies.” If children simply ignore the quantifier, then we would expect the same pattern of performance with all that we saw with some. Similarly, if they incorrectly quantify across the three boxes, then they should now either refuse to answer the question (since no character has all the cookies) or consistently perform at chance across the three trial types. However, if children quantify across the individual boxes, then they should now distinguish between the visible alternatives. In particular, when presented with a box where Cookie Monster has a subset of the cookies and one where he has a total set, children with the correct domain of quantification should interpret all as referring to the latter.

4. Experiment 3

4.1. Methods

4.1.1. Participants

Ten English-speaking children between the ages of 2;6 and 3;5 (mean 2;9) participated in the experiment.

4.1.2. Procedure and Materials

The experiment was identical to the scalar condition in Experiment 2 except that children were asked to “Give me the box where Cookie Monster has all of the cookies.” No children were excluded for failing to select the correct boxes during the Familiarization phase.

4.2. Results and Discussion

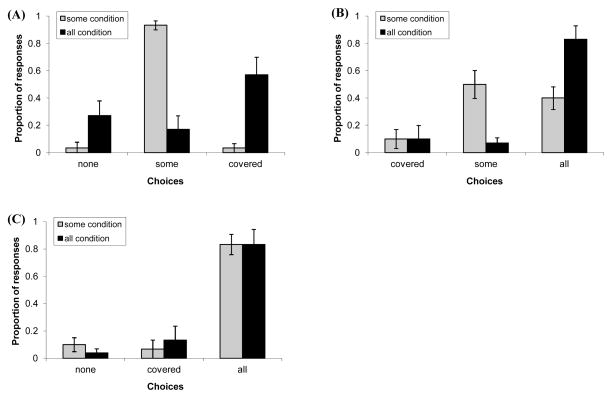
Figure 4 indicates that children’s interpretation of all varied across the three types of trials. In both the all(NONE, ALL) trials and all(SOME, ALL) trials, children overwhelmingly selected the box where Cookie Monster had the total set of cookies (M = 93% and M = 93% respectively), suggesting that they understood the meaning of the quantifier. Similarly, when this visible match was not available in the all(SOME, NONE) trials, children often inferred the presence of a total set in the covered box (M = 53%). The remaining children experienced more confusion, dividing their responses between the box where Big Bird had all of the cookies and Cookie Monster had none (M = 18%) or the box where Cookie Monster had some of them (M = 29%).

Figure 4.

Results for Experiments 2 and 3 in (A) (SOME, NONE) trials, (B) (SOME, ALL) trials, and (C) (NONE, ALL) trials. Light bars indicate children’s responses to some (Experiment 2). Dark bars indicate children’s responses to all (Experiment 3).

We compared children’s preferences in the all condition with those in the Experiment 2 some condition by examining their selection of the total set match across the three trial types. In the (NONE, ALL) trials, there was no difference in preference for the total set across the some and all conditions (Mann–Whitney U = 43.5, n₁ = n₂ = 10, p > .50). While this is consistent with the claim that scalar implicatures were canceled in the some condition, making the total set an acceptable match for some as well as all, it is also consistent to the possibility that children simply ignored the quantifier in their selections. However, preferences in the other two trials provided more definitive evidence. In the (SOME, ALL) trials, children were more likely to select the total set when asked for all compared to some (Mann–Whitney U = 16.0, n₁ = n₂ = 10, p < .01). Similarly, even when the total set was not visible in the (SOME, NONE) trials, children were more likely to infer its presence in the covered box when asked for all compared to some (Mann–Whitney U = 12.5, n₁ = n₂ = 10, p < .01).

Critically, these differences in the some and all conditions demonstrate that children’s interpretations were sensitive to the semantics of the quantifier. Furthermore, the robustness of their preference for the total set in the all condition highlights a bias to interpret these terms as quantifying over the individual boxes. These results clarify our understanding of the findings in Experiment 2 in two ways. First, it suggests that children’s preference for the total set in the some(NONE, ALL) trials reflected the fact that they (like adults) did not generate an implicature in these trials. Second, it suggests that their preference for an exact match in the corresponding two(1,3) trials revealed an interpretation that was based on the number word semantics.

However, we consider additional features of our task that might lead one to question this analysis. First, the use of a within-subjects design in Experiments 2 and 3 introduces the possibility that children’s performance in the critical trials (when the subset/exact alternatives were not visible) may have been influenced by their experience in other trials (when they were visible). While this did not appear to influence their selection of the visible total set in the some(NONE, ALL) trials, it may explain their willingness to select the covered box in the two(1,3V5) trials. Second, the different response patterns for the number and scalar conditions could be influenced by the use of less complex pictures in the number trials. Each box in the scalar trials depicted two sets shared between two characters. In contrast, boxes in the number trials involved only a single set. This asymmetry raises the possibility that children are only able to infer the contents of the covered box when the materials are relatively simple.

In Experiment 4, we addressed these concerns by making two changes to the experiment. First, we removed trials where the subset/exact alternatives were visible and only tested children on ones where they were not visible, the some(NONE, ALL) trials and two(1,3) trials. This ensured that information across trials could not be used to draw inferences about the contents of the covered box. Second, we increased the complexity of the materials in the number condition so that it more closely matched those used in the scalar condition. Figure 5 illustrates that like the some(NONE, ALL) trials, the alternatives in the two(1,3) trials now featured quantities shared between two characters. Finally, to verify the robustness of this task, we tested a separate group of adults who were recruited through Amazon’s Mechanical Turk, a web-based crowdsourcing platform (see Schnoebelen and Kuperman, 2010 for additional information on this method of data collection for linguistic research). If this paradigm continues to cancel scalar implicatures, these adults should pattern like their counterparts in Experiment 1.

Figure 5.

Stimuli for Experiment 4. Each trial featured two open boxes and one closed box. The open boxes depicted Big Bird (on the left), Cookie Monster (on the right) and a set of cookies. (A) In the some(NONE, ALL) condition, participants were asked to “Give me the box where Cookie Monster has some of the cookies.” (B) In the two(1,3) condition, participants were asked to “Give me the box with two of the cookies.”

5. Experiment 4

5.1. Methods

5.1.1. Participants

Twenty English-speaking children between the ages of 2;6 and 3;7 (mean 3;0) and 50 English-speaking adults participated in the experiment. As in Experiment 2, number and scalar trials were manipulated between-subjects (10 children and 25 adults in each condition). The adults were recruited through Amazon’s Mechanical Turk (www.mturk.com).

5.1.2. Procedure and Materials

The materials, design and procedure were similar to those of Experiments 2. For the number trials, Wynn’s (1992) Give-N task was again used to select children who were two-knowers. In the Familiarization phase, participants were introduced to the box task and one child was excluded for failing to select the correct boxes during this portion of the task. During the Test phase, participants were presented with one of the following contexts (see Figure 5):

1. Some(NONE, ALL). On these trials, participants were presented with a box featuring an empty set option (a picture where Cookie Monster had 0 of 4 cookies and Big Bird had 4 of 4 cookies), a total set option (a picture where Cookie Monster had 4 of 4 cookies and Big Bird had 0 of 4 cookies), and a third covered box. Participants were asked to “Give me the box where Cookie Monster has some of the cookies.”

2. Two(1,3). Participants were presented with a box featuring a less-than option (a picture where Cookie Monster had 1 of 4 cookies and Big Bird had 3 of 4 cookies), a more-than option (a picture where Cookie Monster had 3 of 4 cookies and Big Bird had 1 of 4 cookies), and a third covered box. Participants were asked to “Give me the box where Cookie Monster has two of the cookies.”

These configurations ensured that the items in each box were matched for complexity across the scalar and number conditions. Three tokens of these critical trials were presented, each featuring different pairs of characters sharing various objects. These trials were randomized with three filler trials that were similar to those used in the Familiarization phase.

5.2. Results and Discussion

We turn first to adult performance in this task. Figure 6a illustrates that adults in the some(NONE, ALL) trials were more likely to select the box with the total set (M = 60%) over the covered box (M = 31%). In contrast, those in the two(1,3) trials overwhelmingly favored the covered box (M = 92%) over the lower-bounded option (M = 7%). Comparisons across conditions revealed significantly more covered box selections in the two(1,3) trials compared to the some(NONE, ALL) trials (Mann–Whitney U = 3.9, n₁ = n₂ = 25, p < .001) and more lower-bounded matches in the some(NONE, ALL) trials compared to the two(1,3) trials (Mann–Whitney U = 3.8, n₁ = n₂ = 25, p < .001).² Overall these findings confirm that the current context reliably suspends scalar implicatures.

Figure 6.

Results for Experiment 4 for (A) adults and (B) children. Light bars indicate responses when presented with some(NONE, ALL) trials. Dark bars indicate responses when presented with two(1,3) trials.

Next we turn to child performance in these conditions. Figure 6b illustrates that children in the some(NONE, ALL) trials overwhelmingly preferred the box with the total set (M = 90%) over the covered box (M = 7%). This preference mirrors performance in Experiment 2 and suggests that when no clear implicature match was provided, children like adults interpreted some with respect to its semantic meaning. Critically, children in the two(1,3) trials favored the covered box (M = 80%) and rarely selected the lower-bounded option (M = 10%). This preference suggests that when no clear exact match for the number word was provided, children inferred its presence in the covered box. Comparisons across trials revealed significantly more covered box selections in the two(1,3) trials compared to the some(NONE, ALL) trials (Mann–Whitney U = 2.0, n₁ = n₂ = 10, p < .001) and more lower-bounded choices in the some(NONE, ALL) trials compared to the two(1,3) trials (Mann–Whitney U = 1.5, n₁ = n₂ = 10, p < .001).³

While the results of the Experiment 4 revealed the same pattern as we saw in Experiments 1 and 2, there was one clear difference between the studies for the adults. In particular, the proportion of lower-bounded matches was lower than previously found (M = 60% in Experiment 4 vs. M = 87% in Experiment 1). This could reflect differences in the task demands associated with interpreting written language versus speech or differences in the expectations generated by a web-based experiment aimed at adults versus a live procedure in a developmental lab filled with toys. Either factor may have led participants to engage in more metalinguistic reasoning or deeper processing, increasing the number of covered box selections (M = 31% in Experiment 4 vs. M = 13% in Experiment 1).

However, overall these results confirm the patterns found in Experiments 1 and 2. They demonstrate that adults in this task are less likely to generate implicatures with a true scalar term and under these same circumstances, children who have limited knowledge of the number scale strongly preferred to interpret two as EXACTLY TWO. This preference could not have resulted from prior exposure to a visible exact match since this alternative was never presented during the study. Similarly, differences between performance in the scalar and number trials could not reflect variations in task complexity since the materials were closely matched across conditions.

6. General Discussion

The present paper takes a developmental approach to the linguistic question: What do number words mean? We found that 2- and 3-year-olds interpreted two as referring to an exact quantity at the earliest stage of development. Like adults, they were able to reject salient lower-bounded targets and to use the number word to infer the presence of an exact match elsewhere in the array (in the covered box). On the lower-bounded theory, the rejection of a lower-bounded target can only be explained as the effect of an upward-bounding scalar implicature. However, two features of the current results make such an explanation unlikely. First, scalar implicatures are motivated by mutual knowledge of the terms on the scale and their relative informational strength. Yet children gave exact interpretations of two even though they seemed to have little knowledge of the meaning of three. Second, we found that interpretations of number words contrasts with those interpretation of true scalar terms, as both children and adults readily selected ALL as an example of some when there was no other visible alternative.

In the remainder of this discussion, we will examine three remaining issues. First, we discuss the possibility that features of the current task decreased our sensitivity to detect the presence of lower-bounded semantics. Next we examine how evidence from the real-time processing of numbers and scalars can be used to distinguish between the underlying meanings of the two expressions. Finally, we discuss how our current findings bear on methodological and theoretical issues in developmental psychology.

6.1. Additional arguments for lower-bounded semantics

While the present findings provide strong support for exact semantics, a potential concern that one might have is that our use of the Give-N task selectively screened for children who could already generate an exact interpretation via scalar implicature. Recall that children who are two-knowers understand how one and two map onto exact quantities in a Give-N task but are unable to pick out exact quantities for larger sets like three and five. Nevertheless, their failure to give one or two as referents for three and five suggests that they have implicit knowledge that these larger number words refer to quantities greater than two. At first glance, this pattern seems to provide evidence for lower-bounded semantics in the stage before each number is mapped to a specific quantity (three means MORE THAN TWO) and an ability to generate exact interpretations after the mapping is performed.

However, two further considerations lead us to reject this analysis. First, selection of an exact numerical match in the Give-N task is consistent with both exact and lower-bounded accounts since an ultimate preference for an exact interpretation is predicted by both proposals. Critically, prior work has found that adults never give the total set when asked for some, demonstrating that object selection tasks create a context in which scalar implicatures are robustly present (Barner et al., 2009). Thus children’s performance on the Give-N task does not tell us how they would interpret number words in a critical implicature-cancelling context. Second, in the object selection task, 3- to 5-year-olds, like adults, tend to give subsets and not total sets when asked for some (Barner et al., 2009). Nevertheless, children often accept total sets as referents for some in picture selection tasks (Experiment 2 in the current study; Hurewitz et al., 2006) and in judgment tasks (Papafragou & Musolino, 2003; Foppolo et al., under review). These differences suggest that a stable response pattern in the Give-N task does not directly reflect the underlying semantics of number words.

A related concern is the possibility that two-knowers in our task could make an implicature about the meaning of two on the basis of what they know about three. Prior developmental work has shown that children have a limited appreciation of the numerical information encoded by words beyond their knower level (Sarnecka et al., 2007; Le Corre & Carey, 2007; Condry & Spelke, 2008; Huang et al., 2010). For example, Condry and Spelke (2008) found that two-knowers who hear a set labeled as eight incorrectly apply the same label to situations where the set is increased by 1, doubled, or halved. Furthermore, they often switch their label when they saw members of the set rearranged, with no objects subtracted or added. Nevertheless, two-knowers do realize that expressions like three and five describe quantities greater than 2. Thus when asked for two, they could access its lower-bounded semantics (AT LEAST TWO), contrast this with their implicit knowledge of a stronger alternative (three or five means MORE THAN TWO), and generate the scalar implicature (two implies EXACTLY TWO). Thus two could be bounded by implicature even if the child did not know the difference between three and five.

While our findings are logically compatible with this account, it is worth noting the ways in which it diverges, both theoretically and empirically, from prior accounts of implicature. Underlying most theories of implicature is the inference that the listener has expectations about how particular situations will be described (“I ate some” means I didn’t eat all or I would have said “I ate all”). But these expectations will be systematically violated when a two-knower makes predictions about quantities greater than three. The child may encode 5 fish as three or six but the adults around her will label them as five. Consequently most of the direct evidence that the child receives will indicate that larger number words cannot be used to draw the inference that another number does not apply to the set. In the absence of this inference, the child should then exhibit a lower-bounded semantics.

The present study clearly shows that children interpret two exactly before they have an adult like understanding of the meaning of three, ruling out one possible account of how implicature determines the upper bound of numbers. Other accounts are possible but they are clearly distinct from the hypothesis that we tested and eliminated on the basis of these findings.

6.2. The interpretation of number words in real-time processing

Finally, while we have sought to distinguish the meaning of number words by examining children’s patterns of acquisition, our theories may also be informed by converging evidence from how these expressions are processed. Recall that on lower-bounded theories of number word semantics, an exact interpretation involves three steps: a lower-bounded meaning is semantically composed, the relevant alternatives on the scale are computed, and the inference is calculated. These accounts make clear predictions about the time course of comprehension: the lower-bounded semantic meaning should be visible at some point during processing prior to the time at which the scalar implicature is calculated. In contrast, on an exact semantics account, the meanings of number words are exact from the moment they are encountered.

Recent studies examining the time-course of number word interpretation in adults (Huang & Snedeker, 2009a, 2011) and 5-year-old children (2009b) allow us to evaluate such a hypothesis. In these studies, participants heard commands like “Point to the girl that has some of the socks” while viewing displays featuring a girl with 2 of 4 socks (a subset) and a girl with 3 of 3 soccer balls (the total set). Critically, these sentences have a period of ambiguity from the onset of the quantifier to the disambiguating phoneme (“some of the soc-”) where the semantics of some is compatible with both characters. This ambiguity would be eliminated if a scalar implicature were calculated to restrict reference to the girl with the subset of socks. However, following the onset of some, adults and children initially looked to both girls, suggesting that the implicature was not available to restrict reference. Furthermore, while adults calculated the implicature after about 800ms (Huang & Snedeker 2009a, 2011), children showed no sign of ever doing so and instead relied on the final phoneme of the noun (“-ks” in socks) to distinguish between the two referents (Huang & Snedeker, 2009b). Thus both adults and children show a robust temporal lag between semantic processing of some and the calculation of the implicature.

In these same experiments, there were trials that examined the online interpretation of number words. The control trials isolated how quickly children and adults could use the semantically-encoded lower bound of a number to determine reference (“Point to the girl that has three of the socks” in the presence of a girl with 3 socks and a girl with 2 soccer balls). As expected under all theories, both groups rapidly used the meaning of the number word to close in on the correct character. The critical trials probed how quickly participants could access the upper bound of a number word (“Point to the girl that has two of the socks” in the presence of a girl with 2 socks and another with 3 soccer balls). If the upper bound of a number is calculated by an implicature, then we would expect an exact interpretation to be delayed in this condition, just as it was for some. However, shortly after the onset of two, both adults and children preferred to look at the correct referent with exactly 2 items over the distractor with 3 items. These results demonstrate drastically different time-courses for the interpretation of number words and scalar terms across both age groups. These differences provide strong evidence that number word meanings are exact: from the earliest moments of interpretation two has an upper bound while some, a true scalar term, does not.

6.3. Methodological contributions

The present study demonstrates that the covered box task is a useful paradigm for mapping the semantic boundaries of words and phrases. Tasks that assess the meanings of words and expressions typically present participants with a choice of several potential referents. Participants in these tasks generally assume that their job is to select the best option from the set of options presented. However, these studies often focus on the status of marginal category members or pragmatically infelicitous interpretations and for such questions, the task demands of the choice paradigms will typically create one of two problems.

First, if the questionable category members are contrasted with typical category members (“Give me the birds” in a context with sparrows and penguins) the semantic meaning of the term may appear to be narrower than it actually is. In a choice task, participants may prefer typical exemplars and fail to select less typical exemplars, even if both fall within the extension of the tested word or phrase, because they construe their task as choosing the best exemplars rather than all possible exemplars. This problem may be magnified in young children, who face limitations of memory and attention and thus may be more likely to get distracted after making an initial selection. However, if uncontroversial category members are not included in the set of alternatives, a second and equally serious problem arises. The demands of the task may lead subjects to stretch the meanings of words and phrases in ways that do not reflect their true meanings (see Syrett, Kennedy, & Lidz, 2010). If no true referents of a word or expression are presented (“Give me the fish” in a context with dogs and whales), participants may redefine their task as choosing the alternative that is “most like” the request and thus select a referent that is outside the true extension of the expression.

The box task avoids this demand by providing a foil which participants can interpret however they like. Our experiments demonstrate that when participants are given a definite description and are allowed to select an option that they cannot see, they will chose to do so only when none of the visible options match the meaning of the description. Thus the covered box task allows experimenters to test the extension of a description without making any a priori assumptions about the status of atypical exemplars (see Li, Barner, & Huang (2008) and Khan, Pearson, & Snedeker (2010) for a further application). Notably we found that even 2-year-olds made systematic inferences about the contents of the covered box, suggesting that this task is appropriate across a wide age range.

6.4. Implications for cognitive development

The present findings also speak to more general questions concerning the development of language and concepts. Unlike the 2- and 3-year-olds who are in the throes of learning numbers, adults have mastered the meanings of all the words in their count list. Through their experiences with money, measurement, and mathematics, they have come to use these words to express ideas far beyond that of young children. Yet with respect to language development, this research demonstrates a strong continuity between the semantic and interpretive processes of adults and young children. Both endow the number words in their lexicon with exact meanings, and appear to use the same processes to interpret these terms and apply them to sets of entities. Given the vast conceptual changes that occur in the domain of number during childhood (Carey, 2009), this developmental continuity in number word semantics is striking.

Concerning conceptual development, the present findings help to reconcile two large literatures on number words and number concepts. The predominant linguistic theory of number semantics posits a large gap between the basic meanings of numerically quantified noun phrases (which is lower bounded) and the most common use of these phrases to designate set with exact numerical quantities, see Levinson (2000). On this hypothesis, there is little connection between our informal and formal number concepts. On the other hand, research in cognitive development provides a wealth of evidence that children’s mastery of number word meanings directly supports their entry into formal mathematics. Children who have mastered the language of verbal counting perform far better in the kindergarten mathematics curriculum than those who do not, and interventions to enhance their number word mastery lead to improvements in their school mathematics achievement (Case & Griffin, 1996; Siegler, 2007). Moreover, children who have learned to count, but have not yet been taught any arithmetic in school, are spontaneously able to use counting to solve small-number addition problems exactly (Case & Griffin, 1996; Zur & Gelman, 2004) and large-number addition problems approximately (Gilmore & Spelke, 2008). Such achievements would seem to be impossible if the number word meanings that children initially mastered were lower-bounded, or if the number words in ordinary conversations and those in mathematical formalizations were learned separately.

In conclusion, the present study provides good reasons to believe that number words are not bounded by scalar implicature, but instead have exact meanings. By adopting a task in which implicatures are cancelled, we are able to disentangle semantic and pragmatic contributions to interpretation and clearly disassociate the meaning of numbers and true scalar quantifiers. These findings help to resolve a longstanding controversy in linguistics, and they validate a key assumption underlying much of the current developmental work on number word learning.