Short abstract
Increasing interests have been raised toward the potential applications of biodegradable poly(lactic-co-glycolic acid) (PLGA) coatings for drug-eluting stents in order to improve the drug delivery and reduce adverse outcomes in stented arteries in patients. This article presents a mathematical model to describe the integrated processes of drug release in a stent with PLGA coating and subsequent drug delivery, distribution, and drug pharmacokinetics in the arterial wall. The integrated model takes into account the PLGA degradation and erosion, anisotropic drug diffusion in the arterial wall, and reversible drug binding. The model simulations first compare the drug delivery from a biodegradable PLGA coating with that from a biodurable coating, including the drug release profiles in the coating, average arterial drug levels, and arterial drug distribution. Using the model for the PLGA stent coating, the simulations further investigate drug internalization, interstitial fluid flow in the arterial wall, and stent embedment for their impact on drug delivery. Simulation results show that these three factors, while imposing little change in the drug release profiles, can greatly change the average drug concentrations in the arterial wall. In particular, each of the factors leads to significant and yet distinguished alterations in the arterial drug distribution that can potentially influence the treatment outcomes. The detailed integrated model provides insights into the design and evaluation of biodegradable PLGA-coated drug-eluting stents for improved intravascular drug delivery.
Keywords: drug-eluting stents, mathematical modeling, PLGA biodegradable coating, intravascular delivery, drug internalization, interstitial fluid flow, strut embedment
1. Introduction
Drug-eluting stents are commonly used in the coronary angioplasty procedures to both provide structural support and release drug molecules locally at the implanted arterial site for preventing adverse outcomes (such as in-stent restenosis) in the patients [1–3]. Biodurable (or nonerodible) polymers are the predominant type of stent coatings for carrying active drug compounds, whereas recent studies have suggested issues potentially related to the slow drug release in the biodurable coatings and the hypersensitivity to the permanent presence of polymer coating in the arterial wall [4–7]. Improving the design and performance of drug-eluting stents is a long-term research topic. Among the various research directions, the utilization of biodegradable polymer coatings in place of the biodurable coatings has been proposed [8,9]. In particular, biocompatible PLGA, and allows tunable drug release rates based on different polymer molecular weights, has received a high amount of interest in ongoing drug-eluting stents research [10–14]. While most studies were carried out for examination of release under in vitro conditions, further evaluation of PLGA stent coating for in vivo evaluations of implanted stents are necessary and are typically significantly more costly.
Mathematical models and simulations have been widely employed in the research of drug-eluting stents ranging from in vitro drug release evaluation to intravascular delivery investigations. Especially, models for studying the intravascular drug delivery process can help to acquire detailed information about the drug release, delivery, and distribution into the arterial wall, and can provide additional insights into the stent-based drug delivery systems. Some models simplifies the stent coating into a source term for providing drug concentrations, and focus on investigating the arterial drug distribution surrounding the stent struts without explicitly modeling the drug transport in the stent coating. Such models were used in the analysis of convective and diffusive drug transport comparison in the arterial wall [15], mechanics of stent expansion and drug distribution [16], and impact of blood flow on drug deposition in the arterial wall [17,18]. Other models have incorporated the biodurable coating to model the drug release from the coating and subsequent drug uptake in the arterial wall. In those models where the biodurable coating is explicitly modeled with a constant drug diffusivity, drug release, and arterial drug distribution have been investigated considering the effects of drug diffusivities in the coating and in the arterial wall [19–22], coating thickness [19], the strut embedment [20] and compression [23], reversible drug binding [22,24], and multilayer structure of the arterial wall [25,26].
So far little modeling work has been published on intravascular drug delivery using biodegradable stent coatings. A degradable stent coating has been modeled by artificially switching the values of drug diffusivity in the coating reservoir based on a predefined drug concentration threshold [27], which does not mechanistically model the coating erosion process. While various models have been proposed for describing the in vitro drug release coupled with polymer degradation and/or erosion in PLGA drug delivery systems (for microspheres [28–30] and thin film stent coatings [31,32]), such mechanistic models have not been utilized to model the intravascular drug delivery from a PLGA stent coating.
This work presents a mathematical model that describes the integrated process of drug release in PLGA coating and subsequent drug delivery, distribution, and drug pharmacokinetics in the arterial wall. A mechanistic model for drug release in the PLGA coating is adopted that couples the drug diffusion to the PLGA degradation and erosion [32], and the adopted model is integrated with an arterial wall model where the drug pharmacokinetics in the arterial wall is modeled as a reversible binding process [22]. The integrated model further incorporates drug internalization for cellular drug uptake, interstitial fluid flow, and strut embedment as model factors. For drug diffusion in the arterial wall, an anisotropic drug diffusivity is considered and is analytically calculated based on the structural properties of the arterial wall. The model is simulated using the finite element method. The simulations first compare the biodegradable PLGA coating with a biodurable coating for stent-based drug delivery. For a stent with PLGA coating, the model simulations further investigate the impact of drug internalization, interstitial fluid flow in the arterial wall, and stent embedment on drug release in the coating, arterial drug levels, and arterial drug distribution. Development of such a detailed integrated model helps to provide insights into the design and evaluation of biodegradable PLGA coated drug-eluting stents for intravascular drug delivery.
2. Theory and Methods
2.1. Model Development.
In the model scheme, an implanted stent is studied in the artery where the stent struts are evenly placed in the cross section of the lumen (Fig. 1(a)). The strut-arterial wall configuration is based on a previous study of a biodurable polymer coating carried out by the authors [22] and is typical for stents applications [15]. The blood flow is in the direction into the paper plane. Typical square-shaped stent struts are considered [19,25,33]. Due to symmetry, a single stent strut with its surrounding arterial wall domain is extracted for the study to reduce computational cost. The extracted model domain is illustrated in Fig. 1(b), where half of the stent strut is embedded into the arterial wall. Different from the previous study of biodurable coatings [22], here the curvature of the arterial wall is retained rather than simplified as being flat. The Cartesian coordinate system (noted as x, y) is used for describing the domains including the square-shaped stent strut and the stent coating, and the cylindrical coordinate (noted as r, θ) is adopted for the curved arterial wall domain.
Fig. 1.
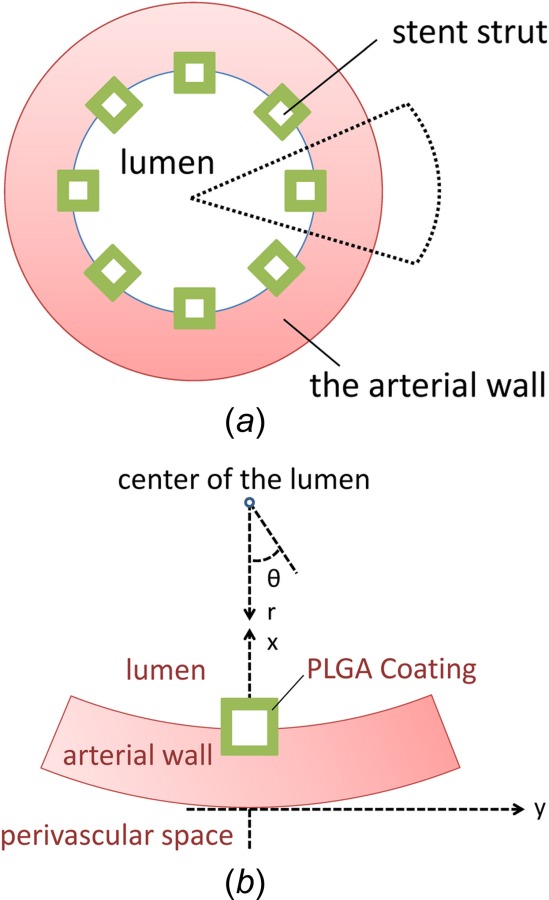
(a) Cross-sectional view of an implanted stent in a coronary artery. (b) Schematic of a single stent strut with PLGA coating half-embedded into the arterial wall. Cartesian coordinate (x, y) and cylindrical coordinate (r, θ) are both illustrated.
The mathematical models for important phenomena governing the drug delivery process are described in Secs. 2.1.1 and 2.1.2. The model for describing drug transport in the biodegradable PLGA coating was adapted from Ref. [32], and the model for drug transport and pharmacokinetics in the arterial wall was developed based on a previous study for biodurable coating [22]. The integrated model provides a tool for evaluating PLGA-coated drug-eluting stents for intravascular drug delivery.
2.1.1. Drug Transport in the PLGA Coating.
The drug release in the PLGA polymer coating is a process coupled to the degradation and erosion of the PLGA polymer matrix. Degradation represents the chemical process that breaks down the polymer chains and results in decreasing PLGA molecular weight, and erosion is the physical process characterized by the polymer mass loss [34]. Both degradation and erosion can facilitate drug molecule diffusion, as molecular weight reduction induces less entanglement of polymer chains in the PLGA bulk, and the mass loss creates pore space. For PLGA microsphere systems, a good number of mathematical models have been proposed in the literature to describe the degradation and erosion process of PLGA microspheres and to take into account the degradation and/or erosion contribution in the drug release process [28–30]. The proposed models typically incorporate a variable drug diffusivity that depends solely on the PLGA molecular weight change [35–38]. An exponential dependency of drug diffusivity on the concentration of undegraded poly(lactic acid) (PLA) was also seem in a model for PLA stent coating [31]. In a recent work of the authors, a model was proposed for drug release in PLGA stent coating that considers contributions to the effective drug diffusivity from both degradation and erosion of PLGA [32], where the importance of dual contributions in the effective drug diffusivity was validated and demonstrated for in vitro sirolimus release from PLGA coating. The model is utilized here to describe the drug diffusion in the PLGA coating coupled to polymer degradation and erosion; readers interested in the detailed derivation of the mathematical model are referred to Ref. [32].
The drug diffusion through both the polymer bulk with decreasing PLGA molecular weight and the pore space with increasing pore volume fraction in the matrix is described by incorporating an effective drug diffusivity. The drug transport in the PLGA coating is modeled by
| (1) |
where D 1,e is the effective drug diffusivity in the PLGA coating and is described by
| (2) |
The effective diffusivity is a function dependent on the changing PLGA molecular weight M w and the evolving coating porosity . D s0 is the initial drug diffusivity in the PLGA polymer before degradation, D l0 is the drug diffusivity in the aqueous phase, M w0 is the initial polymer molecular weight, a is the dependency of drug diffusivity on PLGA molecular weight, and is the drug partition coefficient between PLGA solid and aqueous phase (defined as concentration in aqueous phase divided by concentration in the solid phase at equilibrium).
The PLGA molecular weight change is described by a first-order decay model given by [35–37]
| (3) |
The porosity change, which is related to the mass loss of the coating, was analytically derived as [32]
| (4) |
where is the initial porosity in the PLGA polymer matrix and is assumed zero.
In Eqs. (3) and (4), the k w and k n are degradation rate constants corresponding to weight- and number-average molecular weight change, respectively, and their values were experimentally measured [39]. Equations (1)–(4) provide the complete set of equations for describing drug transport in the PLGA coating. As PLGA undergoes bulk erosion, the coating experiences mass loss while the integral structure is maintained. The coating structure has been reported to maintain integrity during the entire degradation period, until much later time after complete elution of the loaded drug [10]. Therefore, the coating domain can be considered as intact for the time span of interest.
2.1.2. Drug Transport in the Arterial Wall.
Once released into the arterial wall, the drug molecules are exposed to the physiological environment in the arterial wall. While drug molecules diffuse within the arterial wall, various drug-tissue interactions occur that affect the arterial wall drug transport, distribution, and drug uptake [40,41]. The drug-arterial wall interaction has been commonly modeled as a reversible binding reaction of the drug molecules with binding sites present in the arterial wall, as shown in Eq. (5) [22,24,27,41]. In the process, bound drug C B is formed by associating free drug C F with the available binding sites S. The bound drug is immobilized and only the free drug can diffuse. The reversible binding process, however, does not provide a mechanism for drug consumption (e.g., drug uptake by tissue cells), which can be characterized by drug internalization [42–44]. To take this factor into account, drug internalization (Eq. (6)) is modeled in this model which assumes that, once drug molecules are associated with binding sites, the cells take up and metabolize drug molecules as a first-order reaction. The internalization step, as a result, regenerates a binding site S for every internalized drug molecule C l
| (5) |
| (6) |
The drug transport and interactions in the arterial wall are described for the three drug forms in Eqs. (7)–(9). The cylindrical coordinate system is used for the arterial wall domain for handling the curvature (Fig. 1(b))
| (7) |
| (8) |
| (9) |
where S 0 is the initial concentration of binding sites in the arterial wall. Among the three drug forms, only the free drug is able to diffuse within the arterial wall (Eq. (7)). The equation describes two different drug diffusivities in the arterial wall: in the circumferential direction and in the transmural direction. A convective transport term is also included for investigation of the potential impact of transmural interstitial flow in the arterial wall with velocity , which is driven by the pressure difference between the lumen and the perivascular space [45]. For correspondence to scenarios where drug internalization and interstitial fluid flow were not modeled, the factors can be turned off by setting the internalization rate constant k i and the interstitial fluid flow velocity v r to zero.
Because of the elongated shape of smooth muscle cells and the consequent anisotropic arterial wall property, arterial drug diffusion in the transmural direction is hindered, which results in a much smaller apparent drug diffusivity in the transmural direction than that of the circumferential direction [46]. The anisotropic drug diffusivity in the arterial wall has been investigated and revealed impact on drug delivery and distribution in a few studies, where the anisotropic ratio was either treated as a parameter or had empirical values [15,22,25]. Theoretical quantification of the drug diffusivity anisotropic ratio, however, does not seem to be published in the literature. In this model, the anisotropic diffusivity is analytically quantified by adopting the expression for estimating effective diffusivity in periodic composite with impermeable flakes [47]
| (10) |
where α is the aspect ratio of smooth muscle cells (defined as the smaller cell dimension in the circumferential direction divided by the cell thickness in the transmural direction) and is the volume fraction of smooth muscle cells in the arterial wall. With the volume fraction of smooth muscle cells measured as 60–70% [48], and consider an aspect ratio of 3 [49,50], the expression estimates an anisotropic diffusivity ratio /D r of 9.1–15.7. The estimated range correspond to the reported values (around 10) fairly well [15]. For larger aspect ratio of the cells, even higher anisotropic ratio could be expected through the estimate of expression. In this work, an anisotropic ratio of 10 is used throughout the simulations.
2.2. Numerical Simulation.
With appropriate boundary conditions and initial conditions, the integrated model can be solved for the domain described in Fig. 1(b). For the simulation studies, zero drug concentration is assumed at the coating-lumen interface considering a wash-out condition by the bloodstream, and also at the perivascular interface considering drug clearance [15,24]. At the arterial wall-lumen interface, the drug flux into the lumen is assumed as zero considering the barrier effect of the endothelial layer and the typically high hydrophobicity for drugs used in drug-eluting stents (such as sirolimus and paclitaxel) that lead to very limited drug dissipation into the bloodstream from the arterial wall [20,22,27]. The no flux boundary condition is also applied to the left and right boundaries based on symmetry, and at the coating-strut interface. At the coating-arterial wall interface, an equal flux constraint and equal concentration partitioning are applied. For the initial conditions, the drug is initially uniformly distributed only in the coating.
While the models proposed here are generally applicable, the model parameters can vary depending on the different drugs. For the simulation studies, the model parameters are based on sirolimus. However, little information for drug internalization is available. In order to investigate the internalization factor, a range of its rate constant values is considered with respect to the dissociation binding rate constant (Sec. 3.2). The dimensions defining the model domain and the model parameters are summarized in Table 1.
Table 1.
Summary of model parameters
| Parameters of the model domain | ||
|---|---|---|
| Outer diameter of the artery | 3 mm | [20] |
| Thickness of the arterial wall | 200 μm | [24,42] |
| Thickness of the stent strut | 140 μm | [33] |
| Thickness of stent coating | 30 μm | [11] |
| Mesh size for the arterial wall | 5 μm | — |
| Mesh size for the coating | 0.5 μm | — |
| Mesh size for the boundary layers | 0.2 μm | — |
| Parameters of the mathematical model | ||
| Drug diffusivity in the initial PLGA polymer, | 10−5 μm2/s | [32,35] |
| Drug diffusivity in the aqueous phase, | 50 μm2/s | [32,47] |
| Transmural drug diffusivity in the arterial wall, | 10−1 μm2/s | [40] |
| Anisotropic ratio of drug diffusivity in the arterial wall, | 10 | As derived |
| Association rate constant, | 104 l/mol·s | [41,51] |
| Dissociation rate constant, | 10−2 l/s | [41,51] |
| Internalization rate constant, | 0 or as mentioned | — |
| Weight-based PLGA degradation rate constant, | 7.5 × 10−7 l/s | [39] |
| Number-based PLGA degradation rate constant, | 2.5 × 10−7 l/s | [39] |
| Molecular weight dependency of diffusivity, a | 1.714 | [32,36] |
| Drug partitioning coefficient, κ | 10−4 | [32,52] |
| Interstitial flow velocity in the arterial wall, ν | 0 or as mentioned | |
| Initial drug concentration in the coating, C 0 | 10−5 mol/l | [22,24] |
| Initial binding site concentration in the arterial wall, S 0 | 10−5 mol/l | [40] |
The mathematical model with domains shown in Fig. 1(b) was implemented in COMSOL 4.2, which is a simulation platform based on the finite element method. The model domains consist of a single stent strut with coating and the surrounding arterial wall with curvature. The coating and arterial wall domains are meshed as illustrated in Fig. 2, where the actual mesh for simulations was much finer. Considering the much smaller scale of the coating domain, a finer mesh in the coating than the arterial wall is used. Boundary layers with smaller mesh size are also imposed at interfaces with nonzero flux (coating-lumen interface, coating-arterial wall interface, and perivascular interface) to improve the simulation accuracy.
Fig. 2.
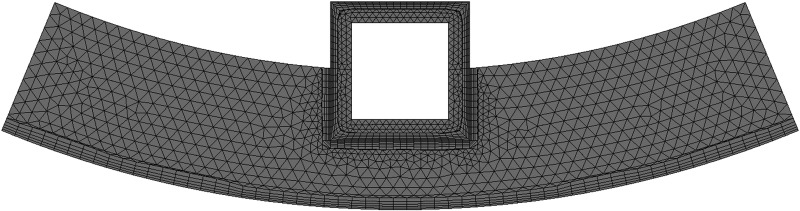
Illustrated mesh of the model domain. (The actual mesh used in simulation is much finer).
A thorough mesh convergence test was carried out for determining the mesh sizes for model simulations (Fig. 3). The convergence test is performed with constant drug diffusivities in the coating and in the arterial wall, and the relative error was calculated for the drug release profile based on an extremely fine reference mesh. The reference mesh uses sizes of 0.2 μm for the coating and 2 μm for the arterial wall, and contains 2 × 106 cells.
Fig. 3.
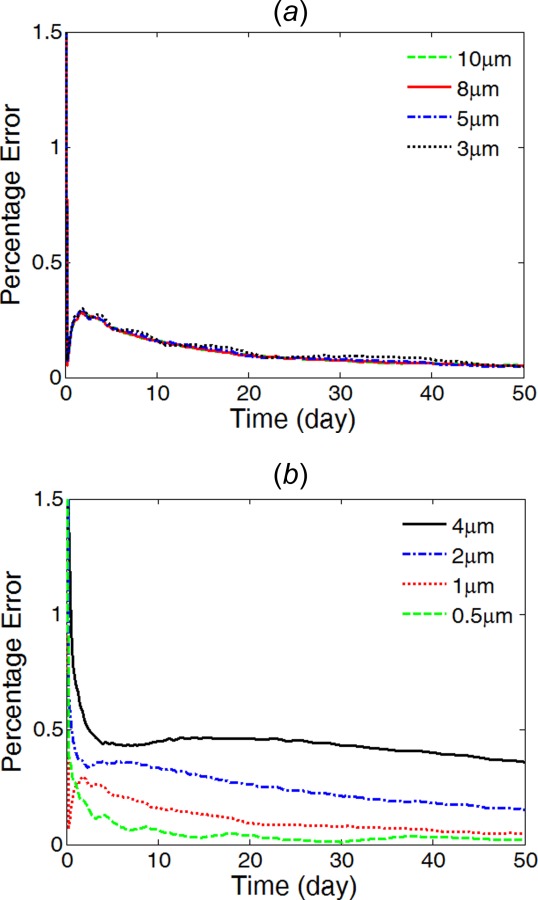
Percentage relative error of different mesh sizes compared with the extremely fine reference mesh. (a) Varying mesh size in the arterial wall with constant mesh size of 1 μm in the coating; and (b) varying mesh size in the coating with constant mesh size of 5 μm in the arterial wall.
In the convergence test, the relative errors were similar and stayed under 0.5% for different mesh size of the arterial wall domain, while the mesh size of the coating is remained the same at 1 μm (Fig. 3(a)). Choosing a mesh size of 5 μm for the arterial wall domain, a mesh size of 0.5 μm was selected for the coating (Fig. 3(b)). The final mesh gives relative error of less than 0.1% and contains 257,712 cells.
3. Results and Discussion
In this section, the model simulations first compare the intravascular drug delivery from a biodegradable PLGA coating with that from a biodurable polymer coating. Following that, using the model developed for PLGA-coated stent, the drug internalization rate, interstitial fluid flow, and strut embedment are individually investigated for their impact on the drug transport and distribution. In the model simulations, unless mentioned, half strut embedment is considered and the internalization rate constant k i and the interstitial fluid flow velocity v r are both set to zero, for the purpose of comparing with previous modeling work and inspecting the impact of individual model factors.
The simulation results are reported for drug release profiles in the coating, average drug levels in the arterial wall for the different drug forms, and the spatial drug concentration distribution in the arterial wall. Specifically, the average drug concentration in the arterial wall is defined as the spatial average of each drug form. The three means of characterizing the drug delivery process are consistent with other modeling works, while offering the possibility for potential comparison with future experimental measurements.
3.1. Comparing PLGA Coating With Biodurable Coating.
In model simulations, the PLGA coating is compared with a biodurable coating for stent-based intravascular drug delivery. In the biodurable stent coating case where the polymer coating stays intact, the drug diffusivity in the coating remains constant at the initial drug diffusivity in the polymer (D s0). The rest of the model parameters are the same for the two scenarios. In the drug release profiles in the coating (Fig. 4), the two scenarios start with similar release rates in the first two days when the PLGA degradation and erosion are insignificant. Following that, the drug release in the PLGA coating quickly exceeds that of the biodurable coating as a result of the increasing degradation and erosion of the coating. The characteristics of the release profiles in intravascular delivery are in good correspondence to what was reported for in vitro release [12,32]. In the simulation comparison, the total drug release is achieved in the PLGA coating at around day 30, while the biodurable coating has only released 20% of its loading and remains at very slow releasing rate.
Fig. 4.
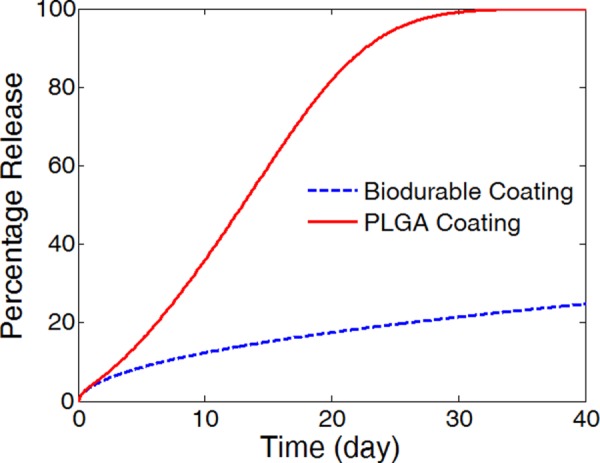
Comparison of simulated drug release profiles for the PLGA stent coating (solid) and the biodurable coating (dashed). (Half strut embedment, k i = 0, and v r = 0).
Corresponding to the difference in the release profiles in the PLGA coating and the biodurable coating, the average drug concentrations in the arterial wall starts off with similar levels for both free drug and bound drug (Fig. 5). The peak drug concentrations appear very early in the biodurable coating case at around day four, and the drug levels gradually decrease. In the PLGA coating case, the drug levels keep increasing as a result of accelerated drug release by degradation and erosion in the coating, and do not arrive at the peaks until around day 22, just a few days prior to total drug release in the coating at day 30. Compared with the biodurable coating case, the drug levels in the PLGA coating case decreased much faster after the peak concentrations. The faster decrease is contributed by the higher drug levels in the arterial wall which leads to a fast drug clearance rate at the perivascular interface. In each case, the trends of concentration evolution for the free drug and the bound drug are highly identical, as a result of the fast reversible binding process in comparison with the drug diffusion [22].
Fig. 5.
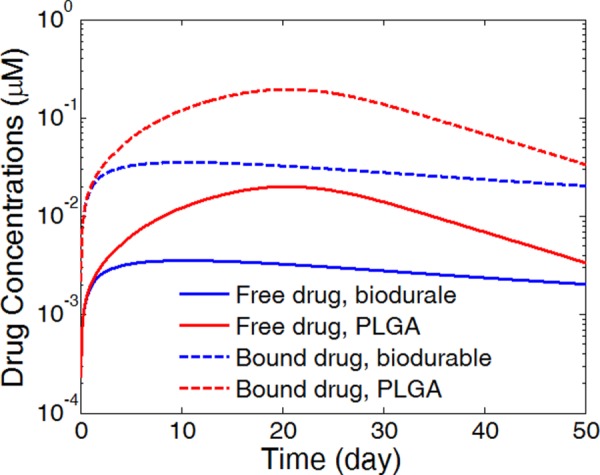
Spatially averaged concentrations of free drug and bound drug in the arterial wall for the PLGA coating case and the biodurable coating case. (Half strut embedment, k i = 0, and v r = 0).
Noticeably, the PLGA coating produces overall much higher drug levels in the arterial wall than the biodurable coating for a prolonged period, governed by the faster drug release rate in the coating. In coronary angioplasty procedures, a sustained drug level in the arterial wall for a prolonged period is necessary for reducing the restenosis. The biodurable coatings are typically found to be limited in sustaining a sufficiently high drug level in the arterial wall after the initial release period, because of the low drug diffusivity and slow drug release [4]. The simulations suggest that the requirement can potentially be achieved by using a degradable PLGA coating through the enhanced release by degradation and erosion.
The arterial drug distributions for both free drug and bound drug are shown for the PLGA coating case at day 25 (Fig. 6), shortly after the drug levels have peaked in the arterial wall. The drug distribution is close to uniform in the circumferential direction, whereas in the transmural direction a gradient is clearly observed closer to the perivascular interface. The better uniformity in the circumferential direction is expected with the anisotropic drug diffusivity which results in fast drug diffusion in the circumferential direction. The observed arterial drug distribution pattern for the PLGA coating case is similar to previous studies of a biodurable coating [22]. The comparison indicates that while the PLGA coating ensures higher overall drug concentrations in the arterial wall than a biodurable coating, the arterial drug distribution pattern is not impacted.
Fig. 6.
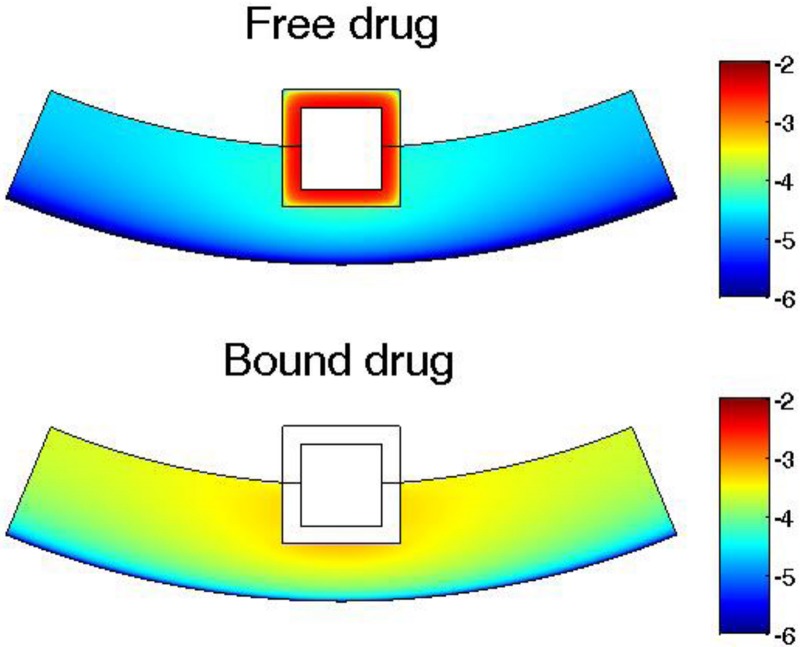
Drug concentration distribution in the arterial wall at 25 days for intravascular drug delivery from a PLGA stent coating. Color bar is in logarithmic scale (mol/m3). (Half strut embedment, k i = 0, and v r = 0).
3.2. Impact of Drug Internalization.
The drug internalization describes the cellular uptake of drug molecules after they associate with the binding sites, and is an important mechanism for drug metabolism in the physiological environment [43,44]. Only limited studies have considered the impact of the internalization process on the stent-based drug delivery [42]. While the drug internalization rate may vary for the different drugs, and such data are lacking in the literature, the proposed model allows different values to be tested for examining and understanding the potential impact of drug internalization. Because the internalization process is in competition with the dissociation step of binding, values of the internalization rate are investigated based on its relative value to the dissociation rate constant. To illustrate the drug internalization process, the average drug levels in the arterial wall are simulated and plotted in Fig. 7 for the three drug forms using the proposed drug internalization model, assuming a small internalization rate relative to the dissociation rate (). The simulation shows an initial build-up for bound drug, which peaks and then diminishes as the bound drug gets internalized. Eventually both free drug and bound drugs are converted to internalized drug. The drug binding and internalization kinetics are closely related to that of the well-recognized enzymatic reactions [53], where in this context the binding sites are acting like enzymes. Throughout the period, the available binding sites are at abundance in the arterial wall, as revealed by the much smaller average bound drug levels (<0.15 μM) compared with that of the overall binding sites concentration (10 μM).
Fig. 7.
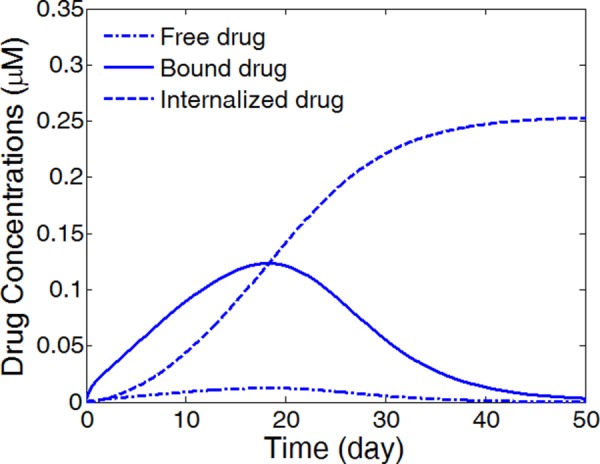
Average concentrations of free drug, bound drug, and internalized drug in the arterial wall for a relatively small internalization rate constant. (Half strut embedment, v r = 0, and ).
Different values for the internalization rate constant are examined to look at its impact on the drug delivery process and the conversion among the three drug forms. While the simulations have shown identical release profiles in the coating for the different internalization rates, Fig. 8 reveals very different drug allocation among the different drug forms for internalized drug (Fig. 8(a)) and bound drug (Fig. 8(b)). For very small internalization rate (), the bound drug level experiences little change compared with the no-internalization case and very low internalized drug level was generated. Increasing the internalization rate constant to , a two orders of magnitude increase in internalize drug level is observed, while the bound drug concentration only experiences a small decrease that is more noticeable at later times. The internalized drug level arrives at constant profiles once the internalization rate constant exceeds , whereas the profiles for the bound drug can still experience drastic decrease for values from to . In all cases, the free drug evolution followed identical trends as the bound drug as a result of the fast reversible binding process and is therefore not illustrated. The simulation results indicate that the arterial drug levels could have a sensitive response with respect to the different rates of drug internalization.
Fig. 8.
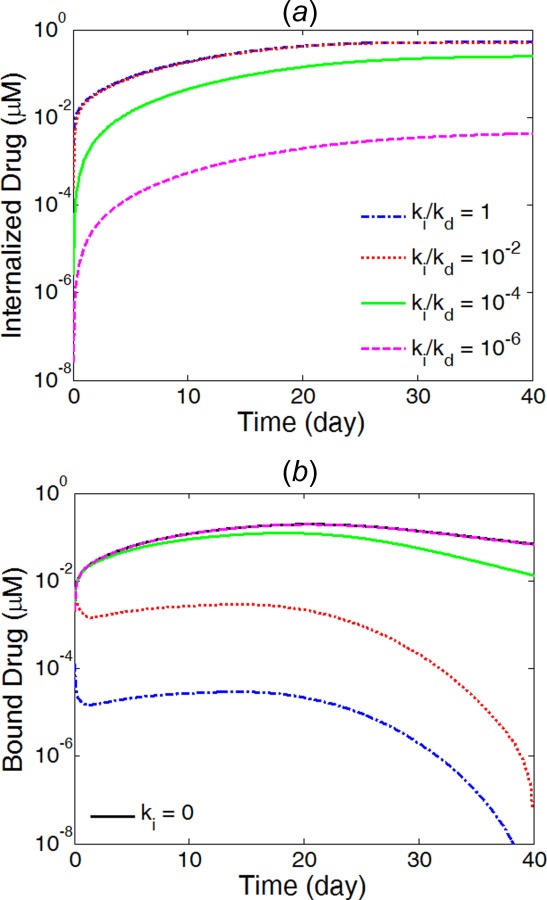
Average concentrations in the arterial wall for internalized drug (a) and bound drug (b) at different internalization rates. (Half strut embedment and v r = 0).
Furthermore, the internalization process changes the arterial drug distribution and significantly affects the drug availability in different regions of the arterial wall (Fig. 9). At small internalization rate (Fig. 9(a)), the arterial wall drug distribution is still close to uniform in the circumferential direction, similar to the case in the no-internalization case. The internalized drug distribution, however, exhibits gradient in both the circumferential and transmural directions and has higher concentration close to the proximity of the stent strut. With increased internalization rate (Fig. 9(b)), the arterial distribution becomes highly nonuniform for both bound drug and internalized drug. In the circumferential direction, the drug levels at areas far away from the stent strut have decreased drastically. As illustrated with the simulations, the consequences of drug internalization could lead to significantly modified arterial drug distribution and reduce the drug availability at arterial sites that are further away from stent strut. The simulations suggest that drug internalization could increase the likelihood of spatial nonuniformity in arterial drug distribution for stent-based drug delivery. As reported in previous studies, the spatial nonuniformity of arterial drug distribution is potentially linked to the growth of more in-stent restenosis at larger interstrut angle [22,54]. Interestingly, the internalization process could aggravate the potential adverse effect of low drug levels at arterial sites further away from stent strut in reducing in-stent restenosis. The amount of impact varies with the internalization rate constant and can be determined for a specific drug (such as sirolimus) when experimental characterization of the rate constant becomes available.
Fig. 9.
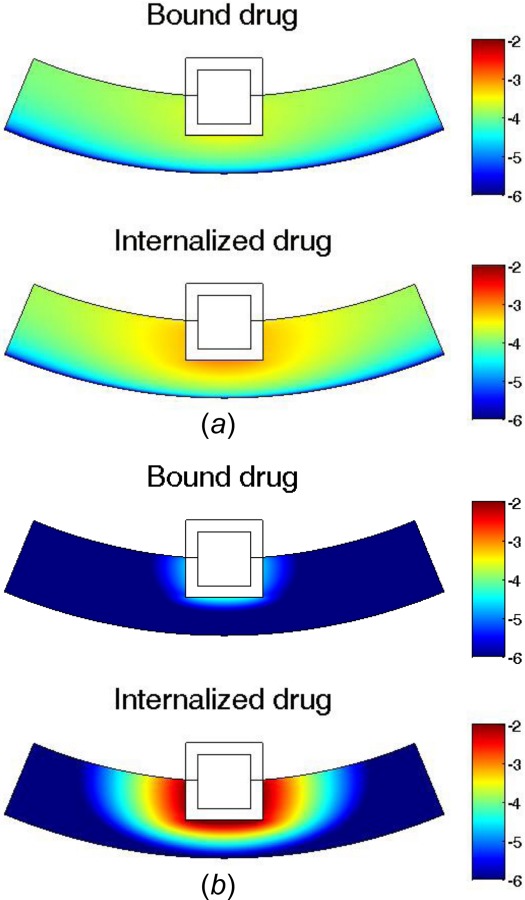
Arterial drug distribution at 25 days for (a) small internalization rate , and (b) fast internalization rate . Color bar is in logarithmic scale (mol/m3). (Half strut embedment and v r = 0).
3.3. Impact of Interstitial Flow.
The interstitial flow within the arterial wall is induced by the pressure difference between the lumen and the perivascular space and is typically very small (in the range of 0.01–0.1 μm/s [45]), and the convective transport term for inside the arterial wall is often left out in the drug transport models of drug-eluting stents [18,20]. A detailed analysis has been carried out to depict the relative importance of convective transport to that of diffusive transport, where drug pharmacokinetics were absent and the impact of convection transport for a hydrophobic drug only starts to become apparent for Peclet number larger than 10 [15]. The interstitial flow velocities can be calculated by Darcy's Law if the pressure difference and the arterial wall permeability are known [55]. While the velocity may differ in different subjects, and the focus of the study was on the impact of the velocity on drug transport rather than accurate calculation of the velocity itself, a range of values reasonable for the system were used [45].
A thorough investigation of the impact of interstitial flow is carried out using our model. As described in Eq. (7), the flow velocity is nonzero only in the transmural direction. While fluid momentum equations are not explicitly solved in this work, the fluid mass conservation equation (the so-called continuity equation) can be used to show that the velocity is inversely dependent on the radius. Considering the small curvature of the arterial wall (that is, a thin wall thickness compared with the radius of the lumen), the variation of the velocity in the transmural direction is negligible, and a constant velocity is assumed in the investigation of the impact of interstitial flow on the drug transport. The simulations show that the drug release profiles in the PLGA coating is not affected by the interstitial fluid flow within the arterial wall for the reported interstitial flow velocities (figure not shown). The absence of variation in the drug release rate is a result of the significantly slower drug diffusion within the PLGA stent coating in comparison to the mechanisms for drug removal at the exterior of the coating, which are contributed by both the drug diffusion in the arterial wall and the wash-out boundary condition at the coating-lumen interface.
The average drug concentrations in the arterial wall, however, are significantly impacted by the presence of convection (Fig. 10). From no interstitial flow to increasing flow velocity, the average drug concentrations for both free and bound drug decrease significantly. While the same drug release rates in the different scenarios indicate that the same amount of drug passed through the coating-arterial wall interface, the presence of interstitial flow increases the transport in the transmural direction and leads to faster drug clearance at the perivascular interface. With interstitial fluid flow, the peaking of the average drug concentrations shift toward earlier times. The Peclet number in the arterial wall is calculated as for interstitial flow velocity (v r) of 0.01 μm/s and wall thickness (L) of 200 μm, which confirms the non-negligible impact of the interstitial flow in drug transport.
Fig. 10.
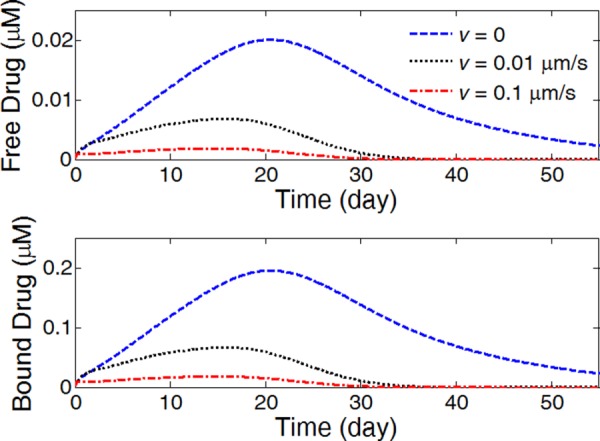
The average drug concentrations in the arterial evolution at different interstitial fluid flow velocities. (Half strut embedment and k i = 0).
The drug distribution shows greatly impaired drug uniformity in the circumferential direction as a result of the convection with even low interstitial flow velocity (0.01 μm/s) (Fig. 11). Compared with the case with no interstitial flow (Fig. 6), the convection results in highly nonuniform distribution in the circumferential direction. Interestingly, the interstitial flow enhances the uniformity in the transmural direction, especially for areas closer to the stent strut. However, the drug coverage in the upper layers are important for reducing in-stent restenosis [56]. Similar to the analysis on the drug internalization, the interstitial flow creates spatial nonuniformity of drug distribution and leads to lowered drug level at arterial sites further away from the stent strut, which could increase the chances of potential adverse outcomes such as in-stent restenosis growth.
Fig. 11.
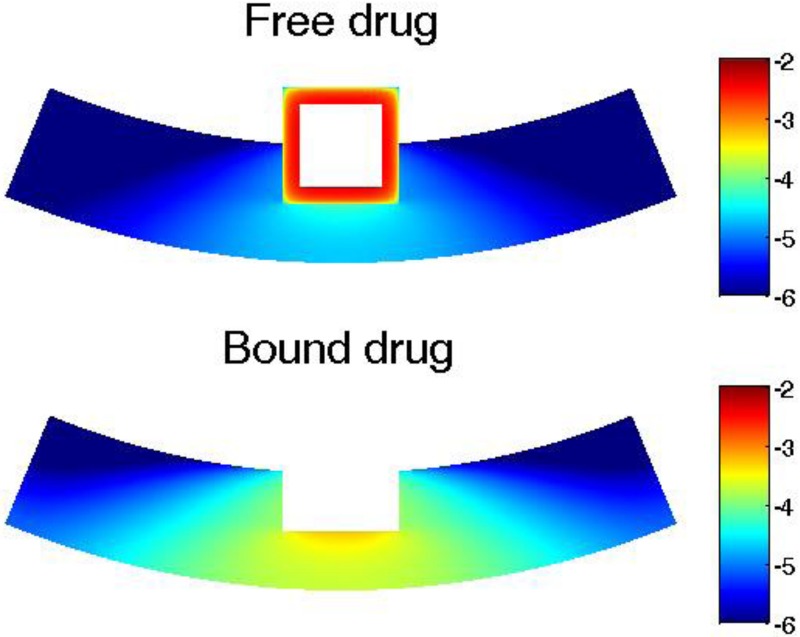
Arterial drug distributions for free drug and bound drug with transmural interstitial flow (v = 0.01 μm/s) at day 20. Color bar is in logarithmic scale (mol/m3). (Half strut embedment and k i = 0).
3.4. Impact of Strut Embedment.
The strut embedment in the arterial wall is another important factor that can affect the drug release in the stent coating and the drug delivery into the arterial wall. Investigation of strut embedment was previously carried out for a biodurable stent coating where the drug binding pharmacokinetics was absent [20]. The model simulations here considered three different scenarios of embedment: contact, half-embedded, and fully embedded. The strut embedment was examined for its impact on the drug release in the PLGA coating and the arterial drug up-take. The arterial wall thickness is used as 300 μm in the simulations in this section.
The simulations show that the drug release profiles in the PLGA coating for the three different strut embedment overlap with each other (figure not shown), similar to what was observed in the cases for different interstitial flow and internalization rates. The observed negligible impact on the drug release profiles in the PLGA coating, again, is due to the rate-limiting step of drug diffusion within the PLGA coating.
The average bound drug concentration in the arterial wall increases with more strut embedment (Fig. 12), which is within expectation, because with more contacting area of the coating with the arterial wall, more of the released drug gets into the arterial wall rather than that depletes into the blood stream. The enhancement of arterial drug levels for higher degrees of strut embedment is in agreement with findings in a previous study of a biodurable coating [20]. Interestingly, the drug concentrations all peak at the same time at around 24 days. The peak drug levels are roughly proportional to the ratio of the contacting area of the stent coating with the arterial wall. The fully embedded case has the highest average drug concentration throughout the time.
Fig. 12.
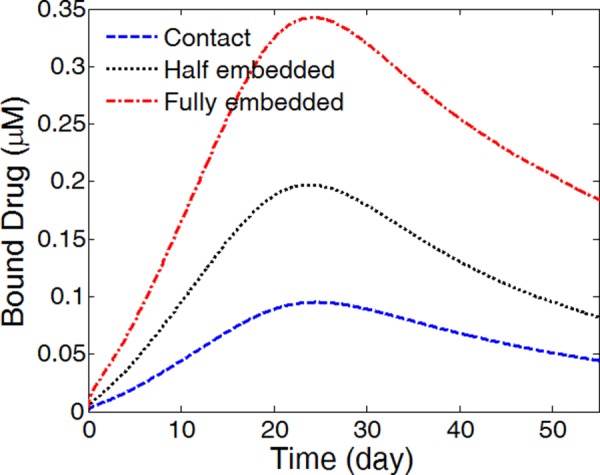
The average bound drug levels in the arterial wall for different strut embedment (k i = 0 and v r = 0)
The arterial drug distribution for bound drug is shown for the three different strut embedments in Fig. 13. A transmural drug concentration gradient is observed in all three cases, with the lowest drug concentration at the perivascular interface due to the drug clearance. In the fully embedded case, drug accumulates and results in the highest drug concentration in the upper layers of the arterial wall. While enhanced drug concentration in the upper layers may be beneficial, the increased degree of strut embedment also indicates more damage to the arterial wall during the stent expansion process, which could potentially counter the benefit of increased drug levels.
Fig. 13.
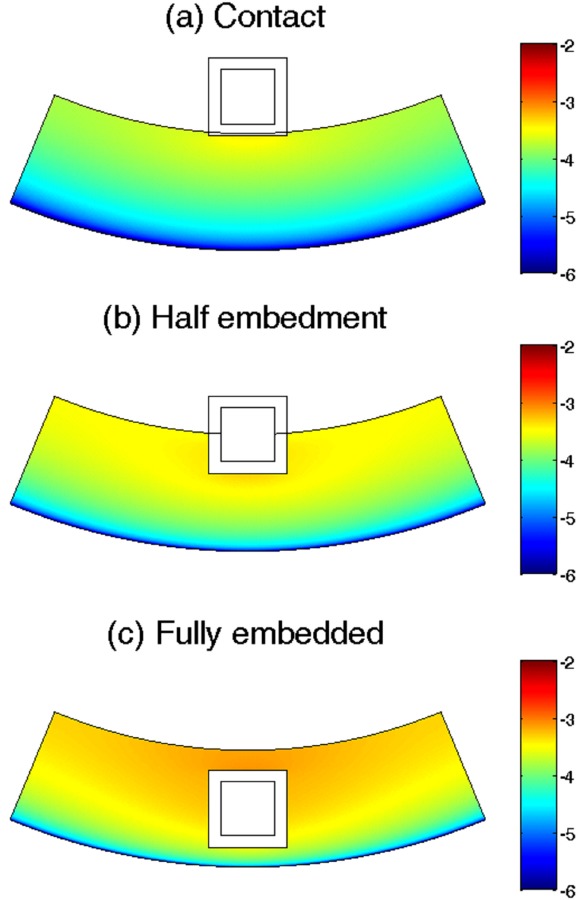
Bound drug distribution in the arterial wall at day 25 for (a) a contacting stent strut, (b) a half-embedded strut, and (c) a fully embedded strut. Color bar is in logarithmic scale (mol/m3). (k i = 0, and v r = 0).
4. Conclusions
The model developed in this work considers a wide and detailed scope of physical, chemical, and biological processes involved in the intravascular drug delivery from a stent with PLGA coating. A mechanistic model for drug release in the biodegradable PLGA coating that couples the drug diffusion with PLGA degradation and erosion was adopted and integrated with subsequent drug transport and distribution in the arterial wall that takes into account anisotropic drug diffusivity and reversible drug binding in the arterial wall. Theoretical estimation of the anisotropic drug diffusivity was also proposed and analyzed with good correspondence to the literature.
The simulation comparison of PLGA coating and biodurable coating has confirmed the difference in drug release rates for intravascular drug delivery, in accordance with expectations gained from in vitro release studies. The comparison revealed the enhanced average drug levels in the arterial wall by utilizing a PLGA stent coating, while the simulations suggested similar patterns of arterial drug distribution compared to the biodurable coating case.
Simulation and analysis of factors including drug internalization, transmural interstitial fluid flow in the arterial wall, and strut embedment were carried out. Negligible change in the drug release profiles in the PLGA coating was observed in all cases, as a result of the slow drug diffusion within the coating compared with drug transport at the coating-lumen interface and coating-arterial wall interface. Higher average drug levels are observed for slower interstitial fluid flow velocities and higher degree of strut embedment. More importantly, each of the investigated factors can significantly change the drug distributions in the arterial wall, which can potentially influence the treatment outcomes. The presence of drug internalization irreversibly consumes and reduces the drug molecules for diffusion, and can localize drug concentrations in the arterial wall neighboring the strut. The transmural interstitial fluid flow, even at very slow velocity, depletes the drug levels at distant arterial sites by convection. Both the drug internalization and interstitial fluid flow can lead to low drug levels at distant arterial wall sites away from the strut, which can potentially impair the drug-eluting stent performance in reducing restenosis. For the different strut embedment, more strut embedment is found to induce higher drug concentration in the upper layer of the arterial wall. While the different model factors were investigated individually in this study in order to acquire insights on their distinct impacts on the drug transport and distribution, when more than one model factor are in consideration, a combination of their individual impact can be expected. For example, when both drug internalization and interstitial flow are present, they will both contribute to reduce the drug availability at the sites far away from the strut in the circumferential direction.
Besides the three factors investigated in detail in this work, other factors related to the pathological conditions, such as plaque, thrombus, and regions of tissue compression due to the stent implantation, may change the drug transport properties in the arterial wall and can also play an important role in the efficacy of treatment with drug-eluting stents. While some studies have been carried out [23,57], such factors were not investigated in this study and further research efforts are necessary. In addition, this study was focused on modeling drug delivery and distribution in the circumferential direction for insights on potentially reducing the nonuniform circumferential restenosis growth [54], and extension of the developed model to 3D to include the drug transport in the axial direction may also be interesting for further investigations.
The developed model here provides the basis of a design tool for evaluating and studying a PLGA coating for stent applications, with the ease of adaptation to more sophisticated scenarios (e.g., consideration of more pathological conditions). Simulations using the model help to provide insights into the drug release and distribution by a stent with PLGA coating, as well as the potential impacts of various factors that can affect the efficacy of drug delivery. With the developed model, optimization of the model parameters, such as different stent strut geometries and coating thickness, can also be performed for exploration on the design of PLGA-coated drug-eluting stents.
Acknowledgment
Support was acknowledged from the National Institutes of Health NIBIB 5RO1EB005181.
Contributor Information
Xiaoxiang Zhu, Department of Chemical Engineering, , Massachusetts Institute of Technology, , 77 Massachusetts Avenue, , Room 66-060, , Cambridge, MA 02139 , e-mail: zhuxx@mit.edu .
Richard D. Braatz, Department of Chemical Engineering, , Massachusetts Institute of Technology, , 77 Massachusetts Avenue, , Room 66-548, , Cambridge, MA 02139 , e-mail: braatz@mit.edu .
References
- [1]. Costa, M. A. , and Simon, D. I. , 2005, “Molecular Basis of Restenosis and Drug-Eluting Stents,” Circulation, 111(17), pp. 2257–2273. 10.1161/01.CIR.0000163587.36485.A7 [DOI] [PubMed] [Google Scholar]
- [2]. Santin, M. , Colombo, P. , and Bruschi, G. , 2005, “Interfacial Biology of In-Stent Restenosis,” Expert Rev. Med. Dev., 2(4), pp. 429–443. 10.1586/17434440.2.4.429 [DOI] [PubMed] [Google Scholar]
- [3]. Khan, W. , Farah, S. , and Domb, A. J. , 2012, “Drug Eluting Stents: Developments and Current Status,” J. Controlled Release, 161(2), pp. 703–712. 10.1016/j.jconrel.2012.02.010 [DOI] [PubMed] [Google Scholar]
- [4]. Venkatraman, S. , and Boey, F. , 2007, “Release Profiles in Drug-Eluting Stents: Issues and Uncertainties,” J. Controlled Release, 120(3), pp. 149–160. 10.1016/j.jconrel.2007.04.022 [DOI] [PubMed] [Google Scholar]
- [5]. Virmani, R. , Guagliumi, G. , Farb, A. , Musumeci, G. , Grieco, N. , Motta, T. , Mihalcsik, L. , Tespili, M. , Valsecchi, O. , and Kolodgie, F. D. , 2004, “Localized Hypersensitivity and Late Coronary Thrombosis Secondary to a Sirolimus-Eluting Stent Should We Be Cautious?,” Circulation, 109(6), pp. 701–705. 10.1161/01.CIR.0000116202.41966.D4 [DOI] [PubMed] [Google Scholar]
- [6]. Daemen, J. , and Serruys, P. W. , 2007, “Drug-Eluting Stent Update 2007 Part I: A Survey of Current and Future Generation Drug-Eluting Stents: Meaningful Advances or More of the Same?,” Circulation, 116(3), pp. 316–328. 10.1161/CIRCULATIONAHA.106.621342 [DOI] [PubMed] [Google Scholar]
- [7]. Lüscher, T. F. , Steffel, J. , Eberli, F. R. , Joner, M. , Nakazawa, G. , Tanner, F. C. , and Virmani, R. , 2007, “Drug-Eluting Stent and Coronary Thrombosis—Biological Mechanisms and Clinical Implications,” Circulation, 115(8), pp. 1051–1058. 10.1161/CIRCULATIONAHA.106.675934 [DOI] [PubMed] [Google Scholar]
- [8]. Acharya, G. , and Park, K. , 2006, “Mechanisms of Controlled Drug Release From Drug-Eluting Stents,” Adv. Drug Delivery Rev., 58(3), pp. 387–401. 10.1016/j.addr.2006.01.016 [DOI] [PubMed] [Google Scholar]
- [9]. Deconinck, E. , Sohier, I. , De Scheerder, I. , and Van Den Mooter, G. , 2008, “Pharmaceutical Aspects of Drug Eluting Stents,” J. Pharm. Sci., 97(12), pp. 5047–5060. 10.1002/jps.21356 [DOI] [PubMed] [Google Scholar]
- [10]. Xi, T. F. , Gao, R. L. , Xu, B. , Chen, L. A. , Luo, T. , Liu, J. , Wei, Y. , and Zhong, S. P. , 2010, “In Vitro and In Vivo Changes to PLGA/Sirolimus Coating on Drug Eluting Stents,” Biomaterials, 31(19), pp. 5151–5158. 10.1016/j.biomaterials.2010.02.003 [DOI] [PubMed] [Google Scholar]
- [11]. Finkelstein, A. , Mcclean, D. , Kar, S. , Takizawa, K. , Varghese, K. , Baek, N. , Park, K. , Fishbein, M. C. , Makkar, R. , Litvack, F. , and Eigler, N. L. , 2003, “Local Drug Delivery Via a Coronary Stent With Programmable Release Pharmacokinetics,” Circulation, 107(5), pp. 777–784. 10.1161/01.CIR.0000050367.65079.71 [DOI] [PubMed] [Google Scholar]
- [12]. Wang, X. T. , Venkatraman, S. S. , Boey, F. Y. C. , Loo, J. S. C. , and Tan, L. P. , 2006, “Controlled Release of Sirolimus from a Multilayered PLGA Stent Matrix,” Biomaterials, 27(32), pp. 5588–5595. 10.1016/j.biomaterials.2006.07.016 [DOI] [PubMed] [Google Scholar]
- [13]. Pan, C.-J. , Tang, J.-J. , Weng, Y.-J. , Wang, J. , and Huang, N. , 2009, “Preparation and In Vitro Release Profiles of Drug-Eluting Controlled Biodegradable Polymer Coating Stents,” Colloids Surf. B, 73(2), pp. 199–206. 10.1016/j.colsurfb.2009.05.016 [DOI] [PubMed] [Google Scholar]
- [14]. Klugherz, B. D. , Jones, P. L. , Cui, X. M. , Chen, W. L. , Meneveau, N. F. , Defelice, S. , Connolly, J. , Wilensky, R. L. , and Levy, R. J. , 2000, “Gene Delivery From a DNA Controlled-Release Stent in Porcine Coronary Arteries,” Nat. Biotechnol., 18(11), pp. 1181–1184. 10.1038/81176 [DOI] [PubMed] [Google Scholar]
- [15]. Hwang, C. W. , Wu, D. , and Edelman, E. R. , 2001, “Physiological Transport Forces Govern Drug Distribution for Stent-Based Delivery,” Circulation, 104(5), pp. 600–605. 10.1161/hc3101.092214 [DOI] [PubMed] [Google Scholar]
- [16]. Zunino, P. , D'angelo, C. , Petrini, L. , Vergara, C. , Capelli, C. , and Migliavacca, F. , 2009, “Numerical Simulation of Drug Eluting Coronary Stents: Mechanics, Fluid Dynamics and Drug Release,” Comput. Methods Appl. Mech. Eng., 198(45–46), pp. 3633–3644. 10.1016/j.cma.2008.07.019 [DOI] [Google Scholar]
- [17]. Kolachalama, V. B. , Tzafriri, A. R. , Arifin, D. Y. , and Edelman, E. R. , 2009, “Luminal Flow Patterns Dictate Arterial Drug Deposition in Stent-Based Delivery,” J. Controlled Release, 133(1), pp. 24–30. 10.1016/j.jconrel.2008.09.075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Balakrishnan, B. , Tzafriri, A. R. , Seifert, P. , Groothuis, A. , Rogers, C. , and Edelman, E. R. , 2005, “Strut Position, Blood Flow, and Drug Deposition—Implications for Single and Overlapping Drug-Eluting Stents,” Circulation, 111(22), pp. 2958–2965. 10.1161/CIRCULATIONAHA.104.512475 [DOI] [PubMed] [Google Scholar]
- [19]. Balakrishnan, B. , Dooley, J. F. , Kopia, G. , and Edelman, E. R. , 2007, “Intravascular Drug Release Kinetics Dictate Arterial Drug Deposition, Retention, and Distribution,” J. Controlled Release, 123(2), pp. 100–108. 10.1016/j.jconrel.2007.06.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Mongrain, R. , Faik, I. , Leask, R. L. , Rodes-Cabau, J. , Larose, E. , and Bertrand, O. F. , 2007, “Effects of Diffusion Coefficients and Struts Apposition Using Numerical Simulations for Drug Eluting Coronary Stents,” ASME J. Biomech. Eng., 129(5), pp. 733–742. 10.1115/1.2768381 [DOI] [PubMed] [Google Scholar]
- [21]. Denny, W. J. , and Walsh, M. T. , 2014, “Numerical Modelling of Mass Transport in an Arterial Wall With Anisotropic Transport Properties,” J. Biomech., 47(1), pp. 168–177. 10.1016/j.jbiomech.2013.09.017 [DOI] [PubMed] [Google Scholar]
- [22]. Zhu, X. , Pack, D. W. , and Braatz, R. D. , 2014, “Modelling Intravascular Delivery from Drug-Eluting Stents With Biodurable Coating: Investigation of Anisotropic Vascular Drug Diffusivity and Arterial Drug Distribution,” Comput. Methods Biomech. Biomed. Eng., 17(3), pp. 187–198. 10.1080/10255842.2012.672815 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Denny, W. J. , and Walsh, M. T. , 2014, “Numerical Modelling of the Physical Factors That Affect Mass Transport in the Vasculature at Early Time Periods,” Med. Eng. Phys., 36(3), pp. 308–317. 10.1016/j.medengphy.2013.11.013 [DOI] [PubMed] [Google Scholar]
- [24]. Sakharov, D. V. , Kalachev, L. V. , and Rijken, D. C. , 2002, “Numerical Simulation of Local Pharmacokinetics of a Drug After Intravascular Delivery With an Eluting Stent,” J. Drug Targeting, 10(6), pp. 507–513. 10.1080/1061186021000038382 [DOI] [PubMed] [Google Scholar]
- [25]. Vairo, G. , Cioffi, M. , Cottone, R. , Dubini, G. , and Migliavacca, F. , 2010, “Drug Release From Coronary Eluting Stents: A Multidomain Approach,” J. Biomech., 43(8), pp. 1580–1589. 10.1016/j.jbiomech.2010.01.033 [DOI] [PubMed] [Google Scholar]
- [26]. Pontrelli, G. , and De Monte, F. , 2010, “A Multi-Layer Porous Wall Model for Coronary Drug-Eluting Stents,” Int. J. Heat Mass Transfer, 53(19–20), pp. 3629–3637. 10.1016/j.ijheatmasstransfer.2010.03.031 [DOI] [Google Scholar]
- [27]. Borghi, A. , Foa, E. , Balossino, R. , Migliavacca, F. , and Dubini, G. , 2008, “Modelling Drug Elution From Stents: Effects of Reversible Binding in the Vascular Wall and Degradable Polymeric Matrix,” Comput. Methods Biomech. Biomed. Eng., 11(4), pp. 367–377. 10.1080/10255840801887555 [DOI] [PubMed] [Google Scholar]
- [28]. Ford Versypt, A. N. , Pack, D. W. , and Braatz, R. D. , 2013, “Mathematical Modeling of Drug Delivery From Autocatalytically Degradable PLGA Microspheres—A Review,” J. Controlled Release, 165(1), pp. 29–37. 10.1016/j.jconrel.2012.10.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29]. Fredenberg, S. , Wahlgren, M. , Reslow, M. , and Axelsson, A. , 2011, “The Mechanisms of Drug Release in Poly(Lactic-Co-Glycolic Acid)-Based Drug Delivery Systems—A Review,” Int. J. Pharm., 415(1–2), pp. 34–52. 10.1016/j.ijpharm.2011.05.049 [DOI] [PubMed] [Google Scholar]
- [30]. Sackett, C. K. , and Narasimhan, B. , 2011, “Mathematical Modeling of Polymer Erosion: Consequences for Drug Delivery,” Int. J. Pharm., 418(1), pp. 104–114. 10.1016/j.ijpharm.2010.11.048 [DOI] [PubMed] [Google Scholar]
- [31]. Prabhu, S. , and Hossainy, S. , 2007, “Modeling of Degradation and Drug Release From a Biodegradable Stent Coating,” J. Biomed. Mater. Res., Part A, 80A(3), pp. 732–741. 10.1002/jbm.a.31053 [DOI] [PubMed] [Google Scholar]
- [32]. Zhu, X. , and Braatz, R. D. , “A Mechanistic Model for Drug Release in PLGA Biodegradable Stent Coatings Coupled With Polymer Degradation and Erosion,” (in revision). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Bailey, S. R. , 2009, “DES Design: Theoretical Advantages and Disadvantages of Stent Strut Materials, Design, Thickness, and Surface Characteristics,” J. Interventional Cardiol., 22(Suppl s1), pp. S3–S17. 10.1111/j.1540-8183.2009.00449.x [DOI] [Google Scholar]
- [34]. Gopferich, A. , 1996, “Mechanisms of Polymer Degradation and Erosion,” Biomaterials, 17(2), pp. 103–114. 10.1016/0142-9612(96)85755-3 [DOI] [PubMed] [Google Scholar]
- [35]. Faisant, N. , Siepmann, J. , and Benoit, J. P. , 2002, “PLGA-Based Microparticles: Elucidation of Mechanisms and a New, Simple Mathematical Model Quantifying Drug Release,” Eur. J. Pharm. Sci., 15(4), pp. 355–366. 10.1016/S0928-0987(02)00023-4 [DOI] [PubMed] [Google Scholar]
- [36]. Raman, C. , Berkland, C. , Kim, K. , and Pack, D. W. , 2005, “Modeling Small-Molecule Release From PLG Microspheres: Effects of Polymer Degradation and Nonuniform Drug Distribution,” J. Controlled Release, 103(1), pp. 149–158. 10.1016/j.jconrel.2004.11.012 [DOI] [PubMed] [Google Scholar]
- [37]. Charlier, A. , Leclerc, B. , and Couarraze, G. , 2000, “Release of Mifepristone from Biodegradable Matrices: Experimental and Theoretical Evaluations,” Int. J. Pharm., 200(1), pp. 115–120. 10.1016/S0378-5173(00)00356-2 [DOI] [PubMed] [Google Scholar]
- [38]. Wada, R. , Hyon, S. H. , and Ikada, Y. , 1995, “Kinetics of Diffusion-Mediated Drug-Release Enhanced by Matrix Degradation,” J. Controlled Release, 37(1–2), pp. 151–160. 10.1016/0168-3659(95)00075-J [DOI] [Google Scholar]
- [39]. Batycky, R. P. , Hanes, J. , Langer, R. , and Edwards, D. A. , 1997, “A Theoretical Model of Erosion and Macromolecular Drug Release from Biodegrading Microspheres,” J. Pharm. Sci., 86(12), pp. 1464–1477. 10.1021/js9604117 [DOI] [PubMed] [Google Scholar]
- [40]. Levin, A. D. , Vukmirovic, N. , Hwang, C. W. , and Edelman, E. R. , 2004, “Specific Binding to Intracellular Proteins Determines Arterial Transport Properties for Rapamycin and Paclitaxel,” Proc. Natl. Acad. Sci. U. S. A., 101(25), pp. 9463–9467. 10.1073/pnas.0400918101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41]. Kolachalama, V. B. , Pacetti, S. D. , Franses, J. W. , Stankus, J. J. , Zhao, H. Q. , Shazly, T. , Nikanorov, A. , Schwartz, L. B. , Tzafriri, A. R. , and Edelman, E. R. , 2013, “Mechanisms of Tissue Uptake and Retention in Zotarolimus-Coated Balloon Therapy,” Circulation, 127(20), pp. 2047–2055. 10.1161/CIRCULATIONAHA.113.002051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42]. Lovich, M. A. , and Edelman, E. R. , 1996, “Computational Simulations of Local Vascular Heparin Deposition and Distribution,” Am. J. Physiol.-Heart Circ. Physiol., 271(5), pp. H2014–H2024. [DOI] [PubMed] [Google Scholar]
- [43]. Castellot, J. J. , Wong, K. , Herman, B. , Hoover, R. L. , Albertini, D. F. , Wright, T. C. , Caleb, B. L. , and Karnovsky, M. J. , 1985, “Binding and Internalization of Heparin by Vascular Smooth Muscle Cells,” J. Cell. Physiol., 124(1), pp. 13–20. 10.1002/jcp.1041240104 [DOI] [PubMed] [Google Scholar]
- [44]. Deux, J.-F. , Meddahi-Pellé, A. , Le Blanche, A. F. , Feldman, L. J. , Colliec-Jouault, S. , Brée, F. , Boudghène, F. , Michel, J.-B. , and Letourneur, D. , 2002, “Low Molecular Weight Fucoidan Prevents Neointimal Hyperplasia in Rabbit Iliac Artery In-Stent Restenosis Model,” Arterioscler., Thromb., Vasc. Biol., 22(10), pp. 1604–1609. 10.1161/01.ATV.0000032034.91020.0A [DOI] [PubMed] [Google Scholar]
- [45]. Wang, D. , and Tarbell, J. , 1995, “Modeling Interstitial Flow in an Artery Wall Allows Estimation of Wall Shear Stress on Smooth Muscle Cells,” ASMEJ. Biomech. Eng., 117(3), pp. 358–363. 10.1115/1.2794192 [DOI] [PubMed] [Google Scholar]
- [46]. Hwang, C. W. , and Edelman, E. R. , 2002, “Arterial Ultrastructure Influences Transport of Locally Delivered Drugs,” Circ. Res., 90(7), pp. 826–832. 10.1161/01.RES.0000016672.26000.9E [DOI] [PubMed] [Google Scholar]
- [47]. Cussler, E. L. , 1997, Diffusion: Mass Transfer in Fluid Systems, Cambridge University, Cambridge, UK. [Google Scholar]
- [48]. Tonar, Z. , Kochová, P. , and Janáček, J. , 2008, “Orientation, Anisotropy, Clustering, and Volume Fraction of Smooth Muscle Cells Within the Wall of Porcine Abdominal Aorta,” Appl. Comput. Mech., 2(1), pp. 145–156. [Google Scholar]
- [49]. Rhodin, J. A. , 2011, “Architecture of the Vessel Wall,” Handbook of Physiology: A Critical, Comprehensive Presentation of Physiological Knowledge and Concepts. Section 2: The Cardiovascular System, Volume II. Vascular Smooth Muscle, D. F. Bohr, A. D. Somlyo, and H. V. Sparks, Jr.(eds.). American Physiological Society, Bethesda, MD, pp. 1–31. [Google Scholar]
- [50]. Roby, T. , Olsen, S. , and Nagatomi, J. , 2008, “Effect of Sustained Tension on Bladder Smooth Muscle Cells in Three-Dimensional Culture,” Ann. Biomed. Eng., 36(10), pp. 1744–1751. 10.1007/s10439-008-9545-5 [DOI] [PubMed] [Google Scholar]
- [51]. Zhang, F. M. , Fath, M. , Marks, R. , and Linhardt, R. J. , 2002, “A Highly Stable Covalent Conjugated Heparin Biochip for Heparin-Protein Interaction Studies,” Anal. Biochem., 304(2), pp. 271–273. 10.1006/abio.2002.5617 [DOI] [PubMed] [Google Scholar]
- [52]. Ferron, G. M. , Conway, W. D. , and Jusko, W. J. , 1997, “Lipophilic Benzamide and Anilide Derivatives as High-Performance Liquid Chromatography Internal Standards: Application to Sirolimus (Rapamycin) Determination,” J. Chromatogr. B: Biomed. Sci. Appl., 703(1–2), pp. 243–251. 10.1016/S0378-4347(97)00415-5 [DOI] [PubMed] [Google Scholar]
- [53]. Fogler, H. S. , 1999, Elements of Chemical Reaction Engineering, Prentice-Hall International, London. [Google Scholar]
- [54]. Takebayashi, H. , Mintz, G. S. , Carlier, S. G. , Kobayashi, Y. , Fujii, K. , Yasuda, T. , Costa, R. A. , Moussa, I. , Dangas, G. D. , Mehran, R. , Lansky, A. J. , Kreps, E. , Collins, M. B. , Colombo, A. , Stone, G. W. , Leon, M. B. , and Moses, J. W. , 2004, “Nonuniform Strut Distribution Correlates With More Neointimal Hyperplasia After Sirolimus-Eluting Stent Implantation,” Circulation, 110(22), pp. 3430–3434. 10.1161/01.CIR.0000148371.53174.05 [DOI] [PubMed] [Google Scholar]
- [55]. Truskey, G. A. , Yuan, F. , and Katz, D. F. , 2004, Transport Phenomena in Biological Systems, Pearson/Prentice Hall, Upper Saddle River, NJ. [Google Scholar]
- [56]. Wessely, R. , Schomig, A. , and Kastrati, A. , 2006, “Sirolimus and Paclitaxel on Polymer-Based Drug-Eluting Stents—Similar but Different,” J. Am. Coll. Cardiol., 47(4), pp. 708–714. 10.1016/j.jacc.2005.09.047 [DOI] [PubMed] [Google Scholar]
- [57]. Balakrishnan, B. , Dooley, J. , Kopia, G. , and Edelman, E. R. , 2008, “Thrombus Causes Fluctuations in Arterial Drug Delivery From Intravascular Stents,” J. Controlled Release, 131(3), pp. 173–180. 10.1016/j.jconrel.2008.07.027 [DOI] [PMC free article] [PubMed] [Google Scholar]


