Photoacoustic excitation profiles of gold nanoparticles

Abstract

The wavelength dependence of the laser-induced photoacoustic signal amplitude has been measured for water dispersions of 10, 61, and 93 nm diameter gold nanospheres. The whole region of the localized surface plasmon resonance has been covered. This “photoacoustic excitation profile” can be overlayed with the extinction spectrum between 450 nm and 600 nm in the case of the smallest nanoparticles. At variance, the larger-sized nanoparticles display a progressive deviation from the extinction spectrum at longer wavelength, where the photoacoustic signal becomes relatively smaller. Considering that photoacoustics is intrinsically insensitive to light scattering, at least for optically thin samples, the results are in agreement with previous theoretical work predicting (i) an increasing contribution of scattering to extinction when the nanoparticle size increases and (ii) a larger scattering component at longer wavelengths. Therefore, the method has a general validity and can be applied to selectively determine light absorption by plasmonic systems.

1. Introduction

Photoacoustic methods are increasingly taking advantage of plasmonic systems, such as gold and silver nanoparticles of various size and shape [1,2]. One of the reasons for this growing interest is the flexibility with which plasmon resonances can be optimized to tune and enhance the optical response [3–8]. This, in turn, can give rise to heat conversion – and to the subsequent pressure wave generating the photoacoustic signal – with an especially high efficiency, due to the large absorption cross section of metal nanoparticles and to their negligible radiative relaxation. These optothermal properties have been the basis for the development of metal nanoparticles as contrast agents for photoacoustic imaging [9–19] and photoacoustic tomography [20–24].

There is a particular aspect of the relationships between optical and thermal properties of nanoparticles which deserves special attention. The excitation wavelength giving rise to the photoacoustic effect must lie within an extinction band, which, for metal nanoparticles, is normally the localized surface plasmon resonance band. In the case of small-sized nanoparticles (<40 nm diameter for gold), absorption and extinction are practically coincident, so that the wavelength dependence of the photoacoustic amplitude will strictly follow the extinction band. This will not be observed, instead, when the nanoparticles size becomes progressively larger, as the scattering contribution to extinction increases [3,5,25]. In fact, scattering of the excitation light does not generate acoustic waves, because it does not involve a transfer of energy from the light field to the nanoparticles; therefore, photoacoustics is intrinsically insensitive to light scattering. This property is not only an advantage when detecting nanoparticles in turbid media [26–28], but it can also be exploited to separate the absorption contribution to extinction within a plasmon resonance band. This idea was already clearly expressed in a classical textbook on the optical properties of small particles [29], together with the proposal to employ traditional chopped-light photoacoustics to resolve absorption from scattering. Similar results can be obtained by all-optical photothermal methods [30,31]. Compared to traditional photoacoustic spectrometry, laser-induced optoacoustic spectroscopy offers an improvement in sensitivity. It requires, on the other hand, the availability of a laser source which can be tuned in a wide wavelength range, completely spanning the relatively broad surface plasmon resonance band. In the present work, we have applied laser-induced photoacoustics to model plasmonic systems, namely, water-dispersed gold nanospheres with 10, 61, and 93 nm diameter, measuring the photoacoustic signal amplitude as a function of the laser excitation wavelength between 440 and 610 nm. We term this measurement a photoacoustic excitation profile. We have also contrasted this excitation profile with that of a dilute chromophore solution, which displays a negligible scattering, and with simulations based on Mie's theory.

2. Experimental methods

Gold nanospheres with 10 nm diameter and potassium permanganate were purchased from Sigma–Aldrich. Gold nanospheres with 61 and 93 nm diameter were synthesized according to Turkevich's method [32]. The nanoparticle dimensions were evaluated by dynamic light scattering measurements (see Supplementary Data). Extinction spectra were measured with a Varian Cary 5 spectrophotometer. Photoacoustic signals were detected with a 1 MHz bandpass Panametrics V103-RM piezoelectric transducer clamped to a standard quartz cuvette for spectrophotometry. The signals were amplified with a Panametrics 5660 B amplifier and averaged with a Tektronix TDS-3054B digitizing oscilloscope. The minimum number of signals was 512 for each average. The sample temperature was kept constant within 0.1 °C with a Lauda Eco RE 415 cryostat and monitored by a thermocouple placed inside the cuvette. The excitation source was a GWU – Lasertechnik GmbH optical parametric oscillator pumped by the third harmonic of a Quanta System Nd:Yag laser for all the measurements but for those presented in Fig. 4, which were obtained with Quanta System Nd:Yag laser-pumped dye lasers. The pulse duration was 10 ns and the repetition rate 10 Hz. The excitation wavelength was measured with a Mut Tristan fiber optic spectrophotometer. The incident laser energy was measured in front of the sample cuvette by a pyroelectric head energy meter before each measurement. The incident laser beam was shaped by a rectangular slit with 1 mm × 10 mm size without focussing in the sample. The fluence was therefore on the order of 0.1 mJ cm⁻². Convolution analysis, performed with commercial software (Sound Analysis, Quantum Northwest Inc.), showed that the temporal profile was the same for a calorimetric reference solution (see below) and for the nanosphere samples, without any detectable delayed component [33]. Therefore, we have simply considered the difference between the first maximum and the first minimum of the signal as the photoacoustic signal amplitude S (see Fig. 1b). Sample integrity was checked by comparing the extinction spectra taken before and after each measurement. Mie theory calculations were performed with the program MiePlot version 4.2.09 by Philip Laven. Size and polydispersity were set according to the parameters obtained by the dynamic light scattering measurements shown in Supplementary Data.

Fig. 4.

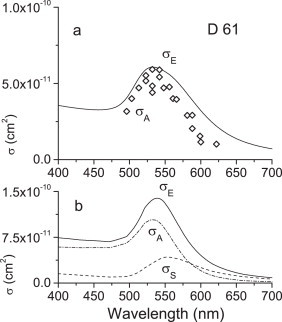
(a) Extinction spectrum (continuous line) of D61 nanospheres in water at T = 22 °C. Photoacoustic excitation profile (diamonds) of the same sample. Every single point of the latter profile is rescaled to the extinction spectrum by comparing the photoacoustic signal amplitude for D61 and potassium permanganate, as in the inset of Fig. 1a, at each wavelength. (b) Extinction (σ_E), absorption (σ_A), and scattering (σ_S) cross sections calculated from Mie theory.

Fig. 1.

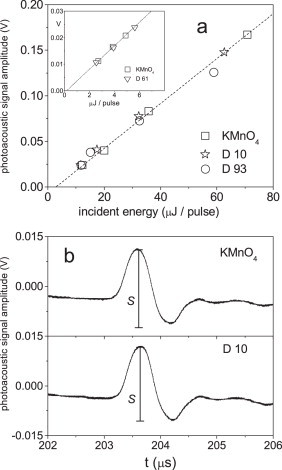
(a) Photoacoustic signal amplitude vs. incident laser energy for the potassium permanganate reference solution and for both D10 and D93 nanospheres samples with 532 nm excitation wavelength at T = 20.6 °C. The amplitudes are normalized with respect to small extinction differences of the samples at 532 nm. A linear fit (dashed line) is superimposed on the potassium permanganate data. The inset shows the same measurement for D61 nanospheres. (b) Laser-induced photoacoustic signals of KMnO₄ and D10 in water at T = 20.6 °C. S indicates the signal amplitude, which is plotted in Fig. 1a. The excitation wavelength was 532 nm. The incident laser power was 14 μJ/pulse. The abscissa represents the signal delay with respect to the trigger which is synchronous with the laser pulse. The position of the signal depends on the speed of sound in water and on the distance between the laser beam and the transducer.

3. Results

3.1. Measurements at a single excitation wavelength

The first step in constructing the photoacoustic excitation profile is to ascertain which physical processes are contributing to the photoacoustic signal amplitude in our experimental conditions. To this end, we first compared the signals from three aqueous dispersions of nanospheres, with 10 nm diameter (D10), 61 nm diameter (D61), and 93 nm diameter (D93), and from a reference compound, at the single excitation wavelength of 532 nm. Theory and practice of laser-induced optoacoustic spectroscopy methods have been previously reviewed [34–36] and we therefore do not describe them in the present article. A common aspect of many photoacoustic measurements is the need to compare the signals of a given sample with those of a so-called calorimetric reference. This is a substance which instantaneously (relative to the time scale of the experiment, i.e., 20 ns in our case) releases all the energy absorbed from the excitation laser as heat. This implies that the calorimetric reference does not photochemically react and that it is not fluorescent. The reference we chose was a potassium permanganate aqueous solution [35].

Fig. 1a shows the photoacoustic amplitude of the nanoparticle samples, and of the potassium permanganate solution, as a function of the incident laser energy. This measurement series allowed us to proof the correctness of the experimental conditions we were employing. Firstly, we could verify the linearity of the relation between signal amplitude and laser energy. A linear fit could be superimposed on the potassium permanganate data, showing the absence of deviations from linearity up to 70 μJ/pulse. The same behavior was displayed by D10 and D61. Small deviations from linearity were only observed at relatively high energy for D93. For this reason, the photoacoustic excitation profiles of all samples were measured keeping the incident laser energy at ∼10 μJ/pulse. Secondly, we could assess the absence of contributions to the signal from photoinduced processes. In fact, in those cases where a photochemical reaction occurs, both reaction enthalpy and reaction volume can change the photoacoustic signal amplitude, adding to, or subtracting from, the signal generated by the heat released following light absorption [35]. Fig. 1b shows representative photoacoustic signals of D10 and of potassium permanganate. We repeated this measurement at various temperatures – for D10 as well as for D93 – always observing a coincidence of the signal amplitudes for the nanoparticles and for the reference solution at each temperature (data not shown). This confirms the absence of contributions from photoinduced processes, and is consistent with previous results obtained for gold nanoshells [37]. We finally note that these results rule out the occurrence of thermal nonlinearities [38,39] and the formation of laser-induced bubbles, which would contribute with an enhanced photoacoustic signal [40,41].

3.2. Wavelength dependence of the reference solution

We first tested our method measuring the photoacoustic excitation profile of the reference potassium permanganate solution. As shown in Fig. 2, the photoacoustic excitation profile corresponds rather closely to the extinction profile. This is what can be expected from a solution of a diluted chromophore which (i) has the characteristic properties of a calorimetric reference and (ii) does not scatter the excitation light appreciably. In fact, owing to the very low scattering by the reference solution, we could neglect the scattering contribution (σ_S) to the extinction cross section (σ_E) in the equation:

$${\sigma }_E={\sigma }_A+{\sigma }_S$$ (1)

where σ_A is the absorption cross section. σ_E in turn was obtained by applying the relationship between cross sections and absorption coefficients μ [42,43]:

$${\mu }_E={\sigma }_{E}N$$ (2)

N, the number density of molecules, was calculated from the reported molar extinction coefficient (2.2 × 10³ M⁻¹ cm⁻¹ at 525 nm) [44]. We chose to rescale the photoacoustic excitation profile and the extinction spectrum at 532 nm, as the fluence-dependent measurements shown in Fig. 1b were performed at this wavelength.

Fig. 2.

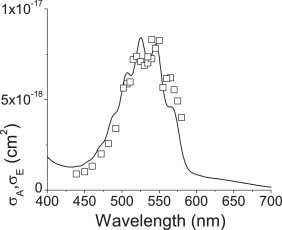
Absorption spectrum (continuous line) of a 1.8 × 10⁻⁵ M solution of potassium permanganate in water at T = 22 °C. Photoacoustic excitation profile (squares) of the same sample. Both profiles are rescaled at 532 nm.

3.2.1. Photoacoustic excitation profiles of gold nanoparticles

As stated in Section 1, it is expected that the photoacoustic excitation profile and the extinction spectrum may not coincide for gold nanoparticles dispersions when the scattering contribution to extinction is remarkable. We intended to add an experimental proof to this prediction by performing a comparison between the photoacoustic excitation profile of D10 and those of D61 and D93.

Fig. 3a presents the photoacoustic excitation profile of D10 nanospheres together with the extinction spectrum of the same sample. Similarly to Fig. 2, the ordinate scale is the extinction cross section σ_E, which, owing to the relatively low dimensions of the nanoparticles, practically coincides with the absorption cross section σ_A in the examined wavelength range. σ_E was obtained from Eq. (2), but in this case N was calculated from the Au content of the dispersion, by means of the available density data, considering the nanoparticles as spherical and monodisperse. The photoacoustic excitation profile was rescaled to the cross section at 532 nm on the basis of the same considerations made for the potassium permanganate solution. The localized surface plasmon resonance band has an extinction maximum at 516 nm. The photoacoustic excitation profile strictly follows the extinction profile between this maximum and the longer wavelength edge. Its apparent maximum, which can be estimated to lie between 500 and 520 nm, is very close to the extinction maximum, as expected if the scattering contribution is negligible.

Fig. 3.

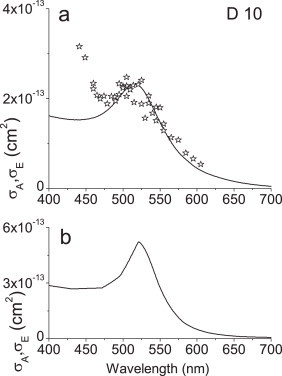
(a) Extinction spectrum (continuous line) of D10 nanospheres in water at T = 22 °C. Photoacoustic excitation profile (stars) of the same sample. Both profiles are rescaled at 532 nm. (b) Extinction (σ_E) and absorption (σ_A) cross sections calculated from Mie theory. The two cross sections are coincident.

Fig. 3b displays the results of a calculation performed on the basis of Mie theory for monodisperse nanospheres with 10 nm diameter. The calculation confirms that σ_A and σ_E are practically coincident for D10, and shows that the wavelength dependence of the cross sections – in particular, the extinction maximum – is very similar to the experimental one. The absolute cross section values are a factor of two higher than our experimental values. There are many possible reasons for this discrepancy. One of them is that the simple physical model considered in the Mie calculation does not fully represent the complexity of the real nanoparticles ensemble, in particular, the nonspherical shape. Moreover, there are significant uncertainties both in the physical constants employed in the Mie calculation of σ_E, and in the experimental determinations of μ_E and N (in particular, the latter relies on the gold content of the sample and on the nanoparticle sphericity as well). This discrepancy is not uncommon: for instance, the experimental and simulated cross sections in the Supplementary Information of Ref. [45] are different by one order of magnitude.

The photoacoustic signal rise at wavelengths shorter than 460 nm is unexpected on the basis of the extinction cross section. In the absence of data below 440 nm, which we could not obtain with our current experimental setup, this increase cannot be presently interpreted. We exclude nonlinear effects because of the linear dependence of the signal on the incident laser power at 443 and at 453 nm (data not shown). Moreover, the transmission of the laser excitation light after crossing the sample follows the extinction spectrum measured by the spectrophotometer (see Supplementary data). This control measurement rules out that the photoacoustic profile deviation is due to a change of the optical properties induced by laser irradiation itself.

Fig. 4a compares the extinction spectrum and the photoacoustic excitation profile of D61 nanospheres. At variance with the results obtained for D10, the D61 photoacoustic profile lies constantly below the extinction profile. A maximum is observed at ∼535 nm, and the displacement from the extinction profile increases at longer wavelength. Fig. 4b shows the calculated cross sections for gold nanospheres with 61 nm diameter. Polydispersity was included in the calculation to take into account the results of the dynamic light scattering analysis (see Supplementary Data). The extinction cross section now receives appreciable contributions from both σ_S and σ_A, with a prevalent weight of the latter at shorter wavelengths. This prediction can explain the experimentally observed displacement of the photoacoustic profile from the extinction.

Fig. 5a displays the extinction spectrum and the photoacoustic excitation profile for the D93 sample. The photoacoustic signal amplitude cannot be overlayed with the extinction spectrum. The latter presents a very broad maximum at ∼545 nm, whereas the photoacoustic signals increase from the longer wavelengths, reaching a plateau around 500 nm, where, in contrast, the extinction is relatively low. The absence of a well-defined maximum in the photoacoustic excitation profile, which is observed for the smaller particles instead, can be due to the steep increase at excitation wavelengths shorter than 460 nm. Fig. 5b shows the calculated cross sections for gold nanospheres with 93 nm diameter. Polydispersity was included in the calculation in this case too. The scattering cross section σ_S gives an increased contribution to the extinction cross section, as expected for larger-sized nanoparticles. Moreover, the maxima of σ_S and σ_A are well separated. We note that the wavelength dependence of the calculated extinction profile is in qualitative agreement with the measured one, whereas the ordinate scale differs by about one order of magnitude. Another discrepancy between the calculated profiles and the experimental findings is the prediction that the scattering contribution at 532 nm should not be negligible, in contrast with the measurements in Fig. 1a which showed the absence of any signal loss due to scattering. In other words, the calculated scattering profile appears more red-shifted than the experimental one. The same considerations about the incomplete coincidence of experimental and calculated parameters, expressed for the case of D10 nanospheres, may be applied here.

Fig. 5.

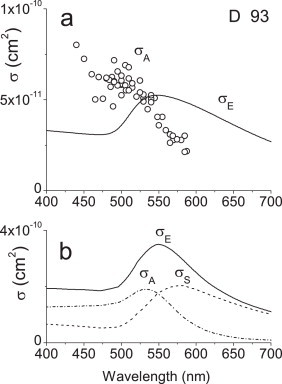
(a) Extinction spectrum (continuous line) of D93 nanospheres in water at T = 22 °C. Photoacoustic excitation profile (circles) of the same sample. Both profiles are rescaled at 532 nm. (b) Extinction (σ_E), absorption (σ_A), and scattering (σ_S) cross sections calculated from Mie theory.

4. Discussion

Our experimental results are in overall agreement with numerous theoretical predictions which have appeared in the literature in the last years. Absorption and scattering efficiencies have been calculated according to various models and methods. Mie's scattering theory [3,25] yields exact results for spherical metal particles under some assumptions, the most important one being that the sphere diameter is much smaller than the light wavelength. Modified methods, like Mie–Gans calculations, have been developed to take into account the nonspherical shape of nanoparticles in real systems [46]. The necessity of performing calculations for any particle shape has led to numerical methods generally labelled as the “discrete dipole approximation” [47,48]. Independently of the calculation method employed, two main features have been generally observed. The first one is that the ratio between scattering and absorption efficiencies increases with the nanoparticle size. For example, the scattering efficiency becomes appreciable for gold nanospheres in the visible wavelength range when the diameter is >40 nm. The second feature is that the wavelength dependence of scattering presents a maximum which is always red-shifted with respect to the absorption maximum. Both characteristics are displayed in the calculated profiles shown in Figs. 3–5b.

Experimental evidence of these predicted optical properties has been shown in previous articles. A photoacoustic imaging setup has been employed to measure the absorption cross sections of various nanostructures at the single wavelength of 638 nm [43]. In fact, accurate σ_A values at this wavelength have been obtained for gold nanorods and mixed-metal nanocages, while scattering cross sections have been obtained by subtracting σ_A from the σ_E values obtained spectrophotometrically. The photoacoustic signal amplitude has been compared to the extinction properties of variously sized and shaped gold nanoparticles at four excitation wavelengths from 650 to 905 nm [49]. The combination of dark-field scattering and photothermal imaging has allowed Link's group [50] to obtain both σ_S and σ_A at the single-nanoparticle level. Size-dependent effects were clearly exposed by the variation of the cross-sections at 532 nm in gold nanospheres with diameter ranging from 43 to 274 nm. At variance with these approaches, we chose to focus on three model nanostructures and to measure the wavelength dependence of σ_A in an extended range.

Our experimental results are in overall agreement with both previous simulations and our ones, moreover, they clearly display the expected differences related to the size of the nanoparticles. D10 nanospheres, owing to a negligible scattering contribution to the extinction, have a relatively narrow plasmon resonance which is superimposable with the photoacoustic excitation profile to a large extent. Similar results have been recently obtained for gold nanospheres with D = 15 nm [51]. At variance, the photoacoustic excitation profiles of D61 and D93 nanospheres cannot be superimposed with the extinction profile. We propose that the observed difference between the photoacoustic excitation profile and the extinction profile is related to the scattering contribution to extinction. This is in agreement with the view, proposed theoretically [52] and verified experimentally [53], that light scattering does not contribute to the generation of the photoacoustic signal, nor does it influence the photoacoustic amplitude, at least for optically thin samples. It would be interesting to compare a photoacoustic excitation profile and a resonance light scattering profile performed on the same nanospheres sample: the former should give σ_A (λ), whereas the latter should yield σ_S (λ), with their sum yielding σ_E (λ) as predicted by Eq. (1). Resonance light scattering profiles, without the photoacoustic counterpart, have been measured for 40 nm gold particles [54] and for silver nanospheres ranging from 29 to 136 nm [42]. In the latter case, particular care was taken in the evaluation of the nanoparticles concentrations, thus allowing to improve the accuracy in determining σ_S. Quantitative results have also been obtained by applying differential pathlength spectroscopy to 40, 50, and 60 nm gold nanospheres and to 47.8 nm × 23.3 nm gold nanorods [55]. The experimentally determined scattering coefficients appeared to be superimposable to those calculated by a discrete dipole approximation method.

The unexpected results at wavelength <460 nm deserve some final comments. Metal nanoparticles can be reshaped by pulsed laser irradiation, with a consequent change of the extinction spectrum. Silver nanoparticles are reduced in size upon 355 nm laser excitation with 60 mJ cm⁻² fluence [56]. Gold nanoparticles – if larger than 14 nm – are reshaped when irradiated at 532 nm with 160 mJ cm⁻² fluence [57]. Besides melting, metal ionization can be involved in the reshaping mechanism [58]. Moreover, gold nanoparticles reshaping depends on the excitation wavelength [45]. We note that the laser fluence in our experiment was <0.1 mJ cm⁻², several orders of magnitude lower than the fluence level leading to nanoparticle breakdown by melting. Following the calculation performed in Ref. [57], a moderate laser-induced temperature rise of 4 K is estimated for our samples. As explained in the Results section and shown in the Supplementary data, laser-induced optical changes are absent at our irradiation level.

Apparently, laser excitation at wavelengths shorter than 460 nm gives rise to a heat release larger than it would be expected on the basis of the extinction spectrum. On the other hand, energy balance dictates that the released heat cannot exceed that of the calorimetric reference when the excitation conditions are identical. One of the differences between excitation wavelengths below or above 460 nm is that interband or intraband transitions, respectively, are excited. This difference has been recognized as the origin of distinct effects of laser excitation at 266, 355, or 532 nm, on laser-induced nanoparticles reshaping in the above-cited Ref. [45]. In that case, the interpretation invoked a reduction of the nanoparticle heat capacity upon interband excitation. Assessing whether this is related to our experimental observations goes far beyond the aim of the present article, and we are therefore planning further experimental and theoretical work to investigate this intriguing aspect of photoacoustic excitation profiles.

5. Conclusions

We have demonstrated that laser-induced photoacoustic spectroscopy can effectively display the wavelength dependence of the absorption and scattering contributions to the extinction in metal nanoparticles by measuring photoacoustic excitation profiles in the localized surface plasmon resonance band. The absorption contribution is obtained directly, comparing the photoacoustic signal to that of a reference compound, whereas the scattering contribution can be evaluated by the difference between extinction and absorption. We have applied the method to gold nanospheres with 10, 61, and 93 nm diameter as model plasmonic systems, for which Mie theory calculations are straightforward, and found a fair correspondence with the expected wavelength dependence in the 450–600 nm range. Possibly the method can be advantageously exploited when the absorption cross sections of new plasmonic systems with uncommon size and composition is to be determined, especially if only the extinction spectra are available and calculations have not been obtained.

Conflict of interest statement

The authors declare that there are no conflicts of interest.

Biographies

Alessandro Feis graduated at the University of Florence in 1985 and received his PhD in Chemistry from the University of Padua in 1990. After working as a postdoctoral fellow at the University of Mainz and at the former Max-Planck-Institut for Radiation Chemistry in Muelheim/Ruhr, he joined the Department of Chemistry of the University of Florence in 1996. He spent a sabbatical year at the Institute for Molecular Structure of the CSIC in Madrid in 2012. His main interests are in optical and optoacoustic spectroscopy, with a focus on Raman spectroscopy of biological molecules.

Cristina Gellini graduated in Chemistry at the University of Florence in 1992 and received her PhD in Chemistry in 1996. In 1997 worked as von Humboldt fellow at the Max Planck Institut für Strahlenchemie in Mülheim an der Ruhr. In 1998 got a postdoc position at the Chemistry Department of the University of Florence where became researcher in 2000. Main scientific interests are focused on the optical characterization of SERS active surfaces, optoacoustic spectroscopy of nanosystems and fluorescence properties of probe-chromophores.

Pier Remigio Salvi received the degree in Chemistry at the University of Florence where is presently full Professor of Chemical Physics. He has been Director of the Chemistry Department “U. Schiff”, University of Florence, in the years 2010–2012. Coauthor of more than 100 publications in internationally refereed journals, his scientific interest along the years include solid-state spectroscopy of molecular crystals, electronic and non linear spectroscopy of aromatic and antiaromatic systems, thermal lensing in molecules, ultrafast relaxation dynamics in porphyrins and photoacoustic spectroscopy of nanomaterials.

Maurizio Becucci born in Florence (Italy) in 1963. Received his PhD in Chemical Sciences. Research and Academic appointments: 2001 to present: Lecturer (Physical Chemistry) at the Department of Chemistry ‘Ugo Schiff’ at the University of Florence (UNIFI), associated member of the European Laboratory for Non-Linear Spectroscopy (LENS); earlier he was scientific staff member of LENS. He is currently Directive Board member of the workgroup for Raman spectroscopy and non-linear optical spectroscopies of the Italian Chemical Society. He is coauthor for more than 80 publications on peer-reviewed, international, scientific journals and he has been invited speaker in many international conferences. His current research interest is related to photophysical and photochemical processes of molecules in the gas phase and the application of spectroscopy for material science.

Appendix A. Supplementary data

The following are the supplementary data to this article: