Markerless EPID image guided dynamic multi-leaf collimator tracking for lung tumors

Abstract

Compensation of target motion during the delivery of radiotherapy has the potential to improve treatment accuracy, dose conformity and sparing of healthy tissue. We implement an online image guided therapy system based on soft tissue localization (STiL) of the target from electronic portal images and treatment aperture adaptation with a dynamic multi-leaf collimator (DMLC). The treatment aperture is moved synchronously and in real-time with the tumor during the entire breathing cycle.

The system is implemented and tested on a Varian TX clinical linear accelerator featuring an AS-1000 electronic portal imaging device (EPID) acquiring images at a frame rate of 12.86 Hz throughout the treatment. A position update cycle for the treatment aperture consists of 4 steps: in the first step at time t = t₀ a frame is grabbed, in the second step the frame is processed with the STiL algorithm to get the tumor position at t = t₀, in a third step the tumor position at t = t + δt is predicted to overcome system latencies and in the fourth step, the DMLC control software calculates the required leaf motions and applies them at time t = t + δt. The prediction model is trained before the start of the treatment with data representing the tumor motion. We analyze the system latency with a dynamic chest phantom (4D motion phantom, Washington University). We estimate the average planar position deviation between target and treatment aperture in a clinical setting by driving the phantom with several lung tumor trajectories (recorded from fiducial tracking during radiotherapy delivery to the lung).

DMLC tracking for lung SBRT without fiducial markers was successfully demonstrated. The inherent system latency is found to be δt = (230 ± 11) ms for a MV portal image acquisition frame rate of 12.86 Hz. The root mean square deviation between tumor and aperture position is smaller than 1 mm.

We demonstrate the feasibility of real-time markerless DMLC tracking with a standard LINAC-mounted (EPID).

1. Introduction

Thoracic and abdominal tumors often exhibit large respiratory motion ranges (Ekberg et al. [5], Seppenwoolde et al. [25], Keall et al. [11]). Intrafractional target motion causes a blurring of the target dose distribution which necessitates the irradiation of additional normal tissue surrounding the tumor volume to achieve full dose coverage of the target. Stereotactic body radiation therapy (SBRT) for non-small cell lung cancers (NSCLC) has been found to be a promising alternative treatment option to surgery (Fakiris et al. [7], Nagata et al. [17]), particularly for early stage NSCLC and inoperable cases. However, radiation toxicity can be a concern (Timmerman et al. [28]). The grade of toxicity has been linked to the irradiated volume and the integrated dose to sensitive structures (e.g. chest wall) (Andolino et al. [1], Matsuo et al. [16]).

Beam tracking (Keall et al. [10]), can effectively “freeze” the tumor motion in the beam reference frame by following it with the treatment beam and can therefore potentially reduce the size of the irradiated volume and/or the maximal dose delivered to critical structures. The procedure may be divided into two separate steps:

1. A method for real-time target motion estimation.

2. A device to shift the radiation beam synchronized to the target position.

The main challenge for step (ii) is to develop a system with acceptable technical specifications concerning leaf position accuracy, velocity and response time. There are currently two research platforms (Tacke et al. [27], Sawant et al. [24]) that provide real-time adjustment of the treatment aperture in response to the signal of a motion capture device.

Other publications have utilized fiducial marker tracking for step (i). Both, the use of electromagnetically excitable markers (Calypso) as well as marker segmentation from x-ray fluoroscopy images have been tested (Sawant et al. [23], Krauss, Nill, Tacke and Oelfke [14]). Using the MV-EPID with soft tissue localization can avoid the patient’s discomfort and any risks associated with fiducial marker placement (including pneumothorax

2. Materials and Methods

2.1. System implementation on Varian platform

A system is presented integrating fast image acquisition, real-time markerless image-based target position estimation (Rottmann et al. [21]), a linear predictor and a DMLC tracking system developed for the Varian platform (Sawant et al. [24]). In Figure 1 a flowchart of this system is shown. In the following a brief overview of the components is given.

Figure 1.

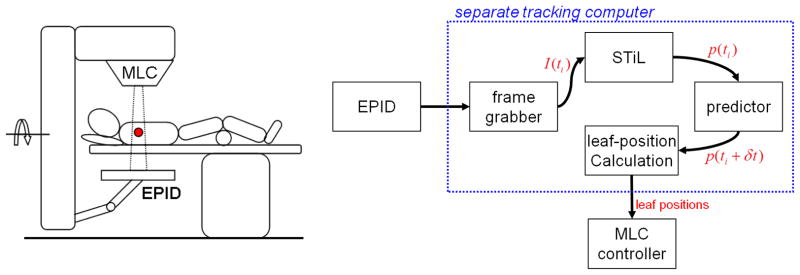
(left) Typical patient setup for continuous MV EPID imaging during lung SBRT delivery. (right) Information flow for the integration of frame grabber, STiL algorithm and DMLC tracker on the clinical platform. All non-clinically approved tools are bundled on a separate computer that receives image data as input through a high density connector cable and provides output in the form of leaf position requests to the MLC controller.

2.1.1. Image acquisition

A frame grabber was provided courtesy of Varian Medical Systems, Inc. along with an application programming interface (API) allowing direct random access memory (RAM) buffer access to images grabbed from the LINAC-integrated image acquisition system. When compared to saving the images first on disk (cf. Fledelius et al. [8], Poulsen et al. [19]), this can reduce the time ΔT_aq needed for image acquisition and allows the seamless integration of the image acquisition process with the other components.

2.1.2. Soft Tissue Localization (STiL)

The STiL algorithm has been described in previous publications (Rottmann et al. [21]) and is embedded in a Matlab^® GUI to have real-time visual feedback for the user. The GUI has an interface accepting incoming frame buffers from the frame grabber API. Figure 2 (right) shows the GUI during tracking of the phantom used in this study. The resulting target positions p(t_i) (red arrow in the figure) are fed into a linear predictor that uses the first N_t positions for training. The forward predicted position p̂(t_i+δt_s) is sent to the DMLC component which calculates and then requests the new leaf-positions by communication with the MLC controller.

Figure 2.

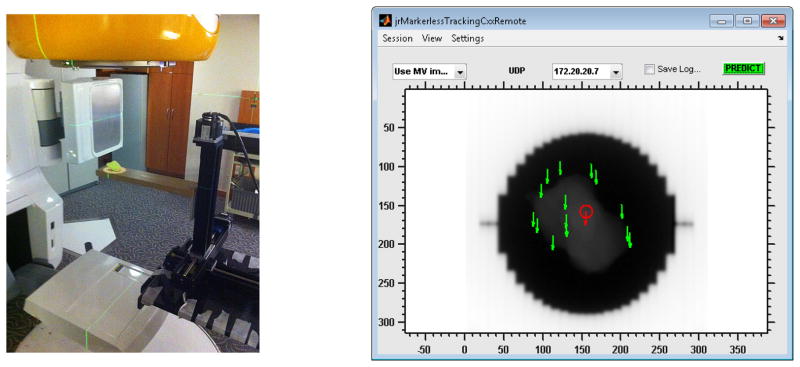
(left) Experimental setup with the Washington University 4D Phantom and a clinical LINAC. The resin tumor model rests on a solid water slab that is mounted to the motion stages of the phantom. The treatment field light is on to show the outline of the radiation field. (right) Screenshot of the Graphical user interface (GUI) for real-time visual feedback during tracking operation. Each green arrow corresponds to a landmark, the red arrow to the average landmark position (which is fed to the predictor). The window/level of the image was adjusted to enhance the display contrast for the tumor model.

2.1.3. Predictor

For any system attempting to compensate tumor motion by image guided target tracking there is an inherent implementation specific time interval that is needed for the process of image acquisition, position calculation and hardware adjustment. In the context of dynamic aperture adaptation we define the system latency δt_s to be the time interval needed for the aperture position to reach a given target position. The aperture will therefore reach the target position p(t_i), calculated from an image acquired at time t_i, at time t = t_i + δt_s introducing a geometric error. The magnitude of this error naturally depends on δt_s and the target velocity.

To reduce the latency induced geometric error, we need to estimate for each target position p(t_i) a future target position p̂(t_i + τ_p). The underlying assumption in finding this estimate is that the target location at time (t_i+τ_p) may be expressed as a function of the N_p previous target positions {p(t_j) | j = (i − N_p), …, i}, i.e. we need to define an adequate prediction function

$$f_p:{(p(t_{i-N_p}),\dots ,p(t_i))}^T\mapsto \widehat{p}(t_i+{\tau }_p)$$ (1)

Several techniques for constructing f_p have been proposed and compared in the literature: Sharp et al. [26] compared linear prediction (LP) with an artificial neural network (ANN) and a Kalman filter (KF) using patient data traces as simulation input. Considering imaging frequencies of 1–30 Hz and latencies from 33–1000 ms they found ANN and LP to give similar results and consistently outperform KF. Ernst and Schweikard [6] proposed the use of support vector regression (SVR) and Ruan [22] proposed a kernel density (KD) based prediction algorithm. Krauss, Nill and Oelfke [13] implemented and compared LP, ANN, SVR and KD including extensive model parameter optimization on the same data set used by Sharp et al. [26] and Krauss, Nill and Oelfke [13]. They found the ANN algorithm to work best, closely followed by SVR and LP and all algorithms performing far better than KD.

Comparing the complexities of the algorithms, we have found linear (ridge) regression to be a rather fast and simple, yet still appropriate method for construction of f_p (cf. Krauss, Nill and Oelfke [13]). In this case the prediction function f_p can be explicitly written as

$$f_p({\mathit{x}}_{\mathit{i}})={\alpha }^T{\mathit{x}}_{\mathit{i}}+{\alpha }_0$$ (2)

if we define x_i := (p(t_i−Np), …, p(t_i)). For practical purposes the constant term α₀ can be omitted if we pre-process all input data to have a mean value of zero. Additionally we can neglect any kind of scaling differences between training data and testing data^‡ if all input data is normalized to have a standard deviation of unity. The transformation is applied to each position p(t_i) in the form of a sliding window operation using the N_p previous positions to calculate the standard deviation σ_i and the mean value m_i

$$\stackrel{\sim }{p}(t_i)=\frac{p(t_i)-m_i}{{\sigma }_i}$$ (3)

if we use

$$m_i=\sum _{k=i-N_p}^i\frac{p(t_k)}{N_p}{\sigma }_i=\sqrt{\frac{1}{(N_p-1)}\sum _{k=i-N_p}^i{(p(t_k)-m_i)}^2}$$ (4)

Considering a set of N_t value pairs of training data: {(x̃_i, ỹ_i) | i = 1, …, N_t} with normalized predicted positions ỹ_i = p̃(t_i + τ_p) that may be calculated by linear interpolation, the weight vector α can be written as an analytic expression:

$$\alpha ={(X^{T}X+\lambda 𝟙)}^{-1}{X}^{T}Y$$ (5)

Here X = (x̃₁, …, x̃_Nt)^T ∈ ( 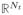× 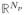) is a matrix containing in each row a training vector x_i, Y = (ỹ₁, …, ỹ_Np)^T is a column vector containing the interpolated target positions at times (t_i+τ_p) and λ is the Tikhonov regularization parameter, which helps to keep the matrix inversion numerically stable for the cases of a poorly conditioned X. There is one free model parameter (λ). Krauss, Nill and Oelfke [13] have found that a patient independent tuning of prediction model parameters is generally adequate, so we follow this approach and tune this parameter with traces that are not later used for prediction.

2.1.4. Dynamic MLC control

The updated aperture position is processed by dynamic multi-leaf collimator (DMLC) tracking software developed for the Varian platform. It has been described in detail by Sawant et al. [24].

2.2. Experimental demonstration with a dynamic motion phantom

We characterized the performance of the integrated system with dynamic phantom studies. For this we employed the Washington University’s 4D phantom, which consists of three orthogonally mounted translation stages that can be programmed to move a platform in an arbitrary 3 D trajectory (cf. Figure 2left). For the target we used a lung tumor model made by rapid prototyping from a resin and placed it on the phantom tray. The tumor model was modeled after a patient’s CT using the GTV outline (cf. Court et al. [4]). The phantom was mounted on the treatment couch of a Varian TX linear accelerator holding the target roughly at an isocentric position (SAD = 100). A circular treatment aperture covering the target completely was chosen and the EPID (AS-1000) was set up at SID = 180 cm, recording at 12.86 Hz with a pixel resolution of (0.43 × 0.43) mm in the isocenter plane.

2.2.1. System latency and its measurement

To determine the look-ahead time, the system latency is measured without the predictor. The dynamic phantom is programmed to drive in a sinusoidal motion with a cycle time of T = 4.5 s and a peak-to-peak amplitude of A = 20 mm in the superior-inferior direction, i.e. in the motion direction of the MLC leaves. With respect to motion range and cycle time, this scenario is a sufficiently realistic simulation of respiratory motion observed clinically during radiotherapy delivery (cf. Berbeco et al. [3]). Running the system without a prediction algorithm in place results in a shift between target position and aperture position of the MV beam that can be easily analyzed from the acquired portal images. Calculating the phase shift Δϕ between a sinusoidal fit to the target positions p_gtv(t_i) and a sinusoidal fit to the treatment aperture position p_mlc(t_i) yields then an estimate for the system latency:

$$\delta t_s=T·\frac{\mathrm{\Delta }\varphi }{2\pi }$$ (6)

2.2.2. Geometric Accuracy with realistic phantom data

To quantify the geometric accuracy of the integrated tracking system (cf. Figure 1 ) three patient lung tumor trajectories were utilized (Berbeco et al. [3]). The trajectories were chosen from a data set of 17 patients that had underwent fiducial marker implantation before being treated for non-small cell lung cancer (NSCLC). The selection criterion was large tumor motion range and (for trajectory 1 and 3) irregularity because we expect these conditions to be the most challenging for MLC leaf travel velocity and predictor performance, respectively. The dynamic motion phantom was programmed with the superior-inferior component of the breathing trajectory. The predictor model was trained in a separate session before the radiation delivery to the phantom. The predictor look-ahead time was set equal to the previously measured system latency (τ_p = δt_s). An overview of all relevant predictor parameters is given in Table 1. For the phantom experiments, the first 100 data points were not latency corrected by the predictor because the prediction vector was chosen to be of this size (N_p = 100). This length of time was chosen to have a sizable sample of points providing results with and without prediction. The timing requirements and alternate schemes are presented in the Discussion section (Section 4).

Table 1.

Parameter values used for the linear prediction algorithm.

parameter	frame rate	τp = δts	λ	Np	Nt	Nwait	Ntest
value	12.86 Hz	250 ms	0.025	100	450	100	450

We use the root mean square error (RMSE) as a measure for the deviation between tumor phantom location and treatment aperture location.

3. Results

3.1. System latency

We observed a system latency of δt_s = (230 ± 11) ms (see Eq. (6)) at an imaging frequency of 12.86 Hz for our experimental implementation. The MLC leaves were positioned in parallel to the dynamic phantom motion. The sinusoidal fits to target and treatment aperture position are shown in Figure 3.

Figure 3.

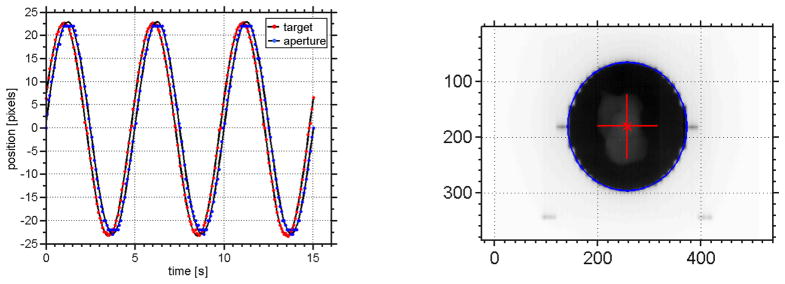
Measurement of system latency at a frame of 12.86 Hz with a dynamic phantom driving a sinusoidal motion in the superior-inferior direction. The motion range was set to 20 mm and the breathing cycle period to T = 4.5 s. (left) Sinusoidal fits to tumor position (red) and aperture position (blue). The latency was found to be δt_s = (230 ± 11) ms (cf. Eq. (6)). (right) A sample EPID image from the latency measurement showing the circular fit to the segmented aperture position (blue) and the target position (red).

3.2. Deviation between target and aperture position

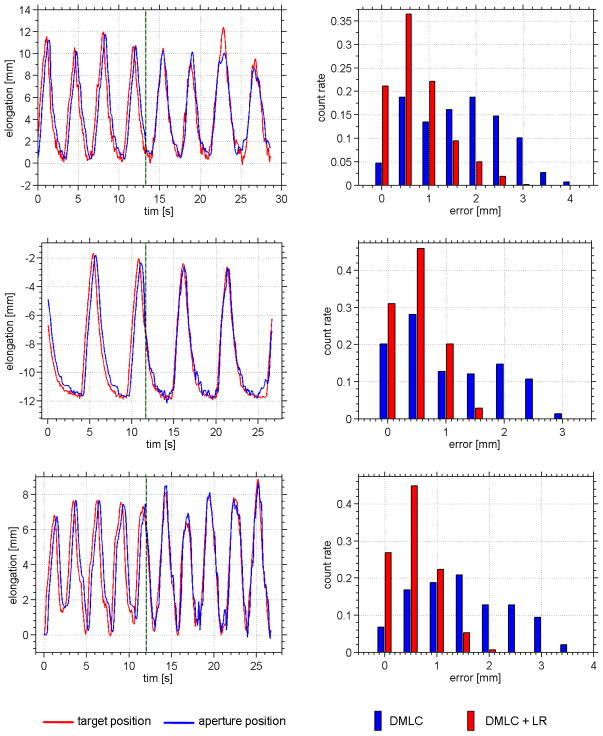
The STiL algorithm operates in real-time and provides target positions to the predictor that allow the treatment aperture to follow the target motion, keeping the aperture centered on the target. The three sample breathing traces used in this study (for driving the dynamic phantom) are shown in Figure 4 with their respective histograms of geometric deviation between tumor and aperture position. It is apparent that the system latency can be effectively compensated. The observed deviations are in line with the geometric accuracy of the markerless soft tissue localization (STiL) algorithm. The overall geometric accuracy is found to be sub-millimeter for all three patient tumor motions. In our previous study, the STiL algorithm provided sub-millimeter localization (without DMLC motion). The histogram also clearly shows a shifts towards smaller deviations once the predictor has started operation. The results are summarized in Table 2. For the investigated traces it is shown that DMLC tracking with a linear predictor can substantially reduce the residual tumor motion.

Figure 4.

Experimental results of the physical phantom study (cf Table 2 ). Each row refers to the delivery of one lung tumor trajectory. The target position (red) and the aperture position (blue) are plotted over time. The black/green dotted line denotes the start of prediction. (right column) Error histograms for each trace before prediction is in place (blue) and after (red). The histogram is normalized to unity integral counts.

Table 2.

Experimental results of DMLC tracking phantom studies. Three different patient’s lung tumor trajectories were used to drive a dynamic chest phantom with a realistic lung tumor model. The deviation between estimated tumor position and beam aperture position is given as root mean square error (RMSE).

trace	static beam RMSE [mm]	DMLC RMSE [mm]	DMLC + LP RMSE [mm]
1	3.4 ± 3.8	1.9 ± 1.9	0.9 ± 0.9
2	3.2 ± 3.2	1.4 ± 1.4	0.6 ± 0.6
3	2.4 ± 2.4	1.8 ± 1.8	0.7 ± 0.7

4. Discussion

In this paper we demonstrate the feasibility of using MV markerless lung tumor tracking in combination with a linear prediction filter to drive real-time dynamic multi-leaf collimator (DMLC) adaptation on a clinical linear accelerator. The presented system employs a previously published DMLC tracking code (Sawant et al. [24]) which we have combined with a markerless soft tissue localization (STiL) algorithm optimized for real-time operation. Furthermore we show that a linear prediction filter can substantially reduce geometric errors caused by the system’s inherent latency.

Using the same DMLC tracking code and similar equipment (Varian Trilogy) but no frame grabber Poulsen et al. [19] reported a system latency of about δt_s = (380±9) ms with a single marker segmentation algorithm. Krauss, Nill, Tacke and Oelfke [14] reported a system latency of 500 ms for their DMLC tracking implementation on the Siemens platform. We attribute our smaller system latency (230 ± 11) ms to the use of the frame grabber and our optimized motion estimation algorithm.

A linear prediction filter was implemented to further reduce the geometric error caused by the system latency. While linear prediction is known to perform less well with irregular breathing patterns, our small latency renders these differences insignificant (Krauss, Nill and Oelfke [13]). For the three lung tumor trajectories (recorded from patients during SBRT deliveries), we saw a reduction in geometric deviation by about 50% with the predictor.

Due to the use of MV-EPID images we can only calculate 2D motion information. However, the neglected direction (depth) has a very shallow dose falloff compared to the other two directions (Nill et al. [18]). Additionally, using the EPID does not give additional imaging dose to a patient (Kilby and Savage [12]). Other publications have suggested using the MV-EPID for lung tumor motion analysis (Richter et al. [20], Rottmann et al. [21], Arimura et al. [2]) and reported accuracy in retrospective user-dependent image analysis scenarios. The algorithm employed in this publication, however, operates fully automatic, i.e. finding landmarks and following these in real-time without prior knowledge or human interaction. The accuracy of the tracking algorithm is of the same range as reported in [21], i.e. better than 1 mm for a dynamic motion phantom.

The accuracy of any real-time tracking of tumors will depend on the fidelity of the localization algorithm. For our method, patient-specific and treatment-specific factors will have some influence on real-time localization due to the visibility of the tumor in MV images. The clinical effect of these factors will be investigated in a separate study of a large patient cohort. The purpose of the current study is to demonstrate the integration of EPID imaging, tumor localization, prediction and DMLC motion on a clinical linear accelerator in a real-time implementation. Prior to clinical application with patients, several challenges will be addressed, including quality assurance, treatment planning and methods for improving the MV imaging capabilities.

While the phantom employed in this demonstration is not anthropomorphic, the tumor model itself is, to our knowledge, more realistic than any other that has been used for this purpose. While the size of the tumor model used in this study is somewhat larger than most tumors that are treated with SBRT, tumor model size will not affect the results in this phantom study.

A pre-treatment training data set can be derived prior to the tracking session. External surrogate data from 4DCT acquisition or tumor motion estimation from pre-treatment cone-beam CT (CBCT) can be used for this purpose [15]. Phase lags between external surrogate motion and tumor motion [9] do not affect the training of the predictor as only the motion pattern information is needed. At the beginning of the tracking session, a period of at least one breathing cycle is required for establishing the tumor trajectory history vector. As SBRT treatments have 4–6 minutes of beam-on time, we don’t see this as a substantial limitation.

5. Conclusions

We have demonstrated fully automatic, real-time, markerless DMLC tracking on a clinical LINAC. Furthermore, we have shown that a linear prediction algorithm can eliminate the system latency, resulting in sub-millimeter accuracy.