Patient-specific modeling of cardiovascular and respiratory dynamics during hypercapnia

Abstract

This study develops a lumped cardiovascular-respiratory system-level model that incorporates patient-specific data to predict cardiorespiratory response to hyper-capnia (increased CO₂ partial pressure) for a patient with congestive heart failure (CHF). In particular, the study focuses on predicting cerebral CO₂ reactivity, which can be defined as the ability of vessels in the cerebral vasculature to expand or contract in response CO₂ induced challenges. It is difficult to characterize cerebral CO₂ reactivity directly from measurements, since no methods exist to dynamically measure vasomotion of vessels in the cerebral vasculature. In this study we show how mathematical modeling can be combined with available data to predict cerebral CO₂ reactivity via dynamic predictions of cerebral vascular resistance, which can be directly related to vasomotion of vessels in the cerebral vasculature. To this end we have developed a coupled cardiovascular and respiratory model that predicts blood pressure, flow, and concentration of gasses (CO₂ and O₂) in the systemic, cerebral, and pulmonary arteries and veins. Cerebral vascular resistance is incorporated via a model parameter separating cerebral arteries and veins. The model was adapted to a specific patient using parameter estimation combined with sensitivity analysis and subset selection. These techniques allowed estimation of cerebral vascular resistance along with other cardiovascular and respiratory parameters. Parameter estimation was carried out during eucapnia (breathing room air), first for the cardiovascular model and then for the respiratory model. Then, hypercapnia was introduced by increasing inspired CO₂ partial pressure. During eucapnia, 7 cardiovascular parameters and 4 respiratory parameters was be identified and estimated, including cerebral and systemic resistance. During the transition from eucapnia to hypercapnia, the model predicted a drop in cerebral vascular resistance consistent with cerebral vasodilation.

1. Introduction

Regulation of breathing and cardiovascular dynamics as well as their interactions are essential for healthy physiological responses to CO₂ challenges. It has been shown that certain mechanisms within the cardio-respiratory regulatory system are compromised in patients suffering from congestive heart failure (CHF) and sleep apnea [1, 2, 3, 4, 5, 6], in particular, it is believed that cerebral CO₂ reactivity is muted in these patients. Moreover, a compromised cerebral CO₂ reactivity may affect the stability of breathing causing ventilatory overshooting during hypercapnia and undershooting during hypocapnia (decreased CO₂ partial pressure) [5, 6]. In the clinic, cerebral CO₂ reactivity is studied by challenging the respiratory system, e.g., by inducing hyper- or hypocapnia. The response to hypercapnia is cerebral vasodilation yielding an increase in cerebral blood flow velocity, while hypocapnia elicits opposite effects. Non-invasive measurements used to assess cerebral CO₂ reactivity include inspired volumetric airflow, expiratory CO₂ partial pressure, heart rate, ejection fraction, arterial blood pressure, and cerebral blood flow velocity. These quantities can be measured dynamically at a high temporal resolution, but they have to be interpreted to assess cerebral vasomotion. One way to combine the available measurements for prediction of cerebral vasomotion is using mathematical modeling.

Several recent studies have provided insight into the mechanisms that govern respiratory function, respiratory system interaction with cardiovascular control, and mutual regulation between ventilation and cerebral blood flow (CBF) and arterial CO₂ partial pressure. Mathematical models that address aspects of the above topics include work by Dong and Langford [7], who developed a model to study factors affecting stable behavior of the cardiovascular-respiratory system in CHF and Lu et al. [8, 9] who applied a combined cardiovascular-respiratory model to study the Valsalva maneuver and factors affecting cerebral blood flow. Relevant experimental studies include work investigating the differential role of CO₂ partial pressures and sympathetic response on vasoconstriction [10], and the role of cerebral reactivity to CO₂ [6]. In addition to understanding basic mechanisms associated with ”healthy” cardio-respiratory interactions, many studies focus on investigating mechanisms associated with pathological cardio-respiratory dynamics. Among the most studied group of patients are those suffering from CHF and sleep apnea (about half the patients with CHF have episodes of sleep apnea).

For CHF patients, an influence of cerebral reactivity on respiratory function could develop as follows. CHF patients can have an elevated brain tissue CO₂ partial pressure after being subjected to a hypercapnic challenge, with this elevation possibly resulting from a muted cerebral CO₂ reactivity. Elevated brain tissue CO₂ resulting from muted or impaired cerebral reactivity can lead to increased respiratory chemosensor stimulation and artificially raised ventilatory drive. Such changes which influence respiratory control responses may contribute to unstable breathing patterns when normal breathing is disturbed by events such as apnea-related asphyxia often observed in CHF patients [11] (arousal-related hyperpnia can have analogous effects). More detailed knowledge of cerebral vascular reactivity and related mechanisms can potentially be obtained with mathematical models that couple ventilatory and cardiovascular system dynamics and control functions combined with appropriate parameter estimation techniques.

To provide adequate physiological insights and allow prediction of specific quantities, the model must include a fair degree of complexity, yet to be able to use the model for analysis of given data, the model should be able to provide reliable model predictions. One way to render a model patient-specific is to use nonlinear optimization to predict a set of model parameters and initial conditions that minimize the least squares error between computed states and the patient-specific data. This process involves solving an inverse problem: predicting the model parameters given the model and the model output. Inverse problems are typically ill-posed and thus difficult to solve reliably. Generally, as the number of measured system quantities increases, the inverse problem becomes easier to solve, yet to minimize patient discomfort and risks, experiments are often limited to a few non-invasive quantities. At the same time, the mathematical models developed to study the system dynamics have to be fairly complex to capture necessary details of the system. Consequently, a relatively large set of parameters are associated with models where only limited data are available. Thus, it may only be possible to estimate a small subset of model parameters. Two techniques are typically employed to identify a small subset of parameters: sensitivity analysis, which predicts how sensitive the model output is to changes in parameter values, and parameter identification or subset selection, which predicts potential correlations among model parameters. If a set of parameters are correlated, only one or a given combination of the parameters can be estimated uniquely.

This study describes a comprehensive method for estimating parameters in a complex physiological model predicting the cardiovascular-respiratory response to hypercapnia in a patient with CHF. To do so, we developed a coupled cardiovascular and respiratory systems model that predicts pulsatile blood pressure, flow, and concentration of gasses (CO₂ and O₂) in the systemic, cerebral, and pulmonary arteries and veins for the patient studied. The model was applied to two respiratory conditions. First, we analyzed dynamics during 5 min of eucapnic breathing, followed by analysis of the transition to hypercapnic breathing. For each experimental condition, parameter sensitivity analysis was used to rank model parameters from the most to the least sensitive, and parameter identification was used to predict a subset of parameters that could be estimated given available data. Section 2 describes efforts needed to develop the cardiovascular (section 2.1) and respiratory (section 2.2) models as well as efforts needed to predict nominal parameters used for these models (section 2.3). Section 3 describes data used for this study, and section 4 describes efforts involved with parameter estimation. Section 5 presents our results during eucapnia (section 5.1) and hypercapnia (section 5.2), section 6 discusses our results, and section 7 summarizes our study.

2. Mathematical modeling

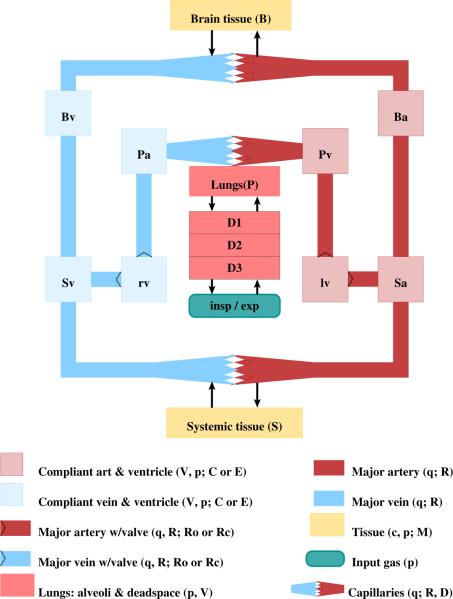
The cardiovascular-respiratory model depicted in Fig. 1 represents a lumped parameter compartmental model designed to predict patient-specific dynamics of cerebral CO₂ reactivity during hypercapnic breathing in a CHF patient. The model consists of two parts: a cardiovascular model that predicts the main quantity of interest cerebral vascular resistance R_B [mmHg s/ml], as well as systemic arterial blood pressure p_Sa [mmHg], middle cerebral blood flow velocity ν_MCA [ml/s], and left ventricular ejection fraction EF. The cardiovascular model is coupled to a respiratory model that predicts expiratory CO₂ partial pressure p_exp,CO2 [mmHg]. These quantities are predicted as a function of heart rate H [beats/s], airflow velocity V̇_IE [ml/s], and concentration of inspired CO₂ [ml_stpd/ml]. The model is designed to predict these quantities for a patient resting in semi-recumbent position. The test protocol involves two stages. The patient first breathes in normal air (approximately zero % CO₂) for 5 min after which a switch to hypercapnic air containing 5% CO₂ is made. This switch in CO₂ concentration is modeled by dynamically changing the concentration of inspired CO₂. The inducement of hypercapnia elicits autonomic and autoregulatory control responses. Autonomic responses to the CO₂ challenge include changes in heart rate, breathing depth and frequency, and minor changes in cardiac contractility and systemic vascular caliber. Effects on the first two quantities (heart rate and airflow) are directly incorporated as model inputs, while the autonomic control quantities (contractility and systemic vascular resistance) are not included in the model. The main autoregulatory response to the CO₂ challenge is regulation of the vessel caliber in the cerebral vasculature. This key response is modeled via prediction of dynamic changes of the cerebral vascular resistance and represents a measure of cerebral CO₂ reactivity. Below, we describe the basic cardiovascular and respiratory models, as well as nominal parameter values. All model quantities are defined in cgs units (cm, grams, and seconds), with the exception of pressure, which is computed in mmHg, standard for the physiology literature.

Figure 1.

Compartmental model of the cardiovascular and respiratory circulations. Systemic (subscript S), brain (subscript B), and pulmonary (subscript P) arteries (subscript a) and veins (subscript ν); Vessels carrying oxygenated blood (systemic arteries and pulmonary veins) are red, while vessels carrying deoxygenated blood (systemic veins and pulmonary arteries) are blue. All vascular compartments represent a group of vessels with similar pressure p [mmHg]. Each vascular compartment is characterized by its volume V [ml] and compliance C [ml/mmHg]. The left (red, subscript lν) and right (blue, subscript rν) ventricles generate pulsatile pressure p_lν, p_rν [mmHg]. These two compartments are defined using time-varying elastance E [mmHg/ml]. Flow q [ml/s] between compartments are opposed by constant resistances [mmHg s/ml]. Gases diffuse from major arteries into the capillaries at a rate D. Tissue compartments (yellow) account for exchange of gases (O₂ and CO₂) with capillaries. Each vascular bed is characterized by a metabolic rate M [ml_stpd/s], and the gas concentrations in the tissues and capillaries are denoted by c [ml_stpd/ml]. The lungs are represented by three dead space compartments each predicting the partial pressure of the gases p_Di,g [mmHg]. The partial pressure of the gases in the inspired air p_I,g, and the CO₂ expiratory partial pressure p_exp,CO2 are marked separately.

2.1. Cardiovascular model

The cardiovascular system (see Fig. 1) is represented by a closed circuit with 3 arterial compartments, 3 venous compartments, and 2 ventricular compartments. Vascular compartments represent systemic arteries and veins in the body and the brain, as well as pulmonary arteries and veins. Each compartment lumps related vessels yielding a representative transmural pressure p(t) [mmHg], volume V(t) [ml], compliance C [ml/mmHg] (constant). Compartments are separated by resistors R [mmHg s/ml], analogous to an RC-circuit. The physiological analogy of compliance is vascular tone, while resistances can be predicted from vascular caliber through Poiseuille's law for flow in a cylinder, where resistance R is inversely proportional to the radius r to the fourth power, R = k/r⁴. It should be noted that each compartment lumps many vessels together, thus a direct computation relating radius to resistance is not feasible.

For each compartment i, the stressed volume V_i,str(t) [ml] is given by

$$V_{i,str}\left(t\right)=V_i\left(t\right)-V_{i,unstr}=C_i{p}_i\left(t\right),$$ (1)

where V_i(t) [ml] is the time-dependent total volume and V_i,unstr [ml] (constant) is the unstressed volume, at zero transmural pressure.

Flows between adjacent compartments are characterized by a constant resistance R [mmHg s/ml] and volumetric flow rate q(t) [ml/s]. Incorporating Ohm's law, the net change in volume for each compartment is given by

$$\frac{d{V}_i\left(t\right)}{dt}=q_{in}\left(t\right)-q_{out}\left(t\right),q_{in}\left(t\right)=\frac{p_{i-1}\left(t\right)-p_i\left(t\right)}{R_{in}},q_{out}\left(t\right)=\frac{p_i\left(t\right)-p_{i+1}\left(t\right)}{R_{out}},$$ (2)

The subscripts i − 1 and i + 1 refer to upstream and downstream compartments in relation to compartment i, respectively. A system of differential equations is obtained by differentiating (1) and equating with (2) to give

$$\frac{d{p}_i\left(t\right)}{dt}=\frac{q_{in}\left(t\right)-q_{out}\left(t\right)}{C_i}.$$ (3)

An equation of this form is associated with each vascular compartment.

The heart is represented by the left and right ventricles, modeled to generate the driving pressures for the systemic and pulmonary systems, respectively. This is realized by imposing a time-varying pressure as a function of ventricular volume. Thus, for the ventricular compartments V_iν we obtain a differential equation by imposing volume conservation, as

$$\frac{d{V}_{iv}\left(t\right)}{dt}=q_{in}\left(t\right)-q_{out}\left(t\right),i=l,r,$$ (4)

where the flows q(t) [ml/s] are determined similarly to (2). We use a time-varying elastance model to compute ventricular pressures p_iν(t) [mmHg] [12, 13, 14, 15],

$$p_{iv}\left(t\right)=E_{iv}\left(t\right)[V_{iv}\left(t\right)-V_{id}],i=l,r,$$ (5)

where V_id [ml] denotes the volume at zero end-systolic pressure [12, 16] and E_iν(t) [mmHg/ml] denotes the time-varying elastance. In the above equations subscript i denotes the left or right ventricle, respectively. For each ventricle, time-varying elastance E(t) [mmHg/ml] is modeled using a piecewise sinusoidal function of the form

$$E\left(t\right)=\{\begin{array}{cc}(E_S-E_D)\left[1-\cos \left(\frac{\pi t}{T_M}\right)\right]∕2+E_D\hfill & 0\le t\le T_M\hfill \\ (E_D-E_D)\left[\cos \left(\frac{\pi (t-T_M)}{T_R}\right)+1\right]∕2+E_D\hfill & T_M\le t\le T_M+T_R\hfill \\ E_D\hfill & T_M+T_R\le t\le T,\hfill \end{array}\phantom{\}}$$ (6)

where T_M and T_R [s] denote the time for end-systolic (maximum) elastance (T_M) and the remaining time to relaxation (T_R). To account for varying heart rate, we express these times as fractions of the heart period T = 1/H[s], i.e., T_M,f = T_M/T and T_R,f = T_R/T. We assume that maximum elastance occurs at the same time for both left and right ventricles, thus the values of the two parameters T_M and T_R [s] remain the same for the two sides of the heart. E_D and E_S [mmHg/ml] denote the end-diastolic and end-systolic elastance of each ventricle. The elastances differ significantly between the right and the left ventricle, in particular for the CHF patient studied in this manuscript. Thus we include four elastance parameters E_D,l,E_D,r and E_S,l,E_S,r [mmHg/ml] and two timing parameters T_M and T_R [s].

Similar to previous studies [17, 18, 19], the cardiac valves (mitral mν, aortic aν, tricuspid tν, and pulmonary pν) are modeled using time-varying resistances R_mν(t), R_aν(t),R_tν(t),R_pν(t) [mmHg s ml] defined as a function of the pressure drop across the valves. A small baseline resistance is used to define an “open” valve (subscript “o”) and a resistance that is several orders of magnitude larger is used to define the “closed” valve (subscript “c”). An exponential function is applied to describe the degree of openness as a function of the pressure gradient. Thus the effective resistance of a valve is defined by

$$R_{valve}\left(t\right)=\min \left[R_{valve,o}+e^{-k(p_{in}\left(t\right)-p_{out}\left(t\right))},R_{valve,c}\right].$$ (7)

The parameter Rvalve,o [mmHg s/ml] is the small resistance allowing flow out of the ventricle, k describes the speed of the transition from open to closed, and Rvalve,c [mmHg s/ml] is a value large enough to effectively shut off the flow through the valve. Since this function is non-smooth at the junctions of the exponential and Rvalve,c, a smoothing function [20] was used. A smooth minimum can be computed as

$${\min }_{\epsilon }\left(x\right)=-\epsilon \log \left(\sum _i\exp (-x_i∕\epsilon )\right),$$ (8)

where 0 < ε < 1 denotes the degree of smoothness (in this study we used ε = 0.5) and x denotes the vector to be minimized. Similarly, a smooth maximum could be computed as max_e(x) = –min_ε(–x).

Cerebral autoregulation, activated during the switch from eucapnic to hyper-capnic breathing, causes cerebral vasodilation, i.e., the caliber and consequently the resistance of vessels in the cerebral vasculature decreases. This decrease in cerebral vascular resistance causes an increase in cerebral blood flow velocity as observed in measurements of associated data (see Fig. 6). Similar to previous studies [17], we included cerebral autoregulation by modeling peripheral vascular resistance in the brain as a piecewise linear function in time of the form

$$\begin{array}{cc}\hfill R_B\left(t\right)=& \sum _{i=1}^n{\gamma }_i{H}_i\left(t\right),\hfill \\ \hfill H_i\left(t\right)=& \{\begin{array}{cc}\frac{t-t_{i-1}}{t_i-t_{i-1}},\hfill & t_{i-1}\le t_i\hfill \\ \frac{t_{i+1}-t}{t_{i+1}-t_i},\hfill & t_i\le t_{i+1}\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (9)

where the unknown function values at nodes γ_i are model parameters.

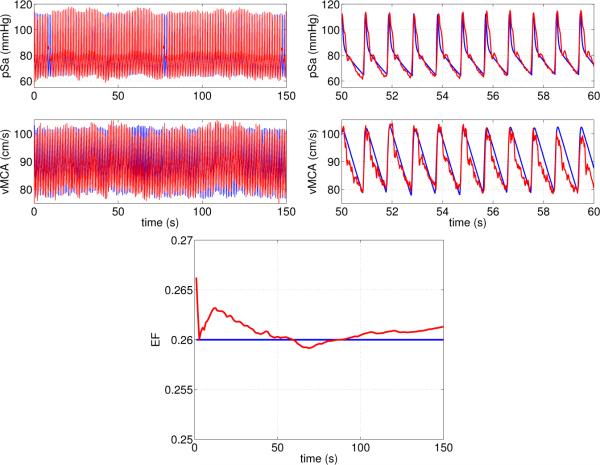
Figure 6.

Steady state simulation results from the cardiovascular model. Graphs show arterial pressure and cerebral blood flow velocity for the full dataset, and a zoom for 50 ≤t ≤ 60 seconds. The bottom panel shows computed and expected ejection fraction EF (set at 26%).

The input to the cardiovascular model is the period of the cardiac cycle T = 1/H, which is obtained from data (see Fig. 2). Note, that this period is not constant but varies with each cardiac cycle. Four quantities constitute the model output, the first being the cerebral vascular resistance (the resistance in the brain, R_B) as described above. Three additional output quantities are compared with the model data. Systemic arterial blood pressure p_Sa is found from the solution of the differential equation (28). Blood flow velocity in the middle cerebral artery ν_MCA is related to the total flow to the brain by

$$v_{MCA}=\frac{q_B}{\kappa },q_B=\frac{p_{Ba}-p_{Bv}}{R_B},$$

where κ is a scaling factor relating volumetric blood flow in the brain to blood flow velocity measured in the middle cerebral artery. We assume that this factor is constant, implying that no active changes in vessel properties (diameter and vascular tone) occur at the level of the major cerebral arteries. The final output is the ejection fraction

$$\mathrm{EF}=\frac{V_{lv,max}-V_{lv,min}}{V_{lv,max}},$$

where V_lν,max and V_lν,min are the maximum and minimum volume of the left ventricle, respectively. Note, since the ventricular volume is a dynamic quantity, the maximum and minimum volumes change over each cardiac cycle. To ensure differentiability, these quantities are computed as smooth minimums and maximums from V_lν (one of the state variables) using the smoothing function (8).

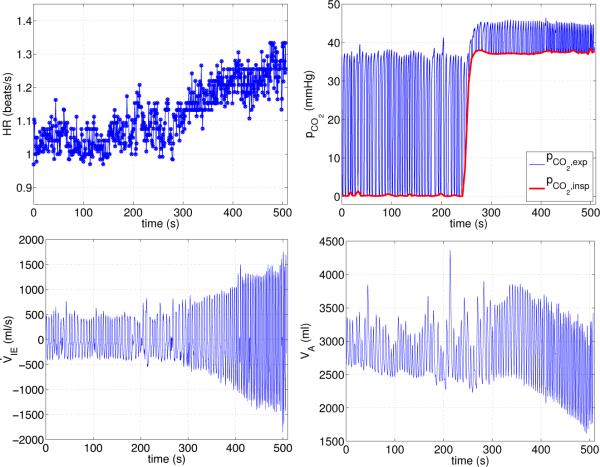
Figure 2.

Input to the model from experimental data. Top row: Heart rate (left panel) and inspired partial pressure of CO₂ (marked with a red line on the right panel). These values are obtained by fitting a smooth spline through minimum values of expiratory CO₂ partial pressures. Bottom row: Inspired airflow (left panel) and alveolar volume (right panel).

All equations for the cardiovascular model are given in Appendix A.1, and parameterization is discussed in the beginning of Section 2.3.

2.2. Respiratory model

The respiratory system (also depicted in Fig. 1) contains tissue and lung com partments. Metabolism, defined here as the consumption of O₂ and production of CO₂, occurs in all tissue and organs. We lump tissue and organs in the same compartment, but divide the mass into two regions: brain tissue B and systemic tissue S. These two regions are each divided into two compartments: a tissue compartment tis where metabolic activity resides and an interfacing capillary compartment cap where gas exchange between tissue and blood occurs, see e.g., [21]. The lungs, where O₂ and CO₂ are exchanged with the environment, are described by an alveolar compartment and three dead space compartments. Standard material balance equations describe the exchange of gases within each compartment and between the tissue compartments and interfacing capillaries.

Tissue equations

The following symbol convention will be used: c represents concentration [ml_gas/mlblood], subscript T represents a generic tissue compartment which can be chosen to be systemic S or brain B tissue, generic gas quantities (O₂ or CO₂) are denoted by g and the gas fractional amount by F. Venous flow [ml/s] is denoted by ν and arterial flow [ml/s] by a. Following this symbol convention, and as mentioned above, we distinguish between two tissue-related compartments: the actual tissue regions Ttis denoted as Stis and Btis, and the capillary blood compartments Tcap denoted as Scap and Bcap. The latter compartments serve as an interface between the tissue compartments and the blood stream. The two tissue compartments are marked in yellow on Fig. 1, while the systemic and brain capillary compartments are indicated as expansions where arteries and veins intersect.

Let the general quantity of a gas g (O₂ or CO₂) in a tissue region T (B or S) be written as A_T,g, then, the total amount of a gas in a tissue region A_T,g [ml] can be found as

$$A_{T,g}=V_{T,g}{C}_{T,g}.$$ (10)

This equation describes A_T,g [ml] as the product of the effective tissue volume V [ml] (constant) available for the gas and the concentration c [ml_gas/mlvolume] of the gas in the volume.

The change in the amount of gas g in the tissue compartment depends on the amount of gas produced or consumed by metabolism M_T,g [ml/s] and the amount added or removed by exchange through diffusion with the capillary compartment. Similarly, the change in the amount of gas in the capillary compartment depends on the removal of gas by the bloodstream q_T [ml/s] and diffusion of gas into or out of the tissue compartment, i.e., by differentiating (10) we obtain

$$\begin{array}{cc}\hfill \frac{d{A}_{Ttis,g}}{dt}=& \frac{d{V}_{Ttis,g}}{dt}{c}_{Ttis,g}+V_{Ttis,g}\frac{d{c}_{Ttis,g}}{dt}\hfill \\ \hfill =& M_{T,g}-D_{T,g}(c_{Ttis,g}-c_{Tcap,g}),\hfill \\ \hfill \frac{d{A}_{Tcap,g}}{dt}=& \frac{d{V}_{Tcap,g}}{dt}{c}_{Tcap,g}+V_{Tcap,g}\frac{d{c}_{Tcap,g}}{dt}\hfill \\ \hfill =& q_{T,g}(c_{a,g}-c_{Tcap,g})+D_{T,g}(c_{Ttis,g}-c_{Ttis,g}-c_{Tcap,g}).\hfill \end{array}$$

In the above equations, D_T,g denotes the diffusion capacity for a gas in a given tissue (depending on partial pressure or concentration of the gas). V_Ttis,g is the effective tissue volume for a gas, V_Tcap,g is the effective capillary blood volume for a gas (approximately 1% of V_Ttis,g), and q_T,g is the blood flow through the capillary compartment. The concentration in the arteries traveling to both the systemic circulation and the brain are the same since no metabolic effects are introduced until exchanges occur between capillary and tissue compartments. Hence we denote the arterial concentration for both regions as c_a,g [ml_gas/ml_blood].

Assuming dV_T,g/dt = 0, the above equations reduce to generic equations predicting exchange between the tissue compartment and capillary blood combined with metabolism

$$V_{Ttis,g}\frac{d{c}_{Ttis,g}}{dt}=M_{T,g}-D_{T,g}(c_{Ttis,g}-c_{Tcap,g})$$ (11)

and exchange between capillary blood and the tissue compartment combined with transport via the bloodstream

$$V_{Tcap,g}\frac{d{c}_{Tcap,g}}{dt}=q_T(c_{a,g}-c_{Tcap,g})+D_{T,g}(c_{Ttis,g}-c_{Tcap,g}).$$ (12)

Assume that tissue compartments can be considered well-mixed and gas concentrations are equilibrated with exiting venous concentrations. Then the gas concentration c_ν,g [ml_gas/ml_blood] in the systemic venous return can be calculated as a mixture of the concentrations from the incoming systemic stream q_S [ml/s] and cerebral venous stream q_Bv [ml/s] as

$$c_{v,g}=\frac{c_{Stis,g}{q}_S+c_{Btis,g}{q}_{Bv}}{q_S+q_{Bv}},$$

where c_S,g and c_B,g [ml_gas/ml_blood] are the systemic and cerebral concentrations of each gas exiting the capillary compartments.

Lung equations

The lungs (also depicted on Fig. 1) are modeled using five compartments including pulmonary capillaries, the alveolar space, and three dead space compartments representing the bronchial airways. The compartment representing the alveolar space has a dynamic volume V_A,g, in which O₂ and CO₂ are exchanged between the lungs and the pulmonary capillaries. Let A denote the alveolar compartment; then the amount of alveolar gas is given by

$$V_{A,g}=V_A{F}_{A,g},$$

the product of alveolar volume V_A [ml] and gas fraction F_A,g. The change in quantity of alveolar gas is represented by a mass balance relation parallel to the one developed for the tissue compartment, taking into account a time-varying alveolar volume. Gas transport is via blood flowing to and from the lungs through pulmonary capillaries, and gas exchange with the environment is carried out via inspiration and expiration. A separation into lung tissue and lung capillary compartments is not included given the rapid and complete loading and unloading of blood gases between the alveoli and the the blood flow through the capillaries surrounding each alveolus. Note that the systemic venous return concentration c_ν,g will be the same as the pulmonary arterial concentration and systemic arterial concentration c_a,g will be the same as pulmonary venous return. Thus, c_ν,g and c_a,g are used to denote the pulmonary arterial and venous concentrations, respectively.

The bronchial airways have been modeled using a rigid anatomical dead space connecting the alveolar space with the atmosphere. This space is divided into three equal-volume compartments which each account for some of the effects of the pulmonary branching. We assume that the compartment marked D₁ is located closest to the mouth with the compartment marked by D₃ closest to the alveolar space. Gas concentrations and partial pressures are predicted in all compartments.

Following these considerations, the mass balance equation for the alveolar compartment can be written as

$$\frac{d{V}_{A,g}}{dt}=F_{A,g}\frac{d{V}_A}{dt}+V_A\frac{F_{A,g}}{dt}=\frac{d{V}_A}{dt}{F}_{i,g}+q_P\nabla (c_{v,g}-c_{a,g}).$$

In the above equation, subscript p marks the pulmonary compartment and F_i,g marks the fraction of gas in the air that is either being inspired into or expired from the alveolar compartment. Hence, i = D₃ during inspiration since inspired air is coming from the adjacent dead space region and i = A during expiration since air leaving the alveoli is alveolar air equilibrated with the pulmonary capillaries. Rearranging to express the rate of change of alveolar gas fraction gives

$$V_A\frac{d{F}_{A,g}}{dt}=\{\begin{array}{cc}\frac{d{V}_A}{dt}(F_{D_3,g}-F_{A,g})+q_P(c_{v,g}-c_{a,g}),\hfill & \text{inspiration}\hfill \\ q_P(c_{v,g}-c_{a,g}),\hfill & \text{expiration}.\hfill \end{array}\phantom{\}}$$

To convert gas fractions to partial pressures (in mmHg) and maintain consistency of units we use the the relationship

$$F_{A,g}=\frac{p_{A,g}}{(p_{amb}-p_{water})}=\frac{p_{A,g}}{713},$$ (13)

where p_amb is the ambient air pressure of 760 mmHg and water vapor partial pressure p_water equals 47 mmHg at body temperature of 37 °C. Because blood gas concentrations are reported in [ml_stpd/ml] (”standard temperature pressure dry”), but alveolar volumes are in btps (”body temperature pressure saturated”), we convert tissue concentrations to btps. One assumption included here is that incoming air is immediately humidified once it enters the nasal passages [22, 23] and that expired air is a composition of alveolar air and dead space air at btps, therefore terms with those quantities are not converted.

Additional modeling considerations concern the relationship between the pulmonary capillaries and the systemic arteries. First, the effective amount of blood in contact with alveolar air is reduced by blood bypassing alveoli and can also be reduced by under-ventilated alveoli. A 2% anatomical shunt is assumed for blood bypassing the alveoli, appropriate for an adult with no known anatomical abnormalities [22, 23]. As a consequence, only 98% of the cardiac output becomes oxygenated, and we alter the alveolar equations accordingly. We note that physiologically, the amount of blood not in effective content with alveolar air can range from 2-5% [22, 23], with the lower end of the range for healthy subjects and the higher end indicating a pathological condition, such as collapsed or obstructed lungs and congenital cardiovascular conditions. Since the subject analyzed here has no known pulmonary or congenital cardiovascular disease associated with CHF, using a 2% shunt is justified. This appears in (14) as the factor 0.98.

Second, we note that the thin alveolar wall allows for almost immediate equilibration of gases between the alveoli denoted by A and the pulmonary capillaries; thus we assume that the concentrations of blood gases are the same in the pulmonary capillaries and in the systemic arteries. Thus, in terms of partial pressures we have p_A,g = p_a,g as an auxiliary equation. Intermediate equations taking into account the modeling considerations and unit conversions discussed above are presented previously in Ellwein [24], with the final alveolar equations given as

$$V_A\frac{d{p}_{a,g}}{dt}=\{\begin{array}{cc}\frac{d{V}_A}{dt}(p_{D_3,g}-p_{a,g})+0.98\cdot 863q_P(c_{v,g}-c_{a,g}),\hfill & \text{inspiration}\hfill \\ 0.98\cdot 863q_P(c_{v,g}-c_{a,g}),\hfill & \text{expiration}.\hfill \end{array}\phantom{\}}$$ (14)

Each of the three compartments making up the anatomical dead space is considered to be well-mixed with units V_btps, in ml. Material balance equations for the dead space compartments reflect changes in gas levels due to airflow, with opposite directions of flow for inspiration versus expiration. The relation (13) holds and equation units are all in btps. Thus following the derivation of (14),

$$\begin{array}{cc}\hfill \text{Inspiration}:V_{D_1}\frac{d{p}_{D_1,g}}{dt}=& \frac{d{V}_A}{dt}(p_{I,g}-p_{D_1,g}),\hfill \\ \hfill V_{D_i}\frac{d{p}_{D_i,g}}{dt}=& \frac{d{V}_A}{dt}(p_{D_{i-1},g}-p_{D_i,g}),i=2,3\hfill \end{array}$$ (15)

$$\begin{array}{cc}\hfill \text{Expiration}:V_{D_i}\frac{d{p}_{D_i,g}}{dt}=& \frac{d{V}_A}{dt}(p_{D_i,g}-p_{D_{i+1},g}),i=2,3\hfill \\ \hfill V_{D_3}\frac{d{p}_{D_3,g}}{dt}=& \frac{d{V}_A}{dt}(p_{D_3,g}-p_{a,g}).\hfill \end{array}$$ (16)

In the above equations, pressure p_I,g [mmHg] denotes the partial pressure of the gas in the inspired air.

O₂ and CO₂ have different affinities for hemoglobin, and therefore behave differently as gases in the air versus dissolved in blood. Gas dissociation laws are used as auxiliary equations to convert alveolar gas pressures to blood gas concentrations. In this study we use equations presented in Batzel et al. [1],

$$\begin{array}{cc}\hfill c_{T,{\mathrm{CO}}_2}=& K_{{\mathrm{CO}}_2}{p}_{T,{\mathrm{CO}}_2}+k_{{\mathrm{CO}}_2},\hfill \\ \hfill c_{T,{\mathrm{O}}_2}=& K_{{\mathrm{O}}_2}{(1-e^{-k_{{\mathrm{O}}_2}{p}_{T,{\mathrm{O}}_2}})}^2.\hfill \end{array}$$

The linear law for CO₂ and the exponential law for O₂ are empirical relationships reflecting the general behavior of each gas, but do not explicitly model gas interdependencies or factors such as pH and temperature.

Inputs for the respiratory model include heart rate and flows predicted by the cardiovascular model as well as inspired volumetric airflow V̇_IE [ml/s] measured during experimentation. Note, V̇_IE is equivalent to the rate of change of alveolar volume dV_T,g/dt [ml/s]. Thus, the alveolar volume can be predicted as

$$V_A=\int {\stackrel{.}{V}}_{IE}dt.$$ (17)

The integration constant is chosen such that the minimum alveolar volume matches the functional residual capacity (FRC) [ml] estimated as a function of height h [cm] and weight w [kg] [25], i.e.,

$$\min \left(V_A\right)=\mathrm{FRC},\mathrm{FRC}=(3.8h∕100-3.41w∕h-2.74)1000.$$

Note that dV_A/dt [ml/s] is positive during inspiration and negative during expiration.

The second input to the respiratory model is the partial pressure of inspired CO₂ (p_{insp, CO2}) determined by estimating a smooth curve through the minima of the expired CO₂ values from experimental data as shown on Fig. 2. The minimum CO₂ level occurs during inspiration, both for inspired normal air and for inspired air with elevated CO₂. In both cases expired air includes the inspired CO₂ plus the quantity of higher-concentration CO₂ generated from metabolism and transferred to alveolar air through the alveolar-capillary exchange. Note, the data automatically includes the switch from eucapnic to hypercapnic breathing.

Only one model output is predicted from the respiratory model, namely, expiratory CO₂ partial pressure (p_expCO2), which is computed as

$$p_{\exp ,{\mathrm{CO}}_2}=f_{alv}{p}_{a,{\mathrm{CO}}_2}+(1-f_{alv})p_{D_1,{\mathrm{CO}}_2}.$$

Expiratory partial pressures are assumed to be nearly equivalent to the dead space pressure in D₁ closest to the mouth, with a slight mixing of alveolar gas. Thus the factor f_alν is introduced to represent the fraction of alveolar gas convected into the expired mixture. For model comparison, p_exp,CO2 is compared to the data for expiratory CO₂ partial pressure. All respiratory equations are listed in Appendix A.2, while parameterization is discussed beginning in Section 2.3.

2.3. Parameterization

2.3.1. Nominal cardiovascular parameters

Nominal parameter values and initial conditions for the cardiovascular model were calculated from data, literature, and using the subject's anthropometric measurements. Parameter values used to predict time-varying elastance include endsystolic and end-diastolic elastance of the left ventricle (E_S,i,E_D,i, i = l,r) [mmHg/ml], as well as fractions denoting the timing of the cardiac cycle (T_M,f ,T_R,f ). Values for the end-diastolic elastance are obtained from estimated diastolic ventricular pressure p_dia, end-diastolic volume EDV, and zero pressure volume V_d [ml] as

$$E_{D,i}=\frac{p_{i,dia}}{{\mathrm{EDV}}_i-V_{d,i}},i=l,r,$$ (18)

where the diastolic ventricular pressures are set using literature values [26]. The subject studied has CHF and is thus expected to have an enlarged left ventricle, while the size of the right ventricle is closer to normal. We estimate these volumes using results for CHF patients without sleep apnea reported by Tkacova et al. [27].

End-systolic elastances are estimated using a similar relation, but as a function of systolic ventricular pressure p_sys [mmHg], end-systolic volume ESV [ml], and zero pressure volume V_d [ml]. Systolic ventricular pressure is obtained from the maximum measured arterial pressure. End systolic volume ESV [ml] is obtained by subtracting stroke volume (SV [ml beat]) from the end-diastolic volume (EDV), while the stroke volume is estimated from end left ventricular diastolic volume and ejection fraction (EF, measured 26% for the subject studied):

$$\mathrm{ESV}=\mathrm{EDV}-\mathrm{SV},\mathrm{SV}=\mathrm{EF}\cdot {\mathrm{EDV}}_{lv}.$$ (19)

The timing fractions T_M,f and T_R,f were estimated from literature values suggested by Ottesen and Danielsen [28] and Heldt [29]. We assume that the ejection of the left and the right sides of the heart are synchronous, thus we use the same values for both ventricles.

Total blood volume (ml) was computed using Baker's formula [30] as a function of body surface area (BSA (m²), estimated from Mosteller's formula [31]) again as a function of height h [cm] and weight w [kg]:

$$V_t=(23.9\cdot \mathrm{BSA}-1.229)1000,\mathrm{BSA}=\sqrt{wh∕3600}.$$ (20)

Distributions of volume and unstressed volumes were obtained using values from Beneken and DeWitt [32].

Mean flows were scaled to cardiac output, which was computed from stroke volume SV and mean heart rate H̄ [beats/s] [26], i.e.,

$$\mathrm{CO}=\mathrm{SV}\cdot \overline{H},$$ (21)

where the mean heart rate was obtained from the measurements. Flows in the circuit were distributed to reflect a 20% cardiac output distribution to the brain, while 80% was directed to the systemic arteries [23, 26].

Mean pressures were obtained from literature values [26, 23] and scaled using available data. Scaling was done such that left ventricular systolic pressure was set to the maximum measured arterial pressure, while the mean systemic arterial pressure were predicted by calculating the mean over the part of the time-series representing eucapnic breathing. We assumed a negligible drop in arterial pressure (1%) between arterial pressure in the aorta and the main arteries in the cerebral vasculature, i.e., p_Ba = 0.99p_Sa.

Resistors were determined using Ohm's law (2) while values for compliances were obtained from a pressure volume relation (1). Both were predicted using mean values for pressure, flow, and volume, i.e.,

$$R_i=\frac{{\overline{p}}_{in}-{\overline{p}}_{out}}{{\overline{q}}_i},C_i=\frac{V_{str,i}}{{\overline{p}}_i},$$ (22)

where stressed volumes for each compartment were determined using values given in the study by Beneken and DeWitt [32].

Finally, the scaling factor κ = ν_MCA/qB relating the model output to the volu-metric flow rate computed by the model is predicted from literature values of diameters of the major cerebral arteries [33]. It should be noted that ν_MCA represents the velocity of the left middle cerebral artery, while q_B represents the volumetric flow to the entire brain, i.e., through all cerebral arteries. Assuming that the major cerebral arteries do not change their diameter or vascular tone, the scaling factor will be constant.

Initial conditions for blood pressures and ventricular volumes used for the differential equations were obtained partly from the data and partly from literature estimates. Initial conditions for arterial pressures were scaled relative to the mean of the measured arterial pressure (as discussed above) assuming that the pressure drop over the larger arteries is small, while initial conditions for venous pressures and the ventricular volumes were were set using standard literature estimates [23, 26].

In summary, the cardiovascular model contains 24 parameters including 9 resistances R = {R_S,R_B,R_Ba,R_Bν,R_P,R_mν,o,R_aν,o,R_tν,o,R_pν,o}, 6 compliances C = {C_Sa,C_Sν,C_Ba,C_Bν,C_Pa, C_pν}, 8 heart parameters θ_heart = {V_dl, V_dr,E_D,l,E_D,r,E_S,l, E_S,r,T_M,f ,T_R,f}, and the scaling factor κ. Nominal parameters and initial conditions for the differential equations are specified in the Appendix, Table 3.

Table 3.

Nominal parameters and initial conditions for the cardiovascular model. Top: auxiliary parameters, center: model parametersl, bottom: initial values for ODE's.

Parameter	Physiologic description	Nominal value	Reference
EDVl [ml]	End-diastolic volume (left ventricle)	312	[27]
EDVr [ml]	End-diastolic volume (right ventricle)	100	[23, 26]
EF	Ejection fraction	0.26	meas
N SV [ml]	Stroke volume	EF · EDVl = 81.1	(19) [23, 26]
ESVl	End-systolic volume (left ventricle)	EDVl – SV = 231	(19) [23, 26]
ESVr	End-systolic volume (right ventricle)	EDVr – SV = 18.9	(19) [23, 26]
H̄ [bpm]	Mean heart rate	mean (Hd) = 62.5	meas
CO [l/min]	Cardiac output	SV · H̄ = 5.07	(21) [23, 26]
pl,sys [mmHg]	Systemic left ventricular pressure	$\max \left(p_{sa}^d\right)=120$	meas
pr,sys [mmHg]	Systemic right ventricular pressure	30	[23, 26]
pl,dia [mmHfg]	Diastolic left ventricular pressure	3	[23, 26]
pr,dia [mmHg]	Diastolic right ventricular pressure	6	[23, 26]
p̄Pa [mmHg]	Mean pulmonary arterial pressure	20	[23, 26]
p̄Pv [mmHg]	Mean pulmonary venous pressure	3.3	[23, 26]
p̄Sa [mmHg]	Mean systemic arterial pressure	$\mathrm{mean}\left(p_{Sa}^d\right)=79.5$	meas
p̄Sv [mmHg]	Mean systemic venous pressure	6.6	[23, 26]
p̄Ba [mmHg]	Mean cerebral arterial pressure	0.99 p̄sa = 78.7	meas
p̄Bv [mmHg]	Mean cerebral venous pressure	7	[23, 26]
q̄S [ml/s]	Mean systemic flow	0.8 CO = 67.6	[23, 26]
q̄Ba, q̄B, q̄Bv [ml/s]	Mean cerebral flow	0.2 CO = 16.6	[23, 26]
q̄Pa, q̄P, q̄Pv [ml/s]	Mean pulm flow	CO = 84.5	[23, 26]
Vt [ml]	Total blood volume	5,408	(20) [32]
V̄Sa [ml]	Mean systemic arterial blood volume	0.1178 Vt = 637	[32]
V̄Sv [ml]	Mean systemic venous blood volume	0.6091 Vt = 3294	[32]
V̄Ba [ml]	Mean cerebral arterial blood volume	0.0237 Vt = 128	[32]
V̄Bv [ml]	Mean cerebral venous blood volume	0.0936 Vt = 521	[32]
V̄Pa [ml]	Mean pulmonary arterial blood volume	0.0288 Vt = 156	[32]
V̄Pv [ml]	Mean pulmonary venous blood volume	0.1243 Vt = 1672	[32]
TM,f	Time to end-systole	0.35	[29]
TR,f	Ventricular relaxation time	TM,f/2 = 0.175	[29]
Vdl [ml]	Zero left ventricular end-diastolic volume	90	[27]
Vdr [ml]	Zero right ventricular end-diastolic volume	10	[12]
ED,l [mmHg/ml]	Left ventricular diastolic elastance	pl,dia/(EDVl – Vdl) = 0.0135	(18)
ED,r [mmHg/ml]	Right ventricular diastolic elastance	pr,dia/(EDVr – Vdr) = 0.0667	(18)
ES,l [mmHg/ml]	Left ventricular systemic elastance	pl,sys/(ESVl – Vdl) = 0.849	(18)
ES,r [mmHg/ml]	Right ventricular systemic elastance	pr,sys/(ESVr – Vdl) = 3.38	(18)
Ri,o [mmHg s/ml]	Open i = mv, ao, tv, pv valve resistance	0.001	est
Ri,c [mmHg s/ml]	Closed i = mv, ao, tv, pv valve resistance	20	est
RS [mmHg s/ml]	Systemic resistance	(p̄Sa – p̄Sv)/q̄S = 1.08	(22)
RB [mmHg s/ml]	Cerebral resistance	(p̄Ba – p̄Bv)/q̄B = 4.25	(22)
RBa [mmHg s/ml]	Cerebral arterial resistance	(p̄Sa – p̄Ba)/q̄Ba = 0.0471	(22)
RBv [mmHg s/ml]	Cerebral venous resistance	(p̄Bv – p̄Sv)/q̄Bv = 0.0237	(22)
RP [mmHg s/ml]	Pulmonary resistance	(p̄Pa – p̄Pv)/q̄P = 0.198	(22)
CSa [ml/mmHg]	Systemic arterial compliance	0.3 V̄Sa/p̄Sa = 2.40	(22) [32]
CSv [ml/mmHg]	Systemic venous compliance	0.08 V̄Sv/p̄Sv = 39.9	(22) [32]
CBa [ml/mmHg]	Cerebral arterial compliance	0.22 V̄Ba/p̄Ba = 0.359	(22) [32]
CBv [ml/mmHg]	Cerebral venous compliance	0.08 V̄Bv/p̄Bv = 5.95	(22) [32]
CPa [ml/mmHg]	Pulmonary arterial compliance	0.58 V̄Pa/p̄Pa = 4.52	(22) [32]
CPv [ml/mmHg]	Pulmonary venous compliance	0.11 V̄Pv/p̄Pv = 22.4	(22) [32]
κ [cm2]	Brain-cerebral flow scaling	0.3	est
$p_{Pa}^I$ [mmHg]	Initial pulmonary arterial pressure	20	[23, 26]
$p_{Pv}^I$ [mmHg]	Initial pulmonary venous pressure	3.3	[23, 26]
$p_{Sv}^I$ [mmHg]	Initial systemic arterial pressure	$\mathrm{mean}\left(p_{Sa}^d\right)=79.5$	meas
$p_{Ba}^I$ [mmHg]	Initial systemic venous pressure	6.6	[23, 26]
$p_{Bv}^I$ [mmHg]	Initial cerebral arterial pressure	$0.99p_{sa}^I=78.7$	meas
$p_{Bv}^I$ [mmHg]	Initial cerebral venous pressure	7	[23, 26]
$V_{lv}^I$ [ml]	Initial left ventricular volume	EDVl = 312	[27]
$V_{rv}^I$ [ml]	Initial right ventricular volume	EDVr = 100	[23, 26]

2.3.2. Nominal respiratory parameters

Nominal respiratory parameters and initial conditions are obtained primarily from literature values scaled to the subject's weight and gender. As is standard practice, all tissue gas volumes and blood gas concentrations are given in stpd, thus units are consistent. Metabolic rates were set using standard allometric scaling proportional to body mass by the power of 3/4 [34, 35] using values in the Appendix, Table 4. We used the lumped metabolic rates for the systemic tissue given in [1, 36, 37] (scaled to the subject's weight and gender) for CO₂ (M_S,CO2) and O₂ (M_S,O2). These studies also report a lumped CO₂ metabolic rate for brain tissue (M_B,CO2). To get a metabolic rate for O₂ in the brain, we used the assumption suggested by Grodins et al. [37] that the brain O₂ metabolic rate is approximately equal to the metabolic rate for CO₂, i.e., we let M_B,O2 = M_B,CO2. For the gas diffusion constants D_T,g, we used values given by Conrad et al. [21]. This study does not report differentiated values between brain and systemic tissue, thus we used the same constant for both organs and both blood gases and in addition the same volume ratio between tissue and capillary compartments for both CO₂ and O₂ systemic and brain compartments with capillary volume 1% of tissue volume.

Table 4.

Nominal parameters and initial conditions for the respiratory model. Top: auxiliary parameters, center: model parameters, bottom: initial values for ODE's.

Parameter	Physiologic description	Nominal value or formula	Reference
w [kg]	Body weight	83.2	meas
MCO2 [mlstpd/s]	Body CO2 tissue metabolism	0.85 MO2 = 4.42	[1, 36, 37]
MO2 [mlstpd/s]	Body O2 tissue metabolism	5.2	[1, 36, 37]
VCO2 [mlstpd]	Body CO2 tissue volume	15,000	[1, 36, 37]
VO2 [mlstpd]	Body CO2 tissue volume	6,000	[1, 36, 37]
MB,CO2 [mlstpd/s]	Brain CO2 tissue metabolism	0.2 MO2 = 1.04	[1, 36, 37]
MB,O2 [mlstpd/s]	Brain O2 tissue metabolism	MB,CO2 = 1.04	[1, 36, 37]
MS,CO2 [mlstpd/s]	Systemic CO2 tissue metabolism	MCO2 – MB, CO2 = 3.38	[1, 36, 37]
MS, O2 [mlstpd/s]	Systemic O2 tissue metabolism	MO2 – MB, O2 = 4.16	[1, 36, 37]
VBtis, CO2 [mlstpd]	Cerebral tissue CO2 volume	900	[1, 36, 37]
VBtis,O2 [mlstpd]	Cerebral tissue O2 volume	1,000	[1, 36, 37]
VStis,CO2 [mlstpd]	Systemic tissue CO2 volume	VCO2 – VBtis,CO2 = 14,100	[1, 36, 37]
VStis,O2 [mlstpd]	Systemic tissue O2 volume	VO2 – VBtis,CO2 = 5,000	[1, 36, 37]
VBcap,CO2 [mlstpd]	Cerebral capillary CO2 volume	fV,cap VBtis,CO2 = 9	[21]
VScap,CO2 [mlstpd]	Systemic capillary CO2 volume	fV,cap VStis,CO2 = 141	est [21]
VBcap,O2 [mlstpd]	Cerebral capillary O2 volume	fV,cap VBtis,O2 = 10	[21]
VScap,O2 [mlstpd]	Systemic capillary O2 volume	fV,cap VStis,O2 = 50	est [21]
VD [mlbtps]	Total dead space volume	181	[38, 36, 37]
KO2 [mlstpd/ml]	O2 dissociation coefficient	0.200	[1, 36, 37]
kO2 [mmHg–1]	O2 dissociation coefficient	0.046	[1, 36, 37]
KCO2 [mlstpd /mmHg/ml]	CO2 dissociation coefficient	0.0065	[1, 36, 37]
kCO2 [mlstpd/ml]	CO2 dissociation coefficient	0.244	[1, 36, 37]
K̃O2 [mlstpd /mmHg/ml]	O2 linearized dissociation coefficient	0.0025	[1, 36, 37]
DT,CO2 [ml/s]	CO2 diffusion coefficient	9/60 w/KCO2 = 1899	[21]
DT,O2 [ml/s]	O2 diffusion coefficient	9/60 w/K̃O2 = 4938	[21]
fV,cap [N.D.]	Tissue-capillary volume fraction	0.01	[21]
$p_{D1,{\mathrm{CO}}_2}^I$ [mmHg]	Initial CO2 partial pressure dead space 1	5	[37, 38]
$p_{D1,{\mathrm{O}}_2}^I$ [mmHg]	Initial O2 partial pressure dead space 1	159	[37, 38]
$p_{D2,{\mathrm{CO}}_2}^I$ [mmHg]	Initial CO2 partial pressure dead space 2	6	[37, 38]
$p_{D2,{\mathrm{O}}_2}^I$ [mmHg]	Initial O2 partial pressure dead space 2	158	[37, 38]
$p_{D3,{\mathrm{CO}}_2}^I$ [mmHg]	Initial CO2 partial pressure dead space 3	7	[37, 38]
$p_{D3,{\mathrm{O}}_2}^I$ [mmHg]	Initial O2 partial pressure sdead space 3	157	[37, 38]
$p_{a,{\mathrm{CO}}_2}^I$ [mmHg]	Initial systemic arterial CO2 partial pressure	40	[39]
$p_{a,{\mathrm{O}}_2}^I$ [mmHg]	Initial systemic arterial O2 partial pressure	100	[40]
$c_{Stis,{\mathrm{CO}}_2}^I$ [mlstpd/ml]	Initial systemic tissue CO2 concentration	0.543	[40]
$c_{Stis,{\mathrm{O}}_2}^I$ [mlstpd/ml]	Initial systemic tissue MO2 concentration	0.128	[40]
$c_{Btis,{\mathrm{CO}}_2}^I$ [mlstpd/ml]	Initial brain tissue CO2 concentration	0.569	[37, 38]
$c_{Btis,{\mathrm{O}}_2}^I$ [mlstpd/ml]	Initial brain tissue O2 concentration	0.112	[37, 38]
$c_{Scap,{\mathrm{CO}}_2}^I$ [mlstpd/ml]	Initial systemic capillary CO2 concentration	cStis,CO2 – MS,CO2 /DT,CO2 = 0.541	(23)
$c_{Scap,{\mathrm{O}}_2}^I$ [mlstpd/ml]	Initial systemic capillary O2 concentration	cStis,O2 – MS,O2 /DT,O2 = 0.127	(23)
$c_{Bcap,{\mathrm{CO}}_2}^I$ [mlstpd/ml]	Initial cerebral capillary CO2 concentration	cBtis,CO2 – MB,CO2 /DT,CO2 = 0.568	(23)
$c_{Bcap,{\mathrm{O}}_2}^I$ [mlstpd/ml]	Initial cerebral capillary O2 concentration	cBtis,O2 – MB,O2 /DT,O2 = 0.111	(23)

Compartment volumes of the various gases were based on values in Batzel [1, 36, 37]. Alveolar volume is a dynamic quantity as shown in (17). Dead space volume was set proportional to the body weight, and the coefficients of the dissociation equations are assumed to be independent of the size of the subject.

Initial conditions for the differential equations were also obtained from literature values. For the alveolar and dead space space compartments initial conditions are given for partial pressures of CO₂ and O₂, respectively. Assuming that the first dead space compartment D₁ is closest to the mouth we assumed that the O₂ concentration in this compartment should be close to that of room air. Assuming a slight decrease in O₂ partial pressure as air is transported through the lungs we let p_D2,O2 = 158 mmHg and p_D3,O2 = 157 mmHg. The CO₂ partial pressure in inspired air is small. Using an average value extracted from the mean of inspired CO₂ data shown in Fig. 2, we chose initial conditions for partial pressures as increasing along the dead space using a similar logic as for oxygen (all initial values summarized in the Appendix, Table 4). These values also agree with those used by Grodins et al. and Khoo et al. [37, 38].

Partial pressure in the alveolar compartments were obtained from values suggested by [39, 40]. These values reflect magnitudes that are between values in inspired air and standard values reported in the lung. For systemic and brain tissue we used initial conditions reported in [40, 37, 38]. Finally, to obtain initial conditions for the capillary compartments we assumed that the system was in steady state, thus we let

$$c_{Tcap,g}=c_{Ttis,g}-M_{T,g}∕D_{T,g}.$$ (23)

In summary, the respiratory portion of the model contains 20 parameters, including 4 metabolic rates M = {M_S,CO2, M_S,O2,M_B,CO2,M_B,O2}, 4 gas tissue volumes V = {V_Stis,CO2,V_Stis,O2,V_Btis,CO2,V_Btis,O2} and 4 gas capillary volumes V = {V_Scap,CO2, V_Scap,O2,V_Bcap,CO2,V_BcapO2}, the lung dead space volume V_D, 4 dissociation constants K = {K_O2,k_O2, K_CO2,k_CO2,}, two diffusion constants D_T,CO2 and D_T,O2, a parameter allowing us to predict gas volume in the capillary compartment f_V,cap, and a fraction f_alν indicating alveolar air in the exiting air stream. Nominal parameter values and initial conditions for the differential equations are specified in the Appendix, Table 4.

3. Experimental methods

The data analyzed in this study include continuous measurements (sampled at 128 Hz) of heart rate H [beats/min], systemic arterial blood pressure (p_Sa [mmHg]), cerebral blood flow velocity ν_MCA [cm/s] measured from the middle cerebral artery (MCA), inspired volumetric airflow V̇_IE [ml/s], and expired partial pressure of CO₂ [mmHg]. In addition we have a measure for left ventricular ejection fraction (EF), as well as anthropometric measurements of height, weight, and gender. These data are obtained from the Pulmonary Physiology Laboratory, Middleton Veterans Hospital, Madison WI. Detailed descriptions of the experimental protocol can be found in [6] but are also summarized below.

Time series data were analyzed from one subject diagnosed with CHF and no sleep apnea syndromes. This subject is a 55 years old male, height 178 cm, weight 82.3 kg with an ejection fraction of 26%. Two breathing protocols were analyzed 1: Eucapnia, denoting the state that the subject breathes room air at room temperature, and 2: Hypercapnia, denoting the state that the subject breathes a constant mixture of air containing 5% CO₂. Under both breathing protocols, the subject was resting in a semi-recumbent position with the head still and eyes open. When steady state signals were observed, eucapnic data were recorded for 250 s. At this point, the CO₂ challenge was initiated and another 250 s of data were recorded during hypercapnia.

To obtain data, the subject was instrumented with a 2-MHz pulsed Doppler ultrasound system (Neurovision 500 M; Multigon Industries, Yonkers, NY) used to continuously measure cerebral blood flow velocity in the proximal segment of the middle cerebral artery (MCA). The MCA was insonated through the right temporal bone window using search techniques described in Otis and Ringelstein [41]. After detection and optimization of the Doppler signal, the probe was mechanically secured using a headband device and probe holder to provide a fixed angle of insonation for the duration of the experiment. The subject was asked to keep his head still and eyes open throughout the experiment. Heart rate was obtained from the electrocardiogram, and arterial pressure (p_Sa [mmHg]) was measured beat by beat in the middle finger of the left hand by photoelectric plethysmography (Finapres, Ohmeda, Louisville CO). Inspired volumetric airflow was measured with a pneumotachograph Model 3700, Hans Rudolph, Kansas City, MO) that was attached to a leak-free nasal mask. Expiratory CO₂ partial pressure (p_exp,CO2 [mmHg]) was sampled from the mask and measured by gas analyzers (#S-3A/I & CD-3; Ametek, Pittsburgh PA). Left ventricular ejection fraction was measured using two-dimensional echocardiography with a Hewlett-Packard echocardiography device (SONOS model 5000).

4. Patient-specific model adaptation

In order to render the model patient-specific, model parameters are estimated to minimize the least squares error between computed and measured values of arterial pressure p_Sa, cerebral blood flow velocity ν_MCA, left ventricular ejection fraction EF, and expiratory CO₂ partial pressure. Similar to previous studies [19, 24] we note that to accurately reproduce cardiovascular dynamics it is important to account for both instantaneous as well as systolic and diastolic values of arterial pressure and cerebral blood flow velocity. The quantities (pressure, velocity, partial pressure of CO₂) are observed at N equally spaced times t_i, according to the frequency of data collection (128 Hz). Similarly, for arterial pressure and cerebral blood flow velocity we have one observation of systolic and diastolic pressure for each of M cardiac cycles. In addition, we have an average value for ejection fraction EF during eucpania.

Each of the predicted model outcomes has an associated data vector, which we denote a superscript (d). Consequently, the data vectors are $p_{Sa}^d$, $v_{\mathrm{MCA}}^d$, $p_{Sa,sys}^d$, $p_{Sa,dia}^d$, $v_{\mathrm{MCA},sys}^d$, $p_{\mathrm{MCA},dia}^d$, EF^d and $p_{exp,{\mathrm{CO}}_2}^d$. To calculate the least squares error, we define two residual vectors R_car and R_resp, containing quantities relevant for the cardiovascular and respiratory models, respectively:

$$\begin{array}{cc}\hfill {\mathbf{R}}_{car}\left(t\right)=& {\left[r_{p_{Sa}},r_{v_{\mathrm{MCA}}},r_{p_{Sa,sys}},r_{p_{Sa,dia}},r_{v_{\mathrm{MCA},sys}},r_{v_{\mathrm{MCA},dia}},r_{\mathrm{EF}}\right]}^T\hfill \\ \hfill {\mathbf{R}}_{resp}\left(t\right)=& {\left[r_{p_{exp},{\mathrm{CO}}_2}\right]}^T,\hfill \end{array}$$ (24)

where each component is scaled to account for the number of elements in the vector and relative to the data, i.e.,

$$r_i\left(t\right)=\frac{1}{\sqrt{K}}{\left[\frac{r_i\left(t_1\right)-r_i^d\left(t_1\right)}{r_i^d\left(t_1\right)},\dots ,\frac{r_i\left(t_K\right)-r_i^d\left(t_K\right)}{r_i^d\left(t_K\right)}\right]}^T,$$

with i = p_Sa,v_MCA, p_Sa,sys, p_Sa,dia,..., p_exp,CO2, and κ = N,M, respectively.

The vector R_car has 2N + 5M entries, while R_resp has N entries. For each of the residual vectors Rj, the least squares cost J is defined by

$$J={\Vert {\mathbf{R}}_j\Vert }_2^2={\mathbf{R}}_j^T{\mathbf{R}}_j,j=car,resp.$$ (25)

Actual parameter estimates were predicted using nonlinear optimization, performed using log-scaled parameters to facilitate convergence:

$${\tilde{\theta }}_{opt}=\arg {\min }_{\tilde{\theta }}J\left(\theta \right),$$

where $\tilde{\theta }=\log \left(\theta \right)$.

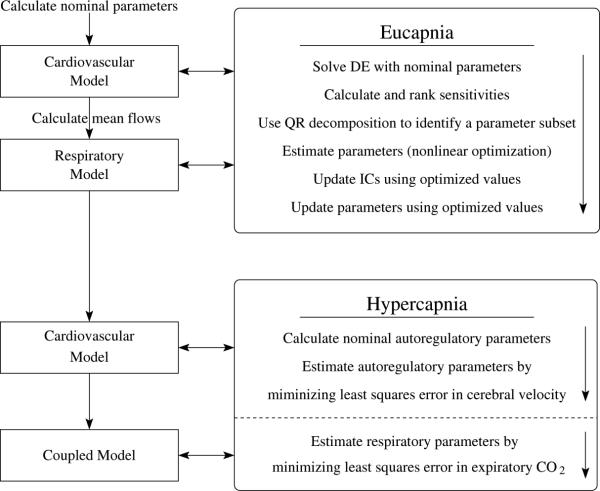
Before solving the least squares problem we used sensitivity analysis and subset selection to identify parameter sensitivity and correlations among model parameters. The two models are coupled loosely: the cardiovascular model does not depend on the respiratory model, but the respiratory model depends on flows predicted by the cardiovascular model. During eucapnia, the flows do not change significantly, consequently mean flows were computed and input to the respiratory model. During hypercapnia, the flows change in response to the CO₂ challenge and thus the fully coupled model were solved at this stage. The process used for model simulations is illustrated in Fig. 3.

Figure 3.

Model analysis flow chart.

4.1. Eucapnia

During eucapnia the subject is resting in semi-recumbent position thus autonomic and cerebral autoregulation has limited effect. As a result, the cardiovascular and the respiratory models can be treated as two separate entities. The cardiovascular model is given heart rate as an input and via solution of Eqs. (27-28) model output is computed. The respiratory model depends on blood flow through the pulmonary, systemic and brain tissue regions. Moreover, respiratory oscillations are about 4-5 times slower than cardiovascular oscillations due to the cardiac cycle [26]. As a result the respiratory dynamics are not expected to change significantly. Consequently, mean values can be computed from the cardiovascular model and input to the respiratory model.

Simulations done under eucapnia are set up to reflect dynamics of a resting subject. Data were collected after the subject had rested for a period of time until stable signals were obtained. The cardiovascular model has fast dynamics, consequently, impact of approximated initial conditions will die out quickly and the model will settle oscillating around steady state. However, the volume of the systemic tissue compartment is large, and as discussed by Farhi [42] it can take more than an hour for the systemic tissue CO₂ to be in steady state. To account for the tissue gas time scale being an order of magnitude longer than the 250 s of eucapnic data, we performed model analysis of steady state dynamics with the last 250 s segment of an extended data set created by replicating the eucapnic data 40 times. Figure 4 shows dynamics of the cardiovascular and respiratory data as a function of time, with the cardiovascular system reaching steady state oscillations within a few seconds, while the respiratory system takes more than an hour to reach steady state.

Figure 4.

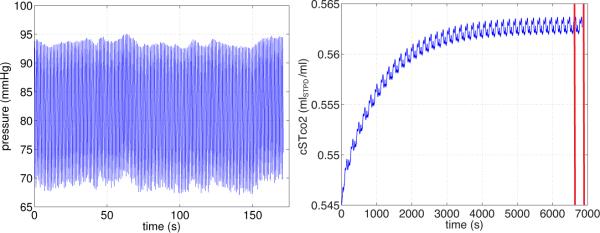
Dynamics of arterial blood pressure p_Sa (left) and tissue concentration of CO₂ (right) during Eucapnia. Note, the cardiovasculatory model settles at steady state oscillations within the first 10 seconds, while the respiratory model takes more than an hour to equilibrate.

4.1.1. Sensitivity analysis

Sensitivity analysis gives a measure of how much the output of a model is affected by changes in the model parameters [18]. For the system discussed here, sensitivities were computed during eucapnia analyzing how sensitive the model output (arterial blood pressure, p_Sa, cerebral blood flow velocity ν_MCA, ejection fraction EF, and expiratory CO₂ partial pressure p_exp,CO) are to the model parameters. Sensitivities were computed for the cardiovascular and the respiratory models separately. Since a number of physiological quantities at several scales were included, sensitivities were computed from the Jacobian defined by

$$S_{j,{\tilde{\theta }}_i}\left(t\right)={\phantom{\mid }\frac{\partial {\mathbf{R}}_{\mathbf{j}}\left(\theta \right)}{\partial {\tilde{\theta }}_i}\mid }_{\theta ={\theta }_0},\text{for}i=1,\dots ,n\text{and}j=car,resp,$$ (26)

where n denotes the number of parameters. Note that the Jacobian is calculated with respect to the log-scaled parameters $\tilde{\theta }$, limiting the effect of varying parameter scales, but the differential equations are evaluated at nominal parameter values θ₀. Sensitivities are local in the model parameters, i.e., if parameter values θ₀ are changed so will the sensitivities. Since the model is nonlinear, the impact of each parameter may change as the values of the model parameters θ₀ change. In the absence of an analysis of this large parameter space, not feasible within the scope of this study, we assume that for well-chosen nominal parameters θ₀ the local sensitivity predictions will persist over a reasonable range of parameter values.

Given that the model states are time-series, the sensitivities will be time-varying as well. However, during eucapnia, we expect both the solution and the sensitivities to oscillate around steady state values. Thus it it reasonable to use ranked sensitivities for comparing the impact of model parameters to the model output. To obtain ranked sensitivities we used the standard 2-norm scaled with the largest sensitivity, i.e.,

$${\overline{S}}_{j,{\tilde{\theta }}_i}={\Vert S_{j,{\tilde{\theta }}_i}\left(t\right)\Vert }_2∕\max \left(S_{j,\tilde{\theta }}\left(t\right)\right),j=car,resp\text{and}i=1,\dots ,n.$$

4.1.2. Subset selection

Solving the inverse problem uniquely is not feasible using the complex model combined with available data, since several combinations of parameters likely give rise to the same solution. To achieve a simpler inverse problem, we limit the set of parameters identified using subset selection to obtain a set of uncorrelated parameters. Numerous methods exist for estimating identifiable parameters as discussed in recent studies [43, 44]. In this study, we used a method based on QR factorization as outlined below. Further details of this method can be found in [19, 45].

Recall that $\tilde{\theta }$ is the vector of n log-scaled model parameters and R is the model residual defined in (24). The subset selection method analyzes the Jacobian, R′ predicted using (26) to find a subset of columns that are “maximally independent”. Singular value decomposition is used to decompose the Jacobian R′ = UΣV^T , such that Σ is a diagonal matrix containing the singular values σ₁ ≥ σ₂ ≥ ...σ_n and V is an orthogonal matrix of corresponding right singular vectors. The number of identifiable parameter values is predicted by the numerical rank ρ of R′, the largest value ensuring that σ_ρ/σ₁ > ε. For our study $\epsilon =\sqrt{{\epsilon }_S}$, where ε_S is the relative tolerance used to solve the differential equations. Using ρ, the matrix of eigenvectors V^T can be partitioned as [V_ρ V_n–ρ]^T. The parameters associated with the ρ highest singular values are then found using QR-decomposition with column pivoting. We first determine a permutation matrix P by $V_{\rho }^{T}P=QR$, where Q is an orthogonal matrix, and the first ρ elements of R form an upper triangular matrix with diagonal elements in decreasing order. Then P is used to reorder the parameter vector θ_{0, ρ} = P^T θ₀. This gives the partition θ₀ = {θ_{0, ρ}, θ_{0, n–ρ}}, where θ_{0, ρ} contains the ρ identifiable parameters. Unidentifiable parameters the vector θ_{0, n–ρ} were kept at their nominal parameter values during the parameter estimation. It should be noted that estimating only identifiable parameters does introduce bias in the computations, but reduces the variance and makes the estimation algorithm more robust [46, 47]. Furthermore, it should be noted that the QR decomposition is not unique but depends on the concrete implementation of the algorithm; however, the algorithm will return a set of identifiable parameters for a given ρ.

4.1.3. Parameter estimation

To estimate the subset of model parameters we used the Levenberg-Marquardt method, a trust-region variant of the gradient based Gauss-Newton optimization method. Parameter estimation involves minimizing the least squares cost J defined in (25). Gauss-Newton is an iterative method [48] that at each iteration uses a solution based on a local linear approximation to compute the next iterate. The theory supporting our method predicts convergence even when the initial parameter estimates are far from the solution, and rapid convergence near the solution.

4.2. Eucapnia followed by hypercapnia

As discussed above great effort was put into achieving a set of model parameters that allowed prediction of steady state dynamics (during eucapnia). As described in the beginning of Section 3, hypercapnia was introduced by changing inspired concentration of CO₂. The response to this change involves activation of the autonomic and cerebral autoregulatory control systems. The autonomic control system acts to increase heart rate and breathing depth and frequency. These changes are included via inputs to the model. Cerebral autoregulation responds via vasodilation decreasing cerebral vascular resistance. This change in cerebral vascular resistance was modeled by redefining the parameter R_B using the piece wise linear function defined in (9), where parameters are defined as the function values at nodes. These parameters were estimated in a second simulation with the cardiovascular model, minimizing the least squares error between predicted and measured values of cerebral blood flow velocity. Using the optimized values for R_B, we re-estimated the identifiable respiratory parameters minimizing the least squares error between computed and measured values of expiratory CO₂ partial pressure. It was necessary for the latter simulation to use the coupled model, since equations predicting respiratory dynamics depend on predicted flows which are no longer constant but change in response to cerebral autoregulation. Note that for simulations done during hypercapnia, subset selection was not repeated.

5. Results

The cardiovascular-respiratory model analyzed in this study is derived in Section 2 (see also Fig. 1). This model uses heart rate, air flow, and inspired CO₂ data as system inputs and predicts pulsatile responses including cerebral vascular resistance, arterial and venous pressures in the systemic and pulmonary systems, partial pressures of CO₂ and O₂ in the lungs, as well as concentrations of these gases in the cerebral and systemic tissues. Parameter estimation is carried out to match data available from cerebral blood flow velocity, expired CO₂, and arterial pressure.

5.1. Eucapnia

5.1.1. Sensitivity analysis

For each of the cardiovascular and respiratory models, we computed and ranked relative sensitivities as described in Section 4.1.1. Results of this analysis (see Fig. 5) showed that both the cardiovascular and respiratory models contain sensitive and insensitive parameters, but that no clear break separates the two groups of parameters. Therefore, we separated parameters using an estimate based on the numerical integration accuracy. Numerical integration was done with accuracy 10⁻⁶, and sensitivities were computed using finite difference Jacobians accurate to the order 10⁻³. Thus, we included parameters with sensitivities greater than 10⁻³ in the subset selection analysis, while rejecting the remaining parameters. The model depends on both sensitive and insensitive parameters, thus the insensitive parameters cannot be taken out of the model. Instead, we kept these parameters fixed at their nominal parameter values. This cutoff choice allowed us to exclude the four valve parameters x_car,insens = {R_tν,o,R_mν,o,R_aν,o,R_pν,o} and 7 respiratory parameters x_resp,insens = {K_O2,k_O2, f_ν,tis,V_B,O2,V_T,O2, f_alv}.

Figure 5.

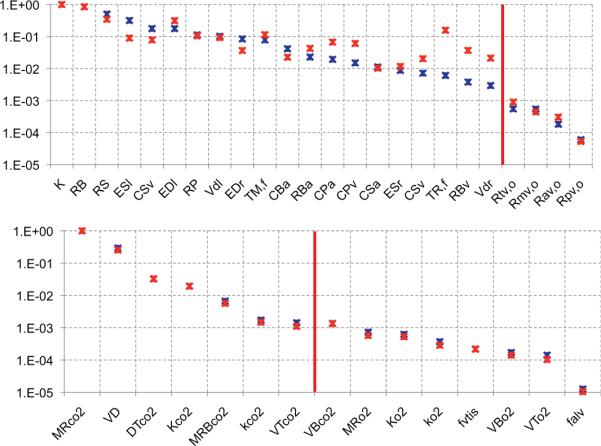
Ranked sensitivities for the cardiovascular and respiratory models. The top graph shows ranking for the cardiovascular model and bottom graph shows ranking for the respiratory model. For both graphs, blue stars denote sensitivities computed using the initial (nominal) parameter values, and the red stars denote sensitivities computed using the optimized parameters. Note, that the y-axis is a log scale.

Note, for the respiratory model, the set of sensitive parameters did not include any parameters related to O₂. This is reasonable given that we had no measurements of partial pressure of O₂. In conclusion, parameters included in the set of sensitive parameters serve as candidates for subset selection as described in detail below.

5.1.2. Subset selection

For each model, we investigated correlations between parameters using subset selection as described in section 4.1.2. For the cardiovascular model, subset selection allowed us to extract six uncorrelated parameters from the set of sensitive parameters including x_car,sub = {R_B,R_S,C_Sa,T_M,f ,E_S,l,E_D,l}. These results were obtained assuming that κ can be kept constant at its nominal parameter value. Including κ in subset selection result in a subset with κ instead of R_B (indicating that κ and R_B are correlated). However, since κ is a scaling factor, while R_B is the model parameter of interest, we chose to keep κ constant allowing identification of R_B. This observation is similar to results reported in previous studies [19, 24].

Nonlinear least squares estimation of the six cardiovascular parameters chosen by subset selection did not allow us to accurately reproduce the dynamics displayed by the data. An analysis of the remaining parameters (not picked by subset selection) revealed that including a seventh parameter, cerebral arterial compliance C_Ba, allowed us to better reproduce the dynamics displayed by the data. Since the objective is to analyze data from a patient with CHF it is reasonable that this parameter should be included. Also typical of CHF is an increased blood volume, which would induce an increased compliance in order to maintain a normal arterial pressure. Note that the systemic arterial compliance was already included in the subset, but that neither of the venous compliances were included. The latter may again be related to the fact that we have no data on the venous side. We remind the reader that subset selection was based on initial parameter values. Therefore, we repeated subset selection with the optimized parameter values, and at this stage C_Ba was included in the subset. Results from subset selection with the respiratory model revealed that we can identify 4 of the sensitive parameters including x_resp,sub = {V_D,M_S,CO2, M_B,CO2,V_B,CO2}. Note, the CO₂ dissociation constants were set at literature values and thus not[notdef]included in the subset selection.

In summary, with subset selection we identified 11 parameters (7 cardiovascular and 4 respiratory) that can be estimated reliably given the data available for this study. This is a significant reduction from the total of 43 model parameters. However, it should be noted that model prediction does depend on the value of all 43 parameters, thus care must be taken to use realistic patient-specific physiological values for the parameters that are not included in the subset.

5.1.3. Parameter estimation

As described in Section 4.1 and shown on Fig. 3 nonlinear estimation was done in two steps. First we estimated the subset of parameters identified for the cardiovascular model, then we estimated the respiratory parameters. For both models, parameters were estimated using the Levenberg-Marquardt variant of the Gauss-Newton optimization method as described in Section 4.1.3. Optimized parameters are given in Table 1 for both the cardiovascular and respiratory models. All data were subsampled at 64 Hz to speed up computations and as discussed in Section 4.1 to allow the respiratory model to reach steady state, computations were done on a data-set repeated 40 times. Though the least squares error between computed and measured values of partial pressure of CO₂ was done only using the last repeat of the respiratory data as discussed. To verify that 40 repetitions of respiratory data was sufficient for achieving steady state, we compared results with those obtained with 60 and 80 repetitions. Parameter estimates with 40 repetitions varied less than 5% from those obtained with 80 repetitions, while the difference in estimates using 60 and 80 repetitions were less than 2%. Moreover, using 80 repetitions almost doubles the computation time, thus we decided that the 5% difference was acceptable. Results showing that with optimized parameters, our model is able to predict observed data are shown in Figs. 6 and 7. Note the model nicely predicts systolic and diastolic values, while the waveform is not reproduced exactly, this is due to the fact, that the circuit model used in this study does not account for wave-propagation, i.e., it is not able to predict the actual waveforms with an incoming and reflected wave. This can be seen from the large scale plots given in the right column of Fig. 9. Moreover, for ejection fraction EF, we only have one measurement given an overall ejection fraction of 26%. There will be variation over steady state, also shown in Fig. 9. On the other hand, respiratory data does not include major phenomena not accounted for by the model, thus the better fit to data as shown in Fig. 7.

Table 1.

Nominal and optimal parameter values for the cardiovascular model (top) and the respiratory model (bottom).

Parameter	Physiologic description	Nominal value	Optimal value
TM,f	Time to end-systole	0.35	0.137
ED,r [mmHg/ml]	Right ventricular diastolic elastance	0.0667	0.0167
ES,l [mmHg/ml]	Left ventricular systemic elastance	0.849	0.507
RS [mmHg s/ml]	Systemic resistance	1.08	0.934
RB [mmHg s/ml]	Cerebral resistance	4.25	2.69
CSa [ml/mmHg]	Systemic arterial compliance	2.40	0.989
CBa [ml/mmHg]	Cerebral arterial compliance	0.358	3.18
MCO2 [mlstpd/s]	Body CO2 tissue metabolism	4.22	4.89
MB,CO2 [mlstpd/s]	Brain CO2 tissue metabolism	1.04	1.24
VBtis,O2 [mlstpd]	Cerebral tissue CO2 volume	900	855
VD [mlbtps]	Total dead space volume	181	201

Figure 7.

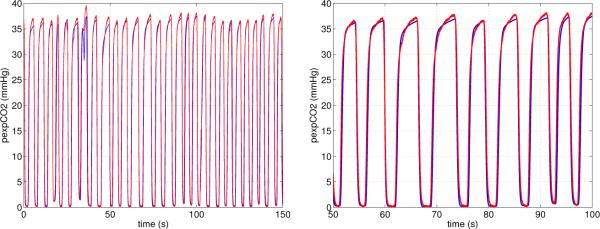
Steady state simulation results from the respiratory model. The graphs show expiratory CO₂ partial pressure as a function of time. The left graph shows results over the complete time-series, while the right graph show a zoom for 50 ≤ t ≤ 100 seconds.

Figure 9.

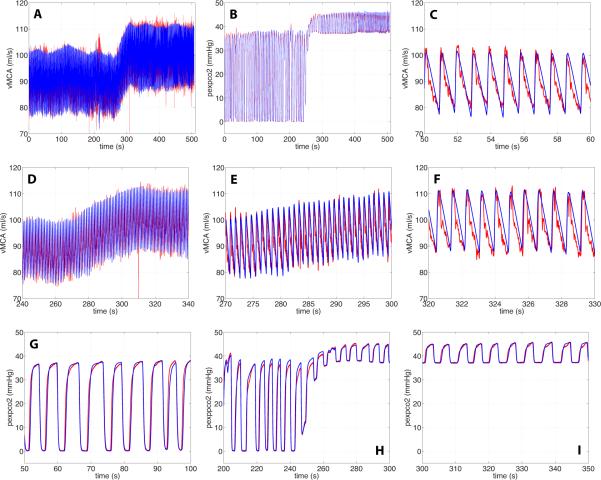
Simulation results from the coupled model with controls. Panels A and B show the entire time-series predicting cerebral blood flow velocity and expiratory CO₂ partial pressure. Panels C-F show zoomed snapshots of cerebral blood flow velocity during normal breathing C, during the transition D and E, and during hypercapnia F. Panels G-I show zoomed snapshots of expiratory CO₂. G shows dynamics during normal breathing, H during the transition, I during hypercapnia. For all graphs the blue line denotes computed results, while the red line mark the associated experimental data.

5.2. Eucapnia followed by hypercapnia

Hypercapnia was induced by increasing inspired CO₂. To predict the effect of cerebral autoregulation, we used nonlinear optimization to estimate parameters representing the cerebral vascular resistance (R_B) under hypercapnic conditions. It should be noted that the cardiovascular model does not depend on the respiratory model, consequently parameters used for prediction of R_B were estimated using the cardiovascular model by minimizing the least squares error between computed and measured values of cerebral blood flow velocity ν_MCA. The predicted time course of the cerebral vascular resistance is shown in Fig. 8, and the associated blood flow velocity in the middle cerebral artery is shown in the top left panel of Fig. 9. Subsequently, we used the coupled model to estimate the subset of respiratory parameters identified during eucapnia. This was done by minimizing the least squares error between measured and computed values of expiratory CO₂ partial pressure. Results of this computation are shown in the remaining panels of Fig. 9. As for the steady state simulations, the model is able to predict the overall dynamics displayed by the data. Systolic and diastolic values were predicted accurately (R² = 0.88 and 0.84, respectively), with R² = 0.72 accounting for the entire waveform. The lower value is obtained because the model cannot predict secondary oscillations due to the lack of its ability to reflect wave propagation. Finally, respiratory dynamics were estimated accurately (R² = 0.96), reflecting that the model closely resembles dynamics observed in data.

Figure 8.

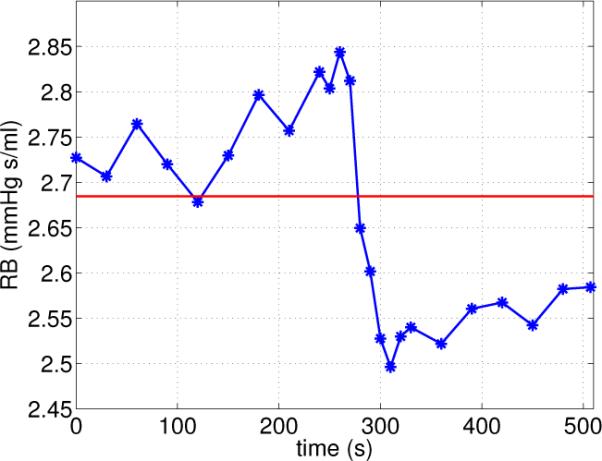
Autoregulation of cerebral vascular resistance R_B. The red horizontal line shows the value obtained during eucapnia, while the time-varying blue line shows dynamics obtained during hypercapnia.

6. Discussion

Results from the cardiovascular and respiratory models (Figs. 6 and 7) showed that the approach used in this study allowed prediction of cerebral CO₂ reactivity, via prediction of cerebral vascular resistance R_B, which can be directly related to cerebral vasodilation. Additionally, the models were able to predict observed data including cerebral blood flow velocity, arterial blood pressure, ejection fraction, and expiratory CO₂ partial pressure. Below we first discuss implications of the results obtained during eucapnia, and then we discuss results obtained during the transition from eucapnia to hypercapnia. We note that the subject studied was chosen since he displayed normal cerebral CO₂ reactivity and aside from CHF did not display other cardiovascular diseases.

Results from the cardiovascular and respiratory models (Figs. 6 and 7) showed that the approach used in this study allowed prediction of cerebral CO₂ reactivity, via prediction of cerebral vascular resistance R_B, which can be directly related to cerebral vasodilation. Additionally, the models were able to predict observed data including cerebral blood flow velocity, arterial blood pressure, ejection fraction, and expiratory CO₂ partial pressure. Below we first discuss implications of the results obtained during eucapnia, and then we discuss results obtained during the transition from eucapnia to hypercapnia. Finally, we note that the subject studied was chosen since he displayed normal cerebral CO₂ reactivity and aside from CHF did not display other cardiovascular diseases.

6.1. Eucapnia

During eucapnia, the cardiovascular model does not depend on any quantities computed by the respiratory model, while the respiratory model depends on blood flows predicted by the cardiovascular model. Since blood flow oscillate around a steady state during eucapnia and respiratory oscillations are significantly slower, it was sufficient to compute average blood flow values over the entire steady state interval and use these as inputs to the respiratory model. We checked results from the two step approach by computing the full dynamics using the coupled cardiovascular-respiratory model. We found that these predictions were indistinguishable from those obtained from sequential solution of the two models. A consequence of this observation is that accounting for pulsatile blood flow (as is done by the coupled model) does not significantly impact respiratory model dynamics.

In addition to computing model outcomes, we also computed all internal states and these were all within physiological bounds. This is important to verify because the nonlinear least squares optimization technique used for parameter estimation does not guarantee that internal states cannot deviate from physiological values, even if predicted values for the parameters optimized are within physiological bounds. Importantly, we compare internal states particular to CHF, characterized in this patient by a severely enlarged left ventricle and reduced ejection fraction at 26%. Optimized parameters revealed that the maximum left ventricular volume was approximately 411 ml and minimum ventricular volume was approximately 309 ml. These values yielding a stroke volume of 102 ml, with an average heart rate of 62.7 beats per minute, this gives an approximate CO of 6.4 L/min (see Appendix Table 3). This number corresponds to the cardiac output obtained from calculating the mean flow in the systemic or pulmonary circulations.

CHF implies reduced heart function however cardiac output can stay near normal levels in the early stages of CHF as the ventricle remodels and other controls work to keep cardiac output normal. In the end, these changes cause damage that reduces cardiac output (see presentation in [49]). For this patient, with left heart failure (but no sleep apnea) left ventricular end diastolic volume (LVEDV) is derived to be (double normal values but physiological for CHF patients without sleep apnea (left heart failure patients with sleep apnea have significantly larger LVEDV [50]). Given that the heart rate is normal and ejection fraction is 26% that implies such a very high LVEDV if cardiac output is to be normal. The fact that heart rate is normal and no other symptoms are present suggests a normal cardiac output (cardiac output data is not available). When cardiac output starts to reduce, as it will eventually in CHF, heart rate can possibly increase to compensate for a while. Thus in this patient it will likely take a very low ejection fraction to cause the kind of reduced cardiac output seen in CHF as the disease progresses.

Moreover, systemic venous pressure, pulmonary arterial pressure, and pulmonary venous pressure were approximately 3.6 mmHg, 27 mmHg, and 6.3 mmHg respectively, all with the range of expected values for a patient with CHF (see Table 2). The total resistance R_Tot = (1/T_BTot + 1/R_S)−1 = 0.70, where R_BTot = R_Ba + R_B + R_Bν is fairly low, but again expected for CHF. The low resistance may be an indicator of poor circulation in the lower extremities. Finally, we noted that during eucapnia approximately 25% of cardiac output was utilized as cerebral blood flow. This is a bit high, however, cerebral blood flow velocity measured for this subject was significantly larger than mean velocities reported in the literature [59]. This could be due to poor circulation in the lower body or exceptionally high values from the transcranial Doppler measurements. However, it could also be a result of the simplified modeling of the cerebral arteries. The blood flow velocity is measured in the middle cerebral arteries, and this has then been scaled (assuming constant area of the major cerebral arteries) to compute a total flow to the brain. Without information about anatomical quantities for the size of the cerebral arteries, this scaling factor is only as accurate as our estimates of patient anatomy. The magnitude of the scaling factor κ would impact the optimized values for the cerebral vascular resistance R_B since these two parameters are correlated as stated earlier. However, if the area of all major cerebral vessels (PCA, MCA and ACA) were measured, then this scaling parameter could be computed explicitly from the data.

Table 2.

Typical (from literature) state changes in CHF for patient with an enlarged left ventricle.

State	Value	Source
Mean pPa [mmHg]	increase	[51]
Mean pPv [mmHg]	increase	[52, 53]
Mean pSa [mmHg]	decrease or stable	[54]
Mean pSv [mmHg]	increase	[53]
Mean plv [mmHg]	steady to increase	[55]
Mean pla [mmHg]	increase	[54]
Left ventricular end-diastolic pressure [mmHg]	increase	[55]
Left ventricular end-systolic pressure [mmHg]	steady or increase	[55]
Left ventricular end-diastolic volume [ml]	increase	[56, 54]
Left ventricular end-systolic volume [ml]	increase	[56, 54]
Left ventricular EF [ml]	decrease	[56, 57]
CO [mlmin]	decrease	[54]
SV [ml]	decrease	[54]
H [beat/min]	increase	[54, 57]
Systemic resistance [mmHg · s /ml]	increase	[53]
Fluid retention [ml]	increase	[53, 58]

For the respiratory quantities, values for dead space p_D,CO2 and p_D,O2, arterial values p_a,CO2 and p_a,O2, and systemic values p_S,CO2 and p_S,O2 (the latter calculated from concentrations and dissociation laws) are reasonable (compare [37, 38, 36]). Dead space values of CO₂ for normal inspired air oscillate between zero (inhaled air) and end-expiratory air approximately the same as alveolar air. Oxygen values follow similar reasonable patterns. It should be noted that brain partial pressures p_B,CO2 and p_B,O2 did not match typical values as well in the optimized case. The value for p_B,CO2 was approximately 44 mmHg (too low) and p_B,O2 approximately 50 mmHg (too high). There are likely several reasons for this. First, the data for cerebral blood velocity for this subject was higher than expected, which would tend to depress brain p_B,CO2 and raise p_B,O2. Second, we did not have data on O₂ which might impact the results. Further, research indicates that cerebral metabolism may be abnormal in patients with CHF, leading to possible metabolic imbalance [60]. In addition, given the complex effects induced by CHF in regards to the relation between heart rate and contractility [61] and the fact that the modeled CO₂ challenge induces only a 10% change in heart rate, we omitted a heart rate dependent change in contractility reflecting a Bowditch effect. The elastance parameters reflecting contractility were optimized for the steady state using subject specific data. We also recognize that the value estimated from literature for the FRC is only valid for individuals with no respiratory conditions, thus an extension of this model to CHF patients co-presenting with respiratory dysfunction would require a modified FRC estimate.

6.2. Eucapnia followed by hypercapnia

As discussed above, our model produced good predictions of behavior during eucapnia. In this section we discuss impact of the transition from eucapnia to hypercapnia. When the body is exposed to air with a high concentration of CO₂, it responds by activating control mechanisms to eliminate excess CO₂. The autonomic regulatory system increases heart rate and breathing depth and frequency while the cerebral autoregulatory system dilates vessels in the brain to allow faster washout of CO₂. The autonomic responses are incorporated in the model via model inputs, and thus, will not be discussed further here. Vasodilation enforced by cerebral autoregulation was modeled via dynamic regulation of cerebral vascular resistance. In physiological terms, the concentration of CO₂ should mediate changes in cerebral vascular resistance. As a first step towards elucidating the dynamics of this physiological connection, we used an empirical model predicting dynamics of cerebral vascular resistance directly by estimating nodes in a piecewise linear spline based on cerebral blood flow. This approach allowed prediction of cardiovascular dynamics independent of the respiratory model. Results showed the expected response behavior that cerebral vascular resistance decreased leading to an associated increase in cerebral blood flow velocity.

To ensure that the respiratory model was able to accurately predict expiratory CO₂ partial pressure, a final simulation was performed re-estimating the subset of respiratory parameters. This simulation did not move respiratory parameters significantly, since the majority of the dynamics were already identified during the steady state simulation.

Another detail which could improve patient-specific results involves adjusting the integration constant arising in (17) which is currently taken as the functional residual capacity (FRC) [ml] (as estimated as a function of height h [cm] and weight w [kg] [25]). This integration constant could be increased to reflect a higher effective basic CO₂ volume due to its higher ability to diffuse into tissues compared to O₂ (see e.g. [38]). Since we were estimating FRC from a general formula we did not include such a correction. When fitting the data to specific patients one could seek to acquire more information to adjust the integration constant to reflect this.

In future work, we plan to incorporate a model predicting R_B(c_B,CO2,t), that is, changes in R_B dependent on cerebral CO₂ level. The current model provides a way to estimate cerebral CO₂ via a model and parameter estimation from data for measured expired CO₂. At this point, R_B is estimated from cerebral blood flow velocity. The link will be complete once a model that connects R_B and cerebral CO₂ is developed. Once this is done, it will be possible to estimate cerebral CO₂ reactivity using non-invasive measurements from CO₂ breathing tests.

7. Conclusion

The results discussed here indicate that the proposed methodology and model can be used for numerically efficient estimation of parameters for any subject with CHF and hence can be also used for quantitatively studying variations between subjects with CHF and subjects who suffer from CHF and central sleep apnea [3, 2, 4, 1], periodic breathing [62, 63], compromised breathing stability [64], greater central and peripheral reactivity to CO₂ [65, 66], and attenuated cerebral vascular reactivity resulting from brain hypoperfusion [66, 67, 68, 6]. Understanding how the control systems are compromised has potential to provide more insight into these diseases. Future studies could include an extension of the proposed method to a cohort of similar patients, to both analyze differences in parameter values across the group at a particular time point and understand the progression of disease progression in time. However, to use this model to compare quantities from a larger population it should be emphasized that the model should be used with care. First, a physiology-based model as a function of tissue CO₂ could improve prediction of cerebral vascular resistance dynamics. One could also expand the complexity of the interactions influencing the dynamics affecting expiratory CO₂. Second, more effort could be put into developing faster methods for parameter estimation.

Moreover, it is important that nominal parameters reflect known characteristics from a subject with CHF, in particular since only a subset of the parameters will be estimated. Therefore, conclusions based on analysis of parameters obtained from several subjects should all be interpreted related to the nominal parameter values used. Furthermore, additional measurements would increase predictability of the model parameters, in particular it would be beneficial to include measurements of cardiac output and estimation of diameters of major cerebral vessels. Knowing these quantities would allow better prediction of systemic and arterial flow as well as help to get better estimation of the scaling factor needed, which would help in prediction of the scaling factor relating flow and velocity in the middle cerebral artery. Finally, it should be noted that parameter estimates predicted here are found using a local method. Thus, there is no guarantee that the predicted values are truly optimal. However, since nominal values were assumed close to the physiological values for the specific subject, estimated values are physiologically relevant. Another use of the subset selection methods applied here, is for model reduction. If the model output is insensitive to a given group of parameters it may be possible to use this information to reduce the model.

Finally, we mention that the analysis of the correlation between parameters using the above methods might potentially suggest new links between systems and hence suggest new physiological information as long as the correlation is not introduced simply as a consequence of the model reduction or model structure.

Appendix

A.1. Cardiovascular model

The following give equations for blood pressures and ventricular volumes. The main symbols are p, V, and C for pressure, volume, and compliance, respectively. Subscript symbols P, S, and B denote pulmonary, systemic, and brain regions, respectively. Subscripts a and ν in vascular pressure equations denote generally arterial and venous, respectively, except for the resistances entering and leaving the heart. In that case R_mν, R_tν, R_aν, and R_pν denote mitral valve, tricuspid valve, aortic valve, and pulmonary valve resistances while lv and rv denote left and right ventricle, respectively, in the ventricular equations.

Blood pressures, ventricular volumes, and intrathoracic pressure

$$\begin{array}{cc}\hfill \frac{d{p}_{Pa}}{dt}=& \left(\frac{p_{rv}-p_{Pa}}{R_{pv}}-\frac{p_{Pa}-p_{Pv}}{R_P}\right)∕C_{Pa}\hfill \\ \hfill \frac{d{p}_{Pv}}{dt}=& \left(\frac{p_{Pa}-p_{Pv}}{R_P}-\frac{p_{Pv}-p_{lv}}{R_{mv}}\right)∕C_{Pv}\hfill \\ \hfill \frac{d{p}_{Sa}}{dt}=& \left(\frac{p_{lv}-p_{Sa}}{R_{av}}-\frac{p_{Sa}-p_{Sv}}{R_S}-\frac{p_{Sa}-p_{Ba}}{R_{Ba}}\right)∕C_{Sa}\hfill \\ \hfill \frac{d{p}_{Sv}}{dt}=& \left(\frac{p_{Sa}-p_{Sv}}{R_S}+\frac{p_{Bv}-p_{Sv}}{R_{Bv}}-\frac{p_{Sv}-p_{rv}}{R_{tv}}\right)∕C_{Sv}\hfill \\ \hfill \frac{d{p}_{Ba}}{dt}=& \left(\frac{p_{Sa}-p_{Ba}}{R_{Ba}}-\frac{p_{Ba}-p_{Bv}}{R_B}\right)∕C_{Ba}\hfill \\ \hfill \frac{d{p}_{Bv}}{dt}=& \left(\frac{p_{Ba}-p_{Bv}}{R_B}-\frac{p_{Bv}-p_{Sv}}{R_{Bv}}\right)∕C_{Bv}\hfill \\ \hfill \frac{d{V}_{lv}}{dt}=& \frac{p_{Pv}-p_{lv}}{R_{mv}}-\frac{p_{lv}-p_{Sa}}{R_{av}}\hfill \\ \hfill \frac{d{V}_{rv}}{dt}=& \frac{p_{Sv}-p_{rv}}{R_{tv}}-\frac{p_{rv}-p_{Pa}}{R_{pv}}\hfill \end{array}$$ (27)

Heart valves

$$\begin{array}{cc}\hfill R_{av}=& \min \left[R_{av,o}+e^{-2(p_{lv}-p_{Sa})},R_{av,c}\right]\hfill \\ \hfill R_{mv}=& \min \left[R_{mv,o}+e^{-2(p_{Pv}-p_{lv})},R_{mv,c}\right]\hfill \\ \hfill R_{pv}=& \min \left[R_{pv,o}+e^{-2(p_{rv}-p_{Pa})},R_{pv,c}\right]\hfill \\ \hfill R_{tv}=& \min \left[R_{tv,o}+e^{-2(p_{Sv}-p_{rv})},R_{tv,c}\right]\hfill \end{array}$$

Ventricular pressures

$$\begin{array}{cc}\hfill p_{lv}\left(t\right)=& E_{lv}\left(t\right)[V_{lv}\left(t\right)-V_{ld}]\hfill \\ \hfill p_{rv}\left(t\right)=& E_{rv}\left(t\right)[V_{rv}\left(t\right)-V_{rd}]\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill E_{lv}\left(t\right)=& \{\begin{array}{cc}{E}_{D,l}+(E_{S,l}-E_{D,l})\left[1-\cos \left(\frac{\pi t}{T_M}\right)\right]∕2\hfill & 0\le t\le T_M\hfill \\ E_{D,l}+(E_{S,l}-E_{D,l})\left[\cos \left(\frac{\pi (t-T_M)}{T_R}\right)+1\right]∕2\hfill & T_M\le t\le T_M+T_R\hfill \\ E_{D,l}\hfill & T_M+T_R\le t\le T,\hfill \end{array}\phantom{\}}\hfill \\ \hfill E_{rv}\left(t\right)=& \{\begin{array}{cc}{E}_{D,r}+(E_{S,r}-E_{D,r})\left[1-\cos \left(\frac{\pi t}{T_M}\right)\right]∕2\hfill & 0\le t\le T_M\hfill \\ E_{D,r}+(E_{S,r}-E_{D,r})\left[\cos \left(\frac{\pi (t-T_M)}{T_R}\right)+1\right]∕2\hfill & T_M\le t\le T_M+T_R\hfill \\ E_{D,r}\hfill & T_M+T_R\le t\le T\hfill \end{array}\phantom{\}}\hfill \end{array}$$

Note, the timing parameters T_M and T_R are the same for both the left and right ventricles. Input to this model is heart rate H. Outcomes from the model is arterial blood pressure p_Sa(t), cerebral blood flow velocity ν_MCA = q_B/k, and ejection fraction EF. Initial values for the differential equations as well as nominal and optimal parameter values are listed in the Appendix, Table 3.

A.2. Respiratory model

The following give equations for partial pressures and concentrations in the respiratory system. The main symbols are p and c for partial pressure and concentration. Subscript symbols S and B refer to the systemic arteries and the brain, subscripts CO₂ and O₂ refer to the two main gases. Metabolic rates are denoted by M and diffusion coefficients by D. Finally, the respiratory model depends on flows q_i predicted by the cardiovascular model.

Systemic tissue

$$\begin{array}{cc}\hfill \frac{d{c}_{Stis,{\mathrm{CO}}_2}}{dt}=& (M_{S,{\mathrm{CO}}_2}-D_{S,{\mathrm{CO}}_2}(c_{Stis,{\mathrm{CO}}_2}-c_{Scap,{\mathrm{CO}}_2}))∕V_{Stis,{\mathrm{CO}}_2}\hfill \\ \hfill \frac{d{c}_{Scap,{\mathrm{CO}}_2}}{dt}=& (q_S(c_{a,{\mathrm{CO}}_2}-c_{Scap,{\mathrm{CO}}_2})+D_{S,{\mathrm{CO}}_2}(c_{Stis,{\mathrm{CO}}_2}-c_{Scap,{\mathrm{CO}}_2}))∕V_{Scap,{\mathrm{CO}}_2}\hfill \\ \hfill \frac{d{c}_{Stis,{\mathrm{O}}_2}}{dt}=& (M_{S,{\mathrm{O}}_2}-D_{S,{\mathrm{O}}_2}(c_{Stis,{\mathrm{O}}_2}-c_{Scap,{\mathrm{O}}_2}))∕V_{Stis,{\mathrm{O}}_2}\hfill \\ \hfill \frac{d{c}_{Scap,{\mathrm{O}}_2}}{dt}=& (q_S(c_{a,{\mathrm{O}}_2}-c_{Scap,{\mathrm{O}}_2})+D_{S,{\mathrm{O}}_2}(c_{Stis,{\mathrm{O}}_2}-c_{Scap,{\mathrm{O}}_2}))∕V_{Scap,{\mathrm{O}}_2}\hfill \end{array}$$

Brain tissue

$$\begin{array}{cc}\hfill \frac{d{c}_{Btis,{\mathrm{CO}}_2}}{dt}=& (M_{B,{\mathrm{CO}}_2}-D_{B,{\mathrm{CO}}_2}(c_{Btis,{\mathrm{CO}}_2}-c_{Bcap,{\mathrm{CO}}_2}))∕V_{Btis,{\mathrm{CO}}_2}\hfill \\ \hfill \frac{d{c}_{Bcap,{\mathrm{CO}}_2}}{dt}=& (q_{Bv}(c_{a,{\mathrm{CO}}_2}-c_{Bcap,{\mathrm{CO}}_2})+D_{B,{\mathrm{CO}}_2}(c_{Btis,{\mathrm{CO}}_2}-c_{Bcap,{\mathrm{CO}}_2}))∕V_{Bcap,{\mathrm{CO}}_2}\hfill \\ \hfill \frac{d{c}_{Btis,{\mathrm{O}}_2}}{dt}=& (M_{B,{\mathrm{O}}_2}-D_{B,{\mathrm{O}}_2}(c_{Btis,{\mathrm{O}}_2}-c_{Bcap,{\mathrm{O}}_2}))∕V_{Btis,{\mathrm{O}}_2}\hfill \\ \hfill \frac{d{c}_{Bcap,{\mathrm{O}}_2}}{dt}=& (q_{Bv}(c_{a,{\mathrm{O}}_2}-c_{Bcap,{\mathrm{O}}_2})+D_{B,{\mathrm{O}}_2}(c_{Btis,{\mathrm{O}}_2}-c_{Bcap,{\mathrm{O}}_2}))∕V_{Bcap,{\mathrm{O}}_2}\hfill \end{array}$$

In the above equations, D_T is the diffusion capacity for a gas, V_Ttis,g is the effective tissue volume for a gas, V_Tcap is the effective systemic capillary blood volume for blood flow through a tissue for a gas (approximately 1% of V_T).

Inspiration

$$\begin{array}{cc}\hfill \frac{d{p}_{D1,{\mathrm{CO}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{I,{\mathrm{CO}}_2}-p_{D1,{\mathrm{CO}}_2})∕V_{D1}\hfill \\ \hfill \frac{d{p}_{D1,{\mathrm{O}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{I,{\mathrm{O}}_2}-p_{D1,{\mathrm{O}}_2})∕V_{D1}\hfill \\ \hfill \frac{d{p}_{D2,{\mathrm{CO}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D1,{\mathrm{CO}}_2}-p_{D2,{\mathrm{CO}}_2})∕V_{D2}\hfill \\ \hfill \frac{d{p}_{D2,{\mathrm{O}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D1,{\mathrm{O}}_2}-p_{D2,{\mathrm{O}}_2})∕V_{D2}\hfill \\ \hfill \frac{d{p}_{D3,{\mathrm{CO}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D1,{\mathrm{CO}}_2}-p_{D3,{\mathrm{CO}}_2})∕V_{D3}\hfill \\ \hfill \frac{d{p}_{D3,{\mathrm{O}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D1,{\mathrm{O}}_2}-p_{D3,{\mathrm{O}}_2})∕V_{D3}\hfill \\ \hfill \frac{d{p}_{a,{\mathrm{CO}}_2}}{dt}=& 863\cdot 0.98\cdot q_P(c_{v,{\mathrm{CO}}_2}-c_{a,{\mathrm{CO}}_2})+{\stackrel{.}{V}}_{ie}(p_{D3,{\mathrm{CO}}_2}-p_{a,{\mathrm{CO}}_2})∕V_A\hfill \\ \hfill \frac{d{p}_{a,{\mathrm{O}}_2}}{dt}=& 863\cdot 0.98\cdot q_P(c_{v,{\mathrm{O}}_2}-c_{a,{\mathrm{O}}_2})+{\stackrel{.}{V}}_{ie}(p_{D3,{\mathrm{O}}_2}-p_{a,{\mathrm{O}}_2})∕V_A\hfill \end{array}$$

Expiration

$$\begin{array}{cc}\hfill \frac{d{p}_{D1,{\mathrm{CO}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D1,{\mathrm{CO}}_2}-p_{D2,{\mathrm{CO}}_2})∕V_{D1}\hfill \\ \hfill \frac{d{p}_{D1,{\mathrm{O}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D1,{\mathrm{O}}_2}-p_{D2,{\mathrm{O}}_2})∕V_{D1}\hfill \\ \hfill \frac{d{p}_{D2,{\mathrm{CO}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D2,{\mathrm{CO}}_2}-p_{D3,{\mathrm{CO}}_2})∕V_{D3}\hfill \\ \hfill \frac{d{p}_{D2,{\mathrm{O}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D2,{\mathrm{O}}_2}-p_{D3,{\mathrm{O}}_2})∕V_{D2}\hfill \\ \hfill \frac{d{p}_{D3,{\mathrm{CO}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D3,{\mathrm{CO}}_2}-p_{a,{\mathrm{CO}}_2})∕V_{D3}\hfill \\ \hfill \frac{d{p}_{D3,{\mathrm{O}}_2}}{dt}=& {\stackrel{.}{V}}_{ie}(p_{D3,{\mathrm{O}}_2}-p_{a,{\mathrm{O}}_2})∕V_{D3}\hfill \\ \hfill \frac{d{p}_{a,{\mathrm{CO}}_2}}{dt}=& 863\cdot 0.98\cdot q_P(c_{v,{\mathrm{CO}}_2}-c_{a,{\mathrm{CO}}_2})∕V_A\hfill \\ \hfill \frac{d{p}_{a,{\mathrm{O}}_2}}{dt}=& 863\cdot 0.98\cdot q_P(c_{v,{\mathrm{O}}_2}-c_{a,{\mathrm{O}}_2})∕V_A\hfill \end{array}$$

Note, instantaneous airflow is obtained from integrating the air flow velocity data as described in equation (17). Inputs to the respiratory model include airflow velocity, average systemic, pulmonary, and cerebral blood flow obtained by solving the cardiovascular model. For the coupled model, these flows are computed at any instant in time. Initial values, and nominal and optimized parameter values for the respiratory model are given in the Appendix, Table 4.