Biophysical implications of lipid bilayer rheometry for mechanosensitive channels

Significance

Given the extensive use of lipid bilayer reconstitution for the study of mechanosensitive channels, it is imperative to understand the biophysical properties of lipid bilayers. We have theoretically and experimentally proven that the traditional micropipette aspiration method fails to accurately describe these properties. Herein we introduce a superior framework, which combines computational modeling with patch fluorometry for the assessment of bilayer properties. Our results show the limitations of Laplace’s law for estimation of tension within a patch membrane. We also demonstrate, in contrast to the cell-attached configuration, there is a significant difference between the stress developed in the outer and in the inner monolayers of the bilayer in the excised patch configuration. These results are of critical importance for patch-clamp electrophysiology in general.

Abstract

The lipid bilayer plays a crucial role in gating of mechanosensitive (MS) channels. Hence it is imperative to elucidate the rheological properties of lipid membranes. Herein we introduce a framework to characterize the mechanical properties of lipid bilayers by combining micropipette aspiration (MA) with theoretical modeling. Our results reveal that excised liposome patch fluorometry is superior to traditional cell-attached MA for measuring the intrinsic mechanical properties of lipid bilayers. The computational results also indicate that unlike the uniform bilayer tension estimated by Laplace’s law, bilayer tension is not uniform across the membrane patch area. Instead, the highest tension is seen at the apex of the patch and the lowest tension is encountered near the pipette wall. More importantly, there is only a negligible difference between the stress profiles of the outer and inner monolayers in the cell-attached configuration, whereas a substantial difference (∼30%) is observed in the excised configuration. Our results have far-reaching consequences for the biophysical studies of MS channels and ion channels in general, using the patch-clamp technique, and begin to unravel the difference in activity seen between MS channels in different experimental paradigms.

Liposome reconstitution has been used for both functional and structural studies of bacterial mechanosensitive (MS) channels (MscL and MscS) for many years (1–4) and also more recently for the study of eukaryotic MS channels (5–8). Most frequently azolectin, a crude extract of phospholipids from animal and plant tissue consisting mainly of phosphatidylcholine (PC), phosphatidylethanolamine (PE), and phosphatidylinositol (PI) (9), has been used for liposome preparations. Given the frequent use of azolectin bilayers for the study of MS channels and the importance of protein–lipid interactions in MS channel gating it is imperative to consider the best way to accurately calculate and assess its material properties. This is also essential for studies of voltage- and ligand-gated ion channels as the activity of these proteins can also be modulated by membrane tension (6–8, 10–12).

The mechanical properties of different types of lipids have been studied extensively using the micropipette aspiration (MA) approach (13–18). These experiments have shown that the mechanical properties of lipids differ considerably and that lipid bilayers exhibit elastic behavior (14, 15, 18, 19). The MA technique is versatile and has the advantage of exerting a wide range of aspiration pressures on a specific portion of a bilayer (20–23). Here we use this technique in combination with finite-element (FE) simulation to examine in depth the mechanical properties of azolectin bilayers in both cell-attached and excised patch configurations (SI Materials and Methods). It is widely known that lipid behavior is vastly different at low (<0.5 mN/m) compared with high tensions, due to thermal shape fluctuations (24). Given that the midpoint activation of most MS channels is higher than 1 mN/m [e.g., ∼12 mN/m for MscL (25, 26) and ∼6.0 mN/m for MscS (26, 27)], characterizing the behavior of lipid bilayers at high-tension ranges is a necessity and is the focus of this study. To do this we introduce two alternative models (elastic and hyperelastic). These models have the advantage, over the traditional model, of including in the calculations the boundary conditions caused by a rigid cylindrical pipette and no assumption for volume conservation during MA. The material properties resulting from these models were imported separately into a continuum FE model (Fig. S1 A–C). This permitted comparisons between the FE model parameters and experimentally derived results to define the best description of the continuum behavior of azolectin bilayers. Using our alternative models, we compare the membrane tension in an azolectin liposome patch estimated using Laplace’s law with the membrane tension obtained from our computations. Furthermore, the stress–strain distribution within the patch area for cell-attached and excised configurations has been compared. We discuss how these findings may provide integral information about a widely used experimental and theoretical paradigm used to study MS channels.

Results and Discussion

To probe the material properties of azolectin bilayers we used patch fluorometry. This technique involves slowly aspirating a lipid membrane into a micropipette, measuring the geometry of the patch, recording the pressure inside the pipette during aspiration, P, and then calculating the liposome’s surface tension and areal strain to determine its mechanical properties, i.e., areal elastic modulus. In this study, to estimate material parameters from patch fluorometry data, the experimental deformation history was fitted to three different analytical models. These models represent different assumptions, namely, (i) model 1, traditionally used in conjunction with MA (28) (based on an equibiaxial tension assumption); (ii) model 2, linear elastic (based on a uniaxial tension assumption); and (iii) model 3, hyperelastic (neo-Hookean) (SI Materials and Methods). For each model we describe the physical parameters calculated for azolectin membrane bilayers under mechanical stress. Although cell membranes are composed of various lipids and proteins and as such are not homogeneous, in this study we examined the continuum behavior of azolectin lipid bilayers, which are a good model, mimicking the basic mechanical properties of cell membranes (26). The framework set out can be applied to any type of lipid bilayer.

Cell-Attached Patch Fluorometry.

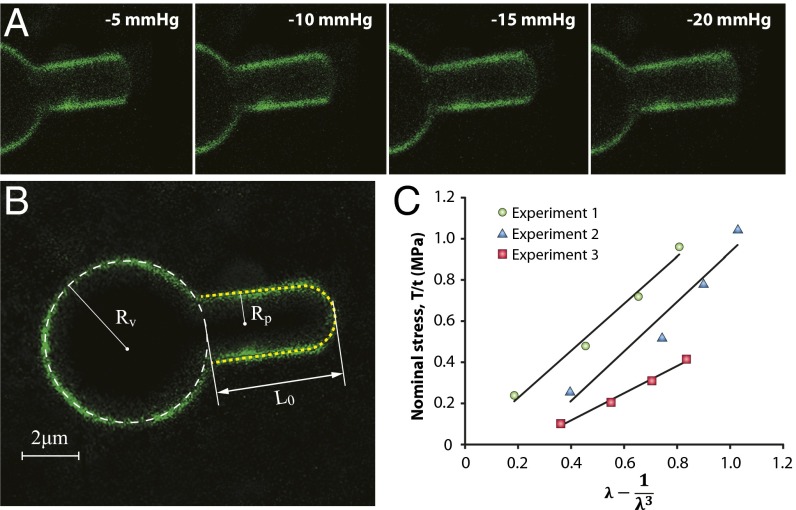
Initially we investigated the material properties of azolectin liposomes containing 0.1% rhodamine-PE, using cell-attached patch fluorometry. During these experiments, due to the shear rigidity of lipid vesicles, below a certain pressure, the vesicle was only marginally deformed by suction. Above this threshold pressure, however, the vesicle moved into the pipette until it reached a point of equilibrium, specifically a pressurized spherical geometry, where area dilation was required for further entry (14). After equilibrium, liposomes were aspirated by applying negative pressure up to a maximum pressure of −20 mmHg in increments of −5 mmHg (Movie S1). At each pressure, the length of liposome patches inside the pipette was measured (Fig. 1 A and B). Our experiments indicated that in some cases the radius of curvature of the liposome patch was slightly larger than the radius of the pipettes used. Hence, to provide an accurate estimation, the method used to calculate membrane tension in stretched membrane patches based on Laplace’s law (14, 16) had to be modified with regard to the radius of the liposome patch (SI Materials and Methods and Fig. S1 D–F).

Fig. 1.

Representative cell-attached patch fluorometry experiment. (A) Confocal images of azolectin liposomal membranes fluorescently labeled by addition of 0.1% rhodamine-PE being stretched by applying four negative pressure steps of −5 to −20 mmHg. (B) L₀ is the initial projection length, and R_v and R_p denote the radius of the liposome and the micropipette, respectively. (C) Stress–strain relationship from the patch fluorometry experiment shows the variation of the nominal in-plane stress in the membrane with respect to a function of the longitudinal stretching ratio, λ − 1/λ³, for three azolectin lipid vesicles of similar diameter (6–8 µm). The relationship is fitted using the linear neo-Hookean hyperelastic model (model 3). λ is the stretching ratio in the longitudinal direction (along the length of the micropipette). These diagrams demonstrate a linear relation between the change in the nominal stress of lipid and the term λ − 1/λ³. The slope allows us to calculate the shear modulus, which is ∼1.0 MPa. R² values are 0.98, 0.94, and 0.99 for experiments 1, 2, and 3, respectively.

After modification of Laplace’s law for the tension calculation, we first assessed the material properties, using model 1. Linear slopes in measurements of area dilation at high tensions were used in the early 1980s as elastic (Hookean) moduli, characterizing the bilayer area-stretch response (28). The membrane area increases linearly as the membrane undulations are reduced by the increasing pressure difference across the pipette opening. Using model 1, from the slopes of the plots of applied tension vs. areal strain, the areal elasticity modulus, $K_A$, of ∼45.5 $\pm 5$ mN/m was calculated (Fig. S2A). Thus, we calculated the average Young’s modulus of azolectin to be ∼13 MPa for small vesicles in the diameter range of 5–8 $\text{μm}$ (Table 1 and Fig. S2A). Surprisingly, these values increased with vesicle size, i.e., 14–20 $\text{μm}$. Elastic modulus is related to bending rigidity, $k_b$, through $k_b=E{t}^3/24$, where t is the bilayer thickness (18, 29, 30). Therefore, the $k_b$ for small vesicles (diameter 5–8 $\text{μm}$) was 2.32 $\times {10}^{-20}$ J (Table 1). These values were much smaller than those of larger azolectin vesicles as well as values previously reported for other types of lipids (15).

Table 1.

Material parameters obtained from curve fitting of patch fluorometry data (cell-attached and excised patch configurations)

Models	Linear elastic, biaxial	Linear elastic, uniaxial	Hyperelastic, neo-Hookean
Small vesicles, diameter 5–8 µm
C10, MPa	—	—	0.5 ± 0.15
E(MPa)	13.0 ± 1.5	3.0 ± 0.7	10.5 ± 3
KA, mN/m	45.5 ± 5	3.0 ± 0.8	10.5 ± 3
kb (J) × 1021	23 ± 3	5.4 ± 1.3	5.4 ± 1.6
Large vesicles, diameter 14–20 µm
C10, MPa	—	—	0.7 ± 11
E(MPa)	32.1 ± 8.0	4.2 ± 1.5	4.1 ± 0.7
KA, mN/m	112.2 ± 29	14.6 ± 5	14.4 ± 2
kb (J) × 1021	57.0 ± 15	7.4 ± 1.9	7.3 ± 1.2
Excised patches
C10, MPa	—	—	0.7 ± 0.07
E(MPa)	4.5 ± 0.6	4.4 ± 0.5	4.3 ± 0.4
KA, mN/m	15.8 ± 2	15.5 ± 2	15.0 ± 2
kb (J) × 1021	8.1 ± 1.1	7.9 ± 0.9	7.6 ± 0.8

C₁₀ is the neo-Hookean material parameter. E and G represent Young’s and the shear moduli, respectively. In the case of lipids, the Poisson ratio is assumed to be 0.5, and then E = 3G. k_b denotes the bending rigidity. All of the data are presented in the form of mean ± SEM.

Although a patch fluorometry experiment does not exhibit all of the ideal uniaxial conditions, one could consider this experiment as a uniaxial tensile test. If we look at the liposome behavior on the patch scale (>1 $\text{μm}$, range of pipette radius) rather than on the lipid raft scale (10–200 nm) (31), the cylindrical pipette disallows the expansion of lipid in the radial direction. Hence, a uniaxial assumption is more appropriate than an equibiaxial assumption for obtaining the stress–strain relationship (SI Materials and Methods). Using the elastic uniaxial assumption (model 2), the nominal stress–strain experimental results are presented in Fig. S2B. From the slopes of these plots we calculated a Young’s modulus of ∼2.5 MPa, which was much lower than that determined by the traditional MA approach (model 1) (Table S1) but very close to what has been measured for egg yolk lipid bilayers (32). This means that model 1 described much stiffer behavior for small azolectin vesicles.

Given that elastic material models are intended for elastic strains that usually remain small (<5–10%) and hyperelastic material models are more appropriate for most biological materials, particularly at large strain magnitudes (>5%) (33), we fitted a linear constitutive hyperelastic model, the neo-Hookean model (model 3, SI Materials and Methods), to our experimental data (Fig. 1C). In this model, the strain energy density, U, is a linear function of deviatoric strain invariants, ${\overline{I}}_1$, and can be derived as

$$U=\frac{G({\overline{I}}_1-3)}{2},$$ [1]

where G is the shear modulus. Unlike the liposome areal change in the longitudinal direction, the area of the patch dome within the pipette does not change notably at any equilibrium position. As a result, one may simplify the boundary and loading conditions inside the pipette as illustrated in Fig. S3. Because the rigid cylindrical pipette does not allow any growth of the patch area in the radial direction, λ₁ = 1. Consequently, due to the boundary conditions of the liposome bilayer within the pipette and the incompressibility of azolectin lipid, λ₃ = 1/λ₂ = 1/λ. Hence, the stress in the longitudinal direction could be expressed as (SI Materials and Methods and Fig. S3)

$$\sigma =\frac{\partial U}{\partial \lambda }=G(\lambda -\frac{1}{{\lambda }^3}).$$ [2]

Based on Eq. 2, the slope of stress vs. a function of the longitudinal stretch ratio, λ − 1/λ³, shows the shear modulus of the azolectin bilayer (∼1 MPa; Fig. 1C and Table 1).

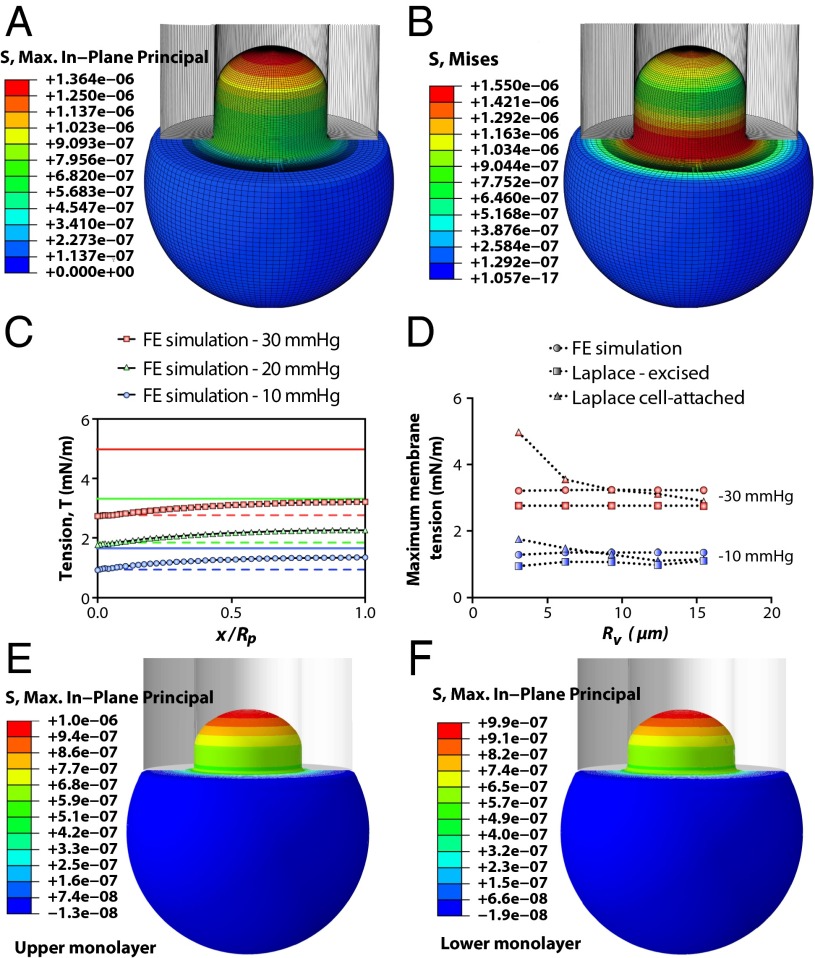
Next, we imported the material properties estimated using models 1–3 into our computational model to see which were the best for describing the continuum behavior of azolectin lipids during aspiration (Fig. 2 A and B). This was achieved by comparing the computed liposome projection lengths, $\mathrm{\Delta }L$, with those observed during patch fluorometry (Table S1). All FE computations were carried out using identical geometries, meshes, loads, and boundary conditions typical of experimental patch fluorometry conditions, including identical liposome diameters, micropipette diameters, and applied pressures (SI Materials and Methods). FE solutions were obtained successfully for all three models at corresponding pressures to those used in the cell-attached patch fluorometry experiments (Table S1 and Movie S2 ). Model 1 predicted $\mathrm{\Delta }L$ values that were far below the experimental values at all pressures. These results clearly show that the material properties obtained based on model 1 (assuming the lipid bilayer as a single elastic slab) are much stiffer than the real behavior of the azolectin lipid bilayers during aspiration. Use of model 2 resulted in $\mathrm{\Delta }L$ values that were in better agreement with those obtained using patch fluorometry. The neo-Hookean material model (model 3) was the most appropriate model for describing the continuum behavior of the azolectin liposomes (Table S1). The principal difference between models 2 and 3 is the consideration of more realistic boundary conditions during derivation of the equations. The main difference between the introduced models (models 2 and 3) and the traditional model (model 1) is the lack of assumption of preserved internal vesicle volume and inclusion of boundary conditions in our calculations for the membrane patch inside the micropipette (15, 34) with both of these being important for the calculation of areal strain (SI Materials and Methods).

Fig. 2.

Spatial profiles of an aspirated liposome calculated using FE simulation. The vesicle has a diameter of 6.2 µm. The inner diameter of the micropipette is 2.8 µm (both are typical sizes encountered experimentally). The suction starts from 0 and reaches a value of −30 mmHg (∼4 kPa), instantaneously (in 0.01 s), and is then kept constant for 0.01 s. The computations are performed for the material parameters of C₁₀ = 0.5 MPa and k_b = 5.36 × 10⁻²¹ J (neo-Hookean model). (A) In-plane maximum principal stress (N/µm² distribution; maximum membrane tensional stress, σ_max, in the apex and the minimum membrane tension, 0.6 σ_max, close to the pipette wall has also been illustrated). (B) Effective stress (von Mises stress) field. (C) Comparison of membrane tension, T, at different points in the patch area using FE analysis in conjunction with the relevant Laplace’s equations for excised patch and cell-attached configurations. FE results demonstrate that there is a differential distribution of tension within a patch; with the above-mentioned geometrical properties, the cell-attached Laplace equation (solid lines) (Eq. S1) is an overestimation of the membrane tension, whereas the excised patch equation (dashed lines) (Eq. S18) underestimates the tension developed in the patch area (x axis: 0, membrane–pipette contact point; 1, patch apex). (D) Comparison of the maximum membrane tensions (in the apex) obtained from FE computation and Laplace’s law formulation at two negative pressures (blue, 10 mmHg; red, 20 mmHg) and for different vesicle sizes, R_v. This result illustrates that R_v is not affecting the actual tension distribution in the patch. However, as R_v increases, the accuracy of Eq. S1 improves up to the point where R_v = ∼9 µm. For much larger vesicles (i.e., R_v ∼ 15 µm), the results from both forms of Laplace’s equation are equal and both underestimate the actual distributed tension in the patch (Fig. S6). (E and F) Spatial profiles of the in-plane stress in an aspirated liposome illustrated in the upper (outer) monolayer and the lower (inner) monolayer, respectively. It is the same model as described in A and B, except that here, each monolayer of the bilayer has been modeled as a separate shell that can slide against another shell. Moreover, the material behavior of the inner and outer layers in the current computational model has two more material constants: their relaxation time of 0.01 and their relaxation shear modulus ratio of 0.9 (SI Materials and Methods).

Although models 2 and 3 provided an excellent representation of the continuum behavior of azolectin liposomes, there were minor discrepancies between the computational and experimental results. These small differences possibly originate from the adhesion tension (35) dependency on the applied pressures within the pipette (36), which for simplicity our FE models did not consider.

Excised Patch Fluorometry.

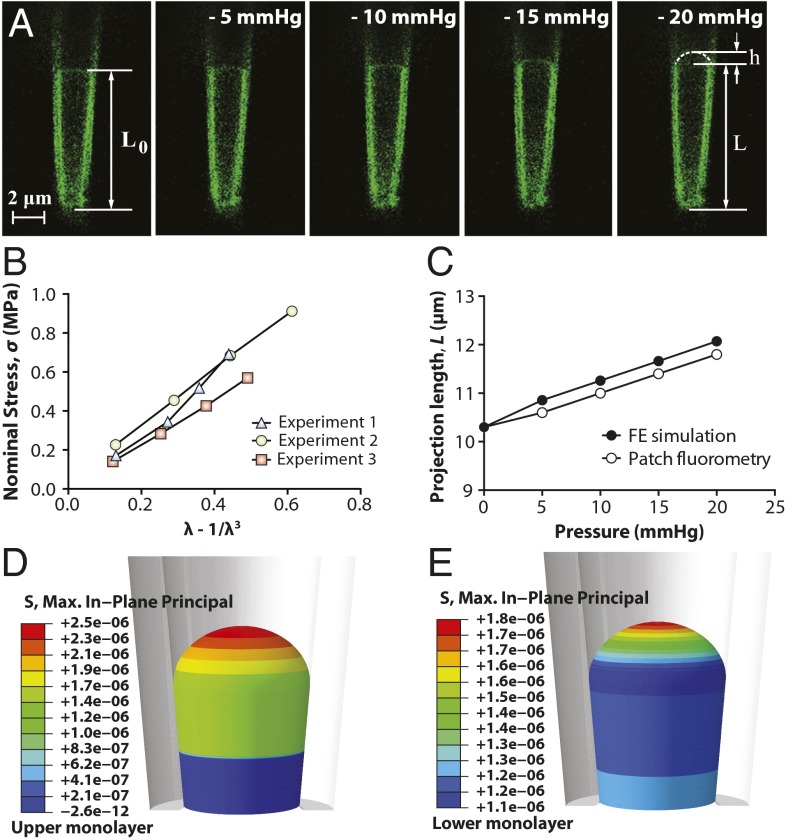
Due to the wide use of the excised patch configuration in the electrophysiological studies of MS channels, we also investigated the material properties of azolectin bilayers, using excised patch fluorometry (Movie S3). There has been a discussion in the literature (37, 38) about the existence of pretension in lipid vesicles (without any concentration or pressure gradient across the membrane). Our results indicate considerable pretension even in small vesicles, which is magnified in larger vesicles (Table S2). Aside from experimental simplicity, excised patch fluorometry has the major benefit of reducing this pretension and more importantly allows suppression of the thermodynamic effects related to volume changes and thermal undulations (“wiggles”) (19, 24, 28, 34, 39), which may affect the rheological behavior of liposomal membranes. Importantly, unlike the cell-attached technique (Fig. 2 and Table S2), in excised patch fluorometry experiments the material properties obtained from all three theoretical models were very similar (Fig. 3 A and B, Fig. S4 A and B, and Table 1). The areal elasticity modulus, $K_A$, for excised azolectin bilayers is ∼15 mN/m. Moreover, comparisons performed between the experimentally measured aspiration lengths of azolectin lipid and those simulated using the neo-Hookean model (model 3) were in very good agreement (Fig. 3C and Fig. S4 C and D).

Fig. 3.

Excised patch fluorometry. (A) Confocal images of a representative excised liposome patch fluorometry experiment. Rhodamine-PE–labeled azolectin liposome excised patch membranes were stretched by applying four negative pressure steps of −5 mmHg to −20 mmHg through the micropipette. L₀ is the initial projection length, L is the deformed projection length of the liposome membrane, and h is the height of the patch dome. (B) Variation of the nominal in-plane stress in the membrane with respect to the unidirectional strain term λ − 1/λ³ based on the neo-Hookean hyperelastic model. λ is the unidirectional stretching ratio in the longitudinal direction. These diagrams demonstrate a linear relation between the change in the nominal stress of lipid and the strain term λ − 1/λ³. (C) Validation of the simulations with the observations from patch fluorometry experiments. Comparisons were made between the measured aspiration lengths of azolectin lipid inside the pipette and those simulated using the neo-Hookean hyperelastic model. The inner diameters of the micropipette are typical sizes encountered experimentally. The computations were performed for the material parameters of C₁₀ = 0.71 MPa and k_b = 5.36 × 10⁻²¹ J (SI Materials and Methods). (D and E) Spatial profiles of the in-plane stress in an excised liposome patch shown in the upper (outer) monolayer and the lower (inner) monolayer, respectively. The computations were performed for the material parameters of C₁₀ = 0.71 MPa and k_b = 5.36 × 10⁻²¹ J (SI Materials and Methods). It is the same model as model described in C, except that here, each monolayer of the bilayer has been modeled as a separate surface that can slide against another surface. Moreover, the material behavior of the inner and outer layers in the current computational model has two more material constants: their relaxation time of 0.01 and their relaxation shear modulus ratio of 0.9 (SI Materials and Methods).

Tension Distribution in Cell-Attached Membrane Patches.

As model 3 resulted in the best description of azolectin rheometry in both configurations, it was used in the following computational stress analysis, which includes investigating tension distribution and deformation of azolectin liposome patches during aspiration. The maximum in-plane stress is highest in the apex, reducing to zero around the site where the micropipette is normally connected to the liposome (Fig. 2A and Movie S2). The largest effective stress field was found in the vicinity of the membrane normal contact with the edge of the micropipette as well as in the apex (Fig. 2B). From this we suggest that these two areas are the most likely places for lipid rupture initiation during aspiration. Given that we assumed the pipette to have a smooth tip, which it does not (40), the most likely place for the rupture initiation in a cell-attached system is near the pipette tip rather than the apex of the patch. From comparison of the vertical displacement field and the in-plane maximum principal strain the apex of the patch had the greatest vertical displacement whereas the elements near the liposome–pipette contact region had the largest strain (Fig. S5). This implies that when a local stress is produced in this area, the lipid membrane is unable to reconfigure itself and reduce the strain. Consequently, it restricts the movement of the elements (in FE simulation) and likely the phospholipids of the membrane (in reality) (18), thereby facilitating membrane rupture (Fig. S3). Hence, the computational results show that the response is mostly dominated by local stretching of the liposome rather than by its shear and/or bending effects near this normal contact area. In fact, the lipid membrane expands in the principal in-plane directions and shrinks in the thickness direction to maintain a constant volume; i.e., ΔA/A = −Δt/t, where A and t are the area and the thickness of the bilayer, respectively. These stress and deformation analyses of geometrically realistic liposomes could be used for an accurate estimation of stresses and strains and to facilitate prospective studies of the role of stress in lipid bilayer rupture during aspiration, particularly relevant for patch-clamp electrophysiology.

Subsequently, we compared the tension values acquired from our FE simulations with those estimated by two widely used forms of Laplace’s law (Eqs. S1 and S18) to assess their levels of accuracy (Fig. 2C). The maximum in-plane tension variation in the membrane, obtained from FE simulations, at three negative pressure steps of −10 mmHg, −20 mmHg, and −30 mmHg in the whole patch area is shown in Fig. 3C. Based on the geometry of the deformed patch from our simulations at each pressure, we calculated the theoretical tension using Laplace’s formulation for the cell-attached configuration using Eq. S1, as well as the relevant form for excised patches using Eq. S18. Our results indicate that the tension value estimated by Eq. S18 was always an underestimation of the maximum actual tension developed in the patch (Fig. 2 C and D). In contrast, the value obtained from Eq. S1 was always above the actual tension for relatively small vesicles (i.e., R_v < 9 µm) and was below the actual tension for larger vesicles. However, both equations provided similar results when the radius of the vesicle was much greater than the micropipette radius, i.e., R_v/R_p > 15 (Fig. 2D and Fig. S6). In contrast to the assumption provided by both equations, the membrane tensional stress was not uniform at different points within the patch area. The highest value is found in the patch apex and the lowest near the pipette wall. These findings were true of a wide range of vesicles, from 3 µm to 16 µm, and are important for the study of MS channels using the patch-clamp technique. Additionally, we modeled the liposome membrane as two independent monolayers being able to slide relative to each other and normally restrained by van der Waals force. We compared the stress–strain profile in the two monolayers under ramp pressure, considering the internal and intermonolayer damping of our model bilayer (SI Materials and Methods). Our results indicate a negligible difference (<2%) between the stress profiles of the two monolayers in the cell-attached model (Fig. 2 E and F). These results are valid for different loading rates and/or material properties (SI Materials and Methods).

Tension Distribution in Excised Membrane Patches.

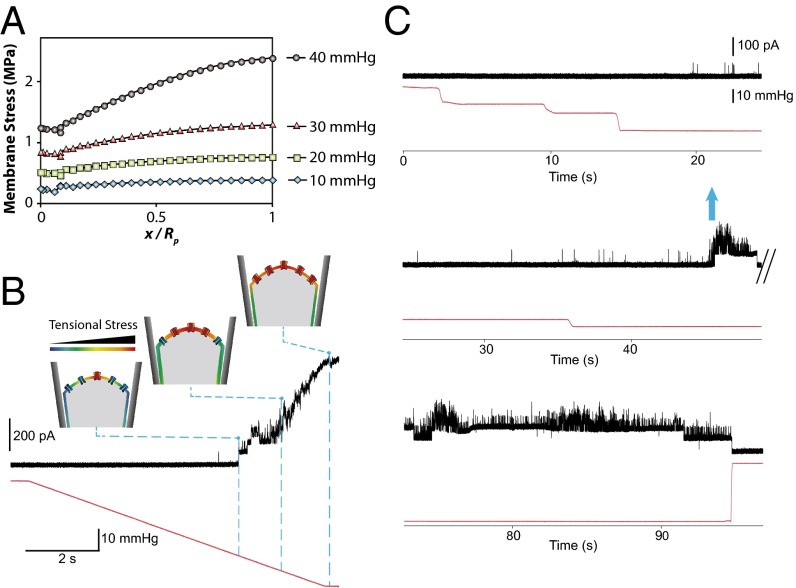
As well as investigating the stress distribution in the membrane in the cell-attached configuration we also studied simulations of the excised patch configuration (Figs. 3 D and E and 4A). Similar to what we simulated for the cell-attached configuration, we modeled the liposome bilayer as two separate monolayers in an excised patch system. Interestingly, unlike the cell-attached results (Fig. 2 E and F), the peak stress in the upper leaflet is ∼30% higher than that in the inner leaflet (Fig. 3 D and E). This dissimilarity may explain differences in activity seen for some MS channels between the cell-attached and excised patch configurations. For example, it may explain the apparent adaptation upon a sustained pressure pulse observed experimentally with both MscL (1) and MscS channels (41) in excised liposome patches. In this experiment we pressurized an excised patch lipid bilayer containing MscL with a tapered pipette. Analogous to cell-attached results, membrane tension reduced from a maximum value in the apex of the patch to its minimum close to the pipette wall (Fig. 4A). In Movie S4 we illustrate how the distribution of tension changed in the membrane during the application of negative pressure. This observation together with our patch-clamp results may explain the very interesting biophysical phenomenon of sequential gating of MscL (Fig. 4 B and C), which may well be relevant for other MS channels. Our electrophysiology recordings demonstrated that when we gradually increased the pressure up to a certain point (i.e., −35 mmHg), the resulting tension was just enough to activate a few channels probably clustered in the apex (highly stressed). As the pressure rose, the area that had reached or passed the activation threshold of MscL increased and thus there was a higher probability for a larger cohort of channels in the patch area to gate. This trend continued until the stress value in the whole patch area exceeded the activation threshold of MscL. At this point the maximum saturating current, a composite of the activity of all functional channels in the patch area, was recorded (Fig. 4B). Moreover, the gating kinetics of MscL under ramp pressure were shown as an S-like activation of the cohort of channels in the patch area. Moreover, we examined how MscL was activated under constant pressure close to the activation threshold. When the negative pressure steps increased gradually, first a single channel opened and then several channels were suddenly activated (Fig. 4C). This “flare-up activation” also seems consistent with the finding that MscL forms clusters in the liposome membrane as previously shown (42).

Fig. 4.

MS channels in the center of the patch sense a higher tensional stress than the channels close to the pipette wall. (A) In-plane maximum principal stress (MPa) distribution in a conical pipette. FE results demonstrate that there is a differential distribution of tensional stress within a patch: maximum membrane tensional stress, σ_max, in the apex and minimum tensional stress, 0.6 σ_max, close to the pipette wall (more details about the FE computations in Figs. S7 and S8). (B) Activation of MscL under a pressure ramp. Currents were recorded at a pipette voltage of +20 mV in a recording solution containing 200 mM KCl, 40 mM MgCl₂, and 5 mM Hepes-KOH, the gating kinetics of MscL under ramp pressure applied to the patch membrane. (C) “Flare-up” activation of MscL under the application of increasing pressure steps (blue arrow). Applied pressure (mmHg) is shown in red.

It has previously been reported that acyl chain length (and hence initial bilayer thickness) affects the gating of numerous channels including MscL; in the case of MscL shorter acyl chains (PC16) facilitate opening, whereas longer chains (PC20) stabilize the closed state (43). Surprisingly, previous work has shown that altering acyl chain length (PC13–PC22) does not appreciably affect the areal elasticity modulus of a lipid bilayer (19, 28). Thus, we performed a set of simulations to investigate the effect of initial membrane thickness on the stress and tension distribution within the membrane patch area (Figs. S7 and S8). The results show that the initial thickness had no effect on membrane tension, but it had a remarkable impact on bilayer stress. The thinner the lipid bilayer, the higher the stress was at any given pressure. Moreover, the stress variation over the patch area was also steeper. We believe that these simulations complement and compound the previous reports of lipid chain length on MscL activity by explaining the effect of bilayer thickness on tensional stress (43, 44).

Conclusions

In summary, patch fluorometry in combination with continuum mechanics modeling has clearly shown that the traditional widely used model (model 1) describes much stiffer continuum behavior for azolectin liposomes, and likely other lipids, during aspiration. The alternative elasticity models we introduce (models 2 and 3) differ principally from the old model (model 1) in the calculation of areal strain, resulting in a more realistic description of the rheological behavior of azolectin lipids. To make sure that the inaccuracy arises from the calculation of areal strain in the traditional approach (model 1), we used excised patch fluorometry, to remove this assumption during the calculation of areal strain. The material properties obtained from these experiments were very similar for all three theoretical models. This confirms the notion that the way that areal strain is calculated in the traditional model is not accurate. Thus, we require new theoretical models to interpret data obtained from the cell-attached MA technique, with our neo-Hookean model (model 3) being a good example. In addition, excised patch fluorometry seems to be an excellent experimental paradigm for investigating the mechanical properties of lipids. Based on our FE simulations we also conclude that although Laplace’s law gives a good approximation of membrane tension in a patch membrane by assuming a constant tension within the patch area, this is not a true reflection of the experimental scenario. First, application of Laplace’s law leads to an overall underestimation of the bilayer tension in excised patch membranes, whereas for the cell-attached equation its accuracy depends on the radius of the individual liposome. Furthermore, Laplace’s law neglects the integral fact that membrane tension is actually decreasing from its maximum value in the apex of the patch dome to its minimum value near the pipette wall. This may be one of the reasons for sequential activation of MscL channels when their activity is recorded upon application of a pressure ramp. More importantly, we showed that unlike in cell-attached configuration, the difference between the stress profiles of the two monolayers of a liposome bilayer is significantly different in the excised patch configuration (∼30%). There is higher stress in the upper monolayer in comparison with the lower one. These results should facilitate prospective studies on the role of bilayer stress not only in the gating of MS channels, but also of voltage- and ligand-gated ion channels. They also caution against the extrapolation of MS channel behavior from one experimental paradigm to another.

Materials and Methods

Liposome Preparation and Patch Fluorometry.

Liposomes made of azolectin [99.9% (wt/wt)] and rhodamine-PE [0.1% (wt/wt)] were prepared using the Nanion Vesicle Prep Pro device. Lipids dissolved in chloroform were placed on electrodes and an electrical field of 5 Hz and 3 V was applied for 120 min. For visualizing the creep, the tips of glass pipettes were bent ∼30°, using a microforge (Narishige) to make them parallel to the bottom of the chamber, and images of patch membranes were taken using a confocal microscope (SI Materials and Methods). All of the data are expressed in the form of mean $\pm \mathrm{SEM}$. To suppress adhesion tension between the glass and lipid bilayer, we coated the pipette with 0.1% BSA (Movie S5).

Electrophysiology.

Liposomes were prepared by the dehydration/rehydration (D/R) method and the MscL proteins were incorporated in the ratio of protein to lipids (1:1,000) as previously described (1, 45). Channel currents were recorded with an AxoPatch 1D amplifier and negative pressure was applied with a syringe or a High Speed Pressure Clamp-1 apparatus (HSPC-1; Ala Scientific) (SI Materials and Methods).

Finite-Element Modeling.

Details of the computational models can be found in SI Materials and Methods. Given the geometric nonlinearities that had to be taken into consideration, we used commercial finite-element analysis (FEA) software (Abaqus/Standard; Dassault Systemes Simulia) for simulations as well as for prediction of the stress and strain distribution in azolectin liposomes exposed to pipette aspiration (Movies S2, S4, S6 and S7). To address the limitations of applying all of the forms of Laplace’s law to calculate membrane tension in membrane patches, FE models of pure azolectin liposomes for both cell-attached (MA technique) and excised patch (patch-clamp experiment) configurations based on their related patch fluorometry data were developed. This approach has been widely used to model micropipette aspiration for several different cell types (46–50).