Global market integration increases likelihood that a future African Green Revolution could increase crop land use and CO₂ emissions

Significance

Agriculture is a key driver of tropical deforestation, and there is heated debate about whether productivity-enhancing crop innovations can slow such environmental degradation. For fixed food demand, globally higher yields will reduce cropland and hence deforestation. However, regional innovations often boost agricultural profitability and lower prices, thereby leading to cropland expansion in the innovating region. This paper develops a framework for understanding the impact of regional innovations on global land use and the environment. Although the historical Green Revolution in Asia, Latin America, and the Middle East is shown to have been land sparing, a future Green Revolution in Africa could lead to global cropland expansion in the context of a more fully integrated global agricultural economy.

Abstract

There has been a resurgence of interest in the impacts of agricultural productivity on land use and the environment. At the center of this debate is the assertion that agricultural innovation is land sparing. However, numerous case studies and global empirical studies have found little evidence of higher yields being accompanied by reduced area. We find that these studies overlook two crucial factors: estimation of a true counterfactual scenario and a tendency to adopt a regional, rather than a global, perspective. This paper introduces a general framework for analyzing the impacts of regional and global innovation on long run crop output, prices, land rents, land use, and associated CO₂ emissions. In so doing, it facilitates a reconciliation of the apparently conflicting views of the impacts of agricultural productivity growth on global land use and environmental quality. Our historical analysis demonstrates that the Green Revolution in Asia, Latin America, and the Middle East was unambiguously land and emissions sparing, compared with a counterfactual world without these innovations. In contrast, we find that the environmental impacts of a prospective African Green Revolution are potentially ambiguous. We trace these divergent outcomes to relative differences between the innovating region and the rest of the world in yields, emissions efficiencies, cropland supply response, and intensification potential. Globalization of agriculture raises the potential for adverse environmental consequences. However, if sustained for several decades, an African Green Revolution will eventually become land sparing.

Increasing world food supplies while minimizing the environmental footprint of agriculture is increasingly recognized as a major challenge (1, 2). Global crop output is estimated to increase significantly by 2050 as a result of population growth and changes in diet (3, 4). This output increase can be achieved through either clearing new land for agriculture or through intensifying production on existing land. Both of these options have major environmental implications, and there is a lively debate on which option offers greater promise (5–7).

One side of the debate is best characterized by Norman Borlaug’s assertion that agricultural innovation is land sparing (8–10). In other words, Borlaug argued that intensifying agricultural production is better for the environment overall because the same amount of food could be produced using less land, thereby sparing land for nature. Waggoner (11), in a report titled “How much land can 10 billion people spare for nature?,” lent further credence to this idea. Stevenson et al. (12), using a global simulation model, made the case that the Green Revolution (GR) spared land. However, these assertions assume that the overall impact on the environment would be lower because of land sparing without considering the greater environmental impact per unit area of higher-intensity production systems. Green et al. (13), in a landmark paper, presented an analytical model for evaluating the biodiversity benefits of land sparing vs. “wildlife-friendly farming” (often termed land-sharing) modes of production. They applied this model in a recent field study to find support for land sparing (14). Others have, however, argued that the analytical model of Green and colleagues is overly simplistic and promoted instead the concept of an “agro-ecological matrix” as an alternate land-sharing mode of production to promote biodiversity (15, 16).

Another recent study investigated the climate impact of the historical intensification of agriculture compared with alternate scenarios of extensive modes of production. They compared CO₂ emissions from clearing of land, CH₄ emissions from rice paddy cultivation, N₂O emissions from agricultural soils, and CO₂, CH₄, and N₂O emissions from fertilizer production and use. Intensification would increase emissions from soils and from fertilizer use but decrease emission from clearing. The study found that differences in CO₂ emissions from land clearing dominated and that the historical intensification of agriculture lowered overall greenhouse gas emissions because of land sparing (17). Given that greenhouse gas emissions from our global food systems constitute a third of total greenhouse gas emissions (18), this is an important contribution to the debate on how to reduce global emissions.

Irrespective of the outcome of the debate surrounding the putative environmental benefits of intensification, another major criticism of the Borlaug hypothesis is that land sparing does not, in fact, occur in practice. The validity of the proposition rests, among other things, on Borlaug’s assumption of a fixed demand for food. Borlaug’s hypothesis has recently been brought into question by a series of studies on land use change that argue in favor of a competing hypothesis—dubbed by some as Jevons’ paradox—which suggests that increases in agricultural productivity will, in fact, be accompanied by an expansion in land area (19, 20). Rudel et al. (19) scrutinized United Nations Food and Agriculture Organization (FAO) data for 961 agricultural sectors in 161 countries over a 15-y period and found little evidence of higher yields being accompanied by reduced area. Ewers et al. (21) similarly analyzed FAO data on crop yields and per capita area for 23 staple crops and total per capita cropland area over a 21-y period and found a weak land-sparing effect in developing countries but no effect in developed countries.

The literature evaluating the Borlaug hypothesis suffers from two major problems. First, the statistical studies suffer from the challenge of estimating what would have happened in the absence of such agricultural innovation (i.e., they are unable to account for the counterfactual world in their analysis). Second, there is a strong tendency in this literature to focus on particular regions of the world (5, 22, 23), thereby ignoring impacts of regional innovations on land use and CO₂ emissions in the rest of the world, where these may fall. Accordingly, this paper introduces a general framework for analyzing the impacts of regional and global innovations on long run agricultural output, prices, land rents, land use, and associated CO₂ emissions. In so doing, it facilitates a reconciliation of the apparently conflicting views of the impacts of agricultural productivity growth on land use, global CO₂ emissions, and environmental quality.

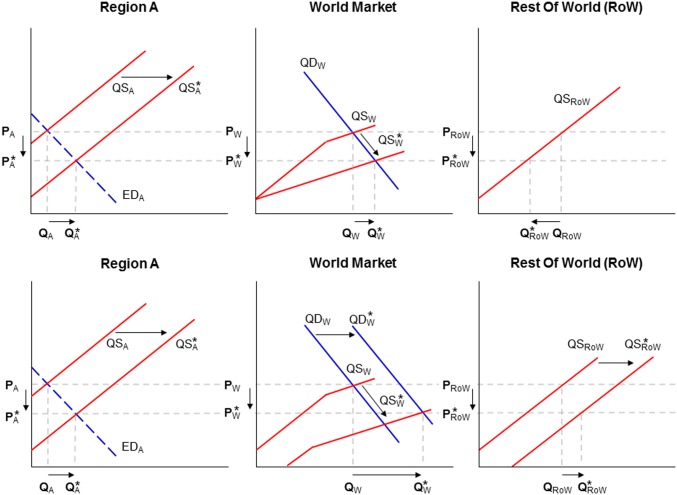
Fig. 1 provides an overview of key elements of the land-sparing debate. The top left panel presents a supply and demand diagram explaining the equilibrium output and price in the innovating region (region A) before and after introduction of an improved agricultural technology (12, 24), which increases yields and shifts the region’s supply curve (QS_A) to the right (to QS*_A). Price is determined in the world market by the intersection of the world supply (QS_W) and world demand (QD_W) curves. The world supply curve represents the horizontal summation of supplies in both region A and in the rest of the world (RoW), represented by the right panel. From this diagram, it is clear that the innovation in A will result in a lower world price (P_W falls to P*_W) and hence a reduction in RoW output and land use. It is this land-sparing impact of region A’s innovation in RoW that is often ignored in the case study-based literature (5). The impact of the innovation on land use in region A is ambiguous, because it is the net outcome of two competing forces. On the one hand, improved technology means fewer inputs are required to produce the same level of output. However, improved technology also lowers costs and induces an expansion in equilibrium output, as shown in the top leftmost portion of Fig. 1. Not only is the impact on land use in region A ambiguous, this regional ambiguity is inherited by the global change in land use, as will be shown later in our analytical solution of this model.

Fig. 1.

Three-panel diagrams depicting the impacts of an improvement in technology in region A on world price and output in the RoW. (Upper) Impact of an improvement in technology in region A alone. The TFP gain shifts supply in A to the right, thereby increasing global supply and depressing world price when taken alone. This outward supply shift depresses production in RoW, which doesn’t benefit from the new technology. A key factor in determining the impact on output and land use in region A is the slope of the excess demand curve (ED_A). (Lower) Impact of simultaneous shifts in world demand and regional supplies in A and in RoW. When the supply shift in A is combined with an outward shift in demand, as well as technological change in RoW, the impact on RoW cropland area is no longer clear cut.

Although the foregoing analysis appears straightforward, it is hardly this simple in practice, because supply in region A is not the only thing that is changing. Consider, for example, the historical period analyzed by Rudel et al. (19). During this period, global food demand was growing strongly due to the combination of population and income growth. This growth translated into an outward shift in global demand (QD_W to QD*_W in Fig. 1, Lower). There was also technological progress in crop production in nearly every region of the world (25). These innovations are represented by the outward shifts in supply in both region A and in RoW, resulting in the global price reduction shown in Fig. 1, Lower. Given the multiplicity of factors at work here, it is difficult to know what would have happened if technological progress in region A had not occurred or if it had been slower. For this, we need a formal model. Accordingly, we use the Simplified International Model of Prices Landuse and the Environment (SIMPLE) model of global agricultural land use (SI Text and Fig. S1) (26) to reexamine the historical record considered by Rudel et al. (19) and Ewers et al. (21), as well as to explore future Green Revolution scenarios. Importantly, this version of SIMPLE has been modified to allow for the segmentation of regional markets (Fig. S1), a point to which we will return below.

Results

The Historical Green Revolution Was Indeed Land and CO₂ Emissions Sparing Compared with a Counterfactual World Without These Agricultural Innovations.

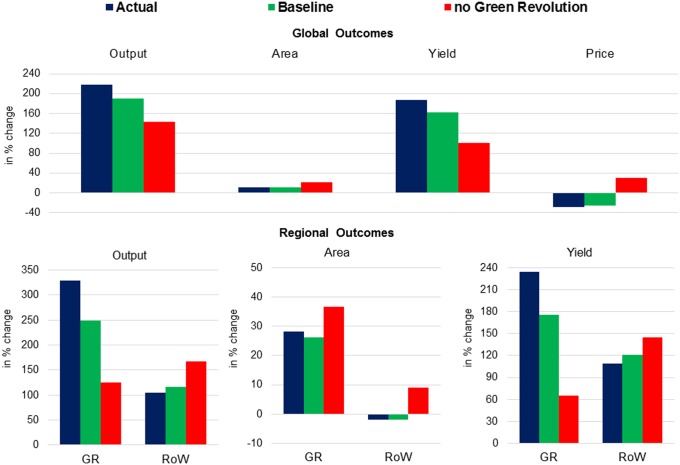
There was a remarkable increase (>200%) in global crop production over the 1961–2006 period as a result of the Green Revolution (Fig. 2, Upper, blue bars for observed global values). Most of this output expansion was achieved through higher yields especially in regions that experienced the Green Revolution. The expansion in cropland area was just 11%, and real crop prices fell by 29% over this historical period. The other important point to note is that both yields and area expanded in the Green Revolution region, whereas in the RoW, aggregate yields expanded and area remained essentially unchanged (Fig. 2: Lower, blue bars for observed regional values). These results are broadly consistent with the observation of Rudel et al. (19), who concluded that “rising yields and declining cultivated areas, does not generally characterize agricultural sectors between 1990 and 2005.” They suggested that this is evidence of technological change failing to be land sparing. However, they were not able to generate a counterfactual against which to consider what would have happened had the technological progress not occurred. This shortcoming motivates the use of SIMPLE to undertake the counterfactual analysis.

Fig. 2.

Observed and simulated changes in global and regional output, yield, cropland area, and prices over the historical period 1961–2006. The baseline simulation (green bar) reflects the presence of the historical Green Revolution in Asia, Latin America, and the Middle East. The counterfactual simulation (red bar) excludes TFP growth attributed to this Green Revolution.

The SIMPLE model’s historical baseline, in the presence of the GR scenario, reproduces output, yield, and price changes at the global level reasonably well (Fig. 2, Upper, green bars). We aggregate outcomes from the 15 regions in SIMPLE into the GR region and RoW, in keeping with Fig. 1. SIMPLE’s predicted yield and output growth in the Green Revolution region is lower than observed, suggesting that we are not capturing all of the complexity of these innovations in historical total factor productivity (TFP; the ratio of an output index to an index of land and nonland inputs) measure used in this model (27). However, overall, this model with segmented regional markets performs better over this historical period than the previous version which assumed integrated world markets (26).

With this historical baseline simulation in hand, we are now in a position to explore a counterfactual scenario that we dub the no Green Revolution (no-GR) scenario. In this case, technological progress in Asia, Latin America, and the Middle East is slower due to the absence of improved germplasm. Rather than crop TFP growing at an annual average rate of 1.6% in Asia and Latin America, it grows at just 0.5% in our counterfactual (12, 28). By subtracting the results of our counterfactual no-GR scenario (red bar in each group of Fig. 2) from the GR scenario (green bars), we obtain a model-based assessment of the impact of the Green Revolution on cropland use, yields, output, and global price over this historical period.

Results in Fig. 2 show that the Green Revolution causes land area in the affected region to be smaller than it would have been without the Green Revolution (26% with GR and 37% without GR). The growth in global output is also notably greater in the case of the Green Revolution. Rather than a reduction in global crop prices as observed in the historical GR baseline, the model simulates a 30% price increase over the 1961–2006 period under the no-GR counterfactual. RoW cropland use is much lower under the GR scenario (−2% with GR and +9% without); hence, we see from Fig. 2 (Upper) that the Green Revolution was indeed land sparing at the global scale compared with the no-GR counterfactual (11% global cropland increase with GR and 21% without GR). Furthermore, the error bars reported in Fig. S2 show that these land use deviations from baseline in the GR region, the RoW, and worldwide are all robust to variation in the SIMPLE model parameters (Tables S1 and S2).

We can also assess the impact of the GR on CO₂ emissions from land cover change. To do so, we multiply the land cover change predicted by SIMPLE by carbon emission factors per hectare estimated using yield and carbon loss estimates from West et al. (29) (SI Text). [Note that unlike Burney et al. (17), here we are only considering CO₂ emissions from land cover change, neglecting emissions from intensification, e.g., N₂O from fertilizer use. Burney et al. (17) found that differences in CO₂ emissions dominate the overall effect on greenhouse gases.] These results are also reported in Fig. S2 and show robust evidence of global CO₂ savings from the GR, with a mean reduction of ∼1,300 MMg. Both of these findings are consistent with the recent work of Stevenson et al. (12), who analyzed this question in the context of their comparative static simulation of a disaggregated global economic model of agriculture.

A Prospective African Green Revolution Would Also be Land and CO₂ Emissions Sparing if World Agricultural Markets Remain Segmented.

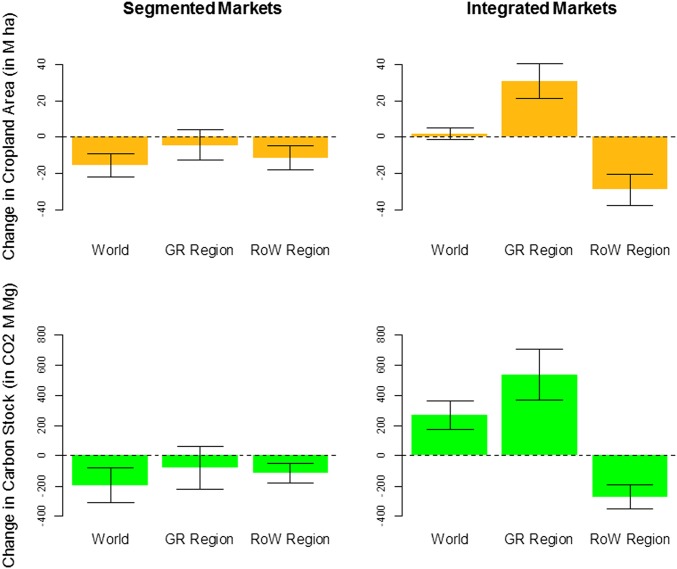
Given the lagging nature of yield growth in Africa, considerable new investment is flowing into research and development in this region, with the goal of launching an African Green Revolution. Such a development could yield significant benefits in terms of enhanced food security, increased rural incomes, and poverty reduction. If successful, will such an advance have a similarly beneficial impact on global land use and CO₂ emissions? To test this hypothesis, we perform two, forward-looking simulations using SIMPLE. In our baseline, we specify changes in population, income, biofuels, and TFP from 2006 to 2051 (Table S3) as described in Baldos and Hertel (30). Baseline TFP growth rates are slower than over the 1961–2006 period, as is expected in the face of higher temperatures and more variable rainfall (31). Our counterfactual simulation is one in which, beginning in 2025, African TFP grows at a higher rate commensurate with the Asian Green Revolution discussed previously. Differences in cropland area between the African Green Revolution and the baseline are reported in the upper left panel of Fig. 3. Error bars correspond to 95% CIs with respect to parameter uncertainty (SI Text). Here, we see that the mean changes in global land use and CO₂ emissions are negative (−16 Mha and −194 MMg) and once again statistically robust. However, unlike the historical Green Revolution, the reductions in land use and emissions in the innovating region (sub-Saharan Africa in this case) are no longer robust to parameter variation.

Fig. 3.

Sensitivity analysis of the regional and global cropland change and their corresponding carbon emissions given a future African Green Revolution under both segmented and integrated markets: difference between with vs. without Green Revolution TFP growth. Error bars reflect 95% CIs obtained from Monte Carlo analysis with respect to parameter uncertainty.

Our numerical simulations with SIMPLE provide the missing counterfactual analyses of the impact of the historical and prospective Green Revolutions on regional and global land use. However, they are necessarily limited, because the results depend not only on the behavioral parameters, but also on the state of the world and the characteristics of the affected region as well as the RoW. To investigate the land-sparing issue at a deeper level, we revert to a theoretical model. A key feature of this theoretical model will be the assumption of fully integrated world markets. This assumption contrasts with evidence that agricultural commodity markets were segmented as a result of high and variable trade barriers during much of the historical period (32). Thus, it is hardly surprising that the distribution of global production predicted by the SIMPLE model under segmented domestic, and international markets better approximates what was observed over the 1961–2006 period (26). However, the world economy is changing rapidly. One of the primary objectives of the Uruguay Round Agreement, which resulted in formation of the World Trade Organization in 1994, was to bring greater discipline to international agricultural trade, and there is evidence that distortions to agricultural trade are being dismantled (33). Therefore, it is of great interest to examine how these findings might be altered in the context of a more fully integrated global economy.

After appropriate condensation of the demand side, adding the assumption of fully integrated world markets and modest simplification of the supply side, the SIMPLE model can be condensed and solved analytically (SI Text and Table S4). In particular, we aggregate across all of the sources of crop demand, including biofuels, as well as direct consumption, input demands in livestock, and crop use in processed foods in each of the 15 model regions. This aggregation has no effect on model behavior and simply results in a single, global demand schedule, as shown in Fig. 1 (middle graph). On the supply side, we aggregate across countries within the GR and no-GR regions. The theoretical model also assumes that the price of nonland inputs is unaffected by the innovation (This assumption tends to exaggerate the potential for endogenous intensification.) With these simplifications, we can now obtain a general theoretical solution to the model expressed in terms of percentage changes in equilibrium prices and quantities as a function of the change in crop TFP (SI Text). The analytical model offers the following insights into the land-sparing nature of agricultural innovations.

Global TFP Growth in Agriculture Will Increase Land Use and CO₂ Emissions if and Only if the World Demand for Crops Responds Strongly to Changes in Price.

If we start by postulating a common rate of technological change worldwide (superscript W denotes global variables), then the percentage change in worldwide land use ($q_L^W$) given a 1% change in global TFP ($t^W$) is given by the following expression (see Table S4 for a full discussion of the terms in this expression):

$$q_L^W/t^W\mathrm{=}\left[{\epsilon }_D^W\mathrm{-}1\right]/\left\{1\mathrm{+}{\sigma }^W\left[\left(1/{\theta }_L^W\right)\mathrm{-}1\right]/\left({\nu }_L^W/{\theta }_L^W\right)\mathrm{+}{\epsilon }_D^W/\left({\nu }_L^W/{\theta }_L^W\right)\right\},$$ [1]

where ${\epsilon }_D^W\mathrm{>}0$ is the absolute value of the global price elasticity of demand for crops. We refer to this as the demand margin of price response. This unit-free measure describes the slope of the world demand schedule in Fig. 1, reporting the percentage change in global demand in response to a 1% change in price (Table S4). If it is greater than one, then demand is termed price elastic as the quantity response is larger than the price change (in percentage terms). The global price elasticity of demand depends on the responsiveness of both consumer demands and livestock and food processing demands for crops. The term ${\sigma }^W\left[\left(1/{\theta }_L^W\right)\mathrm{-}1\right]$ captures the potential for yield increases in response to higher crop prices (the intensive margin of supply response), wherein the parameter ${\sigma }^W$ describes the potential for substituting nonland for land inputs in crop production (elasticity of substitution) and ${\theta }_L^W\mathrm{<}1$ is the share of land in global production costs. The term $\left({\nu }_L^W/{\theta }_L^W\right)$ reflects the potential for cropland expansion given increases in crop prices (the extensive margin of supply response), wherein ${\nu }_L^W$ is the global supply elasticity of cropland. This term represents the percentage change in global cropland supply in response to a one percent change in cropland returns.

Eq. 1 confirms that TFP growth will cause land to expand if and only if world demand for crops is price elastic $\left({\epsilon }_D^W\mathrm{>}1\right)$. This point is well understood in the literature (5); however, our analytical expression offers additional insights. In particular, the magnitude of any expansion or contraction will depend on the cropland area response, the importance of land in total costs, and the potential for substitution of nonland inputs for land. We can say unambiguously that the larger the elasticity of substitution in production $\left({\sigma }^W\right)$, the more muted will be the global cropland area response to TFP growth. For large values of the intensification parameter relative to the price elasticity of demand (i.e., ${\sigma }^W\mathrm{\gg }{\epsilon }_D^W$, so the third term in the denominator is negligible relative to the second), we have the additional result that the land area response to TFP is diminished when the cost share of land in total crop production rises. Finally, note that the denominator in this expression hinges on the relative sizes of the intensive/extensive margins $\left\{{\sigma }^W\left[\left(1/{\theta }_L^W\right)\mathrm{-}1\right]/\left({\nu }_L^W/{\theta }_L^W\right)\right\}$ and the demand/extensive margins $\left[{\epsilon }_D^W/\left({\nu }_L^W/{\theta }_L^W\right)\right]$. As the extensive margin of supply response becomes relatively larger, the denominator in Eq. 1 shrinks and the entire right side of Eq. 1 becomes larger, so that more land will be converted in the wake of a given improvement in productivity.

Of course the focus of the land-sparing debate has been on asymmetric innovations, such as those shown in Fig. 1, Upper, which take us back to the two-region model, where the analysis becomes more nuanced. Eq. 2 gives the analytical expression for the percentage change in global land use in response to a 1% change in TFP in region A alone $\left(t^A\mathrm{>}0\right)$:

$$q_L^W/t^A\mathrm{=}\delta \left({\nu }_L^A/{\theta }_L^A\right)\left({\epsilon }_D^A\mathrm{-}1\right)/\left({\epsilon }_D^A\mathrm{+}{\epsilon }_S^A\right)\mathrm{+}\left(1\mathrm{-}\delta \right)\left({\nu }_L^R/{\theta }_L^R\right)\left(\mathrm{-}{\epsilon }_S^A\mathrm{-}1\right)/\left({\epsilon }_D^A\mathrm{+}{\epsilon }_S^A\right).$$ [2]

In this expression, $\delta$ denotes the share of global cropland area in region A, so $\left(1\mathrm{-}\delta \right)$ is the share of global cropland in RoW. Therefore, the percentage change in global land use is a weighted combination of the change in land use in the two regions. We also introduce a key concept, namely the excess demand elasticity facing region A: ${\epsilon }_D^A\mathrm{=}\left[{\epsilon }_D^W\mathrm{+}\left(1\mathrm{-}\alpha \right){\epsilon }_S^R\right]/\alpha$. This elasticity governs the slope of the $E{D}_A$ schedule in Fig. 1, and it is a central parameter in the two-region model. It reflects the fact that the demand facing region A’s suppliers is really a combination of the price responsiveness of world demand $\left({\epsilon }_D^W\right)$ and supply response in the RoW $\left({\epsilon }_S^R\right)$. In other words, when producers in region A become more productive and world prices fall, not only will global demand increase, but producers in RoW will reduce their production, thereby further accommodating the output expansion in region A. The slope of the excess demand curve depends critically on the relative share of region A in global production, parameterized here by $\alpha$. As $\alpha \mathrm{\to }0$, as would be the case if region A represented a single farm, the excess demand elasticity approaches infinity, implying that a single farmer cannot influence world markets.

Eq. 2 is also where the assumption of integrated markets comes into play. If instead, markets in A and RoW were segmented, the price changes in A would not be fully transmitted into RoW, therefore reducing the responsiveness of both demand and supply in RoW, resulting in a smaller value for ${\epsilon }_D^W$. This two-region analysis offers the following insight.

Jevon's Paradox is Most Likely to Arise When Global Food Demand is Price Responsive and Yields in the GR Region Are Relatively Low.

At this point, it is important to emphasize that it is not possible to say whether global land use change will be positive or negative following a productivity improvement in the affected region. The answer critically depends on the relative size of this region and its land supply response relative to the RoW. The sign of the second term on the right side of Eq. 2 is always negative, indicating that, in the face of the inevitable price decline owing to $t^A\mathrm{>}0$, land area in the rest of the world will decline (recall Fig. 1, Upper, right graph). The ambiguity in global land use arises due to the first term. In particular, a necessary condition for Jevon’s paradox, $\left(q_L^W/t^A\right)\mathrm{>}0$, is that the first term on the right side of Eq. 2 must be positive, and for this, we require an elastic excess demand facing region A, ${\epsilon }_D^A\mathrm{>}1$. However, this is not a sufficient condition for Jevons’ paradox. The first term must also be large enough to dominate the second one. This condition is more likely if, in addition to the elastic excess demand condition (which is likely to come from having a small share of global production: $\alpha \mathrm{\to }0$), region A simultaneously comprises a relatively large share of global cropland such that $\delta \mathrm{\to }1$. Of course, these two conditions can only coexist if yields are very low in the innovating region. In addition, if region A’s cropland supply response is relatively large, i.e., $\left({\nu }_L^A/{\theta }_L^A\right)\mathrm{\gg }\left({\nu }_L^R/{\theta }_L^R\right)$, Jevon’s paradox also becomes more likely. Finally, a larger intensive margin in RoW results in a greater contraction of output in that region and therefore more scope for the low-yielding innovating region to expand its area. However, it is not possible to say anything more precise about the conditions for global area expansion or contraction in this general case (SI Text).

Special cases yield more clear-cut predictions (SI Text). One that is particularly useful to discuss here is the case when both regions have the same supply response. Now the condition for Jevons’ paradox simplifies to

$${\epsilon }_D^W\mathrm{>}\left(Y^A/Y^W\right)\left({\epsilon }_S^W\mathrm{+}1\right)\mathrm{-}{\epsilon }_S^W\mathrm{\Rightarrow }\left(q_L^W/t^A\right)\mathrm{>}0,$$ [3]

where $\left(Y^A/Y^W\right)$ is the ratio of yields in region A to global yields. Therefore, the likelihood of global land area expanding in the face of innovation in region A increases when yields in the affected region are low, relative to the world average yields. The logic is as follows: (i) agricultural area in region RoW falls in the wake of the productivity improvement in A; (ii) the RoW area displaced by increased production in A will be smaller, and thus the smaller is this yield ratio (smaller right side in Eq. 3); and finally (iii) the larger the increase in global demand due to the resultant price decline (larger left side in Eq. 3), the greater the overall increase in global output that needs to be supported.

We can use this framework to shed further insight into the land-sparing nature of the Green Revolution. Table S5 summarizes the parameters underpinning Eq. 2 in the year 2006, aggregated from the 15 regions in SIMPLE to the level of the historical Green Revolution region and RoW. Relative yields in the historical GR region were 40% above the world average in 2006. Based on Eq. 3, this mitigates against Jevons’ paradox. Cropland area response is only about 80% of the world average, increasing the likelihood of TFP growth being land-sparing, based on Eq. 2. The excess demand elasticity (0.98) is also relatively low, again mitigating against Jevons’ paradox based on Eq. 1. Thus, it is no surprise that when we plug the aggregated parameters in Table S5 into Eq. 2, we find that $q_L^W/t^A$ = −0.26 < 0, and this single-equation prediction provides the same land-sparing result obtained from simulation of the full SIMPLE model albeit in the context of segmented markets.

In the Context of Integrated World Markets, an African Green Revolution Will Only Be Land Sparing if It Is Sustained over Several Decades.

The second set of parameters reported in Table S5 sheds light on potential impacts of an African Green Revolution in the context of fully integrated world markets. In particular, compared with the historical Green Revolution region, sub-Saharan Africa covers a smaller share of global cropland area (13%) but has a much stronger cropland area response to price (0.64 vs. 0.44 for the world) and exhibits yield and emissions efficiencies that are relatively low (just 69% and 50% of the global average, respectively). In light of Eq. 2, these factors suggest that an African Green Revolution has the potential to exhibit Jevons’ paradox. Indeed, if we plug the parameters from Table S5 into Eq. 2, we find that $q_L^W/t^A$ = 0.02 > 0, which suggests that the African Green Revolution would be not land sparing if implemented in 2006 in the presence of fully integrated world markets. We can also see from Eq. 2 why the African GR is land sparing in the presence of segmented markets. For Africa, the excess demand elasticity is <1 (0.74: see parenthetic entries in Table S5), thereby suggesting a land-sparing outcome when evaluated using Eq. 2, because both terms on the right side become negative in this case.

At this point in the theoretical analysis, we must introduce an additional complication: the fact that the parameters reported in Eq. 2 are in fact variables that will change as a result of economic growth, as well as a potential Green Revolution. The most obvious instance is that of relative yields. We expect this ratio to rise in the wake of an African GR. Indeed, we can use Eq. 2 to calculate the critical point at which (holding other variables constant) further productivity growth in the region would boost the yield ratio sufficiently to eventually change the sign in this expression. We find that the critical value for the yield ratio is 0.86, which would be achieved after ∼20 y of GR-induced productivity growth.

We can also return at this point to the SIMPLE model, only now assuming fully integrated world markets. As before, we start from the 2006 base and project the global economy forward, first under the baseline assumptions and subsequently assuming that the African GR commences in 2025 and persists through 2050. Results are reported in the right panel of Fig. 3. As anticipated by our theoretical model, the impact on global land use is ambiguous. However, given the insights offered by Eq. 3 and the preceding discussion, it is clear that the longer this GR persists, the more likely it is to become cumulatively land sparing.

In the Context of a Fully Integrated Agricultural Economy, the African Green Revolution Is Likely to Increase CO₂ Emissions from Cropland Cover Expansion.

Within the analytical framework laid out above, it is also possible to derive conditions analogous to Eqs. 1–3 that bear on the question of global CO₂ emissions from land conversion (SI Text). Indeed, the only difference is that, rather than relative yields driving the result (Eq. 3), the key metric is the emissions efficiency of region A, relative to the global value. Emissions efficiency refers to the yield per hectare of increased cropland, relative to the one-time carbon emissions associated with bringing that land into crop production. If this ratio is large in absolute value, then we say that the region has a high emissions efficiency. West et al. (29) calculated these emissions efficiencies (actually, they computed the inverse of our emissions efficiency measure) for a global grid and found that they are three times lower in the tropics compared with the temperate regions and are particularly low in sub-Saharan Africa. Indeed, the emissions efficiency in the sub-Saharan African region is just half of the world average (Table S5). This finding naturally raises a concern about whether an African Green Revolution would increase global CO₂ emissions. Because the remaining terms in Eqs. 1–3 are identical for the change in global emissions, we are left with a strong suspicion that this may indeed be the case.

The lower right panel in Fig. 3 reports the SIMPLE model simulated change in global CO₂ emissions owing to the African Green Revolution, in the presence of fully integrated world markets. From these results, the prospective African Green Revolution boosts CO₂ emissions in that region by enough to dominate the decline in RoW emissions from land use change. The error bars show this result to be robust to parameter uncertainty.

Discussion

The literature on the land use implications of technological change in agriculture has suffered from the absence of a unifying analytical framework and the associated absence of counterfactual scenarios in many studies. As with earlier studies (19), we verify that, indeed, over the 1961–2006 period, increasing yields were accompanied by increased cropland area in Green Revolution-affected regions. At first glance, this appears to be a refutation of the Borlaug hypothesis and an affirmation of Jevon’s paradox. However, once we consider the counterfactual scenario in which agricultural productivity in developing countries grew more slowly, due to the absence of the Green Revolution, we find more global land conversion relative to the real world case and not less. In other words, the historical Green Revolution did indeed spare land over this period compared with the counterfactual. Nonetheless, even in the counterfactual scenario, with slower productivity growth in the region no longer benefitting from the Green Revolution, cropland area and yields still both rise over the historical period. These results clearly demonstrate the fallacy in simply examining correlations between historical yield and area changes in the absence of a proper counterfactual.

When our framework is used to analyze the impacts of a prospective African Green Revolution, we find that, provided global crop markets remain segmented as they have been historically, this would also be land and emissions sparing. However, in the context of integrated global markets, we show that innovations will most likely fail to be land or emissions sparing when they occur in regions with relatively low yields, low emissions efficiencies, and high land supply elasticities. These conditions are precisely those that apply presently in sub-Saharan Africa. However, we do not take these results to imply that the world should refrain from investing in improved agricultural technology for Africa or that policies should limit the extent of market integration. To the contrary, any measures that boost relative yields in the region will eventually ensure that cropland area expansion in sub-Saharan Africa is also land sparing. In addition, measures to discourage conversion of carbon-rich ecosystems to low-yielding crop production will help to boost environmental efficiencies in the region, thereby ensuring that future land use change does not increase global CO₂ emissions.

Materials and Methods

In this paper, we use the SIMPLE model (26) (SI Text) to simulate cropland change over the historical period from 1961 to 2006. The 15 regions (Table S3) are aggregated into two regions for reporting: Green Revolution and Rest of the World (RoW). Each of the 15 regions consumes crops, livestock products, and other processed foods, with the demand characteristics varying by product and also by per capita income in the region. Crop production is based on the combination of land and nonland inputs in variable proportions. By increasing the intensity of nonland inputs per hectare, yields can be increased, given sufficient economic incentive. Production can also be expanded at the extensive margin by converting more cropland. The model is simulated over the 1961–2006 historical period by specifying exogenous changes in population and per capita income by demand region, as well as changes in TFP in crops, livestock, and processed foods production. As in Fig. 1, long run equilibrium is achieved when global crop supply equals demand, subject to the segmentation of regional markets that limits the transmission of global market prices into the domestic economy and therefore reduces the excess demand elasticity facing the innovating region.

There are several important limitations of our methodology (SI Text). First is the assumption that the impact of technological change is limited to the innovating region. What if all crop innovations were perfectly transferable? In this circumstance, innovation in any region A is automatically transferred to RoW, which takes us back to Eq. 1 in which the impact of the innovation is felt globally and the condition for Jevon’s paradox is price elastic global demand—an unlikely condition, given the evidence on consumer demand (34). A second limitation is that the counterfactual we have constructed has been limited to modifying TFP growth. In reality, agricultural innovations may also have influenced population and income growth, which we have kept fixed in our model experiments. Nevertheless we believe that the qualitative results and insights gained from this study are likely robust to alternate constructions of counterfactuals.