Motor coupling through lipid membranes enhances transport velocities for ensembles of myosin Va

Significance

Intracellular cargo transport is carried out by ensembles of cytoskeleton-based molecular motors, such as myosin Va. Physiologically, motor molecules are bound to (and mechanically coupled through) the vesicular membrane, which is a fluid lipid bilayer. Utilizing a combination of experiment and computer simulation, we characterize the influence of three distinct aspects of the vesicular ensemble (vesicle size, membrane composition, and motor density) on cargo transport. We also demonstrate the presence of vesicle populations that travel at velocities up to twice the unloaded velocity of a single motor. These findings serve to bridge the gap between enhanced vesicular velocities measured in vivo and depressed velocities measured in vitro.

Abstract

Myosin Va is an actin-based molecular motor responsible for transport and positioning of a wide array of intracellular cargoes. Although myosin Va motors have been well characterized at the single-molecule level, physiological transport is carried out by ensembles of motors. Studies that explore the behavior of ensembles of molecular motors have used nonphysiological cargoes such as DNA linkers or glass beads, which do not reproduce one key aspect of vesicular systems—the fluid intermotor coupling of biological lipid membranes. Using a system of defined synthetic lipid vesicles (100- to 650-nm diameter) composed of either 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) (fluid at room temperature) or 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) (gel at room temperature) with a range of surface densities of myosin Va motors (32–125 motors per μm²), we demonstrate that the velocity of vesicle transport by ensembles of myosin Va is sensitive to properties of the cargo. Gel-state DPPC vesicles bound with multiple motors travel at velocities equal to or less than vesicles with a single myosin Va (∼450 nm/s), whereas surprisingly, ensembles of myosin Va are able to transport fluid-state DOPC vesicles at velocities significantly faster (>700 nm/s) than a single motor. To explain these data, we developed a Monte Carlo simulation that suggests that these reductions in velocity can be attributed to two distinct mechanisms of intermotor interference (i.e., load-dependent modulation of stepping kinetics and binding-site exclusion), whereas faster transport velocities are consistent with a model wherein the normal stepping behavior of the myosin is supplemented by the preferential detachment of the trailing motor from the actin track.

Myosin Va is a processive, actin-based molecular motor critical for transport, morphology, and positioning of a wide variety of intracellular cargoes and organelles (1, 2). Although a single myosin Va can transport cargo in vitro, intracellular membrane-bound vesicular cargoes have a high surface density of motor proteins (3–5). Ensembles of motors that transport cargo in vitro have been shown to demonstrate enhanced run lengths (6–9) and slower movement, relative to the behavior of a single motor (6, 8–13). Slower velocities are generally attributed to negative interference between motors that arise when rigidly coupled, high duty ratio motors step asynchronously (12). The stepping kinetics of myosin Va are load sensitive, whereby resistive loads slow the stepping rate, whereas assistive loads produce only a modest acceleration (14–16). This asymmetric load dependence causes an overall slowing for a motor ensemble. Indicative of the complexity of the intracellular environment, Efremov et al. (17) have shown that physiological vesicle transport (whether microtubule- or actin-based) does not directly mirror the behavior of the responsible molecular motor but is sensitive to aspects of the cargo itself. In some microtubule-based transport systems, velocities faster than the capacity of the transporting motor have been observed in cells (18, 19). However, motion of the cytoskeletal track may contribute to this enhanced motion (20).

Most studies of in vitro cargo transport have a motor protein ensemble coupled to rigid cargoes such as quantum dots (Qdots) (8, 21), silica beads (12), DNA scaffolds (9, 22, 23), or directly to glass substrates (24). However, intracellular vesicles have fluid membranes that would be expected to allow the vesicle-attached motors (or coupled groups of motors) to diffuse within the membrane, so that motor ensemble transport of lipid-bound vesicles may be distinct from that observed with rigid cargo. Thus, more physiologically relevant studies have used liposomes (25) or isolated vesicles (26) with their in vivo complement of motors (26–28), or even intracellular organelles artificially coupled to a known motor type (17). Here, we attached recombinant myosin Va heavy meromyosin (myoVa) molecules at varying motor density to 100- to 650-nm lipid vesicles with membrane characteristics that were either fluid- or gel-like. When vesicles composed of fluid membranes are transported by an ensemble of myoVa molecules, they demonstrate velocities exceeding both those of identical vesicles transported by a single motor and those of individual, unloaded motors. Gel-like vesicles demonstrate velocities equal to or slower than a single motor. We developed a simulation of vesicular transport that supports at least one simple model wherein reductions in velocity can be attributed to two distinct mechanisms of intermotor interference (i.e., load-dependent modulation of stepping kinetics and binding-site exclusion), whereas enhanced transport velocities result from the concerted effects of myoVa’s stepping and the preferential detachment of the trailing motor in the ensemble from the actin track. This proposed bias in motor detachment and subsequent recentering of the vesicle above the remaining motors would generate an additional forward-directed displacement of the vesicle, providing the additional vesicular velocity. Therefore, we propose that the physical properties of the cargo itself contribute to the emergent transport behavior.

Results

Vesicle Size and Motor Number per Vesicle.

Vesicles of consistent sizes were prepared by a well-established technique in which rehydrated lipid preparations were extruded through filter membranes with defined pore sizes (29). Vesicle size distributions were measured in a flow cytometer by the method of Vorauer-Uhl et al. (30) (Fig. S1). We measured the distribution of vesicle diameters to be within 10% of the pore diameter over the range of 100–650 nm (Fig. S1 B–E). Throughout this manuscript, we refer to the resulting vesicle diameters according to the filter pore size used (i.e., 100-, 200-, 400-, and 650-nm diameters).

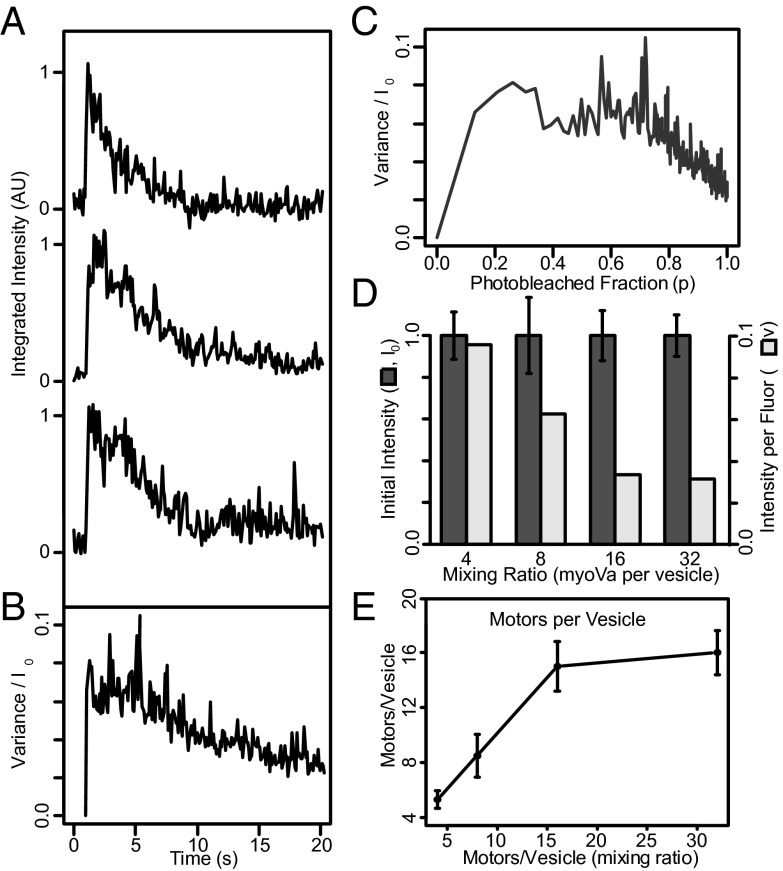
To quantitate the number of motors bound to a vesicle, we used the fluorescence photobleaching approach of Nayak and Rutenberg (31), which is appropriate for estimating the number of fluorescent molecules within a particle when counting individual photobleaching events is difficult. This statistical approach uses variations between photobleaching decay curves for a number of individual particles to estimate the number of fluorophores initially present (see SI Methods for details). For this purpose, nonfluorescent vesicles were mixed with myoVa molecules having an N-terminal YFP (i.e., two YFPs per motor) and a C-terminal biotin, in molar ratios ranging from 4 to 32 motors per vesicle. Fig. 1A shows the vesicle’s integrated fluorescence intensity as a function of time for three 200-nm 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) vesicles, prepared at a mixing ratio of eight myoVas per vesicle. These traces are normalized such that the average initial intensity, <I₀> = 1 and are temporally aligned to the step increases in fluorescence, which indicates the moment the vesicle landed on the glass surface within the total internal reflection fluorescence (TIRF) field. As individual YFPs photobleach, which cannot be resolved due to the large number of YFP (average of 16 YFPs per vesicle for this case), the fluorescence intensity decays to background. The variance between 295 such fluorescence decay curves vs. time is shown in Fig. 1B, which is then converted to variance vs. the photobleached fraction (p) (Fig. 1C), based on the time course of the exponential photobleaching decay. This relationship is bell shaped due to fluorescence intensity variance being minimal at the onset when YFPs have yet to photobleach and minimal once again as the fluorescence decay approaches background. In addition, by integrating the area under this relationship, the fluorescence intensity per YFP (v) (SI Methods) can be estimated (Fig. 1D, light bars). Thus, dividing the initial fluorescence intensity of each vesicle (I₀) (Fig. 1D, dark bars) by twice the calculated intensity per YFP, given two YFPs per myoVa molecule, provides an estimate of the number of myoVa per vesicle over the range of motor-to-vesicle mixing ratios (Fig. 1E). For 200-nm vesicles, the number of bound myoVa motors saturated at 16 and mixing ratios of 4, 8, and 16 myoVas per vesicle resulted in 5.0 ± 0.6, 8.4 ± 1.2, and 15.0 ± 1.4 myoVa molecules bound on average, respectively. For the remainder of this study, we refer to these as 200-nm vesicles having 5, 8, or 15 motors each, on average. A necessary assumption of this approach is that that all fluorophores are subjected to the same excitation intensity, a condition not normally satisfied in the evanescent field of TIRF illumination. However, in this case, the diffusive movement of fluorescent myoVa over the fluid vesicle surface (see below) is 5–6 orders of magnitude faster than the photobleaching rate (∼0.1 s⁻¹). Thus, the illumination intensity is effectively uniform between individual fluorophores during the time course of the experiment. Despite this, we found that this photobleaching approach could not be applied to the 400- and 650-nm vesicles, as their fluorescence intensity continued to increase for some time after landing, instead of following an exponential-like decay. Perhaps this is because these vesicles are much taller than the evanescent TIRF field, or perhaps an indication that these larger vesicles slowly become oblate as they adsorb onto the glass substrate, as shown by Nakano et al. (32). Therefore, for the experiments involving different diameter vesicles, we then relied on our motor number estimates from these 200-nm vesicles (see below).

Fig. 1.

Determination of the number of motors per vesicle. (A) Time courses of integrated fluorescence intensity for three representative 200-nm DOPC vesicles coupled to YFP-labeled myoVa at a mixing ratio of eight myoVas per vesicle. (B) Variance in normalized fluorescence intensity between photobleaching time courses for 295 vesicles. (C) Ensemble averaged variance normalized to initial intensity (σ²/I_o), vs. photobleached fraction [P = e^(−t/τ)]. See SI Methods for details. (D) Mean integrated initial intensity of 200-nm vesicles incubated with myoVa at molar ratios ranging from 4 to 32 motors per vesicle (dark bars; normalized to mean = 1.0). Error bars indicate SEM. The light bars indicate integrated intensity per fluorophore (v) (see SI Methods for details). (E) Resulting number of myoVa motor molecules per vesicle (assuming two YFPs per myoVa motor, i.e., one YFP per myoVa heavy chain).

MyoVa Ensembles Transport Vesicles over Distances Longer than a Single Motor.

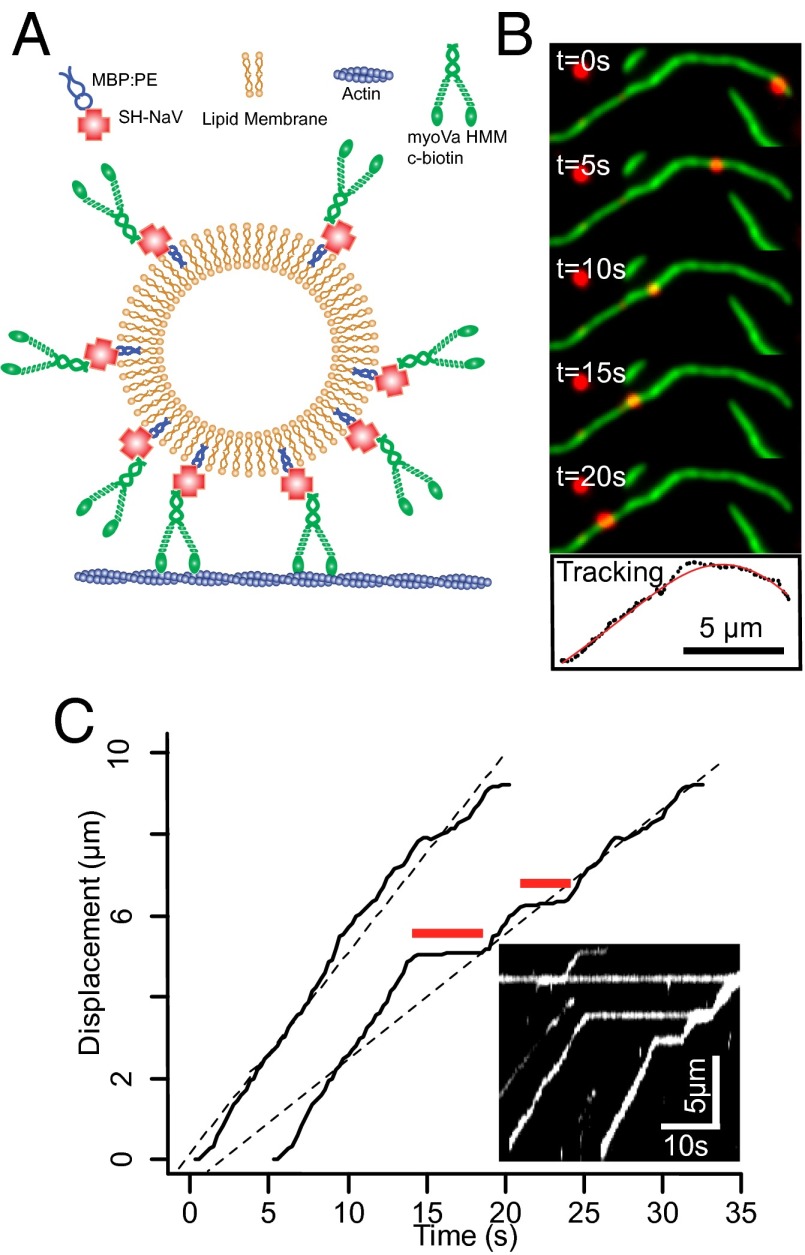
We characterized both individual motor and motor-based vesicular movement on fluorescently labeled actin filaments (Fig. 2 A and B); specifically focusing on how changes in the vesicle properties such as lipid composition (i.e., membrane fluidity), motor surface density, and size affected vesicle run length and velocity.

Fig. 2.

Vesicle model system, motility, tracking, and analysis. (A) Cartoon illustrating attachment of myoVa heavy meromyosin (HMM) molecules to phospholipid vesicles using SH-NaV. (B) Time-lapse of vesicle (red) moving on a single actin filament (green) in a flow cell. The lower panel shows X–Y tracking results (black dots) of the vesicle trajectory, shown with polynomial fit (red curve). (C) Displacement vs. time plot (right trace) demonstrates two “pause” periods (red lines) with an overall velocity of 366 nm/s (determined by regression; dashed black line). Removing the “paused” periods (left trace) yields a velocity (460 nm/s) that describes the periods during vesicle motion. Inset shows a kymograph of multiple vesicles traveling along the same actin filament and pausing at the same location.

During vesicular transport, many runs were interrupted by pauses that persisted for several seconds (Fig. 2C). The pause frequency (calculated as the number of pauses per second of vesicle trajectory) is independent of the vesicle properties, but larger vesicles pause for longer periods of time (P < 0.05; Fig. S2) as do gel-state 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) vesicles compared with fluid-like DOPC vesicles (P < 0.01; Fig. S2). Although the origin of these pauses remains unclear, we do not believe that these pauses are an emergent property of the vesicular ensemble. In fact, many vesicles have their forward motion obstructed by other stalled vesicles, which they then bypass after some time (Fig. 2C, Inset kymograph). Because these pauses would lower the overall average run velocity and were clearly distinguishable, we then excluded the paused periods so that velocity was determined strictly during periods of movement (Fig. 2C).

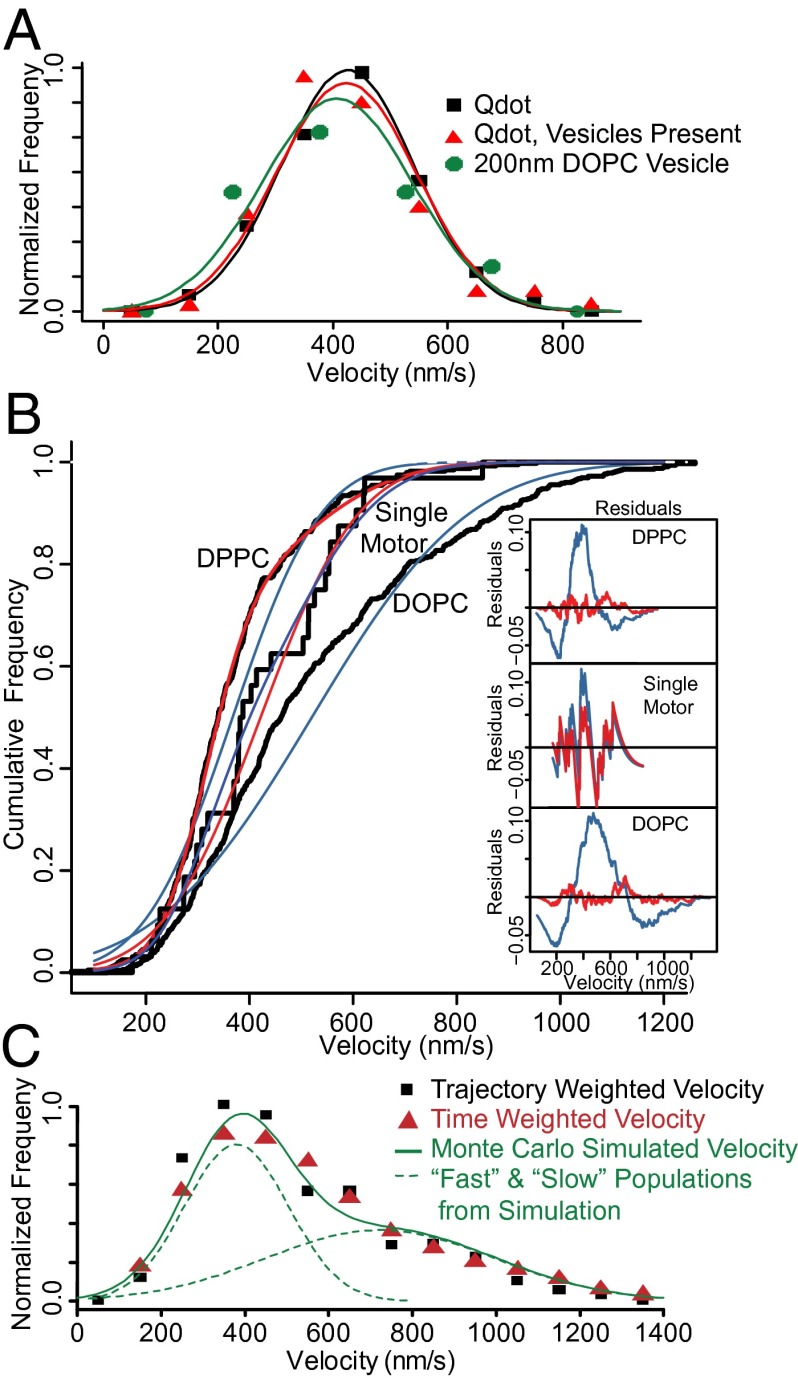
Initially, we established the velocity and run length of individual Qdot-labeled myoVa to be 426 ± 117 nm/s, and 1,716 ± 331 nm, respectively (n = 213). Both of these values were not perturbed (P > 0.05) by the presence of motor-free 200-nm DOPC vesicles in the flow cell, (velocity: 423 ± 122 nm/s; run length: 1,095 ± 390 nm; n = 107; Fig. 3A), indicating that the lipids themselves (or some other component of the preparation) do not perturb the behavior of individual myoVa molecules. To characterize the influence of a larger, vesicular cargo compared with a Qdot on the performance of a single myoVa molecule, we coupled limiting myoVa to 200-nm DOPC vesicles at a 1:4 myoVa-to-vesicle mixing ratio. Assuming Poisson probabilities of motor binding to the vesicles, 88% of vesicles that have motors bound should have only a single attached motor. For these vesicles, both the velocity (421 ± 151; n = 31) and run length (1,438 ± 831 nm) were no different (P > 0.05) than a Qdot-labeled motor (Fig. 3A and Fig. S3) and thus could be used as controls against which all vesicle movements could be compared.

Fig. 3.

Vesicle velocity distributions demonstrate two populations. (A) Velocity distributions are statistically indistinguishable (P > 0.05) for single Qdot-labeled myoVa (black), Qdot-labeled myoVa with 200-nm DOPC vesicles added to the motility buffer (red), and 200-nm DOPC vesicles coupled to a limiting amount of myoVa, such that the majority of vesicles are coupled to a single motor (green). (B) Cumulative frequency distributions demonstrate that the observed velocities of 200-nm DOPC vesicles coupled to a single myoVa molecule are well described as a single-Gaussian population (blue fit to black data), whereas with increased numbers of motors, both DOPC and DPPC vesicle populations (200-nm diameter; eight motors per vesicle) are much better described as the sum of two Gaussian populations (red curves, nearly obscuring black data) than a single Gaussian (blue curves). These fits are supported by the large residuals that result from fitting a single-Gaussian population (Insets, colored to match distributions; tic marks on vertical axis indicate increments of 0.1), and an LLRT (P < 0.001), which indicates that the two-Gaussian fit is appropriate for both vesicle compositions (P < 0.01), but not the single motor case (P > 0.05). (C) Velocity distributions for 200-nm DOPC vesicles with eight motors per vesicle are nearly identical regardless of whether they are calculated on a per-trajectory basis or a “time-weighted” basis, and yield nearly identical fitted values. The green curve indicates the velocity distribution generated by the Monte Carlo simulation of vesicle motility, as well as the two constituent Gaussian populations (dashed lines).

For all conditions tested, vesicles transported by an ensemble of myoVa motors demonstrated robust, long-range movement. On average, 64% of vesicle trajectories were limited by either the actin track length or the experimental recording duration, compared with only 18% for single-motor vesicular transport. Consequently, we used the Kaplan–Meier survival estimator (33) to approximate vesicle run lengths (Fig. S3). Except for the 200-nm diameter, DPPC (gel-state) vesicles with five motors per vesicle, which had a run length (886 ± 135 nm), no different from vesicles transported by a single, myoVa motor (Fig. S3), all other vesicle conditions (i.e., membrane fluidity, motor surface density, and size) resulted in mean estimated run lengths that on average were 2.2-fold longer than that of a vesicle transported by a single motor (Fig. S3).

Vesicle Lipid Composition Influences Transport Velocity.

To compare the effect of lipid composition on vesicle transport, we prepared 200-nm-diameter vesicles of either DOPC (fluid-state) or DPPC (gel-state), at a motor surface density of eight myoVa molecules per vesicle. The mean velocity of these ensemble transported gel-state DPPC vesicles (353 ± 117 nm/s; n = 397; Fig. 3B) was significantly slower (P < 0.001) than those transported by a single myoVa molecule (421 ± 151; n = 31), whereas the fluid-state DOPC vesicles (498 ± 222 nm/s; n = 710) were significantly faster (P < 0.001) than both the otherwise identical gel-state DPPC vesicles and DOPC vesicles transported by a single myoVa.

The velocity distribution for the faster fluid-state DOPC vesicles was characterized by many fast vesicles (≥750 nm/s) that were not observed for either single myoVa or gel-state DPPC vesicles (Fig. 3B). The DOPC velocity distribution was poorly fit as a single Gaussian, which normally describes a vesicle transported by a single myoVa motor (Fig. 3A), as evidenced by the large “wave” in the residuals plot (Fig. 3B, Inset, blue curve). The DOPC velocity distribution was better described [log-likelihood ratio test (LLRT), P < 0.001] as the sum of two Gaussian populations (Fig. 3B, Inset, red curve; Fig. S4): a “slow” population (53% of the total), slower than single motor transport, at 360 ± 100 nm/s and a “fast” population (47% of the total), faster than single motor transport, at 693 ± 223 nm/s. Similarly, the velocity distributions for gel-state DPPC vesicles were better described by two Gaussians (Fig. 3B and Fig. S4: slow: 314 ± 68 nm/s, 63% amplitude; fast: 459 ± 116 nm/s, 37% amplitude; LLRT, P < 0.001). For the gel-state DPPC vesicles, the slow population was once again slower than a single motor. However, the faster population moved at a velocity no different (P > 0.05) than vesicles transported by a single myoVa.

To show that the exceptionally fast DOPC vesicle population was not an artifact of “trajectory weighting” of transient fast velocity events, we also determined velocities using a “time-weighted” or “sliding-window” approach (1-s window, moved 0.25 s for each measurement). Using this approach, the faster population (≥750 nm/s) was again apparent and the overall velocity distribution well fitted by a nearly identical two-Gaussian model (LLRT, P < 0.001): slow: 319 ± 142 (63% of population); fast: 710 ± 270 nm/s (37% of population) (Fig. 3C). Thus, the exceedingly fast velocities were unique to fluid-state DOPC vesicles and were not an analysis artifact.

Finally, we noted that, for DOPC vesicles in particular, the SDs of the vesicular velocity distributions for ensemble transport were nearly double that of the single motor case (222 vs. 151 nm/s). To determine whether this is due to greater variation during individual trajectories or differences between trajectories, we determined the coefficient of variation of the velocity (CV) (defined as SD/mean) both between and within individual trajectories (measured with a 1-s-wide sliding window). For single, Qdot-labeled myoVa motors, the variance between trajectories (CV = 0.27; Fig. S5) is comparable to the variance occurring during individual trajectories (CV = 0.23). Although vesicles transported by motor ensemble demonstrated a similar amount of variation within trajectories, regardless of vesicle type (CV = 0.26 ± 0.03), the variation between trajectories was significantly greater (CV = 0.43 ± 0.10; Fig. S5). This indicates that the source of the additional variance is variability between vesicles, suggesting that some vesicles are inherently faster than others.

Velocity Decreases with Increased Motor Density.

To determine whether the difference in velocity between otherwise-identical fluid-state DOPC and gel-state DPPC vesicles could be attributed to differences in the number of engaged motors, we varied the mixing ratios for myoVa:vesicle conjugation, producing vesicles containing 5, 8, or 15 motors per 200-nm vesicle (Fig. 1E).

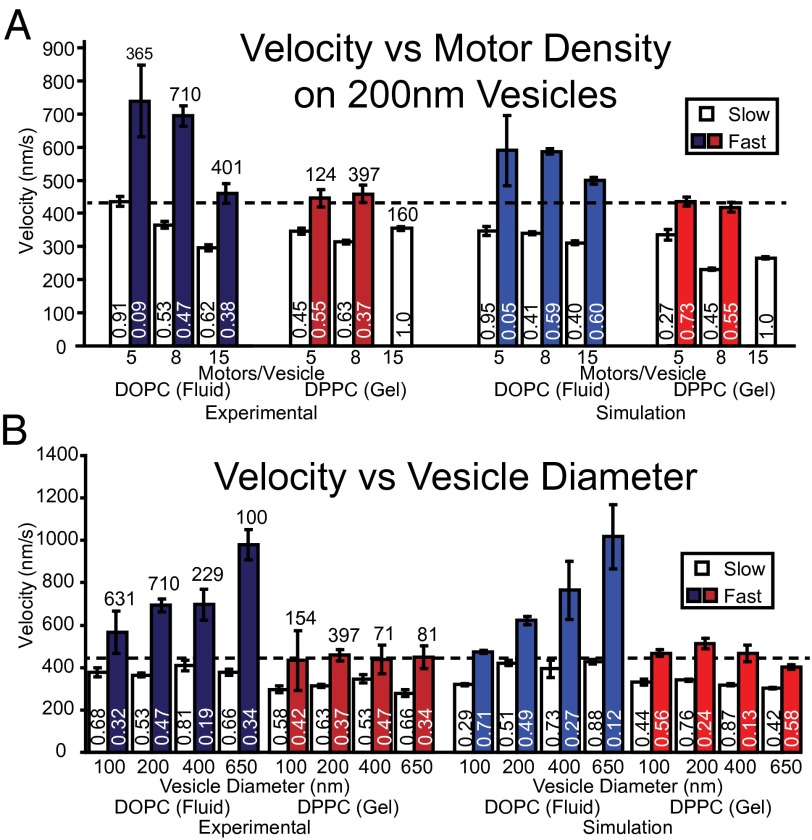
For the fluid-state DOPC vesicles with multiple motors, the velocity distributions were described by fast and slow velocity populations, although both populations slowed with increasing motor density (Fig. 4A). The fast velocity population was significantly faster (P < 0.001) than single-motor vesicular transport, even at the highest motor density (15 motors per vesicle; Fig. 4A). Whereas the slow velocity populations for the 200-nm DOPC vesicles were always slower than vesicles transported by a single motor, except for the least densely motor-populated vesicles (i.e., five motors per vesicle), which equaled that of a single motor (Fig. 4A).

Fig. 4.

Experimental and simulated velocities of fast and slow populations for vesicles of different composition, size, and motor density. Mean velocities for both fast and slow populations from both experiment (left side) and simulation (right side), as a function of motor density for 200-nm vesicles (A) and as a function of vesicle diameter keeping the motor surface density constant at 64 motors per µm² (B). Error bars indicate SEM. Total number of trajectories for each experimental condition is reported above the bars, whereas the relative proportions of the fast and slow populations are reported near the bottom of each bar. The horizontal dashed line indicates the velocity of a 200-nm DOPC vesicle transported by a single myoVa.

For gel-state DPPC vesicles, velocity distributions with five or eight motors per vesicle showed fast and slow velocity populations (Fig. 4A), with the fast population equal to that of a single motor (P > 0.05), whereas the slow populations were 22% slower (P < 0.001) on average than a single motor. When motor density was increased to 15 motors per vesicle, the velocity distribution was no longer best described by two populations but only a single population that was slower (P < 0.001) than single-motor transport by 16% (Fig. 4A).

Fluid-Like Vesicles Travel Faster with Increasing Vesicle Diameter.

The effect of vesicle diameter on velocity was investigated by preparing both fluid-state DOPC and gel-state DPPC vesicles by extrusion using filter membranes with pore diameters between 100 and 650 nm. Based upon vesicle sizes measured in Fig. S1 and our estimate of 8.4 motors per 200-nm vesicle (Fig. 1E), we attempted to keep the motor surface density for the various size vesicles equal to that of the 200-nm vesicles so that 100-nm vesicles would have 2 motors on average, 400-nm vesicles, 39 motors on average, and 650-nm vesicles, 81 motors on average. For fluid-state DOPC vesicles, velocity distributions were described by two populations for all diameters (Fig. 4B), with the slower velocity population (379 nm/s, averaged over all diameters) slower than single-motor transport and insensitive to vesicle diameter. However, the fast velocity population increased dramatically from 565 ± 135 nm/s for 100-nm vesicles to 980 ± 260 nm/s for 650-nm DOPC vesicles (Fig. 4B). In contrast, the gel-state DPPC vesicle velocities were described by two populations, both of which were insensitive to vesicle diameter (Fig. 4B). At all diameters, velocities for the DPPC slow population were on average 309 nm/s, 27% slower (P < 0.001) than single-motor transport. Interestingly, the DPPC fast population moved on average 444 nm/s across all diameters (Fig. 4B), which was not different (P > 0.05) than single-motor vesicle transport.

Supported Lipid Bilayers: Motor Diffusion Determined by Membrane Fluidity.

Are the differences in the fluid-state DOPC and gel-state DPPC transport characteristics related in some way to the motor diffusivity within the vesicle membrane? The theoretical framework of Saffman and Delbrück (34) as well as experimental evidence [e.g., Ramadurai et al. (35)] indicate that the diffusivity of membrane-anchored proteins is largely insensitive to the dimensions of the protein, but are largely governed by the diffusivity of the anchoring lipid within the membrane. Therefore, to characterize the influence of the membrane’s lipid composition on motors’ diffusional freedom, we constructed planar, supported lipid bilayers over glass using the same lipid compositions as for vesicles (Fig. 5A). We then used TIRF microscopy to image Qdot-labeled myoVa molecules that were anchored to these membranes. Single-particle tracking showed 2D Brownian motion for motor molecules attached to fluid-state DOPC membranes (Fig. 5B, Inset), with a diffusion constant of 0.92 ± 0.62 μm²/s (Fig. 5B) as characterized by mean-squared displacement analysis (36). Although work by Sonnleitner et al. (37) indicates that the presence of the rigid substrate may depresses the observed diffusivity in this geometry, relative to unsupported vesicular membranes, our measured value is nearly identical to fluorescence recovery after photobleaching measurements of freely diffusing fluorescent kinesin anchored to a single lipid in a DOPC unilamellar vesicle (38, 39). MyoVa motors attached to gel-state DPPC membranes showed a much lower diffusion constant of 0.0012 μm²/s (Fig. 5C), comparable to reports of the diffusivity of the individual lipids in a DPPC:cholesterol membrane (40).

Fig. 5.

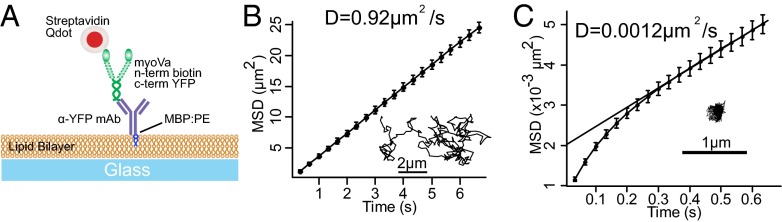
Lipid-anchored myoVas diffuse freely on DOPC membranes. (A) Cartoon illustrating experimental setup of planar supported lipid bilayers. (B) Mean-squared displacement (MSD) analysis and sample trajectory (Inset) of Qdot-labeled myoVa molecule diffusing in a DOPC membrane with an apparent diffusion coefficient, D, shown. However, motors tethered to a bilayer of gel-state DPPC (C) show minimal detectable movement.

Discussion

Intracellular vesicular cargoes are transported by ensembles of motor proteins that are coupled through the vesicular lipid membrane. Using synthetic vesicles transported by a myoVa ensemble, we demonstrate that vesicular transport is not merely a reflection of the motors’ capabilities but is influenced by aspects of the cargo itself, i.e., vesicle size and membrane fluidity, as well as the surface density of motors. When transported by multiple myoVa motors, gel-state DPPC vesicles move more slowly than vesicles driven by a single myoVa motor. Unexpectedly, populations of fluid-state DOPC vesicles attained velocities markedly greater than is observed for a single motor, regardless of its cargo. Because the basis for enhanced velocities was not intuitively obvious, we developed a “Monte Carlo-style” computer simulation to define potential mechanisms that govern myoVa ensemble vesicle transport.

MyoVa Ensembles Transport Vesicles with Slow and Fast Velocity Populations.

Velocity distributions of single myoVa molecules are characterized by a single-Gaussian population (41), regardless of the cargo or presence of lipids in the flow cell (Fig. 3A). However, when multiple motors are present on the cargo, velocity distributions become more complex (Figs. 3B and 4), which may relate to interactions between motor molecules attached to the same cargo. These vesicular velocity distributions were best described as a combination of two populations: one slower than and another equal to or faster than single motor transport, regardless of membrane fluidity, motor surface density, and vesicle size (Figs. 3B and 4). Transport velocities slower than a single, unloaded motor have been reported for ensembles of high duty ratio molecular motors, including myoVa (6, 8, 10–13, 17, 42). Two mechanisms that may slow such transport are (i) load-dependent modulation of motor stepping (43) and (ii) intermotor competition for binding sites on the actin track (8, 42).

Although viscous drag on the cargo may be significant for in vivo transport (24, 44), in the low-viscosity conditions of this study, drag on a 200-nm vesicle is insufficient to significantly alter the velocity of a single motor, compared with a motor carrying only a Qdot (Fig. 3A). This is not surprising, as the viscous drag of the cargo (using Stokes’ Law) is estimated at 0.5–5 fN, which is 2–3 orders of magnitude less than myoVa stall forces (14, 16, 45). A more likely explanation lies with the forces, which motors within the ensemble place on each other as the individual motors step asynchronously along the actin track. Each time a motor takes a step, the other engaged motors are pushed or pulled. Because resistive loads dramatically reduce myoVa’s stepping rate and assistive loads result in little to no change in the motors’ stepping (14–16, 43), the resultant overall stepping rate for a mechanically coupled myoVa ensemble should be slower than a single, unloaded motor.

A second mechanism for slowing transport may result from motor crowding along the track (i.e., “traffic jams”), leading to actin-binding site competition (6, 8, 10, 42). Under this scenario, an individual motor can have its forward step obstructed by another motor bound to the track (46), effectively limiting the stepping rate of the affected motor and, consequently, that of the entire ensemble.

Although load-dependent stepping and binding-site competition can slow vesicle transport, populations of ensemble transported, fluid-state DOPC vesicles exhibit velocities exceeding that of a vesicle transported by a single motor (Figs. 3 and 4). Our findings indicate that the lipids themselves do not directly perturb the transport properties of individual myoVa motors (Fig. 3A). Therefore, we propose that fluid DOPC membranes are able to mediate interactions between myoVa motors in a manner that gel-state DPPC membranes cannot that result in enhanced myoVa-driven vesicle transport velocities.

Model of Vesicle Transport by a MyoVa Ensemble.

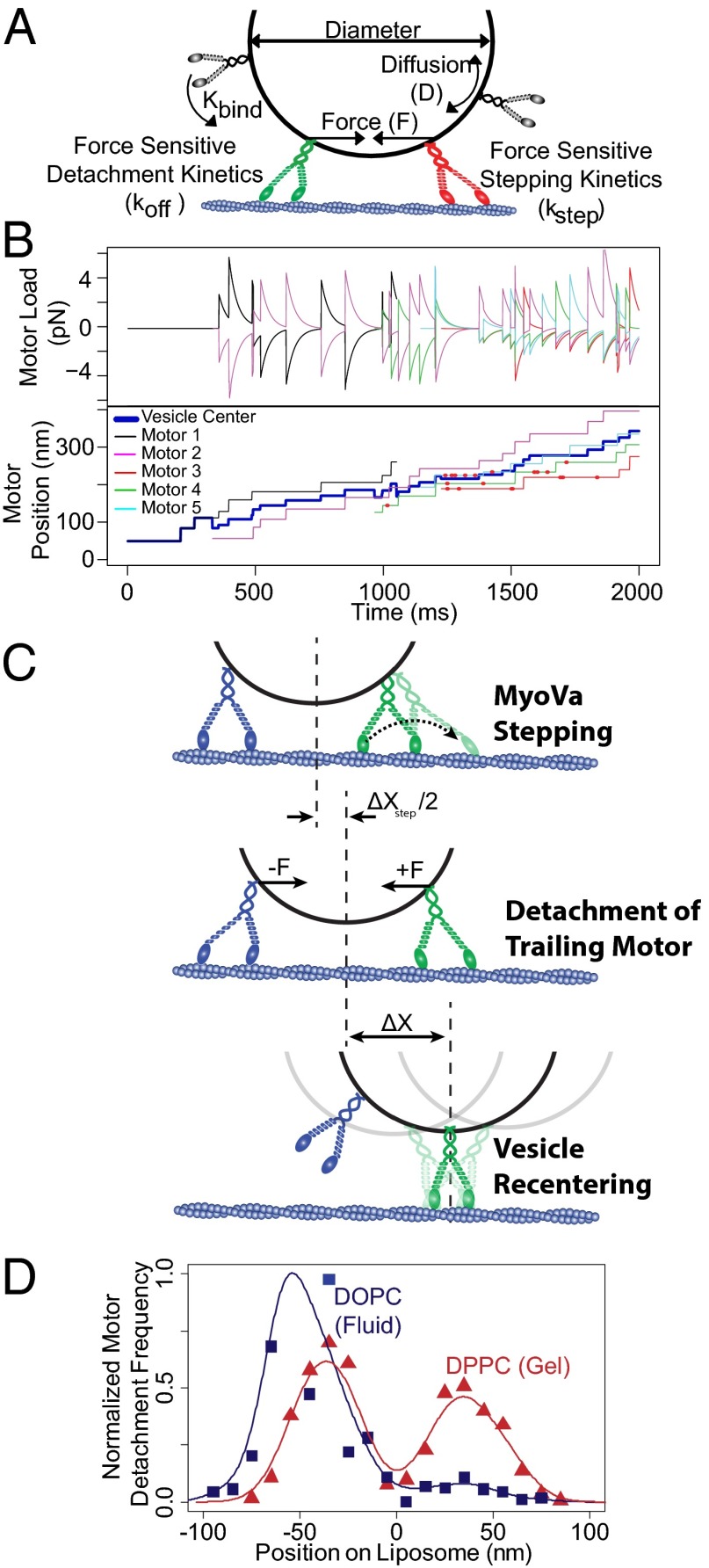
In an attempt to explain the underlying mechanisms that govern vesicle transport by a myoVa ensemble, we developed a simple Monte Carlo simulation (details in SI Methods and Fig. S6) to account for the effects of vesicle membrane fluidity, motor density, and size on vesicle transport. The model follows individual motors within an ensemble as they engage and step processively along the actin track. In doing so, the motor interacts with other engaged motors before detaching from the track (Fig. 6). Although our model is by no means exclusive, we find that other explanations involving perturbations of processive motor stepping dynamics to be less robust in terms of agreement with experimental data. The model incorporates primary data measured in this study in conjunction with literature values of biochemical rates and mechanical properties of single myoVa motors. In brief, the following assumptions and proposed mechanisms underlie the model’s predictive capacities (see SI Methods and Table S1 for model details and parameters): (i) myoVa motors at a given surface density (N) undergo Brownian motion within the vesicle membrane, with the diffusion constant (D) as we measured in the supported lipid bilayers experiments (Fig. 5). This diffusive motion allows the motor to encounter the actin track at a rate (k_bind), described mathematically as a 2D planar search following cell surface receptor:ligand interaction theory (47) as a first approximation, although a more complex 3D search could be considered. Although experimentally, we cannot rule out the possibility that multiple motors bind to the same NeutrAvidin (NaV) molecule, resulting in rigidly cross-linked ensembles on the vesicle surface, within this simulation we consider all motor molecules to be coupled only through the vesicle membrane. (ii) Actin-binding sites are limited to the motor due to (a) the actin filament’s helical structure and its presentation of discrete target zones (Fig. S7 and ref. 46), and (b) the vesicle behaving as a tethered particle, which at times will itself block available actin-binding sites (Fig. S7). (iii) Once the motor encounters a binding site, it binds at a rate, k_on (48), and then steps processively at a load-sensitive rate (k_step) with a step size of 36 ± 9 nm (14). (iv) Two motors cannot bind to the same actin site (i.e., binding-site exclusion distance, c), forcing an actin-bound motor to wait for its next preferential binding site to be vacated by the occupying motor. While waiting, the blocked motor may detach from the track dictated by its run termination rate (k_off), which is most sensitive to assistive loads following the relationship described by Vilfan (49). (v) As a motor attempts to step forward, it generates a positive force (F) that is resisted and shared by other motors in the ensemble (Fig. 6 A and B, Fig. S8, and SI Methods). The load each actin-engaged motor experiences is a function of the number of engaged motors and their spatial relationship on the actin track relative to the vesicle surface (43). These forces undergo relaxation as a simple viscoelastic material, which is due to the “sliding” of the motors’ attachment points through the lipid membrane. The rate of this relaxation is a function of the myosin’s stiffness and the membrane fluidity (Fig. 5 and SI Methods). However, this relaxation is limited by the geometry of the motors, vesicle and actin track, as forces that are perpendicular to the vesicle membrane cannot be relaxed in this manner. (vi) As a tethered particle, the vesicle spatially centers over the engaged motors (Fig. 6C). (vii) Vesicles are considered to be spherical under all conditions.

Fig. 6.

Monte Carlo simulation. (A) Cartoon illustrating interactions of myoVa motor molecules used for Monte Carlo simulation. (B) Representative trajectory of a 200-nm DPPC vesicle, indicating forces experienced by each actin-engaged motor (Upper, positive forces indicate resistive loads) and the spatial arrangement of each actin-engaged motor, as well as the vesicle center (Lower). The red dots indicate events where an attempted processive step was obstructed by the presence of another motor. (C) Cartoon illustrating the proposed mechanisms for enhanced vesicular transport velocity. Processive stepping of either attached motor (only lead motor stepping indicated in figure) results in net forward movement of the cargo. Intermotor forces cause an acceleration of detachment for the trailing motor. Upon trailing motor detachment, Brownian motion of the vesicle leads to a rapid recentering of the vesicle over the remaining bound motor(s), generating a net forward displacement (ΔX). As additional motors engage the track, the process is allowed to repeat. (D) Frequency of motor detachment relative to center position of the liposome. Motor detachment from the track is more frequent among trailing motors on fluid-state DOPC vesicles, whereas there is little detachment bias among leading and trailing motors on gel-state DPPC vesicles.

Modeled vesicle trajectories were Monte Carlo-simulated (Fig. 6B) with 1,000 trajectories generated for each vesicle condition and run lengths and velocities determined. In addition, information about each motor within the ensemble, i.e., its position as well as the direction and magnitude of load it experiences, were recorded and analyzed (Fig. 6B). Although the model does predict run lengths, comparison with the experimental run lengths that were limited by the actin track length and experimental recording time do not provide any insight to the model’s predictive capacity. Therefore, we will limit comparisons of the model predictions to vesicle velocities, which vary dramatically over the range of experimental conditions.

Modeling Emergent Vesicle Transport Properties.

For experimental conditions in which vesicle velocity distributions were described by both a slow and a fast population, the model recapitulated the significant range of observed velocities (Fig. 4 A and B), as well as vesicle conditions in which the velocity was best characterized as a single population (Fig. 4 A and B). The most striking outcome of these modeling efforts was the ability to predict vesicle velocities as much as 1.6-fold faster than single-motor vesicular transport. In both simulation and experiment, these fast velocities were only observed with multimotor fluid-state DOPC vesicles (Figs. 3B and 4). The simulation supports a model in which these enhanced velocities result from the concerted effects of myoVa’s stepping activity and a spatial bias in motor detachment at the vesicle’s trailing edge (Fig. 6D). In this scenario, rapid relaxation of intermotor forces in fluid-state DOPC membranes cause compressive forces (Fig. S8A) between motors to be relaxed very rapidly, whereas configurations that result in tension across the vesicle membrane can be sustained (Fig. S8B), as force vectors become more normal to the vesicle surface. As a result, motors at the leading edge of the vesicle experience predominantly resistive loads (resulting in reduced stepping rates), whereas trailing motors experience predominantly assistive loads (Fig. 6 A and B). Assistive loads slightly accelerate the motor’s stepping rate but more importantly are predicted to increase the motor’s detachment rate from the track as much as 10-fold (up to 4.6 ± 0.5 s⁻¹) (49). In the simulation, after motor detachment, the vesicle acts as a tethered particle and rapidly recenters over the remaining engaged motors (Fig. 6C). This provides an additional vesicle displacement (ΔX ∼ 40 nm) that is forward-biased and acts in concert with the myoVa’s processive stepping to give rise to enhanced vesicular velocities, which exceed the stepping velocity of single myoVa motors (Figs. 3B and 4). The simulation also suggests that this phenomenon is minimized in gel-state DPPC vesicles, as the slower relaxation of the membrane within the model allows sustained compressive forces on the membrane, meaning that not only do motors experience greater forces at any given time point, but forces can be in either the assistive and resistive directions, regardless of the motors’ location on the vesicle. Thus, the model suggests that there is no spatial bias in the location of motor detachment for gel-state DPPC vesicles (Fig. 6D).

Although the mechanisms that contribute to both the slowing and enhancement of vesicle velocities are prescribed within the model, the extent that each mechanism contributes under a given experimental condition vesicle is difficult to tease out. Turning off any of the three mechanisms proposed to alter ensemble transport velocities (load-dependant motor stepping, binding-site competition, or biased motor detachment) within the simulation results in poor predictive capacity across all of the various vesicle conditions studied (Fig. S9). Thus, the model predictions are emergent properties of the system, i.e., the vesicle, the motors, and the physical properties of the motor coupling via the vesicle membrane. However, the model does allow us to make predictions as to how each mechanism contributes to the broad range of velocities observed with changes in vesicle membrane fluidity, motor density, and vesicle size.

Simulations suggest that ensemble transport velocities below that of the single-motor case may result from a combination of both load-dependent modulation of motor stepping and competition between motors for actin-binding sites. In simulations of gel-state DPPC vesicles, track-engaged motors experience absolute time-averaged loads of ∼0.55 pN, which is fivefold greater than that experienced by engaged motors on simulated fluid-state DOPC vesicles (Fig. 7 C and D). Therefore, due to membrane fluidity alone, the motors on gel-state DPPC vesicles would be expected to experience higher resistive loads (Fig. 7 C and D), resulting in slower vesicle populations for the same experimental conditions (Fig. 7 G and H) compared with fluid-state DOPC vesicles (Fig. 4). However, the experimentally observed slow populations among fluid-state DOPC vesicles are slower than transport by a single motor by an average of 16%—an effect much greater than the 2% reduction in the myoVa stepping rate that would be anticipated, as a result of the 0.05- to 0.1-pN time-averaged absolute resistive loads that arise in the simulations (Fig. 7 C and D) (14–16, 45). Thus, the simulations suggest that steric blocking of actin-binding sites is the predominant factor that slows ensemble transport velocities among fluid-state DOPC vesicles (Fig. 7 C, D, G, and H).

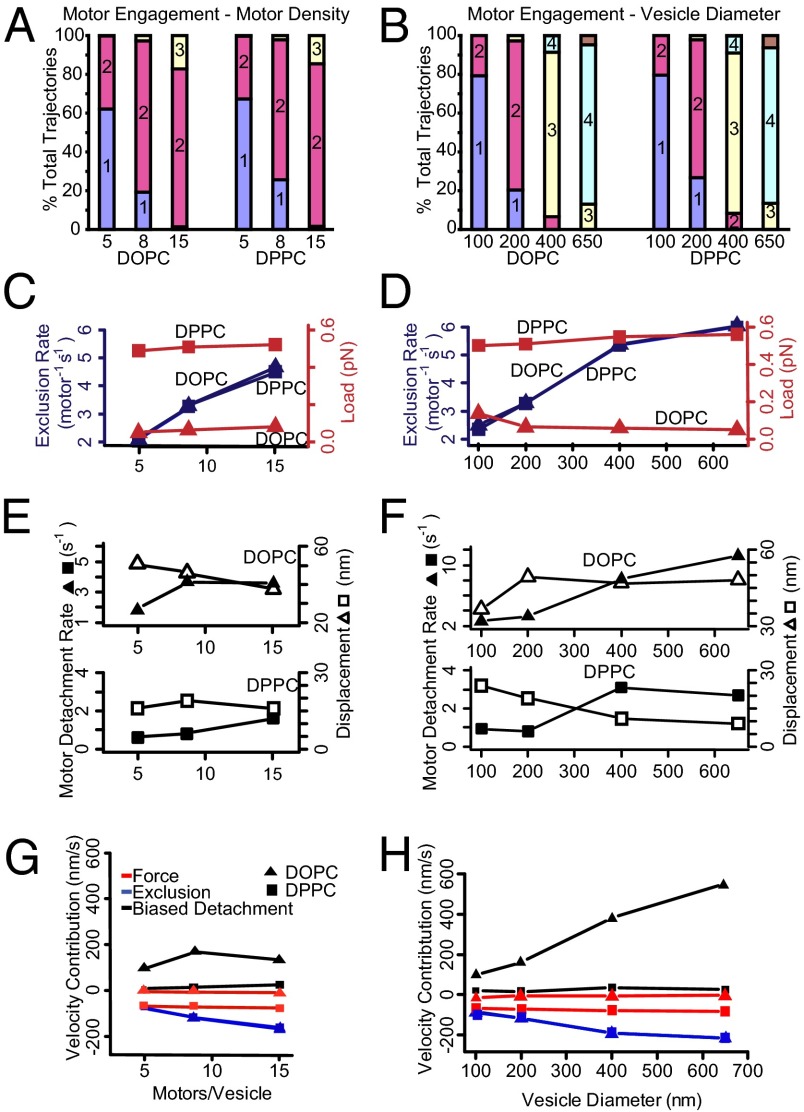
Fig. 7.

Model mechanisms that alter vesicle velocity. (A and B) Median motor engagement is predicted by the simulation on a per-trajectory basis and increases only slightly with increasing motor number and more so with increasing vesicle diameter. The colored bars indicate the proportion of trajectories that have a median number of engaged motors over the course of the trajectory. (C and D) Reductions in velocity are attributable to two main mechanisms—one load-based modulation of motor stepping rate and one based on obstruction of actin-binding sites so as to limit a motor’s forward step. For each vesicle condition simulated, the median absolute load experienced by each motor (red) is strongly influenced by vesicle composition, whereas the frequency of obstructed steps (blue) increases with both motor density and vesicle diameter. (E) The trailing motor detachment rate (closed symbols) is accelerated with increasing motor density on DOPC vesicles. However, the net vesicle movement upon trail motor detachment (ΔX, open symbols) decreases with motor density. Similar trends are predicted for DPPC vesicles but the absolute values are lower. (F) As in E, the trailing motor detachment rate (closed symbols) is dramatically accelerated with DOPC vesicle diameter. However, the net vesicle movement upon trailing motor detachment (ΔX, open symbols) remains nearly constant. Therefore, the enhancement of vesicle velocity for increasing DOPC vesicle diameters is governed by the trailing motor detachment rate (see H). The contribution of this effect is minimal for DPPC vesicles. (G and H) Predicted changes to vesicle velocities attributable solely due to biased detachment of trailing motors (black), load-based modulation of motors’ stepping kinetics (red), and actin-binding site exclusion of motor stepping (blue).

Effect of motor density.

Efremov et al. (17) reported that increasing the density of myoVa on the surface of endogenous peroxisomes (a membranous organelle) resulted in a shift toward faster transport velocities, approaching those of single, unloaded myoVa motors. Conversely, Shubeita et al. (50) found that increasing the density of kinesin motors resulted in a slight reduction in transport velocity of lipid droplets within a Drosophila embryo. Experimentally, we varied the motor surface density on 200-nm vesicles over a 15-fold range (i.e., 1 motor per vesicle to 15 motors per vesicle), a range that is comparable to reported physiological motor densities on intracellular organelles (3–5). Higher motor densities resulted in a shift toward slower transport velocities for both vesicle types, although the velocity distributions were quite different for the fluid-state DOPC vesicles compared with the gel-state DPPC vesicles (Fig. 4). Although, conceptually, this might be due to differences in the number of engaged motors for the two types of membrane fluidity, simulations suggest that fluid-state DOPC and gel-state DPPC vesicles demonstrate nearly identical degrees of motor engagement at each motor density (Fig. 7 A and B). Thus, the model suggests that motor engagement is limited by the geometry of the vesicle and the actin filament, and not the diffusive freedom of the motors on the vesicle surface. This would imply that differences in motor engagement are not responsible for differences between DOPC and DPPC vesicles.

To highlight the model’s predictive capacity, one of the more striking comparisons is the difference in the velocity distributions for fluid-state DOPC vs. gel-state DPPC vesicles with an estimated five motors per vesicle (Fig. 4 A and B). Simulations of both vesicle types showed a number of trajectories that averaged only a single engaged motor (Fig. 7A). If so, then trajectories with velocities equal to that of a single motor would be expected regardless of the membrane fluidity. This may explain the fast velocity population for the gel-like DPPC vesicles and the slow population for the fluid-like DOPC vesicles. For the remaining trajectories in these simulations that are able to (at least occasionally) engage an additional motor, membrane fluidity does affect vesicle velocity. For the gel-like DPPC vesicles, the experimentally observed slow population was 26% slower than the single-motor transport case (Fig. 4A). Interestingly, a similar 25% slowing was reported for two myoVa motors rigidly coupled through a DNA scaffold (23). Thus, mechanical interactions between motors may be the primary determinant of the slow velocities in gel-state DPPC vesicles. For the fluid-like DOPC vesicles, the fast population is nearly twofold faster than a single motor, in both simulated and experimental data. In the simulated trajectories, the enhanced velocity arises from the concerted effects of the myoVa’s stepping and our proposed biased detachment of the trailing motor and the subsequent recentering of the vesicle over the remaining engaged motor (Fig. 7 E and G). Interestingly, with increasing motor density, the fast velocity population of the fluid-state DOPC vesicles approaches the velocity of a single motor. Simulations indicate that this is not due to the presence of only a single engaged motor (Fig. 7A) but is due to offsetting effects of the velocity-enhancing (biased motor detachment) and -reducing (load-dependent stepping and binding-site competition) interactions (Fig. 7 G and H).

Simulations also suggest that heterogeneity in the number of motors conjugated to each vesicle within a preparation may be responsible for the presence of distinct fast and slow populations observed in each experimental condition, with the respective slow populations arising from vesicles with greater numbers of motors. However, we note the lack of a monotonic trend in the proportions of these populations in the experimental data (Fig. 4), suggesting that there may be other sources of heterogeneity in the experimental preparations.

Effect of vesicle size.

One of the most striking experimental findings is that increasing vesicle size dramatically increases the velocity of the fast population of fluid-state DOPC vesicles (Fig. 4B). This is different from the findings of Efremov et al. (17), who report that velocity of intracellular transport of peroxisomes by myoVa is insensitive to cargo size over a comparable range of diameters. Interestingly, Efremov et al. did observe a heavily-tailed velocity distribution for these organelles, reaching velocities as high as 1,500 nm/s, much faster than transport capabilities of a single myoVa motor (Fig. 3A), and similar to our findings. Within our model, these enhanced velocities arise from the concerted effects of myoVa’s processive stepping and biased detachment of trailing motors on DOPC vesicles. After motor detachment, the recentering of the vesicle over the remaining engaged motors results in a forward-biased movement of the vesicle. Simulations support the plausibility of this model, its exclusivity to fluid vesicles, and its sensitivity to both motor density and vesicle diameter. However, we point out that this does not preclude other potential models and explanations for these velocities, such as a bias in the location of where motors engage. Interestingly, our simulations suggest that the increased velocities with DOPC vesicle size results from an increase in the trailing motor detachment frequency, whereas the additional displacement (ΔX) upon vesicle recentering remains constant with vesicle size (Fig. 7 F and H), given that ΔX is dictated by the spacing between engaged motors, which should remain constant as the motor density was kept constant. We observed that vesicle size has no apparent effect on the velocity of gel-state DPPC vesicles, a finding reproduced by our simulation, wherein the number of engaged motors varied substantially. This model prediction suggests that this apparently emergent behavior results from a convolution of varying contributions of the mechanisms that slow (load-dependent stepping and binding-site competition) and enhance (biased motor detachment) ensemble transport within the model (Fig. 4B).

Conclusions

The experiments presented here demonstrate that cargo properties modulate the velocity of transport. Our modeling efforts suggest that this phenomenon can be explained by interactions between track-engaged myoVa motors and the modulation of these interactions by the cargo. Lu et al. (23) recently proposed a model based on data from two-coupled myoVa motors through a DNA scaffold. Their model does predict that coupling of motors through a fluid membrane would affect cargo velocities and that the velocities would be anticipated to increase with vesicle diameter over the range that we report here (100–650 nm) (23). Although our experimental findings support their anticipated trend, their predicted vesicle velocities do not exceed that of a single motor (23), an unexpected finding that we have reported here experimentally (Figs. 3 and 4). Although not necessarily exclusive of other explanations, we propose a model that attributes these enhanced velocities to the concerted effects of the myoVa’s stepping activity and a cargo-mediated biased detachment of the trailing motor. We have demonstrated the plausibility of this model using a Monte Carlo simulation (Fig. 4).

Our findings may help bridge the divide between enhanced velocities seen for physiological cargoes inside cells (18, 19) and the transport of artificial cargoes in vitro by motor ensembles (6–8, 10–13). Interestingly, velocity distributions for intracellular vesicle transport often show heavily tailed distributions that are well described as the sum of multiple, Gaussian populations (18, 19, 51), similar to what we now report in vitro. Physiologically, cells use myoVa and other molecular motors to position and transport a wide array of intracellular cargoes, ranging from single molecules of RNA to the very large membranous endoplasmic reticulum. Each of these cargoes has a distinct size, membrane composition (or no membrane at all), and density of motors. These aspects may act in concert to regulate motor engagement and activity to ensure the proper transport and positioning of these different cargoes within the cell.

Methods

Vesicle Preparation.

Synthetic lipid vesicles offer control over a number of variables including vesicle size, membrane composition, and motor surface density (Fig. 2A). Unilamellar lipid vesicles were formed as follows. Phospholipid vesicles were composed of either DOPC (Tm = −20 °C; fluid state at room temperature) or DPPC (Tm = 41 °C; gel state at room temperature). Vesicles were prepared through two sequential extrusion steps as described by Mayer et al. (52). Briefly, lipid mixtures in chloroform (Avanti Polar Lipids) were prepared with the following molar ratio: 84 parts phospholipid, 5 parts PEG-ylated phospholipid (either 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethylene glycol)-2000] or 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethylene glycol)-2000]—to match the phospholipid composition of the vesicle), 5 parts cholesterol, 5 parts 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-[4-(p-maleimidophenyl)butyramide] (MBP:PE), and 1 part 1,1′-dioctadecyl-3,3,3′3′-tetramethylindocarbocyanine perchlorate (DiI) (a fluorescent dye). Preparations were dried under a nitrogen stream, followed by 1 h under vacuum (Rotovap; Eppendorf). After rehydration with PBS (PBS: 137 mM NaCl, 2.7 mM KCl, 10 mM Na₂HPO₄, 2 mM N KH₂PO₄, pH 7.2) to a final lipid concentration of 5 mg/mL, vesicles were extruded for 20 passes through a 1-μm-pore diameter filter (Whatman) using an Avanti Mini-Extruder (Avanti Polar Lipids). Vesicles were then mixed with thiolated NeutrAvidin (SH-NaV) (1 μM final concentration; see below for preparation) and incubated at room temperature overnight, which allowed covalent conjugation between the maleimide moiety of the membrane constituent MBP:PE and the thiol groups of the SH-NaV (preparation described below). After overnight incubation, vesicles were pelleted by centrifugation at 420,000 × g for 10 min, and the pellet was washed twice with PBS to remove unbound SH-NaV. Washed vesicles were resuspended to 4.25 mg/mL in PBS and extruded 20 passes through an appropriate-sized filter (100-, 200-, 400-, or 650-nm pore diameter filters; Whatman), which determined the final vesicle diameter.

SH-NaV Preparation.

SH-NaV was prepared according to Hermanson (53). Briefly, protected thiol groups were covalently added to NaV (Invitrogen) through incubation with N-succinimidyl-S-acetylthioacetate (SATA) (Sigma-Aldrich; 13 μg/mL final concentration) for 30 min at room temperature. SATA-modified NaV was then purified using a desalting column (Quick Spin Protein Column; Roche Diagnostics). Thiol groups were deprotected with hydroxylamine (50 mM final concentration) for 2 h at room temperature, followed by gel filtration on Sephadex G-25 (Roche Diagnostics). Samples were stored in 100-μL aliquots at −20 °C.

MyoVa Protein and Vesicle:MyoVa Conjugation.

A mouse myoVa construct, truncated after amino acid 1098 to produce a double-headed HMM fragment, was tagged at either the N- or C- terminus with an 88-aa biotin ligase recognition sequence (54, 55). Using a Baculovirus/Sf9 cell system, the myosin heavy chain was coexpressed with calmodulin light chains that were mutated to be calcium insensitive (56). A C-terminal FLAG tag on the myosin heavy chain facilitated protein purification by affinity chromatography (56). For the photobleaching-based motor counting experiments, an alternative form of the construct was produced with a C-terminal biotin ligase sequence and an N-terminal YFP. Thus, each complete myoVa molecule has two YFPs.

MyoVa motor proteins were coupled to vesicles through binding of vesicle-bound SH-NaV to the C-terminal biotin on the myoVa protein. For example, 200-nm vesicles (11.3 nM; see below) were incubated with 90.4 nM myoVa protein (mixing ratio of eight motors per vesicle) for 5 min at room temperature before dilution to 5 pM vesicles (final) in AB-BSA buffer (25 mM imidiazole, 4 mM MgCl₂, 1 mM EGTA, 25 mM KCl, 10 mM DTT, 1 mg/mL BSA, 3.5 mg/mL glucose, 40 μg/mL glucose oxidase, 27 μg/mL catalase, 100 μg/mL creatine phosphokinase, 1 mM creatine phosphate) with 1 mM MgATP for motility analysis. To vary the motor density on vesicles, the myoVa concentration was varied between 45.2 and 180 nM (for 4–16 motors per vesicle). Based on a fluorescence photobleaching assay to determine the number of motors bound to the vesicle (see below; Fig. 1), 200-nm vesicles saturated at 16 motors per vesicle. For experiments with different vesicle diameters, motor concentration was held constant at 90.4 nM, and various-sized vesicles (100- to 650-nm diameter) were prepared by extrusion from a common preparation of 1-µm-diameter vesicles. This ensured a constant surface density of motor proteins.

Determination of Vesicle Size and Number of Bound Motors.

Vesicle size distributions were determined using flow cytometry (30). Briefly, green fluorescent latex beads of different sizes (100- to 1,100-nm diameter; Bangs Laboratories) were analyzed using a LSRII Analytical Cytometer (Becton Dickenson). A linear relationship existed between the particle volume and the height of the side-scatter signal (Fig. S1A). The standard curve was then used to relate the observed side-scatter measurements made for vesicle preparations to a corresponding vesicle volume and hence (assuming spherical vesicles) a diameter.

To determine the number of myoVa motors coupled to each vesicle, we used the fluorescence photobleaching-based approach described by Nayak and Rutenberg (31). A more detailed description of this method is provided in SI Methods.

Supported Lipid Bilayers.

Lipid bilayers on glass slides (Fig. 5A) were prepared according to Tamm and McConnell (57). Briefly, 100-nm-diameter vesicles were formed by extrusion according to the protocol described above. Glass slides (24 mm × 60 mm, No.1; Fisher Scientific) were cleaned in a 1% Liquinox solution in water for 10 min in a bath sonicator (Branson Ultrasonics). Slides were then rinsed extensively in ddH₂O and twice with ethanol. Slides were dried at 150 °C for 1 h, and then air plasma cleaned (Herrick Scientific Corporation) for 10 min. Flow cells were then built as previously described (58), and vesicle suspensions were introduced and allowed to deposit on the cleaned surface for 1 h at room temperature (for DOPC membranes) or 65 °C (for DPPC membranes) in a humidity-controlled chamber. The lipid bilayer formed as the vesicles adsorbed to the surface, burst, and coalesced. To attach myoVa motors to the bilayer (Fig. 2A), we used an alternate myoVa construct with an N-terminal biotin tag and a C-terminal YFP (described in ref. 54). In place of the SH-NaV linkage, we used an anti-GFP antibody with its free thiols (3E6; Sigma-Aldrich), thus allowing 655-nm emitting streptavidin-coated Qdots (Invitrogen) to label the motors at their N terminus for TIRF visualization. Diffusion constants of the Qdot-labeled motors within the bilayer membrane were calculated by mean-squared displacement analysis as described previously (36).

Motility Assay, Imaging, and Data Analysis.

Motility assays for both Qdot-labeled single myoVa molecules and vesicles were performed as described previously (59) in AB-BSA buffer (25 mM KCl, 25 mM imidazole, 1 mM EGTA, 4 mM MgCl₂, 10 mM DTT, 1 mg/mL BSA, 1 mM ATP) at room temperature (21–24 °C). Actin was prepared from chicken pectoralis according to Pardee and Spudich (60) and fluorescently labeled with tetramethylrhodamine B isothiocynate (TRITC) phalloidin (Invitrogen). Movies were collected using a customized Nikon TE2000U microscope equipped with a 1.49 PlanApo objective lens for through-the-objective TIRF illumination, using an argon ion laser (model 163; Spectra Physics) illuminating at either 488 or 514 nm, and a CCD camera (model Turbo 620G; Stanford Photonics) equipped with an image intensifier (model VS4-1845; Video Scope International). Movies were recorded at four frames per second.

Image analysis was performed using ImageJ (version 1.46a) (61). Vesicles were tracked using the ImageJ plugin MTrackJ (62) with cursor snapping to the bright centroid over a 9 × 9 pixel box. Tracks were analyzed using custom-written software according to the following methodology: (i) X–Y coordinates for each track were fitted by regression with a fifth-order polynomial to compensate for track curvature and to minimize off-axis tracking errors (Fig. 2B); (ii) vesicle displacement was determined along the track’s fitted contour length; (iii) using a 1-s-wide (four-frame) sliding window along the displacement vs. time traces, periods of velocity below a 50 nm/s cutoff threshold were identified as pauses (Fig. 2C) and omitted from the displacement vs. time trace for the determination of overall velocity; (iv) finally, velocity was determined by linear regression through pause-free displacement vs. time data (Fig. 2C). Pause frequency was calculated by dividing the number of pauses by the total tracking time for each condition, whereas pause lifetimes were calculated by fitting a single exponential to the lifetime distributions using maximum likelihood.

Run length distributions were fitted using the Kaplan–Meier survival estimator approach (33) (Fig. S3), which is a robust method for estimating run length when a significant number of runs reached the end of the actin track rather than terminating by normally dissociating from the track. To avoid issues that arise from histogram binning, all distributions were fitted using a maximum-likelihood approach implemented in the statistical programming language “R” (63). Normally distributed datasets are reported as mean ± SD, and statistical comparisons were performed using a Student t test. Other distributions are reported as median ± 95% confidence interval and were compared using the Kolmogorov–Smirnov test. Pause lifetimes are compared by parametric survival regression, with the assumption that pause lifetimes were exponentially distributed. The appropriateness of fitting multiple Gaussians to velocity histograms was determined using a log-likelihood ratio test (LLRT), which determines whether the improvement of the fit is significant and not due to “overfitting” the data with additional degrees of freedom present in the double-Gaussian model.