Predicting species’ range limits from functional traits for the tree flora of North America

Significance

A species’ climate niche summarizes the observed climatic conditions at its range limits. This information can be used to predict range shifts of species under climate change, but it does not explain why they occur under a given climate or are absent from another. Functional traits associated with the climate niche, however, allow for such an explanation. We show that key plant functional traits predict the climate ranges of North American trees and discuss the underlying filter mechanisms that define “no-go areas” for specific trait expressions. This approach replaces species idiosyncrasy by the generality of traits, puts biogeography on more functional grounds, and yields products that will serve the improvement of next generation global vegetation models.

Abstract

Using functional traits to explain species’ range limits is a promising approach in functional biogeography. It replaces the idiosyncrasy of species-specific climate ranges with a generic trait-based predictive framework. In addition, it has the potential to shed light on specific filter mechanisms creating large-scale vegetation patterns. However, its application to a continental flora, spanning large climate gradients, has been hampered by a lack of trait data. Here, we explore whether five key plant functional traits (seed mass, wood density, specific leaf area (SLA), maximum height, and longevity of a tree)—indicative of life history, mechanical, and physiological adaptations—explain the climate ranges of 250 North American tree species distributed from the boreal to the subtropics. Although the relationship between traits and the median climate across a species range is weak, quantile regressions revealed strong effects on range limits. Wood density and seed mass were strongly related to the lower but not upper temperature range limits of species. Maximum height affects the species range limits in both dry and humid climates, whereas SLA and longevity do not show clear relationships. These results allow the definition and delineation of climatic “no-go areas” for North American tree species based on key traits. As some of these key traits serve as important parameters in recent vegetation models, the implementation of trait-based climatic constraints has the potential to predict both range shifts and ecosystem consequences on a more functional basis. Moreover, for future trait-based vegetation models our results provide a benchmark for model evaluation.

In 1895 the Danish plant ecologist Eugen Warming defined for the first time the objectives of a functional plant biogeography, when he expressed the need “to investigate the problems concerning the economy of plants, the demands that they make on their environment, and the means that they use to use the surrounding conditions….” He already envisioned how to tackle this: “This subject leads us into deep morphological, anatomical, and physiological investigations; […] it is very difficult, yet very alluring; but only in few cases can its problems be satisfactorily solved at the present time” (1).

Since Warming’s days plant science has progressed beyond the study of just a “few cases.” For more than a century now, botanists and plant ecologists have collected data on morphological, anatomical, and physiological traits (2, 3), and have mapped the distributions of tens of thousands of plant species (e.g., Global Biodiversity Information Facility, www.gbif.org). In addition, climatologists and soil scientists have provided us with high-resolution global maps of the plant’s surrounding condition. With this it has now become feasible to analyze the functional underpinnings of plant distributions for entire regional floras across large-scale environmental gradients (4). It is well established that on regional and global scales, climate determines the distribution not only of plant species but also of form and function (5, 6) because it constitutes the overall physical constraint under which plants must establish and reproduce, before biotic interactions may modulate plant fitness. Plants have evolved a multitude of adaptations to climatic constraints, which are expressed in the diversity of their functional traits. These allow them to tolerate climate extremes such as summer drought or low winter temperatures. In other words, the climate range occupied by plants should be predictable from their functional traits.

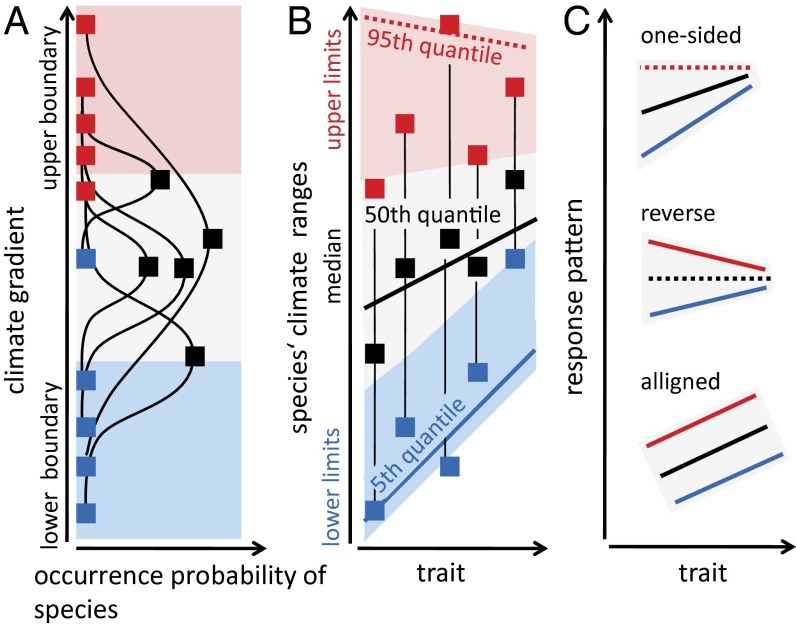
Current species distribution models (SDMs) (7) use correlations between current climate and species distributions, so-called climate envelopes. Even modern dynamic global vegetation models (DGVMs) (8) capable of representing carbon acquisition, water balance, and competitive interactions of plant functional types (PFTs) in great mechanistic detail, still incorporate empirical climate envelopes to constrain PFT distributions. This obvious lack of mechanism is an important limitation when such models are used to predict vegetation shifts under future climate scenarios, especially under novel combinations of climate variables (8). Here, we introduce a unique approach—the “double quantile” approach (Fig. 1 and see Linking Traits to Climate Ranges)—that allows us to predict species distribution limits from functional plant traits. Although still empirical at heart, this approach has distinct advantages: (i) The very nature of the traits emerging as suitable predictors of species distribution limits sheds light on the biological mechanisms. Accordingly, below we are able to put forward concrete hypotheses of the biological underpinnings of trait–climate limit relationships. (ii) Functional traits serve as a common currency across species and thus provide the basis for assimilating the behavior of many species into a single generic predictive framework. (iii) Because this approach replaces idiosyncrasy by generality, the handshake with process-oriented models is greatly facilitated as will be discussed below.

Fig. 1.

(A) Species are distributed along climatic gradients and occupy species-specific climate ranges, which can be characterized by three measures: the upper limit (red squares), the lower limit (blue squares), and the median (black squares) for which the highest species’ occurrence probability is suggested. (B) To explore the response of the climate range measures to traits, we related them separately against the traits using linear quantile regression analysis. We estimated the upper quantiles for the upper limits, the lower quantiles for the lower limits, and the median quantile for the median; a solid line indicates a slope significantly different from zero (increasing or decreasing) and a dotted line represents a nonsignificant slope. The area between the outermost regression lines represents the possible climate range species can occupy across their trait values whereas areas outside these lines describe no-go areas. (C) We distinguish three types of response patterns: (i) one-sided constraint, i.e., significant slope at only one limit (the upper or the lower one); (ii) two-sided constraint with reverse slopes at both limits; and (iii) constant shift with aligned slopes at both limits.

Here, we explore the potential of five functional traits—specific leaf area (SLA), wood density, maximum height, seed mass, and tree longevity—to explain the climate range limits and mean climate preferences of 250 North American tree species covering a temperature gradient from the boreal to the subtropics and a gradient from 65 to 3,000 mm of annual precipitation. Although there has been a first attempt to incorporate trait information in SDMs (9), we present here a unique study using plant functional traits to predict their limiting effect on species’ climate ranges at a taxonomic and climatic scale relevant for DGVMs. We chose to present the relationship between traits and species climate range limits from a trait perspective to highlight their potential for predicting species’ climate niches as a holistic measure of plant performance in response to climate. Unlike previous studies, our double quantile approach places an emphasis on the responses of species-specific climate ranges at the potentially stressful ends of climate gradients, where strong effects of functional traits on range limits can be expected.

Functional Traits: Selection and Relevance.

The five traits represent key functions defining plant strategy axes related to the fundamental tradeoffs of resource acquisition and reproduction (10, 11) and are thus indicative of life history, mechanical, and physiological mechanisms. Furthermore, some of these traits are frequently used as parameters in DGVMs (2). Because these traits vary across climatic gradients (12, 13), they are ideally suited to gain insight into processes shaping tree distributions at continental scales and at the same time to improve predictions on ecosystem functions under climate change. SLA is a key trait of the leaf economic spectrum (14) and defines a species’ resource use strategy from acquisitive to conservative. It is related to growth rate under different climatic conditions (15) and reflects tradeoffs in species’ shade and drought tolerances (16). Wood density is related to the efficiency and safety of water transport (17) and represents a tradeoff between mechanical strength and vertical growth. It is strongly correlated with growth and mortality rates (12). Maximum height describes the maximum recorded height of a species and quantifies species’ carbon gain strategy via light capture (18); it is related to successional status, shade tolerance and responds to gradients in precipitation on a global scale (19). Seed mass correlates positively with seedling survival rates under hazardous conditions during seedling establishment (11) and negatively with dispersal distance and the number of seeds produced per unit energy invested (20). Maximum tree longevity determines species responses to disturbance (21), compensates for reduced fecundity or juvenile survival (22), and relates to defensive investment (23).

Linking Traits to Climate Ranges.

We derive a tree species’ climate range from its natural geographic distribution (24). We use a set of eight bioclimatic variables (Methods) which represent dominant climatic gradients over North America and are widely used in climatic niche modeling (7, 25). To define a species’ climate range (Fig. 1A) we estimate for each bioclimatic variable the lower (5th quantile) and upper limits (95th quantile) and the median (50th quantile) across a species’ distribution range. Using linear quantile regression analysis (26), we regress across all species the three species-specific range measures against each of the five traits separately estimating the lower (10th, 5th), the upper (90th, 95th) and median (50th) regression quantiles, respectively (Fig. 1B). Thus, the 50th quantile regression lines fit to the medians (black line and squares in Fig. 1B) and describe how the mean realized climate niche depends on the trait values. The lower and upper quantile regression lines fit to the lower and upper limits (blue line and squares and red line and squares, respectively). In this double quantile approach, the outer regression lines enclose an area corresponding to the climate range the pool of 250 North American tree species can occupy across the range of their trait values (Fig. 1B). At the same time it identifies “no-go areas” which cannot be occupied by trees with a given trait value. The delineated areas can attain three possible shapes: (i) the area is wedge-shaped when there is a one-sided constraint, i.e., only one outer quantile represents a climatic extreme requiring a trait adaptation. (ii) The area has the form of an acute-angled triangle, when there is a two-sided constraint leading to reverse responses of the outer quantiles. Both triangular shapes, i and ii, imply that the possible climate range of the species pool changes with a given trait value (see Fig. 1C for examples). (iii) The area can have a rhomboid shape when the two-sided constraints are aligned. This implies a shift in the mean climate preference, but no change in the potential climate range per trait value.

Results and Discussion

Patterns of Trait–Climate Range Relationships.

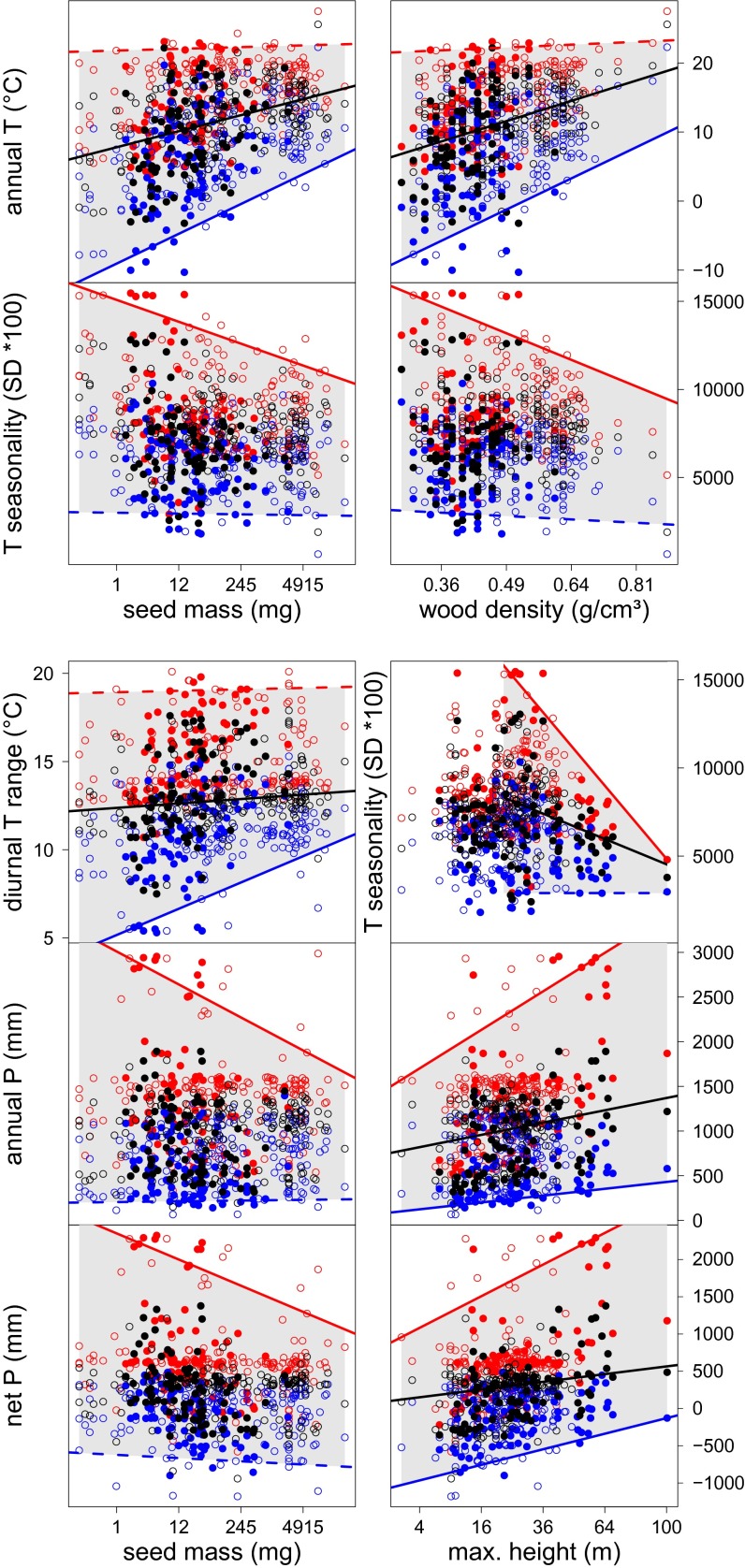
Few significant relationships between functional traits and the median realized climate niche of North American tree species emerge. However, we find strong limiting effects of functional traits on climate range limits estimated as significant upper and/or lower quantile regressions (Fig. 2, Fig. S1, and Table S1). The most obvious (see Methods for nomenclature) and dominant response patterns are one sided but we also find significant aligned patterns as well as less pronounced reverse patterns (Fig. S1). Moreover, there is a clear association between the functional traits and particular response patterns: (i) pronounced one-sided patterns are found for wood density (for 2 of 8 bioclimatic variables) and seed mass (6 of 8) suggesting an adaptation to harsh climates (e.g., cold and dry). This would indicate a strong climate control at the harsh end but not at the rather benign end where biotic control is suggested; (ii) primarily aligned patterns are found for maximum height (3 of 8) suggesting an adaptation to both climatic extremes. This might be an indication of a joint operation of climate control and biotic sorting processes (see also below); and (iii) no obvious responses are found for SLA and longevity, indicating no climate control. It should be noted that the geographical area of North America fully samples the tree species distribution limits toward dry and cold climates, whereas it truncates the distributions toward warmer and moister climates in the tropics. Because of this, the observed patterns might change if the region of interest was extended toward the tropics with datasets that are likely to emerge in the near future (e.g., one-sided may turn into aligned or reverse patterns). In the following, we will structure the presentation of results according to traits and refer to patterns mentioned above.

Fig. 2.

Obvious significant trait–climate range relationships (see Methods for rules) matching the proposed response patterns in Fig. 1C based on climate ranges of 250 North American tree species (open circles represent 166 angiosperms and filled circles represent 84 gymnosperms) or 146 species in case of maximum height vs. T seasonality (see Methods). For each trait–climate combination the responses of the species-specific upper limits (red circles), lower limits (blue circles), and the median (black circles) to the traits are quantified applying linear quantile regression; the 95th quantile (upper limits), the 5th (lower limits), and the 50th quantile (median) are shown; and solid lines indicate slopes significantly different from zero (P < 0.05), dashed lines indicate nonsignificant slopes of the 95th and 5th quantiles, and no line is drawn when slopes of the 50th quantile are nonsignificant. The gray shaded areas between the outermost quantiles correspond to the climate range the species can jointly occupy across the range of their trait values, whereas the white areas correspond to no-go areas.

Wood Density and Seed Mass: Climate-Controlled No-Go Areas.

We observe a one-sided response of mean annual temperature (annual T) to wood density, where only the lower limits increase significantly (Fig. 2 and Table S1) with increasing wood density. Trees with soft wood can occupy regions covering the complete temperature range of North America but species with high wood density only occur in warmer regions. Trees with wood denser than 0.55 g⋅cm⁻³ do not expand into no-go areas with an annual T below 0 °C and the species with the hardest wood (>0.85 g⋅cm⁻³, e.g., Rhizophora mangle and Quercus virginiana) are restricted to subtropical climates with an annual T > 15 °C. There is also a significant positive relationship between wood density and a species’ annual T preference. The significant one-sided pattern also occurs when only angiosperms are considered (Fig. S2) and the more soft-wooded gymnosperms are located well within the triangle formed by the angiosperms (Fig. 2), suggesting a generic response across clades. The mechanism keeping hard-wooded species out of cold regions probably reflects the tradeoff between stability and construction costs (27). Dense wood lends physical stability and is more resistant to interior decay caused by fungi and insects (12). It thus increases longevity particularly in warmer climates where the metabolic activity of decomposers is high. However, the high carbon costs of dense wood slow down growth rates. In cold climates, where carbon gain is limited by short growing seasons, these costs can probably not be met (27), which is mirrored in the one-sided pattern between wood density and temperature seasonality (T seasonality). Species with low wood density are typically fast-growing pioneers which are adapted to exploit the increased light and nutrient availability after disturbance. Disturbances occur across the entire climatic gradient and so do the soft-wooded pioneer species.

Seed mass is another important predictor of species’ climate range limits. The possible climate range the ensemble of species can jointly occupy generally decreases with increasing seed mass for five bioclimatic variables according to a one-sided pattern (Fig. 2). Trees with low seed mass occupy the whole climate range, whereas those with seeds heavier than 150 mg (approximate seed mass of Pinus albicaulis) do not occur in cold climates (annual T <0 °C) and in regions with high annual precipitation (>2,000 mm). Identical one-sided patterns emerge for separate analyses of angiosperms and gymnosperms proving the generic nature of the relationships (Figs. S2 and S3). The functional mechanisms are less clear than for wood density and remain speculative. The short growing season in cold climates might not allow enough time and energy for the development of larger seeds (28).

Maximum Height: No-Go Areas Related to Climate and Biotic Interactions.

Species’ range limits with respect to annual precipitation (annual P) and net precipitation (net P, annual P minus potential evapotranspiration) are related to maximum height according to an aligned pattern (Fig. 2 and Table S1). With increasing maximum height, the medians and limits increase for annual P and net P (Fig. 2). Thus, short trees tend to be rare in regions with high absolute annual P and high net P, whereas tall trees tend to be absent from regions with opposite conditions. Similar patterns emerge when analyzing angiosperms and gymnosperms separately suggesting a generic response across clades (Figs. S2 and S3). Hydraulic limitation of height growth (29) and competition for light (30) are the most likely mechanisms driving these patterns. For water to move vertically, the leaf water potential must decline with height (31). As the required gradient is a linear function of tree height, any reduction in soil water potential has to be met by a parallel reduction in leaf water potential. Because the latter cannot sink below a certain physiological limit, drought translates directly into shorter tree heights (32). Thus, tall trees are missing from dry climates because of physiological constraints which are in agreement with the findings that precipitation controls plant maximum height at the global scale (19). The absence of small trees from very humid climates may be under biotic control, e.g., via selection pressure for tall heights in the race for light under otherwise favorable conditions. The upper T seasonality limits seem to follow a bell-shaped right skewed response with a mode at 22 m, i.e., 20% of the height range. We capture this by applying linear quantile regression to tree species with maximum heights larger than the mode (Fig. 2 and Table S1). Above this threshold, the upper T seasonality limits sharply decrease with maximum height following a one-sided pattern. This relationship keeps trees with large maximum heights out of continental boreal climates with high T seasonality, most likely due to a short growing season combined with a high risk of frost drought during spring.

SLA and Longevity.

For SLA and longevity we find only weak reverse and one-sided responses (Fig. S1 and Table S1). This might be due to the fact that both traits reflect processes operating at local scales, most notably nutrient use efficiency and shade tolerance, responding to strong local heterogeneity in nutrient and light availability, respectively (33). Also temporal changes in these resources and differences in successional niche occupation by species may decouple SLA and longevity from the regional climate. This implies that the differentiation into acquisitive and conservative resource use strategies (high SLA and short tree lifespan vs. low SLA and long tree lifespan) occurs in all climates.

Continental Patterns of Trait Variation and Potential Functional Richness.

Having identified obvious patterns (Fig. 2) and discussed the underlying functional mechanisms of how traits constrain climate limits of North American trees, we are able to map climatic no-go areas for trees of a given wood density, seed mass, and maximum height by applying the quantile regression equations (Table S2) in a reverse mode to gridded climate data. This allows for the identification of maximum attainable trait values in geographic space (Fig. 3, Fig. S4, and Dataset S1) and describes how trait variation will change in response to climate. When trait variation changes in response to climate, the color gradient in Fig. 3 depicts how the maximum trait values decline in the direction of the climate factors; in contrast, dark red depicts regions where trait variation is unconstrained. For wood density and seed mass, dark red regions mean that any trait value within the spectrum defined by the North American species pool (dark red regions in Fig. 3A and Fig. S4) is possible. For maximum height, however, the dark red colored area in Fig. 3B contains some locally humid climates (e.g., the Pacific Northwest) where some low maximum heights tend to be excluded (Fig. 2) as we translated only the lower annual P and net P responses for the map. For example, at low elevation sites, wood density may take on any value between 0.3 and 0.9 g⋅cm⁻³ south of 42° N which is about the latitude of New York (Fig. 3A). At the border to Canada, the maximum attainable wood density is predicted to be 0.54 g⋅cm⁻³ and it decreases to values of 0.32 g⋅cm⁻³ at 60° N (northern border of Manitoba). A very similar pattern, slightly shifted northwards, can be observed for seed mass (Fig. S5). For maximum height, almost the whole spectrum of values (i.e., up to 100.4 m) is predicted for the northwestern coast of North America and the southeastern coast including Florida (Fig. 3B). From Florida northwards the maximum attainable max. height values decrease continuously and fall below 50 m north of the Great Lakes. In the arid lowland regions of the Southwest, the maximum attainable maximum height is reduced to 10 m and below. These results are insensitive to the exclusion of the tall gymnosperm species Sequoia sempervirens, the only species with a maximum height above 70 m (Table S3 and Fig. S5).

Fig. 3.

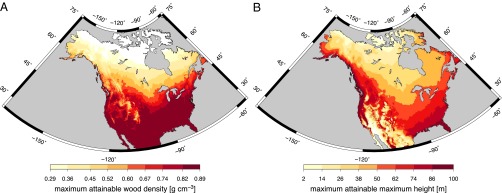
Maps show maximum attainable trait values for wood density (A) and maximum height (B) given the climate (Fig. 2). Dark red depicts regions where trait values are climatically unconstrained whereas the color gradient depicts no-go areas for North American trees as determined by their trait values. White depicts regions outside the considered trait range for which we make predictions. The maximum attainable trait values shown are derived by applying a quantile regression equation (Table S2) to gridded climate data and the subsequent selection of the minimum trait value predicted per grid cell to visualize the strongest climate constraint on trait variation. Gridded climate data used: mean annual T, diurnal T range, T seasonality, annual P, and net P. Maps have a resolution of 5 arcmin and are projected in Albers equal-area conic projection.

These north–south and east–west gradients are in line with trait assembly rules (34) and with trait diversity patterns (4) across large climatic gradients ranging from harsh (boreal and arid) to benign (subtropical and tropical) climate conditions. Under harsh climates, trait ranges are confined to values conveying stress tolerance allowing species to pass strong abiotic filters, whereas in benign climates biotic filters become more important, which are complex and multifaceted. These are most likely reflected by a multitude of traits and may have less of an equalizing effect on single traits than abiotic stressors. In addition, trait values associated with tolerating harsh conditions (e.g., low wood density) may not be subjected to biotic filtering under benign conditions. This results in a higher functional richness and greater trait variation as has been reported for temperate and subtropical relative to boreal climates (4). If this type of response pattern proves to be consistent across many traits, this would lend support to the climate favorability or physiological tolerance hypothesis of functional richness (35), indicating that toward the tropics a larger number of viable trait configurations become possible and that functional richness therefore increases. The relationship between traits and climatic limits thus provides insights into the processes shaping global scale biodiversity patterns.

Limitations and the Way Forward.

The ideal trait for a functional climate range prediction in functional biogeography is one (i) whose function directly reflects the physiological or mechanical mechanism compromising vital rates (growth, survival, and fecundity) at the range limits (10) and (ii) which is available for all species considered in an analysis. One trait satisfying the first condition (but see below) is, e.g., physiological cold-resistance which can be quantified experimentally based on conductivity measurements indicating cell membrane leakage (36). However, this “hard” trait is not available for all 250 North American tree species. Conversely, our five traits are available for all species, but their functional interpretation is rather indirect albeit plausible. Unlike the above example, the relationship between vital rates and climate are rarely controlled by a single trait. Drought tolerance, for instance, is conveyed by a whole suite of traits (37), including, e.g., deep roots for accessing subsoil water, small vessels for cavitation prevention and high seed mass for rapid penetration of dry top soils. Moreover, often several traits jointly define strategy axes based on fundamental tradeoffs (38). All of our five traits are part of such tradeoffs and have been singled out as leader traits representing different bundles of correlated traits, including physiological hard traits (11). We therefore advocate our pragmatic approach that aims to balance functional precision on the one hand and generality and applicability on the other.

Our approach uses species-specific trait means and thus ignores intraspecific trait variation. It is, however, important to note that our trait-based approach is insensitive to intraspecific variation as long as the mechanisms causing inter- and intraspecific variation are the same. The predictions of our study are valid for trees with particular traits no matter whether these vary within (pheno- or genotypes) or between species. We use linear quantile regression to quantify bivariate trait–climate range relationships. Visual inspection of the obvious responses in Fig. 2 shows that quantile relationships indeed tend to be linear when considering at least 75% of the trait range. It is possible that a whole suite of traits and inevitable tradeoffs among these traits can lead to alternative plant designs reaching equal vital rates. This circumstance, in fact, challenges simple bivariate statistical analyses and calls for multivariate approaches, where multidimensional quantiles can be fit to one (or several) climatic niche parameters and for more process-based models accounting for this multidimensional optimization process (39, 40). Nevertheless, our bivariate regression equations have the advantage that they are intuitive, are straight forward to implement in models, and can easily be used to generate maps visualizing climatic filtering on trait variation (e.g., Fig. 3).

Potential for Improving DGVMs.

In classic DGVMs, functional traits are typically used as variables underlying the definition of PFTs (e.g., the evergreen broad-leaved type has elements of leaf longevity and SLA) or as model parameters. For example, SLA is often used to convert carbon allocated to the leaf compartment into leaf area available for light capture (models listed in ref. 2). Wood density is used to translate carbon invested into stem growth into size gain (25, 41). In modern gap models, maximum height is implemented as a site-dependent variable allowing for more pronounced climate-induced changes in productivity (42). Maximum longevity is used to infer mortality rates (LPJ-GUESS model) (43). Seed mass is sometimes used as a proxy for dispersal distance in individual based models (44). In short, our five predictor traits are used as important descriptors of plant functioning in vegetation models. Three of them (seed mass, wood density, and maximum height) also turn out to be suitable predictors of range limits and thus may serve a dual purpose in vegetation models. This is precisely mirroring the response–effect framework of trait influence (10), where traits govern vegetation responses to the environment as well as vegetation effects on ecosystem functioning. Future models taking advantage of both facets of traits may become capable of simultaneously predicting shifts in trait spectra and resulting consequences for ecosystem functioning, and finally via this link the interactions of climate, functional diversity patterns and vegetation feedbacks.

The trait–climate range relationships reported here may not only be useful to improve existing DGVMs but more importantly may serve as benchmark for validating next generation DGVMs (40). In these, trait–climate range relationships emerge as a consequence of the performance of evolving pseudospecies originating from the implementation of tradeoffs in plant functions and functional traits (45). This does not only include the responses of these pseudospecies to climatic constraints, but also the interactions among them exerting an additional biotic filter (46). In these approaches, however, pseudospecies differ from real world species, because (i) not all aspects of plant function (tradeoffs) can be implemented (40, 45), and (ii) they may evolve in the model differently vs. in the real world (47). Models based on pseudospecies require suitable (meta) patterns for model evaluation that are decoupled from observed species or PFT geographic distributions. Such an avenue is provided through the reported trait–climate range relationships and the maps showing continental patterns of trait variation. These shall thus be particularly useful for the evaluation of next generation DGVMs, which will most likely be based entirely on traits and tradeoffs and not necessarily on species or PFT range limits empirically derived from present-day observations.

Methods

We derived species-specific climate ranges from intersecting distribution maps of 250 North American tree species (48) with gridded maps of eight bioclimatic variables, including mean annual T (in degrees Celsius), diurnal T range (in degrees Celsius ), T seasonality (SD of monthly mean temperature values), annual P (in millimeters), P of the coldest quarter (in millimeters), and P of the warmest quarter (in millimeters) with a resolution of 5 arcmin (49). Furthermore, we included growing degree days (GDDs) with a base temperature of 5 °C (50) and net P (in millimeters) as a measure of humidity calculated as annual P minus potential evapotranspiration (51) both in 0.5° resolution. For each bioclimatic variable we derived three species-specific measures: the upper and lower limits and the median which were obtained from the bioclimatic data covering a species range at the 95th, 5th, and 50th quantile, respectively. We used quantiles instead of minimum and maximum values to minimize the effect of outliers caused by potential mismatches intersecting species range maps with climate. We collected the five continuous traits [wood density (in gram per cubic centimeter), seed mass (in milligrams), SLA (in square centimeter per gram), plant maximum height (in meters), and tree longevity (in years)] from literature sources (52, 53), databases (54–56) and, in the case of SLA, species-specific estimates corrected for high intraspecific variation (57). We compiled species-specific mean trait values for each of the 250 tree species as described in Stahl et al. (58). To obtain normally distributed trait values, both seed mass and tree longevity were log transformed, whereas wood density and plant maximum height were square-root transformed. We performed linear quantile regression for each of the three measures against each of the five traits for all eight bioclimatic variables resulting in a total of 40 trait–climate range relationships. To account for nonlinear relationships, we did inspect the patterns visually for strong and obvious linear patterns along at least more than 75% of the range in trait values. In such cases (maximum height vs. T seasonality in Fig. 2), the data were split and quantile regressions applied for that part of the trait range. We classified response patterns according to Fig. 1 when at least one of the two fitted regression lines of the lower/upper limit had a slope significantly different from zero. We classified patterns as “obvious” when the two lower/upper quantiles (gray shaded areas in Figs. S1–S3) had significant slopes (see Table S1 for significance levels of slopes). To evaluate the effect of phylogeny on our results, we repeated the analysis for gymnosperms and angiosperms separately (Fig. S2 and S3). To compare the slopes of the different trait–climate range relationships, we centered and standardized the traits as well as the measures (Table S1). To conduct inferences about slopes of quantile regression estimates, we computed bootstrapped SEs (standard xy pair bootstrap). All analyses were done in R Version 2.11.0 (59) using the quantreg package (60). Finally, we mapped the no-go areas for North American trees as maximum attainable trait values for wood density, seed mass, and maximum height from applying quantile regression equations of the outermost significant estimates (Table S2) to gridded mean annual T, diurnal T range, T seasonality, annual P, and net P. For each trait we created maps from the bioclimatic variables with a significant relationship and extracted the minimum trait value per grid cell across these maps.