Abstract
This study provides evidence that low-intensity ultrasound directly affects nuclear processes, and the magnitude of the effect varies with frequency. In particular, we show that the transcriptional induction of first load-inducible genes, which is independent of new protein synthesis, is frequency dependent. Bovine chondrocytes were exposed to low-intensity below the cavitational threshold) ultrasound at 2,5 and 8 MHz. Ultrasound elevated the expression of early response genes c-Fos, c-Jun and c-Myc, maximized at 5 MHz. The phosphorylated ERK inhibitor PD98059 abrogated any increase in c-series gene expression, suggesting that signaling occurs via the MAPPK/ERK pathway. However, phosphorylated ERK levels did not change with ultrasound frequency, indicating that processes downstream of ERK phosphorylation (such as nuclear transport and chromatin reorganization) respond to ultrasound with frequency dependence. A quantitative, biphasic mathematical model based on Biot theory predicted that cytoplasmic and nuclear stress is maximized at 5.2 ± 0.8 MHz for a chondrocyte, confirming experimental measurements.
Keywords: Low-intensity ultrasound, Resonance, Biphasic mathematical model, Load-inducible genes, MAPPK/ERK, Cell biomechanics
Introduction
The bioeffects of ultrasound (US) have been positively harnessed for use in therapeutic applications, even though the effects are only partly understood (Dalecki 2004; Fowlkes 2008; Nelson et al. 2009). The biological response to US is most often attributed to thermal and cavitational effects (Krasovitski et al. 2011). Researchers are especially interested in cavitation, which may be used to increase cell membrane permeability for applications ranging from targeted drug and gene delivery to induction of apoptosis (Liang et al. 2010; Wu and Nyborg 2008; Yoon and Park 2005). On the other hand, low-intensity US is often used in healing bone fractures and as an alternative therapy to facilitate cartilage repair and restoration (Naito et al. 2010; Rubin et al. 2001; Yang et al. 2005). Certain observed effects, especially those related to fracture healing, cannot be attributed to cavitation, as the intensity of the applied US is below the cavitation threshold (Dalecki 2004). In fact, the American Institute of Ultrasound in Medicine has pointed out that very little is known about US bioeffects below the cavitation threshold (Fowlkes 2008). In addition, both in vivo and in vitro applications of low-intensity US have produced variable results, thus necessitating detailed trials to determine the optimal regimen of low-intensity US in therapeutic applications like wound and fracture healing (de Albornoz et al. 2011).
In addition to in vivo applications of low-intensity US, studies in the last 10 years have shown that cells maintained in in vitro culture can be stimulated by US (Hsu et al. 2007; Nishikori et al. 2002; Parvizi et al. 1999; Zhang et al. 2003). Our work has shown that the stimulation of in vitro chondrocyte cultures by low-intensity continuous US induces a marked increase in the expression of chondrogenic markers, including type II collagen, aggrecan and Sox-9, indicating that US stimulation itself could enhance chondrogenesis in three-dimensional culture (Hasanova et al. 2011). Continuous US stimulation of chondrocytes induced phosphorylation of focal adhesion kinase, Src, p130-Crk-associated substrate (p130Cas), Crk-II and extracellular-regulated kinases (ERK), strongly implicating these intra-cellular signaling molecules in a US-mediated signaling pathway (Whitney et al. 2012). Combined, our findings suggest that US stimulation can modulate the signal transduction pathways that lead to gene regulation or RNA translation of a protein product, or both. However, the frequencydependent modulation of cell function remains largely unexplored.
Our experimental work has shown that the gene and protein expression of chondrocytic markers was enhanced at 5.0 MHz when compared with that at either 1.5 or 8.5 MHz (Noriega et al. 2007). Here, we seek to investigate whether the transcriptional induction of first load-inducible genes, which is independent of new protein synthesis, is frequency dependent. This is significant, as the independence of transcriptional induction from protein synthesis is suggestive of a regulatory role in the cellular response to external stimuli. The first load-inducible genes are called early response or immediate early genes (i.e., c-Jun, c-Fos, c-Myc, EGR1 and BNP), and their transcription is activated rapidly and transiently within minutes of stimulation (Sng et al. 2004). In particular, c-Jun, c-Fos and c-Myc are known to be activated in response to external mechanical stimuli in chondrocytes (Beier et al. 1999; Vincenti and Brinckerhoff 2001), osteoblasts (Greenberg et al. 1985; Sena et al. 2005; Shivaram et al. 2010), stretch in myocytes (Yamazaki et al. 1995) and fetal lung epithelial cells (Copland and Post 2007). However, the frequency dependence has not been evaluated. These genes are regulated at the transcriptional level in a “stretch-responsive” manner, where the activation of c-Jun, c-Fos and c-Myc results in numerous bioeffects that play vital roles in cell proliferation and differentiation (Cole 1986; Sena et al. 2005). Further, pre-treatment of rat mesenchymal stem cells (rMSC) with PD98059 suppressed the stretch-induced gene expression of c-Fos, alluding to the key role of ERK in mediating stretch-induced proliferation of rMSC (Song et al. 2010). ERK belongs to the family of mitogen-activated serine/threonine protein (MAP) kinases and regulates proliferation, differentiation and many other cell processes in response to extracellular signals (Ebner et al. 2006; Ramos 2008). In the study described in this article, we experimentally measured the levels of ERK and load-inducible genes in chondrocytes exposed to US stimulation. So as to shed light on the experimental results and subsequently acquire further insight into the processes underlying the bioeffects of US, a mathematical model was developed to predict the intra-cellular mechanical stresses and strains.
Previous models of bacterial, plant, yeast and animal cells have estimated acoustic resonance frequencies to range between a few hundred kilohertz and 700 MHz (Baaijens et al. 2005; Hartmann and Delgado 2004; Or and Kimmel 2009; Yang and Huang 2001; Zinin and Allen 2009; Zinin et al. 2005). The variability in results can be attributed to the diversity of models used to describe the cell (ranging from encapsulated bubbles to viscoelastic solids), as well as uncertainty in physical properties. Experimentally measured mechanical properties and the inherent heterogeneity of the cell structure must be considered in the model formulation (Mitchison et al. 2008). Biot theory (Allard and Atalla 2009) describes sound propagation in heterogeneous media consisting of a poroelastic frame saturated by a viscous fluid. We use Biot theory to develop a quantitative acoustic model, thereby accounting for the biphasic nature of the system. The interior of a cell is crowded by solid structures and macromolecules, which typically occupy 20%–30% of the total cell volume. The cytosol occupies the remaining space and consists mainly of water. These characteristics warrant a biphasic approach: the cell is modeled as being composed of an elastic solid phase and a fluid phase. Biphasic models have been used successfully to predict the time-dependent response of cells to micropipet aspiration (Bidhendi and Korhonen 2012; Trickey et al. 2006) and unconfined creep compression (Leipzig and Athanasiou 2005). Failure to incorporate biphasic effects will result in the incorrect prediction of mechanical responses.
Although biphasic models have been used to model the cell with respect to finite stresses and strains (Guilak and Mow 2000; Haider and Guilak 2007; Kim et al. 2008), this article is the first to apply Biot theory to the study of US propagation in a cell. We use a chondrocyte cell model to experimentally validate the mathematical model. Finally, we combine the model-based predictions of intra-cellular stresses and strains with the experimental results to postulate that the nucleus may directly sense US stimulation over a specific frequency range (the resonant bandwidth).
Mathematical Modeling
Linearity and harmonic time dependence
The linear wave equation is used as low-intensity US stimulation was used in the experiments; thus, acoustic perturbations are small and higher-order terms are negligible (Kinsler 2000). Furthermore, we applied continuous (as opposed to pulsed) US. We ignored the short duration “transient” component of the acoustic response and only modeled the steady-state acoustics with harmonic time dependence.
Modeling standing waves in the tissue culture well
Stimulation of cells using continuous US is extremely delicate, and care must be taken to ensure repeatable results. We developed a model of the standing wave field in the tissue culture well that accounts for the transmission and reflection of acoustic waves. The standing wave model was used to identify and eliminate possible disturbances that can result in experimental error. The development of the standing wave field model is described in Appendix 1; the model was implemented using MATLAB R2010b (MathWorks, Natick, MA, USA). Cells were sonicated from above, and three distinct acoustic layers exist in the tissue culture well: the culture medium, the polystyrene well bottom and the air gap below the well. The parameters describing the system are given in Table 1.
Table 1. Parameters used in the tissue culture well model.
| Width, h (mm) | Density, ρ (kg/m3) | Bulk modulus, K (MPa) | Shear modulus, G (MPa) | |
|---|---|---|---|---|
| Culture medium* | 6.00 | 992.52 | 2300 | — |
| Polystyrene† | 1.52 | 1050 | 762 | 2000 |
| Air | 1.02 | 1.2 | 0.1 | — |
Assumed to be water at 37° C.
According to the manufacturer's specification.
Acoustic stress and strain in a cell calculated using Biot theory
The basics of Biot theory are summarized in Appendix 2. The following section describes the model development pertaining specifically to a single, spherical cell.
Model geometry
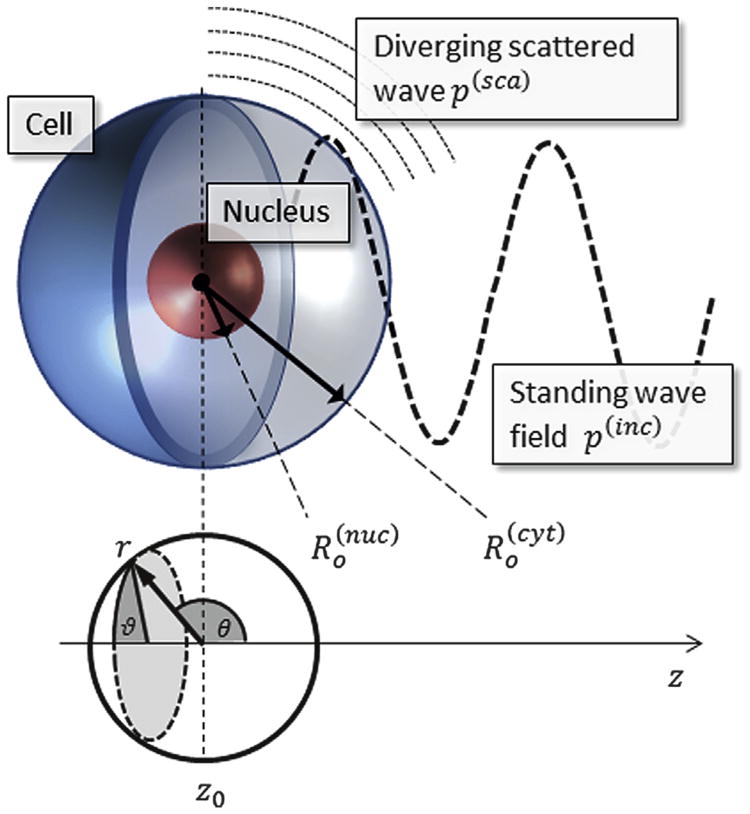
Numerous researchers have shown that the nucleus greatly impacts the mechanical properties of the whole cell (Dahl et al. 2010; Rowat et al. 2006, 2008), so it is important to incorporate this structure into the model geometry. The nucleus consists mostly of tightly packed DNA and proteins, which form chromatin, but it also has its own structural support as well as an encapsulating membrane, the nuclear envelope (Dahl et al. 2010; Rowat et al. 2006). Micropipet aspiration has been performed on isolated nuclei and has shown that the nucleus tends to be three to four times stiffer than the surrounding cytoplasm in chondrocytes (Guilak et al. 2000). To incorporate the effect of the nucleus on the mechanical response, the cell is modeled as four concentric spheres representing the primary elements of the cell, as illustrated in Figure 1. The model thus consists of five domains: the exterior fluid medium and four biphasic parts (cell membrane, cytoplasm, nuclear envelope and nucleus). Our experimental model was bovine chondrocytes, with cell and nuclear radii of 6.5 and 3.5 μm, respectively (Guilak et al. 2000; Trickey et al. 2000). The thicknesses of the plasma membrane and nuclear envelope are 15 and 40 nm, respectively (Vaziri and Mofrad 2007).
Fig. 1.
The model consists of five distinct domains: exterior fluid, with incident standing wave field and a divergent scattered wave; biphasic cell membrane; cytoplasm; nuclear envelope; nucleus. The incident wave p(inc) is invariant in directions perpendicular to the z-axis, leading to azimuthal (ϑ) symmetry.
The US beam has very high directivity, as will be shown in the Results section describing the standing wave field in the tissue culture well. We therefore approximate the standing wave field as two plane waves with equal amplitudes traveling in opposite directions along the z-axis. Choosing the polar axis (θ = 0) to coincide with the z-axis results in azimuthal (ϑ) symmetry, as the standing wave is invariant in the x and y directions. A spherical cell model is sufficient for the current system, as the external acoustic fields have wavelengths that are much greater than the cell diameter (λ > 100 μm); therefore, asymmetry in the cell geometry has a minimal effect on the acoustic response.
Exterior fluid
The acoustic wave in a fluid is fully defined by a pressure wave, which must satisfy the linear wave equation
| (1) |
where Δ is the Laplace operator, and cex is the phase velocity. The US stimulation has harmonic time dependence (eiωt), which transforms the linear wave equation into the Helmholtz equation
| (2) |
with wavenumber kex = ω/cex. In spherical coordinates, with azimuthal symmetry (the angle ϑ in Fig. 1), the solution of the Helmholtz equation can be found by separating variables in terms of spherical harmonics (Hasheminejad 2011):
| (3) |
In Eq. (3), jn(x) and yn(x) are the spherical Bessel functions of the first and second kind, respectively; Pn(x) is the Legendre polynomial of order n; and and are unknown coefficients that are determined by the boundary conditions. The wave can be separated into the incident US stimulation and the wave that is scattered from the cell surface, p(ex) = p(inc) + p(sca). The incident US is treated as a harmonic standing wave with radial frequency ω and antinodal pressure amplitude pA>0. The standing wave is expanded as an infinite series, shown in the equation (Hasheminejad 2011).
| (4) |
where δ is the distance to the closest antinode. The appropriate function describing the diverging scattered wave is the Hankel function, hn(x) = jn(x)+iyn(x) (Hasegawa and Yosioka 1969). Therefore, the scattered wave is given by
| (5) |
In the fluid phase, the displacement vector u is related to pressure by the linearized conservation of momentum equation
| (6) |
with ∇ being the gradient operator and ρ0 the unperturbed density (Kinsler 2000).
Biphasic domains
In Biot theory the acoustic stress and strain are calculated using two irrotational scalar displacement potentials φ1, φ2 and a rotational vectorial displacement potential Ψ (see Appendix 2). The azimuthal symmetry of our model reduces Ψ to a simple scalar potential ψ. Solving the Helmholtz equations associated with each displacement potential yields an equation of the same form as Eq. (3). Once the displacement potentials are known, the stresses and strains in the biphasic domain can be calculated (see Appendix 2).
Boundary conditions
For each value of n (i.e., each term in the series expansion given by Eq. [3]), there are 25 unknowns: one in the exterior fluid, and six for each of the four biphasic domains (two for each of the three waves in each domain). However, for the solution to be physically realizable, we require that the coefficients are zero for every wave in the nucleus domain because . This reduces the number of unknowns to 22n. The boundary conditions are: continuity of solid displacement, fluid flow, normal stress and shear stress. At the interface of the (b)iphasic and (f)luid domains, the boundary conditions are given by the equations (Allard and Atalla 2009):
| (7) |
| (8) |
| (9) |
| (10) |
At the interface between two biphasic layers, we have
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
Applying the boundary conditions above at each of the four interfaces gives 22 equations, which are solved to determine the 22 unknowns. This is done for every value n = 0, 1, 2, …, N in the series expansion given by Eq. (3). Sufficient convergence (defined as the point where the determinant of the system of 22 linear equations was below machine precision) was achieved with N∈ [30, 35].
Model parameters
Biot theory uses parameters that refer to the bulk medium (i.e., the macroscopic properties of the fluid-saturated elastic frame), as well as the pure solid phase and the pure fluid phase. In our case, the “bulk medium” refers to the cytosolic fluid saturated, heterogeneous agglomeration of proteins, organelles and other macromolecules present in each of the regions of the cell, whereas the solid phase refers to the individual structures (i.e., an individual cytoskeletal element, organelle or protein). An extensive literature search was conducted to find a set of feasible material properties specific to chondrocytes.
Most of the parameters used in Biot theory are well known, but some require additional explanation (see Appendix 2). The bulk solid density, ρb = (1−φ)ρs, is the solid mass per volume frame, which in this case is simply the mass concentration of proteins and macromolecules (50–400 mg/mL) (Minton 2001). The drained bulk modulus Kb and Poisson's ratio ν refer to the mechanical properties of the bulk medium as it would be measured when the interstitial fluid is allowed to flow freely in and out of the frame (Nolen-Hoeksema 2000). This is the case during micropipet aspiration and atomic force microscopy measurements. When the fluid is allowed to flow freely, it is easy to see that the frame is highly compressible, and the drained bulk modulus is usually very low. Combining experimentally measured physical properties from a variety of sources, we have established that the bulk modulus of the bulk medium, Kb, is on the order of 0.5 kPa (Baaijens et al. 2005; Bidhendi and Korhonen 2012; Darling et al. 2008; Leipzig and Athanasiou 2005; Shieh and Athanasiou 2006), and Poisson's ratio ν ≈ 0.38. However, the nucleus is known to be around four times stiffer than the cytoplasm (Guilak et al. 2000), and we used the value Kb ≈ 2 kPa. The fluid phase is simply treated as water at 37°C.
The greatest source of uncertainty, as well as model sensitivity, resides in the bulk modulus of the solid phase, Ks, which exhibits large spatial variation throughout the highly heterogeneous cell, composed of a myriad of different proteins, organelles and cytoskeletal structures. The bulk moduli of isolated proteins typically range from 4 to 10 GPa, based on extrapolation from experimentally measured values of protein solutions (Gekko and Hasegawa 1986; Paci and Marchi 1996). For microtubules (one of the main load-bearing structures in cells), Ks has been reported to lie anywhere from 1 MPa to 10 GPa, with values being strongly dependent on experimental conditions and interpretation of data (Kasas et al. 2004). Recent atomistic simulations place the Ks of microtubules between 100 MPa and 1 GPa, depending on the specific structure (Sept and MacKintosh 2010). Similarly, organelles display vastly different compressibility. One study shows a marked decrease in the volume of the mitochondria and rough endoplasmic reticulum during cell compression, whereas the Golgi apparatus resists dilatation (Szafranski et al. 2004). Using a pseudo-homogeneous approximation to take the heterogeneities into account (Berryman 2006; Pride and Berryman 2003), we estimate Ks to be between 1 and 10 MPa.
The plasma and nuclear membranes were treated as biphasic media with extremely high porosity (φ = 0:95) and minimum tortuosity (α∞ = 1), to represent the fact that the major component of the membrane, the lipid bilayer, acts as a fluid (Gutberlet and Katsaras 2001). However, the membrane also contains cyto- and nucleoskeletal elements that can transmit shear, which must be accounted for by incorporating a solid component. Parameters were based on results found by atomistic simulations (Izvekov and Voth 2009; Ovalle-García et al. 2011; Patra et al. 2003).
Values for the flow resistivity of chondrocytes, ϖ, are found in the literature (Guilak and Mow 2000) and it is estimated to lie anywhere between 1010 and 1017. The parameter Λ is the viscous characteristic length and depends on the porous structure. Two approximations of Λ were used to obtain an order-of-magnitude estimate (Allard and Atalla 2009). If pores are nearly circular, Eq. (17) can be used, whereas Eq. (18) is used for fiber bundles (in this case we considered the nucleus to be a bundle of chromatin fibers) (Leuba et al. 1994).
| (17) |
| (18) |
In Eq. (17), c ≈ 1 is a form factor with c = 1 for circular pores. In Eq. (18), L is the total fiber length per unit volume and D is the fiber diameter. Both approximations place Λ in the range Λ ∈ (10−7, 10−13). This range was used in the parameter sensitivity analysis, and it was found that the resonant peak position has negligible dependence on Λ.
All model parameters are summarized in Table 2. The model of acoustic stresses and strains in a single cell was solved using MATLAB R2010b (MathWorks).
Table 2. Material properties used in the Biot theory of wave propagation in porous media.
| Cytoplasm | |||
|---|---|---|---|
| Bulk medium | |||
| Porosity | φ | 0.75 | Minton 2001 |
| Bulk modulus (Pa) | Kb | 0.5 × 103 | Baaijens et al. 2005; Bidhendi and Korhonen 2012; Darling et al. 2008; Leipzig and Athanasiou 2005; Shieh and Athanasiou 2006 |
| Poisson's ratio | ν | 0.38 | Trickey et al. 2006 |
| Tortuosity | α∞ | 1.2 | Kuhn et al. 2011 |
| Flow resistivity (Pa·s/m2) | ϖ | 1015 | Guilak and Mow 2000 |
| Characteristic length (m) | Λ | 10−9 | Eq. (17) |
| Bulk density (kg/m3) | ρb | 300 | Minton 2001 |
| Solid phase | |||
| Bulk modulus (Pa) | KS | 5 × 106 | Berryman 2006; Gekko and Hasegawa 1986; Kasas et al. 2004; Paci and Marchi 1996; Pride and Berryman 2003; Sept and MacKintosh 2010; Szafranski et al. 2004; Tuszynski et al. 2005; Vinckier et al. 1995 |
| Fluid phase* | |||
| Bulk modulus (Pa) | Kf | 2.3 × 109 | Lemmon et al. 2011 |
| Density (kg/m3) | ρf | 992.52 | Lemmon et al. 2011 |
| Viscosity (Pa·s) | μ | 0.7 × 10−3 | Kestin et al. 1978 |
|
| |||
| Nucleus | |||
|
| |||
| Bulk medium | |||
| Porosity | φ | 0.65 | Rowat et al. 2006 |
| Bulk modulus (Pa) | Kb | 2 × 103 | Guilak et al. 2000 |
| Poisson's ratio | ν | 0.38 | † |
| Tortuosity | α∞ | 2 | Kuhn et al. 2011 |
| Flow resistivity (Pa·s/m2) | ϖ | 1015 | Guilak and Mow 2000 |
| Characteristic length (m) | Λ | 10−9 | Eq. 17 |
| Bulk density (kg/m3) | ρb | 400 | ‡ |
| Solid phase | |||
| Bulk modulus (Pa) | KS | 5 × 106 | † |
| Fluid phase* | |||
| See cytoplasm fluid phase | |||
|
| |||
| Cell membrane and nuclear envelope | |||
|
| |||
| Bulk media | |||
| Porosity | φ | 0.95 | § |
| Bulk modulus (Pa) | Kb | 300 × 106 | Izvekov and Voth 2009 |
| Poisson's ratio | ν | 0.48 | Vaziri and Mofrad 2007 |
| Tortuosity | α∞ | 1 | § |
| Flow resistivity (Pa·s/m2) | ϖ | 1015 | Guilak and Mow 2000 |
| Characteristic length (m) | Λ | 10−9 | Eq. (17) |
| Bulk density (kg/m3) | ρb | 40 | ‡ |
| Solid phase | |||
| Bulk modulus (Pa) | KS | 1 × 109 | Sept and MacKintosh 2010 |
| Fluid phase | |||
| Bulk modulus (Pa) | Kf | 300 × 106 | Izvekov and Voth 2009 |
| Density (kg/m3) | ρf | 1000 | Patra et al. 2003 |
| Viscosity (Pa·s) | μ | 0.7 × 10−3 | ‖ |
Standard values for water at 37° C.
Equal Poisson's ratio and solid phase bulk modulus for the cytoplasm and nucleus.
Estimate the solid density in the nucleus/membranes based on the volume fraction solids in the nucleus/membranes compared with the cytoplasm.
Membranes are modeled as biphasic layers with very high porosity, that is, a fluid-like layer that can transmit shear forces.
We used the viscosity of water to calculate the damping across the membranes, which proved to be negligible
Methods
Bovine chondrocytes isolation and culture
Bovine chondrocytes were isolated by digestion of articular cartilage from the knee joints of 6-mo-old calves with pronase and collagenase, as described previously (Noriega and Subramanian 2011). Isolated primary bovine chondrocytes were resuspended in DMEM/F-12 (1:1) (Sigma–Aldrich, St. Louis, MO, USA) supplemented with 10% dimethyl sulfoxide (DMSO, Sigma–Aldrich) and stored in liquid nitrogen until needed. They were allowed to thaw and were expanded in 75-cm2 T-Flasks (Sigma–Aldrich). The culture medium DMEM/F-12 (1:1), supplemented with 10% fetal bovine serum (FBS) (Invitrogen, Carlsbad, CA, USA), 25 μg/mL ascorbic acid (Sigma–Aldrich) and 1× antibiotic–antimyotic (Invitrogen) was changed thrice weekly. Prior to being used for experiments, cells were seeded on 12-well tissue culture plates (Thermo Fisher Scientific, Pittsburg, PA, USA) at a seeding density of 1–2 × 105 cells/well and maintained in culture medium DMEM/F12 (1:1) supplemented with 10% FBS and 1× antibiotic-antimyotic. After a day of incubation in a CO2 incubator, culture medium in all wells was replaced with fresh medium with 0.1% FBS (3.5 mL/well) and incubated again for a day prior to US exposure. All experiments were performed with passage 2 cells.
Ultrasound stimulation
An investigation into the macroscopic effects of US in the bioreactor used in the current research (Subramanian et al. 2013) showed that the employed US stimulation did not result in any thermal or cavitational effects. Reactive oxygen species, a possible byproduct of sonication, was not detected (Subramanian et al. 2013). This provides sufficient reason to believe that any bioeffect reported in this study is not caused by cavitation, but is related to the subtle effects of low-intensity US.
The total US stimulation time was chosen such that the number of cycles is approximately constant (3 × 108 cycles) and is of the same order as in previous work (Noriega et al. 2007; Parvizi et al. 1999). The pressure amplitude of 14 kPa was also kept constant by adjusting the input voltages at a given frequency. The US parameters used are listed in Table 3. Chondrocytes that are not stimulated by US served as controls. On conclusion of the US stimulation step, plates were allowed to incubate in the CO2 incubator for an additional 10 min before protein isolation and 1.5 h before mRNA isolation. Experiments were carried out in triplicate. Protein pooled from four separate wells and mRNA pooled from three separate wells that were treated identically served as a representative replicate. US stimulation was performed as described by Noriega et al. (2007). Briefly, US was applied to the cells (plated in 12-well TCP plates, 16 mm high and 22 mm in diameter) using a non-focused immersion transducer (V300, Panametrics, Waltham, MA, USA) 12.7 mm in diameter and 5-MHz center frequency. The US transducer was placed in the medium directly above the plate, 6 mm above the well bottom. The transducer was sterilized with ethanol before each application.
Table 3. Ultrasonic stimulation parameters.
| Frequency | 2 MHz | 5 MHz | 8 MHz |
|---|---|---|---|
| Transducer input voltage (peak-to-peak) | 6V | 2.5 V | 9.5 V |
| Ultrasound exposure time | 150 s | 60 s | 37.5 s |
| Applications | 1 | 1 | 1 |
| Output pressure | 14 kPa | 14 kPa | 14 kPa |
Chondrocytes were also stimulated by US in the presence of an ERK phosphorylation inhibitor. Chondrocytes were pretreated for 4 h with a 25 μM concentration of ERK inhibitor PD98059 dissolved in sterile DMSO (LC Laboratories, Woburn, MA, USA) before US stimulation was carried out. Three separate controls were done: control with medium alone, vehicle control with DMSO (0.125% v/v) and inhibitor control with 25 μM PD98059.
mRNA gene expression analysis
Experiments were first carried out to ascertain the time-dependent expression of the early response genes on conclusion of the US stimulation. mRNA was collected after 1, 2, 3 and 6 h of US stimulation, and quantitative reverse transcription polymerase chain reaction (qRT-PCR) was employed to quantify the levels of gene expression. Peak gene expression levels were noted between 1 and 2 h post-stimulation; and levels of gene expression were noted to return to baseline after 6 h post-stimulation. Thus, in all studies, mRNA was collected 1.5 h after US exposure. Cell-seeded tissue culture plates were washed with ice-cold Hank's balanced saline solution (HBSS) and incubated with 200 μl/well Trizol reagent (Invitrogen) with periodic mixing for 5 min. Cell homogenate was collected. RNA was isolated from cell homogenate using the Qiagen RNeasy Mini Kit (Qiagen, Valencia, CA, USA). The mRNA level was quantified by using qRT-PCR. The qRT-PCR analysis was carried out using the QuantiFast Probe RT-PCR Kit (Qiagen). Fifty nanograms of total RNA was added per 10-μL reaction vial with RT mix, RT-PCR master mix, sequence-specific primers and Taqman probes. Sequences for all target gene primers and probes were purchased commercially (GAPDH as internal control; Applied Biosystems, Foster City, CA, USA) and are listed in Table 4. qRT-PCR assays were carried out in triplicate on Eppendorf's mastercycler realplex real-time PCR system (Eppendorf North America, Hauppauge, NY, USA). Cycling was initiated by 10 min of cDNA formation by reverse transcriptase enzyme at 50°C and 5 min polymerase activation at 95°C, followed by 40 cycles at 95°C for 30 s, at 55°C for 30 s and at 72°C for 1 min. The threshold was set above the non-template control background and within the linear phase of target gene amplification to calculate the cycle number at which the transcript was detected.
Table 4. Polymerase chain reaction primers and conditions.
| Primers purchased directly from Applied Biosystems Inventory | |||||
|---|---|---|---|---|---|
|
|
|||||
| Sample No. | Gene | Species | Taqman probe dye | Catalog No. | |
| 1 | GAPDH | Bovine | FAM-6 | Bt03210917_g1 | |
| 2 | c-Fos | Bovine | FAM-6 | Bt03244536_m1 | |
| 3 | c-Myc | Bovine | FAM-6 | Bt03260377_m1 | |
|
| |||||
| Custom-designed primer ordered from Applied Biosystems | |||||
|
| |||||
| 4 | Gene | c-Jun | |||
| Accession No. | NM_001077827 | ||||
| Species | Bovine | ||||
| Product length | 124 bp | ||||
| Taqman probe dye | FAM-6 | ||||
|
| |||||
| Primer/probe | Sequence | Tm (°C) | |||
|
| |||||
| Forward Primer (5′–3′) | GTGACGGACTGTTCTATG | 60.9 | |||
| Reverse Primer (5′–3′) | TCTGCTTCAGAATCTTGG | 60.4 | |||
| Taqman Probe (5′–3′) | ACGACCTTCTACGACGATGCC | 69.8 | |||
Protein extraction
Culture medium was removed from chondrocytes incubated for 10 min after US stimulation and from control chondrocytes that did not receive US stimulation; the chondrocytes were rinsed thrice with ice-cold HBSS (Invitrogen) and then incubated in ice-cold Pierce IP lysis buffer (Thermo Scientific Pierce, Rockford, IL, USA) supplemented with 1× Halt protease and phosphatase inhibitor cocktail (Thermo Scientific Pierce). One hundred microliters of IP lysis buffer with Halt inhibitor was added to each well and incubated for 15 min with periodic mixing at 4°C prior to combining the lysate from four wells, which served as replicate of each treatment group. Cell debris was removed, and supernatant was collected in new vials after centrifugation at 15,000g for 10 min at 4°C. The protein concentration of each sample was determined using a QuantiPro BCA Assay Kit (Sigma–Aldrich).
Western blot analysis
Five to ten micrograms of proteins from each sample was subjected to sodium dodecyl sulfate–polyacrylamide gel electrophoresis (SDS-PAGE) analysis using the Nu-PAGE system following the manufacturer's instructions (Invitrogen). Proteins were denatured with NuPAGE lithium dodecyl sulfate sample buffer (LDS; Invitrogen) and then heated at 74°C for 10 min in a heating block. Each denatured protein sample was separated with electrophoresis on NuPAGE 4%–12% Bis-Tris gels (Invitrogen) and transferred to Immobilon-P polyvinyldifluoridene (PVDF) membranes (Millipore, Billerica, MA, USA) using a Pierce fast semidry blotter according to the manufacturer's protocol (Thermo Scientific Pierce). Membranes were blocked in Tris-buffered saline with 0.1% Tween-20 (TBST) containing 0.5% casein for 1 h, and then incubated in TBST containing primary antibody overnight at 4°C under gentle rocking. After being washed, membranes were incubated in TBST containing secondary horseradish peroxidase (HRP)-linked antibodies for 2 h at room temperature. Membranes were rinsed with TBST, and protein bands were visualized using an Immun-star HRP substrate kit (Bio-Rad Laboratories, Hercules, CA, USA) and captured with Amersham Hyperfilm ECL (GE Healthcare, Piscataway, NJ, USA). The primary antibodies used were: p44/42 MAPK (Erk1/2) antibody produced in rabbit (1:1000, Cell Signaling Technology, Danvers, MA, USA) and Phospho-p44/42 MAPK (Erk1/2) (Thr202/Tyr204) antibody produced in rabbit (1:1000; Cell Signaling Technology). Anti-β-actin primary antibody produced in mouse (1:1000; Sigma–Aldrich) was used as a loading control. Secondary antibodies used were: goat anti-rabbit IgG-HRP conjugated anti-rabbit (1:5000; KPL, Gaithersburg, MD, USA) and goat anti-mouse IgG-HRP conjugated (1:5000; KPL). Band intensities were quantified densitometrically using ImageJ software, Version 1.45 s (Abramoff 2004). The values reported were normalized to unstimulated controls. For analysis of the effects of US stimulation on protein levels, data are the means and standard deviations of two independent estimations.
Statistical analysis
One-way analysis of variance (ANOVA) followed by Tukey's post hoc test was performed for statistical analysis of experimental data. p < 0.05 (compared to control) was considered significant.
Results
Experimental results
Load-inducible gene expression is maximized at resonance
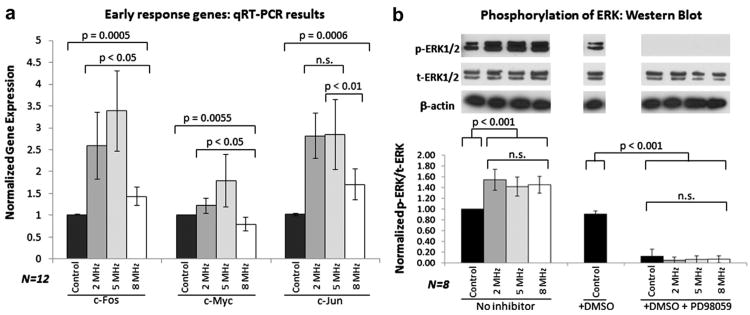
Normalized levels of gene expression of c-Jun, c-Myc and c-Fos at varying US frequencies are shown in Figure 2a (constant pressure amplitude, 14 kPa). At 5 MHz, 3.5-, 3.0- and 1.8-fold higher levels of gene expression of c-Fos, c-Jun and c-Myc, respectively, were noted. Elevated levels of gene expression were also noted at 2 and 8 MHz, but to a lesser extent. The manyfold increase in c-series genes provides strong evidence of the dependence of gene expression on US frequency. Inclusion of the ERK inhibitor, PD98059, led to suppression of the US-induced gene expression of the early response genes. This confirms the role of the MAPPK/ERK signaling pathway (see Fig. 3 [Noriega et al. 2012]) in c-series gene regulation (Whitney et al. 2012).
Fig. 2.
Experimental results with varying-frequency ultrasound (US) stimulation. (a) The expression of early response genes c-Fos, c-Jun and c-Myc after exposure to US with variable frequency was measured. The amount of c-series genes is maximizedatan US frequency of 5 MHz. (b) The c-series genes are activated via the ERK pathway when phosphorylated ERK (p-ERK) enters the nucleus. Expression and phosphorylation of ERK do not change dramatically with US stimulation, and phosphorylation is completely suppressed by the PD98059 inhibitor. DMSO (the PD98059 carrier) does not affect p-ERK levels. Because US frequency does not affect the amount of p-ERK, it would appear that US must enhance some process downstream of ERK phosphorylation. Error bars represent standard deviations. DMSO = dimethyl sulfoxide, n.s. = not statistically significant, qRT-PCR = quantitative reverse transcription polymerase chain reaction.
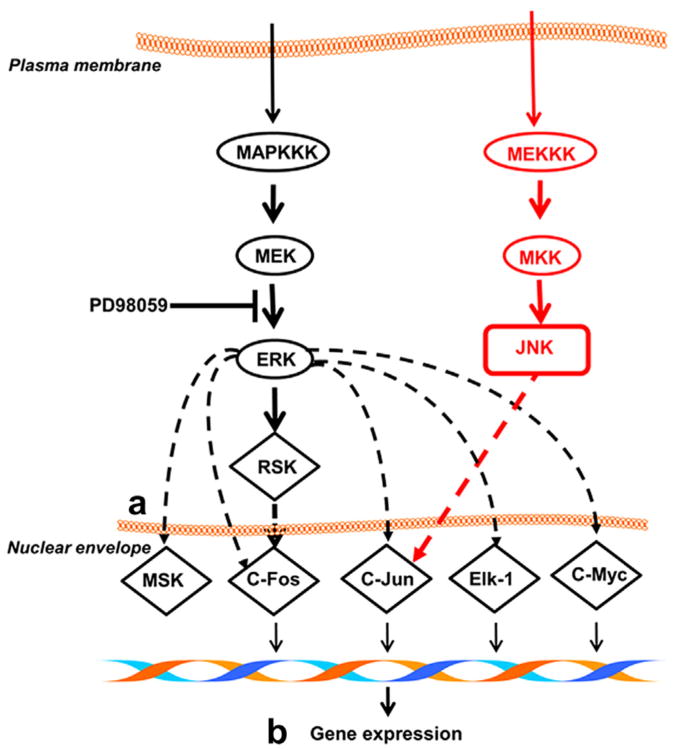
Fig. 3.
Expression of c-Fos, c-Jun and c-Myc is activated when ERK is phosphorylated and enters the nucleus. c-Jun may also be activated through the JNK pathway. The PD98059 inhibitor prevents phosphorylation of ERK. Ultrasound likely affects processes downstream of ERK phosphorylation, which may include (a) transport across the nuclear envelope and (b) chromatin reorganization.
p-ERK concentration is only weakly dependent on frequency
The extent of ERK phosphorylation (p-ERK) in cells under US stimulation is shown in Figure 2b. No significant differences in total ERK (t-ERK) could be detected when compared with controls. Elevated levels of p-ERK were noted in all cells that were subjected to US stimulation, illustrating the role of ERK phosphorylation in mechanotransduction. No appreciable differences in the amount of p-ERK levels were noted between cells subjected to US stimulation at various frequencies. Adding PD98059 abrogated any increase in p-ERK levels. ERK phosphorylation is clearly a prerequisite for the production of c-series genes in response to mechanical stimulation, but the extent of the response is regulated by mechanosensitive processes downstream of phosphorylation in the MAPPK/ERK pathway. One possibility is that US influences p-ERK transport from the cytoplasm to the nucleus. Alternatively (or additionally), mechanical stimulation could result in minor chromatin reorganization, providing access to transcription factors. This postulate is corroborated by previous experimental work conducted in our lab, in which we showed that US stimulation induced chromatin remodeling as measured by dynamic scanning calorimetry (Noriega et al. 2012). The amount of structural reorganization and/or enhanced ERK transport depends directly on nuclear stress and displacement induced by US stimulation. The magnitude of stress and strain was determined by mathematical modeling.
Model results
Prediction of standing wave fields in the tissue culture well
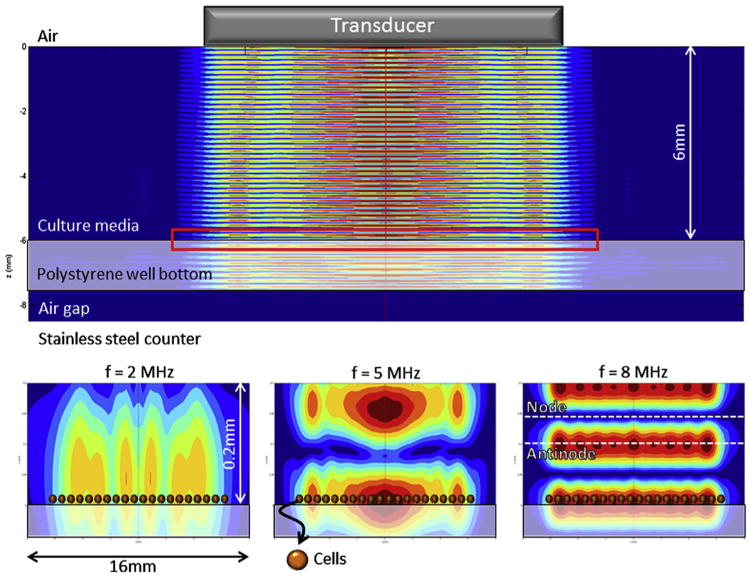
The predicted standing wave field is shown in Figure 4. The US transducer has a radius of 6.35 mm, which is much greater than the wavelength of the acoustic field in water (λ > 100 μm). The result is a highly directive US beam, and we predict minimal reflection from the well walls. The transducer was held 6 mm above the well bottom, but the position may vary slightly between experiments, which will in turn affect the pressure amplitude, but not the position of the nodes. The variation in pressure amplitude will be random and, thus, will bear no statistical significance on the final experimental results.
Fig. 4.
(Top) Acoustic field resulting from application of continuous ultrasound (US) at 5 MHz to the tissue culture well using a transducer. Colors indicate the normalized pressure amplitude. The polystyrene–air interface acts as a complete pressure-release reflector, and standing waves are formed. The red rectangle indicates the region of the closeups displayed in the bottom half. (Bottom) A closeup of the well bottom shows that cells (indicated here by superimposed spheres) are located close to a pressure antinode at US frequencies of 2, 5 and 8 MHz, so experimental results will be comparable. Note that the cell height is drawn to scale in the current figure, but the cell width is not.
Cells located at pressure nodes will be affected differently than cells located at pressure antinodes. The dominant feature in the system affecting the standing wave field is the air gap located directly below the polystyrene well bottom, where almost 100% reflection of US waves occurs (pressure release layer). Pressure nodes are spaced at a set distance from this interface, nλ/2(n∈ℤ), their position depending only on the acoustic wavelength λ and, thus, the US frequency. Figure 4 shows the standing wave fields at frequencies 2, 5 and 8 MHz, cells are always located near pressure antinodes at these frequencies.
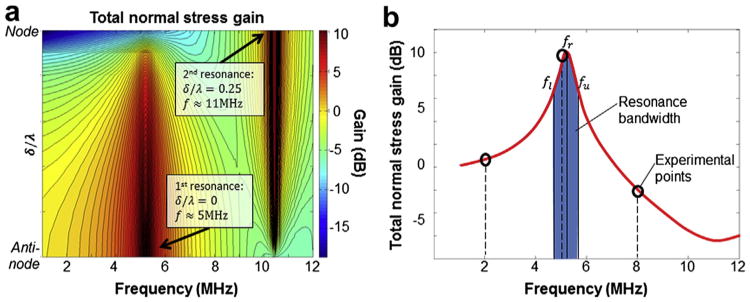
Model predicts cellular resonance in applicable frequency ranges
The main mathematical model results are summarized in Figure 5, which shows the spatially averaged magnitude of the normal stresses in the cytoplasm as a function of frequency and location in the standing wave field (the normal stresses in the solid phase and the pressure in the cytosol are summed). The location in the standing wave is given by δ/λ, where δ is the distance from the nearest pressure antinode and λ is the wavelength:
Fig. 5.
Mathematical model results showing the frequency-dependent stresses in a cell under ultrasound stimulation. (a) The spatially averaged total normal stress gain (in decibels) is shown as a function of frequency and cell position δ/λ. At f = 5 MHz and δ/λ = 0 (antinode), we see a peak corresponding to the first resonance frequency. At f = 11 MHz and δ/λ = 0.25 (node), a second resonance frequency is observed; however, the gain is dependent on the angle θ, and opposite ends of the cell are 180° out of phase with each other (see Fig. 6). (b) The bandwidth is defined as the region fl<f<fu where the normal stress gain is equal to half its maximum value at fu and fl. Experimental points are also indicated (o), showing that only the experiment at 5 MHz lies within the resonance bandwidth.
From Figure 5a we see that the stresses are maximized near f ≈ 5 MHz and δ/λ = 0. We refer to this point as the primary resonance. A second, narrower resonance lies near f ≈ 11MHz and δ/λ = 0.25. Only cells located near antinodes experience the primary resonance; the secondary resonance is exclusive to cells located close to nodes, indicating that the resonance behavior is a function of the cell's position in the standing wave field. A more detailed picture of the resonance frequency at δ/λ = 0 is given in Figure 5b. The resonance frequency lies at f = 5.2MHz, and the bandwidth is Δf = 0.8MHz: cells that are exposed to US within the bandwidth region still benefit from resonance effects. Experiments conducted at 2 and 8 MHz are outside the resonant bandwidth, which would account for the decreased levels of gene expression.
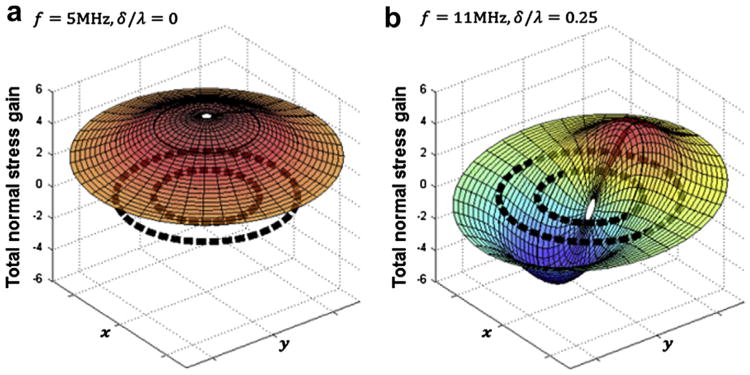
Supplemental animation S1 (online only) shows the stress and strain dynamics for cells stimulated at 2, 5 and 8 MHz. Animation S1 clearly shows that, according to the model predictions, the total normal stress in the cell will be maximized at f = 5MHz and concentrated at the nucleus. Figure 6 (a and b) provide a snapshot of the spatial distribution (r, θ) of total normal stress gain across the entire cell at a moment in time. In Figure 6a (f = 5MHz, antinode), we see that the normal stress is in phase throughout the entire cell and concentrated at the nucleus. In fact, large stress gradients exist near the nuclear envelope. The stress gradients produce net force acting on the nucleus, which oscillates with the US frequency. We propose that these net forces are sensed by the nucleus, resulting in frequency-dependent gene expression. In Figure 6b (f = 11MHz, node) normal stresses are dependent on angle θ and are exactly out of phase on opposite ends of the cell. The phase difference causes shear stress, leading to a different form of mechanical deformation compared with the dilatation at 5 MHz.
Fig. 6.
Snapshot of the oscillating normal stresses in the cell at a moment in time as a function of (r, θ) →(x,y). Dashed black lines indicate the position of the plasma and nuclear membranes. (a) At an antinode, f = 5 MHz, the normal stresses are uniformly distributed throughout the cell, with a maximum in the center (i.e., nucleus). Because of the uniformity of the normal stresses, shear stress is reduced. (b) At a node, f = 11 MHz, the opposing normal stresses causes shear stress in the cell.
The major conclusions of the mathematical model are that stresses and strains in cells are maximized at the resonance frequencies. The location of cells within the standing wave field is also critical, and cellular stimulation varies greatly between positions near pressure nodes and antinodes. For typical chondrocytes, the primary frequency is close to 5 MHz at pressure antinodes and the secondary frequency is near 11 MHz at pressure nodes. At the primary resonance frequency, cells undergo mostly dilatational deformation, and stress gradients are greatest around the nuclear envelope. The stress gradients result in net forces that may be transduced to biochemical signals by the nucleus and subsequently lead to load-inducible gene expression. Because the net forces are frequency dependent, the level of gene expression will also show frequency dependence.
Resonant peaks are sensitive to cell properties
A parameter sensitivity analysis provides information pertaining not only to model uncertainty, but also to the effect of US on various cell types. The primary resonance frequency was calculated for different parameter values, varied one at a time (38 parameters, 53 variations each) as well as simultaneously. To quantify the sensitivity, we defined the variable S, which is the slope of the linear fit to data shown in Figure 7, normalized by the average value of the parameter under investigation. This gives the sensitivity of the resonance frequency (in MHz) to a percentage change in any given parameter. For instance, sensitivity analysis yields S = −5.10 for the cell outer radius. If the radius were to increase from 6.5 to 7 μm (7.6%), the resonance frequency will shift by approximately 0.076 × −5.10 = −0.39 MHz.
Fig. 7.
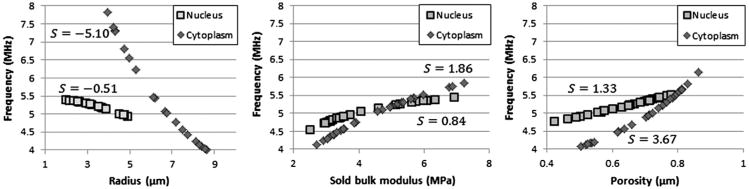
Resonance frequency as a function of the cytoplasmic/nuclear radius, solid-phase bulk modulus and porosity. The sensitivity parameter S is shown for each of the six properties. As expected, the resonance frequency decreases when the cell or nuclear radius increases and exhibits a positive linear relationship with both solid-phase bulk modulus and porosity. In all cases, the resonance frequency lies between 4 and 6 MHz, the exception being cells with outer radii less than 5 μm.
Interestingly, the cell resonance frequency displays very low sensitivity (S < 0.1, 10% change shifts resonance by <0.01 MHz) to most material properties. The exception to this robustness is cell/nuclear radius, fluid-and solid-phase bulk modulus and porosity of both the cytoplasm and the nucleus (see Fig. 7). It is to be expected that the dimensions of a cell will have a notable effect on resonance, an especially important fact when considering different cell types as well as different stages of the cell cycle. Cell porosity (or macromolecular content) is also highly dependent on cell type. However, neither of these parameters can be readily altered in a specific cell. The solid bulk modulus, KS, provides the means for a cell to react to extended mechanical stimulation. Varying KS between 2.5 and 7.5 MPa results in a shift in the resonant peak from 4 to 6 MHz. A single cell may rapidly and transiently cause such a variation through cytoskeletal dynamics, such as actin polymerization and microtubule assembly.
Discussion
Ultrasound stimulation at 2, 5 and 8 MHz increased the expression of early response genes c-Fos, c-Jun and c-Myc, maximized at 5 MHz. The p-ERK level increased with US stimulation, but this increase is not frequency dependent. Although the role of ERK in signal transduction of external stimuli has been demonstrated in a variety of cells, including chondrocytes, our work has shown for the first time that the expression of early response genes caused by low-intensity ultrasound is enhanced at specific frequencies.
The role of the MAPPK/ERK pathway in c-series gene regulation was confirmed when addition of the ERK inhibitor PD98059 reduced the levels of gene expression to those of the non-stimulated control. Taking theoretical and experimental results together suggests that ultrasound at 5 MHz is an effective modulator of certain cellular processes. Our biphasic mathematical model based on Biot theory predicts a primary resonance frequency near 5.2 MHz (bandwidth of 0.8 MHz). The model results enforce the experimental results, as c-series gene expression was maximized at 5 MHz, which is close to the model-predicted resonance frequency. More specifically, the model predicts that stresses and strains are concentrated at the nucleus.
Taking into consideration that the expression of c-series genes is a nuclear process, whereas ERK phos-phorylation is not, we see that US affects various cellular domains differently. ERK phosphorylation increases when the cell experiences mechanical stress, but the amount of p-ERK is independent of the magnitude or frequency of the stimulation. However, expression of c-series genes does change with frequency, which implies that p-ERK transport to the nucleus is enhanced, minor chromatin reorganization occurs, or some other nuclear process is affected. In previous work, we used dynamic scanning calorimetry to show that US does indeed induce minor chromatin reorganization (Noriega et al. 2012), providing more experimental evidence for the ability of the nucleus to directly detect ultrasonic stimulation.
Irrespective of the specifics, the experimental results show that a particular process occurring at the nucleus is sensitive to the frequency of mechanical stimulation, even when the total p-ERK concentration is not. This corroborates the model results, which predicted the concentration of stress and strain at the nucleus. The mechanotransduc-tion pathway thus senses mechanical stimulation at multiple points. Certain steps are “digital,” such as ERK phosphorylation, which increases when the cell experiences mechanical stimulation. Other steps are “analog,” like the nuclear processes preceding c-series gene expression, and vary with ultrasonic frequency. Enhanced nuclear transport at specific frequencies may have further consequences in the study of US-mediated gene delivery.
Cell resonance frequency is sensitive to cell radius, porosity and solid phase bulk modulus. It is important to consider cell radius during sonication of different cell types/cell cycle stages. Furthermore, it is likely that the cell can change its own response to mechanical stimulation by producing transient changes in the solid bulk modulus through cytoskeleton dynamics.
It is clear that cells react to US in subtler ways than can be completely explained by cavitation. The fact that cells, or, specifically, cell nuclei, can sense the frequency and/or magnitude of mechanical stimulation may have far-reaching implications in mechanotransduction research. We see that mechanotransduction, like all forms of cell signaling, occurs through a combination of multiple signaling pathways. Here, ERK phosphorylation is required for c-series gene expression, but the extent of expression is dependent on the nucleus' own ultrasonic perception faculties. Cells may further modulate their response to ultrasonic stimulation by transiently changing their mechanical properties.
Conclusions
We have shown for the first time that ultrasonic frequency must be taken into consideration when investigating the bioeffects of low-intensity ultrasound. We showed that the extent of the cellular response to ultrasound depends on both the frequency of the applied ultrasound and the specific properties of the cell. Clinical trials investigating the effects of therapeutic ultrasound almost always lead to inconclusive results, as cell properties are not taken into account. Our results reveal an additional factor contributing to the healing effects of ultrasound, which must be considered if the positive effects of ultrasound on a cellular level are to be understood and used.
Supplementary Material
Acknowledgments
This work was supported, in part, by American Recovery and Reinvestment Act of 2009 Research Grant 1R21RR024437-01A1 from the Department of Health and Human Services.
Appendix 1. Modeling the Ultrasonic Field in the Tissue Culture Well
To determine the standing wave field in the tissue culture well, we approximate the transducer as a uniformly vibrating piston. We use cylindrical coordinates (r, θ, z), with z being the axial distance from the transducer face. The transducer is circular and centered in the tissue culture well, which means the problem is symmetric around the z-axis and we only use the coordinates (r, z).
Given a medium with density ρ and a transducer vibrating harmonically with radial frequency ω and velocity amplitude νn, the pressure p at any point (r, z) away from the transducer face can be calculated using the equation (Kinsler 2000).
| (A1) |
The wavenumber is , with c being the speed of sound in the medium. dS is an infinitesimal surface element of the transducer, and r′ is, the distance between the point (r, z) and the element dS. Equation (A1) is valid in the near field as well as the far field and can be integrated numerically. We then used a Fourier transform in cylindrical coordinates to decompose the pressure field at z = 0 into plane waves, each with an amplitude A(ξ) and a wavenumber vector [ξ, (k2−ξ)½], as shown in Eq. (A2) (Brekhovskikh and Godin 1992). The original acoustic beam is recovered using Eq. (A3). It is easy to show that Eq. (A3) satisfies the Helmholtz equation with wavenumber k and gives the correct pressure at z = 0.
| (A2) |
| (A3) |
In the implementation, we used a finite number of discrete values ξn so that the integral in Eq. (A3) is replaced by the summation of a series. The reflection and refraction of each plane wave in the system are resolved separately using the transfer matrix method (Allard and Atalla 2009), which requires solving the Helmholtz equation in each of the three layers described below, coupled by appropriate boundary conditions. See Brekhovskikh and Godin (1992) and Allard and Atalla (2009) for details. Finally, the incident, reflected and transmitted plane waves are added together to find the acoustic field generated by the piston transducer.
Appendix 2. Basis of Biot Theory
The model used in this investigation requires some background in the acoustics of porous media. For more details, we refer the reader to Allard and Atalla (2009).
Effective density and tortuosity in porous media with a rigid frame
Consider a fluid (viscosity μ and unperturbed density ρ0) saturating a structure with cylindrical pores parallel to the z-axis, that is, the direction of acoustic wave propagation. The pores have circular cross sections of radius R and rigid walls such that the fluid velocity ν = 0 at the walls. The pressure p is constant across the pore cross section. The linear momentum balance for fluids is given by
| (A4) |
If we assume that the velocity has harmonic time dependence (radial frequency ω) and that the change in velocity in the z direction is negligible in the Laplacian, it can be shown that the average velocity across the pore cross section νz is related to the pressure drop by Eq. (A5), which leads to the definition of the effective density ρ (Eq. [A6]).
| (A5) |
| (A6) |
The effective density is generally a complex number and accounts for damping in the final solution.
The function Gc(s), as well as the variable s, is specific to pores with circular cross sections. However, similar results are obtained for pores of various geometries by making slight changes to the function Gc(s) and the variable s. The flow resistivity ϖ for a layer of porosity φ and cylindrical pores with circular cross sections is given by ϖ = 8μ/φR2 (Allard and Atalla 2009). We can thus substitute ϖ in Eq. (A6) to extend the definition of the effective density to pores with a cross section of arbitrary geometry:
| (A7) |
The function G(s) and variable s is a function of pore geometry. Now consider tortuous pores such that the saturating fluid has a microscopic velocity νm and a macroscopic (average) velocity ν = 〈νm〉; therefore, the average kinetic energy T across a fluid volume is given by (Allard and Atalla 2009).
| (A8) |
The factor of apparent increase in density is called the tortuosity α∞ and is a property of the porous material. Including the tortuosity term leads to the final expression for the effective density:
| (A9) |
The ratio ρ/ρ0 is called the dynamic tortuosity,α(ω). In a real porous layer, the function G(s) cannot be determined analytically, but many approximate models have been suggested. In this work, we use the Johnson et al. (1987) model of dynamic tortuosity, given by
| (A10) |
which also depends on the viscous characteristic length Λ.
Inertial forces and effective densities in porous media with an elastic frame
In the previous section, we considered porous media with a rigid frame, so that the solid-phase velocity νs = 0. To develop the wave equation for “poroelastic” media, we must account for movement of the solid phase. First, we calculate the inertial forces acting on both the solid and fluid phases using a Lagrangian formulation, given that the kinetic energy must be of the form
| (A11) |
where νs and νf are the macroscopic velocities of the solid and fluid phases, respectively. The inertial forces in the solid and fluid phases are found by taking the generalized coordinate derivatives of kinetic energy T, as shown in the following equations:
| (A12) |
| (A13) |
We now derive ρij using two “gedanken” experiments. First, consider the case where the solid and fluid phases move together with the same velocity; then νs = νf = (the microscopic fluid velocity), and kinetic energy is given by
| (A14) |
Here, ρs and ρf are the unperturbed densities of the solid and fluid phases, respectively. Furthermore, the inertial force of the fluid is qf = φρf∂νf/∂t. Keeping in mind that νs = νf = , we can combine this inertial force relationship with Eq. (A13), as well as compare Eqs. (A11) and (A14), which yields the equations
| (A15) |
| (A16) |
Second, consider the case where the fluid flows through a rigid frame, such that νs = 0. From Eq. (A11), as well as the definition of tortuosity (the factor α∞ = ρ/ρ0 which accounts for the ratio between the microscopic and macroscopic velocity, squared), we see that ρ22 is given by
| (A17) |
Equations (A15)–(A17) provide the means to uniquely determine ρij, given ρf, ρs, φ and α∞. If, instead of the static tortuosity α∞, we use the dynamic tortuosity α(ω), we obtain a set of effective densities ρ̃ij, which accounts for viscous forces.
Stress and strain relations in porous media
When considering fluid-saturated porous media, it is important to discriminate between the porous frame, the solid phase and the saturating fluid. For instance, the compressibility of glass wool (the frame) is very high, but the compressibility of glass (solid phase) is not. In the following relationships, refers to the ij th component of the locally averaged stress tensor of the solid frame, whereas is the stress tensor component of the saturating fluid, with p being the fluid pressure and δij the Kronecker delta. The stress and strain relationships pertaining to poroelastic media are given by the following equations (Allard and Atalla 2009):
| (A18) |
| (A19) |
The infinitesimal strain tensor for the solid phase is given by , and the dilatation of both the fluid and solid phases is given by , where i = s,f. The parameters P, Q and R are related to the mechanical properties of the frame, the solid phase and the fluid phase. This is done through two “gedanken experiments.” First, imagine that the frame is jacketed and subjected to a pressure pJ, while the fluid pressure in the pores remains constant at p0, such that and in Eqs. (A18) and (A19). The drained bulk modulus of the frame is defined by
| (A20) |
In the second experiment, the fluid pressure in an unjacketed volume of porous material is increased to pF. The stress is carried by both the solid and fluid phases, such that and (remember that is the average of the local stress tensors). The bulk moduli of the solid and fluid phases are given by
| (A21) |
| (A22) |
Substitution of the values of and from the two “gedanken experiments” into Eqs. (A18) and (A19) yields four equations. We can eliminate Θs, Θf, pJ and pF using Eqs. (A20)–(A22), which gives
| (A23) |
The parameter N is the shear modulus of the solid phase. Equation (A23) can be solved to give P, Q and R, given the porosity φ and the bulk moduli Ki.
Wave equation in porous media
After constructing a force balance using the stress and strain relationships (Eqs. [A18] and [A19]), the inertial forces (Eqs. [A12] and [A13]) and the displacement potentials defined by Eq. (A24), it can be shown that the wave equations for poroelastic media are given by Eqs. (A25) and (A26):
| (A24) |
| (A25) |
| (A26) |
The irrotational scalar and rotational vectorial displacement potentials are given by φi and Ψi, respectively, where superscript i = s,f refers to either the (s)olid or the (f)luid phase. The vector ui is the displacement. The systems represented by Eqs. (A25) and (A26) can be uncoupled using eigenvector decomposition (Eqs. [A27] and [A28]). The resulting system of partial differential equations is solved by separation of variables. This results in three waves in each of the four biphasic domain (Eqs. [A29] and [A30]), two longitudinal waves from Eq. (A25) and one shear wave from Eq. (A26).
| (A27) |
| (A28) |
| (A29) |
| (A30) |
Here, [1, μ1], [1, μ2] and k1,k2 are the eigenvectors and eigenvalues of Eq. (A25), and [1, μ3] and k3 are the first eigenvector and eigenvalue of Eq. (A26) (the second eigenvalue for Eq. [A26] is exactly zero).
Footnotes
The authors declare no conflict of interest.
Supplementary Data: Supplementary data related to this article can be found online at http://dx.doi.org/10.1016/j.ultrasmedbio.2013.01.015.
References
- Abramoff MD, Magalhaes PJ, Ram SJ. Image processing with ImageJ. Biophotonics Int. 2004;11:36–42. [Google Scholar]
- Allard JF, Atalla N. Propagation of sound in porous media: Modelling sound absorbing materials. 2nd. Hoboken, NJ: Wiley; 2009. [Google Scholar]
- Baaijens FP, Trickey WR, Laursen TA, Guilak F. Large deformation finite element analysis of micropipette aspiration to determine the mechanical properties of the chondrocyte. Ann Biomed Eng. 2005;33:494–501. doi: 10.1007/s10439-005-2506-3. [DOI] [PubMed] [Google Scholar]
- Beier F, Leask TA, Haque S, Chow C, Taylor AC, Lee RJ, Pestell RG, Ballock RT, LuValle P. Cell cycle genes in chondrocyte proliferation and differentiation. Matrix Biol. 1999;18:109–120. doi: 10.1016/s0945-053x(99)00009-8. [DOI] [PubMed] [Google Scholar]
- Berryman JG. Measures of microstructure to improve estimates and bounds on elastic constants and transport coefficients in heterogeneous media. Mech Mater. 2006;38:732–747. [Google Scholar]
- Bidhendi AJ, Korhonen RK. A finite element study of micropipette aspiration of single cells: Effect of compressibility. Comput Math Methods Med. 2012;2012:192618. doi: 10.1155/2012/192618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brekhovskikh LM, Godin OA. Acoustics of layered media II: Point source and bounded beams. Berlin/New York: Springer-Verlag; 1992. [Google Scholar]
- Cole MD. The myc oncogene: Its role in transformation and differentiation. Annu Rev Genet. 1986;20:361–384. doi: 10.1146/annurev.ge.20.120186.002045. [DOI] [PubMed] [Google Scholar]
- Copland IB, Post M. Stretch-activated signaling pathways responsible for early response gene expression in fetal lung epithelial cells. J Cell Physiol. 2007;210:133–143. doi: 10.1002/jcp.20840. [DOI] [PubMed] [Google Scholar]
- Dahl KN, Booth-Gauthier EA, Ladoux B. In the middle of it all: Mutual mechanical regulation between the nucleus and the cytoskeleton. J Biomech. 2010;43:2–8. doi: 10.1016/j.jbiomech.2009.09.002. [DOI] [PubMed] [Google Scholar]
- Dalecki D. Mechanical bioeffects of ultrasound. Annu Rev Biomed Eng. 2004;6:229–248. doi: 10.1146/annurev.bioeng.6.040803.140126. [DOI] [PubMed] [Google Scholar]
- Darling EM, Topel M, Zauscher S, Vail TP, Guilak F. Viscoelastic properties of human mesenchymally-derived stem cells and primary osteoblasts, chondrocytes, and adipocytes. J Biomech. 2008;41:454–464. doi: 10.1016/j.jbiomech.2007.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Albornoz PM, Khanna A, Longo UG, Forriol F, Maffulli N. The evidence of low-intensity pulsed ultrasound for in vitro, animal and human fracture healing. Br Med Bull. 2011;100:39–57. doi: 10.1093/bmb/ldr006. [DOI] [PubMed] [Google Scholar]
- Ebner HL, Fiechtner B, Pelster B, Krumschnabel G. Extracellular signal regulated MAP-kinase signalling in osmotically stressed trout hepatocytes. Biochim Biophys Acta. 2006;1760:941–950. doi: 10.1016/j.bbagen.2006.03.017. [DOI] [PubMed] [Google Scholar]
- Fowlkes JB. American Institute of Ultrasound in Medicine consensus report on potential bioeffects of diagnostic ultrasound: Executive summary. J Ultrasound Med. 2008;27:503–515. doi: 10.7863/jum.2008.27.4.503. [DOI] [PubMed] [Google Scholar]
- Gekko K, Hasegawa Y. Compressibility–structure relationship of globular proteins. Biochemistry. 1986;25:6563–6571. doi: 10.1021/bi00369a034. [DOI] [PubMed] [Google Scholar]
- Greenberg ME, Greene LA, Ziff EB. Nerve growth factor and epidermal growth factor induce rapid transient changes in proto-oncogene transcription in PC12 cells. J Biol Chem. 1985;260:14101–14110. [PubMed] [Google Scholar]
- Guilak F, Mow VC. The mechanical environment of the chondrocyte: A biphasic finite element model of cell–matrix interactions in articular cartilage. J Biomech. 2000;33:1663–1673. [PubMed] [Google Scholar]
- Guilak F, Tedrow JR, Burgkart R. Viscoelastic properties of the cell nucleus. Biochem Biophys Res Commun. 2000;269:781–786. doi: 10.1006/bbrc.2000.2360. [DOI] [PubMed] [Google Scholar]
- Gutberlet T, Katsaras J. Lipid bilayers: Structure and interactions. Berlin/New York: Springer; 2001. [Google Scholar]
- Haider MA, Guilak F. Application of a three-dimensional poroelastic BEM to modeling the biphasic mechanics of cell–matrix interactions in articular cartilage (REVISION) Computer Methods Appl Mech Eng. 2007;196:2999–3010. doi: 10.1016/j.cma.2006.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann C, Delgado A. Numerical simulation of the mechanics of a yeast cell under high hydrostatic pressure. J Biomech. 2004;37:977–987. doi: 10.1016/j.jbiomech.2003.11.028. [DOI] [PubMed] [Google Scholar]
- Hasanova GI, Noriega SE, Mamedov TG, Thakurta SG, Turner JA, Subramanian A. The effect of ultrasound stimulation on the gene and protein expression of chondrocytes seeded in chitosan scaffolds. J Tissue Eng Regen Med. 2011;5:815–822. doi: 10.1002/term.384. [DOI] [PubMed] [Google Scholar]
- Hasegawa T, Yosioka K. Acoustic-radiation force on a solid elastic sphere. J Acoust Soc Am. 1969;46:1139–1143. [Google Scholar]
- Hasheminejad SM, Bahari A, Abbasion S. Modeling and simulation of acoustic pulse interaction with fluid-flow hollow elastic sphere through numerical Laplace inversion. Appl Math Model. 2011;35:22–49. [Google Scholar]
- Hsu HC, Fong YC, Chang CS, Hsu CJ, Hsu SF, Lin JG, Fu WM, Yang RS, Tang CH. Ultrasound induces cyclooxygenase-2 expression through integrin, integrin-linked kinase, Akt, NF-kappaB and p300 pathway in human chondrocytes. Cell Signal. 2007;19:2317–2328. doi: 10.1016/j.cellsig.2007.07.006. [DOI] [PubMed] [Google Scholar]
- Izvekov S, Voth GA. Solvent-free lipid bilayer model using multiscale coarse-graining. J Phys Chem B. 2009;113:4443–4455. doi: 10.1021/jp810440c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DL, Koplik J, Dashen R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J Fluid Mech. 1987;176:379–402. [Google Scholar]
- Kasas S, Kis A, Riederer BM, Forro L, Dietler G, Catsicas S. Mechanical properties of microtubules explored using the finite elements method. Chemphyschem. 2004;5:252–257. doi: 10.1002/cphc.200300799. [DOI] [PubMed] [Google Scholar]
- Kestin J, Sokolov M, Wakeham WA. Viscosity of liquid water in range –8-Degrees-C to 150-Degrees-C. J Phys Chem Ref Data. 1978;7:941–948. [Google Scholar]
- Kim E, Guilak F, Haider MA. The dynamic mechanical environment of the chondrocyte: A biphasic finite element model of cell–matrix interactions under cyclic compressive loading. J Biomech Eng. 2008;130:061009. doi: 10.1115/1.2978991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinsler LE. Fundamentals of acoustics. 4th. New York: Wiley; 2000. [Google Scholar]
- Krasovitski B, Frenkel V, Shoham S, Kimmel E. Intramembrane cavitation as a unifying mechanism for ultrasound-induced bioeffects. Proc Natl Acad Sci USA. 2011;108:3258–3263. doi: 10.1073/pnas.1015771108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn T, Ihalainen TO, Hyvaluoma J, Dross N, Willman SF, Langowski J, Vihinen-Ranta M, Timonen J. Protein diffusion in mammalian cell cytoplasm. Plos One. 2011;6:e22962. doi: 10.1371/journal.pone.0022962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leipzig ND, Athanasiou KA. Unconfined creep compression of chondrocytes. J Biomech. 2005;38:77–85. doi: 10.1016/j.jbiomech.2004.03.013. [DOI] [PubMed] [Google Scholar]
- Lemmon EW, McLinden MO, Friend DG. Thermophysical properties of fluid systems. In: Linstrom PJ, Mallard WG, editors. NIST Chemistry WebBook. Gaithersburg, MD: National Institute of Standards and Technology; 2011. NIST Standard Reference Database No. 69. [Google Scholar]
- Leuba SH, Yang G, Robert C, Samori B, van Holde K, Zlatanova J, Bustamante C. Three-dimensional structure of extended chromatin fibers as revealed by tapping-mode scanning force microscopy. Proc Natl Acad Sci USA. 1994;91:11621–11625. doi: 10.1073/pnas.91.24.11621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang HD, Tang J, Halliwell M. Sonoporation, drug delivery, and gene therapy. Proc Inst Mech Eng H. 2010;224:343–361. doi: 10.1243/09544119JEIM565. [DOI] [PubMed] [Google Scholar]
- Minton AP. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J Biol Chem. 2001;276:10577–10580. doi: 10.1074/jbc.R100005200. [DOI] [PubMed] [Google Scholar]
- Mitchison TJ, Charras GT, Mahadevan L. Implications of a poroelastic cytoplasm for the dynamics of animal cell shape. Semin Cell Dev Biol. 2008;19:215–223. doi: 10.1016/j.semcdb.2008.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naito K, Watari T, Muta T, Furuhata A, Iwase H, Igarashi M, Kurosawa H, Nagaoka I, Kaneko K. Low-intensity pulsed ultrasound (LIPUS) increases the articular cartilage type II collagen in a rat osteoarthritis model. J Orthop Res. 2010;28:361–369. doi: 10.1002/jor.20995. [DOI] [PubMed] [Google Scholar]
- Nelson TR, Fowlkes JB, Abramowicz JS, Church CC. Ultrasound biosafety considerations for the practicing sonographer and sonologist. J Ultrasound Med. 2009;28:139–150. doi: 10.7863/jum.2009.28.2.139. [DOI] [PubMed] [Google Scholar]
- Nishikori T, Ochi M, Uchio Y, Maniwa S, Kataoka H, Kawasaki K, Katsube K, Kuriwaka M. Effects of low-intensity pulsed ultrasound on proliferation and chondroitin sulfate synthesis of cultured chondrocytes embedded in Atelocollagen gel. J Biomed Mater Res. 2002;59:201–206. doi: 10.1002/jbm.1226. [DOI] [PubMed] [Google Scholar]
- Nolen-Hoeksema RC. Modulus–porosity relations, Gassmann's equations, and the low-frequency elastic-wave response to fluids. Geophysics. 2000;65:1355–1363. [Google Scholar]
- Noriega S, Budhiraja G, Subramanian A. Remodeling of chromatin under low intensity diffuse ultrasound. Int J Biochem Cell Biol. 2012;44:1331–1336. doi: 10.1016/j.biocel.2012.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noriega SE, Mammedov T, Turner JA, Subramanian A. Intermittent applications of continuous ultrasound on the viability, proliferation, morphology and matrix production of chondrocytes in 3D matrices. Tissue Eng. 2007;13:611–618. doi: 10.1089/ten.2006.0130. [DOI] [PubMed] [Google Scholar]
- Noriega SE, Subramanian A. Consequences of neutralization on the proliferation and cytoskeletal organization of chondrocytes on chitosan-based matrices. Int J Carbohydrate Chem. 2011;2011:809743. [Google Scholar]
- Or M, Kimmel E. Modeling linear vibration of cell nucleus in low intensity ultrasound field. Ultrasound Med Biol. 2009;35:1015–1025. doi: 10.1016/j.ultrasmedbio.2008.11.011. [DOI] [PubMed] [Google Scholar]
- Ovalle-García E, Torres-Heredia JJ, Antillon A, Ortega-Blake I. Simultaneous determination of the elastic properties of the lipid bilayer by atomic force microscopy: Bending, tension, and adhesion. J Phys Chem B. 2011;115:4826–4833. doi: 10.1021/jp111985z. [DOI] [PubMed] [Google Scholar]
- Paci E, Marchi M. Intrinsic compressibility and volume compression in solvated proteins by molecular dynamics simulation at high pressure. Proc Natl Acad Sci USA. 1996;93:11609–11614. doi: 10.1073/pnas.93.21.11609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parvizi J, Wu C, Lewallwen DG, Greenleaf JF, Bolander ME. Low-intensity ultrasound stimulates proteoglycan synthesis in rat chondrocytes by increasing aggrecan gene expression. J Orthop Res. 1999;17:488–494. doi: 10.1002/jor.1100170405. [DOI] [PubMed] [Google Scholar]
- Patra M, Karttunen M, Hyvonen MT, Falck E, Lindqvist P, Vattulainen I. Molecular dynamics simulations of lipid bilayers: Major artifacts due to truncating electrostatic interactions. Biophys J. 2003;84:3636–3645. doi: 10.1016/S0006-3495(03)75094-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pride SR, Berryman JG. Linear dynamics of double-porosity dualpermeability materials: II. Fluid transport equations. Phys Review E. 2003;68:036604. doi: 10.1103/PhysRevE.68.036604. [DOI] [PubMed] [Google Scholar]
- Ramos JW. The regulation of extracellular signal-regulated kinase (ERK) in mammalian cells. Int J Biochem Cell Biol. 2008;40:2707–2719. doi: 10.1016/j.biocel.2008.04.009. [DOI] [PubMed] [Google Scholar]
- Rowat AC, Lammerding J, Herrmann H, Aebi U. Towards an integrated understanding of the structure and mechanics of the cell nucleus. BioEssays. 2008;30:226–236. doi: 10.1002/bies.20720. [DOI] [PubMed] [Google Scholar]
- Rowat AC, Lammerding J, Ipsen JH. Mechanical properties of the cell nucleus and the effect of emerin deficiency. Biophys J. 2006;91:4649–4664. doi: 10.1529/biophysj.106.086454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin C, Bolander M, Ryaby JP, Hadjiargyrou M. The use of low-intensity ultrasound to accelerate the healing of fractures. J Bone Joint Surg Am. 2001;83:259–270. doi: 10.2106/00004623-200102000-00015. [DOI] [PubMed] [Google Scholar]
- Sena K, Leven RM, Mazhar K, Sumner DR, Virdi AS. Early gene response to low-intensity pulsed ultrasound in rat osteoblastic cells. Ultrasound Med Biol. 2005;31:703–708. doi: 10.1016/j.ultrasmedbio.2005.01.013. [DOI] [PubMed] [Google Scholar]
- Sept D, MacKintosh FC. Microtubule elasticity: Connecting all-atom simulations with continuum mechanics. Phys Rev Lett. 2010;104:018101. doi: 10.1103/PhysRevLett.104.018101. [DOI] [PubMed] [Google Scholar]
- Shieh AC, Athanasiou KA. Biomechanics of single zonal chondrocytes. J Biomech. 2006;39:1595–1602. doi: 10.1016/j.jbiomech.2005.05.002. [DOI] [PubMed] [Google Scholar]
- Shivaram GM, Kim CH, Batra NN, Yang W, Harris SE, Jacobs CR. Novel early response genes in osteoblasts exposed to dynamic fluid flow. Philos Trans Ser A. 2010;368:605–616. doi: 10.1098/rsta.2009.0231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sng JC, Taniura H, Yoneda Y. A tale of early response genes. Biol Pharm Bull. 2004;27:606–612. doi: 10.1248/bpb.27.606. [DOI] [PubMed] [Google Scholar]
- Song G, Yuan L, Luo Q, Yang L, Ju Y. ERK1/2 mediates mechanical stretch-induced proliferation of bone marrow-derived mesenchymal stem cells. IFMBE Proc. 2010;31:1125–1128. [Google Scholar]
- Subramanian A, Turner JA, Budhiraja G, Guha Thakurta S, Whitney NP, Nudurupati SN. Ultrasonic bioreactor as a platform for studying cellular response to ultrasound. Tissue Eng Part C Methods. 2013;19:244–255. doi: 10.1089/ten.tec.2012.0199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szafranski JD, Grodzinsky AJ, Burger E, Gaschen V, Hung HH, Hunziker EB. Chondrocyte mechanotransduction: Effects of compression on deformation of intracellular organelles and relevance to cellular biosynthesis. Osteoarthritis Cartilage. 2004;12:937–946. doi: 10.1016/j.joca.2004.08.004. [DOI] [PubMed] [Google Scholar]
- Trickey WR, Baaijens FPT, Laursen TA, Alexopoulos LG, Guilak F. Determination of the Poisson's ratio of the cell: Recovery properties of chondrocytes after release from complete micropipette aspiration. J Biomech. 2006;39:78–87. doi: 10.1016/j.jbiomech.2004.11.006. [DOI] [PubMed] [Google Scholar]
- Trickey WR, Lee GM, Guilak F. Viscoelastic properties of chondrocytes from normal and osteoarthritic human cartilage. J Orthop Res. 2000;18:891–898. doi: 10.1002/jor.1100180607. [DOI] [PubMed] [Google Scholar]
- Tuszynski JA, Luchko T, Portet S, Dixon JM. Anisotropic elastic properties of microtubules. Eur Phys J E. 2005;17:29–35. doi: 10.1140/epje/i2004-10102-5. [DOI] [PubMed] [Google Scholar]
- Vaziri A, Mofrad MR. Mechanics and deformation of the nucleus in micropipette aspiration experiment. J Biomech. 2007;40:2053–2062. doi: 10.1016/j.jbiomech.2006.09.023. [DOI] [PubMed] [Google Scholar]
- Vincenti MP, Brinckerhoff CE. Early response genes induced in chondrocytes stimulated with the inflammatory cytokine interleukin-1beta. Arthritis Res. 2001;3:381–388. doi: 10.1186/ar331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinckier A, Dumortier C, Engelborghs Y, Hellemans L. Dynamical and mechanical study of immobilized microtubules with atomic force microscopy. J Vacuum Sci Technol B. 1995;14:1427–1431. [Google Scholar]
- Whitney NP, Lamb AC, Louw TM, Subramanian A. Integrin-mediated mechanotransduction pathway of low-intensity continuous ultrasound in human chondrocytes. Ultrasound Med Biol. 2012;38:1734–1743. doi: 10.1016/j.ultrasmedbio.2012.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J, Nyborg WL. Ultrasound, cavitation bubbles and their interaction with cells. Adv Drug Delivery Rev. 2008;60:1103–1116. doi: 10.1016/j.addr.2008.03.009. [DOI] [PubMed] [Google Scholar]
- Yamazaki T, Komuro I, Kudoh S, Zou Y, Shiojima I, Mizuno T, Takano H, Hiroi Y, Ueki K, Tobe K. Mechanical stress activates protein kinase cascade of phosphorylation in neonatal rat cardiac myocytes. J Clin Invest. 1995;96:438–446. doi: 10.1172/JCI118054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang RS, Chen YZ, Huang TH, Tang CH, Fu WM, Lu BY, Lin WL. The effects of low-intensity ultrasound on growing bone after sciatic neurectomy. Ultrasound Med Biol. 2005;31:431–437. doi: 10.1016/j.ultrasmedbio.2004.11.010. [DOI] [PubMed] [Google Scholar]
- Yang SK, Huang YC. Erythrocytes damage by ultrasound at different hydrostatic pressures. Biomed Eng Appl Basis Commun. 2001;13:8–13. [Google Scholar]
- Yoon CS, Park JH. Ultrasound-mediated gene delivery. Expert opinion on drug delivery. 2005;7:321–330. doi: 10.1517/17425241003596329. [DOI] [PubMed] [Google Scholar]
- Zhang ZJ, Huckle J, Francomano CA, Spencer RG. The effects of pulsed low-intensity ultrasound on chondrocyte viability, proliferation, gene expression and matrix production. Ultrasound Med Biol. 2003;29:1645–1651. doi: 10.1016/j.ultrasmedbio.2003.08.011. [DOI] [PubMed] [Google Scholar]
- Zinin PV, Allen JS., III Deformation of biological cells in the acoustic field of an oscillating bubble. Phys Rev E. 2009;79:021910. doi: 10.1103/PhysRevE.79.021910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zinin PV, Allen JS, III, Levin VM. Mechanical resonances of bacteria cells. Phys Rev E. 2005;72:061907. doi: 10.1103/PhysRevE.72.061907. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.