Abstract
Electrostatic interactions play an important role in enzyme catalysis by guiding ligand binding and facilitating chemical reactions. These electrostatic interactions are modulated by conformational changes occurring over the catalytic cycle. Herein, the changes in active site electrostatic microenvironments are examined for all enzyme complexes along the catalytic cycle of Escherichia coli dihydrofolate reductase (ecDHFR) by incorporation of thiocyanate probes at two site-specific locations in the active site. The electrostatics and degree of hydration of the microenvironments surrounding the probes are investigated with spectroscopic techniques and mixed quantum mechanical/molecular mechanical (QM/MM) calculations. Changes in the electrostatic microenvironments along the catalytic environment lead to different nitrile (CN) vibrational stretching frequencies and 13C NMR chemical shifts. These environmental changes arise from protein conformational rearrangements during catalysis. The QM/MM calculations reproduce the experimentally measured vibrational frequency shifts of the thiocyanate probes across the catalyzed hydride transfer step, which spans the closed and occluded conformations of the enzyme. Analysis of the molecular dynamics trajectories provides insight into the conformational changes occurring between these two states and the resulting changes in classical electrostatics and specific hydrogen-bonding interactions. The electric fields along the CN axes of the probes are decomposed into contributions from specific residues, ligands, and solvent molecules that make up the microenvironments around the probes. Moreover, calculation of the electric field along the hydride donor–acceptor axis, along with decomposition of this field into specific contributions, indicates that the cofactor and substrate, as well as the enzyme, impose a substantial electric field that facilitates hydride transfer. Overall, experimental and theoretical data provide evidence for significant electrostatic changes in the active site microenvironments due to conformational motion occurring over the catalytic cycle of ecDHFR.
1. Introduction
Electrostatic interactions have been shown to play a vital role in enzyme catalysis. These interactions assist in the binding of ligands and facilitate the enzyme-catalyzed chemical reactions by keeping the reacting species positioned properly as well as stabilizing the transition state in some cases.1−9 Moreover, these electrostatic interactions are expected to be significantly modulated by the conformational changes that occur over the catalytic cycle.4,7,10,11 In particular, the electrostatic environment in the active site is likely to change as the ligands bind, the chemical reaction occurs, and the ligands are released. Quantifying the electrostatic contributions to the individual catalytic steps, as well as the impact of conformational changes on the electrostatic interactions, is a challenging yet important goal in the field of enzyme catalysis.
To gain a better understanding of the catalytic role of electrostatics and conformational motions, we probed the changes in the active site electrostatic environment resulting from structural rearrangements that occur along the catalytic cycle of Escherichia coli dihydrofolate reductase (ecDHFR). This enzyme catalyzes the NADPH-dependent conversion of 7,8-dihydrofolate (DHF) to 5,6,7,8-tetrahydrofolate (THF). X-ray crystallographic, nuclear magnetic resonance (NMR), theoretical, and photophysical studies have shown that ecDHFR exhibits significant structural rearrangements along the catalytic cycle.5,12−14 Thus, ecDHFR is a highly suitable system for studying how conformational changes can affect the active site electrostatic environment, which can then modulate enzyme catalysis.
Recently, thiocyanate and other vibrational probes have been incorporated into a number of biological systems to investigate the local electrostatic environments.15−20 Boxer and co-workers have explored the use of nitrile (CN) probes to detect differences in the electric field projected along the CN axis in proteins upon ligand binding, protein folding, and protein–protein association.18,21−25 Using this method, they showed that the electrostatic environment in the active site of Δ5-3-ketosteroid isomerase (KSI) exhibits limited rearrangement upon photoexcitation of a ligand, where this excitation was proposed to mimic the movement of charge during the catalyzed chemical transformation.21 The authors concluded that the KSI active site is electrostatically preorganized for catalysis in its tertiary protein structure and that major rearrangement is not necessary for catalysis. This observation is not unexpected due to the relatively rigid structure of KSI26−28 that limits substantial conformational mobility, thereby limiting electrostatic rearrangement. However, calculations have shown that further active site reorganization, manifesting as small conformational changes that position the reacting species for chemistry, is still required in KSI to enable the catalyzed proton transfer reactions.28 In contrast to KSI, which exhibits limited protein motion along the catalytic cycle, ecDHFR is known to undergo significant conformational changes along the catalytic cycle, suggesting that larger changes in electrostatics could play a more significant role in all steps of the catalytic cycle.
To examine the electrostatic interactions within the active site of ecDHFR, we incorporated thiocyanate probes at site-specific locations. Using vibrational and 13C NMR spectroscopic techniques, as well as computer simulations, we analyzed the electrostatics and degree of hydration of the microenvironments surrounding the probes. The electrostatic interactions arising from the active site microenvironments surrounding the small, catalytically nonintrusive probes led to different observed CN vibrational stretching frequencies and 13C NMR chemical shifts along the catalytic cycle. Experimental data clearly show changes in the active site electrostatic environment due to structural rearrangements. Further insights were obtained through mixed quantum mechanical and molecular mechanical (QM/MM) analyses of classical molecular dynamics (MD) simulations. These calculations were able to reproduce the experimentally measured vibrational frequency shifts reported by the probes across the enzyme-catalyzed hydride transfer step of the catalytic cycle.5,12 Moreover, the electrostatic contributions from the active site microenvironments surrounding the probe were decomposed into the major components (individual residues and ligands). In addition, the experimentally validated theoretical model allowed us to examine the electric field along the hydride transfer pathway between the substrate and cofactor, a property that is catalytically important yet unattainable experimentally. This integrated approach provides valuable insights into the interplay between electrostatic and conformational changes along the catalytic cycle of ecDHFR.
2. Methods
2.1. Experimental Methods and Materials
7,8-Dihydrofolate (DHF)29 and [(4′R)-2H]NADPH (NADPD)30 were prepared according to previously described procedures. β-Nicotinamide adenine dinucleotide phosphate reduced tetra(cyclohexylammonium) salt (NADPH), β-Nicotinamide adenine dinucleotide phosphate hydrate (NADP+), potassium cyanide-13C (99 atom % 13C), methotrexate, methotrexate-agarose, dithiothreitol (DTT), folic acid (≥97%; FOL), sodium phosphate monobasic monohydrate (98–102%), and 5,5′-dithiobis(2-nitrobenzoic acid) (Ellman’s reagent) were purchased from Sigma-Aldrich and used without further purification. (6S)-5,6,7,8-tetrahydrofolic acid (THF) was obtained from Schircks Laboratories. Sodium phosphate dibasic heptahydrate and 2-nitro-5-thiocyanatobenzoic acid (97%; NTCB) were purchased from EMD and TCI America, respectively. pH values were measured using an Accumet model 13-620-300 standard combination electrode calibrated with VWR certified standard aqueous buffers (pH = 4, 7, and 10). All of the experiments, including kinetics and spectroscopic measurements, were done in pH 7.0 50 mM sodium phosphate buffer unless otherwise specified.
2.2. Specific ecDHFR Constructs
First, the two native cysteines (C85 and C152) in wild-type (WT) ecDHFR were mutated to Ala and Ser, respectively, to generate ΔCys ecDHFR using the Stratagene QuikChange site-directed mutagenesis kit and the WT ecDHFR template as described elsewhere.31 Primer sequences were 5′-C GAA GCC ATC GCG GCG GCT GGT GAC GTA CCA G-3′ (C85A) and 5′-C TCG CAT AGC TAT TCA TTC GAA ATC CTC G-3′ (C152S). The choice of amino acid substitution was based on a previous report showing that the C85A/C152S substitution on ecDHFR induced minimal perturbation to the enzymatic activity.32 Selective incorporation of cysteine was achieved through subsequent mutations using the following primers: 5′-CA ATC GGT AGG CCT TGC CCC GGC CGC AAA AAT ATT ATC-3′ (L54C) and 5′-G ATT ATG GGG CGC CAT TGC TGG GAA TCA ATC G-3′ (T46C). Plasmid construction, protein expression, and purification of mutant DHFRs were performed according to published protocols.31
2.3. SCN and S13CN Labeling
Labeling of the single-cysteine ecDHFR constructs (ΔCys L54C and ΔCys T46C, denoted as L54C-CN and T46C-CN, respectively) was achieved using a modified version of a published procedure.33 Inside an Amicon Ultra-4 10K nominal molecular weight limit (NWML) centrifugal filter tube, approximately 400 μM of each ecDHFR construct was mixed with four times excess of NTCB in 4 mL of 0.1 M sodium phosphate buffer at pH 7.4. The mixture was allowed to react at room temperature for 10 min, and reaction progress was monitored by the appearance of the phenolic product using a UV–vis spectrophotometer. The protein mixture was then concentrated by spinning at 5K rpm in a centrifuge at 4 °C. The protein sample was then washed twice with 12 mM KCN in pH 7.0 50 mM sodium phosphate buffer, with a concentration step after each wash. This was followed by washing the protein sample with 50mM pH 7.0 sodium phosphate buffer two more times before concentrating the protein solution down to ∼0.8 mL, which was then applied onto a size exclusion column (Econo-Pac 10DG; Bio-Rad) that was pre-equilibrated with pH 7.0 50 mM sodium phosphate buffer. The isolated labeled proteins were concentrated in an Amicon Ultra-4 10K NMWL centrifugal filter tube. The intact masses of SCN labeled and unmodified samples were confirmed by ESI-MS, which yield deconvoluted m/z values of 17965 (L54C)/17978 (T46C) and 17940 (L54C)/17953 (T46C) Da, respectively. The theoretical molecular weights for the unmodified samples are 17941 (L54C)/17953 (T46C) Da.
Similar preparation procedures were used for the S13CN labeled samples. A mixture containing 10 mM Ellman’s reagent and 0.5 M K13CN in pH 7.0 0.1 M sodium phosphate buffer was prepared at room temperature for 15 min. This mixture was then allowed to react with a sample of the unlabeled protein in an Amicon Ultra-4 10K NMWL for 10 min at room temperature. The final concentrations of a typical reaction mixture were 500 μM protein, 5 mM Ellman’s reagent, and 0.25 M K13CN. The subsequent purification and isolation steps were similar to those for SCN labeling, except that K13CN was used for washes rather than KCN. Successful labeling was confirmed spectroscopically by the release of one equivalent of the phenolic product as well as 13C NMR comparison with the unlabeled proteins.
2.4. Enzyme Kinetics
The pre-steady-state hydride transfer reaction was monitored on an Applied Photophysics stopped-flow spectrophotometer thermostated at 25 °C. All of the enzymatic reactions were performed in 50 mM sodium phosphate buffer pH 7.0. One of the syringes in the stopped-flow analyzer was loaded with 20 μM enzyme, 250 μM NADPH, and 2 mM DTT. The other syringe contained 200 μM DHF and 2 mM DTT. After combining DHFR and NADPH as described above, the mixtures were prepared on ice for 5 min prior to the onset of the chemical reaction. Upon mixing, the final concentrations of the individual species in the reaction chamber were halved. The conversion of DHF to THF was followed by the loss of fluorescence resonance energy transfer from the enzyme to NADPH. The reaction mixture was excited at 290 nm, and the emission was measured using a 400 nm cutoff output filter.34 The measure of absorbance vs time trace (of burst phase) was fit to standard single exponential decay to obtain the hydride transfer rate (khyd). The kinetic isotope effect (KIE) for the hydride transfer rate was also determined under the same experimental conditions, with the exception that NADPD was used instead of NADPH in comparative experiments. Steady-state enzyme turnover kinetics (kcat) were studied following similar experimental conditions, with the exception that the reaction progress was monitored at 340 nm. Under each condition, at least 5 independent kinetic runs were conducted, and the average rate constants were used for analysis.
2.5. FTIR Measurements
FTIR spectra were obtained at room temperature using a Mattson Research Series FTIR Spectrometer (Madison Instruments, Inc.) equipped with a liquid-nitrogen cooled HgCdTe (MCT) detector (Infrared Associates, Inc.). Cyanylated DHFR samples ([protein] = 1.7–2.5 mM) were mixed with appropriate ligands (1:10 mol equiv) in aqueous buffer and placed in a liquid cell with two CaF2 windows separated by a 56 μm Teflon spacer. All nitrile (CN) stretch absorbance spectra for cyanylated DHFR samples consisted of 2000 scans and the data were collected with 1.0 cm–1 resolution. The CN stretch absorbance spectra for cyanylated DHFR samples were obtained by subtracting a spectrum of the aqueous buffer solution from the protein spectrum. The baseline for each spectrum was corrected by fitting a fifth-order polynomial fit to the data, as done previously by Fafarman et al.22 and McMahon et al.35 The fifth-order polynomial local fit functions were obtained by defining roots at least 15 cm–1 from the peak maximum, meaning the experimental data and fits were forced to be equal at points more than 15 cm–1 from the central frequency. All published spectra are the averages of two independently prepared protein samples after the baseline has been corrected and the peak height has been normalized to one. The peak positions obtained from independently prepared protein samples typically differed by <0.5 cm–1, which is substantially less than the variation among peak positions due to the protein binding or releasing the ligands. Detailed experimental setup and data analysis are provided in the Supporting Information.
2.6. 13C NMR Experiments
13C NMR spectra were collected on a Bruker AV-III-600 (150.9 MHz 13C frequency) at 25 °C. Samples were prepared with 1.6 mM of the S13CN labeled protein, 8 mM ligands, and 50 mM potassium phosphate (pH 7.0) in water. A sealed capillary tube containing 1 M acetone in D2O was inserted into the NMR tube that holds the protein sample. This provided both a locked solvent and an internal standard. Chemical shifts were also checked with an external standard of tetramethylsilane. Spectral data were acquired for ∼3000–4000 scans. The 1D 13C NMR spectral data obtained for each sample were compared with its corresponding 13C DEPT 45° (distortionless enhancement by polarization transfer) data to confirm the identity of the assigned peaks. Under the same experimental conditions, we were unable to detect the 13C NMR signals corresponding to the SCN probes for samples containing either the nonisotopically enriched SCN label or the unlabeled proteins.
2.7. X-ray Crystal Structures
Crystals of E. coli T46C-CN and L54C-CN DHFR variants were obtained by the hanging-drop vapor diffusion method using conditions similar to those previously described.12 Detailed methods, data collection, and refinement statistics are provided in the Supporting Information.
2.8. Computational Methods
We calculated the IR spectra for the CN stretching mode of the incorporated thiocyanate probes using a two-step method. First we propagated classical MD trajectories for the entire solvated enzyme with bound ligands. The configurations sampled from the MD trajectory were then analyzed using a series of QM/MM single point energy calculations to determine the CN stretching potential energy curve. The QM region was treated with a semiempirical method that was reparameterized for the calculation of nitrile vibrational frequencies, and the MM region was represented as a collection of atomic point charges. The instantaneous vibrational wave functions and associated frequencies from the energy level splittings were obtained from the CN stretching potential energy curve using a grid-based numerical approach. The simulated IR spectra were calculated using the fluctuating frequency approximation, which includes the dynamical contributions of the protein motion to the simulated lineshapes.36 A full description of the methodology can be found in our previous application to KSI,37 with some minor adjustments that will be discussed below.
2.9. MD Simulations
We propagated classical MD trajectories for the cysteine-free T46C-CN and L54C-CN ecDHFR mutants using the GROMACS program.38 We simulated both probe mutants in two different states along the catalytic cycle. The first state has folate (FOL) bound in the substrate pocket and the nicotinamide adenine dinucleotide phosphate cofactor bound in the oxidized form (NADP+). In this state, the Met20 loop is in the closed conformation, which is thought to facilitate the hydride transfer reaction by positioning the ligand and cofactor while excluding solvent molecules.12 This state has been shown to structurally mimic the reactive Michaelis complex (E:DHF:NADPH) prior to hydride transfer.39 Although we can simulate the reactive Michaelis complex without hydride transfer occurring, we simulated the E:FOL:NADP+ ternary complex to compare directly with the experimentally measured IR spectra. The second state that we simulated has the product THF and NADP+ bound. In this state, the Met20 loop is in the occluded conformation, and the nicotinamide ring of NADP+ is excluded from the active site. These two states are used to model the closed to occluded transition that occurs across the hydride transfer step of the ecDHFR catalytic cycle.
The initial structures for the MD simulations were obtained from crystal structures solved with the nitrile probes included for both the L54C-CN and T46C-CN variants (PDB accession codes 4P68 and 4P66, respectively). The crystal structures have methotrexate bound in the substrate binding pocket and NADPH bound in the active site. In both of these structures, the Met20 loop is in the closed conformation. This state is thought to mimic the transition state for the hydride transfer reaction.40 For the simulations in the closed conformation (NADP+/FOL), the folate molecule was incorporated by aligning the folate substrate with the corresponding heavy atoms of the methotrexate ligand from the crystal structure. For the simulations in the occluded conformation (NADP+/THF), we used the initial coordinates of a WT crystal structure of ecDHFR complexed with NADPH and 5,10-dideazatetrahydrofolate (ddTHF) (PDB 1RX6).12 The thiocyanate probes were incorporated into the occluded structure by aligning the backbone atoms of the five previous and five subsequent residues to the cyanylated cysteine residue in the new crystal structure that contains the probe to the corresponding backbone atoms of the 1RX6 structure. We then replaced the specific residue with the aligned cyanalated cysteine and optimized the probe residue geometry and position using a steepest-descent algorithm in GROMACS, while the ligands, the crystallographic water molecules, and the rest of the enzyme were held fixed. The substrate ligand (ddTHF) was replaced by THF by aligning the corresponding heavy atoms in ddTHF and THF, and the oxidized cofactor was modeled by aligning the heavy atoms of NADP+ with the NADPH from the crystal structure. The modeled ligands were also optimized using the steepest-descent algorithm with the enzyme and the crystallographic water molecules held fixed.
For all of the MD simulations, we used the AMBER99SB force field to compute the potential energy and forces for the protein.41,42 The bonded and nonbonded parameters for the NADP+ cofactor43 were consistent with those from our previous work.11 The FOL and THF charges were calculated using the restrained electrostatic potential (RESP) method,44 and the bonded and van der Waals parameters were obtained from the generalized AMBER force field (GAFF).45 For methyl thiocyanate and the cyanylated cysteine residue, the bonded parameters were obtained from Cho et al.,46 and the nonbonded parameters were obtained from Lindquist and Corcelli,47 as used in our previously published work on KSI.37
Each of the enzymatic systems was solvated with TIP3P water48 in a truncated octahedral box, where the sides of the box were at least 10.0 Å from every atom in the enzymatic complex, including the crystallographic waters. After solvation, we added 12 sodium atoms using the GROMACS genion utility to neutralize the system before simulation. All bonds involving a hydrogen atom were constrained to their equilibrium bond lengths using the LINCS algorithm as implemented in GROMACS.49 Nonbonded van der Waals interactions were calculated with a cutoff of 1.0 nm, and electrostatic interactions were calculated using the particle-mesh Ewald method.50
After the initial preparation of each system, we followed a well-defined equilibration procedure. The solvent configurations were minimized using the steepest-descent algorithm in GROMACS with the enzyme and ligands held fixed to mitigate any possible bad contacts between the solvent and solute molecules. The solvent molecules and counterions were then equilibrated for 50 ps at 300 K in the canonical (constant NVT) ensemble with the protein and ligands still fixed. After solvent equilibration, the entire system was then minimized using the steepest-descent algorithm. Subsequently, the system was equilibrated using a simulated annealing procedure in which the initial velocities were generated according to a Boltzmann distribution at 50 K. The system was equilibrated in the isothermal–isobaric ensemble (constant NPT) at 50 K for 50 ps, and then the temperature was increased up to 300 K in increments of 50 K with 50 ps of equilibration at each temperature. After this simulated annealing procedure, an additional 1 ns of equilibration in the constant NPT ensemble was performed, and finally 1 ns of equilibration in the constant NVT ensemble was performed. During the simulations, the Nosé–Hoover thermostat51,52 was used to maintain the temperature, and the Parrinello–Rahman barostat53 was used for the constant NPT simulations.
The production trajectories were propagated in the canonical ensemble at 300 K with a time step of 1 fs and a total simulation time of 1 ns for each independent trajectory. Configurations were saved at every time step and were analyzed using the QM/MM methodology described below. For each mutant and catalytic state, we propagated at least two independent trajectories with different initial configurations. The data for a single trajectory are presented in the main paper, while data from additional trajectories are provided in the Supporting Information. The results for independent trajectories associated with the same system were found to be consistent within the numerical errors of the methodology.
2.10. QM/MM Nitrile Frequency Calculations
The methodology used to calculate the vibrational frequency of the nitrile group is similar to that used in our previous work.37 Here we highlight the differences between the methods used in our previous work and the methods employed in the present work. As in our previous work, we calculated the vibrational frequency by generating the one-dimensional potential energy curve along the CN stretching mode using a QM/MM method. The potential energy is calculated along the CN vibrational coordinate by freezing all of the atomic centers in the system and moving only the nitrogen atom to stretch the CN distance from 1.0 to1.4 Å with a step size of 0.05 Å. The QM calculations were performed with the MM region treated as atomic point charges that polarize the QM region. These atomic point charges were the same as those used in the MD simulations and were obtained from the AMBER99SB force field for the standard amino acid residues, the TIP3P force field for the water molecules, and the RESP calculations for the ligands. The choice of the QM region for each probe studied in this work will be discussed below. In our previous work,37 the one-dimensional potential energy curve for the CN stretching mode was fit to a Morse function, and the energy levels were calculated analytically from the Morse parameters. In the present work, the potential energy curve was fit to a third-order B-spline potential,54 and the vibrational wave functions and energy levels were calculated numerically using the Fourier grid Hamiltonian (FGH) method.55,56 An advantage of the FGH method is that it does not assume any functional form of the potential energy curve and therefore avoids the bias associated with fitting to the Morse function, which depends on only three parameters.
In principle, any electronic structure method can be used to calculate the vibrational stretching potential, but the level of theory must be computationally tractable for the millions of configurations that are required to obtain statistically converged IR spectra. As in our previous work, we used a reparameterized version of the semiempirical PM3 method.57 In this semiempirical method, some of the computationally expensive integrals in Hartree–Fock theory are approximated by analytical functions that contain empirical parameters. These empirical parameters can be varied to reproduce properties from either electronic structure theory calculations or experimental measurements. Because we altered our approach to use the FGH numerical method to calculate the vibrational frequencies, we reoptimized the PM3 parameters. The reparameterization procedure is similar to that from our previous studies, and a full description is provided in the Supporting Information. We also confirmed that the new set of parameters reproduces the results for KSI from our previous work when the FGH numerical method is used for calculating the vibrational frequencies. Table S6 provides the calculated frequencies for the two different vibrational probes in KSI that were studied previously.37
2.11. Electrostatics Calculations
To assist in the analysis of the vibrational frequency calculations, we calculated the average electric field at the midpoint of the CN bond in the thiocyanate group from our MD simulations. The vibrational Stark effect between two states is described by
| 1 |
Here h is Planck’s constant, ΔνCN is the shift in vibrational frequency between the two states, ΔE⃗env is the difference in the electric field vector at the nitrile bond as a result of the change in the environment, Δμ⃗CN is the difference dipole moment for the vibrational mode that lies along the CN bond axis, and θ is the angle between these two vectors. The magnitude of Δμ⃗CN is the Stark tuning rate, which is a measure of the susceptibility of the probe to changes in the local electric field. Boxer and co-workers have measured the Stark tuning rate for thiocyanate probes in various environments, including in proteins, to be ∼0.7 cm–1/(MV/cm).58 We emphasize that this equation accounts only for the classical electrostatic effects of the environment and does not account for the quantum mechanical aspects of effects such as specific hydrogen-bonding interactions and polarization. While these phenomena have significant classical components, they also have nonclassical aspects that can be incorporated into the calculations by treating interacting residues quantum mechanically, as will be discussed below.
Recent work explores the role of a local field correction factor59 that scales the externally applied electric field to obtain the local field experienced by the probe, which is typically larger because of the polarization of the local environment induced by the applied electric field. This local field correction factor has been estimated to be between 1.1 and 1.3 for protein environments,60,61 but recent investigations have suggested that it may be as large as 1.8.59 We have not considered the role of the local field correction factor in our analysis of the electric fields in DHFR due to the lack of consensus about its value for a protein environment. Moreover, applying the local field corrections would result in changes that are within the error bars of our calculations.
To calculate the electric field at the nitrile bond, a virtual particle was positioned at the midpoint of the CN axis during the MD trajectory. This virtual particle had no electrostatic or van der Waals interactions with other particles, and the bond, angle, and dihedral parameters were set to zero. The configurations from the MD trajectory were saved, and subsequently the forces acting on all particles were recalculated for these configurations when the charge on the virtual particle was set to +1. The electric field, E⃗VP, at the virtual particle location was calculated as
| 2 |
where F⃗VP is the force acting on the virtual particle and qVP is the charge of the virtual particle. The total electric field vector, as well as the component along the CN axis, was calculated for each configuration along the MD trajectory. Calculation of the component of the electric field along the CN axis allows us to calculate the change in the vibrational frequency due to classical electrostatics using eq 1. The remaining frequency change can be attributed to the quantum mechanical aspects of specific hydrogen-bonding interactions and polarization effects. These effects can be investigated by using a classical polarizable force field59,62,63 or by treating the interacting residues quantum mechanically. Note that the experimentally measured and theoretically calculated frequency shifts can be compared directly, but the breakdown into the classical electrostatics and quantum mechanical aspects is available only from the theoretical calculations.
We also analyzed the contributions of individual residues and ligands to the electric field at the midpoint of the CN bond. Because the classical electric field is the sum of the individual contributions from each atom, the electric field can be decomposed into contributions from each protein residue and ligand. Analysis of the contributions from specific residues provides insight into the impact of conformational changes occurring during the closed to occluded transition associated with hydride transfer.
3. Results and Discussion
3.1. Probe Incorporation
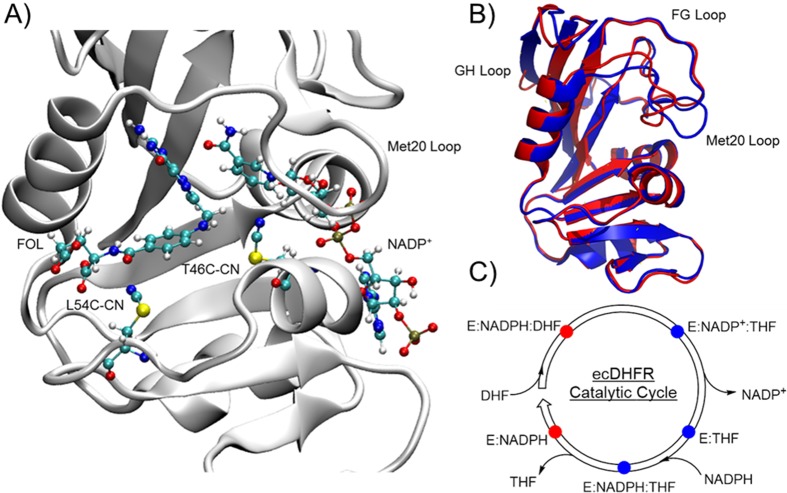
We generated the T46C-CN and L54C-CN mutants by site-specifically incorporating a thiocyanate probe at each position (Figure 1). The T46C-CN probe is situated in close proximity to the junction between the two reacting ligands, DHF and NADPH, allowing us to monitor the microenvironment close to the reaction center.12 The L54C-CN probe is located ∼9 Å from the center of the hydride donor–acceptor (D–A) axis. This probe monitors the folate binding pocket, and its spectral character is expected to respond to the formation of the ternary Michaelis–Menten complex upon folate binding, as well as the release of THF in the enzyme turnover step.
Figure 1.
(A) Superposition of the T46C-CN and L54C-CN ecDHFR mutants in the closed conformation with folate and NADP+ bound, where only the thiocyanate residue is shown for the L54C-CN mutant. (B) ecDHFR in the closed (red) and the occluded (blue) conformations exhibited by the (C) five major complexes in its catalytic cycle.
The enzyme activity of the two ecDHFR variants was evaluated by their ability to catalyze the NADPH-dependent reduction of DHF and the enzyme turnover rates at pH 7.0 and 25 °C. The catalytic efficiencies of the T46C-CN (khyd = 120 ± 10 s–1; kcat = 6.5 ± 0.5 s–1) and L54C-CN (khyd = 250 ± 20 s–1; kcat = 28 ± 3 s–1) variants were comparable to that of WT ecDHFR (khyd = 220 s–1; kcat = 12 s–1).34,64 We also found the ΔCys ecDHFR (C85A/C152S; khyd = 215 ± 8 s–1; kcat = 10.3 ± 0.8 s–1) variant to exhibit activity similar to the WT enzyme. Table S1 summarizes the kinetic data obtained for the various ecDHFR constructs. Furthermore, Figure S1 shows that the crystal structures of the ternary complexes of the T46C-CN and L54C-CN mutants in the closed conformation overlap well with the WT crystal structure. These observations suggest that the incorporation of the SCN probes into the selected locations of the active site does not significantly alter the structure or activity of the enzyme.
It should be noted that we also incorporated the SCN probe at the I50 position (ΔCys-I50C-CN). However, such a modification decreased the hydride transfer rate by ∼10 times at pH 7.0 and 25 °C. We felt that the degree of enzyme activity reduction in ΔCys-I50C-CN might result in a less accurate representation of the electrostatic environment in the active site of the WT enzyme. Thus, further investigations were not performed for the ΔCys-I50C-CN construct. It is expected that even small modifications to the crowded active site can have large effects on enzyme activity.
3.2. Active Site Microenvironments Along ecDHFR Catalytic Cycle
The ecDHFR catalytic cycle contains the five major species (Figure 1C) that reflect the significant conformational changes in the active site Met20 loop (Figure 1B).5,12 The Met20 loop moves from a closed conformation in the ternary Michaelis–Menten complex (E:NADPH:DHF) to an occluded conformation in the initial ternary product complex (E:NADP+:THF). The enzyme remains in the occluded conformation in the two subsequent product-containing species (E:THF and E:NADPH:THF), until the Met20 loop reverts back to the closed conformation upon the rate-limiting34 release of THF to generate E:NADPH (Figure 1C). NMR relaxation dispersion experiments have found that the rates of the Met20 loop conformational change are temporally similar to their corresponding enzymatic processes.5 In other words, the hydride transfer and enzyme turnover rates are similar to the values determined from the NMR experiments for the conformational transitions that connect the relevant enzyme complexes. While the major change in the Met20 loop conformation appears to be induced by the formation of the product THF,65 theoretical simulations have shown that minor structural rearrangements of the ligands and protein, not restricted to the Met20 loop, are necessary to progressively optimize the substrate orientations and the active site environment along the reaction coordinate of the hydride transfer reaction.1,11 Herein, we utilized the SCN probes to experimentally monitor the changes in the local microenvironments in two locations in the active site over the five major catalytic species.
The five complexes that constitute the catalytic cycle of ecDHFR (Figure 2) were generated using 1.5–2.5 mM of the enzyme and at least five times excess of the ligands in pH 7.0 phosphate buffer. These concentrations should be more than sufficient to push the equilibria toward full complexation,5,34,64 thus allowing us to obtain vibrational FTIR spectra of the five major complexes that constitute the ecDHFR catalytic cycle, as well as for the apoenzyme and the E:NADPH:FOL complex. Note that the E:NADPH:DHF state is modeled by E:NADP+:FOL, as discussed in the literature.39 For each enzyme complex, the IR spectrum was obtained in duplicate/triplicate using separately prepared samples, and these spectra were found to be very reproducible (data in Supporting Information). After correcting the IR data for baseline and subsequently normalizing the amplitude of the peak to 1.0, we determined the maximum frequency (νmax) from the first derivative of the corrected IR peak. The peak position is a measure of the transition energy between the vibrational ground state and first excited state of the thiocyanate probe. The transition energy is sensitive to the electric field along the CN bond because the vibrational potential energy function is perturbed by the local electrostatic environment (surrounding residues, ligands, and solvent molecules) which modulates the energy difference between the vibrational quantum states. Color coding the frequency of maximum absorption detected in each complex illustrates the changes in the local electrostatic interactions experienced by the CN probe over the catalytic cycle (Figure 2).
Figure 2.
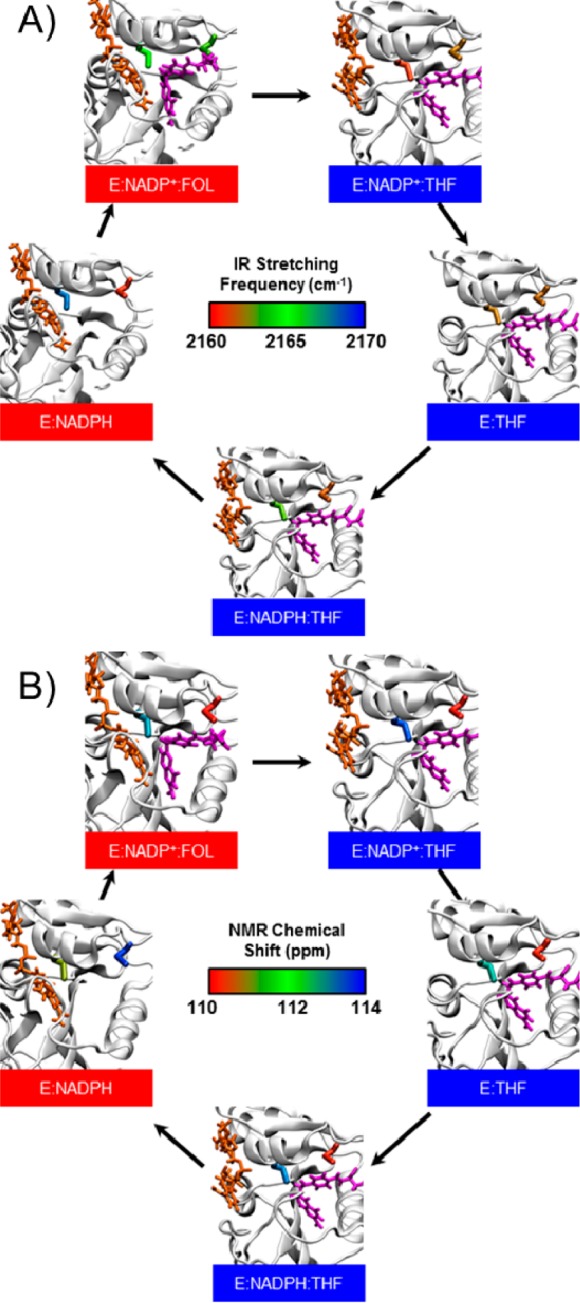
(A) FTIR (SCN) and (B) NMR (S13CN) measurements along the catalytic cycle of ecDHFR. The color scales for the FTIR and NMR data have units of cm–1 and ppm, respectively. The cofactor is orange, and the substrate/product is purple in all complexes (the coloring of the cofactor and substrate/product does not correspond to the color scales that represent the NMR shift or IR frequency). Enzyme complex labels in blue are in the occluded conformation, and those in red are in the closed conformation. The measured values for IR frequency and NMR chemical shift are provided in Table S4.
Figure 2 indicates that the local environment of each CN probe changes significantly over several key steps in the catalytic cycle: formation of the ternary Michaelis–Menten model ground state complex, the hydride transfer step, and the rate-limiting release of THF. The largest frequency shifts observed for the T46C-CN probe occurred across the two most important steps in the catalytic cycle: (1) upon the conversion between the model Michaelis–Menten E:NADP+:FOL complex and the initial E:NADP+:THF product complex (−4.1 cm–1), which is analogous to the hydride transfer step; (2) across the enzyme turnover step, which is the release of THF (5.5 cm–1). For the L54C-CN probe, the most significant change occurred upon the formation of the ternary E:NADP+:FOL complex (2.4 cm–1). Crystal structures of the WT enzyme have shown that the T46 and L54 residues retain their positions and orientations in the five catalytic complexes, suggesting that the inserted CN probes likely experience limited freedom of movement in the active site.12 MD simulations confirm that there are no major conformational changes in the probe orientation during 5 ns trajectories. Therefore, the observed changes in the microenvironments as the system moves through the various complexes in the catalytic cycle are likely due to protein conformational rearrangements that induce changes in the electrostatic interactions between the probes and their surroundings. Note also that the redox state of the cofactor (NADPH/NADP+) has very little effect on both the IR and 13C NMR data (Table S4).
In many cases, we also observed changes in the peak width [full-width at half-maximum (fwhm); Table S4], which usually reflects the variation of chemical environments sampled by the probe as well as the strength of intermolecular interactions such as hydrogen bonding. For example, the L54C-CN probe, which is located in the folate binding site, reported peak widths that are approximately two times smaller in complexes with bound FOL or THF. This observation is consistent with the probe sampling a less fluctuating and more well-defined electrostatic environment resulting from the various interactions that organize the FOL/THF to bind in the active site. There is also some evidence indicating that the E:NADPH complex and the apoenzyme exhibit a greater degree of hydrogen bonding between a solvent water molecule and the L54C-CN probe. One indication of this phenomenon is obtained from inspection of the 13C NMR-IR relationship, which shows that the data for the above two complexes deviate from the rest of the data in a manner that implicates greater specific solvent hydrogen-bonding interactions (Figure S4). MD simulations support the presence of additional solvent hydrogen-bonding interactions in these two complexes for the L54C-CN probe, with a water molecule hydrogen bonded to the nitrile probe in nearly half of the configurations. We also observed a slightly broader IR peak in the E:NADPH:FOL complex, which can be attributed to the slow reduction of FOL over the course of the IR measurement. This is not unexpected since the L54C-CN probe is located in the folate binding pocket. These trends are less obvious for the T46C-CN probe, which seems to be located in a more fluctuating environment, as indicated by the relative IR peak widths.
We also prepared the isotopically enriched Cys-13CN variants (T46C-13CN and L54C-13CN) to obtain the complementary 13C NMR data for all of the studied complexes. While the magnitude of the observed changes are different because the 13C NMR chemical shift is less sensitive to specific solvent hydrogen-bonding interactions than is the CN vibrational stretching frequency,18,23 the 13C NMR data illustrate similar trends to those shown by the corresponding IR data. In particular, we observed a changing microenvironment around the S13CN probes as the enzyme evolves through the catalytic cycle (Figure 2B). Similar to the IR data, the microenvironment detected at the T46C-13CN probe exhibits larger changes along the catalytic cycle than that at the L54C-13CN probe. This trend is expected due to the proximity of the T46C-13CN site to the regions of the substrates that undergo the hydride transfer reaction. Overall, the experimental data summarized as Figure 2 clearly demonstrate a dynamic electrostatic environment in the active site of ecDHFR across its catalytic cycle. The differences in the microenvironments of the two probes and the way they change among the different complexes, especially between the closed and occluded conformations, in the ecDHFR catalytic cycle also provide an indication of the highly heterogeneous nature of the enzyme active site.
3.3. Computer Simulations
To identify the various environmental contributions that give rise to the observed CN stretching vibrational frequency shifts along the catalytic cycle, we conducted QM/MM simulations to monitor the electrostatic interactions experienced by the probes for the complexes along the catalytic cycle. These data provide information about how the microenvironments of the probes reorganize across individual steps of the catalytic cycle. We simulated the IR spectra of the T46C-CN and L54C-CN mutants of ecDHFR for two different complexes along the catalytic cycle: (1) the ternary complex with the reactant analog FOL and NADP+ bound, which mimics the E:NADPH:DHF state prior to hydride transfer; (2) the ternary complex with the product THF and NADP+ bound, which is the E:NADP+:THF state following hydride transfer.
3.3.1. Microenvironment Proximal to the Reaction Center
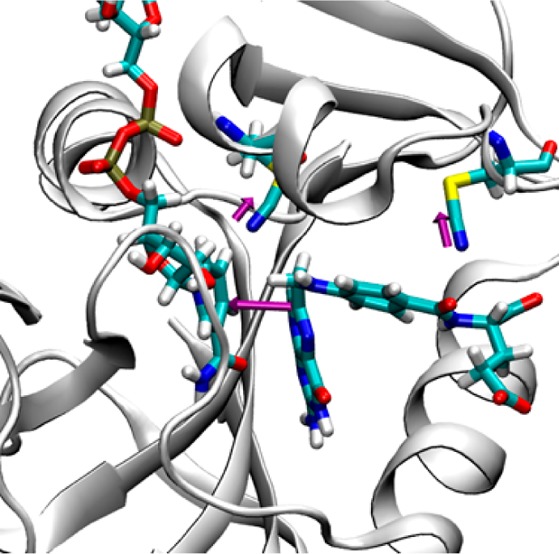
First we examined the local environment around the T46C-CN probe, which is located near the midpoint between the two bound ligands (Figure 1A). The QM region includes the T46C-CN residue, the substrate (either FOL or THF), and the nearest water molecule to the nitrile nitrogen, as depicted in Figure 3A. The QM region was determined by calculating the CN frequency including the entire probe microenvironment in the QM region for a subset of the configurations sampled and comparing these results to those obtained with smaller QM regions. The details of the procedure used to determine the QM region are provided in the Supporting Information.
Figure 3.
Configurations from MD simulations for the (A) T46C-CN and (B) L54C-CN ecDHFR mutants. The residues with thicker lines are included in the QM region for the QM/MM calculations of vibrational frequencies.
Figure 4A presents the calculated and experimentally measured IR spectra for the T46C-CN mutant for both the closed (NADP+/FOL) and occluded (NADP+/THF) states. The calculated IR spectrum for the closed conformation (solid black curve) has a maximum at 2165.8 cm–1, which is within 1.8 cm–1 of the measured peak in the experiments. The agreement between the calculated and experimental absolute frequencies is potentially fortuitous, but the level of agreement is similar to that calculated in our previous studies of KSI.37 The fwhm of the calculated IR spectrum for the closed conformation is 11 cm–1, which is in good agreement with the experimentally measured line width of 14 cm–1. The calculated IR spectrum for the occluded product state (solid red curve) has a maximum at 2162.1 cm–1. The calculated shift between these two states is −3.7 cm–1, which is in excellent agreement with the experimentally measured shift of −4.1 cm–1. Note that our MD simulations and CN frequency calculations are performed on the nanosecond time scale. The probe could experience multiple additional conformations on the longer time scale associated with the IR measurements. During our MD simulations of 5 ns, no major structural rearrangements of the probe orientation occurred, indicating that we are only sampling a single conformational state. Since the starting configurations for our simulations were based on crystal structures that include the probe, we expect to be sampling the most stable and therefore the dominant configuration of the probe. Moreover, the agreement between the calculated and experimental CN frequency shifts provides further validation of the methodology.
Figure 4.
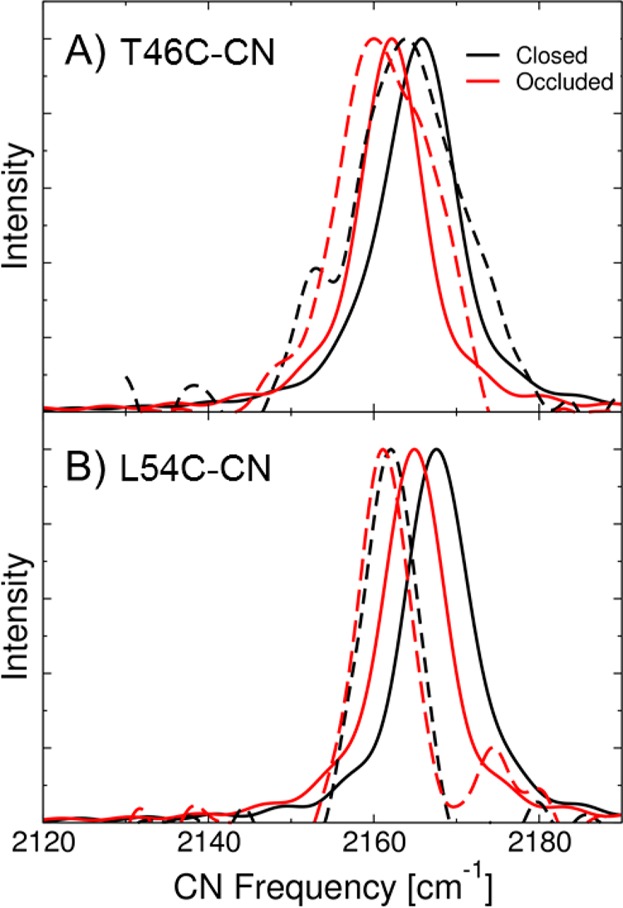
Calculated and experimentally measured IR spectra of the CN vibrational stretching frequency for the (A) T46C-CN and (B) L54C-CN ecDHFR systems with NADP+/FOL bound (closed conformation; black line) and with NADP+/THF bound (occluded conformation; red line). The solid lines are the simulated spectra from the QM/MM calculations, and the dotted lines are the measured spectra from the FTIR experiments.
In addition to the IR spectra, we calculated the electric field at the midpoint of the CN bond for configurations sampled by the MD trajectory using the methodology described above. From these calculations, we can correlate the measured vibrational frequency shifts to changes in electrostatics from the protein environment. Figure 5A depicts the calculated electric field along the CN axis for the two states. The average projected electric field for the closed (NADP+/FOL) and occluded (NADP+/THF) states are −15.9 and −19.0 MV/cm, respectively. Using the experimental Stark tuning rate of 0.7 cm–1/(MV/cm) in conjunction with eq 1, the difference of −3.1 MV/cm corresponds to a shift in the vibrational frequency of −2.2 cm–1. The difference between this frequency shift arising from only classical electrostatics and the actual shift of ca. −4.0 cm–1 obtained from both calculations and experiments is attributed to the quantum mechanical aspects of hydrogen-bonding interactions and polarization effects that are not included in the linear relation given by eq 1.
Figure 5.
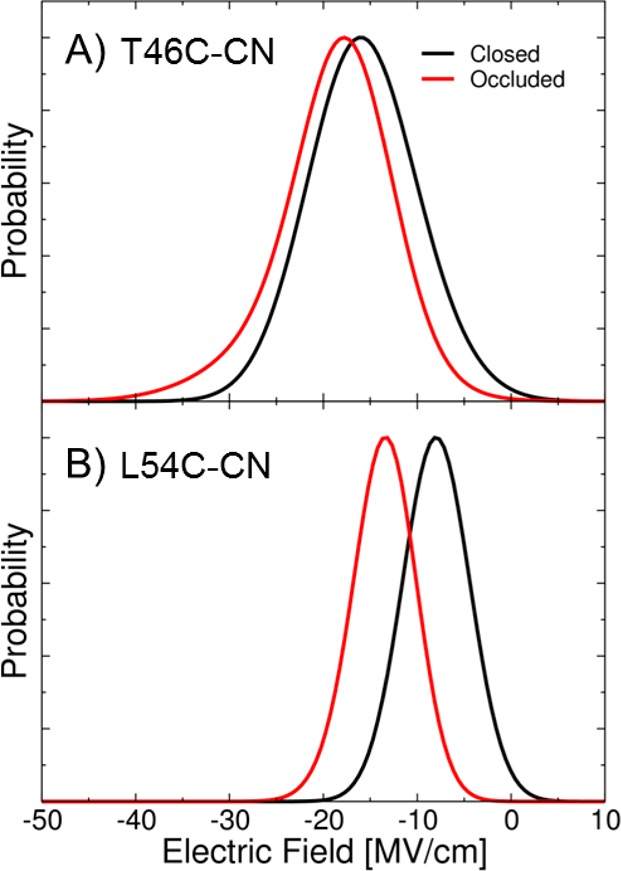
Calculated electric field along the CN bond at the midpoint of this bond for the (A) T46C-CN and (B) L54C-CN ecDHFR systems with NADP+/FOL bound (closed conformation; black line) and with NADP+/THF bound (occluded conformation; red line).
Previously it has been shown experimentally18,22 and computationally37,66 that significant deviations of ∼10 cm–1 from the vibrational frequency shifts predicted by eq 1 can occur when the nitrile probe participates in specific hydrogen-bonding interactions. According to our MD simulations, the T46C-CN thiocyanate probe is solvent accessible in both the closed and occluded conformations and directly hydrogen bonds to a water molecule, as depicted in Figure 3A. In both protein conformations, the nitrile probe is also able to act as a hydrogen-bond acceptor from the amine group in the substrate (FOL/THF) backbone. Note that the observation of hydrogen-bonding interactions with the probe for these two states is consistent with the experimental IR-NMR correlation data in Figure S4.
Thus, the difference between the frequency shift of −2.2 cm–1 predicted from eq 1, which includes only classical electrostatic effects, and the shift of −3.7 cm–1 obtained from the QM/MM calculations of the full system can be attributed to hydrogen-bonding interactions with the water molecule and polarization effects from the water molecule and the substrate (FOL/THF). To confirm this hypothesis, we performed the QM/MM frequency analysis with only the probe residue (T46C-CN) in the QM region (i.e., switching the water molecule and the substrate from the QM region to the MM region). In this case, the calculated frequency shift between the two states was −2.6 cm–1, which agrees well with the −2.2 cm–1 shift obtained from eq 1.
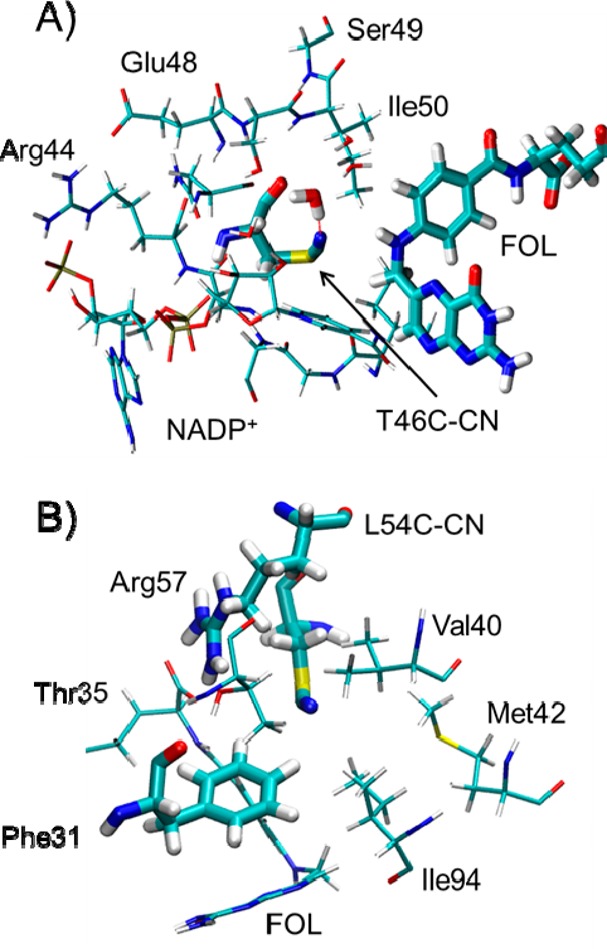
Beyond the calculation of the total electric field at the probes, we can decompose the field along the CN axis into contributions from individual residues in the enzymatic complexes. In essence, this methodology allows us to decompose the microenvironment surrounding the CN probe into the constituent parts, which then allows us to identify the major contributing components. For the T46C-CN probe (Figure 3A), the sum of the contributions from the main contributors given in Table 1 corresponds to a change in electric field along the CN axis of −2.9 MV/cm, which is consistent with the change of −3.1 MV/cm calculated with the entire enzyme. The contributions from the residues in the closed conformation are shown pictorially in Figure 6A, where the residues that are colored blue contribute positively and those that are colored red contribute negatively to the total field along the CN bond. For the T46C-CN probe, the NADP+ cofactor and the nearest water molecule are the dominant contributors to the change in the electric field along the CN axis, although Asn18 and Ser49 also make significant contributions (Table 1). The presence of a positive charge on the nicotinamide ring and the short ∼4 Å distance between the nitrile nitrogen and the aromatic nitrogen in the nicotinamide ring lead to a strong contribution to the electric field in the closed conformation. After the transition to the occluded conformation, the cofactor is excluded from the active site, and the magnitude of the contribution to the field from the nicotinamide ring is much smaller due to the larger distance of ∼14 Å between the two nitrogen atoms. This effect of the movement of NADP+ on the electric field at the probe demonstrates how atomic motions can significantly alter the local electrostatics in the active site. Moreover, the −3.2 MV/cm change in the electric field contributed by Asn18 and Ser49 is consistent with the structural rearrangement from the closed to the occluded conformation. Specifically, the amide nitrogen of Asn18 is ∼1.5 Å closer to the nitrile probe in the closed conformation than in the occluded conformation, and the hydroxyl group of Ser49 is ∼1.0 Å closer to the nitrile probe in the closed conformation.
Table 1. Calculated Contributions from Specific Residues to the Electric Field along the CN Bond for the T46C-CN ecDHFR Mutant in the Closed and Occluded Conformations.
|
ECN,a MV/cm |
ΔECN,b MV/cm | ||
|---|---|---|---|
| residue | closed (NADP+/FOL) |
occluded (NADP+/THF) |
shift |
| Asn18 | 2.65 | –0.52 | −3.17 |
| Ser49 | 4.23 | 1.01 | −3.22 |
| Ile50 | 1.79 | 1.53 | −0.26 |
| FOL | –0.66 | –3.51 | −2.85 |
| NADP+ | –19.43 | –5.35 | 14.08 |
| H2O | 2.14 | –5.32 | −7.46 |
Component of the electric field along the CN bond.
Changes in the electric field along the CN bond in going from the closed conformation (NADP+/FOL) to the occluded conformation (NADP+/THF).
Figure 6.
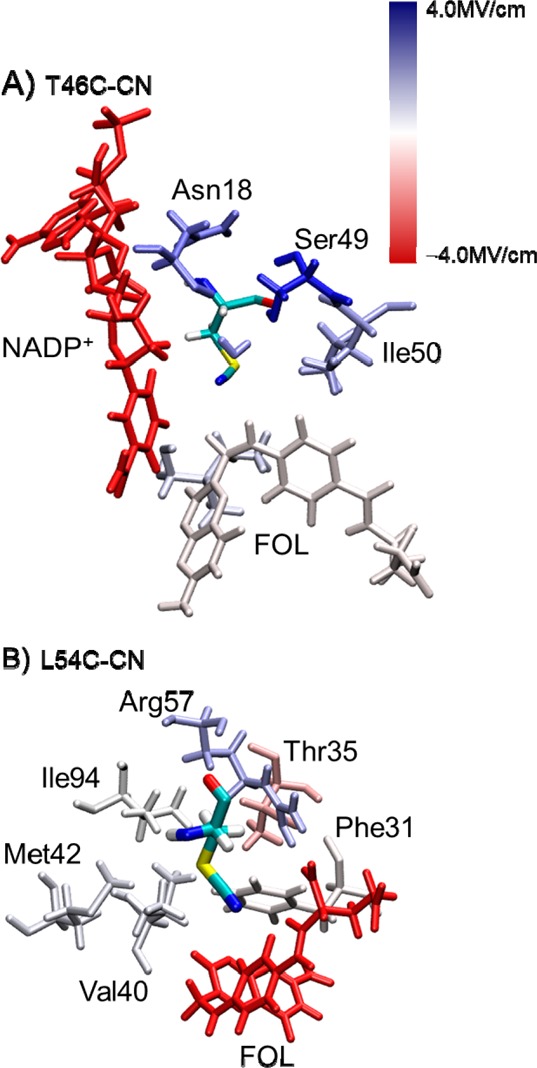
Contributions to the calculated electric field along the CN bond at the midpoint of this bond for the (A) T46C-CN and (B) L54C-CN ecDHFR systems with NADP+/FOL bound and the Met20 loop in the closed conformation. The color for each residue corresponds to the calculated values in Tables 1 and 2, respectively, using the color scale provided, although residues contributing a magnitude >4.0 MV/cm are depicted in the darkest color. The residues that contribute negatively to the field are colored red, the residues that contribute positively to the field are colored blue, and the residues that have no net contribution to the field along the CN bond are colored white.
Additionally, following the closed to occluded transition, the CN probe becomes more accessible to the solvent. The contribution to the electric field along the CN axis from the closest water molecule changes by −7.46 MV/cm during this transition. Moreover, the sign of the average electric field along the CN axis due to this water molecule is different for the closed and occluded conformations, with a value of 2.14 MV/cm for the closed conformation and −5.32 MV/cm for the occluded conformation. Analysis of the MD trajectories indicates that a water molecule is hydrogen bonded to the nitrile probe ∼26% of the time in the closed (NADP+/FOL) conformation and ∼52% of the time in the occluded (NADP+/THF) conformation. Representative snapshots from MD simulations are shown in Figure S5. The positive contribution to the electric field along the CN axis from the nearest water molecule in the closed conformation is due to configurations in which the nearest water molecule has its negatively charged oxygen atom pointing toward the nitrile. These configurations are stabilized by the hydrogen-bonding interaction of the water molecule with the hydroxyl group of Ser49, as shown in Figure S5. The negative contribution to the field in the occluded conformation arises from configurations in which a hydrogen atom of the nearest water molecule is oriented toward the probe, forming a hydrogen bond between the water molecule and the CN group. Thus, this computational approach is also able to probe the detailed active site hydration status, which is not easily accessible with experimental means.
3.3.2. Microenvironment around Substrate Binding Pocket
We performed the same analysis for the L54C-CN mutant to examine the microenvironment near the folate binding pocket. Figure 4B depicts the calculated and experimentally measured vibrational spectra for the L54C-CN mutant in both the closed (NADP+/FOL) and occluded (NADP+/THF) states. The L54C-CN probe is distal from the active site, and it is located in a relatively hydrophobic pocket near the carboxylate tail of the substrate, as shown in Figure 1. The QM region used for this mutant includes the L54C-CN residue, Phe31, and Arg57, as depicted in Figure 3B. The QM region was determined by calculating the CN frequency including the entire probe microenvironment in the QM region for a subset of the configurations sampled and comparing these results to those obtained with smaller QM regions. The details of the procedure used to determine the QM region are provided in the Supporting Information. The calculated frequency shift between the two states for the L54C-CN probe is −2.5 cm–1, which is in reasonable agreement with the shift of −1.0 cm–1 measured experimentally.
Figure 5B depicts the calculated electric fields along the CN bond for the L54C-CN mutant in the two states. The calculated average electric fields along the CN probe in the closed and occluded conformations are −8.4 and −13.8 MV/cm, respectively. Using the experimental Stark tuning rate of 0.7 cm–1/(MV/cm) in conjunction with eq 1, this shift of −5.4 MV/cm corresponds to a shift in vibrational frequency of −3.8 cm–1 due to only classical electrostatic interactions. To model the situation with only classical electrostatic interactions, we calculated the shift in the vibrational frequency when only the residue containing the thiocyanate group (L54C-CN) is treated quantum mechanically and the remainder of the system, including Phe31 and Arg57, is represented as classical point charges. The calculated frequency shift when only the probe residue is treated quantum mechanically is −3.5 cm–1, which is consistent with the value of −3.8 cm–1 obtained from eq 1. However, this frequency shift is greater than the shift of −2.5 cm–1 calculated with the larger QM region. The greater shift predicted by the purely classical electrostatic model indicates that the polarization effects due to the Phe31 and Arg57 residues decrease the vibrational frequency shift relative to that predicted by classical electrostatics.
Table 2 provides the contribution to the electric field along the CN axis for several key residues near the L54C-CN probe. The sum of these contributions is −7.3 MV/cm, which is slightly higher than the change of −5.4 MV/cm calculated with the entire enzyme, indicating that other residues are also contributing to this field. In a similar manner to the analysis for the T46C-CN mutant, the contributions from these residues are illustrated in Figure 6B. The Arg57 residue exhibits the largest change between the two states with a net shift of −6.58 MV/cm. In the closed conformation, the line connecting the midpoint of the CN bond to the protonation site of the positively charged Arg57 is nearly perpendicular to the CN axis, resulting in almost zero contribution to the electric field along the CN axis. The change in the electric field contribution by Arg57 is likely due to a geometrical shift that moved the positive charge on Arg57 away from this orthogonal orientation with respect to the probe in the occluded conformation. Interestingly, while the substrate exerts a large contribution to the electric field along the CN axis, this contribution remains nearly constant between the two states. The stable orientation of the CN axis relative to the negatively charged carboxylate moiety in the bound substrate results in negligible change in the contribution of the substrate to the electric field at the CN probe.
Table 2. Calculated Contributions from Specific Residues to the Electric Field along the CN Bond for the L54C-CN ecDHFR Mutant in the Closed and Occluded Conformations.
|
ECN,a MV/cm |
ΔECNb, MV/cm | ||
|---|---|---|---|
| residue | closed (NADP+/FOL) |
occluded (NADP+//THF) |
shift |
| Phe31 | –0.28 | 0.03 | 0.31 |
| Thr35 | –0.75 | 0.60 | 1.35 |
| Val40 | 0.16 | –2.11 | −2.27 |
| Met42 | 0.33 | –0.65 | −0.98 |
| Arg57 | 0.80 | –5.78 | −6.58 |
| Ile94 | 0.33 | –0.71 | −1.04 |
| FOL | –13.21 | –11.27 | 1.95 |
Component of the electric field along the CN bond.
Changes in the electric field along the CN bond in going from the closed conformation (NADP+/FOL) to the occluded conformation (NADP+/THF).
3.3.3. Electric Field along the Hydride Transfer Donor–Acceptor Axis
While the calculated electric fields along the CN axes of the probes provide a measure of the electrostatic microenvironments within the active site, the electric field along the hydride transfer D–A axis is more directly connected to catalysis. Encouraged by the good agreement between the experimental and the simulated data described above, we applied the same methodology to evaluate the total electric field at the midpoint of the D–A axis and the field projected along the D–A axis in the closed (E:NADP+:FOL) state. The field projected along the D–A axis is −48.9 MV/cm. The negative value of the field indicates that it points from the substrate to the cofactor and that this field will facilitate the transfer of a negatively charged hydride from the cofactor to the substrate. In other words, the projection and the magnitude of the field along the D–A axis in the ternary Michaelis complex is highly favorable for the hydride transfer reaction to occur. The substrate and cofactor contribute a total of −32.4 MV/cm to the field along the D–A axis. The rest of the protein contributes approximately an additional ∼31% (−15.4 MV/cm) of the total field. Also, the solvent molecules and ions contribute an additional −1.1 MV/cm to the field along the D–A axis.
This analysis suggests that a major function of the enzyme is to bring the substrate and cofactor into a configuration that realizes the highly favorable field for facilitating the hydride transfer reaction (Figure 7). In the absence of the enzyme, it would be less probable for the reacting species, NADPH and DHF, to achieve the same relative orientation in solution. Moreover, this analysis provides a new perspective on the role of electrostatic catalytic contributions in DHFR. It is currently impossible to experimentally measure the electric field along the D–A axis, but the calculations provide reasonable estimates. A favorable electric field of −15.4 MV/cm from the protein and −32.4 MV/cm from the ligands along the D–A axis could potentially reduce the free energy barrier by several kcal/mol.67 While these values suggest a substantial catalytic contribution generated from the active site electrostatic environment, it is important to acknowledge that the full mechanism of catalysis is far more complex than a simplistic evaluation based solely on the electric field along the D–A axis.
Figure 7.
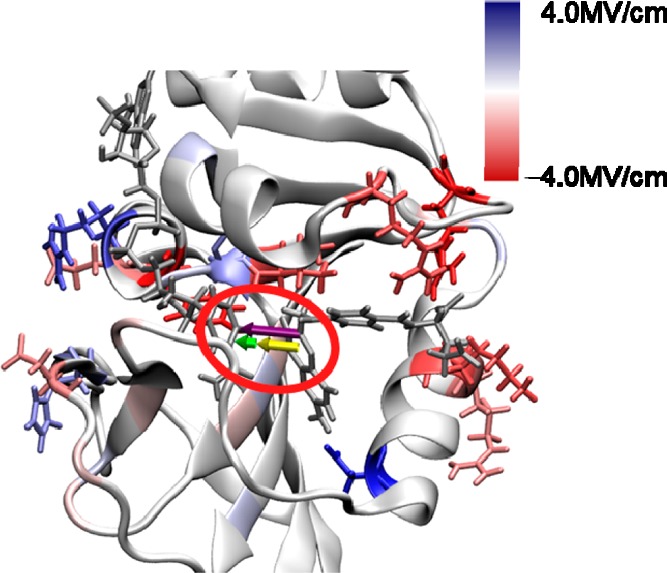
Depiction of the component of the electric field along the hydride transfer D–A axis calculated from an MD simulation of WT ecDHFR with NADP+/FOL bound and the Met20 loop in the closed conformation. The color for each residue corresponds to the calculated electric field values using the color scale provided, although residues contributing a magnitude >4.0 MV/cm are depicted in the darkest color. The three arrows in the red oval represent the total electric field of −48.9 MV/cm (purple), the field of −32.4 MV/cm resulting from the ligands (yellow), and the field of −16.5 MV/cm resulting from the rest of the system (green) projected along the D–A axis.
We also decomposed this field into the contributions from all of the protein residues, and our analysis identified many residues that contribute to the electric field along the D–A axis. Figure 7 depicts the contributions from each of the residues to the field along the D–A axis. The residues that are colored blue contribute positively and those that are colored red contribute negatively to the field pointing from the substrate to the cofactor along the D–A axis. The residues that are shown with side chains contribute to the field with a magnitude >1 MV/cm. The numerical values for the contributions are provided in Table S9. Interestingly, there is a strong degree of overlap between the residues that strongly contribute to the field along the D–A axis and the network of coupled motions that has been identified for DHFR catalysis.68 The residues Ile14, Tyr100, and Asp122 contribute −1.2, −4.2, and −2.4 MV/cm, respectively, and were all implicated in the network of coupled motions. Additional residues that strongly contribute to the electric field along the D–A axis are Lys32 (−3.2 MV/cm), Arg52 (−3.9 MV/cm), and Arg57 (−4.2 MV/cm). The residues that contribute strongly against the field along the D–A axis include Asp27 (5.4 MV/cm), Arg98 (3.4 MV/cm), and His124 (3.0 MV/cm). All of these residues represent potential targets to alter the electrostatic contribution to catalysis.
4. Conclusions
We investigated the changing electrostatic environment at two different thiocyanate probes inserted into the active site of ecDHFR for five complexes along the catalytic cycle. Our results illustrate a changing electrostatic environment near the hydride transfer site (T46C-CN) as well as a smaller change in key regions of the folate binding pocket (L54C-CN). The changes in electrostatic environment are associated with conformational changes occurring along the catalytic cycle of ecDHFR. Experimental evidence for the changing electrostatic environment includes both IR frequency and 13C NMR measurements, which interrogate the electric field along the CN axis and the total electric field at the probe. These experimental data demonstrate fundamental aspects of the electrostatic landscape for catalysis in ecDHFR.
Molecular dynamics simulations provided an atomic-level picture of the local environment experienced by the thiocyanate probes in complexes that model the states prior to and subsequent to the hydride transfer reaction. The QM/MM vibrational frequency calculations reproduced the experimentally measured frequency shifts for these two states, which span the closed to occluded transition associated with hydride transfer. Analysis of the MD trajectories provided insight into the conformational changes occurring between these two states. The factors leading to the vibrational frequency shifts were broken down into classical electrostatic effects, specific hydrogen-bonding interactions, and polarization effects. Thus, the vibrational frequency shifts are not simply a manifestation of the classical electric fields but rather include additional contributions from the environment. Moreover, the electric fields along the CN axis of the probes were decomposed into contributions from specific residues, ligands, and solvent molecules. The electric field along the hydride D–A axis was also calculated with the experimentally validated methodology. The calculations illustrate that the cofactor and substrate, as well as the enzyme, impose a substantial electric field along the D–A axis that facilitates hydride transfer.
Overall, experimental and theoretical data provide evidence for significant electrostatic changes in the microenvironments that constitute the heterogeneous ecDHFR active site as the enzyme progresses along the catalytic cycle. The electrostatic interactions between the protein and the ligands assist in orienting the reacting species in a geometry that maintains a large electric field favoring hydride transfer from the cofactor to the substrate. The enzyme active site environment also provides a significant portion (∼1/3) of the total electric field that facilitates the hydride transfer reaction, suggesting the catalytic importance of enzymatic conformational changes that alter the active site electrostatics. Future work will investigate the five trapped states along the catalytic cycle for the two probes studied in this work as well as additional probe sites in the ecDHFR system to provide a comprehensive picture of the electrostatic landscape for the entire catalytic cycle.
Acknowledgments
This work was supported by US National Institutes of Health Grants GM092946 (C.T.L., S.J.B.) and GM056207 (J.P..L., P.H., S.H.S.). R.J.S. and J.B.A. acknowledge support from the US National Science Foundation through grant number CHE-0846241. C.T.L. and J.B.F. would like to acknowledge postdoctoral fellowships from The Natural Sciences and Engineering Research Council of Canada and Canadian Institutes of Health Research, respectively. X-ray diffraction data were collected at the Cornell High Energy Synchrotron Source (CHESS), which is supported by the National Science Foundation and the National Institutes of Health/National Institute of General Medical Sciences under NSF award DMR-0936384, using the Macromolecular Diffraction at CHESS (MacCHESS) facility, which is supported by award GM103485 from the National Institutes of Health, through its National Institute of General Medical Sciences.
Supporting Information Available
Kinetic data, IR collection and spectra fitting procedures, crystal structure collection data, IR and NMR spectra parameters, PM3 reparameterization procedures, results for a second set of independent trajectories, QM/MM partitioning data, and contributions from specific residues to the electric field along the D–A axis. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Contributions
∥ These authors contributed equally.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Hammes G. G.; Benkovic S. J.; Hammes-Schiffer S. Biochemistry 2011, 50, 10422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammes-Schiffer S.; Benkovic S. J. Annu. Rev. Biochem. 2006, 75, 519. [DOI] [PubMed] [Google Scholar]
- Henzler-Wildman K. A.; Thai V.; Lei M.; Ott M.; Wolf-Watz M.; Fenn T.; Pozharski E.; Wilson M. A.; Petsko G. A.; Karplus M.; Hübner C. G.; Kern D. Nature 2007, 450, 838. [DOI] [PubMed] [Google Scholar]
- Kosugi T.; Hayashi S. J. Am. Chem. Soc. 2012, 134, 7045. [DOI] [PubMed] [Google Scholar]
- Boehr D. D.; McElheny D.; Dyson H. J.; Wright P. E. Science 2006, 313, 1638. [DOI] [PubMed] [Google Scholar]
- Doshi U.; McGowan L. C.; Ladani S. T.; Hamelberg D. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 5699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Meseguer R.; Marti S.; Ruiz-Pernia J. J.; Moliner V.; Tunon I. Nat. Chem. 2013, 5, 566. [DOI] [PubMed] [Google Scholar]
- Warshel A.; Sharma P. K.; Kato M.; Xiang Y.; Liu H. B.; Olsson M. H. M. Chem. Rev. 2006, 106, 3210. [DOI] [PubMed] [Google Scholar]
- Kamerlin S. C.; Warshel A. Proteins 2010, 78, 1339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benkovic S. J.; Hammes G. G.; Hammes-Schiffer S. Biochemistry 2008, 47, 3317. [DOI] [PubMed] [Google Scholar]
- Liu C. T.; Hanoian P.; French J. B.; Pringle T. H.; Hammes-Schiffer S.; Benkovic S. J. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 10159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawaya M. R.; Kraut J. Biochemistry 1997, 36, 586. [DOI] [PubMed] [Google Scholar]
- Antikainen N. M.; Smiley R. D.; Benkovic S. J.; Hammes G. G. Biochemistry 2005, 44, 16835. [DOI] [PubMed] [Google Scholar]
- Wong K. F.; Selzer T.; Benkovic S. J.; Hammes-Schiffer S. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 6807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waegele M. M.; Culik R. M.; Gai F. J. Phys. Chem. Lett. 2011, 2, 2598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weitman H.; Roslaniec M.; Frimer A. A.; Afri M.; Freeman D.; Mazur Y.; Ehrenberg B. Photochem. Photobiol. 2001, 73, 110. [DOI] [PubMed] [Google Scholar]
- Taft R. W.; Kamlet M. J. Org. Magn. Resonance 1980, 14, 485. [Google Scholar]
- Fafarman A. T.; Sigala P. A.; Herschlag D.; Boxer S. G. J. Am. Chem. Soc. 2010, 132, 12811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Getahun Z.; Huang C. Y.; Wang T.; De Leon B.; DeGrado W. F.; Gai F. J. Am. Chem. Soc. 2003, 125, 405. [DOI] [PubMed] [Google Scholar]
- Kim H.; Cho M. Chem. Rev. 2013, 113, 5817. [DOI] [PubMed] [Google Scholar]
- Jha S. K.; Ji M.; Gaffney K. J.; Boxer S. G. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 16612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fafarman A. T.; Sigala P. A.; Schwans J. P.; Fenn T. D.; Herschlag D.; Boxer S. G. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, E299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagchi S.; Fried S. D.; Boxer S. G. J. Am. Chem. Soc. 2012, 134, 10373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suydam I. T.; Snow C. D.; Pande V. S.; Boxer S. G. Science 2006, 313, 200. [DOI] [PubMed] [Google Scholar]
- Bagchi S.; Boxer S. G.; Fayer M. D. J. Phys. Chem. B 2012, 116, 4034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Q.; Abeygunawardana C.; Mildvan A. S. Biophys. J. 1996, 70, Su164. [Google Scholar]
- Zhao Q. J.; Li Y. K.; Mildvan A. S.; Talalay P. Biochemistry 1995, 34, 6562. [DOI] [PubMed] [Google Scholar]
- Chakravorty D. K.; Soudackov A. V.; Hammes-Schiffer S. Biochemistry 2009, 48, 10608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blakley R. L. Nature 1960, 188, 231. [Google Scholar]
- Jeong S. S.; Gready J. E. Anal. Biochem. 1994, 221, 273. [DOI] [PubMed] [Google Scholar]
- Cameron C. E.; Benkovic S. J. Biochemistry 1997, 36, 15792. [DOI] [PubMed] [Google Scholar]
- Rajagopalan P. T.; Zhang Z.; McCourt L.; Dwyer M.; Benkovic S. J.; Hammes G. G. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 13481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fafarman A. T.; Webb L. J.; Chuang J. I.; Boxer S. G. J. Am. Chem. Soc. 2006, 128, 13356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fierke C. A.; Johnson K. A.; Benkovic S. J. Biochemistry 1987, 26, 4085. [DOI] [PubMed] [Google Scholar]
- McMahon H. A.; Alfieri K. N.; Clark C. A. A.; Londergan C. H. J. Phys. Chem. Lett. 2010, 1, 850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukamel S.Principles of nonlinear optical spectroscopy; Oxford University Press: New York, 1995. [Google Scholar]
- Layfield J. P.; Hammes-Schiffer S. J. Am. Chem. Soc. 2013, 135, 717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. J. Chem. Theory Comput. 2008, 4, 435. [DOI] [PubMed] [Google Scholar]
- Osborne M. J.; Schnell J.; Benkovic S. J.; Dyson H. J.; Wright P. E. Biochemistry 2001, 40, 9846. [DOI] [PubMed] [Google Scholar]
- Bystroff C.; Kraut J. Biochemistry 1991, 30, 2227. [DOI] [PubMed] [Google Scholar]
- Hornak V.; Abel R.; Okur A.; Strockbine B.; Roitberg A.; Simmerling C. Proteins: Struct., Funct., Bioinf. 2006, 65, 712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornell W. D.; Cieplak P.; Bayly C. I.; Gould I. R.; Merz K. M.; Ferguson D. M.; Spellmeyer D. C.; Fox T.; Caldwell J. W.; Kollman P. A. J. Am. Chem. Soc. 1996, 118, 2309. [Google Scholar]
- Holmberg N.; Ryde U.; Bulow L. Protein Eng. 1999, 12, 851. [DOI] [PubMed] [Google Scholar]
- Bayly C. I.; Cieplak P.; Cornell W. D.; Kollman P. A. J. Phys. Chem. 1993, 97, 10269. [Google Scholar]
- Wang J. M.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. J. Comput. Chem. 2004, 25, 1157. [DOI] [PubMed] [Google Scholar]
- Oh K. I.; Choi J. H.; Lee J. H.; Han J. B.; Lee H.; Cho M. J. Chem. Phys. 2008, 128, 154504. [DOI] [PubMed] [Google Scholar]
- Lindquist B. A.; Corcelli S. A. J. Phys. Chem. B 2008, 112, 6301. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. J. Chem. Phys. 1983, 79, 926. [Google Scholar]
- Hess B. J. Chem. Theory Comput. 2008, 4, 116. [DOI] [PubMed] [Google Scholar]
- Darden T.; York D.; Pedersen L. J. Chem. Phys. 1993, 98, 10089. [Google Scholar]
- Nose S. Mol. Phys. 1984, 52, 255. [Google Scholar]
- Hoover W. G. Phys. Rev. A 1985, 31, 1695. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Phys. Rev. Lett. 1980, 45, 1196. [Google Scholar]
- Knott G. D.Interpolating cubic splines; Birkhauser: Boston, 2000. [Google Scholar]
- Marston C. C.; Balint-Kurti G. G. J. Chem. Phys. 1989, 91, 3571. [Google Scholar]
- Balint-Kurti G. G.; Ward C. L.; Marston C. C. Comput. Phys. Commun. 1991, 67, 285. [Google Scholar]
- Stewart J. J. P. J. Comput. Chem. 1989, 10, 209. [Google Scholar]
- Fafarman A. T.; Sigala P. A.; Schwans J. P.; Fenn T. D.; Herschlag D.; Boxer S. G. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, E299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fried S. D.; Wang L. P.; Boxer S. G.; Ren P. Y.; Pande V. S. J. Phys. Chem. B 2013, 117, 16236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wortmann R.; Bishop D. M. J. Chem. Phys. 1998, 108, 1001. [Google Scholar]
- Andrews S. S.; Boxer S. G. J. Phys. Chem. A 2000, 104, 11853. [Google Scholar]
- Ren P. Y.; Ponder J. W. J. Phys. Chem. B 2003, 107, 5933. [Google Scholar]
- Lamoureux G.; Harder E.; Vorobyov I. V.; Roux B.; MacKerell A. D. Chem. Phys. Lett. 2006, 418, 245. [Google Scholar]
- Bhabha G.; Lee J.; Ekiert D. C.; Gam J.; Wilson I. A.; Dyson H. J.; Benkovic S. J.; Wright P. E. Science 2011, 332, 234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weikl T. R.; Boehr D. D. Proteins 2012, 80, 2369. [DOI] [PubMed] [Google Scholar]
- Waegele M. M.; Gai F. J. Phys. Chem. Lett. 2010, 1, 781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- It has been pointed out that every 10 MV/cm field parallel to “a dipolar transition state that separates a unit charge over a distance of 1 Å” can potentially contribute to the reduction of the transition-state energy by 9.6 kJ/mol (2.3 kcal/mol), as verified by simple arithmetic.24
- Agarwal P. K.; Billeter S. R.; Rajagopalan P. T. R.; Benkovic S. J.; Hammes-Schiffer S. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 2794. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.